Abstract
The main goal of this research is to provide a novel model that describes an optically heated layer of an excited non-local microelongated semiconductor material. In a rotating field, the model is examined as the photo-excitation processes occur. The model presents the microelongation scalar function, which describes the microelement processes according to the micropolar-thermoelasticity theory. The model analyses the interaction situation between optical-thermomechanical waves under the impact of rotation parameters when the microelongation parameters are taken into consideration according to the photo-thermoelasticity theory. During the electronic and thermoelastic deformation, the fundamental governing equations were obtained in dimensionless form, and they were investigated using the harmonic wave methodology. Two-dimensional general solutions for the fundamental fields of an isotropic, homogeneous, and linear non-local microelongated semiconductor medium are derived (2D). The free surface of the medium is subjected to several conditions to produce complete solutions due to the laser pulse. The physical properties of silicon (Si) material are used to show numerical modeling of the main fields. Some comparisons are made and graphically shown under the impact of various relaxation time and rotational parameters.
1. Introduction
Recently, the significance of semiconductors has become more apparent as a result of advances in materials research. Modern industries, particularly those such as sensors and transistors that depend on the existence of weak electric currents, have significantly improved from the creation of semiconductors. Normal conditions prevent semiconductors from being sufficiently insulating or excellent conductors of electricity, such as glass or copper. However, these materials’ internal resistance starts to diminish when they are subjected to a steady rise in temperature as a result of being influenced by light or laser beams. As a result, there was a rise in interest in researching the physical characteristics of semiconductors in the second part of the 20th century. It turns out that these materials’ intrinsic characteristics, particularly their internal composition, alters when the temperature changes (microelements) [1]. The transport of light-excited electrons to the surface causes so-called electronic deformation (ED), which gives rise to the photothermal (PT) hypothesis. On the other hand, the thermoelasticity hypothesis suggests that thermoelastic deformation (TD) is brought on by internal particle vibrations. The PT theory and the thermoelastic theory overlap, and a photo-thermoelasticity theory emerges as a result of the earlier ED and TD deformations. Because the microelements of the semiconductor are what causes the change in internal resistance, the impact of the microinertia process on them should be considered during the interference procedures (changing internal structure) [2].
Due to changes in the internal structure of semiconductors caused by the heat effect, the impact of microelongation parameters has been studied. The four degrees of freedom in a microelongated semiconductor are obtained. The third one is caused by the rotating movement (microelongation) of the electrons during the ED deformation, whereas the other three depend on the change that occurs during the TD deformation [3]. In this instance, the micropolar theory is built on these degrees of freedom (director) to explain the behavior of semiconductors [3]. When the microstretch and micropolar theories of the semiconductor are examined, the directors are rigid. When the directors are orthogonal and contraction, the microelongational theory of material emerges as a particular instance. Eringen [4] introduced the micropolar theory by taking into consideration the elastic body’s microstructure. On the other hand, Eringen [5] presented a new microstretch-thermoelasticity model that explains how the thermoelasticity theory and the microstretch parameters interact. For elastic bodies subjected to the effects of external fields, the generalized microstretch thermoelasticity theory is researched in many applications [6,7,8,9,10,11]. Ramesh et al. [12] investigated stretching sheets under Casson fluid flow with a variable porous medium thickness. The hydromechanics of viscoelastic porous media with a single relaxation period was studied using a viscoelastic boundary layer flow by Ezzat and Abd-Elaal [13]. Ailawalia et al. [14,15,16] developed thermo-elastic microelongated governing equations to study the plane-strain deformation of an elastic material with an internal heat source. The microelongated elastic medium is used to obtain the wave propagations inside the medium under the effect of an internal heat source [17,18]. According to the thermoelasticity theory, the double porosity structure is developed using the micropolar theory of the elastic body [19].
When the impact of an absorbed laser beam on a sample of a semiconductor material was examined, the photothermal (PT) theory came into existence [20]. According to photoacoustic spectroscopy analysis, the PT theory is employed to determine the physical characteristics of semiconductors [21,22,23,24]. Hobiny and Abbas [25] investigated the deformation of a semiconductor medium in two dimensions as a result of photothermal and thermoelastic interactions. Todorovic et al. [26,27] studied the optical characteristics of a semiconducting microcantilever medium within the framework of the electronic deformation process. The relationship between the photothermal technique and the thermoelasticity theory of semiconductors was then described in different models by several authors [28,29,30,31,32,33,34,35,36]. According to photothermal excitation methods, Mahdy et al. [37] investigated the microstretch elastic semiconductor medium under the influence of a rotation field. The electromagnetic field was employed by Lotfy and El-Bary [38] to examine the photo-thermo-microstretch semiconductor elastic media.
Using the global balancing rules and the second law of thermodynamics, Eringen and Edelen [39] created the nonlocal elasticity theory. In the beginning, screw dislocation and surface waves in solids were studied using the theory of nonlocal elasticity [40]. In the framework of the nonlocal thermoelastic model, the transient thermoelastic responses of a slab with temperature-dependent thermal are investigated [41]. In the framework of nonlocal dual phase lag, Kumar et al. [42] proposed a dynamical model for a non-local biothermoelastic medium with diffusion. The impacts on the characteristic waves were acquired after they studied fundamental theorems in the form of fundamental solutions.
The main purpose of presenting this subject is to analyze the influence of micro-elongation parameters in the context of the research of non-local semiconductor materials within the framework of photo-thermoelasticity theory, which has not been treated previously. In the present work, a microelongated non-local semiconductor material is examined in a rotating field according to the photo-thermoelasticity theory. In this instance, the non-local semiconductor medium’s microinertia and microelements are taken into account. According to the 2D deformation, the governing basic equations are presented in the dimensionless and rotational fields. The generalized rotational photo-thermo-microelongated (RPTM) of the semiconductor medium is a novel model that was recently proposed. The main wave propagations of physical fields within the medium are obtained using the normal mode approach and numerical closed form with some boundary constraints. With some comparisons under the influence of the rotation field and non-local parameters under the micro-elongation parameters, the numerical simulation of wave propagations is graphically depicted.
2. Mathematical Model and Main Equations
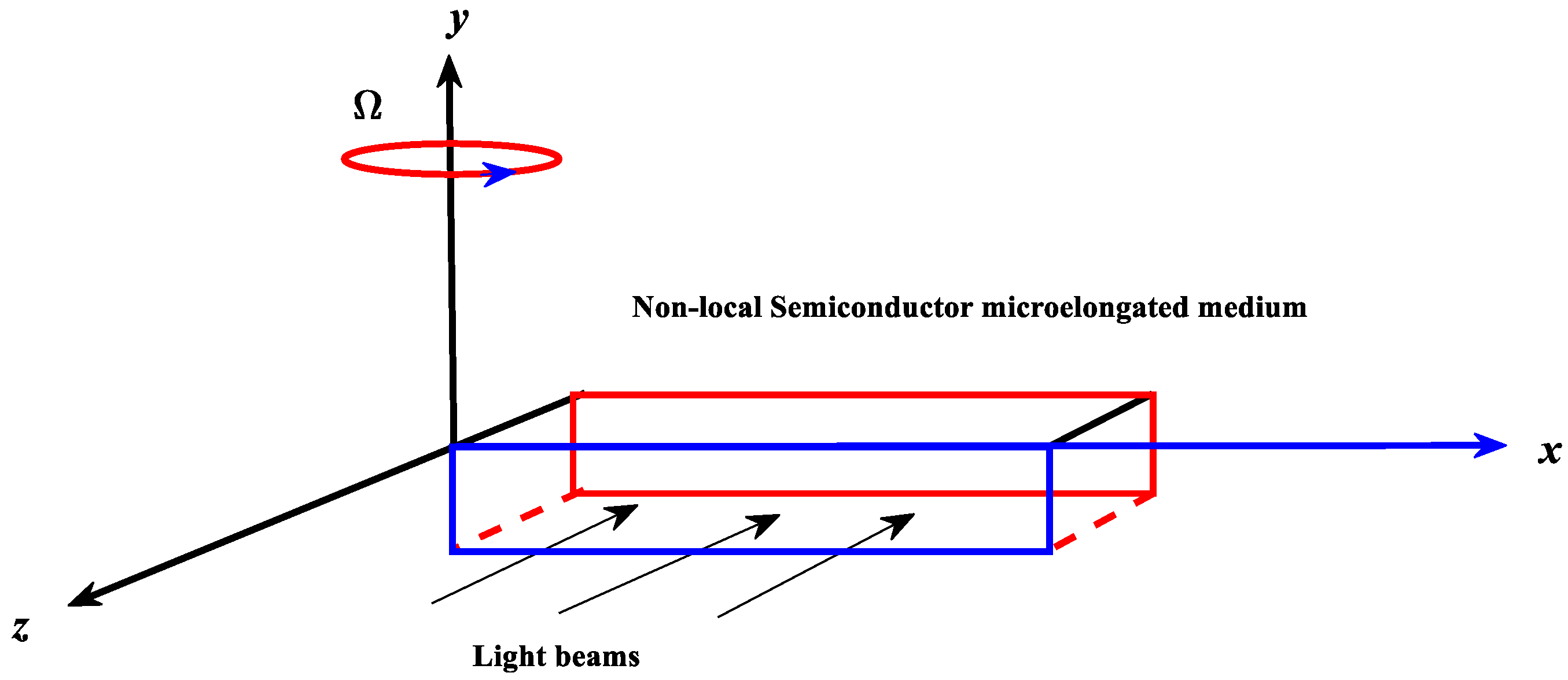
Four main quantities may be presented based on the Cartesian coordinates (Figure 1). The carrier density , which describes the propagation of plasma waves, is the optical function. The heat , which measures the thermal (temperature) effect, may be used to depict the thermal distribution. The displacement (elastic) vector can be used to introduce the elastic wave dispersion. The function is the scalar microelongational function, which describes the influence of elongation if a uniform rotating field () is introduced to the non-local semiconductor medium ( is in the direction of the y-axis, Figure 1). When the non-local semiconductor medium is homogeneous, isotropic, and linear, the fundamental equations for the RPTM theory may be expressed in the following way, according to 2D deformations [1,2].
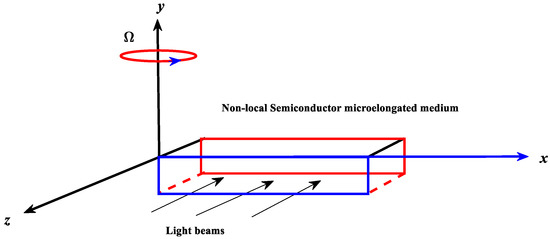
Figure 1.
Geometry of the problem.
According to photo-thermoelasticity theory, the non-local semiconductor microelongated constitutive relations in tensor form are [14,15,16,17,18]:
The optical equation that describes how heat and plasma waves interact may be written as [25]:
When the medium experiences microelongation following processes involving microelements, the non-local motion ( is the non-local parameter) and microinertia equations under the influence of the rotating field can be presented as [43,44]:
According to elastic body theory, the heat conduction equation for a non-local microelongated semiconductor medium may be formulated as [18]:
The fundamental fields can be selected in cases of 2D disturbance based on two-space coordinates and time , according to ED and TE deformations. As a result, in the xz-plane, the elastic vector and the microelongational scalar function may be written as follows:
The strain relation takes the form:
where , represents thermal expansions that depend on the microelongation properties. The main controlling Equations (2)–(5) can be analyzed in 2D, which can be rewritten as
The parameters and are two selected constants that determine the various RPTM theories (coupled-dynamical model (CD) when [40], Lord and Shulman (LS) model when [41], and Green and Lindsay (GL) model when [42]) with thermal relaxation times. The following dimensionless quantities can be considered as follows for even more simplification:
Therefore, the fundamental equations may be converted using Equation (12) to the following form (without superscripts), which results in:
Depending the functions of potential scalar and vector space-time function , Helmholtz’s theorem can be formulated in terms of the displacement components as
The previous Equations (14)–(17) may be rearranged in the following way using Equation (18):
You may rewrite the 2D non-local constitutive relations as
where
3. Solutions to the Problem
All physical quantities may be divided into the categories described below because harmonic waves propagate in the xz-plane, for which the function can be formulated in 2D as follows [37,38,39,40,41]:
where is taken in z-direction, which describes the wave number; the amplitude is , , and is a constant that describes the complex time-frequency. Equations (13) and (19)–(22) with transformation (24) yield the following:
where
The tenth order ordinary differential equation (ODE) that results from solving Equations (25)–(29) may be expressed as follows:
where
The following demonstrates the factorization methodology used to obtain the solutions to Equation (31):
The roots denote by .
The roots of Equation (31) can be used to rewrite the linear solutions in the general form of the main quantities as
where , , , and represent the unknown coefficients, and the other coefficients are
The displacement elastic components in analytical expressions can be rewritten as
The stresses relation in analytical expressions of terms can be represented as
4. Boundary Conditions
According to some boundary conditions that may be selected at the boundary () of the microelongated non-local surface, the general parameters in this section can be determined [45].
Very little heat is lost into the surrounding region as a result of pulsed laser stimulation’s ability to change temperature immediately, or at least over a short time. As a result, pulsed laser excitation is advantageous for studies of absorption. It is also recognized that a range of physical reactions, some of which need energy, may take place when a laser beam illuminates a non-local solid surface. A portion of the energy from the laser light is transformed into heat when it strikes a material. This kind of heat creation sends heat waves across the substance, which have certain impacts (e.g., photothermal effects). The exposure of the medium’s surrounding plane () to laser pulses is also taken into account. The following heat condition may be taken into account in this situation [46]:
where and .
In Equation (41), is the laser pulse energy per unit length, is the surface reflectivity, is the radius of the Gaussian beam, is the rise-time of the laser pulse, and represents the extinction coefficient; it is helpful to assume a surface source for laser heating of materials. It is important to note that the maximum amount of light energy that a laser may emit during one of its pulses is .
The two mechanical conditions on the non-local surface () are
The elongation can be introduced at the free non-local surface () as
However, when the concentration of electrons is established, the recombination processes allow the plasma state to be selected, which may be rewritten as follows:
It is simple to construct the equations that must be satisfied by parameter by substituting their solutions into the boundary conditions (, and ):
The values of four unknown constants may be found by applying the matrix inverse process. Deformations, the temperature field, and all other physical characteristics of the medium may thus be obtained.
5. Discussion and Numerical Results
The physical field variables under examination will be graphically depicted to interpret the numerical results, and comparisons are conducted for various values of physical parameters such as the rotation parameter, the laser pulse rise-time parameter, and relaxation times (thermal memories). In this instance, silicon (Si)-based non-local microelongated semiconductor medium input parameters are simulated numerically. The numerical outcomes can be shown graphically using MATLAB (2022a). A graphical simulation using the following Si parameters, which are given in Table 1, may be created using the SI units of the physical constants of Si [47,48,49,50,51,52]:

Table 1.
The physical constants of Si material in SI units.
The laser parameters used in this calculation are [45]
The calculations of the main field wave propagations in this study are obtained using non-dimensional real quantities. When the wave number is utilized by the mechanical load , numerical simulations are done in the range (distance refers to the depth of the medium) at and (where and ).
5.1. Impact of Thermal and Elastic Memories
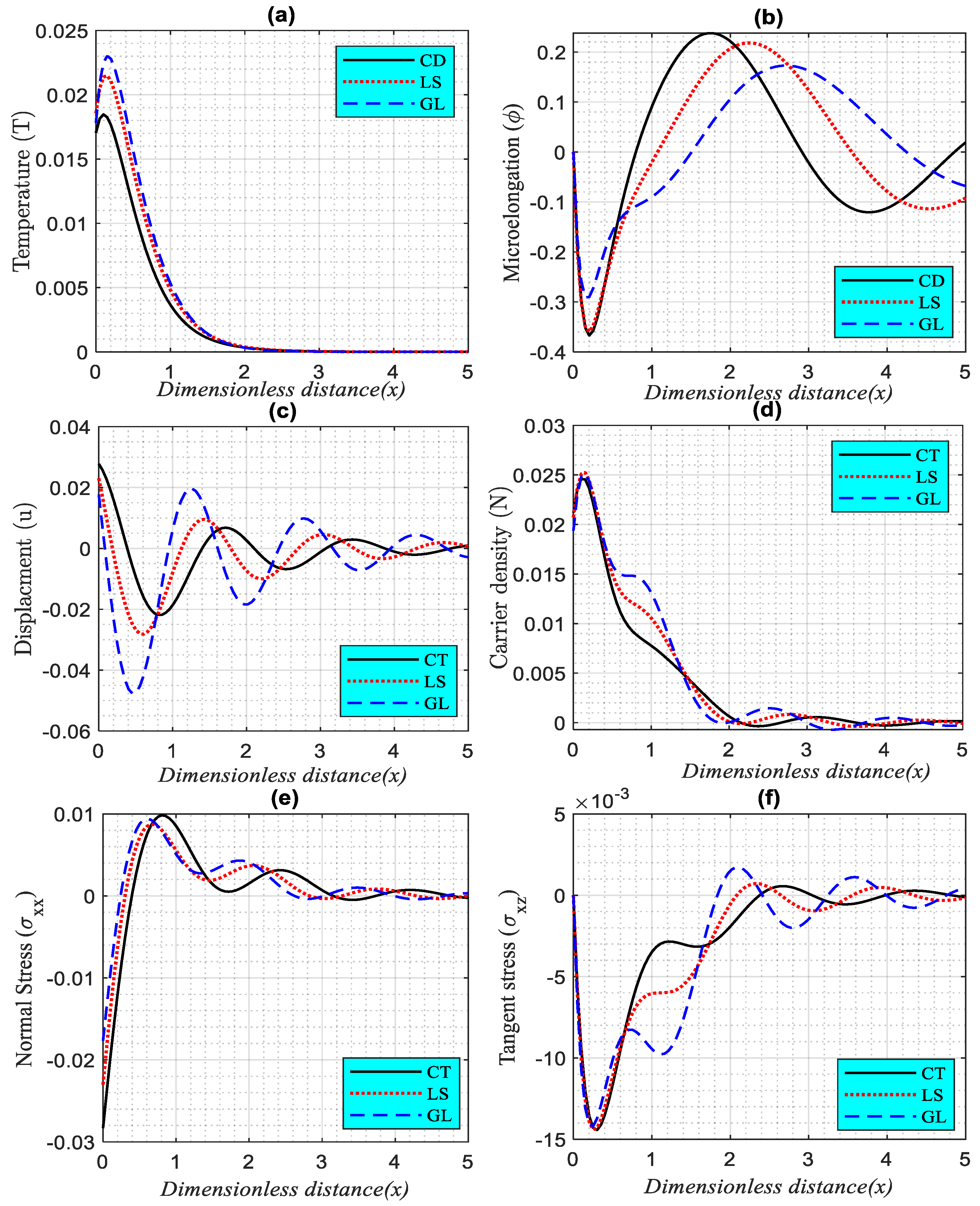
Figure 2a–f depicts how a change in horizontal distance in the range affects the wave propagation of fundamental physical variables with different relaxation times under the impact of rotation filed and laser pulses. In this instance, several models in the theory of photo-thermoelasticity are used to determine the impact of the relaxation times (three models: CD, LS, and GL). Six subfigures (Figure 2a–f) illustrate wave propagation as thermal waves (heat distributions), microelongation distributions, elastic waves (displacement), plasma waves (carrier intensity), and mechanical waves ( and ) at set values of the short time. The boundary conditions at the free surface of the exciting non-local microelongated semiconductor are satisfied by the physical distributions shown in Figure 2a-f. Due to the thermal loads of the laser pulses, the distribution of thermal waves starts at a positive value on the surface and increases until it reaches its maximum value in the first range. The wave behavior according to the CD, LS, and GL models of the thermal wave and plasma wave (exponential behavior) gradually declines in the second range until it reaches the minimum value with the zero line. On the other hand, the behavior of the wave distribution according to the different models agrees with the experimental findings that appear in the two subfigures (temperature, and carrier density) [53,54]. The variation of microelongation, elastic, and tangent stress distributions against the distance for three various photo-thermoelasticity models is shown in the second, third, and sixth subfigures (CD, LS, and CD). It is determined that when the values of the relaxation durations increase, the wave propagation of the microelongation, elastic (displacement), and tangent stress distributions decrease in the beginning until they reach the minimum values near the surface. However, in the second range, all three distributions increase and decrease periodically with wave behavior until approaching the zero line (the equilibrium state is due to the decrease in the thermal effect of laser pulses). The normal mechanical stress wave () begins at the negative value on the surface satisfying the surface condition. Due to the laser pulse (thermal impact) and due to TE and ED, the normal stress distribution increases gradually until it reaches the maximum value. The wave-propagation distribution begins to gradually decrease with distance from the surface to reach the minimum value, then increasing and decreasing alternately until the distribution vanishes completely with the zero line as the distance increases. According to differences in the values of the thermal relaxation durations, all wave propagations are different.
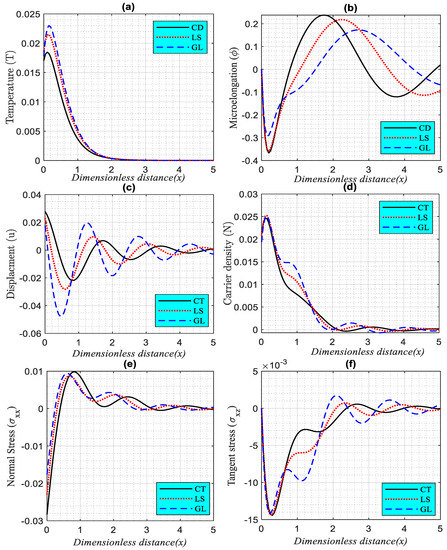
Figure 2.
(a–f). The variation of the main physical fields versus the horizontal distance according to the differences in thermal relaxation times under the effect of rotation parameter.
5.2. Impact of the Laser Pulse Rise-Time Parameter
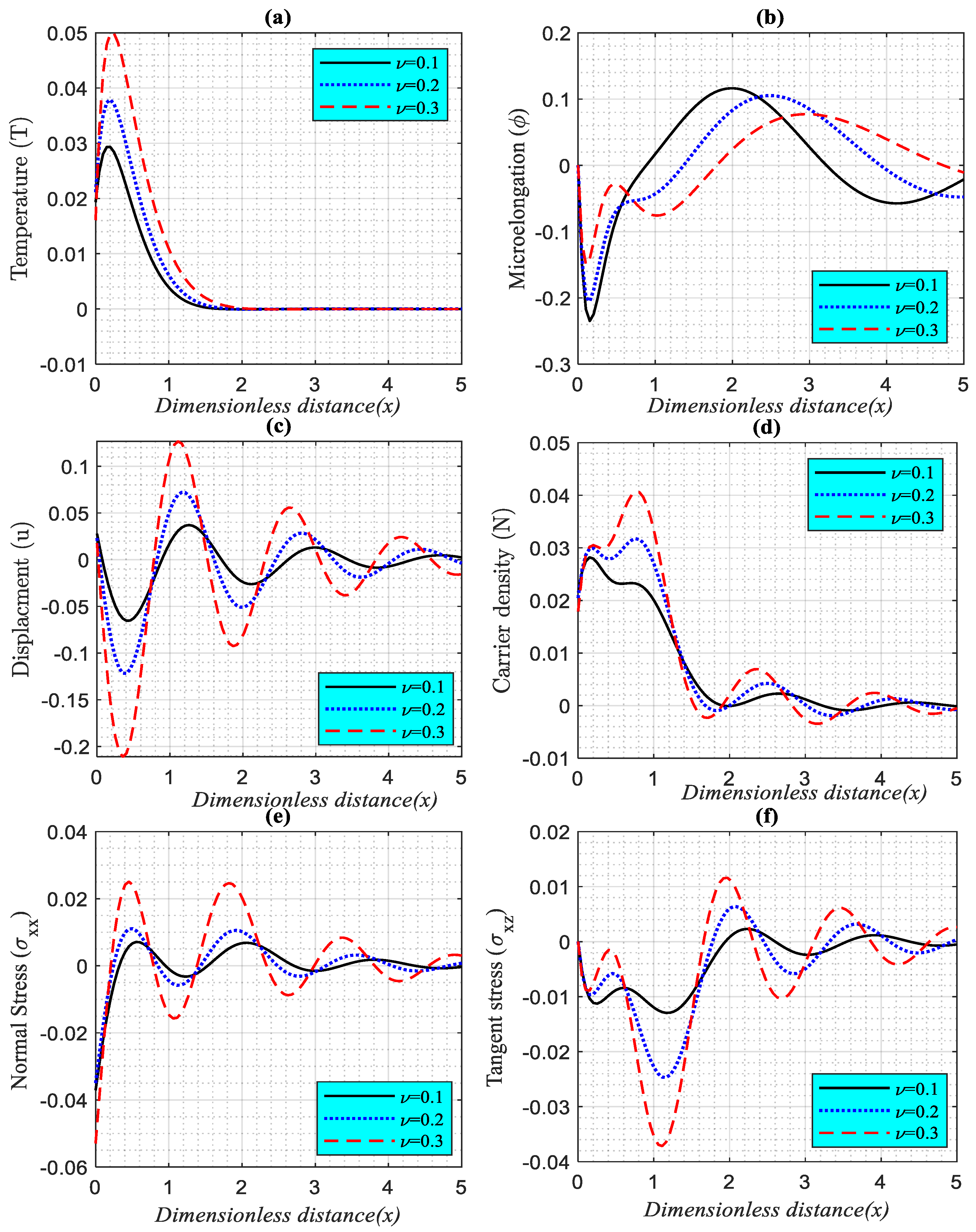
The rise time of picosecond laser pulses is known to be correlated with the pulse energy, measurement range, and maximum laser energy density at the silicon surface. The second figure (Figure 3a–f) displays the relationship between the framework quantities under study and the laser pulse rise-time parameter for three distinct values of equal to , , and . As can be seen in the subfigures, all physical quantities satisfy boundary conditions, and as approaches infinity, all curves coincide under the influence of the rotation field according to the GL model. The numerical outcomes demonstrate that the greatest temperature of the structure is consistently found close to the front of the heat, mechanical, and plasma waves and subsequently decreases with increasing depth into the medium. Using femtosecond laser technology, an unusual mechanical force is produced. In contrast to continuous or long-pulse laser heat generation, where the heat treatment process causes the majority of damage to other components, femtosecond lasers may produce high-quality surfaces with a small amount of abrasion. This is due to how mechanical forces are produced and how lattices deform rapidly. This shows that the electron-to-phonon interactions prevail at time scales of tens of femtoseconds, where the photothermal mechanical model, which incorporates all of these effects, can describe the ultrafast photothermal response throughout a range of nearly three orders of magnitude. Furthermore, it may explain this pattern down to tens of picoseconds, when phonon-to-phonon interactions are the dominant kind of interaction. The main field’s distribution behavior is seen to be strongly influenced by the laser-pulse rising time factor. The Figure clearly shows that as the parameter is increased, the size of the amplitude fields increases. As a result, photo-excitation transport processes strengthen the heat and plasma waves, causing them to peak close to the surface.
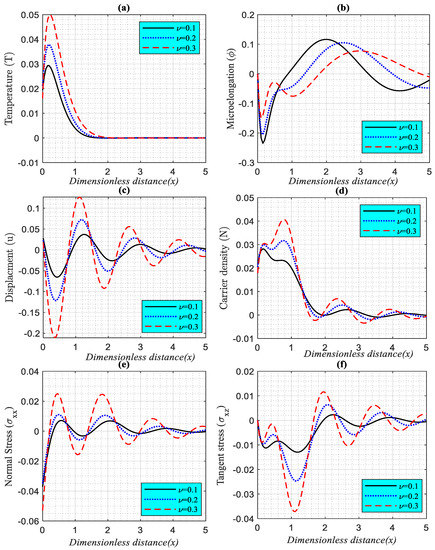
Figure 3.
(a–f). The variation of the main physical fields versus the horizontal distance according to the differences in the laser pulse rise-time parameters under the effect of rotation parameter.
5.3. Impact of Rotation Parameter
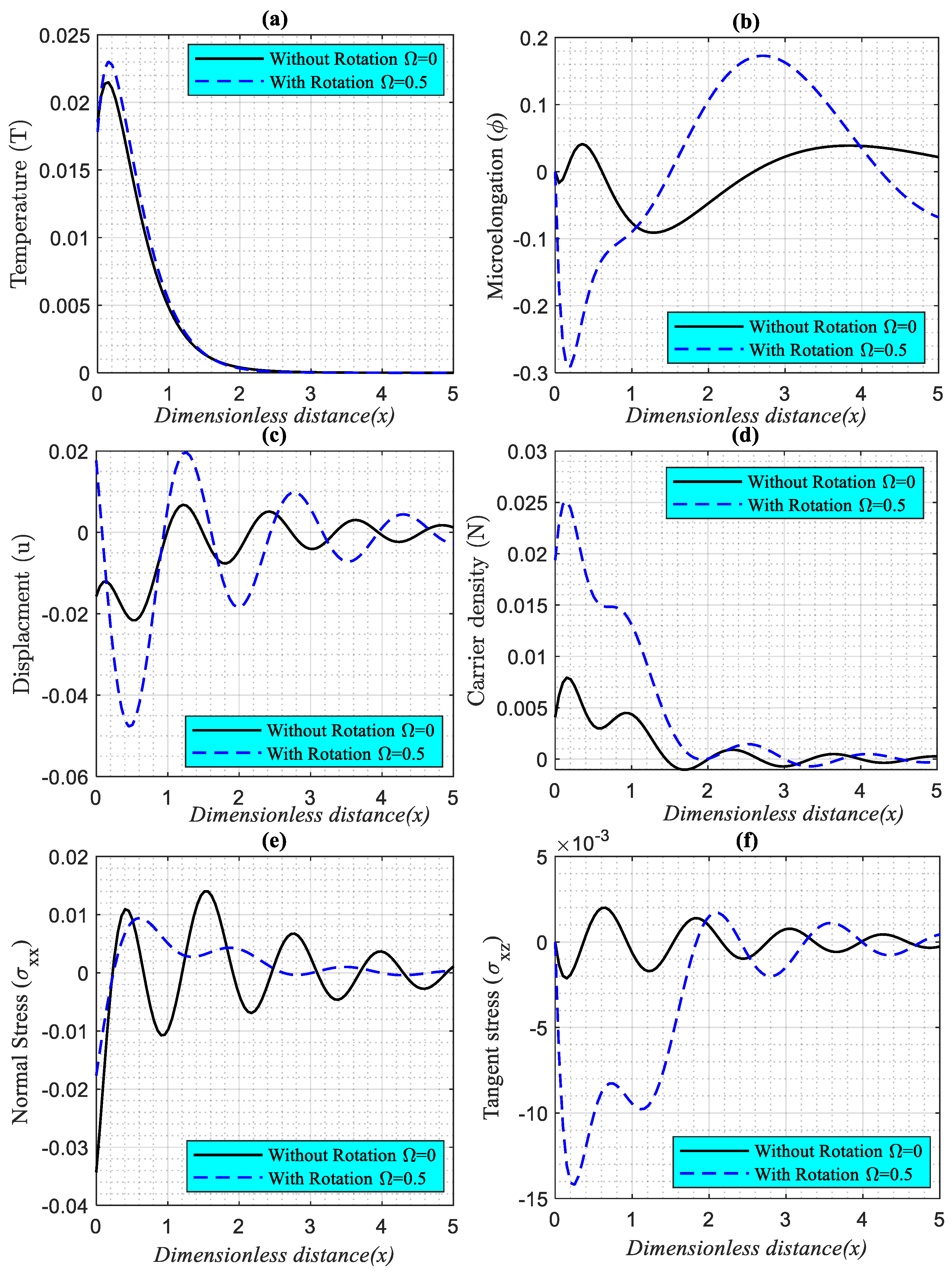
The variations of thermal, microelongation, elastic, plasma, and mechanical ( and ) wave propagation for given values of dimensionless time (), in the range in two cases, are shown in Figure 4a–f (six subfigures). According to the GL model, these two situations occur when the medium is investigated with () and without () that represent the rotation effect. The rotation field parameter may be seen to have a considerable influence on all wave propagations of the investigated fields in this figure. The wave propagations in the different two values of rotation take place at finite speeds, which is compatible with physical principles.
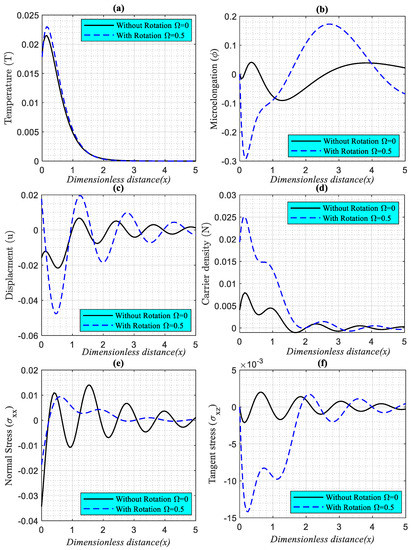
Figure 4.
(a–f). The variations the main physical fields versus the horizontal distance in case of the GL model with rotation field influence and without rotation field influence.
6. Conclusions
For given values of the input physical parameters, an analytical formulation for an isotropic, homogeneous non-local microelongated semiconducting elastic media under the effect of a rotating field and laser pulses is described and graphically represented. The photo-thermoelasticity theory is used to describe the interactions between thermal, mechanical, microelongation, and carrier intensity in the main equations in 2D. In the context of photo-excitation transport mechanisms, the microelongated semiconductor material is investigated. According to various thermal memory, three models of the photo-thermoelasticity theory are taken into consideration (CD, LS, and GL). For the non-local silicon microelongate semiconducting medium, numerical simulations are created using a few set-boundary conditions. Under the generalised photo-thermoelasticity theory, the wave’s propagation properties in the nonlocal microelongated semiconductor structure are investigated. It has been noted that any physical distribution of waves in motion tends to approach equilibrium. Additionally, it was shown that relaxation time significantly affects how the waves of the physical quantities under investigation propagate. For both thermal and mechanical boundary conditions, the variations in physical quantities have a similar character. On the other hand, the distribution of the waves that are propagating has a distinct influence of the rotation parameter and laser pulse rise-time parameter. As the value of the parameter laser pulse rise-time increases, the values of temperature, microelongation, and mechanical and normal displacement also increase. The rising time of the laser pulse has been shown to be a fundamental factor that significantly influences all field distributions. The strength of the laser steadily lowers as it penetrates deeper due to silicon’s high absorption of laser energy. The existence of a photothermal excitation under the rotating field caused all physical variables’ behaviour to change. Microelongated non-local semiconductor silicon is incredibly important for research and is frequently utilized in a wide range of contemporary electronic devices, including diodes, accelerometers, inertial sensors, and electric circuits.
Author Contributions
S.E.-S.: methodology, software; K.L.: validation, formal analysis; S.E.-S.: investigation, resources; K.L.: data curation; A.A.E.-B.: writing—review and editing; W.A.: visualization, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia grant number RI-44-0336, and the APC was funded by Ministry of Education in Saudi Arabia.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0336.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Lame’s elastic semiconductor parameters. | |
| The deformation potential difference. | |
| Unit vector in the direction of y-axis. | |
| Reference temperature in its natural state. | |
| The volume thermal expansion. | |
| The microelongational stress tensor. | |
| The density of the microelongated sample. | |
| Coefficients of linear thermal expansion. | |
| Cubical dilatation. | |
| Specific heat of the microelongated material. | |
| The thermal conductivity. | |
| The carrier diffusion coefficient. | |
| The carrier lifetime. | |
| The energy gap. | |
| Components of strain tensor. | |
| Two scalar functions. | |
| The microinertia of microelement. | |
| Microelongational material parameters. | |
| Thermal relaxation times. | |
| The scalar microelongational function. | |
| Components of the microstretch vector | |
| Stress tensor component | |
| Kronecker delta | |
| Angular velocity |
References
- Chteoui, R.; Lotfy, K.; El-Bary, A.A.; Allan, M.M. Hall Current Effect of Magnetic-Optical-Elastic-Thermal-Diffusive Non-Local Semiconductor Model during Electrons-Holes Excitation Processes. Crystals 2022, 12, 1680. [Google Scholar] [CrossRef]
- Saeed, A.M.; Lotfy, K.; Ahmed, M.H. Thermal-Optical Mechanical Waves of the Excited Microelongated Semiconductor Layer in a Rotational Field. Mathematics 2022, 10, 4660. [Google Scholar] [CrossRef]
- Eringen, A.C. Microcontinuum field theories. In Foundations and Solids; Springer: New York, NY, USA, 1999; Volume 1. [Google Scholar]
- Eringen, A.C. Linear theory of micropolar elasticity. J. Math. Mech. 1966, 15, 909–923. [Google Scholar]
- Eringen, A.C. Theory of thermo-microstretch elastic solids. Int. J. Eng. Sci. 1990, 28, 1291–1301. [Google Scholar] [CrossRef]
- Singh, B. Reflection and refraction of plane waves at a liquid/thermo-microstretch elastic solid interface. Int. J. Eng. Sci. 2001, 39, 583–598. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Lotfy, K. The influence of gravity on 2-D problem of two temperature generalized thermoelastic medium with thermal relaxation. J. Comput. Theor. Nanosci. 2015, 12, 2587–2600. [Google Scholar] [CrossRef]
- De Cicco, S.; Nappa, L. On the theory of thermomicrostretch elastic solids. J. Therm. Stress. 1999, 22, 565–580. [Google Scholar]
- Othman, M.I.; Lotfy, K. On the plane waves of generalized thermo-microstretch elastic half-space under three theories. Int. Comm. Heat Mass Trans. 2010, 37, 192–200. [Google Scholar] [CrossRef]
- Lotfy, K.; Abo-Dahab, S.M. Two-dimensional problem of two temperature generalized thermoelasticity with normal mode analysis under thermal shock problem. J. Comput. Theor. Nanosci. 2015, 12, 1709–1719. [Google Scholar] [CrossRef]
- Othman, M.; Lotfy, K. Effect of rotating on plane waves in generalized thermo-microstretch elastic solid with one relaxation time. Multidiscip. Model. Mat. Str. 2011, 7, 43–62. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Prasannakumara, B.; Gireesha, B.J.; Rashidi, M.M. Casson fluid flow near the stagnation point over a stretching sheet with variable thickness and radiation. J. Appl. Fluid Mech. 2016, 9, 1115–1122. [Google Scholar] [CrossRef]
- Ezzat, M.; Abd-Elaal, M.Z. Free convection effects on a viscoelastic boundary layer flow with one relaxation time through a porous medium. J. Frankl. Inst. 1997, 334, 685–706. [Google Scholar] [CrossRef]
- Shaw, S.; Mukhopadhyay, B. Periodicaly Varying Heat Source Response A Funct. Graded Microelongated Medium. Appl. Math. Comput. 2012, 218, 6304–6313. [Google Scholar]
- Shaw, S.; Mukhopadhyay, B. Moving heat source response in a thermoelastic micro-elongated Solid. J. Eng. Phys. Thermophys. 2013, 86, 716–722. [Google Scholar] [CrossRef]
- Ailawalia, P.; Sachdeva, S.; Pathania, D. Plane strain deformation in a thermo-elastic microelongated solid with internal heat source. Int. J. Appl. Mech. Eng. 2015, 20, 717–731. [Google Scholar] [CrossRef]
- Sachdeva, S.; Ailawalia, P. Plane strain deformation in thermoelastic micro-elongated solid. Civil Environ. Res. 2015, 7, 92–98. [Google Scholar]
- Ailawalia, P.; Kumar, S.; Pathania, D. Internal heat source in thermoelastic micro-elongated solid under Green Lindsay theory. J. Theor. Appl. Mech. 2016, 46, 65–82. [Google Scholar] [CrossRef]
- Marin, M.; Vlase, S.; Paun, M. Considerations on double porosity structure for micropolar bodies. AIP Adv. 2015, 5, 037113. [Google Scholar] [CrossRef]
- Gordon, J.P.; Leite, R.C.C.; Moore, R.S.; Porto, S.P.S.; Whinnery, J.R. Long-transient effects in lasers with inserted liquid samples. Bull. Am. Phys. Soc. 1964, 119, 501–510. [Google Scholar] [CrossRef]
- Kreuzer, L.B. Ultralow gas concentration infrared absorption spectroscopy. J. Appl. Phys. 1971, 42, 2934. [Google Scholar] [CrossRef]
- Tam, A.C. Ultrasensitive Laser Spectroscopy; Academic Press: New York, NY, USA, 1983; pp. 1–108. [Google Scholar]
- Tam, A.C. Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 1986, 58, 381. [Google Scholar] [CrossRef]
- Tam, A.C. Photothermal Investigations in Solids and Fluids; Academic Press: Boston, MA, USA, 1989; pp. 1–33. [Google Scholar]
- Hobinya, A.; Abbas, I. A GN model on photothermal interactions in a two-dimensions semiconductor half space. Results Phys. 2019, 15, 102588. [Google Scholar] [CrossRef]
- Todorović, D.M.; Nikolić, P.M.; Bojičić, A.I. Photoacoustic frequency transmission technique: Electronic deformation mechanism in semiconductors. J. Appl. Phys. 1999, 85, 7716–7726. [Google Scholar] [CrossRef]
- Song, Y.; Todorovic, D.M.; Cretin, B.; Vairac, P. Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int. J. Solids Struct. 2010, 47, 1871. [Google Scholar] [CrossRef]
- Lotfy, K. The elastic wave motions for a photothermal medium of a dual-phase-lag model with an internal heat source and gravitational field. Can. J. Phys. 2016, 94, 400–409. [Google Scholar] [CrossRef]
- Lotfy, K. A Novel Model of Photothermal Diffusion (PTD) fo Polymer Nano- composite Semiconducting of Thin Circular Plate. Phys. B Condenced Matter 2018, 537, 320–328. [Google Scholar] [CrossRef]
- Lotfy, K.; Kumar, R.; Hassan, W.; Gabr, M. Thermomagnetic effect with microtemperature in a semiconducting Photothermal excitation medium. Appl. Math. Mech. Engl. Ed. 2018, 39, 783–796. [Google Scholar] [CrossRef]
- Lotfy, K.; Gabr, M. Response of a semiconducting infinite medium under two temperature theory with photothermal excitation due to laser pulses. Opt. Laser Technol. 2017, 97, 198–208. [Google Scholar] [CrossRef]
- Lotfy, K. Photothermal waves for two temperature with a semiconducting medium under using a dual-phase-lag model and hydrostatic initial stress. Waves Random Complex Media 2017, 27, 482–501. [Google Scholar] [CrossRef]
- Lotfy, K. A novel model for Photothermal excitation of variable thermal conductivity semiconductor elastic medium subjected to mechanical ramp type with two-temperature theory and magnetic field. Sci. Rep. 2019, 9, 3319. [Google Scholar] [CrossRef]
- Lotfy, K. Effect of Variable Thermal Conductivity during the Photothermal Diffusion Process of Semiconductor Medium. Silicon 2019, 11, 1863–1873. [Google Scholar] [CrossRef]
- Abbas, I.; Alzahranib, F.; Elaiwb, A. A DPL model of photothermal interaction in a semiconductor material. Waves Random Complex Media 2019, 29, 328–343. [Google Scholar] [CrossRef]
- Khamis, A.; El-Bary, A.; Lotfy, K.; Bakali, A. Photothermal excitation processes with refined multi dual phase-lags theory for semiconductor elastic medium. Alex. Eng. J. 2020, 59, 1–9. [Google Scholar] [CrossRef]
- Mahdy, A.M.S.; Lotfy, K.; El-Bary, A.A.; Alshehri, H.M. Thermal-microstretch elastic semiconductor medium with rotation field during photothermal transport processes. Mech. Based Des. Struct. Mach. 2021. [Google Scholar] [CrossRef]
- Lotfy, K.; El-Bary, A.A. Magneto-photo-thermo-microstretch semiconductor elastic medium due to photothermal transport process. Silicon 2021, 14, 4809–4821. [Google Scholar] [CrossRef]
- Eringen, A.; Edelen, D. On nonlocal elastic. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Kumar, R.; Ghangas, S.; Vashishth, A. Fundamental and plane wave solution in non-local biothermoelasticity diffusion theory. Coupled Syst. Mech. 2021, 10, 521–538. [Google Scholar]
- Biot, M. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solid. 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.; Lindsay, K. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Abouelregal, A.; Sedighi, H.; Eremeyev, V. Thermomagnetic behavior of a semiconductor material heated by pulsed excitation based on the fourth-order MGT photothermal model. Contin. Mech. Thermodyn. 2022. [Google Scholar] [CrossRef]
- Deresiewicz, H. Plane waves in a thermoelastic solid. J. Acoust. Soc. Am. 1957, 29, 204–209. [Google Scholar] [CrossRef]
- Chadwick, P.; Snedon, I. Plane waves in an elastic solid conducting heat. J. Mech. Phys. Solids 1958, 6, 223–230. [Google Scholar] [CrossRef]
- Chadwick, P. Thermoelasticity: The dynamic theory. In Progress in Solid Mechanics; Hill, R., Sneddon, I.N., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1960; Volume I, pp. 263–328. [Google Scholar]
- Lotfy, K.; Hassan, W.; Gabr, M.E. Thermomagnetic effect with two temperature theory for photothermal process under hydrostatic initial stress. Results Phys. 2017, 7, 3918–3927. [Google Scholar] [CrossRef]
- Mandelis, A.; Nestoros, M.; Christofides, C. Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt. Eng. 1997, 36, 459–468. [Google Scholar] [CrossRef]
- Lotfy, K.; Abo-Dahab, S.M.; Tantawi, R.; Anwer, N. Thermomechanical Response Model of a Reflection Photo thermal Diffusion Waves (RPTD) for Semiconductor Medium. Silicon 2020, 12, 199–209. [Google Scholar] [CrossRef]
- Lotfy, K.; Hassan, W.; El-Bary, A.A.; Kadry, M.A. Response of electromagnetic and Thomson effect of semiconductor mediu due to laser pulses and thermal memories during photothermal excitation. Results Phys. 2020, 16, 102877. [Google Scholar] [CrossRef]
- Liu, J.; Han, M.; Wang, R.; Xu, S.; Wang, X. Photothermal phenomenon: Extended ideas for thermophysical properties characterization. J. Appl. Phys. 2022, 131, 065107. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).