Research on Mesoscale Nucleation and Growth Processes in Solution Crystallization: A Review
Abstract
:1. Introduction
2. Mesoscale Structure during Nucleation
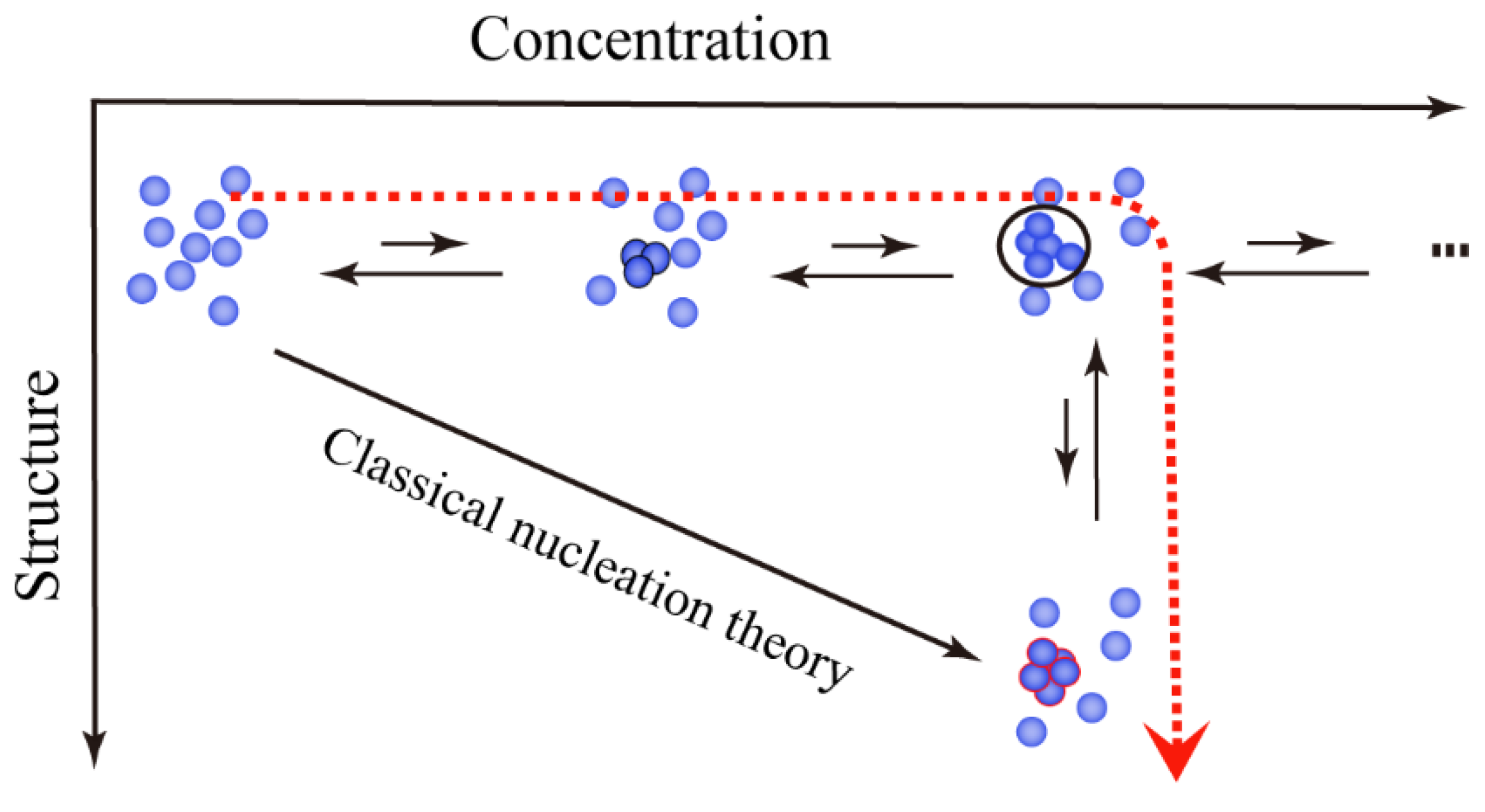
2.1. Ordered Clusters in Classical Nucleation Theory
2.2. Disordered Clusters in Two-Step Nucleation Theory
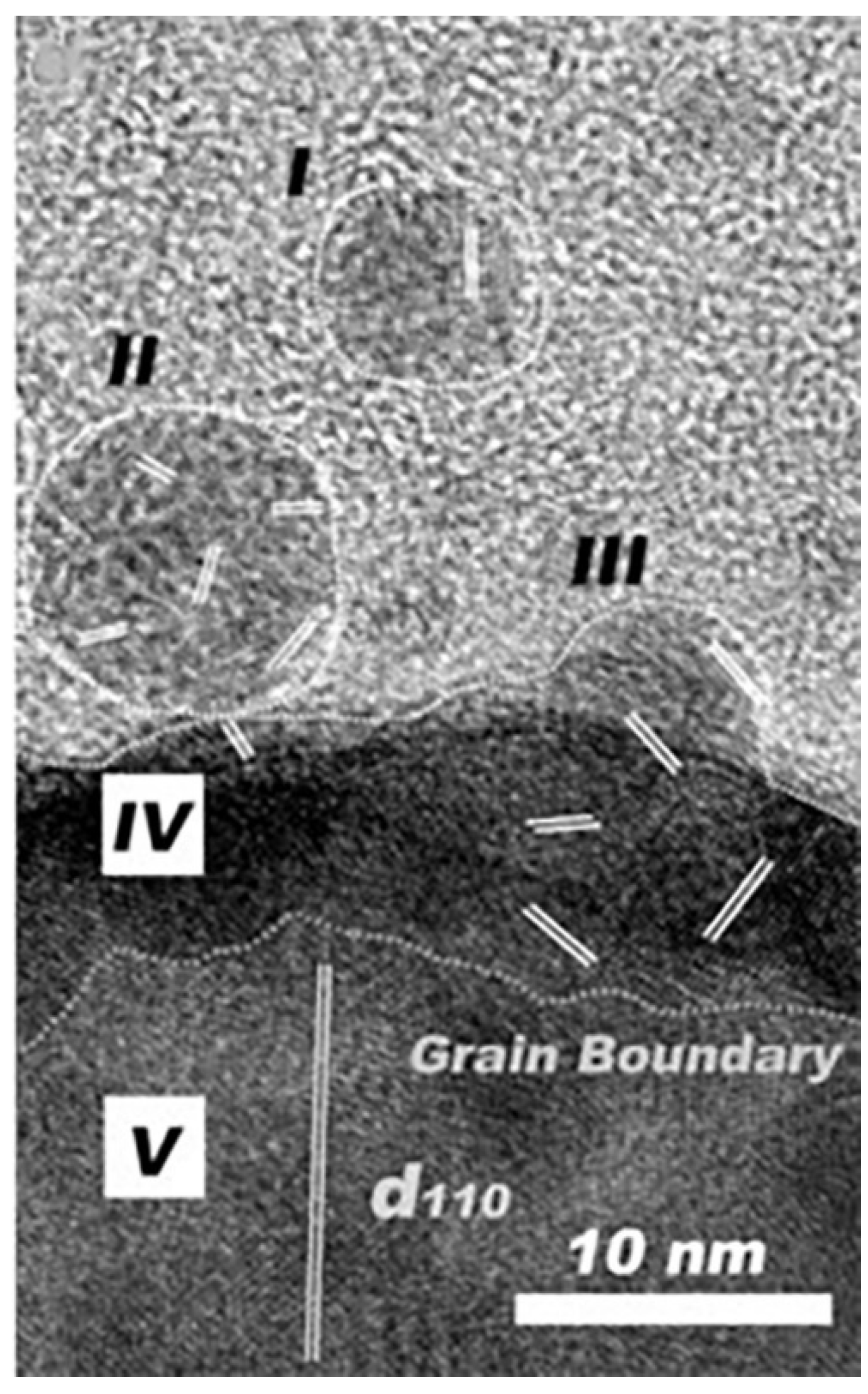
2.3. Prenucleation Clusters in Prenucleation Clusters Theory
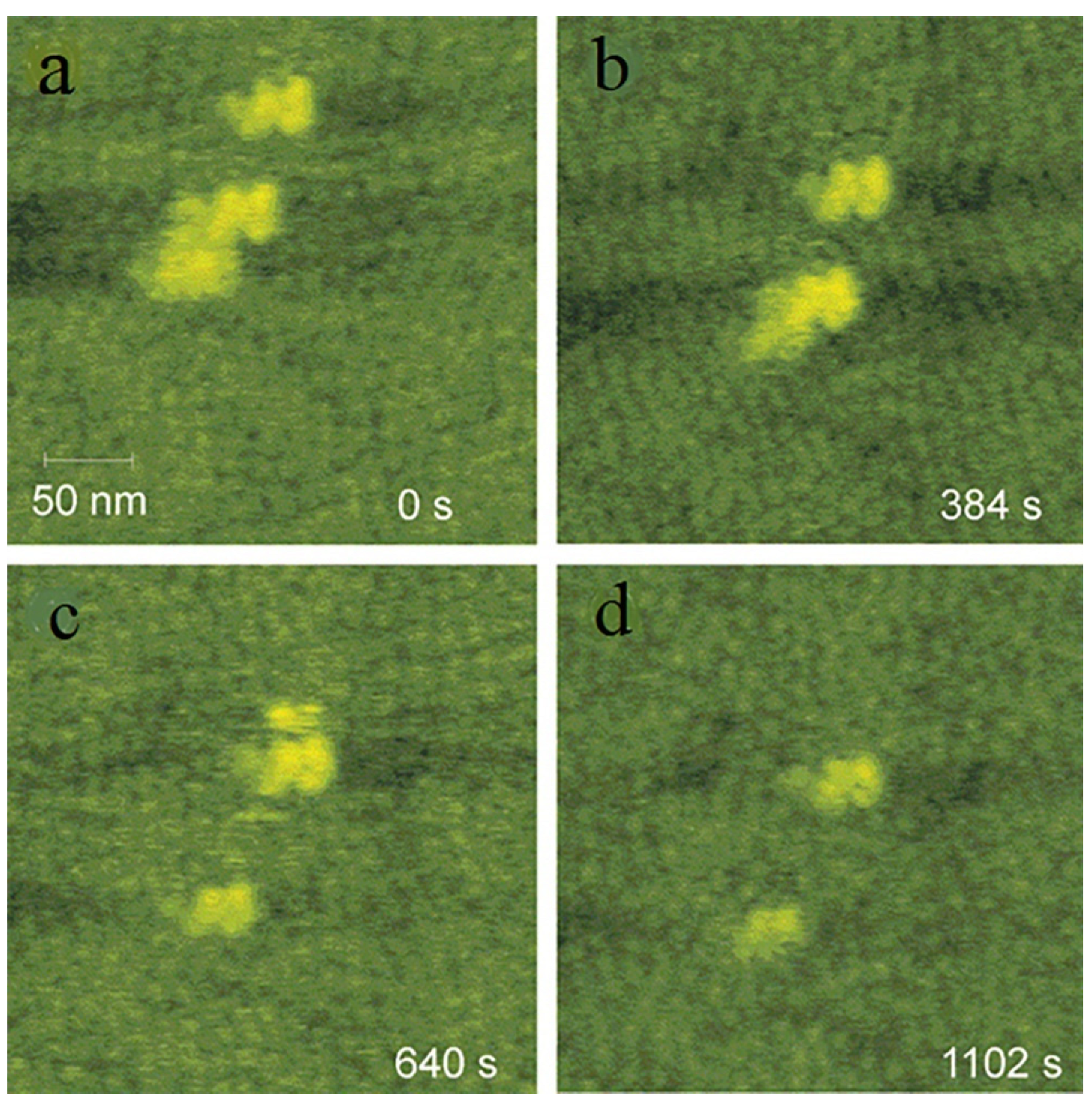
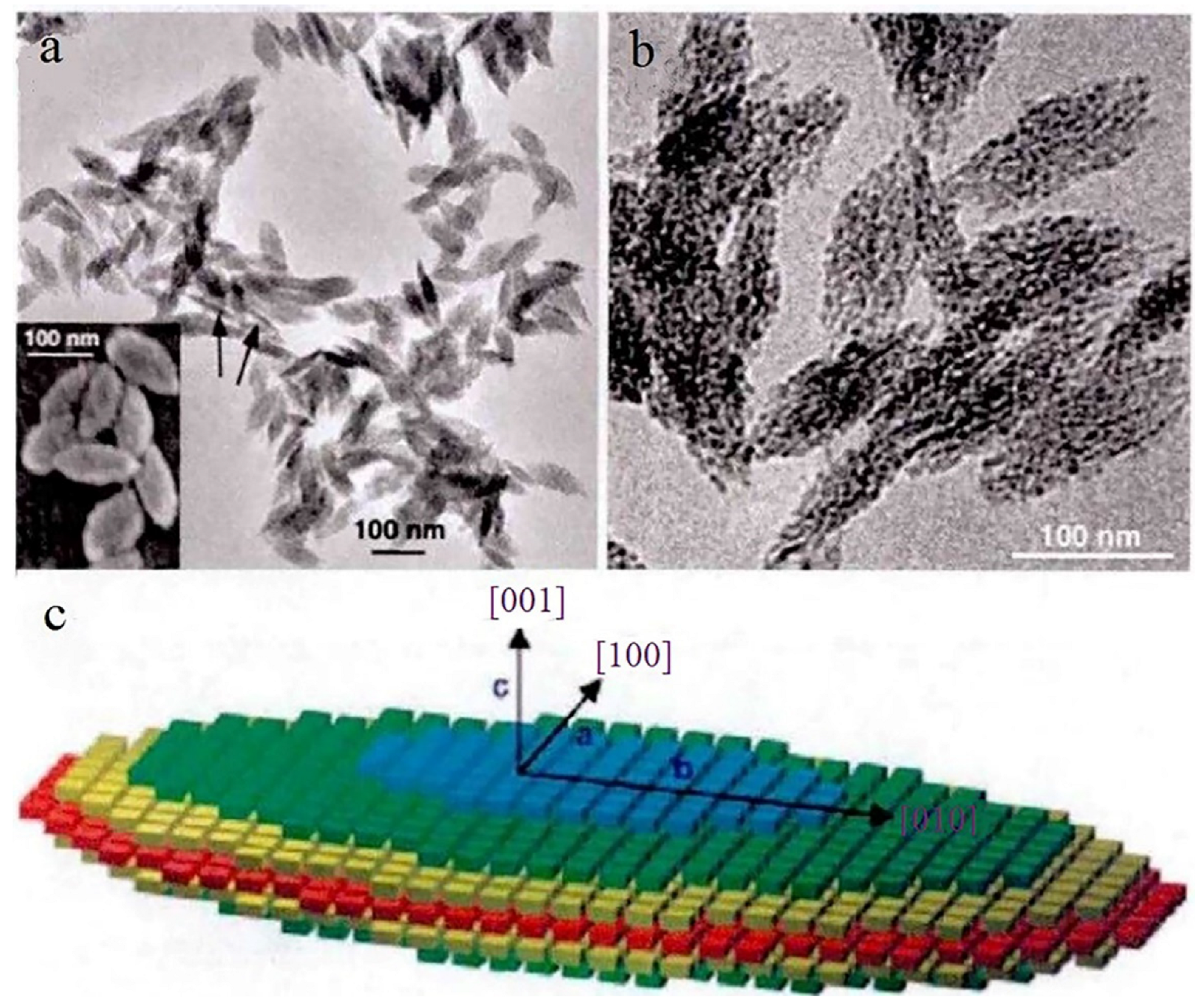
2.4. Particles in Particle Agglomeration Theory
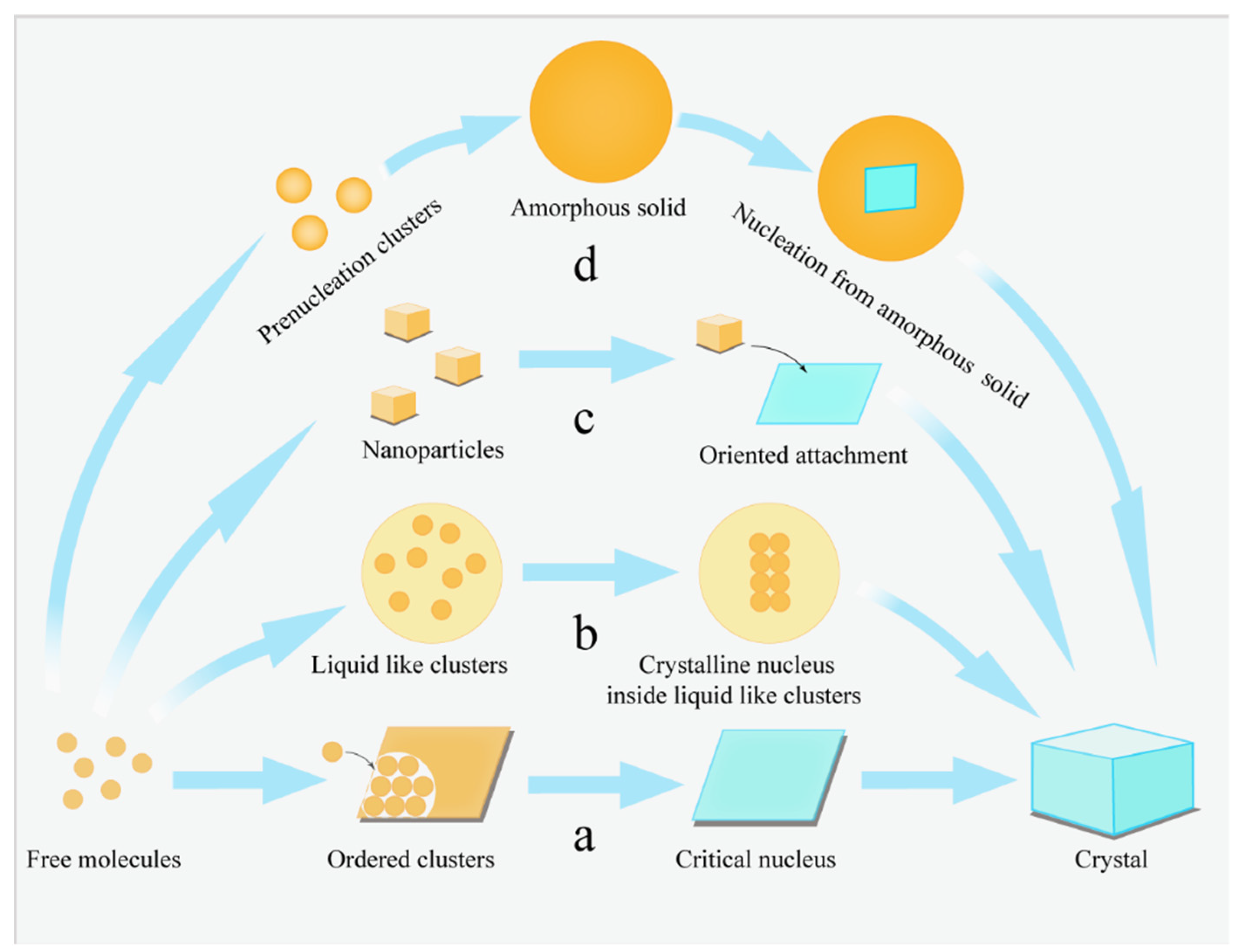
3. Mesoscale Structure during Growth
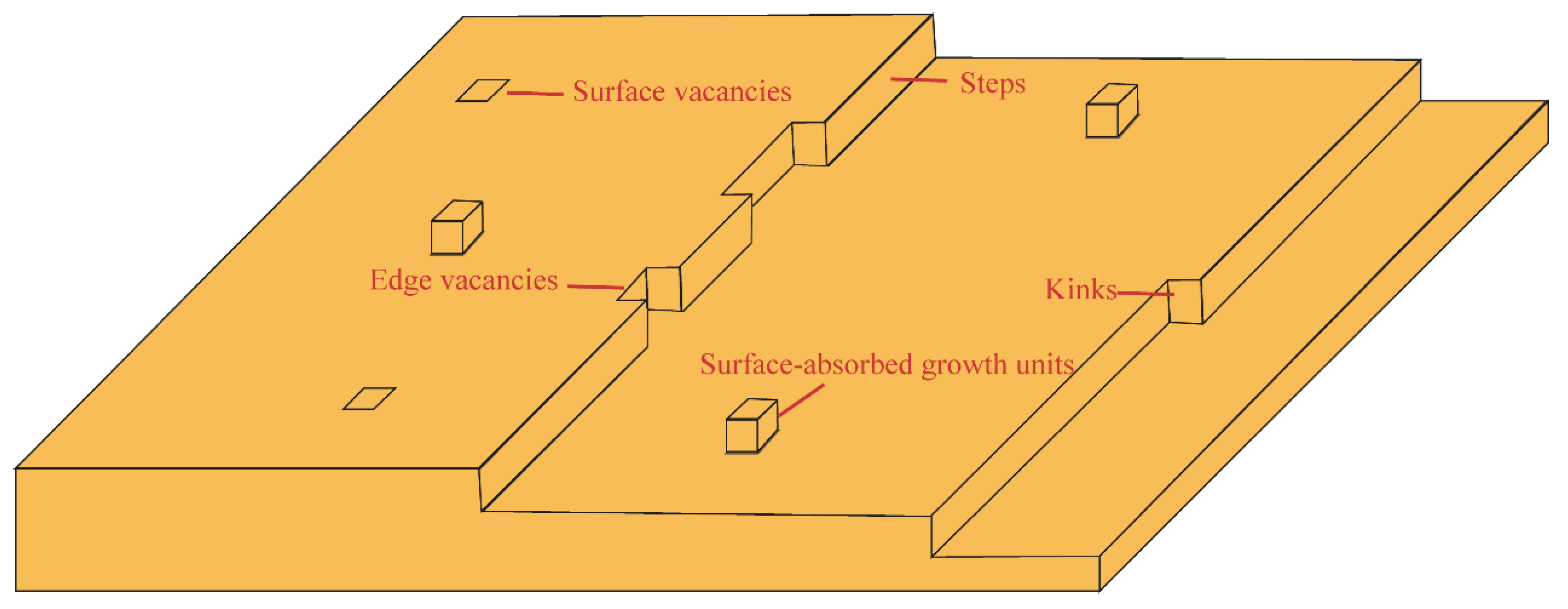
3.1. Units in Classical Growth Theory
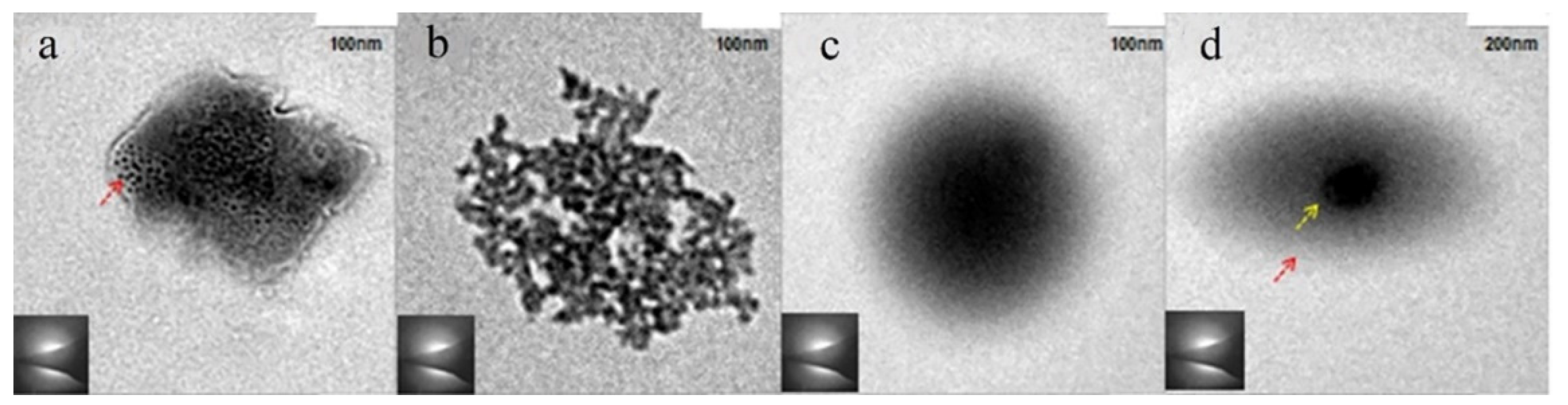
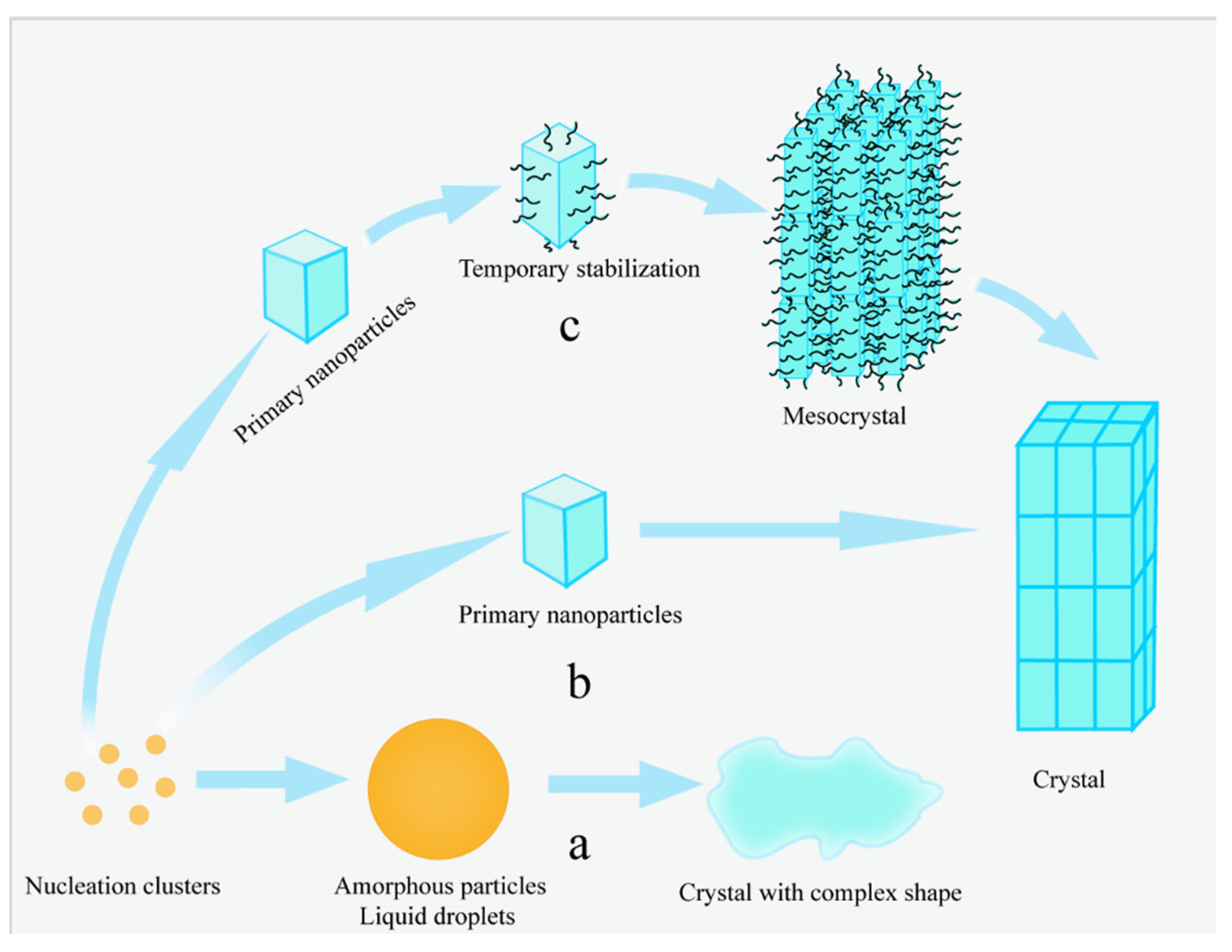
3.2. Amorphous Precursors in Amorphous Precursor Growth Theory
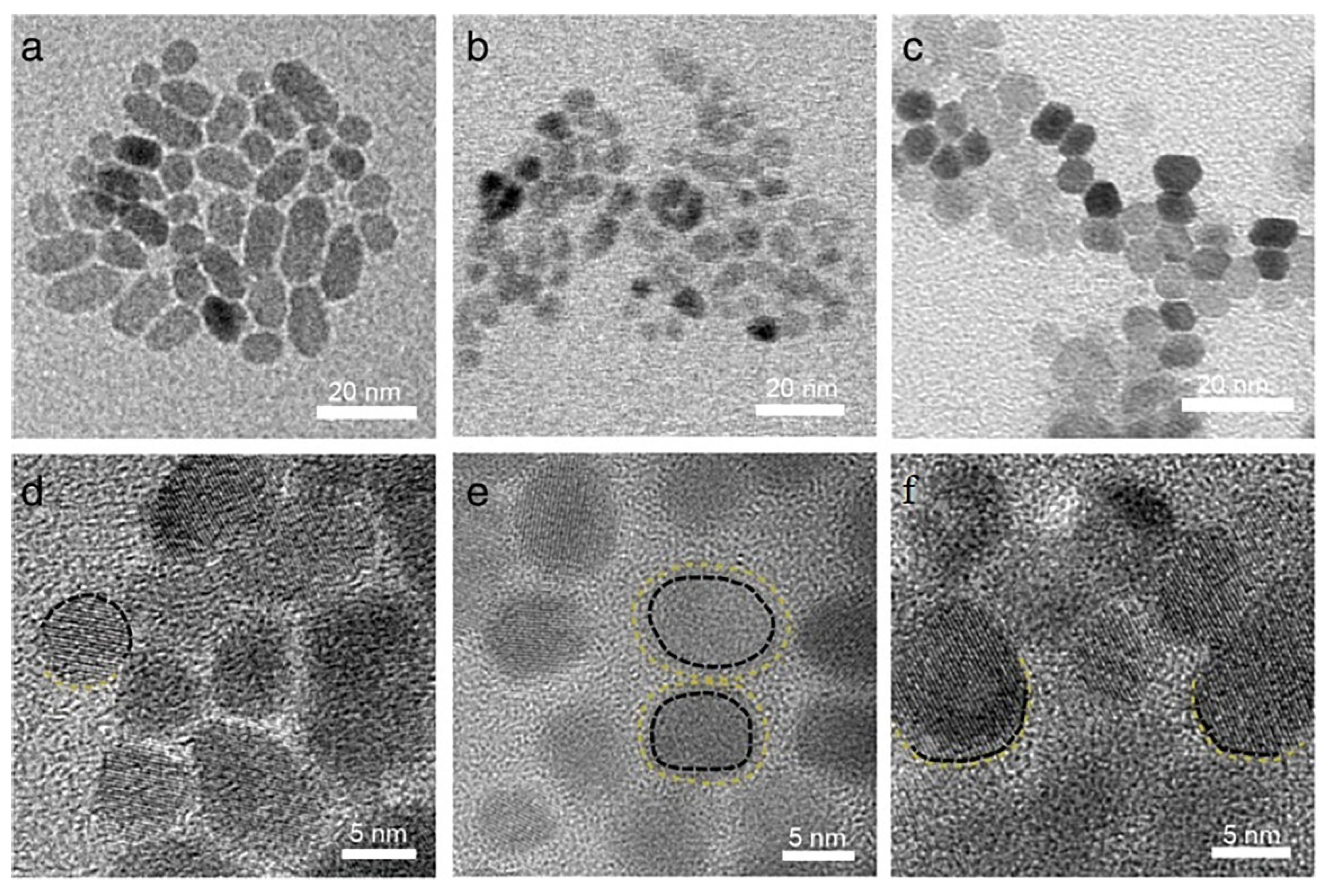
3.3. Nanoparticles in Particle Attachment Growth Theory
3.4. Mesocrystals in Mesocrystal Growth Theory
4. EMMS Model and Crystal Nucleation and Growth
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kato, S.; Furukawa, S.; Aoki, D.; Goseki, R.; Oikawa, K.; Tsuchiya, K.; Shimada, N.; Maruyama, A.; Numata, K.; Otsuka, H. Crystallization-induced mechanofluorescence for visualization of polymer crystallization. Nat. Commun. 2021, 12, 126. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Fang, Y.; Zhao, W.; Han, R.; Wen, J.; Liu, S. Molten-Salt-Assisted CsPbI3 Perovskite Crystallization for Nearly 20%-Efficiency Solar Cells. Adv. Mater. 2021, 33, 2103770. [Google Scholar] [CrossRef] [PubMed]
- Mu, X.; Wu, F.; Tang, Y.; Wang, R.; Li, Y.; Li, K.; Li, C.; Lu, Y.; Zhou, X.; Li, Z. Boost photothermal theranostics via self-assembly-induced crystallization (SAIC). Aggregate 2022, e170, 2692–4560. [Google Scholar] [CrossRef]
- Cui, W.; He, Z.; Zhang, Y.; Fan, Q.; Feng, N. Naringenin Cocrystals Prepared by Solution Crystallization Method for Improving Bioavailability and Anti-hyperlipidemia Effects. AAPS PharmSciTech 2019, 20, 115. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Zhang, Q.; Li, X. Crystallization Kinetics of α-Hemihydrate Gypsum Prepared by Hydrothermal Method in Atmospheric Salt Solution Medium. Crystals 2021, 11, 843. [Google Scholar] [CrossRef]
- Frenkel, J. A general theory of heterophase fluctuations and pretransition phenomena. J. Chem. Phys. 1939, 7, 538–547. [Google Scholar] [CrossRef]
- Volmer, M. Nucleus formation in supersaturated systems. Z. Phys. Chem. 1926, 119, 277–301. [Google Scholar] [CrossRef]
- Santra, M.; Singh, R.S.; Bagchi, B. Polymorph selection during crystallization of a model colloidal fluid with a free energy landscape containing a metastable solid. Phys. Rev. E 2018, 98, 032606. [Google Scholar] [CrossRef]
- Janković, B.; Marinović-Cincović, M.; Dramićanin, M. Kinetic study of isothermal crystallization process of Gd2Ti2O7 pre-cursor’s powder prepared through the Pechini synthetic approach. J. Phys. Chem. Sol. 2015, 85, 160–172. [Google Scholar] [CrossRef]
- Chang, H.; Bootharaju, M.S.; Lee, S.; Kim, J.H.; Kim, B.H.; Hyeon, T. To inorganic nanoparticles via nanoclusters: Nonclassical nucleation and growth pathway. Bull. Korean Chem. Soc. 2021, 42, 1386–1399. [Google Scholar] [CrossRef]
- Houben, L.; Weissman, H.; Wolf, S.G.; Rybtchinski, B. A mechanism of ferritin crystallization revealed by cryo-STEM tomography. Nature 2020, 579, 540–543. [Google Scholar] [CrossRef] [PubMed]
- Wiedenbeck, E.; Kovermann, M.; Gebauer, D.; Cölfen, H. Liquid metastable precursors of ibuprofen as aqueous nucleation intermediates. Angew. Chem. Int. Ed. 2019, 58, 19103–19109. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Kwauk, M. Exploring complex systems in chemical engineering—the multi-scale methodology. Chem. Eng. Sci. 2003, 58, 521–535. [Google Scholar] [CrossRef]
- Huang, W.; Li, J.; Edwards, P.P. Mesoscience: Exploring the common principle at mesoscales. Natl. Sci. Rev. 2018, 5, 27–32. [Google Scholar] [CrossRef]
- Grossmann, L.; King, B.T.; Reichlmaier, S.; Hartmann, N.; Rosen, J.; Heckl, W.M.; Björk, J.; Lackinger, M. On-surface photopolymerization of two-dimensional polymers ordered on the mesoscale. Nat. Chem. 2021, 13, 730–736. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the equilibrium of heterogeneous substances. Am. J. Sci. 1878, 3, 441–458. [Google Scholar] [CrossRef]
- Farkas, L. Keimbildungsgeschwindigkeit in übersättigten Dämpfen. Z. Phys. Chem. 1927, 125, 236–242. [Google Scholar] [CrossRef]
- Becker, R.; Döring, W. Kinetische behandlung der keimbildung in übersättigten dämpfen. Ann. Phys. 1935, 416, 719–752. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Goonetilleke, E.C.; Huang, X. Temperature-dependent kinetic pathways of heterogeneous ice nucleation competing between classical and non-classical nucleation. Nat. Commun. 2021, 12, 4954. [Google Scholar] [CrossRef]
- Banner, D.J.; Firlar, E.; Rehak, P.; Phakatkar, A.H.; Foroozan, T.; Osborn, J.K.; Sorokina, L.V.; Narayanan, S.; Tahseen, T.; Baggia, Y. In Situ Liquid-Cell TEM Observation of Multiphase Classical and Nonclassical Nucleation of Calcium Oxalate. Adv. Funct. Mater. 2021, 31, 2007736. [Google Scholar] [CrossRef]
- Katz, J.L. The critical supersaturations predicted by nucleation theory. J. Stat. Phys. 1970, 2, 137–146. [Google Scholar] [CrossRef]
- Shore, J.D.; Perchak, D.; Shnidman, Y. Simulations of the nucleation of AgBr from solution. J. Chem. Phys. 2000, 113, 6276–6284. [Google Scholar] [CrossRef]
- Adamski, T. Commination of crystal nucleation by a precipitation method. Nature 1963, 197, 894. [Google Scholar] [CrossRef]
- Yau, S.-T.; Vekilov, P.G. Direct observation of nucleus structure and nucleation pathways in apoferritin crystallization. J. Am. Chem. Soc. 2001, 123, 1080–1089. [Google Scholar] [CrossRef]
- Erdemir, D.; Lee, A.Y.; Myerson, A.S. Nucleation of crystals from solution: Classical and two-step models. Acc. Chem. Res. 2009, 42, 621–629. [Google Scholar] [CrossRef] [PubMed]
- Davey, R.J.; Schroeder, S.L.; Ter Horst, J.H. Nucleation of organic crystals—a molecular perspective. Angew. Chem. Int. Ed. 2013, 52, 2166–2179. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.-Z.; Niu, L.-Y.; Zhang, H.; Chen, Y.-Z.; Yang, Q.-Z. Exploration of the two-step crystallization of organic micro/nano crystalline materials by fluorescence spectroscopy. Mater. Chem. Front. 2018, 2, 1323–1327. [Google Scholar] [CrossRef]
- Fang, H.; Hagan, M.F.; Rogers, W.B. Two-step crystallization and solid–solid transitions in binary colloidal mixtures. Proc. Natl. Acad. Sci. USA 2020, 117, 27927–27933. [Google Scholar] [CrossRef] [PubMed]
- ten Wolde, P.R.; Frenkel, D. Enhancement of protein crystal nucleation by critical density fluctuations. Science 1997, 277, 1975–1978. [Google Scholar] [CrossRef]
- Duff, N.; Peters, B. Nucleation in a Potts lattice gas model of crystallization from solution. J. Chem. Phys. 2009, 131, 184101. [Google Scholar] [CrossRef]
- Sun, X.; Garetz, B.A.; Myerson, A.S. Polarization switching of crystal structure in the nonphotochemical laser-induced nucleation of supersaturated aqueous l-histidine. Cryst. Growth Des. 2008, 8, 1720–1722. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Erdemir, D.; Evans, J.M.; Ilavsky, J.; Amenitsch, H.; Segre, C.U.; Myerson, A.S. SAXS study of the nucleation of glycine crystals from a supersaturated solution. Cryst. Growth Des. 2005, 5, 523–527. [Google Scholar] [CrossRef]
- Vekilov, P.G. The two-step mechanism of nucleation of crystals in solution. Nanoscale 2010, 2, 2346–2357. [Google Scholar] [CrossRef]
- Harano, K.; Homma, T.; Niimi, Y.; Koshino, M.; Suenaga, K.; Leibler, L.; Nakamura, E. Heterogeneous nucleation of organic crystals mediated by single-molecule templates. Nat. Mater. 2012, 11, 877–881. [Google Scholar] [CrossRef]
- Leunissen, M.E.; Christova, C.G.; Hynninen, A.P.; Royall, C.P.; Campbell, A.I.; Imhof, A.; Van Blaaderen, A. Ionic colloidal crystals of oppositely charged particles. Nature 2005, 437, 235–240. [Google Scholar] [CrossRef]
- Savage, J.R.; Dinsmore, A.D. Experimental evidence for two-step nucleation in colloidal crystallization. Phys. Rev. Lett. 2009, 102, 198302. [Google Scholar] [CrossRef]
- Pouget, E.M.; Bomans, P.H.; Goos, J.A.; Frederik, P.M.; de With, G.; Sommerdijk, N.A. The initial stages of template-controlled CaCO3 formation revealed by cryo-TEM. Science 2009, 323, 1455–1458. [Google Scholar] [CrossRef]
- Gower, L.B. Biomimetic model systems for investigating the amorphous precursor pathway and its role in biomineralization. Chem. Rev. 2008, 108, 4551–4627. [Google Scholar] [CrossRef]
- Betts, F.; Posner, A. An X-ray radial distribution study of amorphous calcium phosphate. Mater. Res. Bull. 1974, 9, 353–360. [Google Scholar] [CrossRef]
- Gebauer, D.; Kellermeier, M.; Gale, J.D.; Bergström, L.; Cölfen, H. Pre-nucleation clusters as solute precursors in crystallisation. Chem. Soc. Rev. 2014, 43, 2348–2371. [Google Scholar] [CrossRef] [Green Version]
- Gebauer, D.; Cölfen, H. Prenucleation clusters and non-classical nucleation. Nano Today 2011, 6, 564–584. [Google Scholar] [CrossRef]
- Kellermeier, M.; Rosenberg, R.; Moise, A.; Anders, U.; Przybylski, M.; Cölfen, H. Amino acids form prenucleation clusters: ESI-MS as a fast detection method in comparison to analytical ultracentrifugation. Faraday Discuss. 2012, 159, 23–45. [Google Scholar] [CrossRef]
- Lu, J.; Li, Z.; Jiang, X. Polymorphism of pharmaceutical molecules: Perspectives on nucleation. Front. Chem. Eng. Chin. 2010, 4, 37–44. [Google Scholar] [CrossRef]
- Lin, T.-J.; Chiu, C.-C. Structures and infrared spectra of calcium phosphate clusters by ab initio methods with implicit solvation models. Phys. Chem. Chem. Phys. 2018, 20, 345–356. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, X.; Dong, C.; Sun, Y.; Yu, J. Investigation of amorphous calcium carbonate’s formation under high concentration of magnesium: The prenucleation cluster pathway. J. Cryst. Growth 2018, 494, 8–16. [Google Scholar] [CrossRef]
- Habraken, W.J.; Tao, J.; Brylka, L.J.; Friedrich, H.; Bertinetti, L.; Schenk, A.S.; Verch, A.; Dmitrovic, V.; Bomans, P.H.; Frederik, P.M. Ion-association complexes unite classical and non-classical theories for the biomimetic nucleation of calcium phosphate. Nat. Commun. 2013, 4, 1507. [Google Scholar] [CrossRef]
- Trinh, T.T.H.; Khuu, C.Q.; Wolf, S.E.; Nguyen, A.-T. The multiple stages towards crystal formation of L-glutamic acid. J. Cryst. Growth 2020, 544, 125727. [Google Scholar] [CrossRef]
- Wang, F.; Richards, V.N.; Shields, S.P.; Buhro, W.E. Kinetics and mechanisms of aggregative nanocrystal growth. Chem. Mater. 2014, 26, 5–21. [Google Scholar] [CrossRef]
- De Yoreo, J.J.; Gilbert, P.U.; Sommerdijk, N.A.; Penn, R.L.; Whitelam, S.; Joester, D.; Zhang, H.; Rimer, J.D.; Navrotsky, A.; Banfield, J.F. Crystallization by particle attachment in synthetic, biogenic, and geologic environments. Science 2015, 349, 6760. [Google Scholar] [CrossRef]
- Baumgartner, J.; Dey, A.; Bomans, P.H.; Le Coadou, C.; Fratzl, P.; Sommerdijk, N.A.; Faivre, D. Nucleation and growth of magnetite from solution. Nat. Mater. 2013, 12, 310–314. [Google Scholar] [CrossRef] [PubMed]
- Mirabello, G.; Ianiro, A.; Bomans, P.H.; Yoda, T.; Arakaki, A.; Friedrich, H.; de With, G.; Sommerdijk, N.A. Crystallization by particle attachment is a colloidal assembly process. Nat. Mater. 2020, 19, 391–396. [Google Scholar] [CrossRef]
- Park, J.; Elmlund, H.; Ercius, P.; Yuk, J.M.; Limmer, D.T.; Chen, Q.; Kim, K.; Han, S.H.; Weitz, D.A.; Zettl, A. 3D structure of individual nanocrystals in solution by electron microscopy. Science 2015, 349, 290–295. [Google Scholar] [CrossRef]
- Polte, J.; Erler, R.; Thunemann, A.F.; Sokolov, S.; Ahner, T.T.; Rademann, K.; Emmerling, F.; Kraehnert, R. Nucleation and growth of gold nanoparticles studied via in situ small angle X-ray scattering at millisecond time resolution. ACS Nano 2010, 4, 1076–1082. [Google Scholar] [CrossRef]
- Crespo, D.; Pradell, T.; Clavaguera-Mora, M.; Clavaguera, N. Microstructural evaluation of primary crystallization with diffusion-controlled grain growth. Phys. Rev. B 1997, 55, 3435. [Google Scholar] [CrossRef]
- Brüning, K.; Schneider, K.; Roth, S.V.; Heinrich, G. Kinetics of strain-induced crystallization in natural rubber: A diffusion-controlled rate law. Polymer 2015, 72, 52–58. [Google Scholar] [CrossRef]
- Wang, K.; Leng, Y.; Lu, X.; Ren, F.; Ge, X.; Ding, Y. Theoretical analysis of protein effects on calcium phosphate precipitation in simulated body fluid. CrystEngComm 2012, 14, 5870–5878. [Google Scholar] [CrossRef]
- Volmer, M. Zum problem des kristallwachstums. Z. Phys. Chem. 1922, 102, 267–275. [Google Scholar] [CrossRef]
- Burton, W.-K.; Cabrera, N.; Frank, F. The growth of crystals and the equilibrium structure of their surfaces. Philos. Trans. R. Soc. 1951, 243, 299–358. [Google Scholar]
- Malkin, A.; Kuznetsov, Y.G.; Land, T.; DeYoreo, J.; McPherson, A. Mechanisms of growth for protein and virus crystals. Nat. Struct. Biol. 1995, 2, 956–959. [Google Scholar] [CrossRef]
- Nozawa, J.; Uda, S.; Guo, S.; Hu, S.; Toyotama, A.; Yamanaka, J.; Okada, J.; Koizumi, H. Two-dimensional nucleation on the terrace of colloidal crystals with added polymers. Langmuir 2017, 33, 3262–3269. [Google Scholar] [CrossRef]
- Weng, J.; Huang, Y.; Hao, D.; Ji, Y. Recent advances of pharmaceutical crystallization theories. Chin. J. Chem. Eng. 2020, 28, 935–948. [Google Scholar] [CrossRef]
- Chernov, A. Present-day understanding of crystal growth from aqueous solutions. Prog. Cryst. Growth Charact. Mater. 1993, 26, 121–151. [Google Scholar] [CrossRef]
- Kalt, H.; Rühle, W.; Reimann, K.; Rinker, M.; Bauser, E. Alloy-disorder-induced intervalley coupling. Phys. Rev. B 1991, 43, 12364. [Google Scholar] [CrossRef]
- Ming, N.-B. Defect mechanisms of crystal growth and their kinetics. J. Cryst. Growth 1993, 128, 104–112. [Google Scholar] [CrossRef]
- Rodriguez-Navarro, C.; Burgos-Cara, A.; Lorenzo, F.D.; Ruiz-Agudo, E.; Elert, K. Nonclassical crystallization of calcium hydroxide via amorphous precursors and the role of additives. Cryst. Growth Des. 2020, 20, 4418–4432. [Google Scholar] [CrossRef]
- Yang, J.; Koo, J.; Kim, S.; Jeon, S.; Choi, B.K.; Kwon, S.; Kim, J.; Kim, B.H.; Lee, W.C.; Lee, W.B. Amorphous-phase-mediated crystallization of Ni nanocrystals revealed by high-resolution liquid-phase electron microscopy. J. Am. Chem. Soc. 2019, 141, 763–768. [Google Scholar] [CrossRef] [PubMed]
- Uskoković, V. Disordering the disorder as the route to a higher order: Incoherent crystallization of calcium phosphate through amorphous precursors. Cryst. Growth Des. 2019, 19, 4340–4357. [Google Scholar] [CrossRef]
- DiMasi, E.; Kwak, S.-Y.; Amos, F.F.; Olszta, M.J.; Lush, D.; Gower, L.B. Complementary control by additives of the kinetics of amorphous CaCO3 mineralization at an organic interface: In-situ synchrotron X-ray observations. Phys. Rev. Lett. 2006, 97, 045503. [Google Scholar] [CrossRef]
- Penn, R.L.; Banfield, J.F. Imperfect oriented attachment: Dislocation generation in defect-free nanocrystals. Science 1998, 281, 969–971. [Google Scholar] [CrossRef]
- Penn, R.L.; Banfield, J.F. Morphology development and crystal growth in nanocrystalline aggregates under hydrothermal conditions: Insights from titania. Geochim. Cosmochim. Acta 1999, 63, 1549–1557. [Google Scholar] [CrossRef]
- Tsukiyama, K.; Takasaki, M.; Oaki, Y.; Imai, H. Evolution of Co3O4 nanocubes through stepwise oriented attachment. Langmuir 2019, 35, 8025–8030. [Google Scholar] [CrossRef] [PubMed]
- Gehrke, N.; Cölfen, H.; Pinna, N.; Antonietti, M.; Nassif, N. Superstructures of calcium carbonate crystals by oriented attachment. Cryst. Growth Des. 2005, 5, 1317–1319. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, Z.; Lan, Y.; Ren, G.; Chen, D.; Huang, F.; Hong, M. A multistep oriented attachment kinetics: Coarsening of ZnS nanoparticle in concentrated NaOH. J. Am. Chem. Soc. 2006, 128, 12981–12987. [Google Scholar] [CrossRef] [PubMed]
- Kurz, W.; Rappaz, M.; Trivedi, R. Progress in modelling solidification microstructures in metals and alloys. Part II: Dendrites from 2001 to 2018. Int. Mater. Rev. 2021, 66, 30–76. [Google Scholar] [CrossRef]
- Cho, K.-S.; Talapin, D.V.; Gaschler, W.; Murray, C.B. Designing PbSe nanowires and nanorings through oriented attachment of nanoparticles. J. Am. Chem. Soc. 2005, 127, 7140–7147. [Google Scholar] [CrossRef]
- Pacholski, C.; Kornowski, A.; Weller, H. Self-assembly of ZnO: From nanodots to nanorods. Angew. Chem. Int. Ed. 2002, 41, 1188–1191. [Google Scholar] [CrossRef]
- Cao, D.; Gong, S.; Shu, X.; Zhu, D.; Liang, S. Preparation of ZnO nanoparticles with high dispersibility based on oriented attachment (OA) process. Nanoscale Res. Lett. 2019, 14, 210. [Google Scholar] [CrossRef]
- Zhu, C.; Liang, S.; Song, E.; Zhou, Y.; Wang, W.; Shan, F.; Shi, Y.; Hao, C.; Yin, K.; Zhang, T. In-situ liquid cell transmission electron microscopy investigation on oriented attachment of gold nanoparticles. Nat. Commun. 2018, 9, 421. [Google Scholar] [CrossRef]
- Li, X.H.; Li, J.X.; Li, G.D.; Liu, D.P.; Chen, J.S. Controlled synthesis, growth mechanism, and properties of monodisperse CdS colloidal spheres. Chem. Eur. J. 2007, 13, 8754–8761. [Google Scholar] [CrossRef]
- Liu, Z.; Pan, H.; Zhu, G.; Li, Y.; Tao, J.; Jin, B.; Tang, R. Realignment of nanocrystal aggregates into single crystals as a result of inherent surface stress. Angew. Chem. 2016, 128, 13028–13032. [Google Scholar] [CrossRef]
- Ye, Y.; Chen, C.; Li, W.; Guo, X.; Yang, H.; Guan, H.; Xi, G. Highly sensitive W18O49 mesocrystal Raman scattering substrate with large-area signal uniformity. Anal. Chem. 2021, 93, 3138–3145. [Google Scholar] [CrossRef]
- Li, L.; Liu, C.Y. Organic small molecule-assisted synthesis of high active TiO2 rod-like mesocrystals. CrystEngComm 2010, 12, 2073–2078. [Google Scholar] [CrossRef]
- Zhou, L.; O’Brien, P. Mesocrystals: A new class of solid materials. Small 2008, 4, 1566–1574. [Google Scholar] [CrossRef]
- Zhou, L.; O’Brien, P. Mesocrystals—Properties and Applications. J. Phys. Chem. Lett. 2012, 3, 620–628. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, H.; Shao, X.; Li, D.; Yu, H.; Han, M. Three-Dimensionally Oriented Aggregation of a Few Hundred Nanoparticles into Monocrystalline Architectures. Adv. Mate. 2005, 17, 42–47. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, L.; Zeng, Y.; Jia, C.; Lin, J.; Yates, M.Z.; Guan, B. Formation of spherical calcium sulfate mesocrystals: Orientation controlled by subunit growth. CrystEngComm 2019, 21, 5973–5979. [Google Scholar] [CrossRef]
- Tan, B.; Zhang, X.; Li, Y.; Chen, H.; Ye, X.; Wang, Y.; Ye, J. Anatase TiO2 Mesocrystals: Green Synthesis, In Situ Conversion to Porous Single Crystals, and Self-Doping Ti3+ for Enhanced Visible Light Driven Photocatalytic Removal of NO. Chem. Eur. J. 2017, 23, 5478–5487. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, D.; Feng, Y.; Zhang, F.; Chen, L.; Du, Y.; Ivey, D.G.; Wei, W. Tuning anisotropic ion transport in mesocrystalline lithium orthosilicate nanostructures with preferentially exposed facets. NPG Asia Mater. 2018, 10, 606–617. [Google Scholar] [CrossRef]
- Keßler, S.; Reinalter, E.R.; Ni, B.; Cölfen, H. Rational Design of Environmentally Compatible Nickel Hexacyanoferrate Mesocrystals as Catalysts. J. Phys. Chem. C 2021, 125, 26503–26511. [Google Scholar] [CrossRef]
- Ruiz-Agudo, C.; Ruiz-Agudo, E.; Putnis, C.V.; Putnis, A. Mechanistic principles of barite formation: From nanoparticles to micron-sized crystals. Cryst. Growth Des. 2015, 15, 3724–3733. [Google Scholar] [CrossRef]
- Wang, T.; Cölfen, H.; Antonietti, M. Nonclassical crystallization: Mesocrystals and morphology change of CaCO3 crystals in the presence of a polyelectrolyte additive. J. Am. Chem. Soc. 2005, 127, 3246–3247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, F.; Ye, Z.; Kong, L.; Liu, P.; Zhang, Y.; Zhang, H.; Tang, Y. Facile Morphology and Porosity Regulation of Zeolite ZSM-5 Mesocrystals with Synergistically Enhanced Catalytic Activity and Shape Selectivity. Nanomaterials 2022, 12, 1601. [Google Scholar] [CrossRef] [PubMed]
- Estrin, Y.; Beygelzimer, Y.; Kulagin, R.; Gumbsch, P.; Fratzl, P.; Zhu, Y.; Hahn, H. Architecturing materials at mesoscale: Some current trends. Mater. Lett. 2021, 9, 399–421. [Google Scholar] [CrossRef]
- Guo, L.; Wu, J.; Li, J. Complexity at Mesoscales: A common challenge in developing artificial intelligence. Engineering 2019, 5, 924–929. [Google Scholar] [CrossRef]
- Li, J. Particle-Fluid Two-Phase Flow: The Energy-Minimization Multi-Scale Method; Metallurgical Industry Press: Beijing, China, 1994. [Google Scholar]
- Ge, W.; Chen, F.; Gao, J.; Gao, S.; Huang, J.; Liu, X.; Ren, Y.; Sun, Q.; Wang, L.; Wang, W. Analytical multi-scale method for multi-phase complex systems in process engineering—Bridging reductionism and holism. Chem. Eng. Sci. 2007, 62, 3346–3377. [Google Scholar] [CrossRef]
- Li, J.; Ge, W.; Wang, W.; Yang, N.; Liu, X.; Wang, L.; He, X.; Wang, X.; Wang, J.; Kwauk, M. From Multiscale Modeling to Meso-science; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lu, B.; Niu, Y.; Chen, F.; Ahmad, N.; Wang, W.; Li, J. Energy-minimization multiscale based mesoscale modeling and applications in gas-fluidized catalytic reactors. Rev. Chem. Eng. 2019, 35, 879–915. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Y. Mesoscale-Structure-Dependent EMMS Drag Model for an SCW Fluidized Bed: Formulation of Conservation Equations Based on Structures in Subphases. Ind. Eng. Chem. Res. 2021, 60, 18136–18153. [Google Scholar] [CrossRef]
- Li, J.; Ge, W.; Wang, W.; Yang, N.; Huang, W. Focusing on mesoscales: From the energy-minimization multiscale model to mesoscience. Curr. Opin. Chem. Eng. 2016, 13, 10–23. [Google Scholar] [CrossRef]
- Li, J.; Huang, W.; Chen, J.; Ge, W.; Hou, C. Mesoscience based on the EMMS principle of compromise in competition. Chem. Eng. J. 2018, 333, 327–335. [Google Scholar] [CrossRef]
- Wang, W.; Lu, B.; Geng, J.; Li, F. Mesoscale drag modeling: A critical review. Curr. Opin. Chem. Eng. 2020, 29, 96–103. [Google Scholar] [CrossRef]
- Geng, J.; Tian, Y.; Wang, W. Exploring a unified EMMS drag model for gas-solid fluidization. Chem. Eng. Sci. 2022, 251, 117444. [Google Scholar] [CrossRef]
- Xu, T.; Jiang, X.; Yang, N.; Zhu, J. CFD simulation of internal-loop airlift reactor using EMMS drag model. Particuology 2015, 19, 124–132. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y.; Li, X.; Liu, L.; Wei, L.; Liu, Y.; Gao, J. Study of hydrodynamic characteristics of particles in liquid–solid fluidized bed with modified drag model based on EMMS. Adv. Powder Technol. 2014, 25, 1103–1110. [Google Scholar] [CrossRef]
- Wu, N.; Ji, X.; Li, L.; Zhu, J.; Lu, X. Mesoscience in supported nano-metal catalysts based on molecular thermodynamic modeling: A mini review and perspective. Chem. Eng. Sci. 2021, 229, 116164. [Google Scholar] [CrossRef]
- Yang, T.; Han, Y.; Li, J. Manipulating silver dendritic structures via diffusion and reaction. Chem. Eng. Sci. 2015, 138, 457–464. [Google Scholar] [CrossRef]
- Han, M.; Xu, J.; Ren, Y.; Li, J. Simulations of flow induced structural transition of the β-switch region of glycoprotein Ibα. Biophys. Chem. 2016, 209, 9–20. [Google Scholar] [CrossRef]
- Wang, H.; Han, Y.; Li, J. Dominant role of compromise between diffusion and reaction in the formation of snow-shaped vaterite. Cryst. Growth Des. 2013, 13, 1820–1825. [Google Scholar] [CrossRef]
- Li, J.; Huang, W. From multiscale to mesoscience: Addressing mesoscales in mesoregimes of different levels. Annu. Rev. Chem. Biomol. Eng. 2018, 9, 41–60. [Google Scholar] [CrossRef]
- Ge, W.; Wang, W.; Yang, N.; Li, J.; Kwauk, M.; Chen, F.; Zhou, G. Meso-scale oriented simulation towards virtual process engineering (VPE)—The EMMS paradigm. Chem. Eng. Sci. 2011, 66, 4426–4458. [Google Scholar] [CrossRef]
- Ge, W.; Guo, L.; Liu, X.; Meng, F.; Xu, J.; Huang, W.L.; Li, J. Mesoscience-based virtual process engineering. Comput. Chem. Eng. 2019, 126, 68–82. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, K.; Qin, X.; Li, M.; Liu, Y.; An, Y.; Yang, W.; Chen, M.; Ouyang, J.; Gong, J. Research on Mesoscale Nucleation and Growth Processes in Solution Crystallization: A Review. Crystals 2022, 12, 1234. https://doi.org/10.3390/cryst12091234
Wang X, Li K, Qin X, Li M, Liu Y, An Y, Yang W, Chen M, Ouyang J, Gong J. Research on Mesoscale Nucleation and Growth Processes in Solution Crystallization: A Review. Crystals. 2022; 12(9):1234. https://doi.org/10.3390/cryst12091234
Chicago/Turabian StyleWang, Xiaowei, Kangli Li, Xueyou Qin, Mingxuan Li, Yanbo Liu, Yanlong An, Wulong Yang, Mingyang Chen, Jinbo Ouyang, and Junbo Gong. 2022. "Research on Mesoscale Nucleation and Growth Processes in Solution Crystallization: A Review" Crystals 12, no. 9: 1234. https://doi.org/10.3390/cryst12091234
APA StyleWang, X., Li, K., Qin, X., Li, M., Liu, Y., An, Y., Yang, W., Chen, M., Ouyang, J., & Gong, J. (2022). Research on Mesoscale Nucleation and Growth Processes in Solution Crystallization: A Review. Crystals, 12(9), 1234. https://doi.org/10.3390/cryst12091234









