Experimental Investigation of Phase Equilibria in the Ti—Al—Zr System at 1000–1300 °C
Abstract
1. Introduction
| Phase, Temperature Range (°C) | Space Group; Strukturbericht Designation | Lattice Parameters (nm) |
|---|---|---|
| βTi,Zr, <1855–863 | Imm; A2 | a0 = 0.33065 for pure Ti [27] |
| a0 = 0.36090 for pure Zr [28] | ||
| a0 = 0.3228 at 35.1 at. % Ti, 23.7 at. % Al, 41.2 at. % Zr [24] | ||
| αTi, 1491–1120 and <1170 | P63/mmc; A3 | a0 = 0.29506; c0 = 0.46835 [27] |
| Ti3Al (α2), <1200 | P63/mmc; D019 | a0 = 0.5765; c0 = 0.4625 [29] |
| a0 = 0.5783; c0 = 0.4667 at 52.1 at. % Ti, 28.0 at. % Al, 19.9 at. % Zr [24] | ||
| TiAl (γ), <1456 | P4/mmm; L10 | a0 = 0.4000; c0 = 0.4075 at 50 at. % Al [30] |
| a0 = 0.4080; c0 = 0.4087 at ~42 at. % Ti, ~47 at. % Al, ~11 at. % Zr [31] | ||
| a0 = 0.3974; c0 = 0.4072 at 41.5 at. % Ti, 50.6 at. % Al, 7.9 at. % Zr [24] | ||
| Zr5Al3, <1400–1000 | I4/mcm; D8m | a0 = 1.1044; c0 = 0.5391 [28] |
| Zr5Al3, (<1000?) | P63/mcm; D88 | a0 = 0.8174; c0 = 0.5698 [28] |
| a0 = 0.8217; c0 = 0.5704 at 30.5 at. % Ti, 39.2 at. % Al, 30.3 at. % Zr [24] | ||
| ZrAl2, <1624 | P63/mmc; C14 | a0 = 0.52824; c0 = 0.87482 [28] |
| a0 = 0.5273; c0 = 0.8827 at 8.7 at. % Ti, 60.1 at. % Al, 31.2 at. % Zr [24] | ||
| β0 | Pmm; B2 | a0 = 0.333(6) at 50 at. % Ti, 25 at. % Al, 25 at. % Zr [11] |
2. Materials and Methods
3. Results and Discussion
| Alloy | Condition | Ti (at. %) | Al (at. %) | Zr (at. %) | C wt. % ppm | O wt. % ppm | N wt. % ppm |
|---|---|---|---|---|---|---|---|
| Z1 | as-cast | 69.3 | 20.6 | 10.1 | 110 | 350 | <50 |
| Z2 | as-cast | 63.2 | 27.4 | 9.4 | 160 | 370 | <50 |
| 1000 °C/ 100 h | 61.8 | 28.4 | 9.8 | 147 | 510 | <50 | |
| Z4 | as-cast | 44.0 | 40.8 | 15.2 | 137 | 340 | <50 |
| 1000 °C/ 100 h | 38.3 | 44.7 | 16.5 | 111 | 455 | <50 | |
| 1300 °C/ 24 h | 40.6 | 43.3 | 16.1 | 89 | 300 | <50 | |
| Z5 * | as-cast | 48.8 ± 0.2 | 46.1 ± 0.3 | 5.1 ± 0.01 | 127 ± 10 | 110 ± 30 | <50 |
| 1000°C/ 100 h | 48.8 | 46.1 | 5.1 | 100 | 200 | <50 | |
| Z6 | as-cast | 44.7 | 45.1 | 10.2 | 120 | 400 | <50 |
| 1300 °C/ 24 h | 45.1 | 44.6 | 10.3 | 89 | 480 | <50 | |
| Z7 | as-cast | 37.0 | 47.3 | 15.7 | 79 | 180 | <50 |
| 1300 °C/ 24 h | 38.1 | 46.6 | 15.3 | 77 | 240 | <50 |
3.1. Partial Isothermal Section at 1000 °C
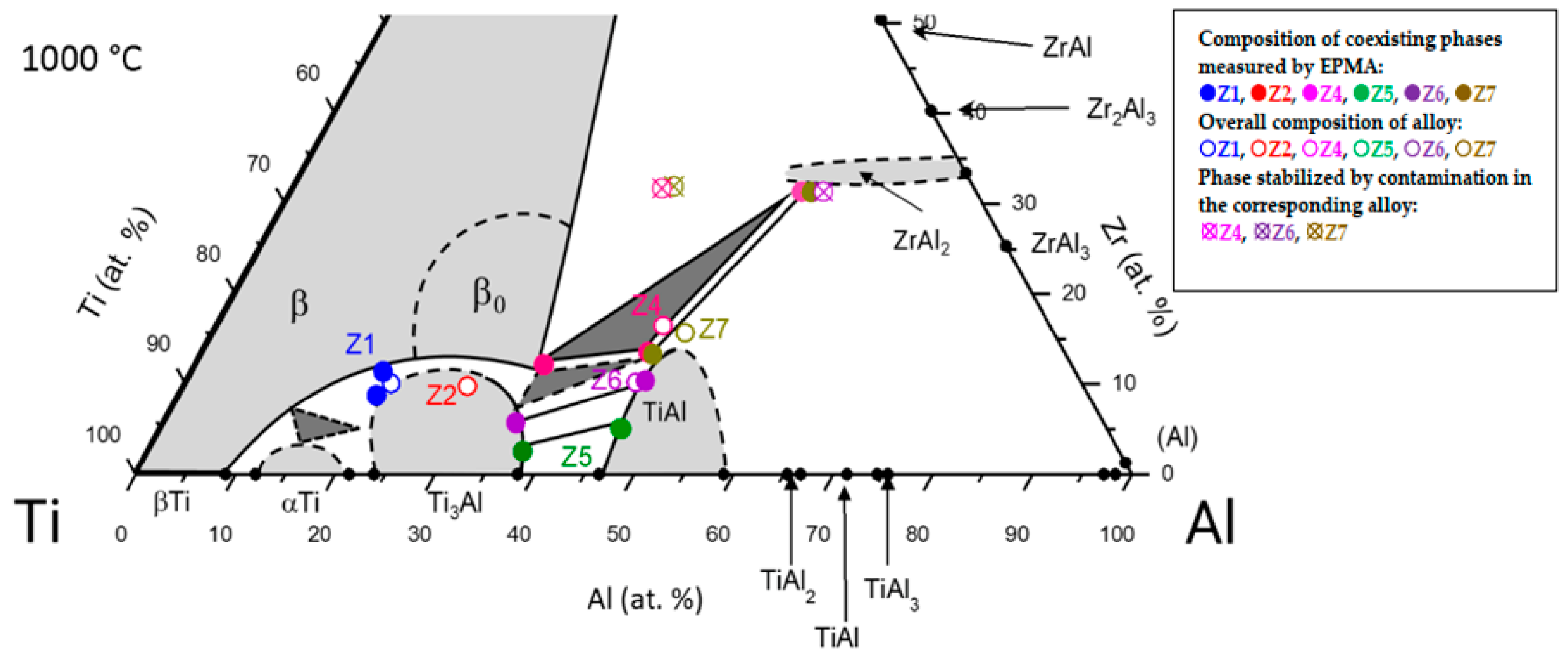
| Alloy | HT (h) | Composition | Lattice Parameters (nm) | Impurity (wt. ppm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Phases | Ti (at. %) | Al (at. %) | Zr (at. %) | Phases | a0 | c0 | C | O | N | ||
| Z1 | 1000 | βTi, Zr or β0 | 69.5 ± 0.2 | 19.1 ± 0.3 | 11.4 ± 0.2 | αTi * | 0.29420 (1) | 0.47307 (3) | |||
| 0.2952 | 0.472 | ||||||||||
| Ti3Al | 71.4 ± 0.3 | 19.8 ± 0.3 | 8.8 ± 0.2 | Ti3Al | 0.58982 (2) | 0.46911 (2) | |||||
| 0.5878 | 0.4707 | ||||||||||
| Z2 | 100 | Ti3Al | 63.2 ± 0.6 | 27.4 ± 0.2 | 9.4 ± 0.5 | Ti3Al | 0.58700 (7) | 0.46979 (5) | 147 | 510 | <50 |
| Z4 | 100 | ZrAl2 | 17.5 ± 0.7 | 51.3 ± 0.4 | 31.2 ± 0.4 | ZrAl2 | 0.53756 (1) | 0.87478 (3) | 111 | 455 | <50 |
| 0.537 | 0.8745 | ||||||||||
| TiAl | 41.8 ± 0.3 | 44.7 ± 0.2 | 13.5 ± 0.3 | TiAl | 0.40963 (2) | 0.40976 (4) | |||||
| 0.411 | 0.408 | ||||||||||
| β0 | 53.0 ± 0.3 | 34.9 ± 0.2 | 12.1 ± 0.2 | β0 | 0.327 (1) | ||||||
| 0.3268 | |||||||||||
| Z5 | 100 | TiAl | 48.7 ± 0.4 | 46.2 ± 0.3 | 5.1 ± 0.3 | TiAl | 0.40453 (4) | 0.40900 (7) | 100 | 200 | <50 |
| Ti3Al | 59.9 | 37.5 | 2.6 | Ti3Al | 0.5813 (4) | 0.4651 (6) | |||||
| Z6 | 1000 | TiAl | 43.6 ± 0.9 | 46.0 ± 0.5 | 10.4 ± 0.5 | TiAl | 0.40737 (4) | 0.41061 (6) | |||
| Ti3Al | 59.0 ± 0.3 | 35.3 ± 0.3 | 5.7 ± 0.1 | Ti3Al | 0.5825 (2) | 0.4666 (3) | |||||
| Z7 | 1000 | ZrAl2 | 16.5 ± 0.4 | 52.2 ± 0.6 | 31.3 ± 0.3 | ZrAl2 | 0.53688 (2) | 0.87237 (5) | |||
| TiAl | 41.7 ± 0.7 | 45.1 ± 0.5 | 13.2 ± 0.3 | TiAl | 0.40942 (2) | 0.40955 (2) | |||||
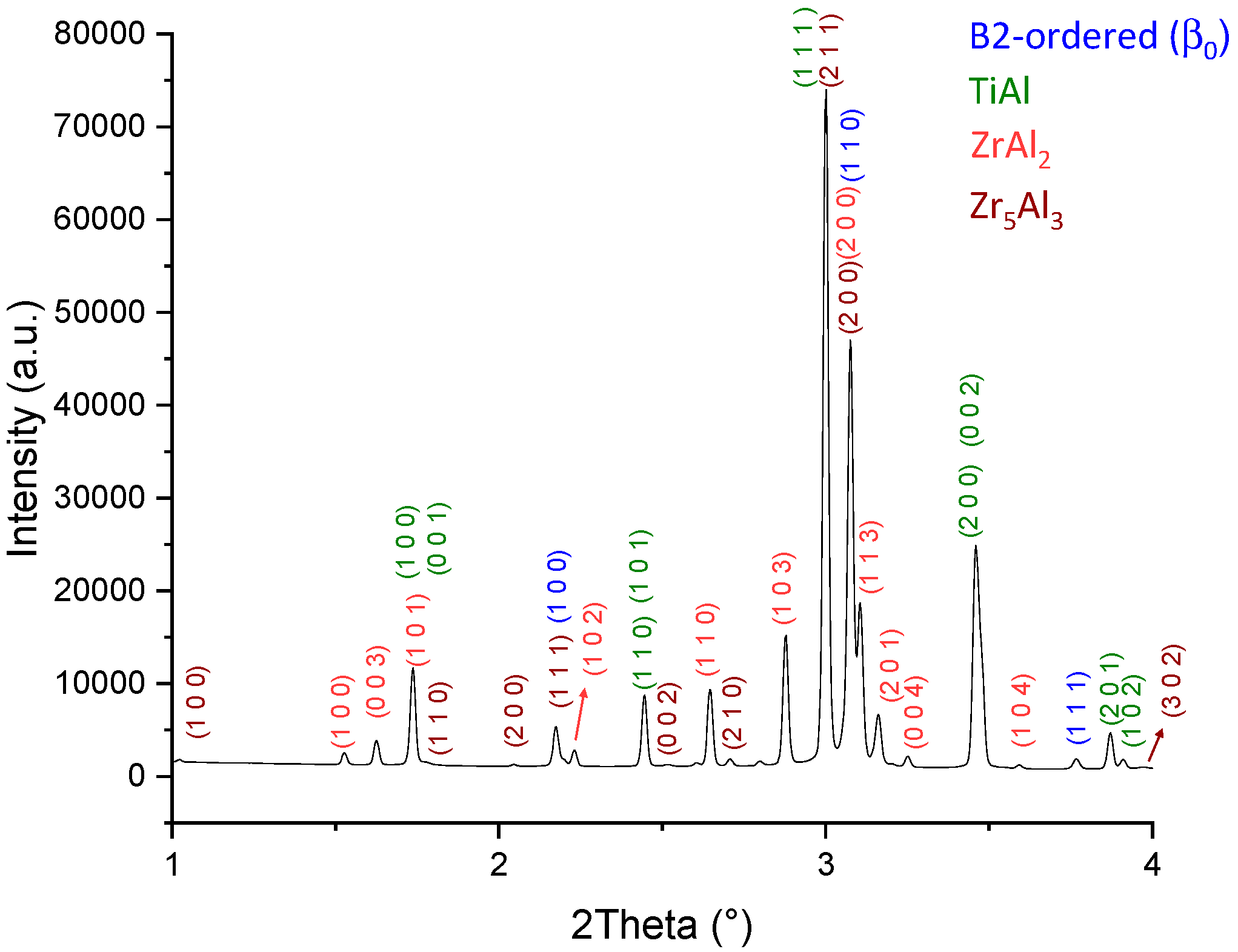


3.2. Partial Isothermal Section at 1100 °C
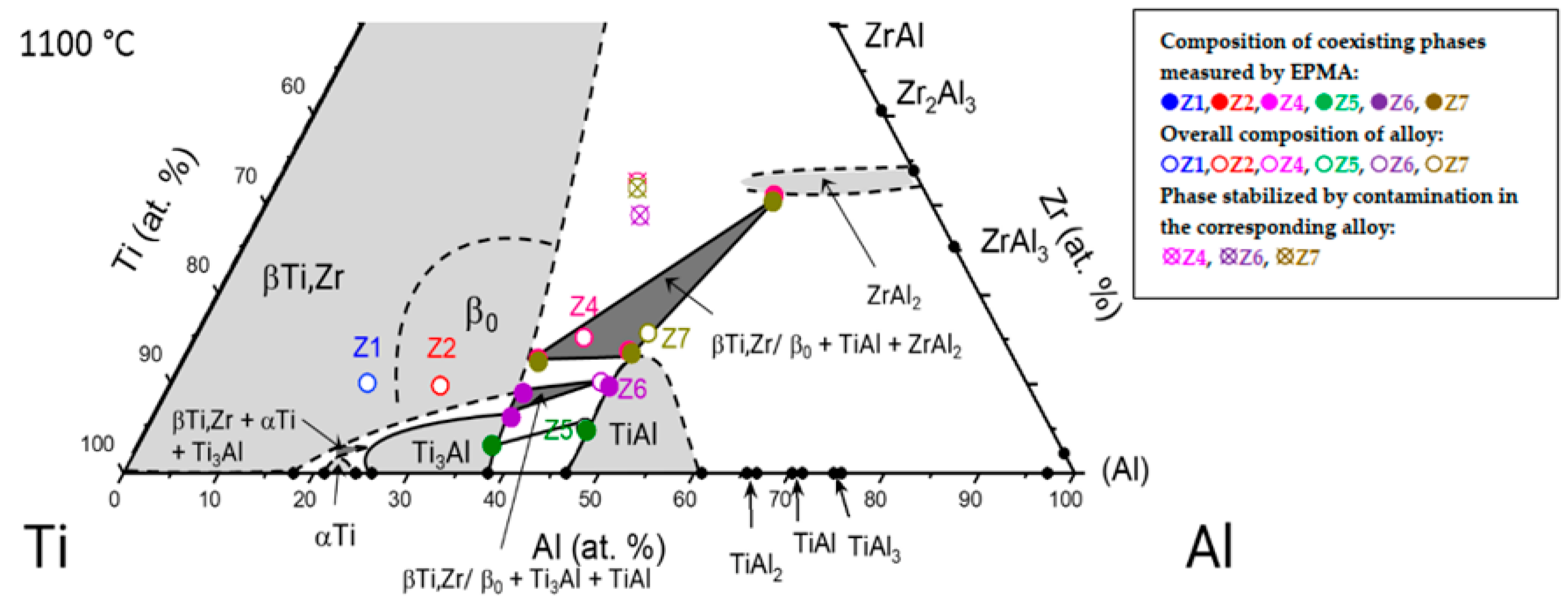
| Alloy | Composition | Lattice Parameters (nm) | |||||
|---|---|---|---|---|---|---|---|
| Phases | Ti (at. %) | Al (at. %) | Zr (at. %) | Phases | a0 | c0 | |
| Z4 | ZrAl2 | 16.0 ± 0.6 | 52.9 ± 0.3 | 31.1 ± 0.5 | ZrAl2 | 0.53461 (1) | 0.87451 (2) |
| TiAl | 40.0 ± 0.6 | 46.3 ± 0.2 | 13.7 ± 0.5 | TiAl | 0.4095 (1) | 0.4115 (4) | |
| β0 | 50.0 ± 0.5 | 37.2 ± 0.3 | 12.8 ± 0.3 | β0 | 0.322 (8) | ||
| Z5 | TiAl | 48.9 ± 0.9 | 46.3 ± 0.6 | 4.8 ± 0.3 | TiAl | 0.40443 (3) | 0.40845 (5) |
| Ti3Al | 59.7 ± 0.6 | 37.2 ± 0.5 | 3.1 ± 0.1 | Ti3Al | 0.5798 (1) | 0.4665 (2) | |
| Z6 | TiAl | 43.5 ± 0.2 | 46.8 ± 0.2 | 9.7 ± 0.2 | TiAl | 0.40716 (4) | 0.41024 (6) |
| Ti3Al | 56.1 ± 0.3 | 37.6 ± 0.2 | 6.3 ± 0.1 | Ti3Al | 0.5822 (2) | 0.4680 (3) | |
| β (or β0) | 53.5 ± 0.3 | 37.5 ± 0.1 | 9.0 ± 0.2 | β (or β0) | n.d. | ||
| Z7 | ZrAl2 | 16.5 ± 0.3 | 53.1 ± 0.3 | 30.4 ± 0.3 | ZrAl2 | 0.53771 (1) | 0.87419 (3) |
| TiAl | 39.9 ± 0.4 | 46.7 ± 0.4 | 13.4 ± 0.2 | TiAl | 0.41051 (2) | 0.41094 (2) | |
| β0 | 50.1 ± 0.5 | 37.4 ± 0.4 | 12.5 ± 0.2 | β0 | 0.327 (1) | ||
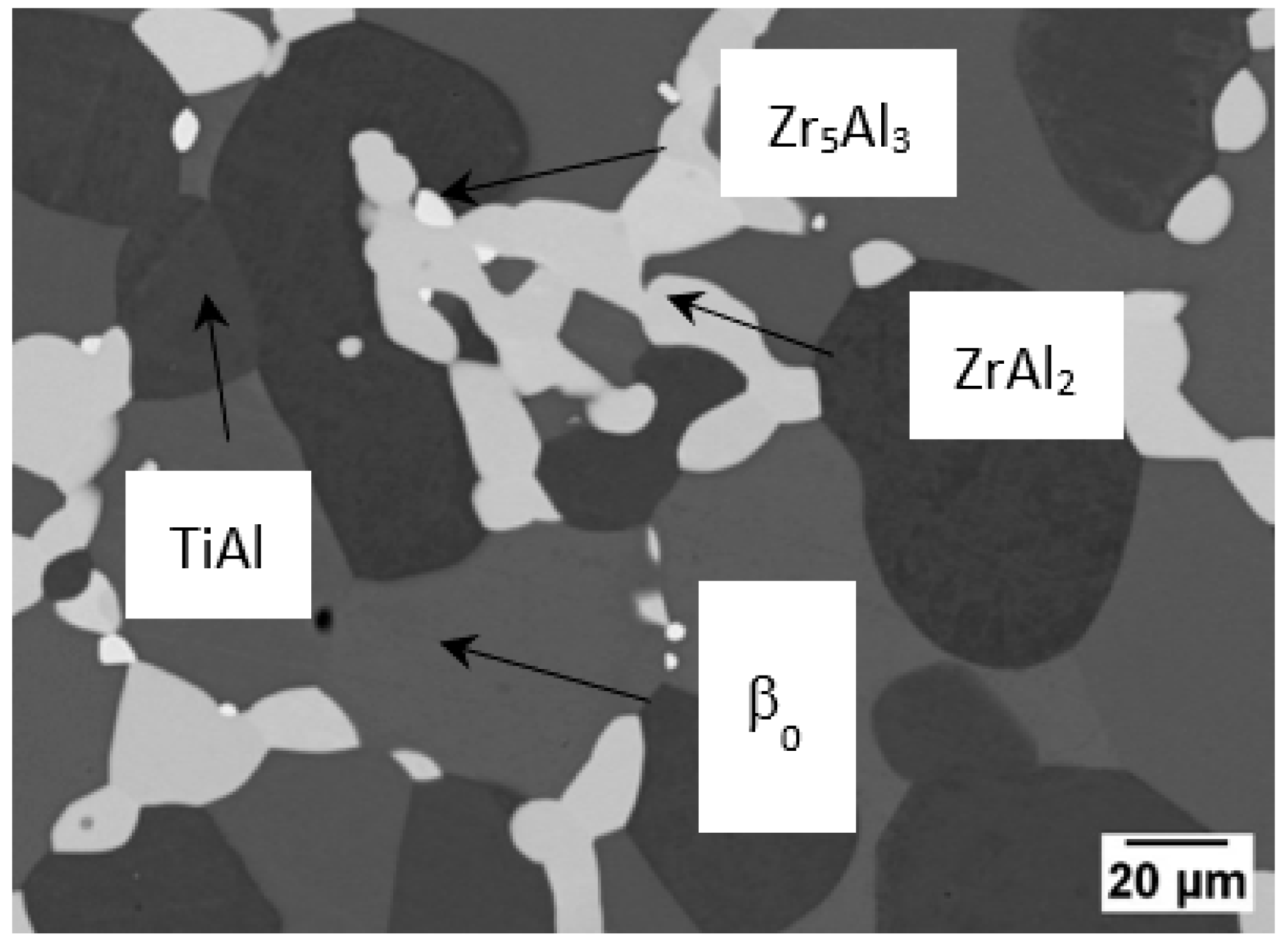
3.3. Partial Isothermal Section at 1200 °C

| Alloy | Composition | Lattice Parameters (nm) | Impurity (wt. ppm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Phases | Ti (at. %) | Al (at. %) | Zr (at. %) | Phases | a0 | c0 | C | O | N | |
| Z4 | ZrAl2 | 15.9 ± 0.4 | 54.3 ± 0.5 | 29.8 ± 0.2 | ZrAl2 | 0.53439 (1) | 0.87378 (2) | 140 | 250 | <50 |
| TiAl | 38.5 ± 0.3 | 47.9 ± 0.3 | 13.6 ± 0.1 | TiAl | 0.40916 (7) | 0.4119 (1) | ||||
| β0 | 47.7 ± 0.7 | 39.4 ± 0.6 | 12.9 ± 0.3 | β0 | 0.327 (1) | |||||
| Z5 | TiAl | 48.0 ± 0.3 | 46.7 ± 0.3 | 5.3 ± 0.2 | TiAl | 0.40459 (5) | 0.40867 (8) | 120 | 240 | <50 |
| 0.4049 | 0.4072 | |||||||||
| αTi | 56.1 ± 0.4 | 40.1 ± 0.4 | 3.8 ± 0.1 | αTi | 0.2900 (1) | 0.4646 (4) | ||||
| Ti3Al * | 0.579 | 0.4638 | ||||||||
| Z6 | TiAl | 42.7 ± 0.5 | 47.2 ± 0.7 | 10.1 ± 0.4 | TiAl | 0.40397 (4) | 0.40868 (7) | 110 | 770 | <50 |
| 0.4078 | 0.4085 | |||||||||
| β0 | 52.0 ± 0.7 | 38.8 ± 0.8 | 9.2 ± 0.3 | β0 | 0.338 (2) | |||||
| 0.3253 | ||||||||||
| Z7 | ZrAl2 | 16.6 ± 0.3 | 53.0 ± 0.4 | 30.4 ± 0.3 | ZrAl2 | 0.53614 (5) | 0.8742 (2) | 100 | 360 | <50 |
| 0.5357 | 0.873 | |||||||||
| TiAl | 38.9 ± 0.6 | 47.1 ± 0.5 | 14.0 ± 0.2 | TiAl | 0.40908 (3) | 0.41162 (5) | ||||
| 0.410 | 0.4095 | |||||||||
| β0 | 49.3 ± 0.3 | 37.9 ± 0.3 | 12.8 ± 0.2 | β0 | 0.326 (5) | |||||
| 0.32665 | ||||||||||

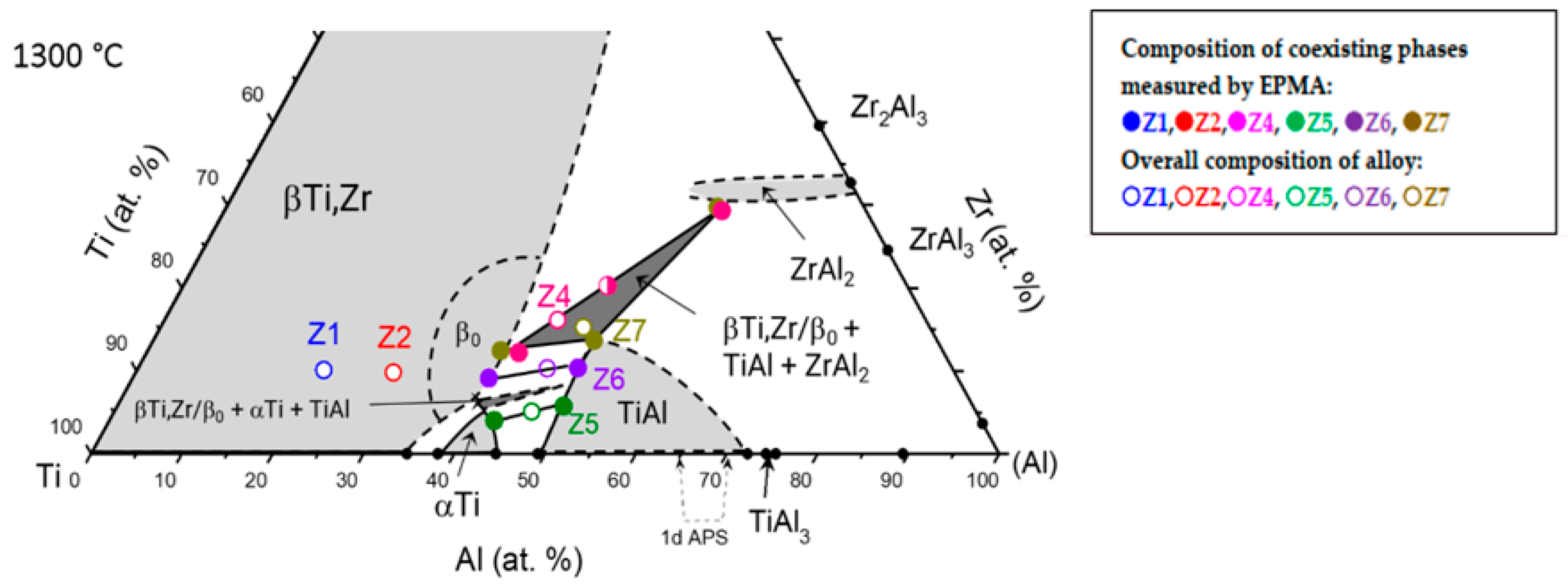
3.4. Partial Isothermal Section at 1300 °C
| Alloy | Composition | Lattice Parameters (nm) | Impurity (wt. ppm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Phases | Ti (at. %) | Al (at. %) | Zr (at. %) | Phases | a0 | c0 | C | O | N | |
| Z4 | ZrAl2 | 15.9 ± 0.3 | 54.8 ± 0.3 | 29.3 ± 0.2 | ZrAl2 | 0.53530 (1) | 0.87245 (3) | 89 | 300 | <50 |
| β0 | 46.8 ± 0.4 | 41.0 ± 0.2 | 12.2 ± 0.3 | β0 | 0.326 (1) | |||||
| TiAl | n.d. | n.d. | n.d. | TiAl | n.d. | n.d. | ||||
| Z5 | TiAl | 45.1 ± 0.4 | 49.2 ± 0.3 | 5.7 ± 0.2 | TiAl | 0.40383 (3) | 0.40858 (4) | 86 | 220 | <50 |
| αTi | 53.6 ± 0.8 | 42.4 ± 0.6 | 4.0 ± 0.2 | αTi | 0.28931 (4) | 0.4639 (1) | ||||
| Z6 | TiAl | 41.2 ± 0.3 | 48.4 ± 0.3 | 10.4 ± 0.2 | TiAl | 0.40689 (3) | 0.41080 (5) | 89 | 480 | <50 |
| β0 (or β) | 51.6 ± 0.9 | 39.3 ± 0.7 | 9.1 ± 0.3 | β (or β0) | 0.325 (3) | |||||
| Z7 | ZrAl2 | 16.2 ± 0.4 | 54.1 ± 0.6 | 29.7 ± 0.4 | ZrAl2 | 0.53430 (1) | 0.87287 (3) | 77 | 240 | <50 |
| TiAl | 37.7 ± 0.3 | 48.6 ± 0.4 | 13.7 ± 0.3 | TiAl | 0.40852 (2) | 0.41081 (2) | ||||
| β0 | 48.7 ± 0.9 | 38.9 ± 0.9 | 12.4 ± 0.2 | β0 | 0.325 (1) | |||||



3.5. DTA Analysis—Phase Transformation Temperatures
| Alloy | Al (at. %) | Zr (at. %) | Heated to °C | Onset (°C); Strength of the Peak | Reaction | Ref. |
|---|---|---|---|---|---|---|
| Z1 | 20.6 | 10.1 | 1400 | 1028; ss | βTi,Zr/β0 <−> Ti3Al + βTi,Zr/β0 | |
| 995; s | Ti3Al + βTi,Zr/β0 <−> Ti3Al | |||||
| Z2 | 28.4 | 9.8 | 1400 | 1083 (±3); ss | β(Ti,Zr)/β0 <−> Ti3Al | |
| Z4 | 44.7 | 16.5 | 1400 | 1316; ss | L <−> βTi,Zr + ZrAl2 | [60] |
| 1235; s | ? | |||||
| 890; s | ? | |||||
| 850; s | ? | |||||
| Z5 | 46.1 | 5.1 | 1400 | ~1185; w | αTi + TiAl <−> Ti3Al + TiAl | |
| Z6 | 45.1 | 10.2 | 1400 | 1353; ss | L <−> L + βTi,Zr | [60] |
| 1314; s | L <−> TiAl + βTi,Zr | [60] | ||||
| ~1190; w | β0 + TiAl <−> β0 + TiAl + Ti3Al | |||||
| Z7 | 47.3 | 15.7 | 1400 | 1367; ss | L <−> βTi,Zr + ZrAl2 | [60] |
| 1312; ss | L <−> TiAl + βTi,Zr | [60] | ||||
| 1219; s | ? |
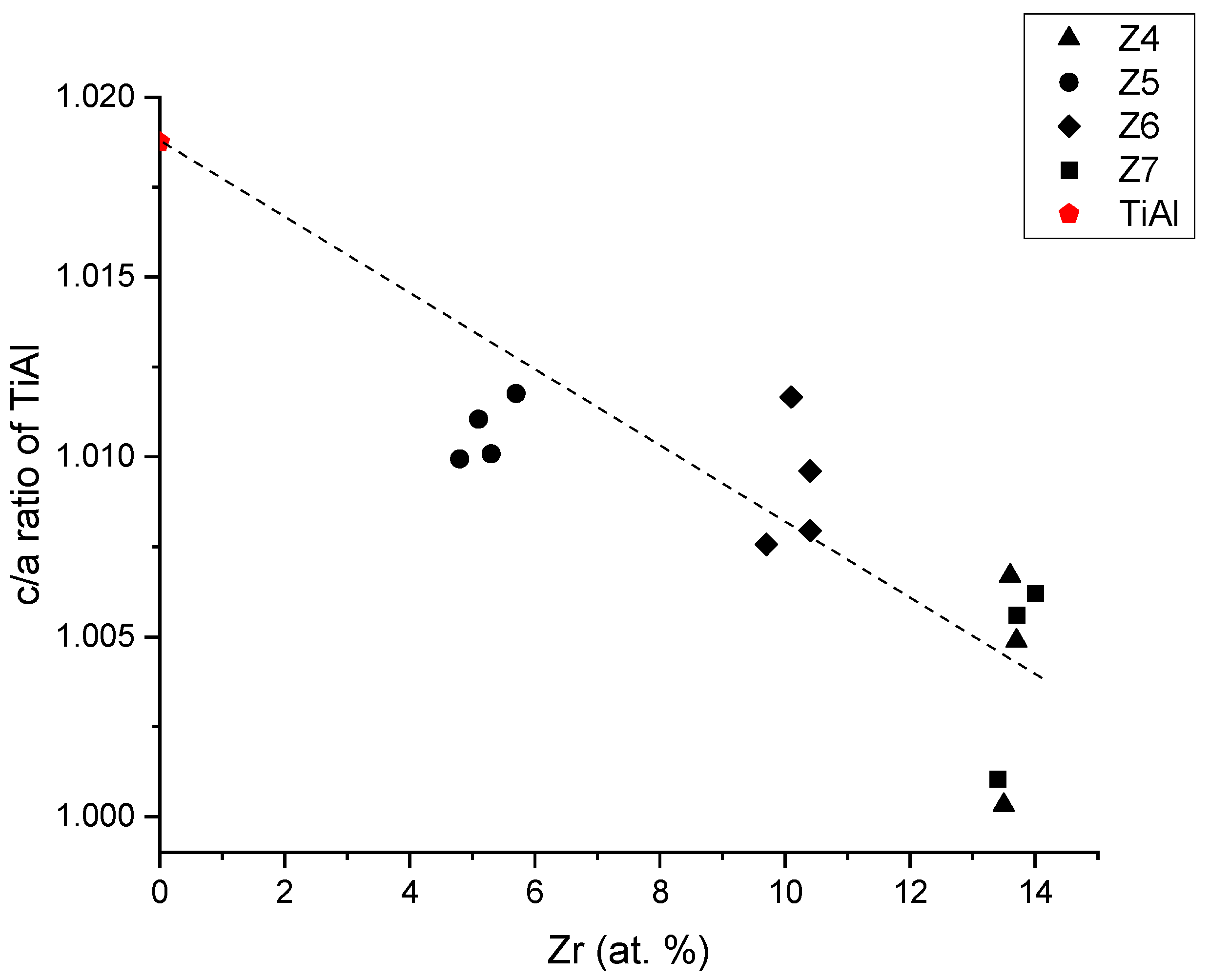
3.6. Effect of Addition of Zr on the Lattice Parameters of TiAl
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bewlay, B.; Weimer, M.; Kelly, T.; Suzuki, A.; Subramanian, P. The science, technology, and implementation of TiAl alloys in commercial aircraft engines. MRS Online Proc. Libr. 2013, 1516, 49–58. [Google Scholar] [CrossRef]
- Clemens, H.; Mayer, S. Design, processing, microstructure, properties, and applications of advanced intermetallic TiAl alloys. Adv. Eng. Mater. 2013, 15, 191–215. [Google Scholar] [CrossRef]
- Clemens, H.; Smarsly, W.; Güther, V.; Mayer, S. Advanced intermetallic titanium aluminides. In Proceedings of the 13th World Conference on Titanium; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 1189–1200. [Google Scholar]
- Neumeier, S.; Bresler, J.; Zenk, C.; Haußmann, L.; Stark, A.; Pyczak, F.; Göken, M. Partitioning behavior of Nb, Ta, and Zr in fully lamellar γ/α2 titanium aluminides and its effect on the lattice misfit and creep behavior. Adv. Eng. Mater. 2021, 23, 2100156. [Google Scholar] [CrossRef]
- Bresler, J.; Neumeier, S.; Ziener, M.; Pyczak, F.; Göken, M. The influence of niobium, tantalum and zirconium on the microstructure and creep strength of fully lamellar γ/α2 titanium aluminides. Mater. Sci. Eng. A 2019, 744, 46–53. [Google Scholar] [CrossRef]
- Kainuma, R.; Fujita, Y.; Mitsui, H.; Ohnuma, I.; Ishida, K. Phase equilibria among α (hcp), β (bcc) and γ (L10) phases in Ti–Al base ternary alloys. Intermetallics 2000, 8, 855–867. [Google Scholar] [CrossRef]
- Allen, M.; Güther, V.; Lindemann, J.; Kardos, S. Solid Solution Strengthening of TiAl Alloys with Zirconium. In Proceedings of the Intermetallics 2021, Bad Staffelstein, Germany, 4–8 October 2021; pp. 73–74. [Google Scholar]
- Wimler, D.; Lindemann, J.; Reith, M.; Kirchner, A.; Allen, M.; Vargas, W.G.; Franke, M.; Klöden, B.; Weißgärber, T.; Güther, V. Designing advanced intermetallic titanium aluminide alloys for additive manufacturing. Intermetallics 2021, 131, 107109. [Google Scholar] [CrossRef]
- Cheng, T.; Willis, M.; Jones, I. Effects of major alloying additions on the microstructure and mechanical properties of γ-TiAl. Intermetallics 1999, 7, 89–99. [Google Scholar] [CrossRef]
- Sornadurai, D.; Panigrahi, B.; Sastry, V.S. Ramani, Crystal structure and X-ray powder diffraction pattern of Ti2ZrAI. Powder Diffr. 2000, 15, 189–190. [Google Scholar] [CrossRef]
- Premkumar, M.; Prasad, K.S.; Singh, A.K. Structure and stability of the B2 phase in Ti–25Al–25Zr alloy. Intermetallics 2009, 17, 142–145. [Google Scholar] [CrossRef]
- Muradyan, G.; Dolukhanyan, S.; Aleksanyan, A.; Ter-Galstyan, O.; Mnatsakanyan, N. Regularities and Mechanism of Formation of Aluminides in the TiH2-ZrH2-Al System. Russ. J. Phys. Chem. B 2019, 13, 86–95. [Google Scholar] [CrossRef]
- Miyajima, Y.; Ishikawa, K.; Aoki, K. Hydrogen-induced amorphization in Ti–Al–Zr compounds with D019, B2 and FCC structures. Mater. Trans. 2002, 43, 1085–1088. [Google Scholar] [CrossRef][Green Version]
- Cheng, T.; Loretto, M. The decomposition of the beta phase in Ti–44Al–8Nb and Ti–44Al–4Nb–4Zr–0.2 Si alloys. Acta Mater. 1998, 46, 4801–4819. [Google Scholar] [CrossRef]
- Ballor, J.; Li, T.; Prima, F.; Boehlert, C.J.; Devaraj, A. A review of the metastable omega phase in beta titanium alloys: The phase transformation mechanisms and its effect on mechanical properties. Int. Mater. Rev. 2022, 1–20. [Google Scholar] [CrossRef]
- Huang, Z. Ordered ω phases in a 4Zr–4Nb-containing TiAl-based alloy. Acta Mater. 2008, 56, 1689–1700. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, D.; Wu, X. Thermal stability of the omega phase in Zr-containing TiAl alloys. J. Alloys Compd. 2009, 475, 134–138. [Google Scholar] [CrossRef]
- Huang, Z. Thermal stability of Ti–44Al–4Nb–4Zr–0.2 Si–1B alloy. Intermetallics 2013, 42, 170–179. [Google Scholar] [CrossRef]
- Kattner, U.R. The Calphad method and its role in material and process development. Tecnol. Metal. Mater. Min. 2016, 13, 3. [Google Scholar] [CrossRef]
- Kahrobaee, Z.; Palm, M. Critical Assessment of the Al-Ti-Zr System. J. Phase Equilibria Diffus. 2020, 41, 687–701. [Google Scholar] [CrossRef]
- Deng, Z.; Zhao, D.; Huang, Y.; Chen, L.; Zou, H.; Jiang, Y.; Chang, K. Ab initio and CALPHAD-type thermodynamic investigation of the Ti-Al-Zr system. J. Min. Metall. Sect. B 2019, 55, 427–437. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, W.; Xu, G.; Zeng, X.; Cui, Y. Thermodynamic assessment of the Ti–Al–Zr system and atomic mobility of its bcc phase. Calphad 2020, 70, 101801. [Google Scholar] [CrossRef]
- Lü, K.L.; Yang, F.; Xie, Z.Y.; Liu, H.S.; Cai, G.M.; Jin, Z.P. Isothermal section of Al−Ti−Zr ternary system at 1073 K. Trans. Nonferrous Met. Soc. China 2016, 26, 3052−3058. [Google Scholar] [CrossRef]
- Yang, F.; Xiao, F.H.; Liu, S.G.; Dong, S.S.; Huang, L.H.; Chen, Q.; Cai, G.M.; Liu, H.S.; Jin, Z.P. Isothermal section of Al–Ti–Zr ternary system at 1273 K. J. Alloys Compd. 2014, 585, 325–330. [Google Scholar] [CrossRef]
- Shirokova, N.I.; Nartova, T.T.; Kornilov, I.I. Исследoвание равнoвесия и свoйств сплавoв Ti-Zr-Al (Investigation of the phase equilibrium and properties of Ti-Zr-Al alloys). Izv. Akad. Nauk. SSSR. Met. 1968, 1968, 183–187. [Google Scholar]
- Thermo-Calc Software AB, Next Generation TiAl Alloys Advanced by New European Consortium. Available online: https://thermocalc.com/blog/next-generation-tial-alloys-advanced-by-new-european-consortium/ (accessed on 28 March 2019).
- Massalski, T.B. Binary Alloy Phase Diagrams, 2nd ed.; ASM International: Metals Park, OH, USA, 1990. [Google Scholar]
- Schuster, J. Al-Zr binary phase diagram evaluation. In MSI Eureka; Effenberg, G., Ed.; Materials Science International Services GmbH (MSI): Stuttgart, Germany, 2004. [Google Scholar]
- Blackburn, M.J. The ordering transformation in titanium: Aluminum alloys containing up to 25 at. pct Al. Trans. Metall. Soc. AIME 1967, 239, 1200–1208. [Google Scholar]
- Braun, J.; Ellner, M.; Predel, B. Experimental investigation of the structure and stability of the phase TiAl. Z. Metallkd. 1995, 86, 870–876. [Google Scholar]
- Kasahara, K.; Hashimoto, K.; Doi, H.; Tsujimoto, T. Crystal structure and hardness of TiAl phase containing zirconium. Nippon. Kinzoku Gakkaishi J. Jpn. Inst. Met. 1987, 51, 278–284. [Google Scholar]
- Distl, B.; Dehm, G.; Stein, F. Effect of oxygen on high-temperature phase equilibria in ternary Ti-Al-Nb Alloys. Z. Anorg. Allg. Chem. 2020, 646, 1151–1156. [Google Scholar]
- T’sai, L.S.; Hogness, T.R. The diffusion of gases through fused quartz. J. Phys. Chem. 2002, 36, 2595–2600. [Google Scholar] [CrossRef]
- Kainuma, R.; Palm, M.; Inden, G. Solid-phase equilibria in the Ti-rich part of the Ti-Al system. Intermetallics 1994, 2, 321–332. [Google Scholar] [CrossRef]
- Powder Diffraction File PDF-2, Release 2004; International Center for Diffraction Data: Newtown Square, PA, USA, 2004.
- Giannuzzi, L.A.; Stevie, F.A. Introduction to Focused Ion Beams Instrumentation, Theory, Techniques and Practice; Springer: New York, NY, USA, 2005. [Google Scholar]
- Mayer, J.; Giannuzzi, L.A.; Kamino, T.; Michael, J. TEM sample preparation and FIB-induced damage. MRS Bull. 2007, 32, 400–407. [Google Scholar] [CrossRef]
- Schell, N.; King, A.; Beckmann, F.; Fischer, T.; Müller, M.; Schreyer, A. The high energy materials science beamline (HEMS) at PETRA III. In Materials Science Forum; Trans Tech Publications Ltd.: Bäch, Switzerland, 2014; pp. 57–61. [Google Scholar]
- Schell, N. Synchrotron-Based Capabilities for Studying Engineering Materials at PETRA-III. Synchrotron Radiat. News 2017, 30, 29–34. [Google Scholar] [CrossRef]
- Hammersley, A. FIT2D: A multi-purpose data reduction, analysis and visualization program. J. Appl. Crystallogr. 2016, 49, 646–652. [Google Scholar] [CrossRef]
- Malfliet, A.; Kozlov, A.; Lebrun, N. Ti-Zr binary phase diagram evaluation. In MSI Eureka; Effenberg, G., Ed.; Materials Science International services GmbH (MSI): Stuttgart, Germany, 2015; pp. 1–12. [Google Scholar]
- Palm, M. Al-Ti binary phase diagram evaluation. In MSI Eureka; Effenberg, G., Ed.; Materials Science International services GmbH (MSI): Stuttgart, Germany, 2020. [Google Scholar]
- Schuster, J.C.; Palm, M. Reassessment of the binary Aluminium-Titanium phase diagram. J. Phase Equilibria Diffus. 2006, 27, 255–277. [Google Scholar] [CrossRef]
- Kim, S.-J.; Kematick, R.; Yi, S.; Franzen, H. On the stabilization of Zr5Al3 in the Mn5Si3-type structure by interstitial oxygen. J. Less Common Met. 1988, 137, 55–59. [Google Scholar] [CrossRef]
- Kwon, Y.U.; Rzeznik, M.A.; Guloy, A.; Corbett, J.D. Impurity stabilization of phases with the manganese silicide (Mn5Si3)-type structure: Questions regarding lanthanum-tin (La5Sn3) and zirconium silicide (Zr5Si3). Chem. Mater. 1990, 2, 546–550. [Google Scholar] [CrossRef]
- Stein, F.; Sauthoff, G.; Palm, M. Phases and phase equilibria in the Fe-Al-Zr system. Z. Metallkd. 2004, 96, 469–485. [Google Scholar] [CrossRef]
- Tanda, D.; Tanabe, T.; Tamura, R.; Takeuchi, S. Synthesis of ternary L10 compounds of Ti–Al–Zr system and their mechanical properties. Mat. Sci. Eng. A 2004, 387–389, 991–995. [Google Scholar] [CrossRef]
- Banerjee, S.; Mukhopadhyay, P. Phase Transformations: Examples from Titanium and Zirconium Alloys; Elsevier: Oxford, UK, 2010. [Google Scholar]
- Mayer, S.; Petersmann, M.; Fischer, F.D.; Clemens, H.; Waitz, T.; Antretter, T. Experimental and theoretical evidence of displacive martensite in an intermetallic Mo-containing γ-TiAl based alloy. Acta Mater. 2016, 115, 242–249. [Google Scholar] [CrossRef]
- Nartova, T.T.; Shirokova, N.I. Phase equilibria and heat resistance of Ti-Zr-Al alloys. Izv. Akad. Nauk. SSSR. Met. 1970, 1970, 194–198. [Google Scholar]
- Shirokova, N.I.; Nartova, T.T. Investigation of the phase equilibrium and properties of alloys of the titanium corner of the system Ti-Zr-Al. In Titanovyye Splavy dlya Novoy Tekhniki; Sazhin, N.P., Ed.; Nauka: Moscow, 1968; pp. 101–106. [Google Scholar]
- Kornilov, I.I.; Boriskina, N.G. Study of the phase structure of the alloys of the system Ti-Al-Zr along the Ti3Al-Zr section. In Metallovedeniye Titana; Kornilov, I.I., Ed.; Nauka: Moscow, 1964; pp. 58–66. [Google Scholar]
- Pylaeva, Y.N.; Volkova, M.A. Study of the alloys of the ternary system Ti-Al-Zr. In Metallovedeniye Titana; Kornilov, I.I., Ed.; Nauka: Moscow, 1964; pp. 38–42. [Google Scholar]
- Kornilov, I.I.; Nartova, T.T.; Savel’yeva, M.M. Phase equilibrium of alloys of the section Ti3Al-Zr of the ternary system Ti-Al-Zr. In Metallovedeniye Titana; Kornilov, I.I., Ed.; Nauka: Moscow, Russia, 1964; pp. 53–57. [Google Scholar]
- Sandlin, D.R.; Klung, H.A. A Phase Study of a Selected Portion of the Ti-Al-Zr Ternary System including Lattice Parameter Determination for the Ti-Al Gamma Phase; School of Engineering, Air Force Institute of Technology, Air University, Wright-Patterson Airforce Base: Fairborn, OH, USA, 1961. [Google Scholar]
- Troup, D.H. An Investigation of the Gamma Phase of the Binary Titanium-Aluminum Alloy with Zirconium Additions; School of Engineering, Air Force Institute of Technology, Air University, Wright-Patterson Airforce Base: Fairborn, OH, USA, 1962; pp. 1–89. [Google Scholar]
- Jiang, X.; Zhou, Y.; Feng, Z.; Xia, C.; Tan, C.; Liang, S.; Zhang, X.; Ma, M.; Liu, R. Influence of Zr content on β-phase stability in α-type Ti–Al alloys. Mater. Sci. Eng. A 2015, 639, 407–411. [Google Scholar] [CrossRef]
- Fan, F.; Gu, Y.; Xu, G.; Chang, H.; Cui, Y. Diffusion Research in BCC Ti-Al-Zr Ternary Alloys. J. Phase Equilibria Diffus. 2019, 40, 686–696. [Google Scholar] [CrossRef]
- Spragins, S.; Myers, J.; Saxer, R. Influence of Zirconium Additions on the Epsilon Phase of the Titanium-Aluminium System. Nature 1965, 207, 183–184. [Google Scholar] [CrossRef]
- Abreu, D.; Silva, A.; Santos, J.; Barros, D.; Barros, C.; Chaia, N.; Nunes, C.; Coelho, G. Liquidus projection of the Al–Ti–Zr system. J. Alloys Compd. 2020, 849, 156463. [Google Scholar] [CrossRef]
- Davies, F.C. The Effects of Ternary Additions on Lattice Parameters in the Gamma Phase of Titanium-Aluminum Alloy System. PhD Thesis, School of Engineering, Air Force Institute of Technology, Air University, Wright-Patterson Airforce Base, Fairborn, OH, USA, 1959. cited in (1962 Tro). [Google Scholar]
- Hashimoto, K.; Doi, H.; Kasahara, K.; Tsujimoto, T.; Suzuki, T. Effects of third elements on the structures of TiAl-based alloys. Nippon. Kinzoku Gakkaishi J. Jpn. Inst. Met. 1988, 52, 816–825. [Google Scholar] [CrossRef]
- Kawabata, T.; Fukai, H.; Izumi, O. Effect of ternary additions on mechanical properties of TiAl. Acta Mater. 1998, 46, 2185–2194. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kahrobaee, Z.; Rashkova, B.; Hauschildt, K.; Palm, M. Experimental Investigation of Phase Equilibria in the Ti—Al—Zr System at 1000–1300 °C. Crystals 2022, 12, 1184. https://doi.org/10.3390/cryst12091184
Kahrobaee Z, Rashkova B, Hauschildt K, Palm M. Experimental Investigation of Phase Equilibria in the Ti—Al—Zr System at 1000–1300 °C. Crystals. 2022; 12(9):1184. https://doi.org/10.3390/cryst12091184
Chicago/Turabian StyleKahrobaee, Zahra, Boryana Rashkova, Katja Hauschildt, and Martin Palm. 2022. "Experimental Investigation of Phase Equilibria in the Ti—Al—Zr System at 1000–1300 °C" Crystals 12, no. 9: 1184. https://doi.org/10.3390/cryst12091184
APA StyleKahrobaee, Z., Rashkova, B., Hauschildt, K., & Palm, M. (2022). Experimental Investigation of Phase Equilibria in the Ti—Al—Zr System at 1000–1300 °C. Crystals, 12(9), 1184. https://doi.org/10.3390/cryst12091184





