Next Article in Journal
Polytypes of sp2-Bonded Boron Nitride
Previous Article in Journal
3D Porous MXene Films for Advanced Electromagnetic Interference Shielding and Capacitive Storage
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 12
Issue 6
10.3390/cryst12060781
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of Braid Angle and Material Modulus on the Negative Poisson’s Ratio of Braided Auxetic Yarns

by
Arif A. Shah
1,2,*,
Muhammad Shahid
1,
John G. Hardy
2,3,
Naveed A. Siddiqui
4,
Andrew R. Kennedy
5,
Iftikhar H. Gul
1,
Shafi Ur Rehman
1 and
Yasir Nawab
6
1
School of Chemicals and Materials Engineering, National University of Sciences & Technology, Islamabad 44000, Pakistan
2
Department of Chemistry, Lancaster University, Lancaster LA1 4YB, UK
3
Materials Science Institute, Lancaster University, Lancaster LA1 4YB, UK
4
Centre for Excellence in Science and Technology (CESAT), Islamabad 44000, Pakistan
5
Engineering Department, Lancaster University, Lancaster LA1 4YW, UK
6
School of Engineering and Technology, National Textile University, Faisalabad 37610, Pakistan
*
Author to whom correspondence should be addressed.
Crystals 2022, 12(6), 781; https://doi.org/10.3390/cryst12060781
Submission received: 26 April 2022 / Revised: 24 May 2022 / Accepted: 25 May 2022 / Published: 27 May 2022
(This article belongs to the Section Organic Crystalline Materials)
Browse Figures
Versions Notes

Abstract

:
Fibers and textiles are ubiquitous in our daily lives, with mechanical properties that match the design specifications for the task for which they are intended; the development of yarns with a negative Poisson’s ratio (NPR) is a hot topic of current research, owing to their potential for use in high-performance textiles (e.g., military, sports, etc.). This study described a simple approach to constructing braided, helically interlaced yarns. When a torque is applied, the yarns prevent the wrapped component from dislodging from the core. The geometry and auxetic behavior of the braided helical structure was analyzed for two different combinations of core materials with similar wrap materials and different braiding angles. Two elastomeric materials (polyurethane (PU) and polyester) served as monofilament cores, while two stiffer multifilament wrap yarns (ultrahigh molecular weight polyethylene (UHMWPE) and polyethylene terephthalate (PET)) served as wrap yarns. In addition, the behavior of yarns braided at seven different angles was investigated to determine the materials’ response to the applied braided configuration’s NPR. The NPR was influenced by the core and wrap materials used and the braiding angle. The NPR value was greater for a core comprising more excellent elasticity (e.g., PU versus polyester); a smaller wrap angle and a slower braiding speed also led to a higher NPR value. The maximum NPR value of −1.70 was obtained using a PU core wrapped at a 9° angle and a strain value of 0.5.

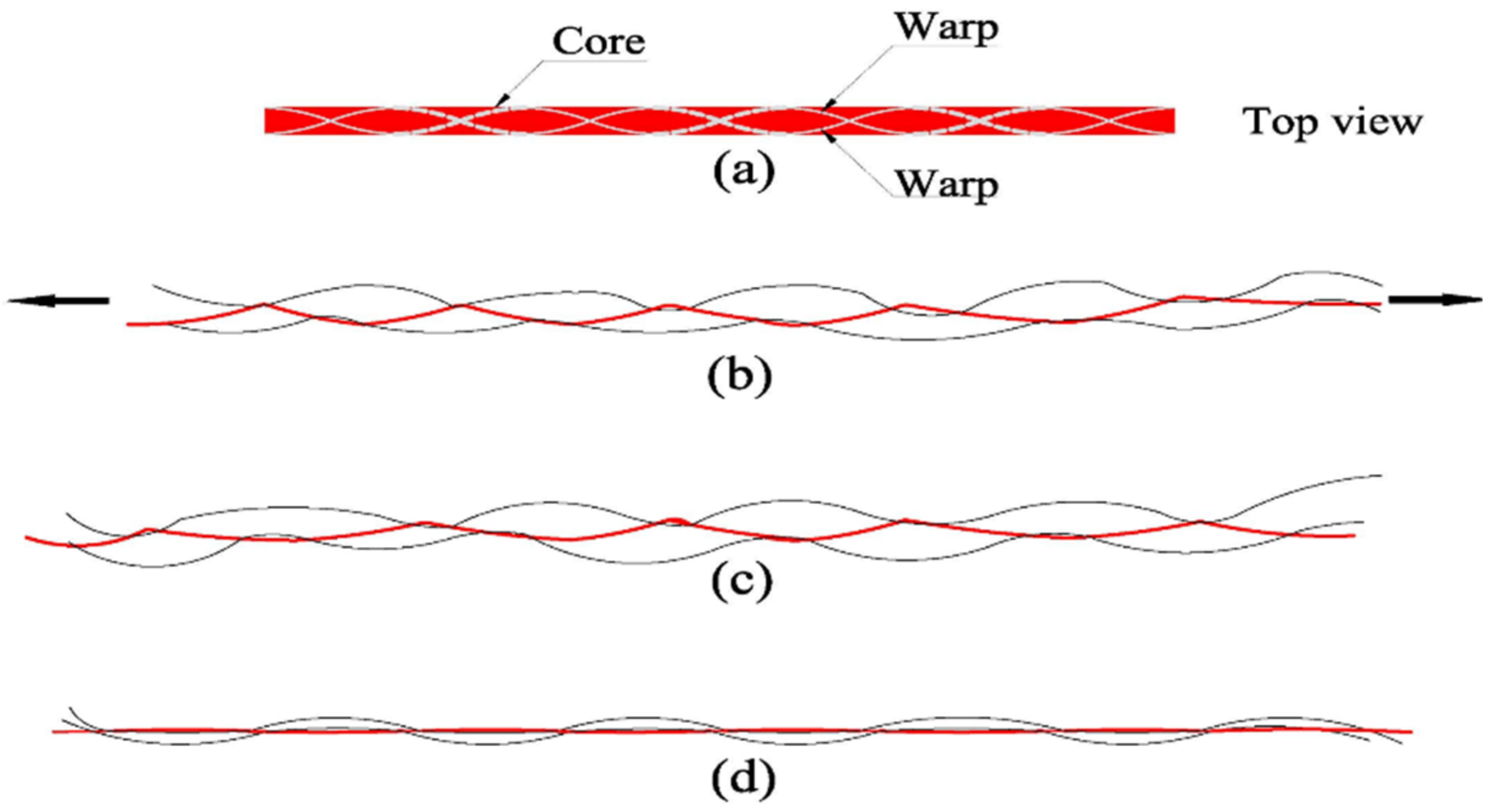
1. Introduction

Materials that exhibit a negative Poisson’s ratio (NPR) under tensile load are known as auxetic [1]. In contrast to most conventional materials, auxetic materials become thicker upon stretching and narrower when compressed, as shown in Figure 1. They expand laterally when subjected to tensile loads and compress under compression loads. These can be described in simple words as the materials, when stretched in one direction, expand in the direction transverse to the loading direction. It follows that if the load is reversed from stretching to compression, the materials contract in transverse direction [2]. The first auxetic material (although the concept of auxeticity was not known at that time) was investigated from the thermodynamically stable model for elastic properties of a two-dimensional isotropic system of hard cyclic hexamers with a negative Poisson’s ratio (NPR) studied by Monte Carlo (MC) simulations and then solved rigorously at zero temperature [3,4]. These models, along with the work by Lakes et al., marked an important milestone in the development of auxetic materials [5]. The MC methods were attractive since they did not require any microscopic definition of pressure or tension (stress) and in the experiments, the size and shape of the selected material (box) varied under constant thermodynamic pressure and/or tension conditions. These auxetic materials are the subject of intense research interest with their mechanical properties like impact resistance, Young’s modulus and shear modulus, energy absorption, indentation resistance, fracture toughness, sound absorption, vibration damping, hardness (increased compared to conventional materials), and the sync-elastic behavior (dome shape formation) of sheets and panels [6,7,8,9,10,11,12,13,14,15,16].
Auxetic materials have numerous applications in different fields of daily life. An interesting example is the expanding Hoberman sphere used for shelters and buildings; sports shoes with an auxetic shoe upper improve the comfort level and fit according to the complex size and shape of the foot at rest and during sporting activity. The aerospace and transport sector employs auxetic materials for vibration damping, shape morphologies (curved components, e.g., nose cone), blast curtains, and impact protection components. Cleanable filters are auxetic materials, and auxetic materials have also found applications in healthcare and biomedicine as arterial prostheses, artificial spinal disc implants, dilators and stents, drug-delivery systems, ultrasonic imagers, hip implant devices, and scaffolds for tissue engineering [17].
There are materials with an NPR of natural and synthetic origins, including but not limited to single crystals, e.g., NAT type Zeolite [18,19], and cubic metals [20]. An NPR effect was observed in ferromagnetic films (Fe, Ni, Co, and permalloy) [21,22], metal, and polymeric foams [5,23]. Currently, over 450 crystalline materials with an NPR are known in which more than 300 crystals have cubic anisotropy [24,25]. Cow teats [26] for which at strains below 0.1, the Poisson’s ratio of skin measured biaxially is very much greater than 1.0, and cat skin [27], various types of honeycomb structures including re-entrant structure, double arrowhead, the star-shaped structure, and the sinusoidal ligament’s structure etc. [6,28,29,30,31], foam with different materials and shapes such as tubular foams [32,33], and various types of 2D, 3D composites [34,35,36,37,38,39,40,41] are considered as natural auxetic materials. Synthetic materials including polymeric materials that exhibit auxeticity were first reported by Caddock and Evans in 1989 [42]. They also modified the PTFE microstructure by expansion during the sintering process and subsequently used this process for polypropylene (NPR of −0.22 at 1.6% strain) [43], nylon, and UHMWPE (indentation resistance enhanced by 2.5 times at low loads, NPR value of −0.32 at low strain) [44]. Auxetic fibers of PP, PE, and nylon provide opportunities for enhanced reinforcement of composite materials [45], and such auxetic fibers were used to produce woven textile fabrics for commercial applications in sports, medicine, and defense. Woven textile structures can exhibit auxetic behavior through the fabric thickness due to a geometric effect, and such behavior has been studied by modeling [46]; a Poisson’s ratio of −0.6 was measured across the fabric width by tailoring the knitted textiles from Nomex and polyester fibers [47]; in all cases, auxetic behavior was attributed to the geometric effects.
Recently, extensive numerical analysis and modeling has been performed by many researchers in the field of auxetic materials [48,49,50,51,52]. Hoover et al. simulated the dynamic analyses of auxetic behavior of mesoscopic model structures by using DYNA 3D and PARADYN numerical analysis. Kasal et al. used the latest 3D printing technology for experimental and numerical analysis of dowel pins for furniture joints. The NPR effect of cylinders was investigated with the geometrical orientation correlation between rigid components by Pikhitsa et al. The latest research on auxetic materials focuses on the addition of nanomaterials to study their effect on an NPR. The Monte Carlo simulation study of the elastic properties of the f.c.c. hard sphere crystals with periodic array of nano inclusion filled by hard spheres of another diameter caused incredibly significant change in the elastic properties. This hybrid inclusion enhanced the auxeticity [53]. Grima et al. worked on the wine-rack like carbon allotropes with tetrasubstituted phenyls and cyclobutadiene centers and studied their compressibility properties. It was shown that some of these systems exhibit negative linear compressibility while others show near zero compressibility [54]. The elastic properties, structural stability, and deformation behavior of graphene-based diamondlike phases were studied by Lisovenko et al. using the molecular dynamic simulations method. Their results revealed that considering the molecular dynamic approach from the stability point of view, two out of eight graphene-based diamondlike phases were found to be stable. In a nonelastic regime, stable diamondlike phases can be stretched to 0.012 and compressed to 0.1 [55]. Study of elliptical inclusion to rotating rigid square revealed that the centers of ellipses form a square lattice of the unit lattice constant. The influence of geometry and material characteristics on the effective mechanical properties found an NPR of −1 for anisotropic inclusion of low Young’s modulus. The observed changes in both the Poisson’s ratio and the Young’s modulus were complex functions of composite parameters [56].
Sloan et al. [57] studied the auxetic effect at the yarn stage. They observed that helical auxetic yarns (HAY) could be fabricated by simply winding or twisting different conventional filaments with spinning machines in direct contrast to the auxetic fibers produced by more complicated processing. The double helix yarn (DHY) was the first reported HAY in auxetic textiles and was produced by winding a stiff yarn around a softcore yarn. Wright et al. [58] carried out a finite element analysis and an experimental study to investigate the influence of structural and material parameters on the auxetic performance of the DHY. Iftikhar et al. performed the numerical analysis of the binding yarn float length for a 3D auxetic structure [59]. Sibal et al. [60] also proposed a DHY system to predict the auxetic behavior through an energy minimization approach, and Bhattacharya et al. [61] investigated core-indentation effects on the auxetic behavior of the DHY.
Knitted and woven fabrics and composites have been produced from HAY and DHY [62]. There are two approaches to fabricating auxetic textiles from the yarns: In the first approach, conventional yarns are knitted or weaved in a special geometrical arrangement, e.g., plain, twill, satin, and matt design, to get the auxetic effects. Hu et al. studied the behaviour of single and double stretched auxetic woven fabric made from nonauxetic yarn based on foldable geometry [63]. In the second approach, the auxetic yarns manufactured by various simple processes are used directly to fabricate woven or knitted textiles from these yarns. Many researchers reported that the auxetic yarn in the weft direction can control the structural performance of the fabric. Nazir et al. conducted experiments for multifilament PP and aramid fiber Kevlar for different geometrical structures such as plain, 2/2 matt, 2/2 twill, and 3/1 twill. The 2/2 matt and plain-woven fabric showed higher NPR effect and structural stability as compared to the twill design [64]. Recently, investigation about the experimental analysis of auxetic woven fabrics with a basket weave structure and a derivative weave structure was reported [65]. Analyzing the elastic recovery of the fabric, weave structures, and wrap density of the auxetic yarn revealed that the derivative structure arranging the yarns in a series of zigzags can reach the maximum negative Poisson’s ratio of −0.585. Gao et al. used a super elastic PU core with high modulus nylon 6.6 to develop HAY with an NPR value of −5.6. The material modulus and elasticity exhibited a high NPR effect. Subsequently, warp wise and weft wise fabrics were also manufactured from this auxetic yarn [66]. These auxetic fabrics with variable permeability under tensile loading could be further explored for applications such as filters, drug-delivery systems, smart bandages, and blast-proof curtains to catch the debris coming up from bomb explosions. Miller et al. [35] developed the first auxetic woven fabric from dual helix yarns which was subsequently used as reinforcement for composite by coating with silicone rubber matrix. The in-plane Poisson’s ratio of the fabric changed from positive 0.06 to negative −0.1 by using DHY with a maximum NPR value of −2.1.
Introducing auxetic effects at the yarn stage is interesting because relatively simple techniques fabricate the auxetic yarns. Various geometric structures of auxetic yarns have been investigated. Thus far, HAY, semi auxetic yarn (SAY), auxetic plied yarn (APY), DHY, and interlaced helical yarn (IHY) structures have been reported. Yarn wrappers (a rotating spinner consisting of three spools for feed yarn, a rotating circular disc wrapper and winder setup and a braiding machine) are commonly employed to produce yarns with various wrap angles and structures. To overcome problems like slippage of the wrap yarn from the core during fabrication, which would result in poor yarn structures of the two-component helical auxetic yarns, a 3-component auxetic system was introduced by Zhang et al. [67]: they coated a sheath over the HAY; however, the auxetic effect decreased with larger coating thickness.
Sloan et al. [57] suggested using polyurethane as the core fiber and polyamide as the wrap fiber to produce DHY. Their results showed that the auxetic behavior was strongly affected by the starting wrap angle of the yarns, both in terms of the magnitude and the strain range. Liu et al. [68] fabricated a novel interlaced helical yarn (IHY); the two-component yarn with a helical wrapping structure exhibited auxetic behavior with a unique performance, having a relatively higher stability structure due to the interlacing of three yarns during braiding. The results of the auxetic effects of IHY with HAY using a similar combination of materials as wrap and core and similar initial wrap angle were also compared, which exhibited structural stability and profound auxetic effects for IHY over HAY.
Here, we reported the results of a comparative study of braided auxetic yarns fabricated from two stiffer yarns with two different compliant cores on a braiding machine. The auxetic effect was investigated using various processing parameters during fabrication (angle/speed of the bobbins/machinery, core/wrap materials etc.) and characterized by imaging and mechanical testing.

2. Experimental Section

Two compliant core materials were used: monofilament polyurethane and polyester cords with low stiffness and multifilament UHMWPE and PET yarns with sufficient stiffness. The properties of the core and wrap materials (as provided by the manufacturers) are listed in Table 1. Two stiff wrap yarns were helically wrapped around a compliant core yarn to fabricate the various braided yarns. The linear density of the auxetic yarn samples with a PU core was 0.51 g/m, while samples with a polyester core had a linear density of 0.18 g/m.
A braiding machine (Figure 2) was used to fabricate and achieve a stable regular yarn structure. Two spindles moving in opposite directions were used to fabricate braided helical yarns. The assembly consisted of a control feed rate mechanism with a fixed base at the bottom for the core yarn, rotating spindles for the wrap bobbins driven by reversible motors, and a fixed take-up bobbin at the top to collect the wound yarn. The braid angle was adjusted by controlling the feed of the yarn components, either by varying the main motor rpm from 70 rpm to 154 rpm at an interval of 15 rpm or by changing the yarn take-up speed (which was kept constant at 1 rpm in our experiment). The number of twists in the entire length of the braided geometry of the yarn could be controlled by the braiding machine, and the twist level could be modified by keeping the rotation speed constant while decreasing the yarn drawing speed or vice versa.
Software ImageJ was used to measure the braid angles at different points, taken from microscope images shown in Figure 3. Yarns with seven different braiding angles (ca. 9°, 11°, 13°, 17°, 19°, 21°, and 23°) were prepared and named according to these angles as shown in Table 2.
Tensile testing of these yarns was performed using a universal testing machine (UTM -Zwick Roell Z100, Ulm, Germany) with a 5 kN load cell, and an extensometer was attached to measure the displacements accurately. Precise diameters of core and wrap fibers were obtained using an SEM (JSM 7800 F, JEOL, Tokyo, Japan) operating at 5 kV accelerating voltage. Measurements were made for 3 random samples of each monofilament fiber taken from the spool as supplied by the manufacturer at a higher magnification that was sputter-coated with gold, at a thickness of 10 nm, using a Q150 RS coater (Quorum Technologies, Lewes, UK). The SEM micrographs are shown in Figure 4.
The gauge length for all the samples was fixed at 100 mm. The software Test Expert-3 was used for measuring the applied load and linear separation of the clamps. The specimens were mounted vertically and tested, using a pretension of 0.5 N. One end of the yarn was secured in the upper clamp, while the other end secured in lower clamps was pretensioned before closing to remove all the slack without appreciable stretching. The braided samples were stretched until the breaking of the wrap, as it failed preferentially. A crosshead speed of 10 mm/min was set, allowing greater accuracy in the yarns’ image acquisition.
Auxeticity was determined using a high magnification (750 MP) DSLR camera (Cannon, Tokyo, Japan) and extensometer to record longitudinal strains accurately. The camera was fixed at a working distance of 250 mm from the sample to take images for better control over the field of view at a fixed resolution. The field of view was selected at the start of testing and remained fixed throughout the tensile test. Images were taken at 4-s intervals with constant regular strain intervals throughout the test. Yarns were visually inspected before testing to ensure consistency of braid angle and conformance of the wrap with the core along the entire sample gauge length.
Images were captured at a strain interval of 0.03 to 0.04 for longitudinal and lateral strains measurements. These images were analyzed in ImageJ, an open-source image analysis tool. ImageJ can calculate area and pixel value statistics for user-defined selections and intensity-thresholder objects. It can also measure distances and angles. The software processed these images to calculate the difference in length due to the elongation. Similarly, the change in diameter of the auxetic yarn (i.e., core and wrap) was also calculated, which varied due to the interchange in positions between the core and wrapped yarn. The images were used to measure the outer contour diameter of the yarns, DI in the initial pre-strain and DL in the longitudinal strain of εL. Then the radial/lateral strain εR was calculated from Equation (1) [57], and the Poisson’s ratio for the yarns was calculated using engineering strains εR and ɛL according to Equation (2).
εR = (DL/DI − 1) × 100%
ʋ = −εR/εL

3. Results and Discussion

The load vs. extension plots for the individual fiber/yarn are shown in Figure 5. UHMWPE and PET had significantly greater modulus and ultimate tensile strengths than PU and polyester. On the other hand, PU and polyester appeared to have greater longitudinal displacements than UHMWPE and PET. UHMWPE requires a significantly higher breaking load of 80 N than a polyester cord, PET, or PU elastomer. On the other hand, the PU elastomer is significantly more elastic than the other stiffer yarns, exhibiting greater than 100% extension under a load of approximately 30 N. As a result of combining these properties, the braided yarns exhibit the auxetic effect. Figure 6a,b illustrates the standard deviations for all three sets of experiments regarding force and applied strain for the individual components.
Initially, the carousel setup was used to wind the wrap yarns around the core helically; however, after manufacturing auxetic yarns with low structural stability due to wrap slippage from the core, we switched to a braiding machine with 48 spindles (Figure 2).

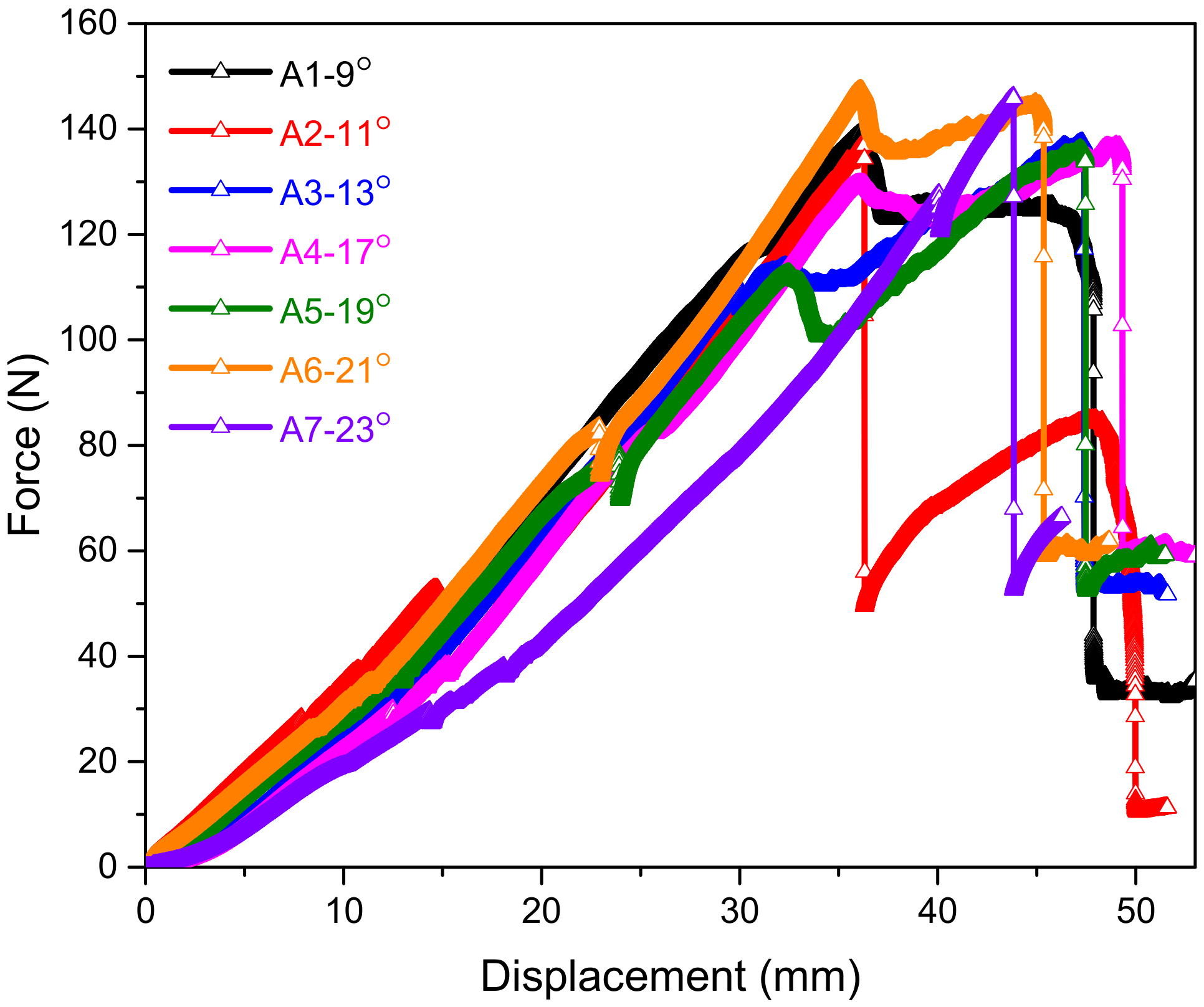
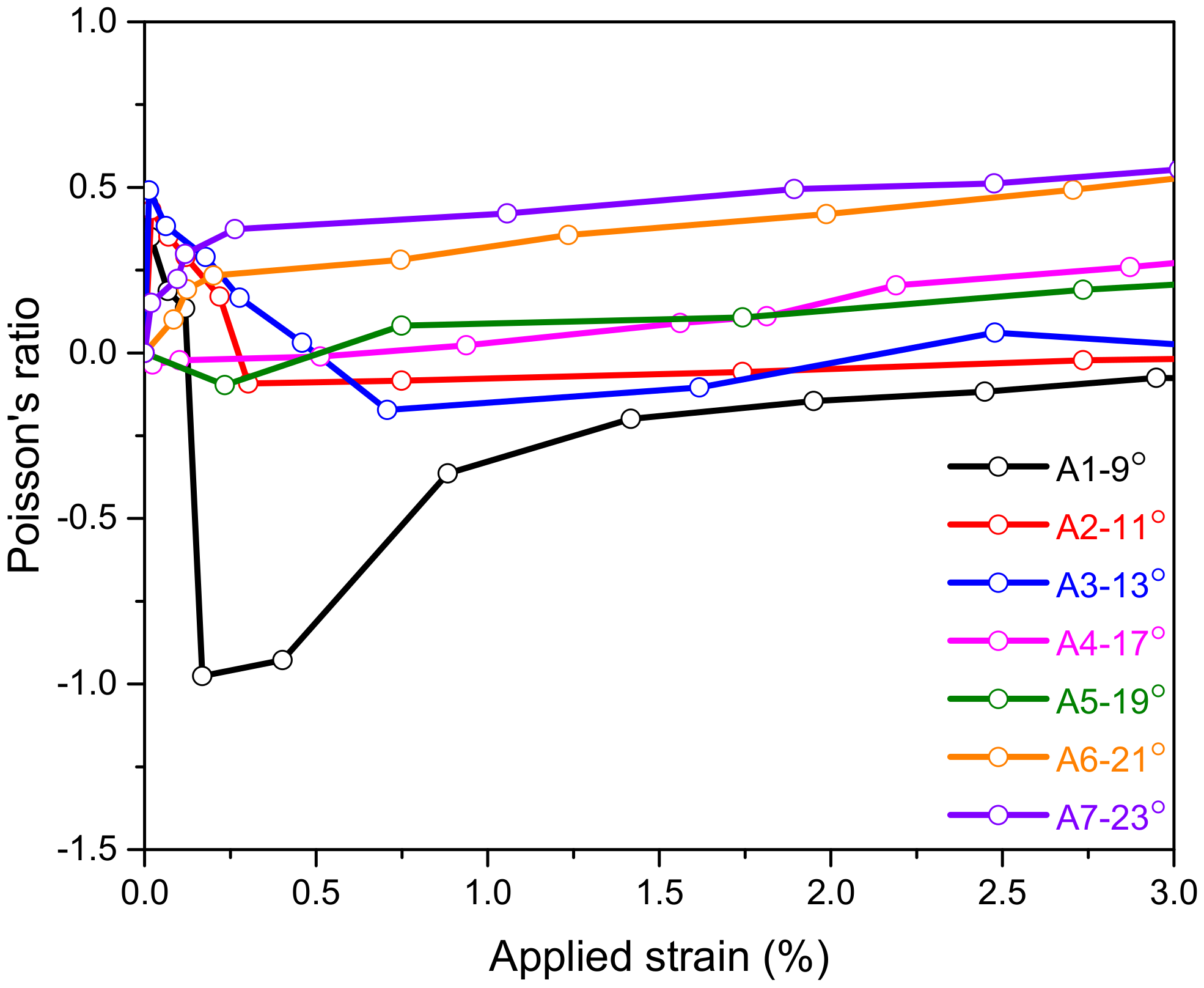
3.1. Braided Yarn with Polyester Core

Moreover, Figure 7 depicts the load vs. extension curves for all seven braided samples made from polyester core with two wraps (designated as A-1 to A-7 in Table 2). When the load was applied, the wrap yarns straightened from their helical configuration, while the core yarn converted to a helical configuration due to its lower stiffness. The braided yarn’s 150 N breaking load was three times that of the polyester cord core alone, which was 50 N. Between 125 N and 150 N (depending on the braid angles of 9° to 23°), the wrap yarns became straightened, which resulted in the wrap filaments being ruptured. A smaller number of turns on the lower angle braided yarn provided less resistance and allowed greater extension under applied load. The braided yarn exhibited auxetic effects in line with the model suggested by Liu et al. [68].
It is well-known from the literature that most common materials have positive Poisson’s ratio values. While the Poisson’s ratios of the individual cores and wraps used in this study were positive, they became negative when braided. Additionally, a large wrap to core angle resulted in more turns per unit area of the core yarn (interlacement using a braider). As the twist count of wrap yarns increased, it tended to cause increased deformation of the core yarn, making it more difficult to interchange with the wraps, resulting in only the core yarn contributing to the auxetic yarn’s strength, resulting in a lower NPR value. In contrast, fewer turns increased the probability of the braided yarn changing shape, resulting in larger auxetic effects. Thus, the braided auxetic yarn (BAY) properties were determined mainly by the component materials and their geometrical structure, such as the angle selection. Reduced braid angles resulted in increased auxetic behavior. Larger auxetic behavior resulted from lower braid angles. The effect of applied strain on the Poisson’s ratio (ʋ) determined for samples A-1 to A-7 with angles 9° to 23°, respectively, for the braided auxetic yarn with polyester cord as core and UHMWPE and PET as wrap materials, is shown in Figure 8.
Initially, at low strains, the A-1 yarn sample at 9° showed positive ʋ to a specific limit, which dropped linearly with increasing strain. The yarn with initial lower angle reached the minimum positive Poisson’s ratio and the maximum NPR. At strain below 0.05, a rapid increase in ʋ for the structure was observed following a sharp decrease. This was the onset of the auxetic behaviour; however, the yarn showed auxetic effects at a very small strain rate. Besides, the Poisson’s ratio of the complex yarns with the minimum initial braided angle changed from positive to negative firstly, due to the interactive compression between the yarn components, which can achieve balance quickly with lower axial strain when the core is interlaced helical wrapped by the two stiff yarns symmetrically with a smaller initial angle. The auxetic effect continued further with applied strain and a maximum NPR value of −0.98 was observed at strain rate of 0.17. The auxetic effect decreased with further increasing the strain until failure of either of the wrap component. Thus, the contour dimension of the complex yarn rapidly increased to its maximal value. Therefore, the lower initial wrap angle played a positive role in achieving the complex yarns with better auxetic effect. This behaviour of the BAY was characteristic of the geometry. Increasing the angle to 11° as in sample A-2, a similar low strain behaviour with rapid increase and subsequent decrease in ʋ to a value of −0.09 was exhibited. The change in the angle affected the auxetic behaviour of the yarn. Further increasing the yarn angle to 13° for sample A-3, the initial positive increase in ʋ followed by a gradual decrease to NPR value of −0.17 with increasing strain was observed. The maximum auxetic effect was exhibited by sample A-1 at a lower angle and lower strain values. The NPR values with variable strain values are shown in Table 3. An increasing trend with increasing the angle is observed, i.e., for higher angles, even at low strain value, the NPR values reduce and gradually attain a positive value or nonauxetic effect.
The variation in the NPR values was due to the yarn structure with the increasing number of turns of the wrap yarns, which limited the core yarn to change its shape in line with the model suggested by Liu et al. [68]. It is evident from Figure 8 that a higher wrap to core angle causes a larger number of twists of wrap yarn per unit length of the core among the tested values of angle. This, in turn, resulted in greater lengths of wrap yarns with the same length of core yarn. During the application of strain, greater elongation in the core was also obtained, resulting in an increased wrap to core angle. This higher elongation caused increased change in the length. The higher axial changes compared to transversal change led to lowering the NPR values with increased wrap to core angles and vice versa.

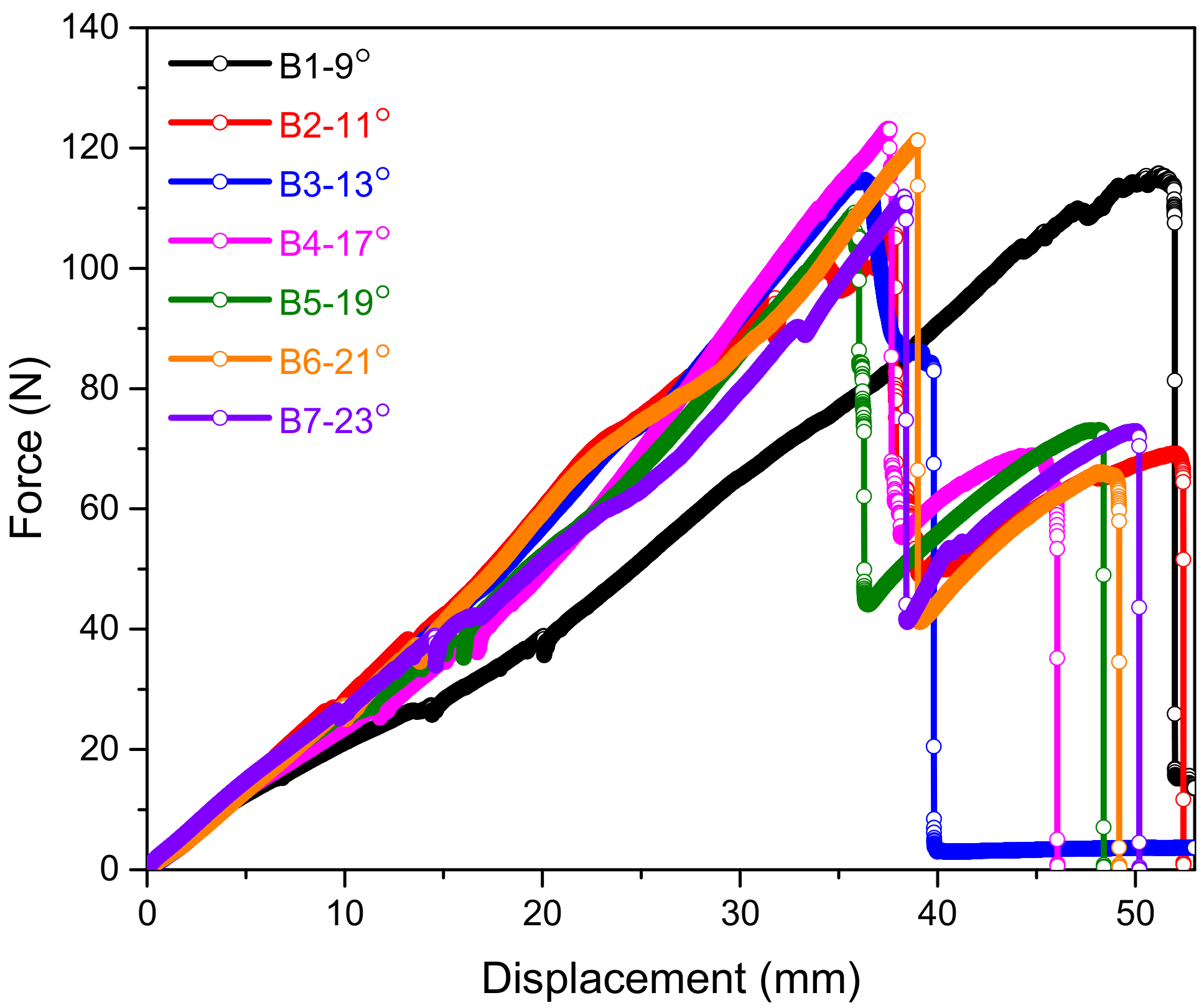
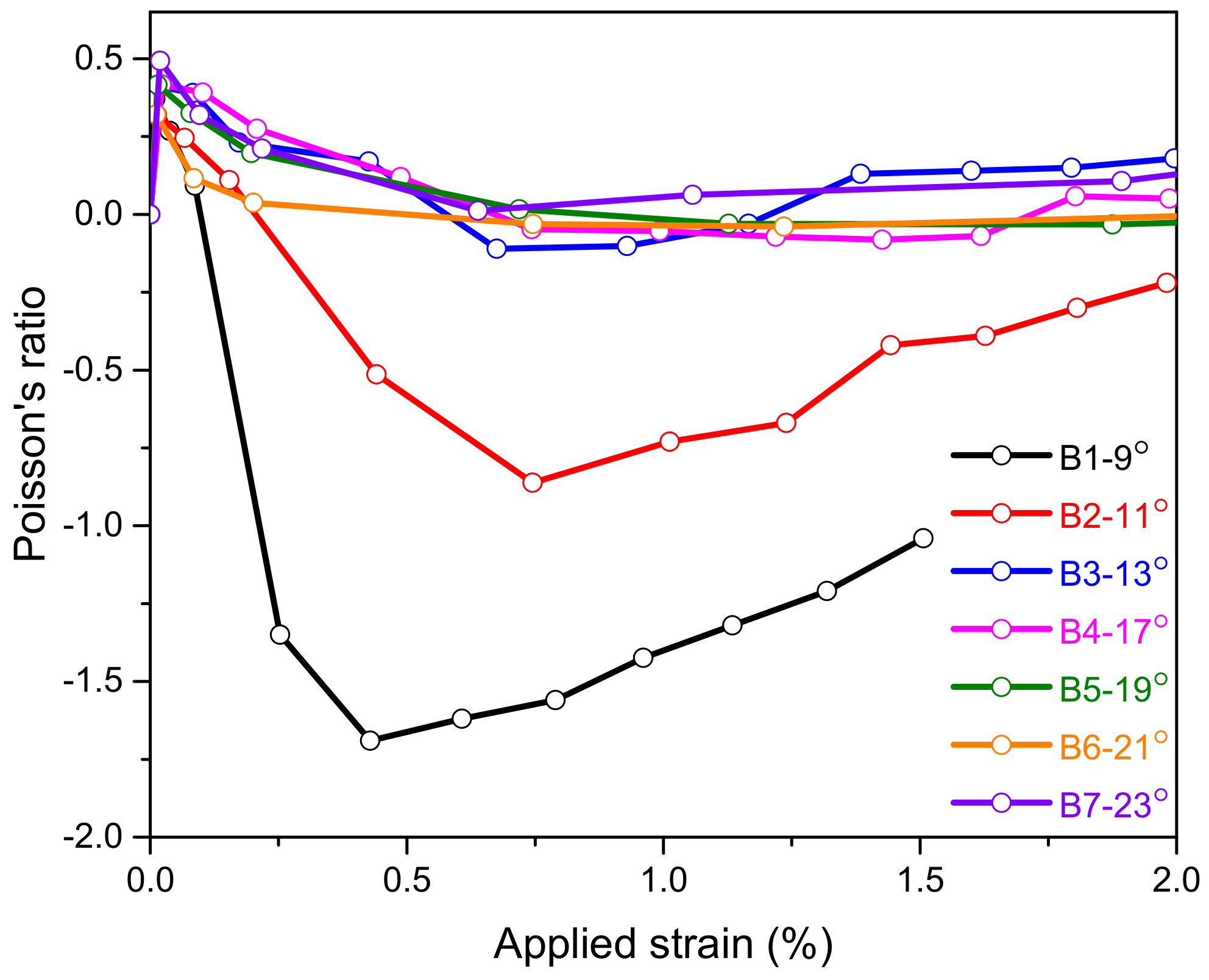
3.2. Braided Yarn with PU Core

In the free state, Figure 9 shows a stable structure of the braided yarn with two stiffer yarns interlaced symmetrically around the PU core yarn. The varying motor speeds correspond to the varying braid angles, for example, 70 rpm equals 9°, 85 rpm equals 11°, etc. The number of yarn twists could be observed at various motor speeds and angles. The greater the angle, the more twists there are and vice versa.
Figure 10 illustrates the relationship between applied load and extension for samples B-1 to B-7 containing PU elastomer as the core and similar wraps to those found in the category ‘A’ yarns. The breaking loads of various samples braided at various angles ranged between 60 and 125 N; the breaking loads were observed to be 500% greater than the breaking load of the PU core alone. Increased breaking loads were caused by material properties and the observed shape change from helical to linear, which resulted in the core straightening during load application due to the wraps’ increased stiffness. Figure 11 demonstrates the mechanism of shape change (a–d). The wrap yarns are initially interlaced around the core’s outer surface. When axially stretched under tensile load, the stiffer yarns symmetrically distributed around the core produce the pulling force and wrap increasingly tightly around the core to achieve force and moment equilibrium. At this point, the cross-section of the core has contracted, and the diameter has decreased. Then, as the axial strain increased, the difference in elastic modulus between the yarn components caused the stiff yarns to transition from helical wrap to straight, whereas the core transitioned from a straight to a bending position, exhibiting a sinusoidal curve. As a result, the complex yarn’s contour dimension increases rapidly to its maximum value, resulting in auxeticity. Further stretching reduces the diameter while the compliant core straightens to the point of wrap yarn breakage. This finding corroborates well with Liu et al.’s work [68]. Wrap yarns were straightened and then ruptured at a force between 60 and 125 N. Increased wrap to core angle corresponds to increased turns per unit area of core yarn. With increasing wrap yarn turns, it becomes more difficult for the core yarn to share the load with the wraps, and thus only the core yarn contributed to the composite yarn’s strength. In contrast, fewer twists increased the likelihood of exhibiting auxetic effects via shape-change behavior.
Poisson’s ratio vs. strain behavior for samples B-1 to B-7 is shown in Figure 12. The selected braid angles ranged between 9° and 23°. The experiment was performed for all seven samples. Maximum auxetic effect was exhibited at lower angle and lower strain value. At higher angles, an increasing number of turns of the wrap yarns limited the core yarn to change its shape, thereby reducing the probability of auxetic effect.
The Poisson’s ratio at different strain values for all seven PU elastic core samples with two wraps are tabulated in Table 4. It is evident that the Poisson’s ratio value varies with the applied strain.
The investigation of 14 braided yarn samples with seven braided angles revealed significant NPR values at low applied strains that gradually decreased as applied strains increased. Additionally, it was discovered that the initial lower braid angle was critical for attaining the maximum NPR values, implying that the braid angle directly affected the NPR. This was most likely caused by interactive compression between the yarn components, which achieved positional interchange at lower strains when the core was wrapped in two stiffer yarns braided helically with a smaller initial braid angle. Thus, the braided yarn’s contour dimension rapidly increased to its maximum value, resulting in the maximum NPR. According to a few researchers, for example [57], the modulus ratio between the core and the wrap is one of the primary factors contributing to the increased NPR value. Due to the stiffer yarn with a higher tensile modulus, UHMWPE had the highest NPR value. The contrast between the core and wrap materials also aided in developing auxetic behavior. When the stiff yarn’s modulus was greater at low strain, it shifted from the braided helical state to wrapping the core to straighten, resulting in a greater deformation, and its radial strain rapidly increased to its maximal value, thus contributing towards an improved NPR effect. All the samples investigated in this study failed due to the rupture of wrap yarns.

4. Conclusions

In this study, a selection of braided yarns was examined to determine the effects of braid angle and material properties on Poisson’s ratio. The braided yarns with a lower initial braid angle and stiff wrap yarns with a higher tensile modulus had better auxetic properties at lower strains. The three samples A-1, A-2, and A-3 with polyester cord as the core showed lower NPR values of −0.98, −0.09, and −0.17, respectively, at lower strain values. At higher angles, the auxetic effect decreased to zero. Samples with a PU core showed a higher auxetic effect with greater NPR values of −1.70, −0.86, and −0.11. Both the yarns showed auxetic behavior. In contrast, the stronger auxetic effect was observed in the greater elasticity yarn braided with wraps of greater modulus. The braided yarn had a breaking strength of 150 N, which was three times greater than the core polyester cord’s load of 50 N. We believe auxetic fibers and their composites have significant potential for use in high-value-added applications supporting advances in technical and medical technologies [69,70,71,72,73,74,75,76,77] that can support the United Nations Sustainable Development Goals (UN SDGs), particularly UN SDG (decent work and economic growth), (industry, innovation, and infrastructure), and (reduced inequalities).

Author Contributions

Conceptualization, Y.N. and J.G.H.; Methodology, Y.N.; Software, I.H.G.; Validation, N.A.S.; Formal Analysis, A.R.K.; Investigation and original draft writing, A.A.S.; Resources, Y.N.; Review and editing, M.S. and J.G.H.; Supervision, M.S. and N.A.S.; Funding Acquisition, M.S.; Visualization, S.U.R. and A.R.K. All authors have read and agreed to the published version of the manuscript.

Funding

We thank the Higher Education Commission of Pakistan for an International Research Support Initiative Program (IRSIP) scholarship to support A.A.S.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest. The sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

References

  1. Evans, K.E.; Nkansah, M.A.; Hutchinson, J.I.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124–125. [Google Scholar] [CrossRef]
  2. Lim, T.C. Auxetic Materials and Structures. Engineering Materials; Springer: Singapore, 2015. [Google Scholar]
  3. Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
  4. Wojciechowski, K.W. Two-dimensional isotropic system with a negative Poisson’s ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
  5. Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
  6. Robert, F.A. An isotropic three-dimensional structure with Poisson’s ratio = −1. J. Elast. 1985, 15, 427–430. [Google Scholar]
  7. Alderson, K.; Evans, K. The fabrication of microporous polyethylene having a negative Poisson’s ratio. Polymer 1992, 33, 4435–4438. [Google Scholar] [CrossRef]
  8. Alderson, K.; Pickles, A.; Neale, P.; Evans, K. Auxetic polyethylene: The effect of a negative Poisson’s ratio on hardness. Acta Metall. Mater. 1994, 42, 2261–2266. [Google Scholar] [CrossRef]
  9. Evans, K.; Nkansah, K.; Hutchinson, J.I. Auxetic foams: Modelling negative Poisson’s ratios. Acta Metall. Mater. 1994, 42, 1289–1294. [Google Scholar] [CrossRef]
  10. Evans, K.; Alderson, A. Auxetic materials: Functional materials and structures from lateral thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
  11. Scarpa, F.; Adhikari, S.; Wang, C. Nanocomposites with auxetic nanotubes. Int. J. Smart Nano Mater. 2010, 1, 83–94. [Google Scholar] [CrossRef] [Green Version]
  12. Gorodtsov, V.A.; Lisovenko, D.S. Auxetics among materials with cubic anisotropy. Mech. Solids 2020, 55, 461–474. [Google Scholar] [CrossRef]
  13. Lim, T.C. Mechanics of Metamaterials with Negative Parameters; Springer: Singapore, 2020. [Google Scholar]
  14. Luo, C.; Han, C.Z.; Zhang, X.Y.; Zhang, X.G.; Ren, X.; Xie, Y.M. Design, manufacturing and applications of auxetic tubular structures: A review. Thin-Walled Struct. 2021, 163, 107682. [Google Scholar] [CrossRef]
  15. Jopek, H. Finite element analysis of tunable composite tubes reinforced with auxetic structures. Materials 2017, 10, 1359. [Google Scholar] [CrossRef] [Green Version]
  16. Kelkar, P.U.; Kim, H.S.; Cho, K.H.; Kwak, J.Y.; Kang, C.Y.; Song, H.C. Cellular auxetic structures for mechanical metamaterials: A review. Sensors 2020, 20, 3132. [Google Scholar] [CrossRef]
  17. Alderson, A. A triumph of lateral thought. Chem. Ind. 1999, 17, 384–391. [Google Scholar]
  18. Williams, J.J.; Smith, C.W.; Evans, K.; Lethbridge, Z.A.D.; Walton, R.L. An analytical model for producing negative Poisson’s ratios and its application in explaining off-axis elastic properties of the NAT-type zeolites. Acta Mater. 2007, 55, 5697–5707. [Google Scholar] [CrossRef]
  19. Grima, J.N.; Cassar, R.N.; Gatt, R.J. On the effect of hydrostatic pressure on the auxetic character of NAT-type silicates. Non-Cryst. Solids 2009, 355, 1307–1312. [Google Scholar] [CrossRef]
  20. Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafstrom, S. Negative Poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
  21. Epishin, A.; Fedelich, B.; Finn, M.; Künecke, G.; Rehmer, B.; Nolze, G.; Leistner, C.; Petrushin, N.; Svetlov, L. Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C. Crystals 2021, 11, 152. [Google Scholar] [CrossRef]
  22. Milstein, F.; Huang, K. Existence of a negative Poisson ratio in fcc crystals. Phys. Rev. B. 1979, 19, 2030–2033. [Google Scholar] [CrossRef]
  23. Friis, E.A.; Lakes, R.S.; Park, J.B. Negative Poisson’s ratio polymeric and metallic foams. Mater. Sci. 1988, 12, 4406–4414. [Google Scholar] [CrossRef]
  24. Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Negative Poisson’s ratio for cubic crystals and nano/microtubes. Phys. Mesomech. 2014, 17, 97–115. [Google Scholar] [CrossRef]
  25. Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Auxetic mechanics of crystalline materials. Mech. Solids 2010, 45, 529–545. [Google Scholar] [CrossRef]
  26. Lees, C.; Vincent, J.E.V.; Hillerton, J.E. Poisson’s ratio in skin. Biomed. Mater. Eng. 1991, 1, 19–23. [Google Scholar] [CrossRef] [PubMed]
  27. Frohlich, L.M.; Labarbera, M.; Stevens, W.P.J. Poisson’s ratio of a crossed fibre sheath: The skin of aquatic salamanders. Zoology 1994, 232, 231–252. [Google Scholar] [CrossRef]
  28. Gaspar, N.; Ren, X.J.; Smith, C.W.; Grima, J.N.; Evans, K. Novel honeycombs with auxetic behaviour. Acta Mater. 2005, 53, 2439–2445. [Google Scholar] [CrossRef]
  29. Liu, Y.; Hu, H. A review on auxetic structures and polymeric materials. Sci. Res. Essays 2010, 5, 1052–1063. [Google Scholar]
  30. Attard, D.; Manicaro, E.; Gatt, R.; Grima, J.N. On the properties of auxetic rotating stretching squares. Phys. Status Sol. B 2009, 246, 2045–2054. [Google Scholar] [CrossRef]
  31. Lim, T.C.; Acharya, R.U. An hexagonal array of fourfold interconnected hexagonal nodules for modeling auxetic microporous polymers: A comparison of 2D and 3D models. J. Mater. Sci. 2009, 44, 4491–4494. [Google Scholar] [CrossRef]
  32. Chan, N.; Evans, K.J. Indentation resilience of conventional and auxetic foams. Cell. Plast. 1998, 34, 231–260. [Google Scholar] [CrossRef]
  33. Lim, T.C. Auxeticity of concentric auxetic-conventional foam rods with high modulus interface adhesive. Materials 2018, 11, 223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Evans, K.; Donoghue, J.P.; Alderson, K.L. The Design, Matching and Manufacture of Auxetic Carbon Fibre Laminates. J. Compos. Mater. 2004, 38, 95–106. [Google Scholar] [CrossRef]
  35. Miller, W.; Hook, P.B.; Smith, C.W.; Wang, X.; Evans, K. The manufacture and characterisation of a novel, low modulus, negative Poisson’s ratio composite. Compos. Sci. Technol. 2009, 69, 651–655. [Google Scholar] [CrossRef]
  36. Kocer, C.; McKenzie, D.R.; Bilek, M.M. Elastic properties of a material composed of alternating layers of negative and positive Poisson’s ratio. Mater. Sci. Eng. A 2009, 505, 111–115. [Google Scholar] [CrossRef]
  37. Bezazi, A.; Boukharouba, W.; Scarpa, F. Mechanical properties of auxetic carbon/epoxy composites: Static and cyclic fatigue behaviour. Phys. Status Sol. B 2009, 246, 2102–2110. [Google Scholar] [CrossRef]
  38. Cicala, G.; Recca, G.; Oliveri, L.; Grube, D.J.; Scarpa, F.; Perikleous, Y. Auxetic Hexachiral Truss Core Reinforced with Twisted Hemp Yarns: Out of Plane Shear Properties. In Proceedings of the 16th International Conference on Composite Structures (ICCS 16), Porto, Portugal, 28–30 June 2011. [Google Scholar]
  39. Alderson, A.; Alderson, K.L.; Ravirala, N. Design and Modelling of Mechanical and Thermal Responses of Novel Auxetic Honeycomb Cores for Structural Composites. In Proceedings of the 16th International Conference on Composite Structures (ICCS 16), Porto, Portugal, 28–30 June 2011. [Google Scholar]
  40. Gorodtsov, V.A.; Lisovenko, D.S. Out-of-Plane Tension of Thin Two-Layered Plates of Identically Oriented Hexagonal Crystals. Phys. Mesomech. 2021, 24, 146–154. [Google Scholar] [CrossRef]
  41. Volkov, M.A.; Demin, A.I.; Gorodtsov, V.A.; Lisovenko, D.S. Effective elastic properties variability for two-layered plates of hexagonal and cubic crystals under longitudinal tension. Compos. Struct. 2021, 274, 114300. [Google Scholar] [CrossRef]
  42. Caddock, B.; Evans, K.J. Microporous materials with negative Poisson’s ratios. I. Microstructure and mechanical properties. Phys. D Appl. Phys. 1989, 22, 1877. [Google Scholar] [CrossRef]
  43. Pickles, A.P.; Alderson, K.L.; Evans, K. The effects of powder morphology on the processing of auxetic polypropylene (PP of negative Poisson’s ratio). Polym. Eng. Sci. 1996, 36, 636–642. [Google Scholar] [CrossRef]
  44. Alderson, K.L.; Webber, R.S.; Evans, K. Novel variations in the microstructure of auxetic ultra-high molecular weight polyethylene. Part 2: Mechanical properties. Polym. Eng. Sci. 2000, 40, 1906–1914. [Google Scholar] [CrossRef]
  45. Ravirala, N.; Alderson, K.L.; Davies, P.J.; Simkins, V.R.; Alderson, A. Negative Poisson’s ratio polyester fibers. Text. Res. J. 2006, 76, 540–546. [Google Scholar] [CrossRef]
  46. Shanahan, M.E.R.; Piccirelli, N. Elastic behaviour of a stretched woven cloth. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1059–1064. [Google Scholar] [CrossRef]
  47. Ugbolue, S.C.; Kim, Y.K.; Warner, S.B.; Fan, Q.; Yang, C.L.; Kyzymchuk, O.; Feng, Y.J. The formation and performance of auxetic textiles. Part I: Theoretical and technical considerations. Text. Inst. 2010, 101, 660–667. [Google Scholar] [CrossRef]
  48. Hoover, W.G.; Hoover, C.G. Searching for auxetics with DYNA3D and ParaDyn. Phys. Stat. Sol. B 2005, 242, 585–594. [Google Scholar] [CrossRef] [Green Version]
  49. Pikhitsa, P.V. Architecture of cylinders with implications for materials with negative Poisson ratio. Phys. Status Sol. B 2007, 244, 1004–1007. [Google Scholar] [CrossRef]
  50. Shah, I.A.; Khan, R.; Koloor, S.S.R.; Petrů, M.; Badshah, S.; Ahmad, S.; Amjad, M. Finite Element Analysis of the Ballistic Impact on Auxetic Sandwich Composite Human Body Armor. Materials 2022, 15, 2064. [Google Scholar] [CrossRef]
  51. Liu, H.; Kollosche, M.; Yan, J.; Zellner, E.M.; Bentil, S.A.; Rivero, I.V.; Wiersema, C.; Laflamme, S. Numerical investigation of auxetic textured soft strain gauge for monitoring animal skin. Sensors 2020, 20, 4185. [Google Scholar] [CrossRef]
  52. Kasal, A.; Kuskun, T.; Smardzews, J. Experimental and numerical study on withdrawal strength of different types of auxetic dowels for furniture joints. Materials 2020, 13, 4252. [Google Scholar] [CrossRef]
  53. Narojczyk, J.W.; Wojciechowski, K.W.; Smardzewski, J.; Imre, A.R.; Grima, J.N.; Bilski, M. Cancellation of auxetic properties in fcc hard sphere crystals by hybrid layer-channel nanoinclusions filled by hard spheres of another diameter. Materials 2021, 14, 3008. [Google Scholar] [CrossRef]
  54. Degabriele, E.P.; Attard, D.; Grima-Cornish, J.N.; Caruana-Gauci, R.; Gatt, R.; Evans, K.E.; Grima, J.N. On the Compressibility Properties of the Wine-Rack-Like Carbon Allotropes and Related Poly (phenylacetylene) Systems. Phys. Status Sol. B 2019, 256, 1800572. [Google Scholar] [CrossRef] [Green Version]
  55. Rysaeva, L.K.; Lisovenko, D.S.; Gorodtsov, V.A.; Baimova, J.A. Stability, elastic properties and deformation behaviour of graphene-based diamond-like phases. Comput. Mater. Sci. 2020, 172, 109355. [Google Scholar] [CrossRef]
  56. Poźniak, A.A.; Wojciechowski, K.W.; Grima, J.N.; Mizzi, L. Planar auxeticity from elliptic inclusions. Compos. Part B 2016, 94, 379–388. [Google Scholar] [CrossRef]
  57. Wright, J.R.; Sloan, M.R.; Evans, K.J. Tensile properties of helical auxetic structures: A numerical study. Appl. Phys. 2010, 108, 044905. [Google Scholar] [CrossRef]
  58. Sloan, M.R.; Wright, J.R.; Evans, K. The helical auxetic yarn—A novel structure for composites and textiles; geometry, manufacture and mechanical properties. Mech. Mater. 2011, 43, 476–486. [Google Scholar] [CrossRef]
  59. Iftekhar, H.; Waseem Ullah Khan, R.M.; Nawab, Y.; Hamdani, S.T.A.; Panchal, S. Numerical Analysis of Binding Yarn Float Length for 3D Auxetic Structures. Phys. Status Sol. B 2020, 257, 2000440. [Google Scholar] [CrossRef]
  60. Sibal, A.R. Design strategy for auxetic dual helix yarn systems. Mater. Lett. 2015, 161, 740–742. [Google Scholar] [CrossRef]
  61. Bhattacharya, S.; Zhang, G.H.; Ghita, O.; Evans, K. The variation in Poisson’s ratio caused by interactions between core and wrap in helical composite auxetic yarns. Compos. Sci. Technol. 2014, 102, 87–93. [Google Scholar] [CrossRef] [Green Version]
  62. Liu, Y. Negative Poisson’s ratio weft-knitted fabrics. Text. Res. J. 2010, 80, 856–863. [Google Scholar]
  63. Zulifqar, A.; Hua, T.; Hu, H. Development of uni-stretch woven fabrics with zero and negative Poisson’s ratio. Text. Res. J. 2018, 88, 2076–2092. [Google Scholar] [CrossRef]
  64. Nazir, M.U.; Shaker, K.; Hussain, R.; Nawab, Y. Performance of novel auxetic woven fabrics produced using Helical Auxetic Yarn. Mater. Res. Express 2019, 6, 085703. [Google Scholar] [CrossRef]
  65. Chen, J.; Du, Z.; Li, T. Performance of novel auxetic woven fabrics produced using Helical Auxetic Yarn. Text. Res. J. 2020, 90, 809–823. [Google Scholar] [CrossRef]
  66. Gao, Y.; Liu, S.; Wu, M.; Chen, X.; Studd, R. Manufacture and Evaluation of Auxetic Yarns and Woven Fabrics. Phys. Status Sol. B 2020, 257, 1900112. [Google Scholar] [CrossRef]
  67. Zhang, O.G.H.; Ghita, O.; Evans, K. The fabrication and mechanical properties of a novel 3-component auxetic structure for composites. Compos. Sci. Technol. 2015, 117, 257–267. [Google Scholar] [CrossRef] [Green Version]
  68. Liu, S.; Du, Z.; Xie, K.; Liu, G.; Yang, S. A novel interlaced-helical wrapping yarn with negative Poisson’s ratio. Fibers Polym. 2018, 19, 2411–2417. [Google Scholar] [CrossRef]
  69. Liu, S.; Pan, X.; Zheng, D.; Du, Z.; Liu, G.; Yang, S. Study on the structure formation and heat treatment of helical auxetic complex yarn. Text. Res. J. 2019, 89, 1003–1012. [Google Scholar] [CrossRef]
  70. Gao, Y.; Chen, X.; Studd, R. Experimental and numerical study of helical auxetic yarns. Text. Res. J. 2021, 91, 11–12. [Google Scholar] [CrossRef]
  71. Ali, M.; Zeeshan, M.; Qadir, M.B.; Riaz, R.; Ahmad, S.; Nawad, Y.; Anjum, A.S. Development and mechanical characterization of weave design based 2D woven auxetic fabrics for protective textiles. Fibers Polym. 2018, 19, 2431–2438. [Google Scholar] [CrossRef]
  72. Liu, S.; Gao, Y.; Chen, X.; Du, Z. A theoretical study on the effect of structural parameter on tensile properties of helical auxetic yarns. Fibers Polym. 2019, 20, 1742–1748. [Google Scholar] [CrossRef]
  73. Kabir, S.; Kim, H.; Lee, S. Characterization of 3D printed auxetic sinusoidal patterns/nylon composite fabrics. Fibers Polym. 2020, 20, 1372–1381. [Google Scholar] [CrossRef]
  74. Gao, Y.; Ma, P.; Li, K.; Xu, J. Characterization of a 3D Auxetic Warp-knitted Spacer Fabric by Synchrotron Radiation X-ray Computed Tomography. Fibers Polym. 2020, 21, 930–933. [Google Scholar] [CrossRef]
  75. Xin, X.; Liu, L.; Liu, Y.; Leng, J. 4D printing auxetic metamaterials with tunable, programmable, and reconfigurable mechanical properties. Adv. Funct. Mater. 2020, 30, 2004226. [Google Scholar] [CrossRef]
  76. Ali, M.N.; Rehman, I.U. An Auxetic structure configured as oesophageal stent with potential to be used for palliative treatment of oesophageal cancer; development and in vitro mechanical analysis. J. Mater. Sci. Mater. Med. 2011, 22, 2573–2581. [Google Scholar] [CrossRef] [PubMed]
  77. Vinay, C.V.; Varma, D.S.M.; Chandan, M.R.; Sivabalan, P.; Jaiswal, A.K.; Swetha, S.; Sionkowska, A.; Kaczmarek, B. Study of castor oil-based auxetic polyurethane foams for cushioning applications. Polym. Int. 2020, 70, 1631–1639. [Google Scholar] [CrossRef]
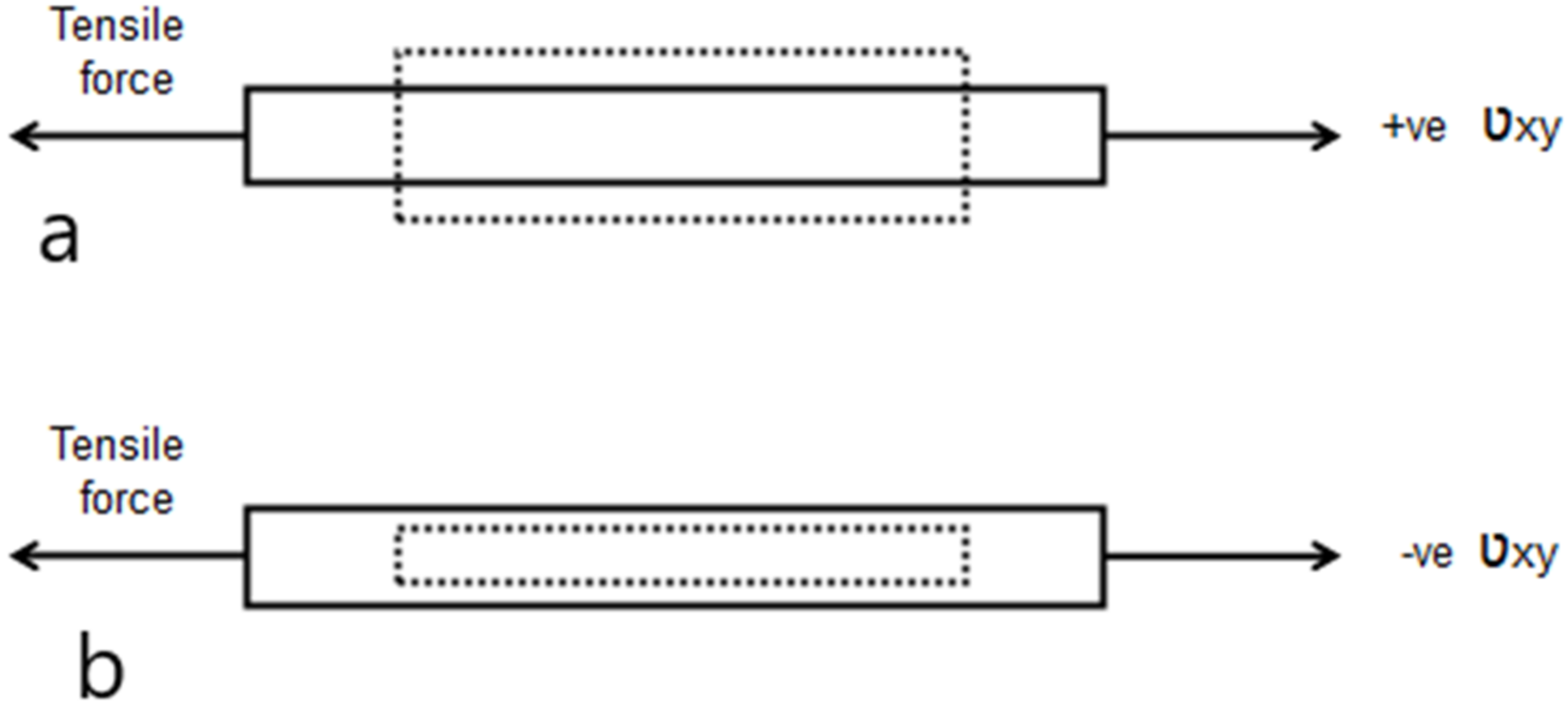
Crystals 12 00781 g001 550
Figure 1. The comparison of (a) conventional material and (b) auxetic material under the influence of tensile force.
Figure 1. The comparison of (a) conventional material and (b) auxetic material under the influence of tensile force.
Crystals 12 00781 g001
Crystals 12 00781 g002 550
Figure 2. Custom-designed braiding machine used for braided yarn fabrication.
Figure 2. Custom-designed braiding machine used for braided yarn fabrication.
Crystals 12 00781 g002
Crystals 12 00781 g003 550
Figure 3. Measured angles for twists for both the wraps with PU core.
Figure 3. Measured angles for twists for both the wraps with PU core.
Crystals 12 00781 g003
Crystals 12 00781 g004 550
Figure 4. SEM micrographs of as received yarns. (a) PU elastomer. (b) PET. (c) UHMWPE.
Figure 4. SEM micrographs of as received yarns. (a) PU elastomer. (b) PET. (c) UHMWPE.
Crystals 12 00781 g004
Crystals 12 00781 g005 550
Figure 5. Load-displacement curves for individual yarns.
Figure 5. Load-displacement curves for individual yarns.
Crystals 12 00781 g005
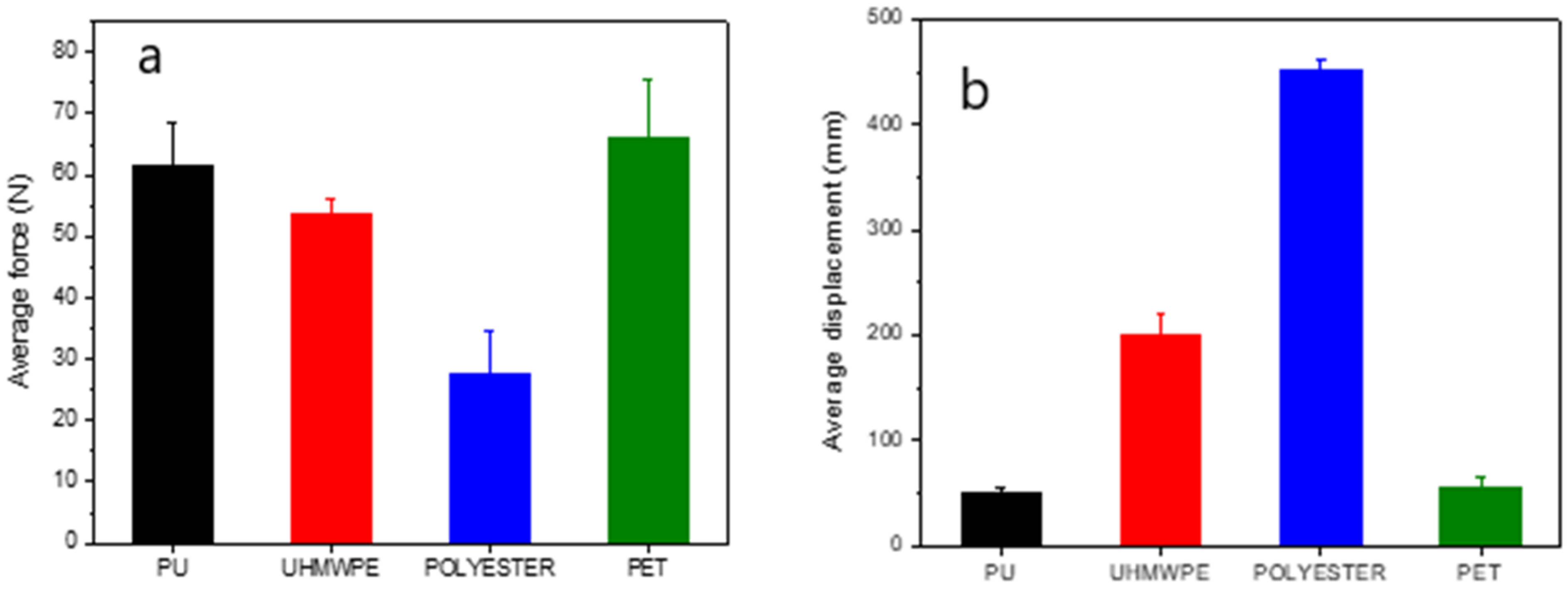
Crystals 12 00781 g006 550
Figure 6. Standard deviations regarding (a) force and (b) displacement.
Figure 6. Standard deviations regarding (a) force and (b) displacement.
Crystals 12 00781 g006
Crystals 12 00781 g007 550
Figure 7. Load-displacement curves for polyester core-based yarn A-1 to A-7.
Figure 7. Load-displacement curves for polyester core-based yarn A-1 to A-7.
Crystals 12 00781 g007
Crystals 12 00781 g008 550
Figure 8. Poisson’s ratio vs. applied strain for polyester core-based yarn samples A-1 to A-7.
Figure 8. Poisson’s ratio vs. applied strain for polyester core-based yarn samples A-1 to A-7.
Crystals 12 00781 g008
Crystals 12 00781 g009 550
Figure 9. Braided auxetic yarns with PU core in the unloaded free state developed at different speeds.
Figure 9. Braided auxetic yarns with PU core in the unloaded free state developed at different speeds.
Crystals 12 00781 g009
Crystals 12 00781 g010 550
Figure 10. Load-displacement curves for PU core-based yarn sample B-1 to B-7.
Figure 10. Load-displacement curves for PU core-based yarn sample B-1 to B-7.
Crystals 12 00781 g010
Crystals 12 00781 g011 550
Figure 11. (a–d) Deformation mechanism in auxetic yarn with PU elastomer.
Figure 11. (a–d) Deformation mechanism in auxetic yarn with PU elastomer.
Crystals 12 00781 g011
Crystals 12 00781 g012 550
Figure 12. Poisson’s ratio vs. extension for PU core-based yarn samples B-1 to B-7.
Figure 12. Poisson’s ratio vs. extension for PU core-based yarn samples B-1 to B-7.
Crystals 12 00781 g012
Table
Table 1. Properties (as provided by the manufacturer) for the individual yarn components.
Table 1. Properties (as provided by the manufacturer) for the individual yarn components.
Type of Fiber/YarnFiber/Yarn Diameter (µm)Linear DensityElongation at Break (%)Breaking Load (N)Young’s Modulus (MPa)
g/mdtex
PU Elastomer, TROFIL® Monofil Technik GmbH, Hennef, Germany6000.36356065050114 ± 2
PET, Morssinkhof® Sustainable Products, Emmen, Netherlands240.11112013.884.3420 ± 30
UHMWPE, Dyneema® SK-75, Almere, Netherlands130.044112.5614022,500
Polyester cord, Beads Park China, Guangzhou, China8000.0333608054.2630
Table
Table 2. The yarns sample identification.
Table 2. The yarns sample identification.
Sample IDCore MaterialPlanned Braid Angle (°)Measured Braid Angle (°)Sample IDCore MaterialPlanned Braid Angles (°)Measured Braid Angle (°)
A-1Polyester cord99 + 0.09 B-1PU elastomer99 + 0.17
A-21111 + 0.09B-21111 + 0.21
A-31313 + 0.17B-31313 + 0.13
A-41717 − 0.05B-41717 + 0.40
A-51919 + 0.25B-51919 + 0.23
A-62121 + 0.21B-62121 − 0.11
A-72323 + 0.32B-72323 + 0.19
Table
Table 3. The NPR for minimum strain values for polyester cord core braided yarns.
Table 3. The NPR for minimum strain values for polyester cord core braided yarns.
Sample IDMeasured Braid Angle (°)Strain ValuePoisson’s Ratio
A-19 + 0.09 0.17−0.98
A-211 + 0.090.31−0.09
A-313 + 0.170.71−0.17
A-417 + 0.210.512−0.01
A-519 + 0.120.234−0.09
A-621 + 0.410.08+0.10
A-723 + 0.140.019+0.15
Table
Table 4. The NPR for minimum strain values for PU elastomer cores braided yarns.
Table 4. The NPR for minimum strain values for PU elastomer cores braided yarns.
Sample IDMeasured Braid Angle (°)Strain ValuePoisson’s Ratio
B-19 + 0.170.427−1.70
B-211 + 0.210.75−0.86
B-313 + 0.130.71−0.11
B-417 + 0.091.426−0.081
B-519 + 0.271.875−0.032
B-621 + 0.351.235−0.039
B-723 + 0.140.639+0.012
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Shah, A.A.; Shahid, M.; Hardy, J.G.; Siddiqui, N.A.; Kennedy, A.R.; Gul, I.H.; Rehman, S.U.; Nawab, Y. Effects of Braid Angle and Material Modulus on the Negative Poisson’s Ratio of Braided Auxetic Yarns. Crystals 2022, 12, 781. https://doi.org/10.3390/cryst12060781

AMA Style

Shah AA, Shahid M, Hardy JG, Siddiqui NA, Kennedy AR, Gul IH, Rehman SU, Nawab Y. Effects of Braid Angle and Material Modulus on the Negative Poisson’s Ratio of Braided Auxetic Yarns. Crystals. 2022; 12(6):781. https://doi.org/10.3390/cryst12060781

Chicago/Turabian Style

Shah, Arif A., Muhammad Shahid, John G. Hardy, Naveed A. Siddiqui, Andrew R. Kennedy, Iftikhar H. Gul, Shafi Ur Rehman, and Yasir Nawab. 2022. "Effects of Braid Angle and Material Modulus on the Negative Poisson’s Ratio of Braided Auxetic Yarns" Crystals 12, no. 6: 781. https://doi.org/10.3390/cryst12060781

APA Style

Shah, A. A., Shahid, M., Hardy, J. G., Siddiqui, N. A., Kennedy, A. R., Gul, I. H., Rehman, S. U., & Nawab, Y. (2022). Effects of Braid Angle and Material Modulus on the Negative Poisson’s Ratio of Braided Auxetic Yarns. Crystals, 12(6), 781. https://doi.org/10.3390/cryst12060781

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop