NAi/Li Antisite Defects in the Li1.2Ni0.2Mn0.6O2 Li-Rich Layered Oxide: A DFT Study
Abstract
:1. Introduction
2. Methods
2.1. Computational Method
2.2. Thermodynamic Model
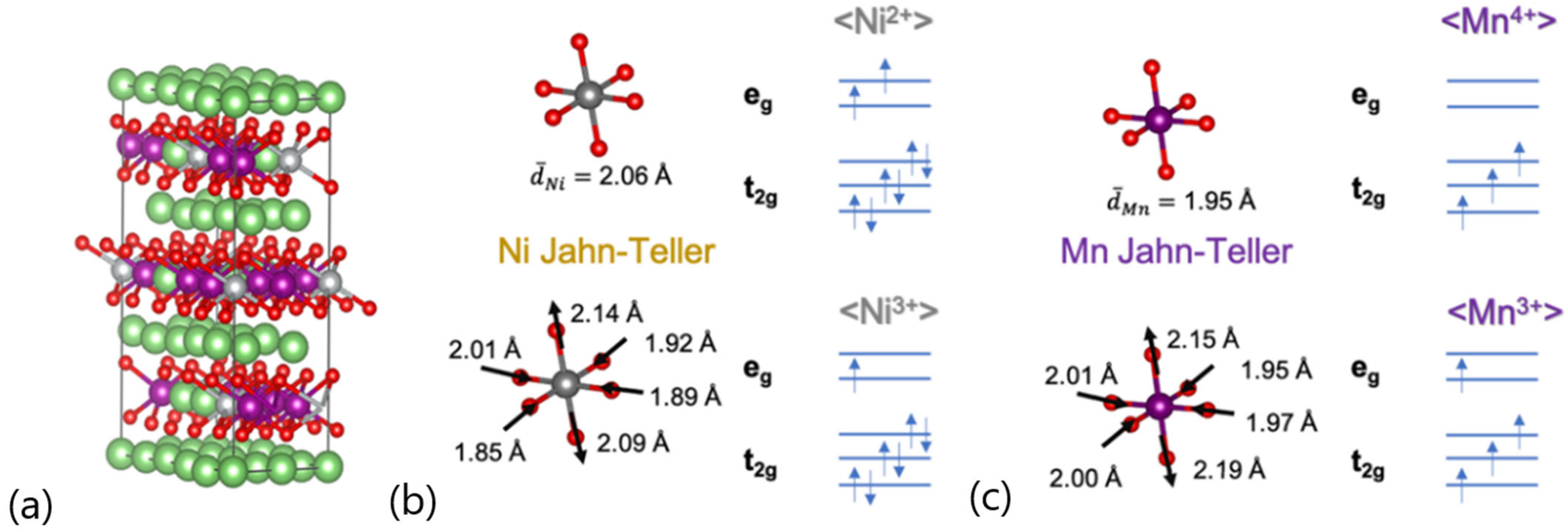
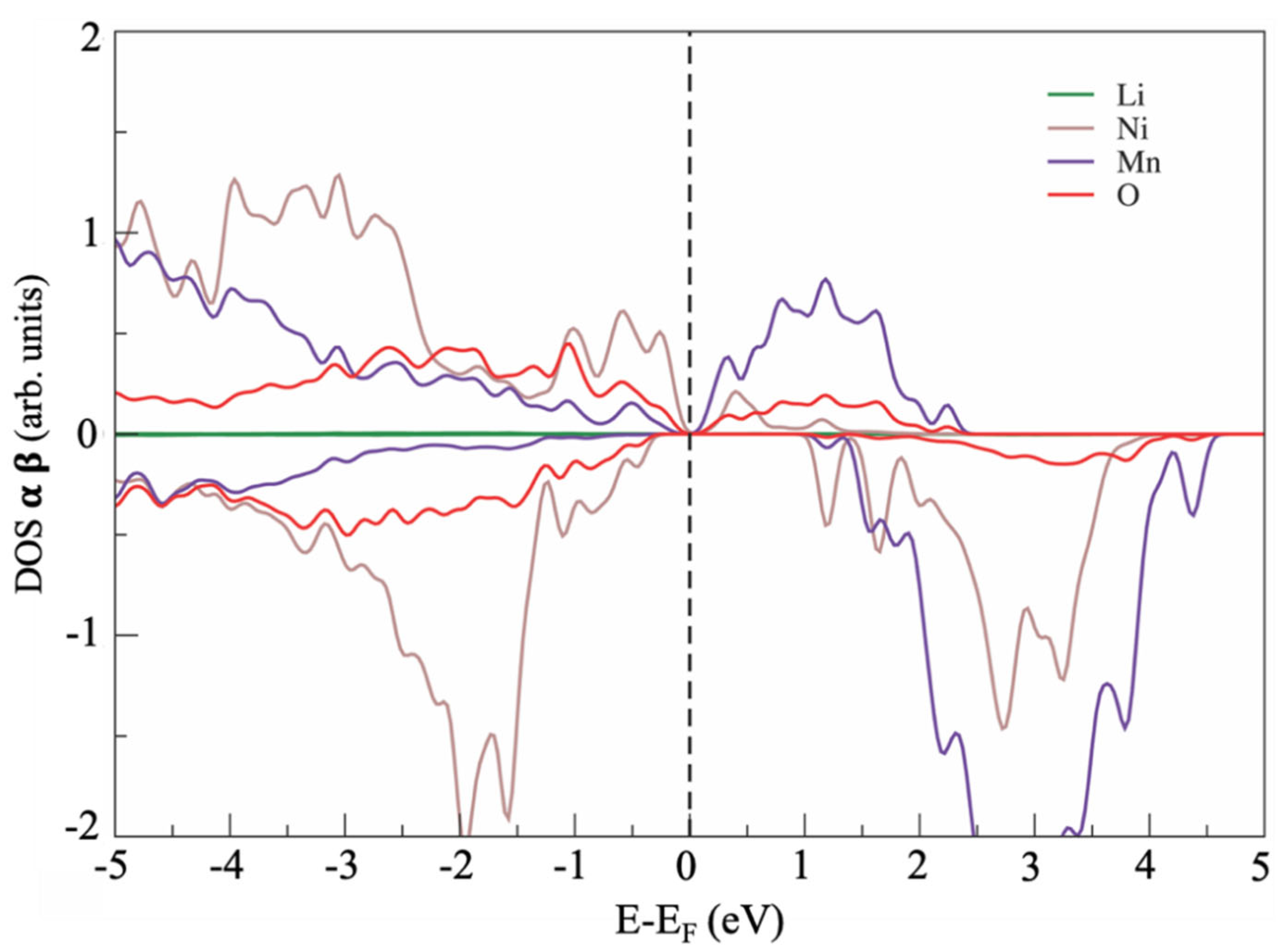
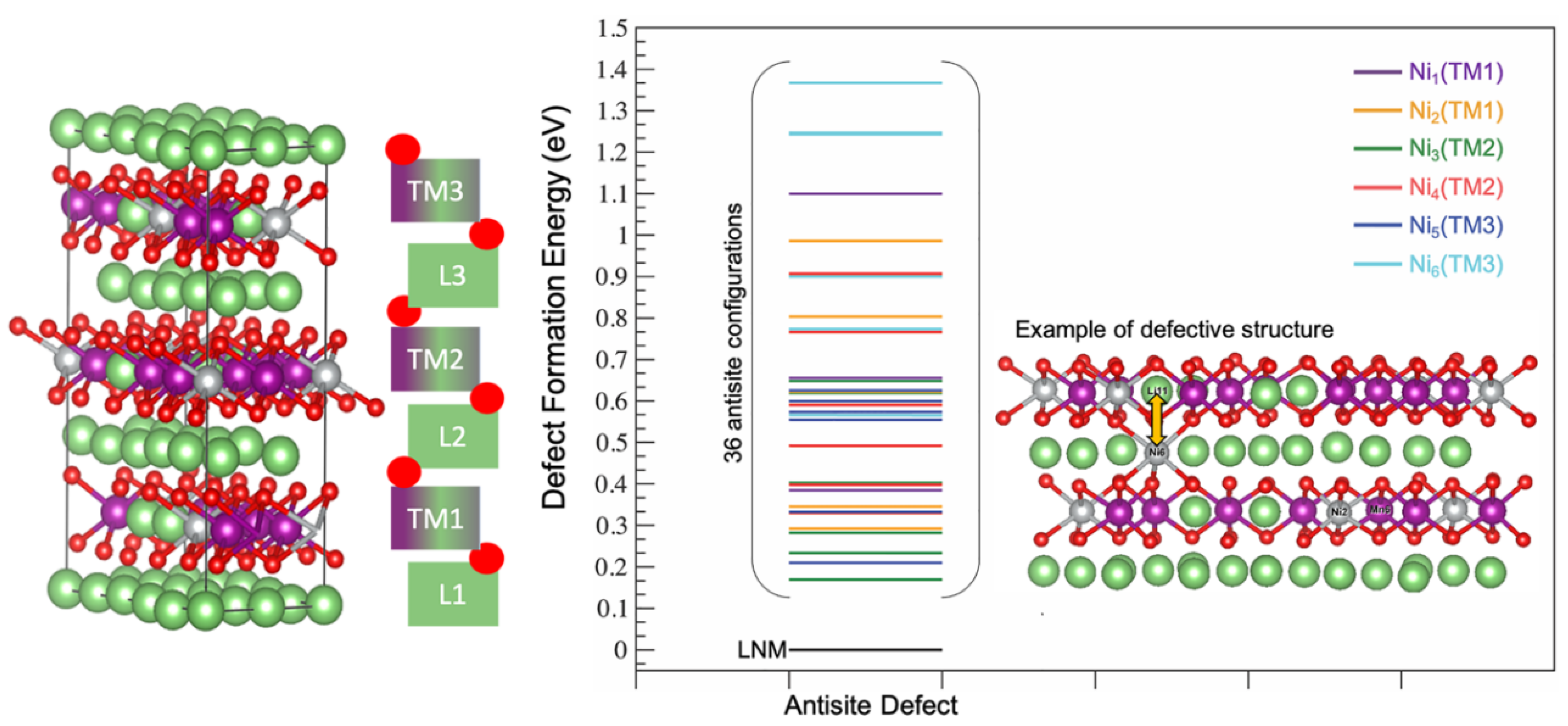
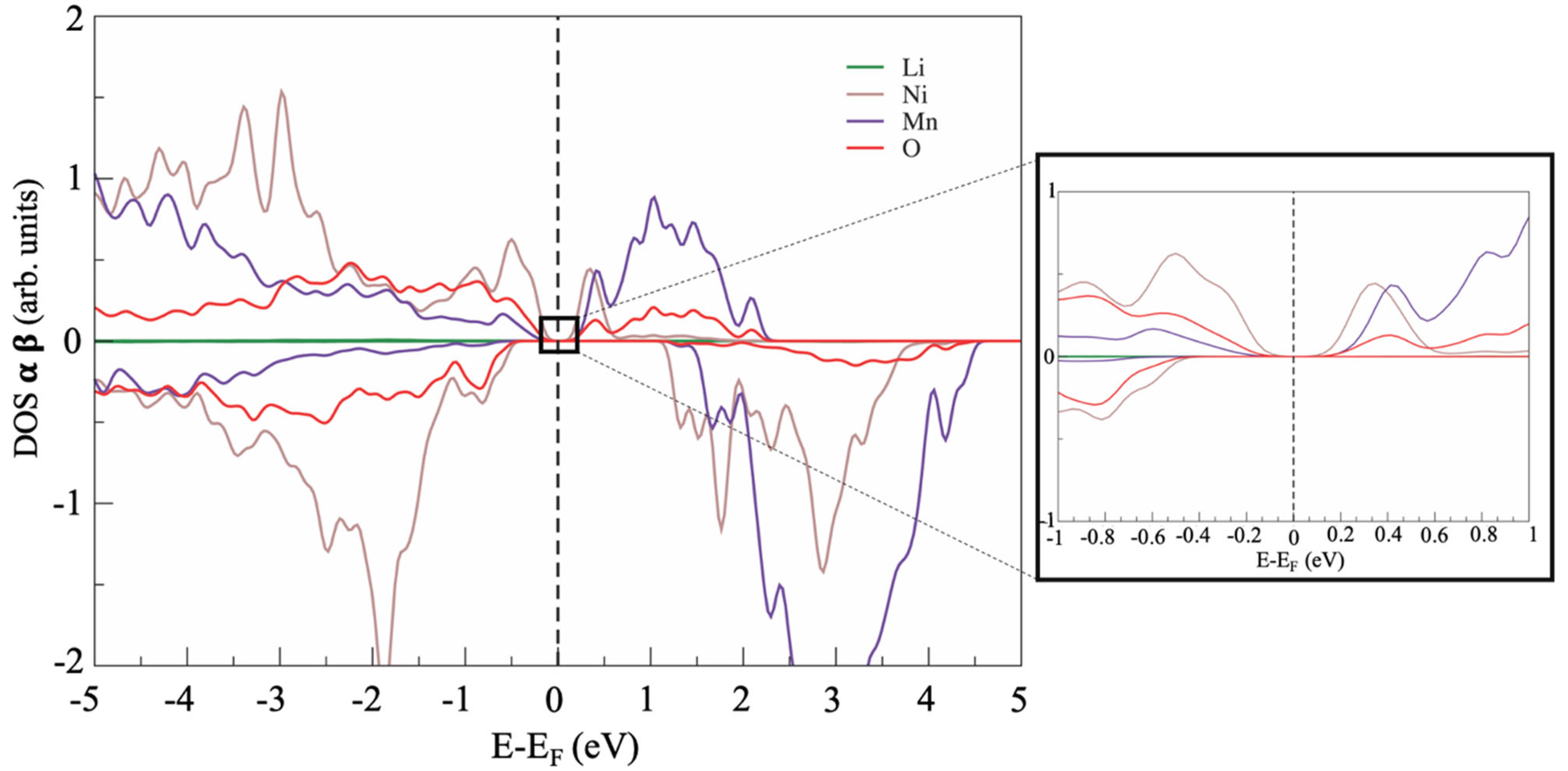
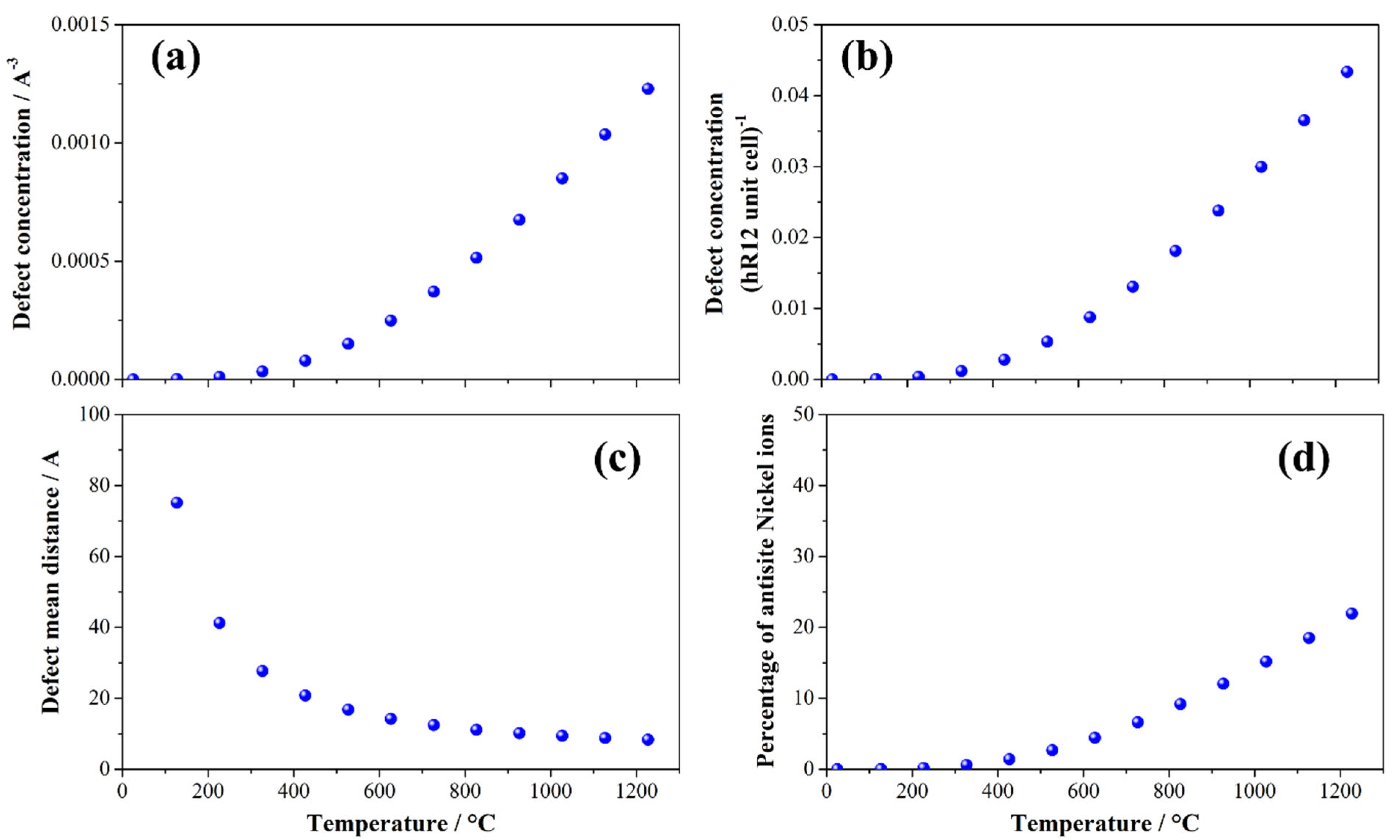
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pierini, A.; Brutti, S.; Bodo, E. Reactive Pathways toward Parasitic Release of Singlet Oxygen in Metal-Air Batteries. Npj Comput. Mater. 2021, 7, 126. [Google Scholar] [CrossRef]
- Meggiolaro, D.; Gigli, G.; Paolone, A.; Vitucci, F.; Brutti, S. Incorporation of Lithium by MgH2: An Ab Initio Study. J. Phys. Chem. C 2013, 117, 22467–22477. [Google Scholar] [CrossRef]
- Meggiolaro, D.; Gigli, G.; Paolone, A.; Reale, P.; Doublet, M.L.; Brutti, S. Origin of the Voltage Hysteresis of MgH 2 Electrodes in Lithium Batteries. J. Phys. Chem. C 2015, 119, 17044–17052. [Google Scholar] [CrossRef]
- Tuccillo, M.; Palumbo, O.; Pavone, M.; Muñoz-García, A.B.; Paolone, A.; Brutti, S. Analysis of the Phase Stability of LiMO2 Layered Oxides (M = Co, Mn, Ni). Crystals 2020, 10, 526. [Google Scholar] [CrossRef]
- Paolone, A.; Brutti, S. Performances of Different DFT Functionals to Calculate the Anodic Limit of Fluorinated Sulphonyl-Imide Anions for Lithium Cells. In The Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 2090. [Google Scholar]
- di Muzio, S.; Paolone, A.; Brutti, S. Thermodynamics of the Hydrolysis of Lithium Salts: Pathways to the Precipitation of Inorganic SEI Components in Li-Ion Batteries. J. Electrochem. Soc. 2021, 168, 100514. [Google Scholar] [CrossRef]
- Tuccillo, M.; Mei, L.; Palumbo, O.; Muñoz-García, A.B.; Pavone, M.; Paolone, A.; Brutti, S. Replacement of Cobalt in Lithium-Rich Layered Oxides by n-Doping: A Dft Study. Appl. Sci. 2021, 11, 10545. [Google Scholar] [CrossRef]
- ben Yahia, M.; Lemoigno, F.; Rousse, G.; Boucher, F.; Tarascon, J.-M.M.; Doublet, M.-L.L. Origin of the 3.6 V to 3.9 V Voltage Increase in the LiFeSO4F Cathodes for Li-Ion Batteries. Energy Environ. Sci. 2012, 5, 9584. [Google Scholar] [CrossRef]
- Dalverny, A.-L.; Filhol, J.-S.; Doublet, M.-L. Interface Electrochemistry in Conversion Materials for Li-Ion Batteries. J. Mater. Chem. 2011, 21, 10134. [Google Scholar] [CrossRef]
- Saubanere, M.; McCalla, E.; Tarascon, J.-M.; Doublet, M.-L. The Intriguing Question of Anionic Redox in High-Energy Density Cathodes for Li-Ion Batteries. Energy Environ. Sci. 2016, 9, 984–991. [Google Scholar] [CrossRef]
- Lombardo, T.; Duquesnoy, M.; El-Bouysidy, H.; Årén, F.; Gallo-Bueno, A.; Jørgensen, P.B.; Bhowmik, A.; Demortière, A.; Ayerbe, E.; Alcaide, F.; et al. Artificial Intelligence Applied to Battery Research: Hype or Reality? Chem. Rev. 2021. [Google Scholar] [CrossRef]
- Forero-Saboya, J.D.; Tchitchekova, D.S.; Johansson, P.; Palacín, M.R.; Ponrouch, A. Interfaces and Interphases in Ca and Mg Batteries. Adv. Mater. Interfaces 2022, 9, 2101578. [Google Scholar] [CrossRef]
- Armstrong, A.R.; Lyness, C.; Panchmatia, P.M.; Islam, M.S.; Bruce, P.G. The lithium intercalation process in the low-voltage lithium battery anode Li1+xV1−xO2. Nat. Mater. 2011, 10, 223–229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morgan, L.M.; Islam, M.M.; Yang, H.; O’Regan, K.; Patel, A.N.; Ghosh, A.; Kendrick, E.; Marinescu, M.; Offer, G.J.; Morgan, B.J.; et al. From Atoms to Cells: Multiscale Modeling of LiNixMnyCozO2 Cathodes for Li-Ion Batteries. ACS Energy Lett. 2022, 7, 108–122. [Google Scholar] [CrossRef]
- Cai, Z.; Ji, H.; Ha, Y.; Liu, J.; Kwon, D.-H.; Zhang, Y.; Urban, A.; Foley, E.E.; Giovine, R.; Kim, H.; et al. Realizing Continuous Cation Order-to-Disorder Tuning in a Class of High-Energy Spinel-Type Li-Ion Cathodes. Matter 2021, 4, 3897–3916. [Google Scholar] [CrossRef]
- Jun, K.J.; Sun, Y.; Xiao, Y.; Zeng, Y.; Kim, R.; Kim, H.; Miara, L.J.; Im, D.; Wang, Y.; Ceder, G. Lithium Superionic Conductors with Corner-Sharing Frameworks. Nat. Mater. 2022. [Google Scholar] [CrossRef]
- Yang, J.H.; Kim, H.; Ceder, G. Insights into Layered Oxide Cathodes for Rechargeable Batteries. Molecules 2021, 26, 3173. [Google Scholar] [CrossRef]
- Voronina, N.; Sun, Y.-K.; Myung, S.-T. Co-Free Layered Cathode Materials for High Energy Density Lithium-Ion Batteries. ACS Energy Lett. 2020, 5, 1814–1824. [Google Scholar] [CrossRef]
- Divakaran, A.M.; Minakshi, M.; Bahri, P.A.; Paul, S.; Kumari, P.; Divakaran, A.M.; Manjunatha, K.N. Rational Design on Materials for Developing next Generation Lithium-Ion Secondary Battery. Prog. Solid State Chem. 2021, 62, 100298. [Google Scholar] [CrossRef]
- Ferro, P.; Bonollo, F. Materials Selection in a Critical Raw Materials Perspective. Mater. Des. 2019, 177, 107848. [Google Scholar] [CrossRef]
- European Commission Methodology for Establishing the EU List of Critical Raw Materials; Publications Office of the European Union: Luxembourg, 2017.
- Simonelli, L.; Sorrentino, A.; Marini, C.; Ramanan, N.; Heinis, D.; Olszewski, W.; Mullaliu, A.; Birrozzi, A.; Laszczynski, N.; Giorgetti, M.; et al. Role of Manganese in Lithium- and Manganese-Rich Layered Oxides Cathodes. J. Phys. Chem. Lett. 2019, 10, 3359–3368. [Google Scholar] [CrossRef]
- Celeste, A.; Tuccillo, M.; Santoni, A.; Reale, P.; Brutti, S.; Silvestri, L. Exploring a Co-Free, Li-Rich Layered Oxide with Low Content of Nickel as a Positive Electrode for Li-Ion Battery. ACS Appl. Energy Mater. 2021, 4, 11290–11297. [Google Scholar] [CrossRef]
- Celeste, A.; Brescia, R.; Greco, G.; Torelli, P.; Mauri, S.; Silvestri, L.; Pellegrini, V.; Brutti, S. Pushing Stoichiometries of Lithium-Rich Layered Oxides Beyond Their Limits. ACS Appl. Energy Mater. 2022, 5, 1905–1913. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, K.A.; Deng, Z.; Allard, L.F.; Manthiram, A.; Ferreira, P.J. Atomic Structure of a Lithium-Rich Layered Oxide Material for Lithium-Ion Batteries: Evidence of a Solid Solution. Chem. Mater. 2011, 23, 3614–3621. [Google Scholar] [CrossRef]
- Lo, W.-T.; Yu, C.; Leggesse, E.G.; Nachimuthu, S.; Jiang, J.-C. Understanding the Role of Dopant Metal Atoms on the Structural and Electronic Properties of Lithium-Rich Li1.2Mn0.6Ni0.2O2 Cathode Material for Lithium-Ion Batteries. J. Phys. Chem. Lett. 2019, 10, 4842–4850. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Kim, G.-T.; Diemant, T.; Kuenzel, M.; Schür, A.R.; Gao, X.; Qin, B.; Alwast, D.; Jusys, Z.; Behm, R.J.; et al. Reducing Capacity and Voltage Decay of Co-Free Li1.2Ni0.2Mn0.6O2 as Positive Electrode Material for Lithium Batteries Employing an Ionic Liquid-Based Electrolyte. Adv. Energy Mater. 2020, 10, 2001830. [Google Scholar] [CrossRef]
- Ren, Q.; Xie, H.; Wang, M.; Ding, X.; Cui, J.; Luo, D.; Liu, C.; Lin, Z. Deciphering the Effects of Hexagonal and Monoclinic Structure Distribution on the Properties of Li-Rich Layered Oxides. Chem. Commun. 2021, 57, 3512–3515. [Google Scholar] [CrossRef]
- Nakamura, T.; Gao, H.; Ohta, K.; Kimura, Y.; Tamenori, Y.; Nitta, K.; Ina, T.; Oishi, M.; Amezawa, K. Defect Chemical Studies on Oxygen Release from the Li-Rich Cathode Material Li1.2Mn0.6Ni0.2O2−δ. J. Mater. Chem. A 2019, 7, 5009–5019. [Google Scholar] [CrossRef]
- Jarvis, K.A.; Deng, Z.; Allard, L.F.; Manthiram, A.; Ferreira, P.J. Understanding Structural Defects in Lithium-Rich Layered Oxide Cathodes. J. Mater. Chem. 2012, 22, 11550–11555. [Google Scholar] [CrossRef]
- Xie, Y.; Meng, S.; Chen, X.; Liang, X.; Jin, Y.; Xiang, L. Synergetic Effect of High Ni Ratio and Low Oxygen Defect Interface Zone of Single Crystals on the Capacity Retention of Lithium Rich Layered Oxides. J. Colloid Interface Sci. 2021, 594, 485–492. [Google Scholar] [CrossRef]
- Bareño, J.; Balasubramanian, M.; Kang, S.H.; Wen, J.G.; Lei, C.H.; Pol, S.; Petrov, I.; Abraham, D.P. Long-Range and Local Structure in the Layered Oxide Li1.2Co0.4Mn0.4O2. Chem. Mater. 2011, 23, 2039–2050. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Chen, C.; Yang, K.; Cao, B.; Xu, S.; Yang, N.; Zhao, W.; Chen, H.; Zhang, M.; et al. Recent Progress in Li and Mn Rich Layered Oxide Cathodes for Li-Ion Batteries. J. Energy Chem. 2021, 61, 368–385. [Google Scholar] [CrossRef]
- Koyama, Y.; Arai, H.; Tanaka, I.; Uchimoto, Y.; Ogumi, Z. High Temperature Defect Chemistry in Layered Lithium Transition-Metal Oxides Based on First-Principles Calculations. J. Power Sources 2013, 244, 592–596. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, X.; Zhang, J.; Wang, D.; Ding, C.; Zhu, Y.; Gao, P.; Huang, X.; Wen, G. Spherical Layered Li-Rich Cathode Material: Unraveling the Role of Oxygen Vacancies on Improving Lithium Ion Conductivity. J. Power Sources 2020, 462, 228171. [Google Scholar] [CrossRef]
- Wu, F.; Kim, G.-T.; Kuenzel, M.; Zhang, H.; Asenbauer, J.; Geiger, D.; Kaiser, U.; Passerini, S. Elucidating the Effect of Iron Doping on the Electrochemical Performance of Cobalt-Free Lithium-Rich Layered Cathode Materials. Adv. Energy Mater. 2019, 9, 1902445. [Google Scholar] [CrossRef]
- Yu, H.; Kim, H.; Wang, Y.; He, P.; Asakura, D.; Nakamura, Y.; Zhou, H. High-Energy “composite” Layered Manganese-Rich Cathode Materials via Controlling Li2MnO3 Phase Activation for Lithium-Ion Batteries. Phys. Chem. Chem. Phys. 2012, 14, 6584–6595. [Google Scholar] [CrossRef]
- Boulineau, A.; Gutel, T. Revealing Electrochemically Induced Antisite Defects in LiCoPO4: Evolution upon Cycling. Chem. Mater. 2015, 27, 802–807. [Google Scholar] [CrossRef]
- Hu, J.; Xiao, Y.; Tang, H.; Wang, H.; Wang, Z.; Liu, C.; Zeng, H.; Huang, Q.; Ren, Y.; Wang, C.; et al. Tuning Li-Ion Diffusion in α-LiMn1–XFexPO4 Nanocrystals by Antisite Defects and Embedded β-Phase for Advanced Li-Ion Batteries. Nano Lett. 2017, 17, 4934–4940. [Google Scholar] [CrossRef]
- Maier, J.; Amin, R. Defect Chemistry of LiFePO4. J. Electrochem. Soc. 2008, 155, A339. [Google Scholar] [CrossRef]
- Jamil, S.; Li, C.; Fasehullah, M.; Liu, P.; Xiao, F.; Wang, H.; Bao, S.; Xu, M. Ni/Li Antisite Induced Disordered Passivation Layer for High-Ni Layered Oxide Cathode Material. Energy Storage Mater. 2022, 45, 720–729. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, S.; Liao, J.; Wang, S.; He, X.; Pan, B.; He, H.; Chen, C. Facilitating Lithium-Ion Diffusion in Layered Cathode Materials by Introducing Li + /Ni 2+ Antisite Defects for High-Rate Li-Ion Batteries. Research 2019, 2019, 2198906. [Google Scholar] [CrossRef] [Green Version]
- Hoang, K.; Johannes, M. Defect Physics and Chemistry in Layered Mixed Transition Metal Oxide Cathode Materials: (Ni, Co, Mn) vs. (Ni, Co, Al). Chem. Mater. 2016, 28, 1325–1334. [Google Scholar] [CrossRef]
- Kandhasamy, S.; Nallathamby, K.; Minakshi, M. Role of Structural Defects in Olivine Cathodes. Prog. Solid State Chem. 2012, 40, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Wu, D.; Hu, M.; Tian, Y.; Wei, J.; Zhou, Z. Could Li/Ni Disorder Be Utilized Positively? Combined Experimental and Computational Investigation on Pillar Effect of Ni at Li Sites on LiCoO2 at High Voltages. Electrochim. Acta 2014, 146, 784–791. [Google Scholar] [CrossRef]
- Li, F.; Liu, Z.; Shen, J.; Xu, X.; Zeng, L.; Zhang, B.; Zhu, H.; Liu, Q.; Liu, J.; Zhu, M. A Nanorod-like Ni-Rich Layered Cathode with Enhanced Li+ Diffusion Pathways for High-Performance Lithium-Ion Batteries. J. Mater. Chem. A 2021, 9, 2830–2839. [Google Scholar] [CrossRef]
- Li, F.; Liu, Z.; Shen, J.; Xu, X.; Zeng, L.; Li, Y.; Zhang, D.; Zuo, S.; Liu, J. Ni-Rich Layered Oxide with Preferred Orientation (110) Plane as a Stable Cathode Material for High-Energy Lithium-Ion Batteries. Nanomaterials 2020, 10, 2495. [Google Scholar] [CrossRef]
- Xie, Y.; Jin, Y.; Xiang, L. Li-Rich Layered Oxides: Structure, Capacity and Voltage Fading Mechanisms and Solving Strategies. Particuology 2022, 61, 1–10. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Shimizu, R.; Cheng, D.; Nguyen, H.; Paulsen, J.; Kumakura, S.; Zhang, M.; Meng, Y.S.; Li, Y.; et al. Elucidating the Effect of Borate Additive in High-Voltage Electrolyte for Li-Rich Layered Oxide Materials. Adv. Energy Mater. 2022, 12, 2103033. [Google Scholar] [CrossRef]
- Jarvis, K.; Wang, C.-C.; Varela, M.; Unocic, R.R.; Manthiram, A.; Ferreira, P.J. Surface Reconstruction in Li-Rich Layered Oxides of Li-Ion Batteries. Chem. Mater 2017, 29, 7668–7674. [Google Scholar] [CrossRef]
- Chen, C.-J.; Kong, W.; Mori, T.; Peterson, V.K.; Sharma, N.; Lee, P.-H.; Wu, S.-H.; Wang, C.-C.; Song, Y.-F.; Liu, R.-S. The Origin of Capacity Fade in the Li2 MnO3 LiMO2 (M = Li, Ni, Co, Mn) Microsphere Positive Electrode: An Operando Neutron Diffraction and Transmission X-ray Microscopy Study. J. Am. Chem. Soc. 2016, 138, 8824–8833. [Google Scholar] [CrossRef]
- Kugel, K.I.; Khomskii, D.I. The Jahn-Teller Effect and Magnetism: Transition Metal Compounds. Sov. Phys. Uspekhi 1982, 25, 621–641. [Google Scholar] [CrossRef]
- Shannon, R.D.; Prewitt, C.T. Effective Ionic Radii in Oxides and Fluorides. Acta Cryst. 1969, B25, 925–946. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Minakshi, M.; Singh, P.; Appadoo, D.; Martin, D.E. Synthesis and Characterization of Olivine LiNiPO4 for Aqueous Rechargeable Battery. Electrochim. Acta 2011, 56, 4356–4360. [Google Scholar] [CrossRef] [Green Version]
- Ivanova, S.; Zhecheva, E.; Stoyanova, R.; Nihtianova, D.; Wegner, S.; Tzvetkova, P.; Simova, S. High-Voltage LiNi1/2Mn3/2O4 Spinel: Cationic Order and Particle Size Distribution. J. Phys. Chem. C 2011, 115, 25170–25182. [Google Scholar] [CrossRef]
- Chi, L.H.L.H.; Dinh, N.N.N.N.; Brutti, S.; Scrosati, B. Synthesis, Characterization and Electrochemical Properties of 4.8 V LiNi0.5Mn1.5O4 Cathode Material in Lithium-Ion Batteries. Electrochim. Acta 2010, 55, 5110–5116. [Google Scholar] [CrossRef]
| Rhombohedral Unit Cell Parameters | |
|---|---|
| LNM Defect-Free (Unit Cell Angles α = β = 90°, γ = 120°) | |
| a (Å) | 2.930 (2.907) [7] |
| c (Å) | 14.22 (14.498) [7] |
| (Å3/f.u.) | 35.26 (35.36) [7] |
| Electronic Structure: Magnetic Moments | |
| Mean value: 1.555 µB (i.e., Ni2+) 16.7% of nickel ions show 1.001 µB (i.e., Ni3+; Jahn–Teller) | |
| Mean value: 3.249 µB (i.e., Mn4+) 5.56% of manganese ions show 3.890 µB (i.e., Mn3+; Jahn–Teller) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuccillo, M.; Costantini, A.; Celeste, A.; García, A.B.M.; Pavone, M.; Paolone, A.; Palumbo, O.; Brutti, S. NAi/Li Antisite Defects in the Li1.2Ni0.2Mn0.6O2 Li-Rich Layered Oxide: A DFT Study. Crystals 2022, 12, 723. https://doi.org/10.3390/cryst12050723
Tuccillo M, Costantini A, Celeste A, García ABM, Pavone M, Paolone A, Palumbo O, Brutti S. NAi/Li Antisite Defects in the Li1.2Ni0.2Mn0.6O2 Li-Rich Layered Oxide: A DFT Study. Crystals. 2022; 12(5):723. https://doi.org/10.3390/cryst12050723
Chicago/Turabian StyleTuccillo, Mariarosaria, Angelo Costantini, Arcangelo Celeste, Ana Belén Muñoz García, Michele Pavone, Annalisa Paolone, Oriele Palumbo, and Sergio Brutti. 2022. "NAi/Li Antisite Defects in the Li1.2Ni0.2Mn0.6O2 Li-Rich Layered Oxide: A DFT Study" Crystals 12, no. 5: 723. https://doi.org/10.3390/cryst12050723
APA StyleTuccillo, M., Costantini, A., Celeste, A., García, A. B. M., Pavone, M., Paolone, A., Palumbo, O., & Brutti, S. (2022). NAi/Li Antisite Defects in the Li1.2Ni0.2Mn0.6O2 Li-Rich Layered Oxide: A DFT Study. Crystals, 12(5), 723. https://doi.org/10.3390/cryst12050723










