Feedback Control of Crystal Size Distribution for Cooling Batch Crystallization Using Deep Learning-Based Image Analysis
Abstract
:1. Introduction
2. Image Analysis Based Feedback Control of CSD
2.1. Experimental Setup
2.2. Measurement of Crystal Size Distribution
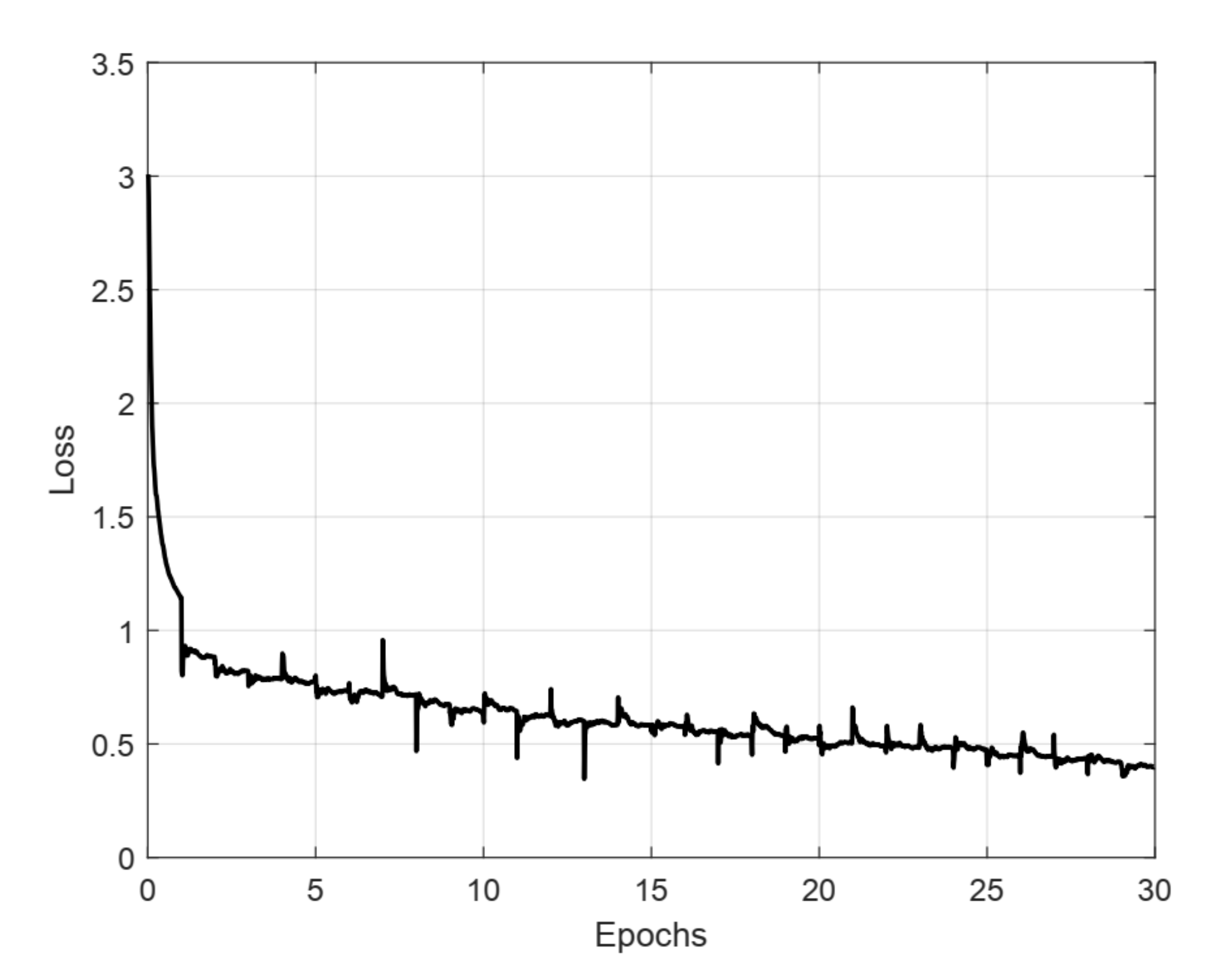
2.2.1. Deep Learning Based Image Analysis Method
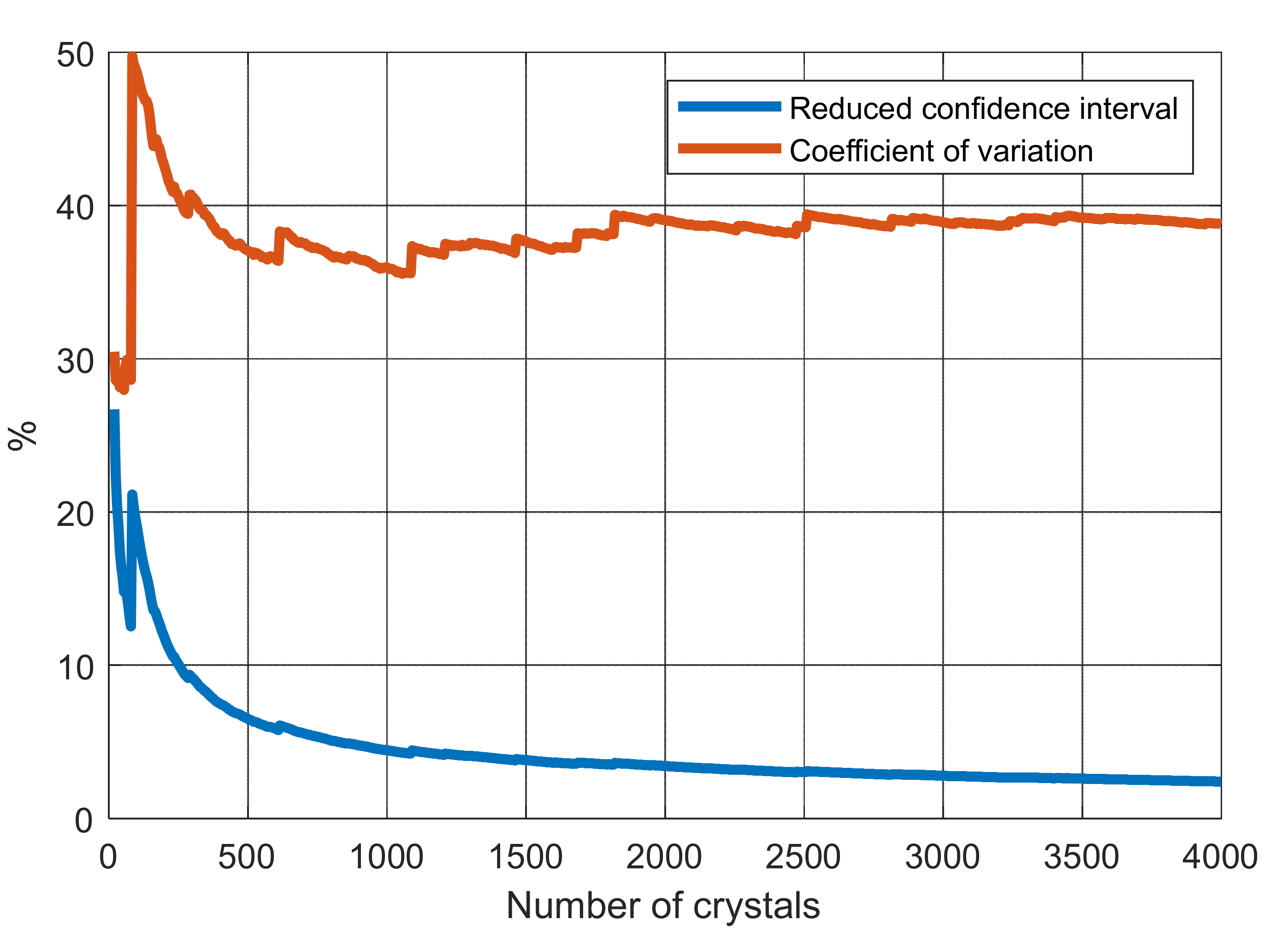
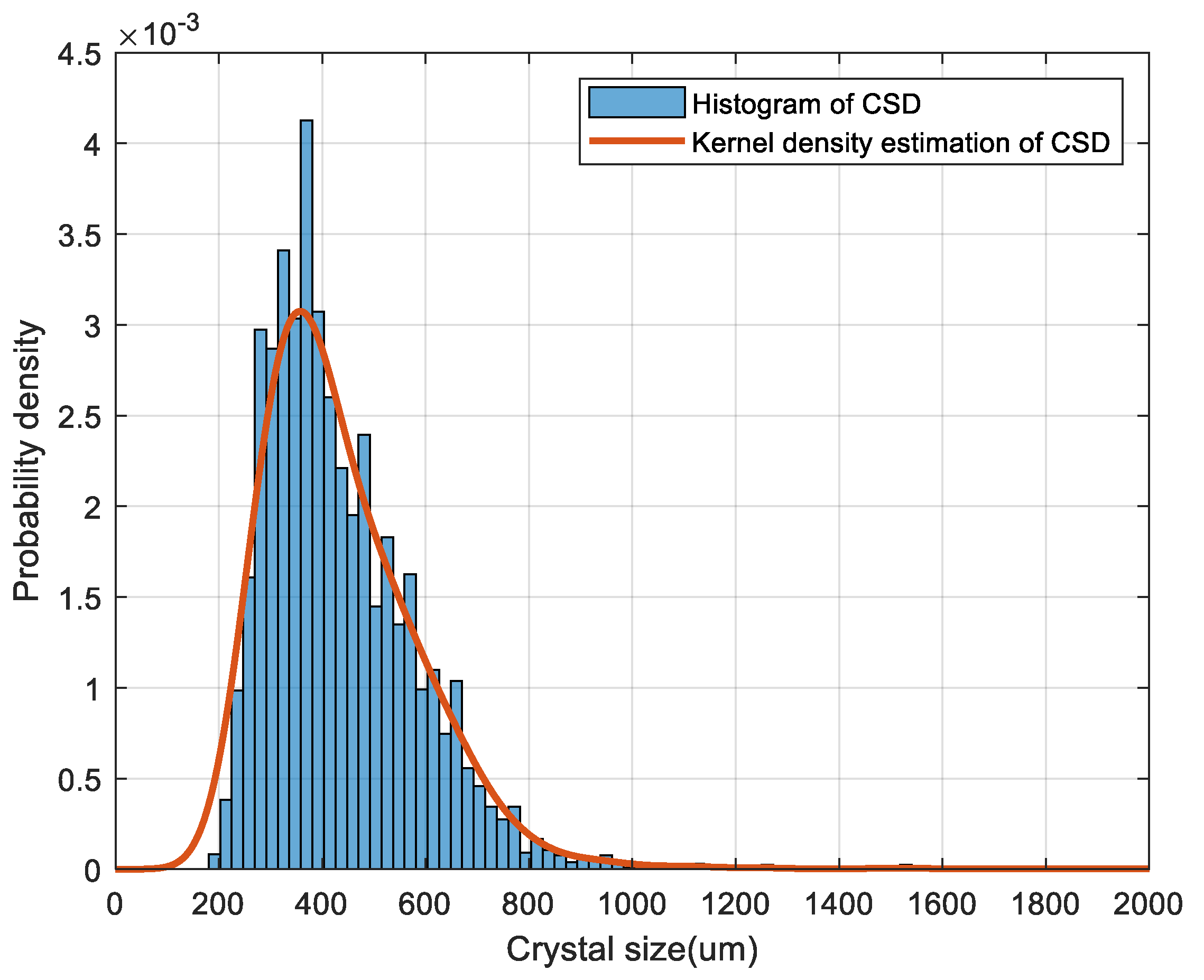
2.2.2. Kernel Density Estimation of Experimental Histogram
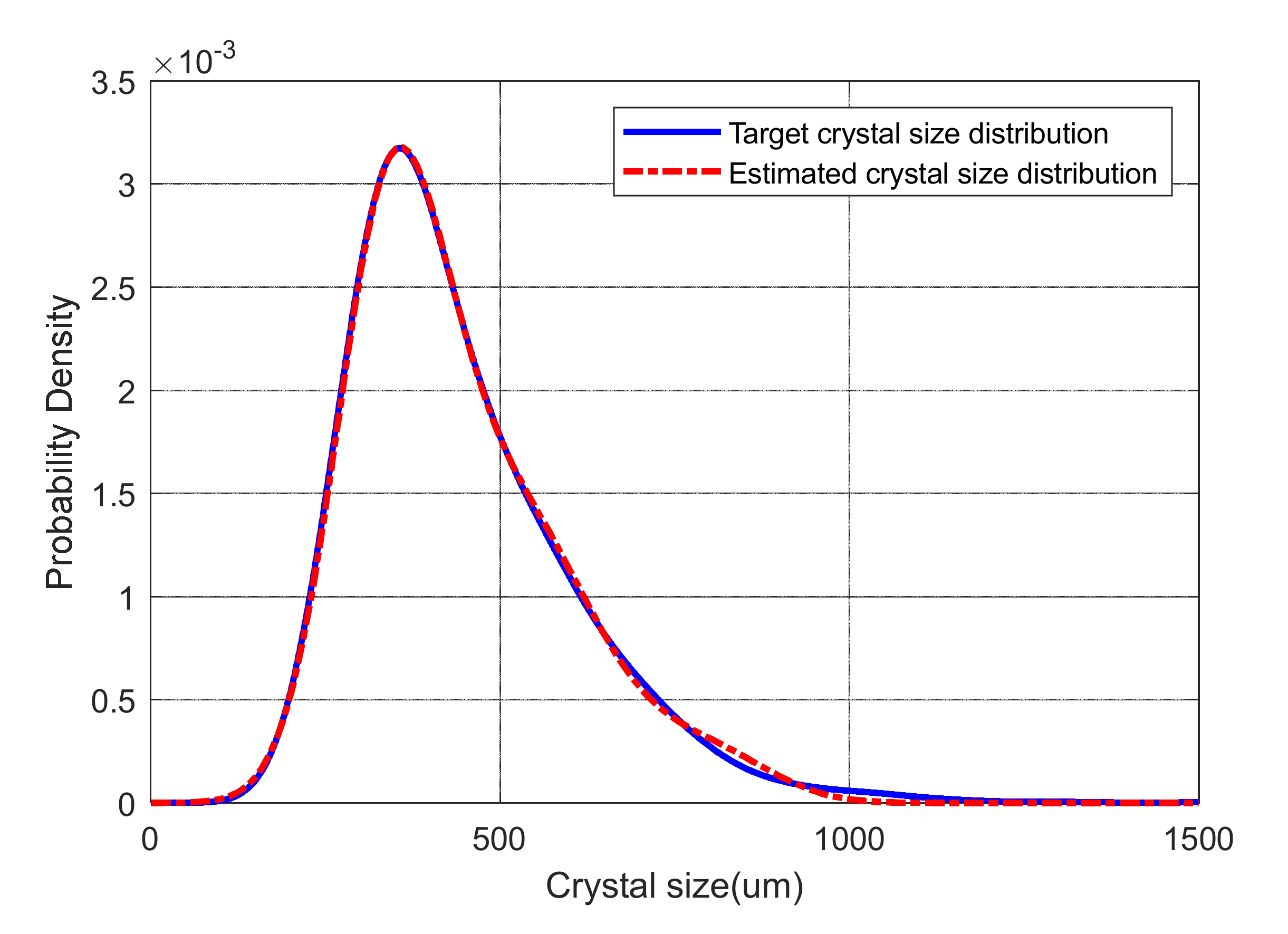
2.3. Feedback Control Algorithm of Crystal Size Distribution
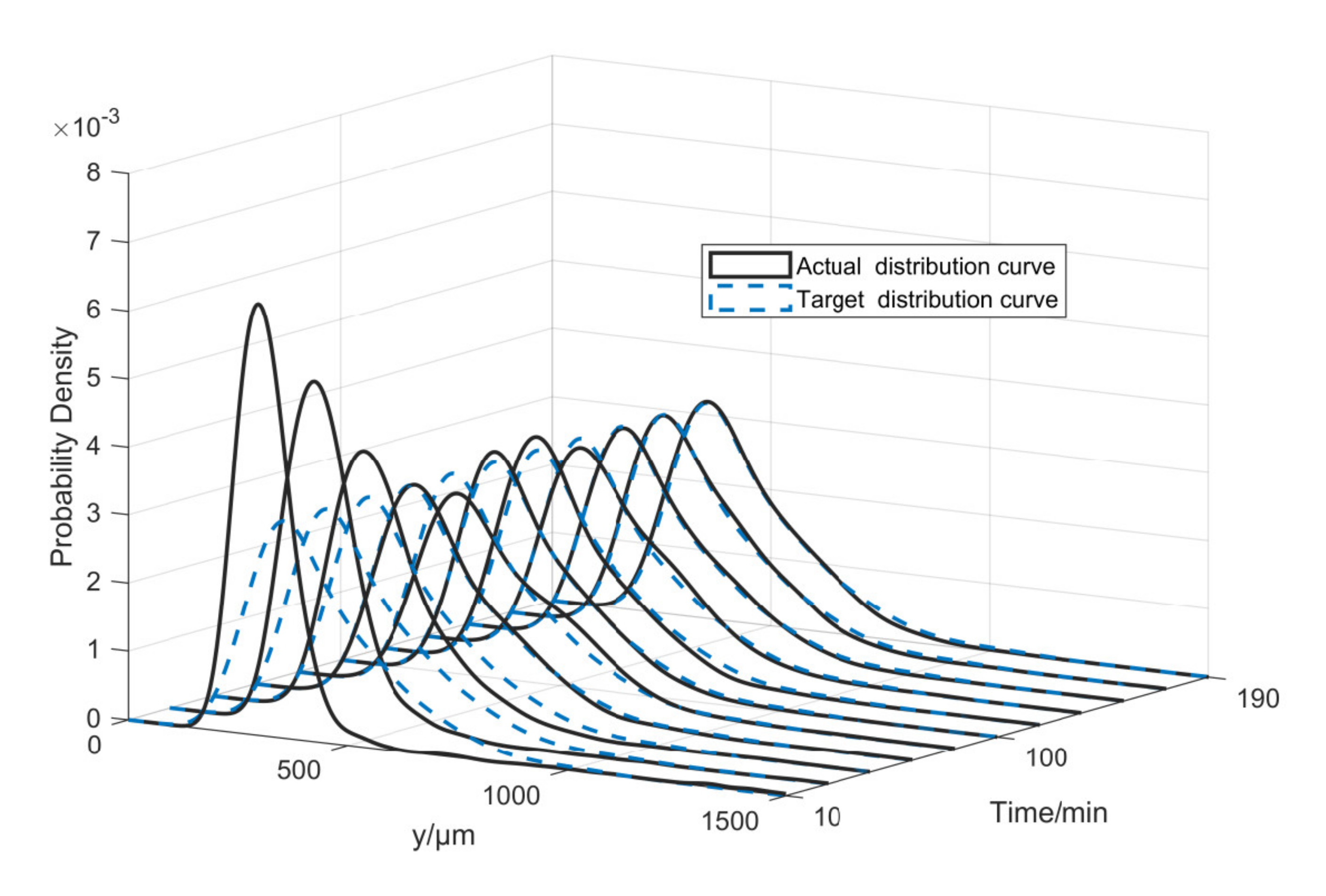
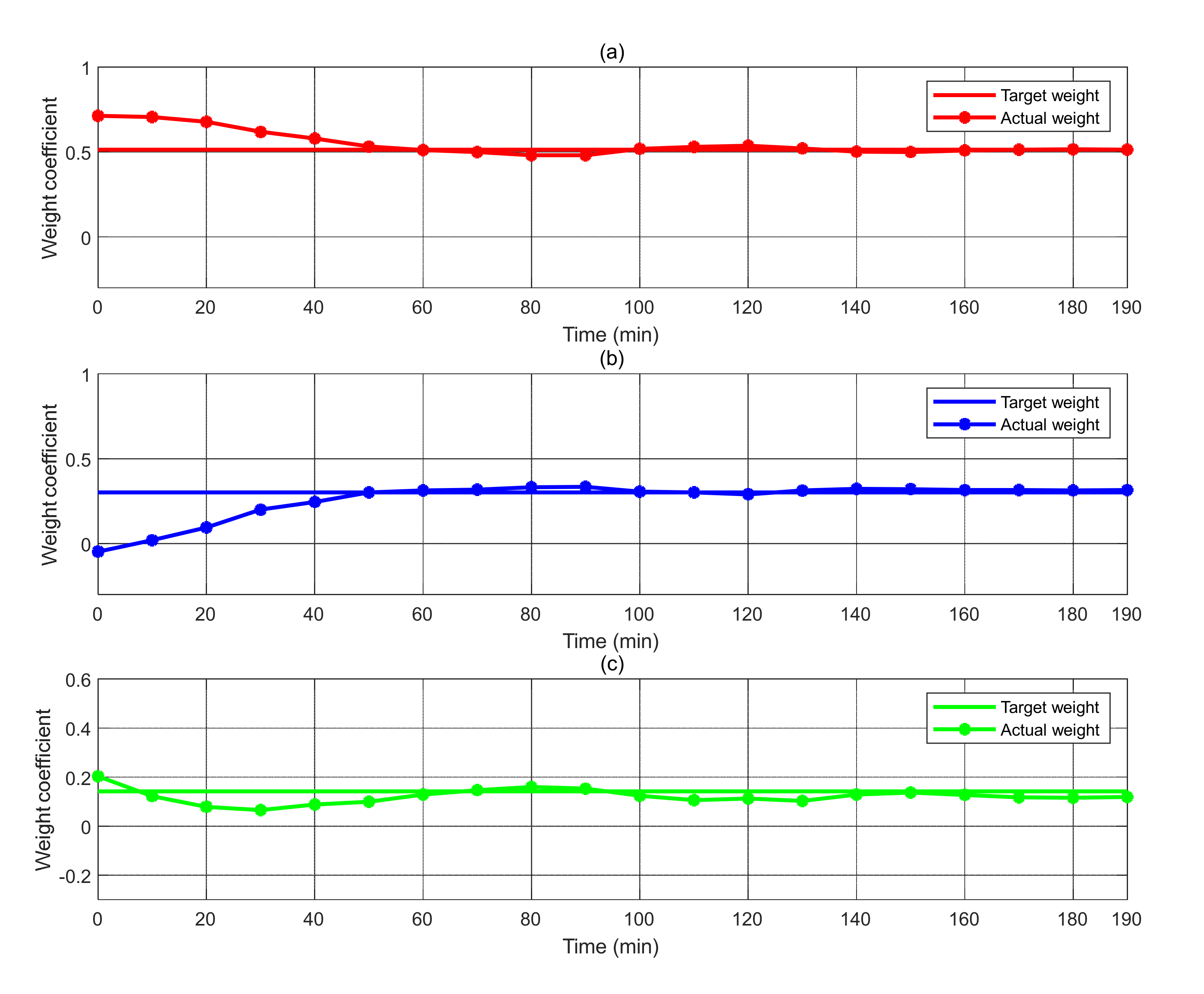
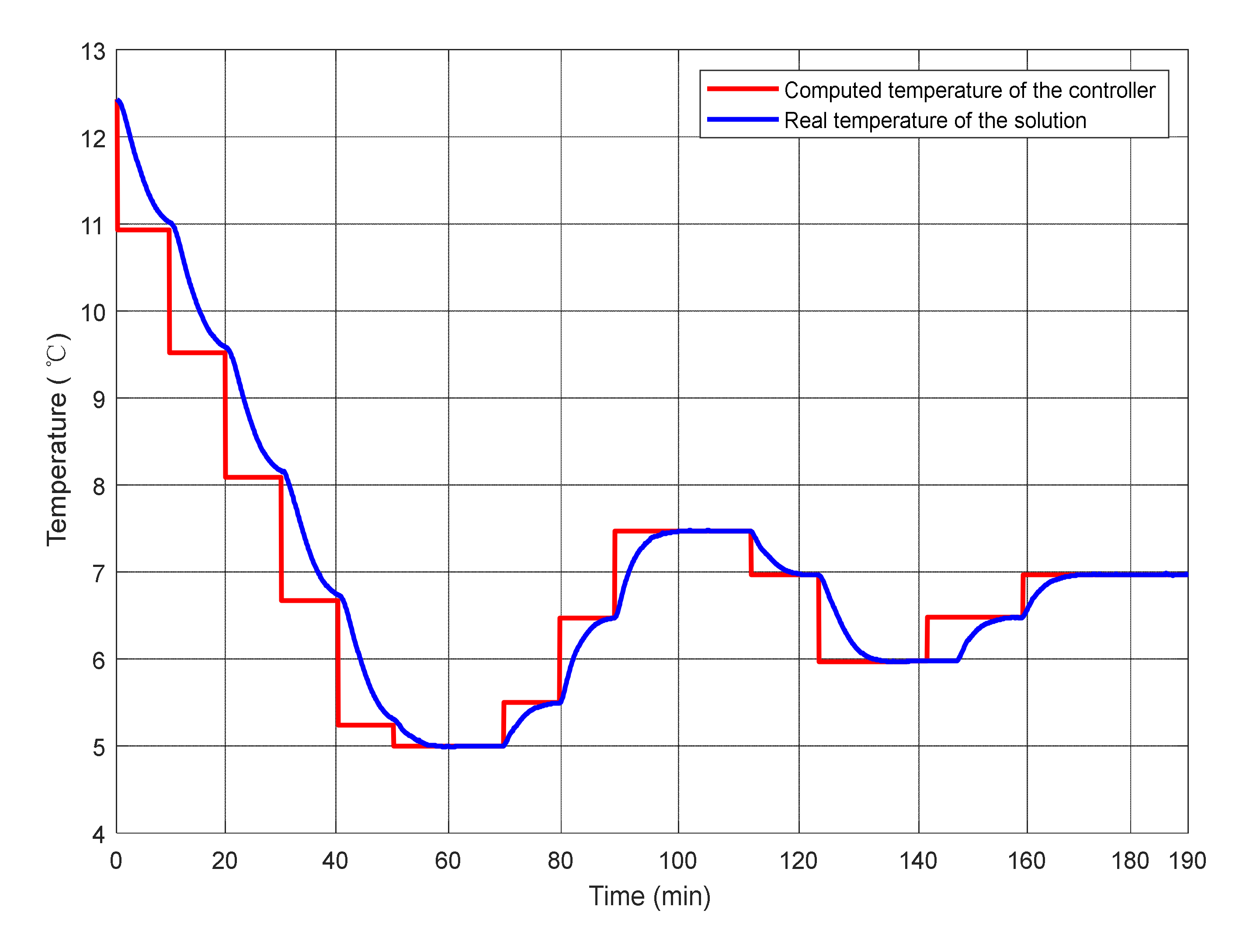
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baratti, R.; Tronci, S.; Romagnoli, J.A. A Generalized Stochastic Modelling Approach for Crystal Size Distribution in Antisolvent Crystallization Operations. AICHE J. 2017, 63, 551–559. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Braatz, R.D. Advances and New Directions in Crystallization Control. Annu. Rev. Chem. Biomol. Eng. 2012, 3, 55–75. [Google Scholar] [CrossRef] [Green Version]
- Crowley, T.J.; Meadows, E.S.; Kostoulas, E.; Doyle, F.J., III. Control of Particle Size Distribution Described by a Population Balance Model of Semibatch Emulsion Polymerization. J. Process Control. 2000, 10, 419–432. [Google Scholar] [CrossRef]
- Hulburt, H.M.; Katz, S. Some Problems in Particle Technology: A Statistical Mechanical Formulation. Chem. Eng. Sci. 1964, 19, 555–574. [Google Scholar] [CrossRef]
- Randolph, A.D.; Larson, M. A, Theory of Particulate Processes, 2nd ed.; Academic Press: San Diego, CA, USA, 1988; pp. 80–108. [Google Scholar]
- Grosso, M.; Galan, O.; Baratti, R.; Romagnoli, J.A. A Stochastic Formulation for the Description of the Crystal Size Distribution in Antisolvent Crystallization Processes. AICHE J. 2010, 56, 2077–2087. [Google Scholar] [CrossRef]
- Cogoni, G.; Tronci, S.; Mistretta, G.; Baratti, R.; Romagnoli, J.A. Stochastic Approach for the Prediction of PSD in Nonisothermal Antisolvent Crystallization Processes. AICHE J. 2013, 59, 2842–2881. [Google Scholar] [CrossRef]
- Semino, D.; Ray, W.H. Control of systems described by population balance equations—I. Controllabity analysis. Chem. Eng. Sci. 1995, 50, 1805–1824. [Google Scholar] [CrossRef]
- Chiu, T.; Christofides, P.D. Nonlinear Control of Particulate Processes. AICHE J. 1999, 45, 1279–1297. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Miller, S.M.; Witkowski, W.R. Model Identification and Control of Solution Crystallization Processes: A Review. Ind. Eng. Chem. Res. 1993, 32, 1275–1296. [Google Scholar] [CrossRef]
- Hermanto, M.W.; Chiu, M.S.; Braatz, R.D. Nonlinear Model Predictive Control for the Polymorphic Transformation of L-Glutamic Acid Crystals. AIChE J. 2009, 55, 2631–2645. [Google Scholar] [CrossRef]
- Mesbah, A.; Landlust, J.; Huesman, A.E.M.; Kramer, H.J.M.; Jansens, P.J.; Van den Hof, P.M.J. A Model-Based Control Framework for Industrial Batch Crystallization Processes. Chem. Eng. Res. Des. 2010, 88, 1223–1233. [Google Scholar] [CrossRef]
- Wang, H.; Jian, H.Z. Bounded Stochastic Distributions Control for Pseudo-ARMAX Stochastic Systems. IEEE Trans. Autom. Control. 2001, 46, 486–490. [Google Scholar] [CrossRef]
- Park, M.J.; Dokucu, M.T.; Doyle, F.J. Regulation of the Emulsion Particle Size Distribution to an Optimal Trajectory Using Partial Least Squares Model-Based Predictive Control. Ind. Eng. Chem. Res. 2004, 43, 7227–7237. [Google Scholar] [CrossRef]
- Wang, H. Minimum Entropy Control of Non-Gaussian Dynamic Stochastic Systems. IEEE Trans. Autom. Control. 2002, 47, 398–403. [Google Scholar] [CrossRef]
- Guo, L.; Wang, H. PID Controller Design for Output PDFs of Stochastic Systems Using Linear Matrix Inequalities. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2005, 35, 65–71. [Google Scholar]
- Li, M.; Zhou, P.; Liu, Y.; Wang, H. Data-Driven Predictive Probability Density Function Control of Fiber Length Stochastic Distribution Shaping in Refining Process. IEEE Trans. Autom. Sci. Eng. 2020, 17, 633–645. [Google Scholar] [CrossRef]
- Zhu, J.; Gui, W.; Yang, C.; Xu, H.; Wang, X. Probability Density Function of Bubble Size based Reagent Dosage Predictive Control for Copper Roughing Flotation. Control. Eng. Pract. 2014, 29, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hansen, T.B.; Simone, E.; Nagy, Z.; Qu, H. Process Analytical Tools to Control Polymorphism and Particle Size in Batch Crystallization Processes. Org. Process Res. Dev. 2019, 27, 855–865. [Google Scholar] [CrossRef] [Green Version]
- Simone, E.; Saleemi, A.N.; Nagy, Z.K. In Situ Monitoring of Polymorphic Transformations Using a Composite Sensor Array of Raman, NIR, and ATR-UV/vis Spectroscopy, FBRM, and PVM for an Intelligent Decision Support System. Org. Process Res. Dev. 2015, 19, 167–177. [Google Scholar] [CrossRef]
- Tadayyon, A.; Rohani, S. Control of Fines Suspension Density in the Fines Loop of a Continuous KCI Crystallizer Using Transmittance Measurement and an FBRM (R) Probe. Can. J. Chem. Eng. 2000, 78, 663–673. [Google Scholar] [CrossRef]
- Abu Bakar, M.R.; Nagy, Z.K.; Saleemi, A.N.; Rielly, C.D. The Impact of Direct Nucleation Control on Crystal Size Distribution in Pharmaceutical Crystallization Processes. Cryst. Growth Des. 2009, 9, 1978–1984. [Google Scholar] [CrossRef]
- Szilágyi, B.; Agachi, P.S.; Nagy, Z.K. Chord Length Distribution Based Modeling and Adaptive Model Predictive Control of Batch Crystallization Processes Using High Fidelity Full Population Balance Models. Ind. Eng. Chem. Res. 2018, 57, 3320–3332. [Google Scholar] [CrossRef] [Green Version]
- Szilágyi, B.; Borsos, Á.; Pal, K.; Nagy, Z.K. Experimental implementation of a Quality-by-Control (QbC) Framework Using a Mechanistic PBM-based Nonlinear Model Predictive Control Involving Chord Length Distribution Measurement for the Batch Cooling Crystallization of L-ascorbic Acid. Chem. Eng. Sci. 2019, 195, 335–346. [Google Scholar] [CrossRef] [Green Version]
- Borsos, Á.; Szilágyi, B.; Agachi, P.Ş.; Nagy, Z.K. Real-Time Image Processing Based Online Feedback Control System for Cooling Batch Crystallization. Org. Process Res. Dev. 2017, 21, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Ruf, A.; Worlitschek, J.; Mazzotti, M.R. Modeling and Experimental Analysis of PSD Measurements through FBRM. Part. Part. Syst. Charact. 2000, 17, 167–179. [Google Scholar] [CrossRef]
- Li, M.Z.; Wilkinson, D. Determination of Non-spherical Particle Size Distribution from Chord Length Measurements. Part 1: Theoretical analysis. Chem. Eng. Sci. 2005, 60, 3251–3265. [Google Scholar] [CrossRef]
- Sarkar, D.; Doan, X.T.; Ying, Z.; Srinivasan, R. In Situ Particle Size Estimation for Crystallization Processes by Multivariate Image Analysis. Chem. Eng. Sci. 2009, 64, 9–19. [Google Scholar] [CrossRef]
- El Arnaout, T.; Cullen, P.J.; Sullivan, C. A Novel Backlight Fiber Optical Probe and Image Algorithms for Real Time Size-shape Analysis during Crystallization. Chem. Eng. Sci. 2016, 149, 42–50. [Google Scholar] [CrossRef]
- Lu, Z.M.; Zhu, F.C.; Gao, X.Y.; Chen, B.C.; Gao, Z.G. In situ Particle Segmentation Approach based on Average Background Modeling and Graph-cut for the Monitoring of L-glutamic Acid Crystallization. Chemom. Intell. Lab. Syst. 2018, 178, 11–23. [Google Scholar] [CrossRef]
- De Anda, J.C.; Wang, X.Z.; Lai, X.; Roberts, K.J.; Jennings, K.H.; Wilkinson, M.J.; Watson, D.; Roberts, D. Real-time Product Morphology Monitoring in Crystallization Using Imaging Technique. AIChE J. 2005, 51, 1406–1414. [Google Scholar] [CrossRef]
- Zhang, B.; Willis, R.; Romagnoli, J.A.; Fois, C.; Tronci, S.; Baratti, R. Image-based Multi Resolution- ANN Approach for Online Particle Size Characterization. Ind. Eng. Chem. Res. 2014, 53, 7008–7018. [Google Scholar] [CrossRef]
- Ghadipasha, N.; Romagnoli, J.A.; Tronci, S.; Baratti, R. A Model-based Approach for Controlling Particle Size Distribution in Combined Cooling-antisolvent Crystallization Processes. Chem. Eng. Sci. 2018, 190, 260–272. [Google Scholar] [CrossRef]
- Ghadipasha, N.; Romagnoli, J.A.; Tronci, S.; Baratti, R. On-line Control of Crystal Properties in Nonisothermal Antisolvent Crystallization. AICHE J. 2015, 61, 2188–2201. [Google Scholar] [CrossRef]
- Serbetci, A.; Akgul, Y.S. End-to-end training of CNN ensembles for person re-identification. Pattern Recognit. 2020, 104, 107319. [Google Scholar] [CrossRef]
- Chu, P.; Li, Z.; Lammers, K.; Lu, R.; Liu, X. Deep learning-based apple detection using a suppression mask R-CNN. Pattern Recognit. Lett. 2021, 147, 206–211. [Google Scholar] [CrossRef]
- Gao, Z.; Wu, Y.; Bao, Y.; Gong, J.; Wang, J.; Rohani, S. Image Analysis for In-line Measurement of Multidimensional Size, Shape, and Polymorphic Transformation of L-Glutamic Acid Using Deep Learning-Based Image Segmentation and Classification. Cryst. Growth Des. 2018, 18, 4275–4281. [Google Scholar] [CrossRef]
- Manee, V.; Zhu, W.; Romagnoli, J.A. A Deep Learning Image-Based Sensor for Real-Time Crystal Size Distribution Characterization. Ind. Eng. Chem. Res. 2019, 58, 23175–23186. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Pons, M.N.; Vivier, H.; Delcour, V.; Authelin, J.; Pailleres-Hubert, J. Morphological Analysis of Pharmaceutical Powders. Powder Technol. 2002, 128, 276–286. [Google Scholar] [CrossRef]
- Faria, N.; Pons, M.N.; De Azevedo, S.F.; Rocha, F.A.; Vivier, H. Quantification of the Morphology of Sucrose Crystals by Image Analysis. Powder Technol. 2003, 133, 54–67. [Google Scholar] [CrossRef]
- Li, M.; Zhou, P.; Wang, L.; Yuan, Y. A Data-Driven Multiobjective Predictive Optimal Control of Refining Process with non-Gaussian Stochastic Distribution Dynamics. IEEE Trans. Ind. Inform. 2021, 17, 7269–7278. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, Y.; Metaxas, D.; Dollar, P. Semantic Amodal Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, C.; Wang, L.; Xiao, S.; Zhu, Y. Feedback Control of Crystal Size Distribution for Cooling Batch Crystallization Using Deep Learning-Based Image Analysis. Crystals 2022, 12, 570. https://doi.org/10.3390/cryst12050570
Gan C, Wang L, Xiao S, Zhu Y. Feedback Control of Crystal Size Distribution for Cooling Batch Crystallization Using Deep Learning-Based Image Analysis. Crystals. 2022; 12(5):570. https://doi.org/10.3390/cryst12050570
Chicago/Turabian StyleGan, Chenyang, Liangyong Wang, Shunkai Xiao, and Yaolong Zhu. 2022. "Feedback Control of Crystal Size Distribution for Cooling Batch Crystallization Using Deep Learning-Based Image Analysis" Crystals 12, no. 5: 570. https://doi.org/10.3390/cryst12050570
APA StyleGan, C., Wang, L., Xiao, S., & Zhu, Y. (2022). Feedback Control of Crystal Size Distribution for Cooling Batch Crystallization Using Deep Learning-Based Image Analysis. Crystals, 12(5), 570. https://doi.org/10.3390/cryst12050570





