Fullerene in a Magnetic Field
Abstract
:1. Introduction
2. Materials and Methods
Conservation of Total Energy in the System
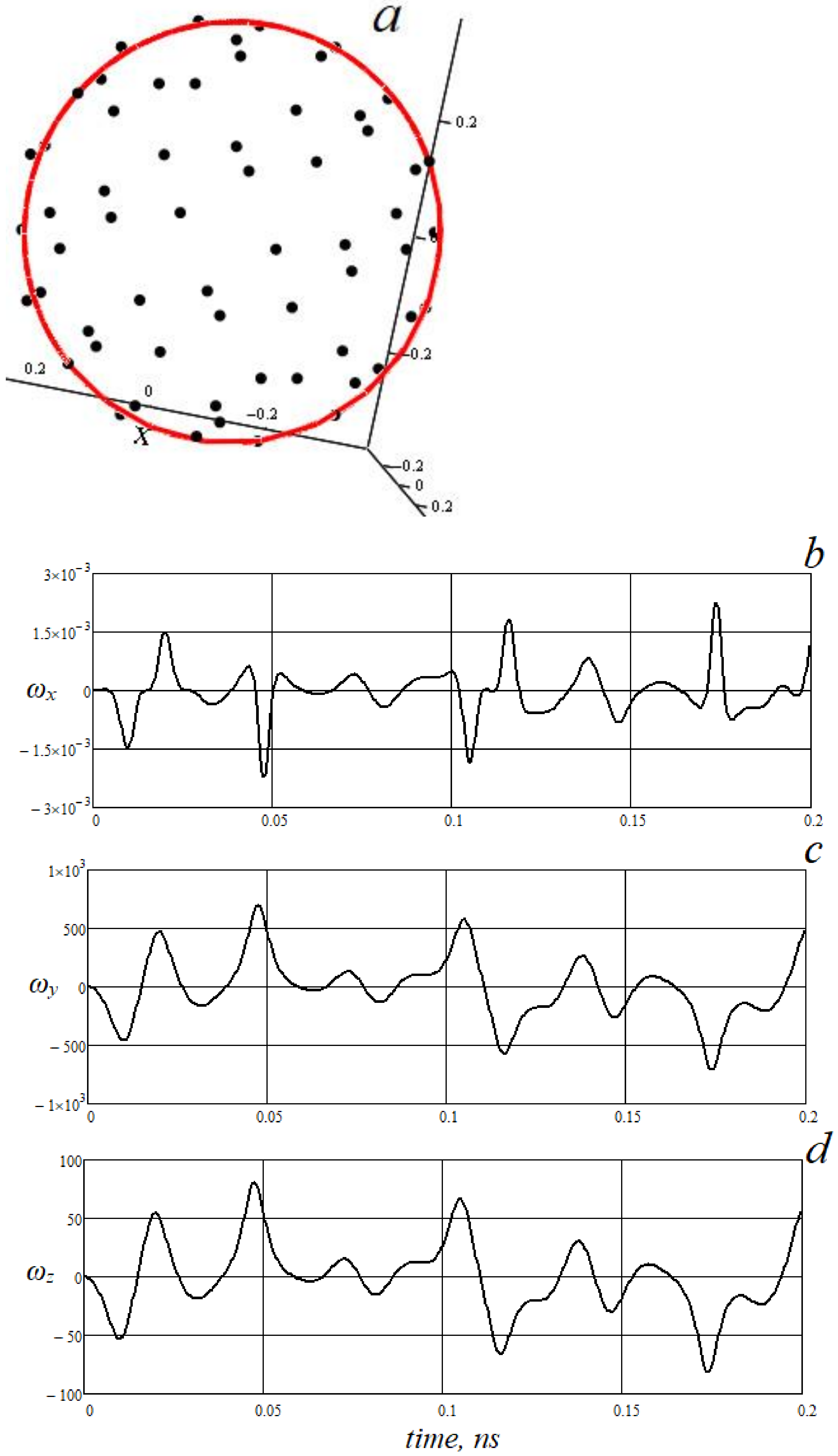
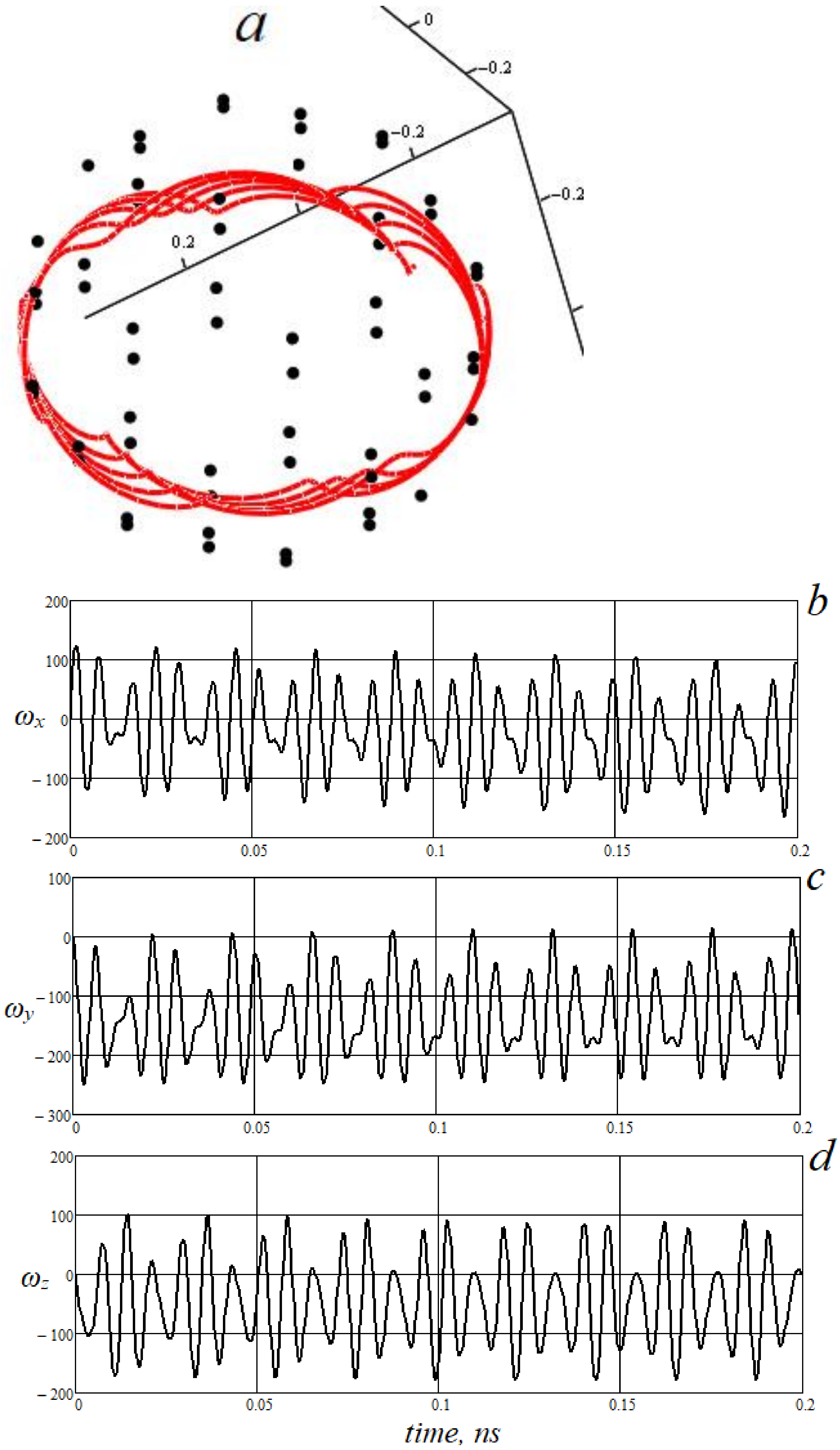
3. Results of Calculations
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fowler, P.W.; Manolopoulos, D.E. An Atlas of Fullerenes; Clarendon: Oxford, UK, 1995. [Google Scholar]
- Guan, J.; Jin, Z.; Zhu, Z.; Chuang, C.; Jin, B.Y.; Tománek, D. Local curvature and stability of two-dimensional systems. Phys. Rev. B 2014, 90, 245403. [Google Scholar] [CrossRef] [Green Version]
- Harris, P.J.F. Fullerene Polymers: A Brief Review. C—J. Carbon Res. 2020, 6, 71. [Google Scholar] [CrossRef]
- Thakral, S.; Mehta, R.M. Fullerenes: Introduction and Overview of Their Biological Properties. Indian J. Pharm. Sci. 2006, 68, 13. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, Y.; Hao, J.; Dong, S. Magnetic fullerene-DNA/hyaluronic acid nanovehicles with magnetism/reduction dual-responsive triggered release. Biomacromolecules 2017, 18, 1029–1038. [Google Scholar] [CrossRef]
- Mallik, S.; Mattauch, S.; Dalai, M.K.; Brückel, T.; Bedanta, S. Effect of magnetic fullerene on magnetization reversal created at the Fe/C60 interface. Sci. Rep. 2018, 8, 5515. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, G.H.; Huh, S.H.; Jeong, J.W.; Ri, H.C. Excellent magnetic properties of fullerene encapsulated ferromagnetic nanoclusters. J. Magn. Magn. Mater. 2002, 246, 404–411. [Google Scholar] [CrossRef]
- Takenobu, T.; Chi, D.H.; Margadonna, S.; Prassides, K.; Kubozono, Y.; Fitch, A.N.; Kato, K.; Iwasa, Y. Synthesis, structure, and magnetic properties of the fullerene-based ferromagnets Eu3C70 and Eu9C70. J. Am. Chem. Soc. 2003, 125, 7, 1897–1904. [Google Scholar] [CrossRef]
- Giacalone, F.; Martin, N. Fullerene polymers: Synthesis and properties. Chem. Rev. 2006, 106, 12, 5136–5190. [Google Scholar] [CrossRef]
- Bhakta, P.; Barthunia, B. Fullerene and its applications: A review. J. Indian Acad. Oral. Med. Radiol. 2020, 32, 159–163. [Google Scholar] [CrossRef]
- Bubenchikov, A.M.; Bubenchikov, M.A.; Mamontov, D.V.; Lun-Fu, A.V. Md-Simulation of Fullerene Rotations in Molecular Crystal Fullerite. Crystals 2019, 9, 496. [Google Scholar] [CrossRef] [Green Version]
- Bubenchikov, A.M.; Bubenchikov, M.A.; Lun-Fu, A.V.; Ovchinnikov, V.A. Gyroscopic effects in fullerite crystal upon deformation. Eur. Phys. J. Plus 2021, 136, 388. [Google Scholar] [CrossRef]
- Bubenchikov, M.A.; Bubenchikov, A.M.; Lun-Fu, A.V.; Ovchinnikov, V.A. Dynamics of Fullerenes in the Molecular Crystal of Fullerite. Phys. Status Solidi A 2021, 218, 2000174. [Google Scholar] [CrossRef]
- Bubenchikov, M.; Ovchinnikov, V.; Mamontov, D. Numerical study of precession characteristics of rotating fullerene-C60 in intermolecular interaction. AIP Conf. Proc. 2020, 2212, 020013. [Google Scholar] [CrossRef]
- Bubenchikov, M.A.; Lun-Fu, A.V.; Ovchinnikov, V.A. Precession of fullerite rotating node at simplest deformations of crystal fragment. AIP Conf. Proc. 2021, 2337, 020005. [Google Scholar] [CrossRef]
- Bubenchikov, A.M.; Bubenchikov, M.A.; Ovchinnikov, V.A. Gyroscopic effect in intermolecular collision with the C60 fullerene molecule. J. Phys. Conf. Ser. IOP Publ. 2020, 1537, 012007. [Google Scholar] [CrossRef]
- Sepahvand, S.; Farhadi, S. Fullerene-modified magnetic silver phosphate (Ag3PO4/Fe3O4/C60) nanocomposites: Hydrothermal synthesis, characterization and study of photocatalytic, catalytic and antibacterial activities. RSC Adv. 2018, 8, 10124–10140. [Google Scholar] [CrossRef] [Green Version]
- Bubenchikov, A.M.; Bubenchikov, M.A.; Mamontov, D.V.; Chelnokova, A.S.; Chumakova, S.P. Movement of fullerenes and their dimers inside carbon nanotubes. Fuller Nanotub. Carbon Nanostructures 2021, 29, 803–809. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lun-Fu, A.; Borodin, V.; Bubenchikov, M.; Bubenchikov, A.; Mamontov, D. Fullerene in a Magnetic Field. Crystals 2022, 12, 521. https://doi.org/10.3390/cryst12040521
Lun-Fu A, Borodin V, Bubenchikov M, Bubenchikov A, Mamontov D. Fullerene in a Magnetic Field. Crystals. 2022; 12(4):521. https://doi.org/10.3390/cryst12040521
Chicago/Turabian StyleLun-Fu, Alexandr, Vladislav Borodin, Mikhail Bubenchikov, Alexey Bubenchikov, and Dmitriy Mamontov. 2022. "Fullerene in a Magnetic Field" Crystals 12, no. 4: 521. https://doi.org/10.3390/cryst12040521
APA StyleLun-Fu, A., Borodin, V., Bubenchikov, M., Bubenchikov, A., & Mamontov, D. (2022). Fullerene in a Magnetic Field. Crystals, 12(4), 521. https://doi.org/10.3390/cryst12040521





