Interaction between a Screw Dislocation and Two Unequal Interface Cracks Emanating from an Elliptical Hole in One Dimensional Hexagonal Piezoelectric Quasicrystal Bi-Material

Abstract

Utilizing conformal transformation, a screw dislocation interacting with two unequal interface cracks emanating from an elliptical hole in a one-dimensional hexagonal piezoelectric quasicrystal bi-material was studied. The analytic expressions of the interface stresses, electric displacement and stress intensity factors were obtained. With the help of the generalization of the Peach–Koehler formula for quasicrystals, the image force acting on the dislocation due to the presence of the interface was then determined. Numerical examples are given to show the effects of the coupling elastic constants of the phonon field and phason field on the field intensity factors.

1. Introduction

As new functional and structural materials, quasicrystals (QCs) have been extensively used in many fields due to their special structures and excellent properties. Since quasicrystals were discovered by Shechtman et al. [1], the generalized elasticity theory of quasicrystals has been explored by many researchers [2,3]. Lubensky et al. [4] studied the motion of dislocation in quasicrystals, which revealed a close relationship with hydrodynamic equations. Jarić and Mohanty [5] developed a density-functional method for calculating the elastic moduli of icoshedral quasicrystals. Widom and Phillips [6] investigated the atomic structure of model decagonal quasicrystals. Fan and Sun [7] studied the problems with moving screw dislocations and straight dislocations in one-dimensional (1D) hexagonal QCs. Using the Stroh method, Radi and Mariano [8] studied the crack problem in two-dimensional (2D) QCs. Rogowski [9] studied the mode III fracture problem of cracks originating from an elliptical hole and obtained the exact analytical solutions of the field intensity factors and energy release rate. Li [10] considered the elasticity problem of one-dimensional hexagonal quasicrystals with planar cracks. Lazar and Agiasofitou [11] provided fundamental quantities for the generalized elasticity and dislocation theory of quasicrystals. Gao et al. [12] studied some of the defects in cubic QCs. Liu et al. [13], Wang and Zhong [14] studied the interactions between dislocations and cracks in 1D QCs and 2D QCs, respectively. Li and Liu [15] studied the interactions between dislocations and elliptical holes in three-dimensional (3D) QCs.

Quasicrystalline materials with piezoelectric effects have been widely investigated [16,17,18,19]. Guo et al. [20,21] studied the elliptical hole problem in QC piezoelectric materials based on the conformal mapping method. Tupholme [22] considered the anti-plane crack problem in 1D hexagonal piezoelectric quasicrystal materials through the continuous dislocation layer method. Zhou and Li [23] investigated the Yoffe-type moving crack problem in 1D hexagonal piezoelectric quasicrystal materials. These are very helpful to understand the mechanical properties of quasicrystal piezoelectric materials. However, there are few reported results on the interaction of defects in piezoelectric QCs materials.

The interaction between a screw dislocation and two unequal interface cracks emanating from the elliptical hole in one-dimensional hexagonal piezoelectric quasicrystal bi-material is considered in this paper. The analytical expressions for the stress intensity factors are presented in detail.

2. Basic Formulation

For point group 6 mm 1D hexagonal piezoelectric QC, supposing its polarized direction and quasi-periodic direction are along the $z$ axis in the 3D space coordinate system with an isotropic $xoy$ plane, the basic equations for the anti-plane problem can be written as follows [18].

Constitutive equations:

$$\{\begin{array}{c}{\sigma }_{z\beta }=2C_{44}{\epsilon }_{z\beta }+R_3{\omega }_{z\beta }-e_{15}{E}_{\beta }\\ H_{z\beta }=2R_3{\epsilon }_{z\beta }+K_2{\omega }_{z\beta }-d_{15}{E}_{\beta }\\ D_{\beta }=2e_{15}{\epsilon }_{z\beta }+d_{15}{\omega }_{z\beta }+{\lambda }_{11}{E}_{\beta }\end{array}$$

(1)

Geometry equations:

$${\epsilon }_{z\beta }=\frac{1}{2}{u}_{z,\beta }, {\omega }_{z\beta }=w_{z,\beta }, E_{\beta }=-{\varphi }_{,\beta }$$

(2)

Equilibrium equations (regardless of body force):

$${\sigma }_{z\beta ,\beta }=0, H_{z\beta ,\beta }=0,D_{\beta ,\beta }=0$$

(3)

where the commas represent partial differentiation and the repeated indices denote summation; ${\sigma }_{z\beta }$, ${\epsilon }_{z\beta }$ and $u_z$ denote the stress, strain and displacement of the phonon field, respectively; $\beta =x,y$; $H_{z\beta }$, ${\omega }_{z\beta }$ and $w_z$ refer to the stress, strain and displacement of phason the field, respectively; $D_{\beta }$, $E_{\beta }$ and $\varphi$ represent the electric displacement, the electric field and the electric potential, respectively; $C_{44}$, $K_2$ and $R_3$ are the elastic constants of the phonon field, phason field and coupling elastic constant of the phonon-phason field, respectively; $e_{15}$ and $d_{15}$ stand for the piezoelectric constants of the phonon field and the phason field, respectively; ${\lambda }_{11}$ denotes the dielectric permittivity.

According to Equations (1)–(3), the governing equations can be obtained as

$$B{\nabla }^{2}u=0$$

(4)

where $u={\left(u_z,w_z,\varphi \right)}^{\mathrm{T}}$, ${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$ is the 2D Laplace operator and

$$B=\left(\begin{array}{ccc}{C}_{44}& R_3& e_{15}\\ R_3& K_2& d_{15}\\ e_{15}& d_{15}& -{\lambda }_{11}\end{array}\right)$$

(5)

According to the properties of the analytic function, the analytic function vector $u$ can be expressed by the imaginary part of the analytic function vector $f(z)$ with the complex variable $z=x+iy$, i.e.,:

$$u=\mathrm{Im}f(z)$$

(6)

where Im denotes the imaginary part of a complex function.

After introducing the generalized strains $Z_x={[{\epsilon }_{zx},{\omega }_{zx},-E_x]}^{\mathrm{T}}$, $Z_y={[{\epsilon }_{zy},{\omega }_{zy},-E_y]}^{\mathrm{T}}$ and the generalized stresses ${\Sigma }_x={[{\sigma }_{zx},H_{zx},D_x]}^{\mathrm{T}}$, ${\Sigma }_y={[{\sigma }_{zy},H_{zy},D_y]}^{\mathrm{T}}$, we can obtain

$$Z_y+i{Z}_x=f^{\prime }(z)$$

(7)

$${\Sigma }_y+i{\Sigma }_x=B{f}^{\prime }(z)$$

(8)

where the superscript prime indicates the derivative with respect to the argument.

Using Equation (8), the normal component of the electric displacement and the forces along the arbitrary arc$AB$ can be represented as

$$T={\displaystyle {\int }_A^B{\Sigma }_{x}dy-}{\Sigma }_{y}dx=-B\mathrm{Re}{[f(z)]}_A^B$$

(9)

where Re denotes the real part of a complex function.

3. Statement of the Problem and Its Solution

The mechanical model considered here is as follows (Figure 1).

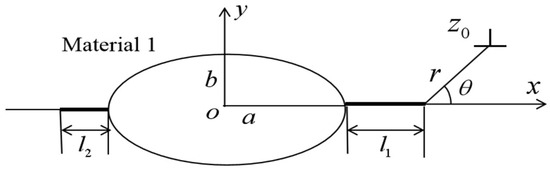
Figure 1. A screw dislocation interaction with two unequal interface cracks emanating from an elliptical hole in a QC piezoelectric bi-material.

Consider a quasi-crystal piezoelectric bi-material that consists of two dissimilar transversely isotropic media with respect to the poling direction ($z$-direction). It is assumed that the upper plane is material 1 and the lower plane is material 2. There are two asymmetrical interface cracks, given in Figure 1. Here, $a$ and $b$ denote the lengths of the major semi-axis and the minor semi-axis of the elliptical hole, respectively; $l_1$ and $l_2$ denote the lengths of the two cracks. A screw dislocation with Burgers vector $b={(b_3,b_{\perp },b_{\varphi })}^{\mathrm{T}}$, where the dislocation line perpendicular to the $z$-plane is located at $z_0=a+l_1+r{e}^{i\theta }$ in material 1, where $b_3$, $b_{\perp }$ stand for the displacement jump values of phonon field and phason field, respectively, $b_{\varphi }$ means the electric-potential jump value [24].

The boundary conditions of the present problem can be expressed as

$${\displaystyle {\int }_l}d{u}^{(1)}=b, {\displaystyle {\int }_l}{\Sigma }_y^{(1)}{d}_x-{\Sigma }_x^{(1)}{d}_y=0$$

(10)

$$u^{(1)}(z)=u^{(2)}(z), T^{(1)}(z)=T^{(2)}(z), z\in L^{\prime }$$

(11)

$$T^{(1)}(z)=T^{(2)}(z)=0, z\in L$$

(12)

where the superscript, (1) and (2), denote the quantities of material 1 and material 2, respectively; $L$ is the surface of hole and crack; and $L^{\prime }$ is the remainder of the interface, which is the perfect bonding between the material 1 and material 2.

In order to obtain the expressions of the complex function $f(z)$, we introduce a new conformal mapping function:

$$\zeta =G(z)=\frac{g(z)-\frac{b_1+a_1}{2}+\sqrt{(g(z)-a_1)(g(z)-b_1)}}{\frac{b_1-a_1}{2}}$$

(13)

where

$$g(z)=\frac{z}{a+b}+\frac{b}{z+\sqrt{z^2-a^2+b^2}}$$

(14)

and

$$a_1=-\frac{a+l_2}{a+b}-\frac{b}{a+l_2+\sqrt{b^2+2a{l}_2+l_2^2}},b_1=\frac{a+l_1}{a+b}-\frac{b}{a+l_1+\sqrt{b^2+2a{l}_1+l_1^2}}$$

(15)

The conformal mapping transforms the outside of the elliptical hole with two unequal cracks in the $z$-plane into the interior of a unit circle $\gamma$ in the $\zeta$-plane.

In the $\zeta$-plane, the Equations (11) and (12) can be rewritten as

$$u^{(1)}(\zeta )=u^{(2)}(\zeta ), T^{(1)}(\zeta )=T^{(2)}(\zeta ), \zeta \in L^{\prime }$$

(16)

$$T^{(1)}(\zeta )=T^{(2)}(\zeta )=0, \zeta \in \gamma$$

(17)

Assume the complex functions $f^{(j)} (j=1,2)$ in the $\zeta$-plane have the form

$$f^{(j)}(\zeta )=f_b{}^{(j)}(\zeta )+f_m{}^{(j)}(\zeta )$$

(18)

where $f_b{}^{(j)}(\zeta )$, $(j=1,2)$ represent the functions associated with the solutions for one-dimensional hexagonal piezoelectric quasicrystal bi-material subjected to a screw dislocation, while $f_m{}^{(j)}(\zeta )$ represent the functions corresponding to the perturbed fields due to the crack.

Assume that the functions $f_b{}^{(j)}(\zeta )$ can be given as

$$f_b^{(1)}(\zeta )=f_0^{(1)}(\zeta )+f_p^{(1)}(\zeta ) ,f_b^{(2)}(\zeta )=f_p^{(2)}(\zeta )$$

(19)

where $f_0^{(1)}(\zeta )$ represent the function corresponding to the unperturbed field and is analytic except for the point of ${\zeta }_0$; $f_p^{(j)}(\zeta ) (j=1,2)$ denotes the perturbed fields in the material $j$.

From Equation (10), $f_0^{(1)}(\zeta )$ is given as

$$f_0^{(1)}(\zeta )=\frac{1}{2\pi }b\ln (\zeta -{\zeta }_0)$$

(20)

Substituting Equations (6) and (9) into Equation (16), we obtain

$$\mathrm{Im}[f_b{}^{(1)}(\zeta )]=\mathrm{Im}[f_b{}^{(2)}(\zeta )], B^{(1)}\mathrm{Re}[f_b{}^{(1)}(\zeta )]=B^{(2)}\mathrm{Re}[f_b{}^{(2)}(\zeta )]$$

(21)

Utilizing Equations (19) and (21), noting that $\overline{\zeta }=\zeta$ holds along the real axis, we have

$$f_b{}^{(1)}(\zeta )=\frac{1}{2\pi }[I\ln (\zeta -{\zeta }_0)+{\Pi }_{12}\ln (\zeta -{\overline{\zeta }}_0)]b$$

(22)

$$f_b{}^{(2)}(\zeta )=\frac{1}{2\pi }(I-{\Pi }_{12})b\ln (\zeta -{\zeta }_0)$$

(23)

where the overbar means the conjugate, $I$ is a $3\times 3$ unit matrix and

$${\Pi }_{12}={(B^{(2)}+{{\rm B}}^{(1)})}^{-1}(B^{(2)}-{{\rm B}}^{(1)})$$

(24)

By taking Equations (9), (17), (18), (22) and (23) and noting $\overline{\zeta }={\zeta }^{-1}$ holds along the unit circle $\gamma$, one can obtain

$$f_m^{(1)}(\zeta )=-\frac{1}{2\pi }[I\ln (\zeta -{\overline{\zeta }}_0^{-1})+{\Pi }_{12}\ln (\zeta -{\zeta }_0^{-1})-(I+{\Pi }_{12})\ln \zeta ]b$$

(25)

$$f_m^{(2)}(\zeta )=-\frac{1}{2\pi }(I-{\Pi }_{12})[\ln (\zeta -{\overline{\zeta }}_0^{-1})-\ln \zeta ]b$$

(26)

Substituting Equations (22), (23), (25) and (26) into Equation (18), the complex potential in the $\zeta$-plane is expressed as follows.

$$\begin{array}{l}{f}^{(1)}(\zeta )=\frac{1}{2\pi }[I\ln (\zeta -{\zeta }_0)+{\Pi }_{12}\ln (\zeta -{\overline{\zeta }}_0)-I\ln (\zeta -{\overline{\zeta }}_0^{-1})\\ -{\Pi }_{12}\ln (\zeta -{\zeta }_0^{-1})+(I+{\Pi }_{12})\ln \zeta ]b\end{array}$$

(27)

$$f^{(2)}(\zeta )=\frac{1}{2\pi }(I-{\Pi }_{12})[\ln (\zeta -{\zeta }_0)-\ln (\zeta -{\overline{\zeta }}_0^{-1})+\ln \zeta ]b$$

(28)

With Equations (8), (27) and (28), the complex expressions of the generalized stresses can be obtained as

$$\begin{array}{l}{\Sigma }_y^{(1)}+i{\Sigma }_x^{(1)}=\frac{1}{2\pi }{B}^{(1)}b{G}^{\prime }(z)\frac{1}{\sqrt{(g(z)-a_1)(g(z)-b_1)}}\\ \times [I(\frac{\zeta }{\zeta -{\zeta }_0}+\frac{1}{1-\zeta {\overline{\zeta }}_0})+{\Pi }_{12}(\frac{\zeta }{\zeta -{\overline{\zeta }}_0}+\frac{1}{1-\zeta {\zeta }_0})]\\ \end{array}$$

(29)

$$\begin{array}{l}{\Sigma }_y^{(2)}+i{\Sigma }_x^{(2)}=\frac{1}{2\pi }{B}^{(2)}{G}^{\prime }(z)\frac{1}{\sqrt{(g(z)-a_1)(g(z)-b_1)}}\times (I-{\Pi }_{12})[\frac{\zeta }{\zeta -{\zeta }_0}+\frac{1}{1-\zeta {\overline{\zeta }}_0}]b\\ \end{array}$$

(30)

4. Stress Intensity Factors (SIFs) and Image Force of the Dislocation

The SIFs in the phonon and phason fields and the electric displacements intensity factors at the right crack tip are defined as

$$K=\left\{\begin{array}{c}{K}_{\sigma }\\ K_H\\ K_D\end{array}\right\}=\underset{z\to a+l_1}{\lim }\sqrt{2\pi (z-a-l_1)}{\Sigma }_y^{(j)}=\frac{1}{\sqrt{2\pi (b_1-a_1)}}{B}^{eff}{G}^{\prime }(a+l_1)\times [\frac{1}{1-{\zeta }_0}+\frac{1}{1-{\overline{\zeta }}_0}]b$$

(31)

The matrix $B^{eff}$ is

$$B^{eff}=2B^{\left(2\right)}{(B^{\left(2\right)}+B^{\left(1\right)})}^{-1}{B}^{\left(1\right)}=2B^{\left(1\right)}{(B^{\left(2\right)}+B^{\left(1\right)})}^{-1}{B}^{\left(2\right)}$$

(32)

The Peach–Koehler force for quasicrystals plays an important role in the defect mechanics of quasicrystals. The Peach–Koehler force, an important quantity for the theory of dislocations of quasicrystals, is derived in [11]. Li and Fan [25] obtained the force between two parallel screw dislocations by extending the Peach-Koehler force to quasicrystals. We therefore discuss the generalized Peach-Koehler force for piezoelectric quasicrystals.

Consider two stress field systems, S and T, both of which represent singularities corresponding to the physical defects in a linear elastic piezoelectric quasicrystal (Figure 2):

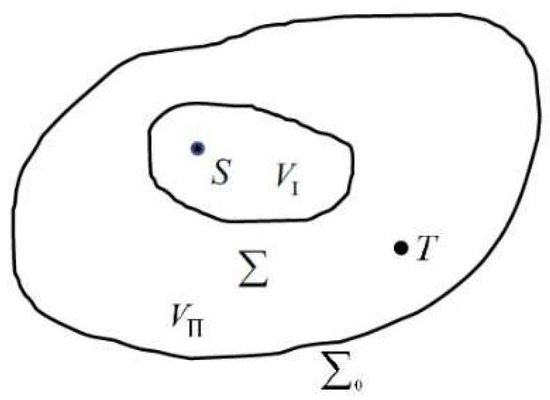
Figure 2. Electro-elastic singularities S and T in a piezoelectric quasicrystal, where $\mathsf{\Sigma }$ is any surface enclosing S.

The total interaction enthalpy can be written as

$$E_{\mathrm{tot}}={\displaystyle {\int }_{V_{\mathrm{I}}+V_{\mathrm{II}}}[\frac{1}{2}(}{\sigma }_{ij}^S{\epsilon }_{ij}^T+H_{ij}^S{w}_{ij}^T-D_i^S{E}_i^T)+\frac{1}{2}({\sigma }_{ij}^T{\epsilon }_{ij}^S+H_{ij}^T{w}_{ij}^S-D_i^T{E}_i^S]]dV$$

(33)

By using divergence theorem, the total interaction enthalpy can be rewritten as

$$E_{\mathrm{tot}}={\displaystyle {\int }_{\Sigma }[}{\sigma }_{ij}^S{u}_i^T+H_{ij}^S{w}_i^T+D_j^S{\varphi }^T-{\sigma }_{ij}^T{u}_i^S-H_{ij}^T{w}_i^S-D_j^T{\varphi }^S]dS\hspace{1em}\hspace{1em}$$

(34)

We are interested in calculating the total interaction enthalpy and calculate the force acting on a dislocation. Choose a contour C surrounding the dislocation, as shown in Figure 3.

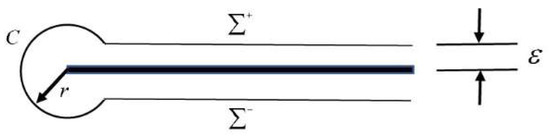
Figure 3. Contour surrounding piezoelectric quasicrystal dislocation core and slip plane.

We assume that the fields associated with T are continuous in the neighborhood of the contour C. Following Bilby and Shelbie [26], calculating the contributions from the integrals on contours ${\mathsf{\Sigma }}^{+}$ and ${\mathsf{\Sigma }}^{-}$ as $\epsilon \to 0$, Equation (34) becomes

$$E_{\mathrm{tot}}=b_i^{\parallel }{\displaystyle {\int }_{{\mathsf{\Sigma }}^{+}}{\sigma }_{ij}^T{n}_{j}dS}+b_i^{\perp }{\displaystyle {\int }_{{\mathsf{\Sigma }}^{+}}{H}_{ij}^T{n}_{j}dS}+b_{\varphi }{\displaystyle {\int }_{{\mathsf{\Sigma }}^{+}}{D}_j^T}{n}_{j}dS$$

(35)

$b_i^{\parallel },b_i^{\perp }$ represent the displacement jump values of the phonon field and phason field in the $x_i$ direction, respectively.

If giving the dislocation a virtual incremental displacement $\delta {\xi }_k$, the general expression for the force acting on a dislocation in a piezoelectric quasicrystal is

$$F_k=-\frac{\delta E_{\mathrm{tot}}}{\delta {\xi }_k}=-(b_j^{\parallel }{\sigma }_{ij}^T+b_j^{\perp }{H}_{ij}^T+b_{\varphi }{D}_j^T){\epsilon }_{jkl}{s}_l$$

(36)

in which ${\epsilon }_{jkl}$ is an alternating tensor and $s_l$ is a unit vector parallel to the dislocation line.

According to Equation (36), the image forces exerted on the dislocation due to the presence of the crack can be obtained as

$$F_x-i{F}_y=b^{\mathrm{T}}\left[ \Sigma { }_{yp}^{\left(1\right)}\left(z_0\right)+i{\Sigma }_{xp}^{\left(1\right)}\left(z_0\right)\right]$$

(37)

where ${\Sigma }_{kp}^{\left(1\right)}\left(z_0\right)\left(k=x,y\right)$ denotes the perturbation stresses of the phonon fields, the perturbation stresses of the phason fields and the perturbed electric displacements at the dislocation point $z_0$. Subtracting ${\Sigma }_{k0}^{\left(1\right)}\left(z_0\right)$ for a screw dislocation in infinite material with $B^{\left(1\right)}$ from the corresponding ${\Sigma }_k^{\left(1\right)}\left(z_0\right)$, the perturbed stresses of the phonon and phason fields and electric displacements are obtained.

With Equations (8) and (10), we have

$${\Sigma }_{y0}^{\left(1\right)}\left(z_0\right)+i{\Sigma }_{x0}^{\left(1\right)}\left(z_0\right)=\frac{1}{2\pi }{B}^{\left(1\right)}\frac{1}{z-z_0}b$$

(38)

Therefore, the image force acting on the screw dislocation in material 1 is

$$\begin{array}{l}{F}_x-i{F}_y=\frac{1}{2\pi }{b}^{\mathrm{T}}\frac{B^{(1)}{g}^{\prime }(z_0)}{\sqrt{(g(z_0)-a_1)(g(z_0)-b_1)}}[I(\frac{1}{2}-\frac{2g(z_0)-a_1-b_1}{4\sqrt{(g(z_0)-a_1)(g(z_0)-b_1)}}\\ -\frac{g^{″}(z_0)\sqrt{(g(z_0)-a_1)(g(z_0)-b_1)}}{2{\left[g^{\prime }(z_0)\right]}^2}-\frac{1}{{\zeta }_0{\overline{\zeta }}_0-1})+{\Pi }_{12}(\frac{{\zeta }_0}{{\zeta }_0-{\overline{\zeta }}_0}-\frac{1}{{\zeta }_0^2-1})]b\end{array}$$

(39)

some special cases of these results are discussed in detail below.

(1)

If $b=0$, $l_1=l_2$, Equation (29) degenerates into

$$\begin{array}{l}{\Sigma }_y^{(1)}+i{\Sigma }_x^{(1)}=\frac{1}{2\pi }{B}^{(1)}\frac{1}{\sqrt{z^2-{(a+l_1)}^2}}[I\frac{{\zeta }_1}{{\zeta }_1-{\zeta }_{10}}\\ +{\Pi }_{12}\frac{{\zeta }_1}{{\zeta }_1-{\overline{\zeta }}_{10}}+I\frac{1}{1-{\zeta }_1{\overline{\zeta }}_{10}}+{\Pi }_{12}\frac{1}{1-{\zeta }_1{\zeta }_{10}}]b\\ \end{array}$$

(40)

where ${\zeta }_1=\frac{z+\sqrt{z^2-{(a+l_1)}^2}}{a+l_1}$, ${\zeta }_{10}=\frac{z_0+\sqrt{z_0^2-{(a+l_1)}^2}}{a+l_1}$. Equation (40) represents the case of the interaction between a screw dislocation and the length of the $2(a+l_1)$ interface crack in the infinite quasicrystal piezoelectric bi-material.

(2)

If $l_2=l_1=0$, Equation (29) can be reduced to the case of a screw dislocation interacting with an elliptical hole in the infinite quasicrystal piezoelectric bi-material.

$$\begin{array}{l}{\Sigma }_y^{(1)}+i{\Sigma }_x^{(1)}=\frac{1}{2\pi \sqrt{z^2-a^2+b^2}}{C}^{(1)}[I\frac{{\zeta }_2}{{\zeta }_2-{\zeta }_{20}}\\ +\Pi \frac{{\zeta }_2}{{\zeta }_2-{\overline{\zeta }}_{20}}+I\frac{1}{1-{\zeta }_2{\overline{\zeta }}_{20}}+\Pi \frac{1}{1-{\zeta }_2{\zeta }_{20}}]b\\ \end{array}$$

(41)

where ${\zeta }_2=\frac{z+\sqrt{z^2-a^2+b^2}}{a+b}$, ${\zeta }_{20}=\frac{z_0+\sqrt{z_0^2-a^2+b^2}}{a+b}$.

The results can be further reduced to the case of a screw dislocation interacting with an elliptical hole when the material is the pure elastic bi-material. This is consistent with the results in [27].

(3)

If $l_1=l_2=0$, $a=b$, Equation (29) becomes

$$\begin{array}{l}{\Sigma }_y^{(1)}+i{\Sigma }_x^{(1)}=\frac{1}{2\pi }{B}^{(1)}\frac{z^2-a^2}{2a{z}^2}\frac{1}{\sqrt{(g_1(z)-a_2)(g_1(z)-b_2)}}[I\frac{{\zeta }_3}{{\zeta }_3-{\zeta }_{30}}\\ +{\Pi }_{12}\frac{{\zeta }_3}{{\zeta }_3-{\overline{\zeta }}_{30}}+I\frac{1}{1-{\zeta }_3{\overline{\zeta }}_{30}}+{\Pi }_{12}\frac{1}{1-{\zeta }_3{\zeta }_{30}}]b\\ \end{array}$$

(42)

where

${\zeta }_3=\frac{g_1(z)-\frac{b_2+a_2}{2}+\sqrt{(g_1(z)-a_2)(g_1(z)-b_2)}}{\frac{b_2-a_2}{2}}$, ${\zeta }_{30}=\frac{g_1(z_0)-\frac{b_2+a_2}{2}+\sqrt{(g_1(z_0)-a_2)(g_1(z_0)-b_2)}}{\frac{b_2-a_2}{2}}$, $a_2=-\frac{a+l_1}{2a}-\frac{a}{2a+2l_1}$, $b_2=\frac{a+l_1}{2a}+\frac{a}{2a+2l_1}$ and $g_1(z)=\frac{z}{2a}+\frac{a}{2z}$.

Equation (42) presents the interaction between a screw dislocation and a circular hole when the material is the pure elastic bi-material. This is consistent with the results in [28].

(4)

If $a=0$, Equation (29) reduces to

$$\begin{array}{l}{\Sigma }_y^{(1)}+i{\Sigma }_x^{(1)}=\frac{1}{2\pi }{B}^{(1)}\frac{1}{\sqrt{(g_2(z)-a_3)(g_2(z)-b_3)}}[I\frac{{\zeta }_4}{{\zeta }_4-{\zeta }_{40}}\\ +{\Pi }_{12}\frac{{\zeta }_4}{{\zeta }_4-{\overline{\zeta }}_{40}}+I\frac{1}{1-{\zeta }_4{\overline{\zeta }}_{40}}+{\Pi }_{12}\frac{1}{1-{\zeta }_4{\zeta }_{40}}]b\\ \end{array}$$

(43)

where

${\zeta }_4=\frac{g_2(z)-\frac{b_3+a_3}{2}+\sqrt{(g_2(z)-a_3)(g_2(z)-b_3)}}{\frac{b_3-a_3}{2}}$, ${\zeta }_{40}=\frac{g_2(z_0)-\frac{b_3+a_3}{2}+\sqrt{(g_2(z_0)-a_3)(g_2(z_0)-b_3)}}{\frac{b_3-a_3}{2}}$, $a_3=-\frac{1}{b}\sqrt{l_2^2+b^2}$, $b_3=\frac{1}{b}\sqrt{l_1^2+b^2}$ and $g_2(z)=\frac{1}{b}\sqrt{z^2+b^2}$.

Equation (43) shows the results of the interaction between a screw dislocation and an interface crisscross crack.

(5)

When $l_2=0$, one has that $a_1=-1$ from Equation (15). In this case, the Equation (29) can be simplified as

$$\begin{array}{l}{\Sigma }_y^{(1)}+i{\Sigma }_x^{(1)}=\frac{1}{2\pi }{B}^{(1)}\left[\frac{a}{a^2-b^2}-\frac{bz}{(a^2-b^2){(z^2-a^2+b^2)}^{\frac{1}{2}}}\right]\frac{1}{\sqrt{(g(z)+\mathrm{1})g(z)-b_1)}}\\ \times [I\frac{\zeta }{\zeta -{\zeta }_0}+{\Pi }_{12}\frac{\zeta }{\zeta -{\zeta }_0}+I\frac{1}{1-\zeta {\overline{\zeta }}_0}+{\Pi }_{12}\frac{1}{1-\zeta {\overline{\zeta }}_0}]b\\ \end{array}$$

(44)

This is the result of a single-interface crack originating from the edge of an elliptical hole. In particular, when $a$ tends to zero, the result of a screw dislocation interacting with the interface T-shaped crack can be obtained from Equation (44).

(6)

If $l_2=l_1$, the stress field of the interaction between a screw dislocation and two symmetrical cracks originating from an elliptical hole can be simulated from Equation (29):

$$\begin{array}{l}{\Sigma }_y^{(1)}+i{\Sigma }_x^{(1)}=\frac{1}{2\pi }{B}^{(1)}\left[\frac{a}{a^2-b^2}-\frac{bz}{(a^2-b^2){(z^2-a^2+b^2)}^{\frac{1}{2}}}\right]\frac{1}{\sqrt{g^2(z)-b_1^2}}\\ [I\frac{{\zeta }_5}{{\zeta }_5-{\zeta }_{50}}+{\Pi }_{12}\frac{{\zeta }_5}{{\zeta }_5-{\overline{\zeta }}_{50}}+I\frac{1}{1-{\zeta }_5{\overline{\zeta }}_{50}}+{\Pi }_{12}\frac{1}{1-{\zeta }_5{\zeta }_{50}}]b\\ \end{array}$$

(45)

where ${\zeta }_5=\frac{g(z)-\sqrt{g^2(z)-b_1^2}}{b_1}$, ${\zeta }_{50}=\frac{g(z_0)-\sqrt{g^2(z_0)-b_1^2}}{b_1}$.

5. Numerical Examples

The effects of the material constants on the field intensity factors and image forces are illustrated in this section. Table 1 lists the material properties of the bi-materials [29,30,31,32].

Table 1. Material properties of two 1D hexagonal piezoelectric QCs.

	${\mathit{C}}_{44} (\mathbf{GPa})$	${\mathit{K}}_2 (\mathbf{GPa})$	${\mathit{e}}_{15} (\mathbf{C}\cdot {\mathbf{m}}^{-2})$	${\mathit{d}}_{15} (\mathbf{C}\cdot {\mathbf{m}}^{-2})$	${\mathit{\lambda }}_{11} ({10}^{-9}{\mathbf{C}}^2{\mathbf{N}}^{-1}{\mathbf{m}}^{-2})$
Material 1	50	0.3	−0.318	−0.16	0.0826
Material 2	70.19	24	11.6	1.16	5

In the computation, we might set the coupling constant of material 2 $R_3^{(2)}=0.8846 \mathrm{GPa}$ [33].

The other parameters are selected as follows:

$b_{{}_3}=1.6\times {10}^{-9} \mathrm{m}$, $b_{\perp }=10.7 \times {10}^{-9} \mathrm{m}$, $b_{\varphi }=1\times {10}^{-9} \mathrm{V}$.

Figure 4 and Figure 5 show the variations of the normalized phonon and phason SIFs with the angular position $\theta$ of the dislocation for different values of $R_3^{(1)}$ at $a=0.01 \mathrm{m}$, $b=0.005 \mathrm{m}$, $l_1=0.005 \mathrm{m}$, $l_2=0.008 \mathrm{m}$. We found that the SIFs are negative in this condition, which shows that screw dislocation can reduce the shielding effect. The shielding effect increases as the value of the coupling constants $R_3^1$ increases, but decreases as the value of $\theta$ increases.

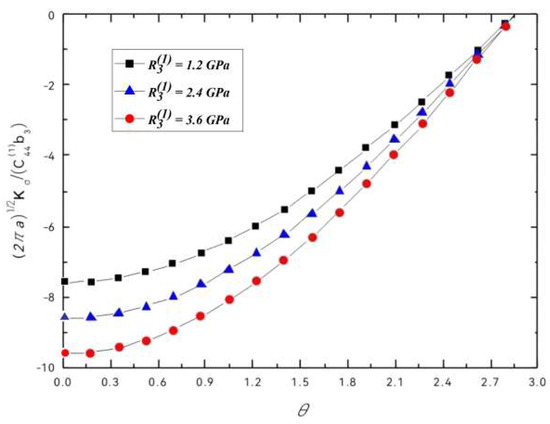
Figure 4. Normalized phonon SIFs ${(2\pi a)}^{1/2}{K}_{\sigma }/(C_{44}^{(1)}{b}_3)$ vs. $\theta$.

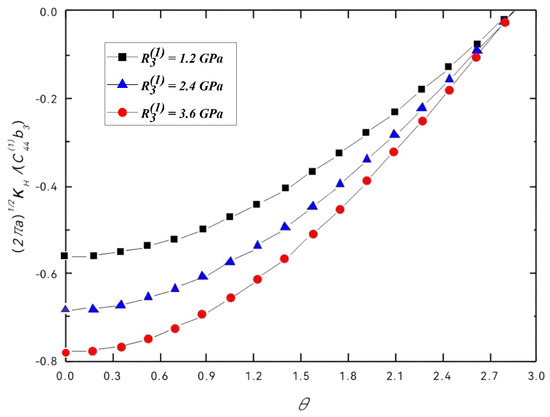
Figure 5. Normalized phason SIFs ${(2\pi a)}^{1/2}{\mathit{K}}_H/(C_{44}^{(1)}{b}_3)$ vs. $\theta$.

Figure 6 and Figure 7 show the variations of the normalized phonon and phason stress intensity factors with $r/a$ for different values of $R_3^{(1)}$ at $a=0.01 \mathrm{m}$, $b=0.005 \mathrm{m}$, $l_1=0.005 \mathrm{m}$, $l_2=0.008 \mathrm{m}$. We found that the SIFs are negative in this condition, which shows that screw dislocation can reduce the shielding effect. The shielding effect increases as the value of the coupling constants $R_3^1$ increases, but decreases as the value of $r/a$ increases.

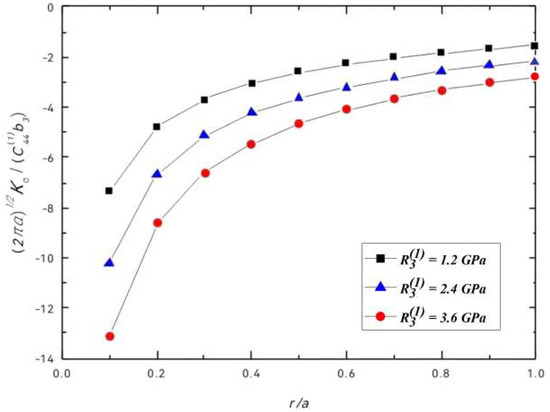
Figure 6. Normalized phonon SIFs ${(2\pi a)}^{1/2}{\mathit{K}}_{\sigma }/(C_{44}^{(1)}{b}_3)$ vs. $r/a$.

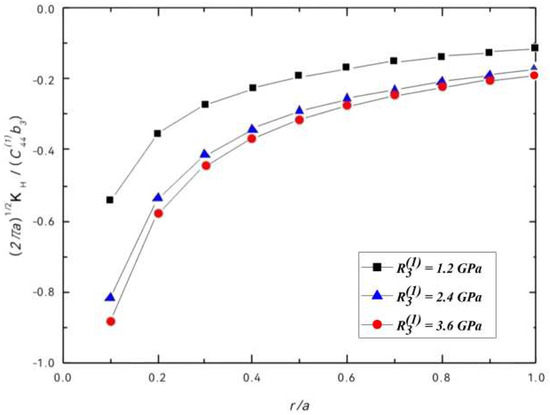
Figure 7. Normalized phason SIFs ${(2\pi a)}^{1/2}{\mathit{K}}_H/(C_{44}^{(1)}{b}_3)$ vs. $r/a$.

Figure 8 and Figure 9 give the relation between the normalized image force and $r/a$ for selected elevation angles θ. As shown in Figure 6, we found that the value of the normalized image force in the x-axis direction decreases with the increase in $\theta$ and increases with the increase in $r/a$. The crack always attracts the dislocation in the x-axis direction. As shown in Figure 9, we found that whether the image force in the y-axis direction is attractive or repulsive is difficult to determine because it is affected by the position of the dislocation.

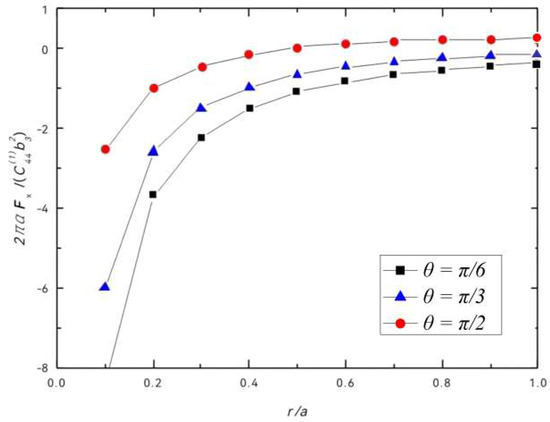
Figure 8. Normalized image force $2\pi a{\mathit{F}}_x/(C_{44}^{(1)}{b}_3^2)$ vs. $r/a$.

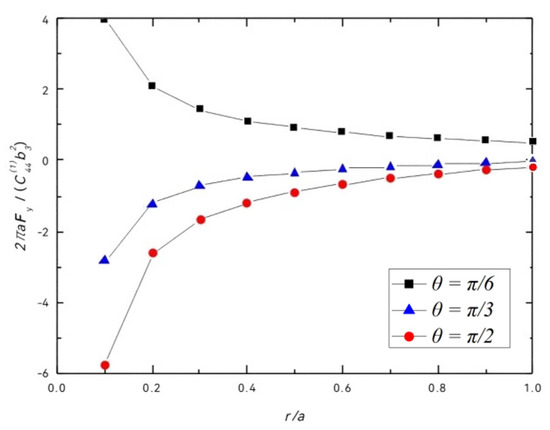
Figure 9. Normalized image force $2\pi a{\mathit{F}}_y/(C_{44}^{(1)}{b}_3^2)$ vs. $r/a$.

6. Conclusions

The interaction between screw dislocation and two unequal cracks in one-dimensional hexagonal piezoelectric quasicrystal bi-materials was studied using the complex function method. The complex expressions for the stresses and electric displacements are given in this article. The results of this paper are consistent with those in some literatures. Numerical examples show that the coupling elastic constant of the phonon and phason fields has a significant effect on the stress intensity factor. The method adopted in this paper can be extended to other problems of interactions between defects in quasicrystals.