Rate-Controlling Microplastic Processes during Plastic Flow in FCC Metals: Origin of the Variation of Strain Rate Sensitivity in Aluminum from 78 to 300 K
Abstract
:1. Introduction
1.1. Background to Microplastic Processes for Metal Formability
1.2. Theoretical Basis of Thermodynamic Strain Rate Sensitivity
2. Modus Operandi
2.1. Thermodynamic Bases for the Temperature (T) Dependence of Activation Work (τν = k/S)
2.2. The Role of Internal Stress in Stress-Aided Thermal Activation
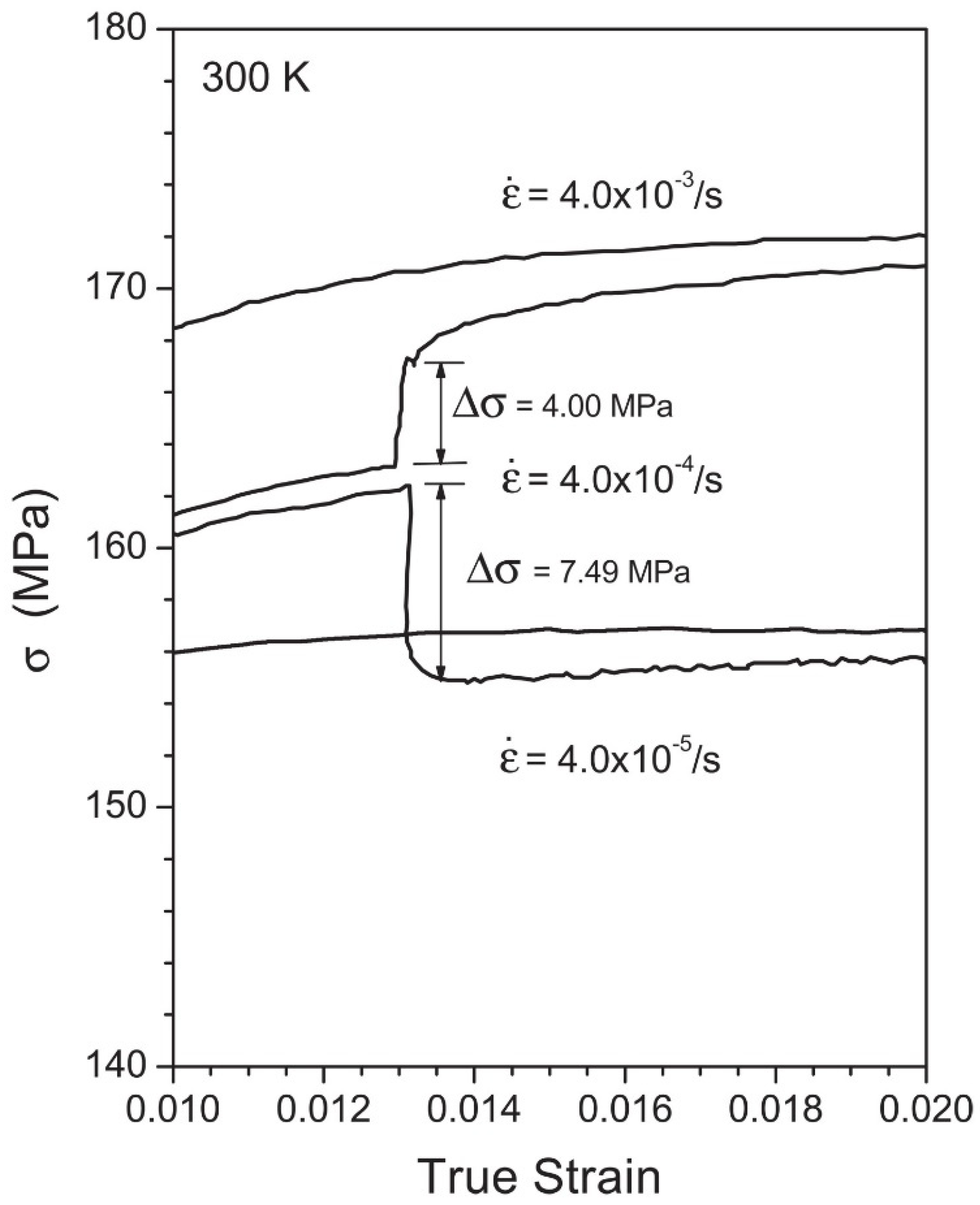
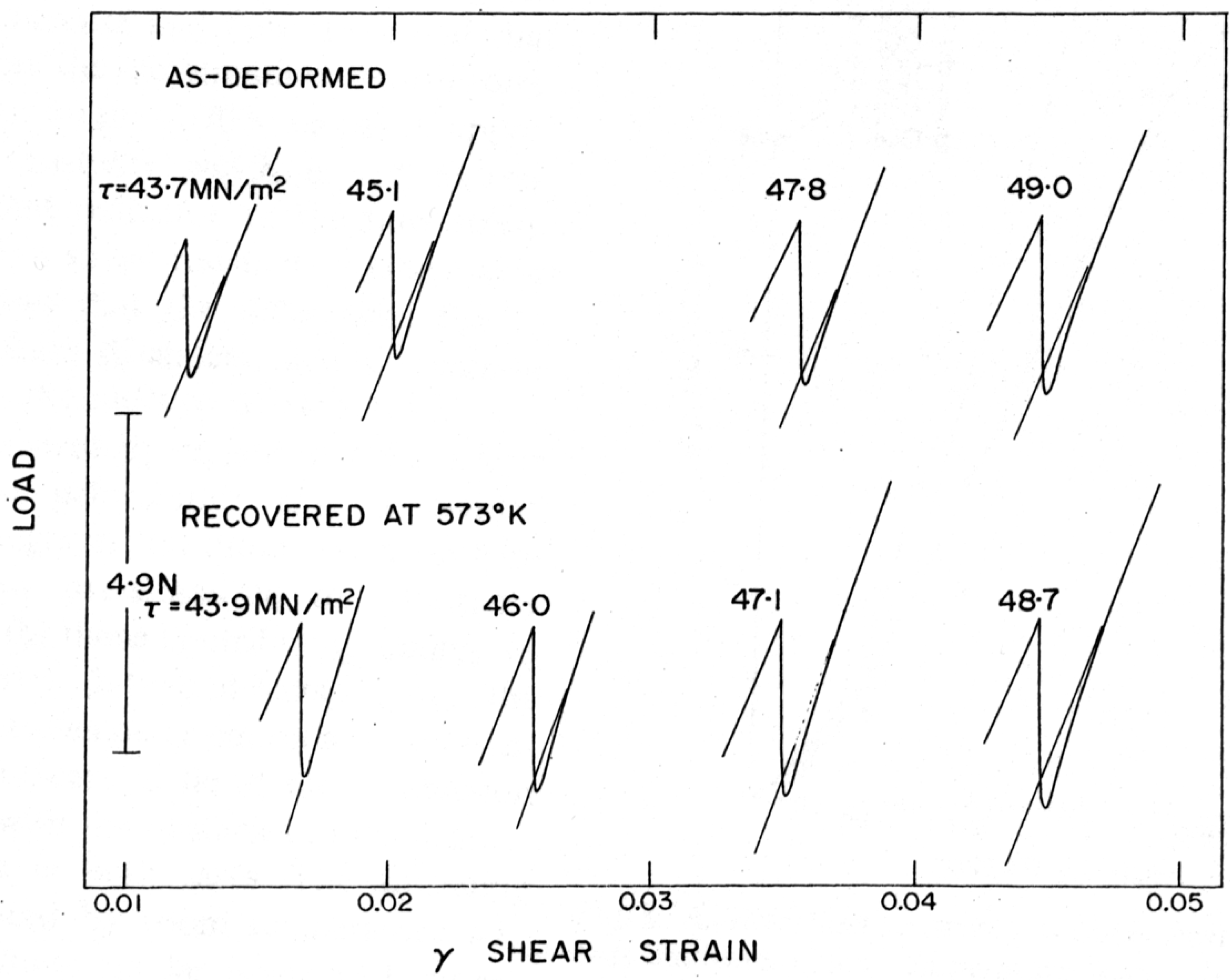
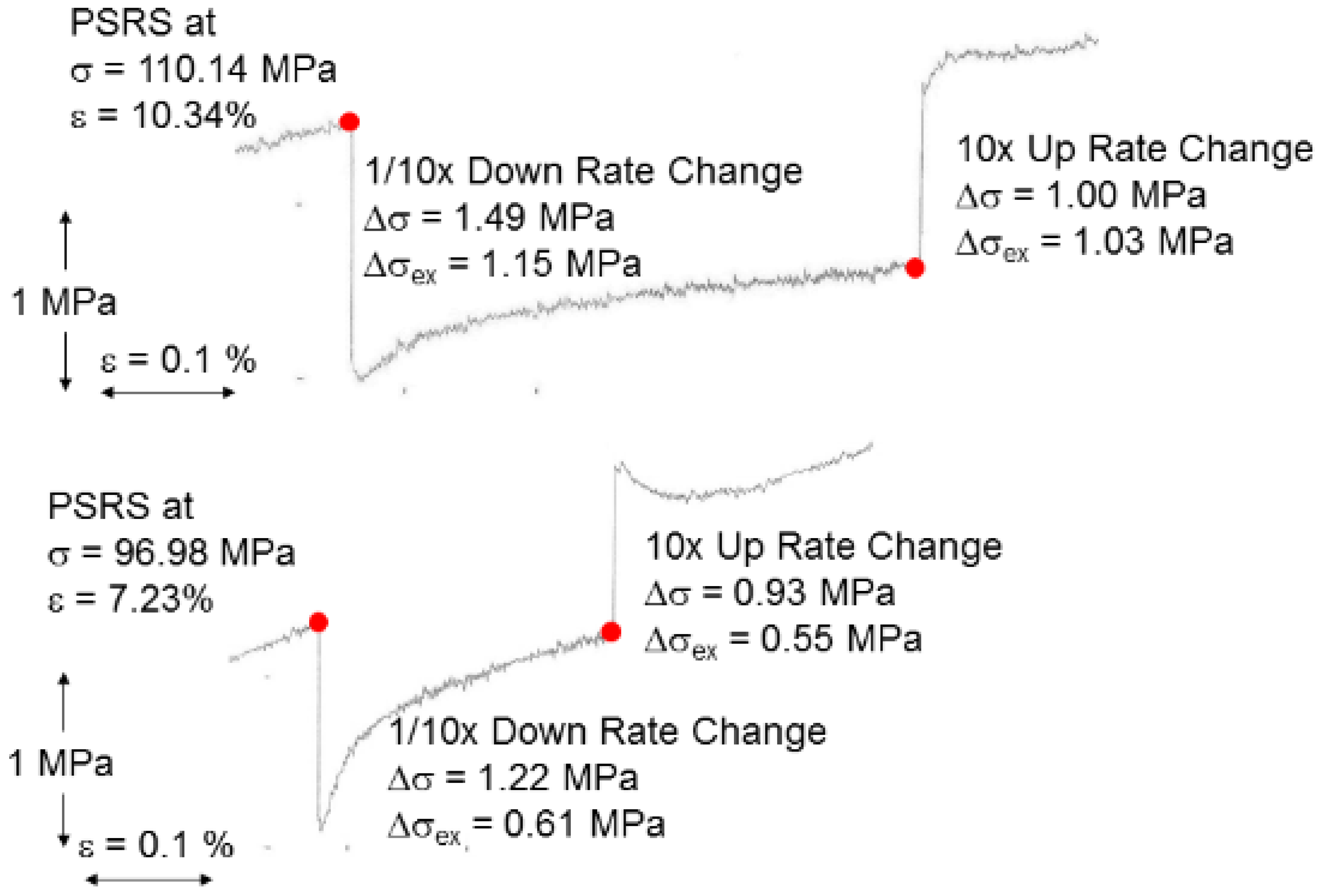
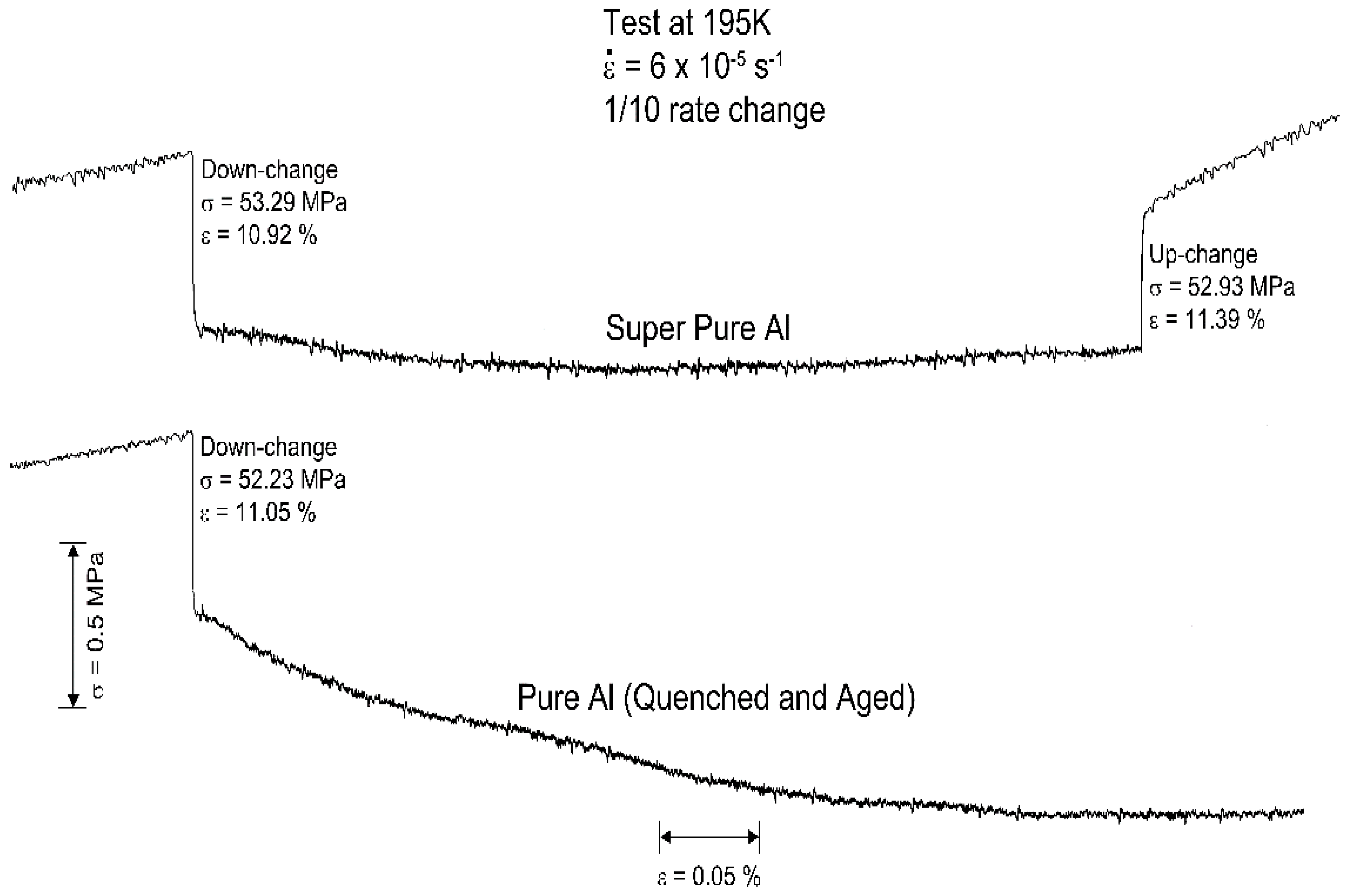
2.3. Forensic Summaries of Temperature and Strain-Rate Change Experiments
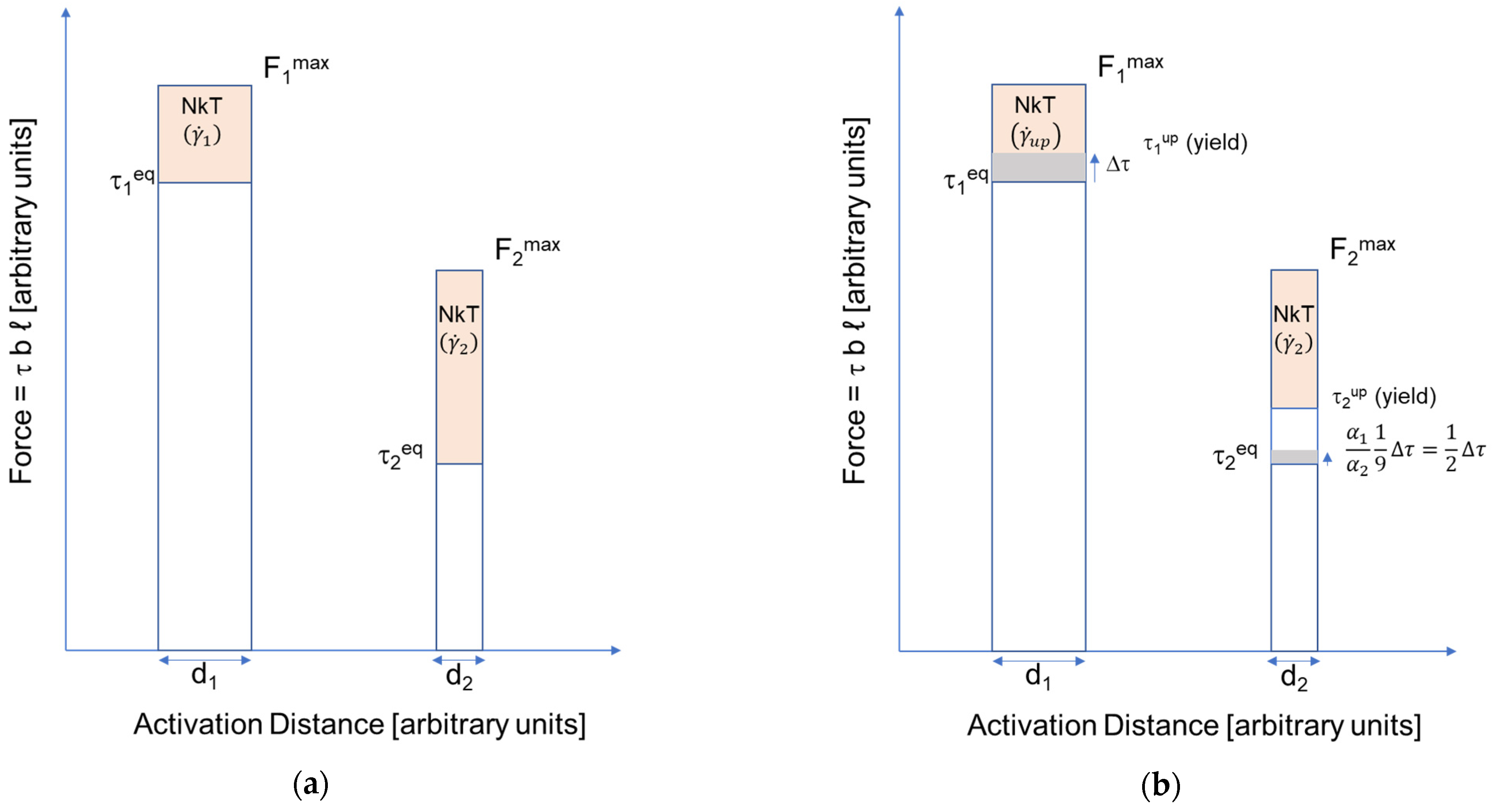
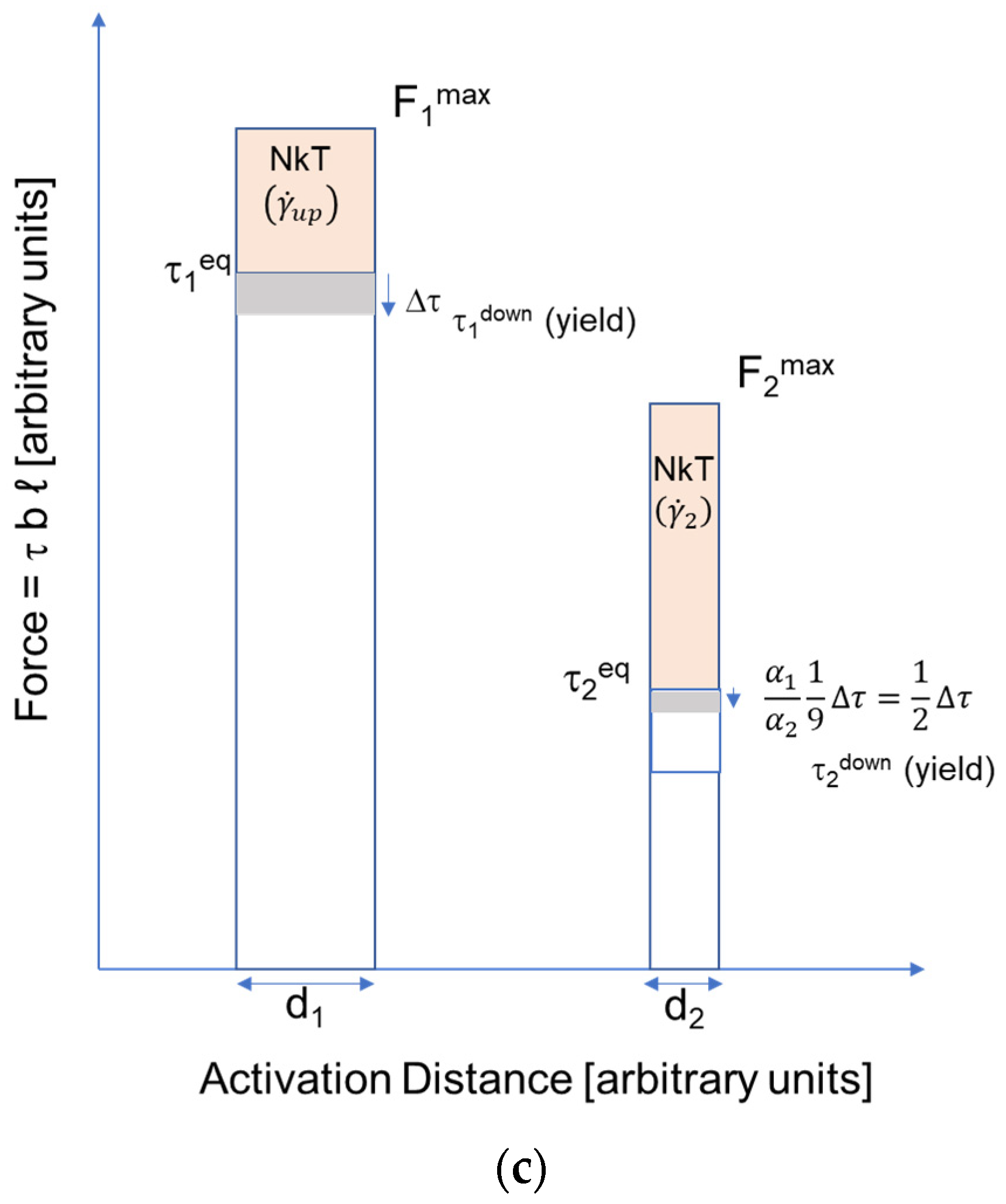
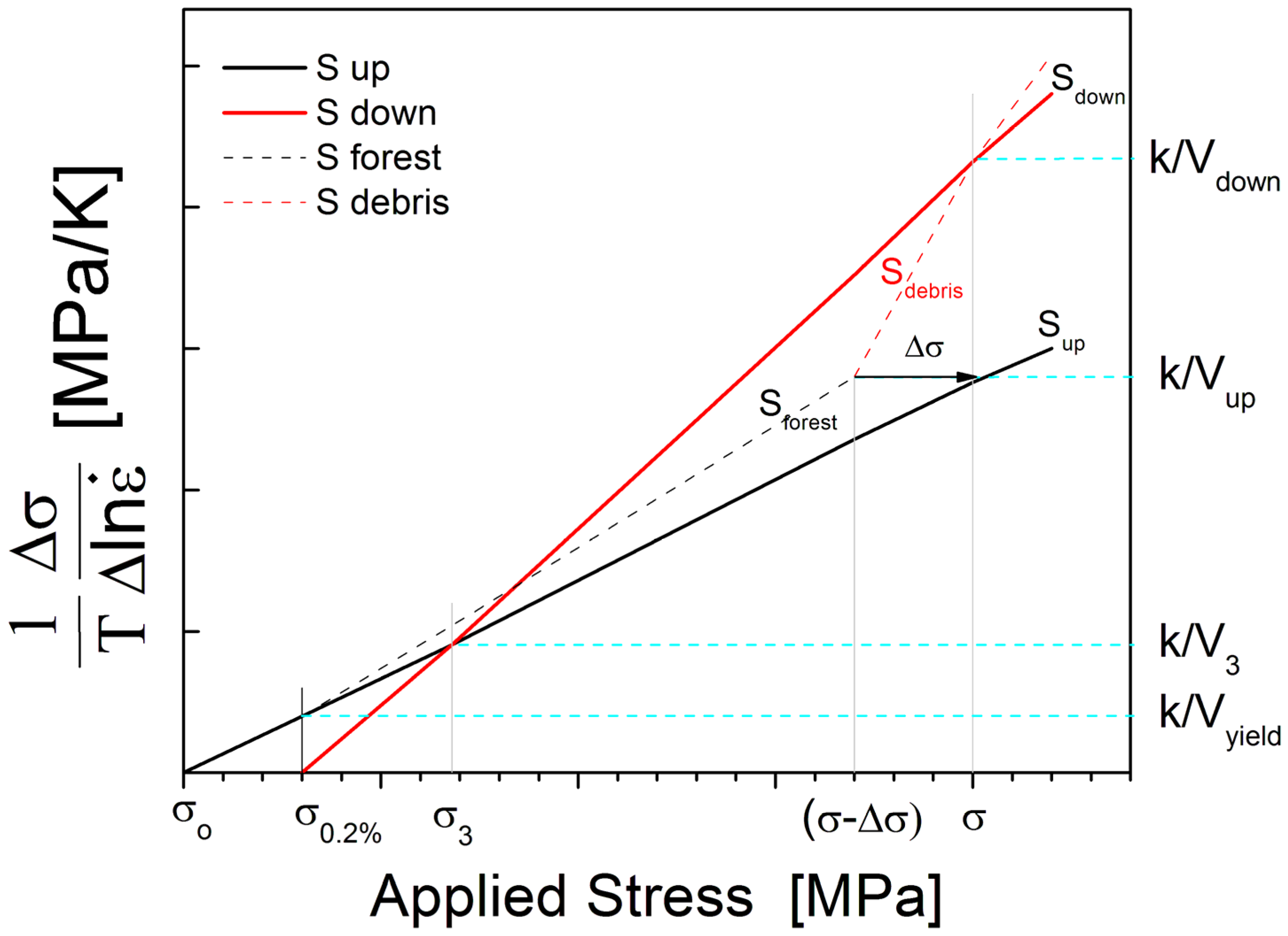
2.4. Schematic Analyses of the Haasen Plot Using Additivity of 1/ν
3. Experimental Methods
4. Results
4.1. Migration of Deformation-Produced Vacancies to Various Sinks at 195 K
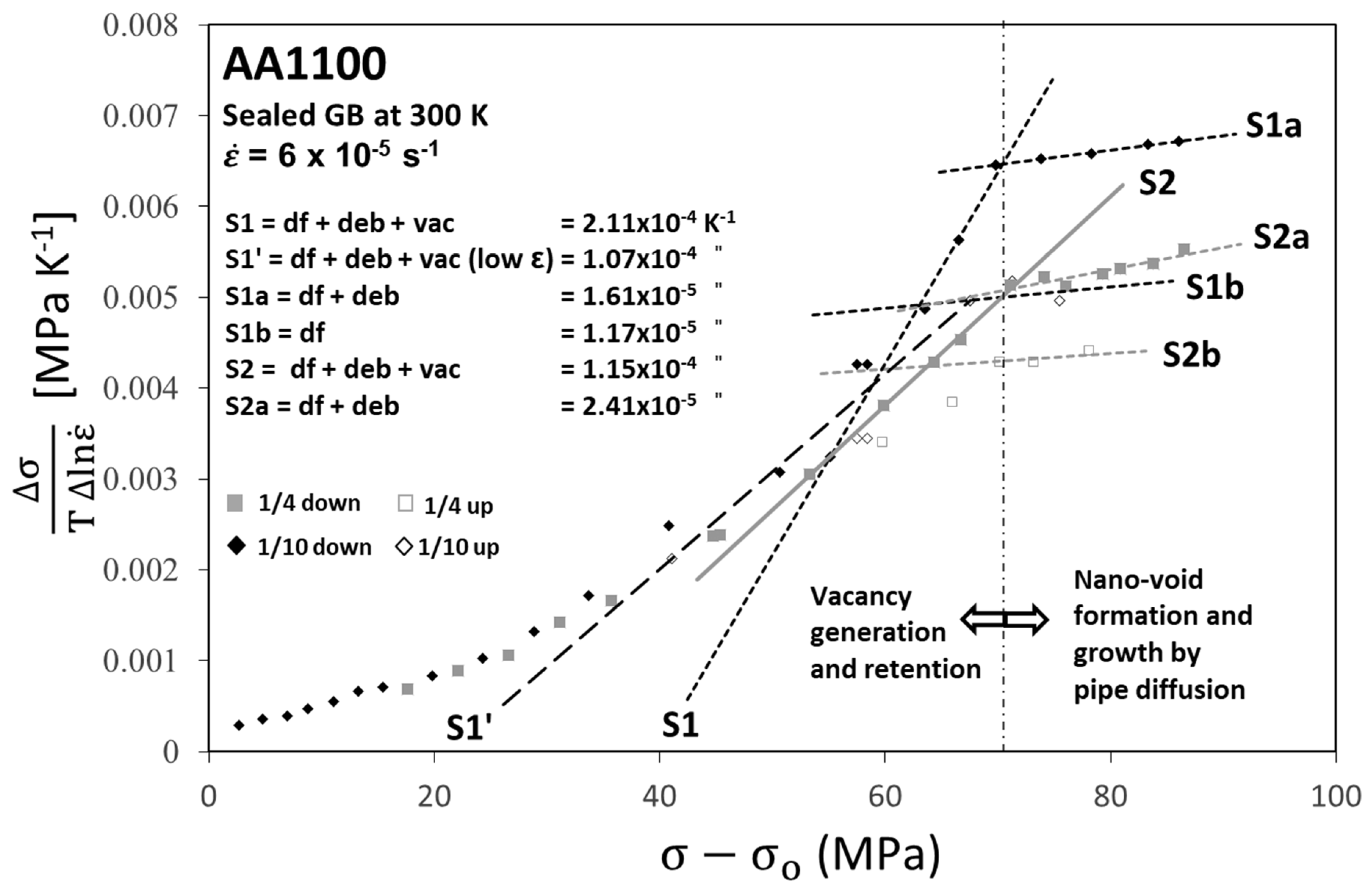
4.2. Dynamic Formation of Nano-Voids Enhanced by Vacancy Creation at Dislocation Intersections
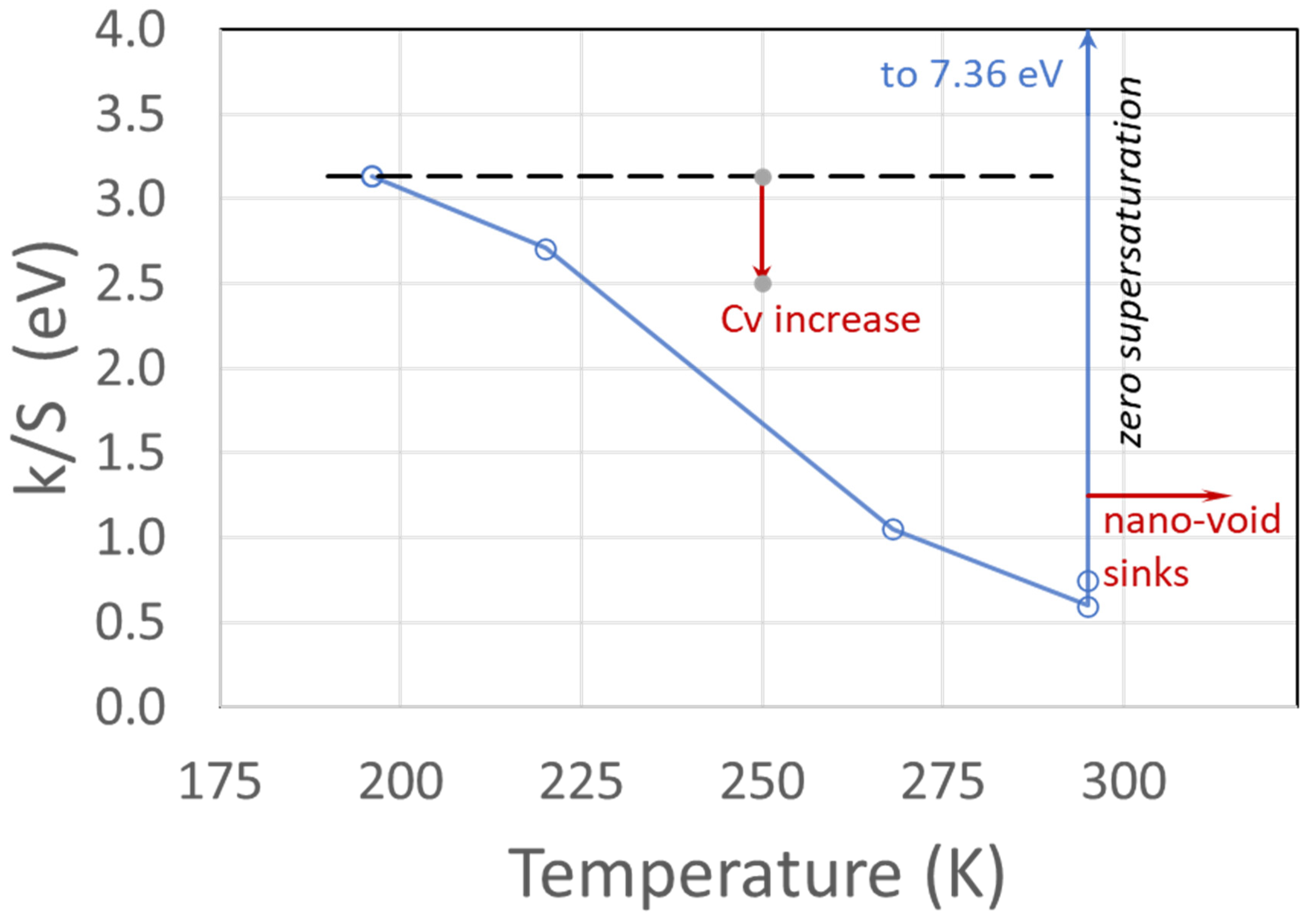
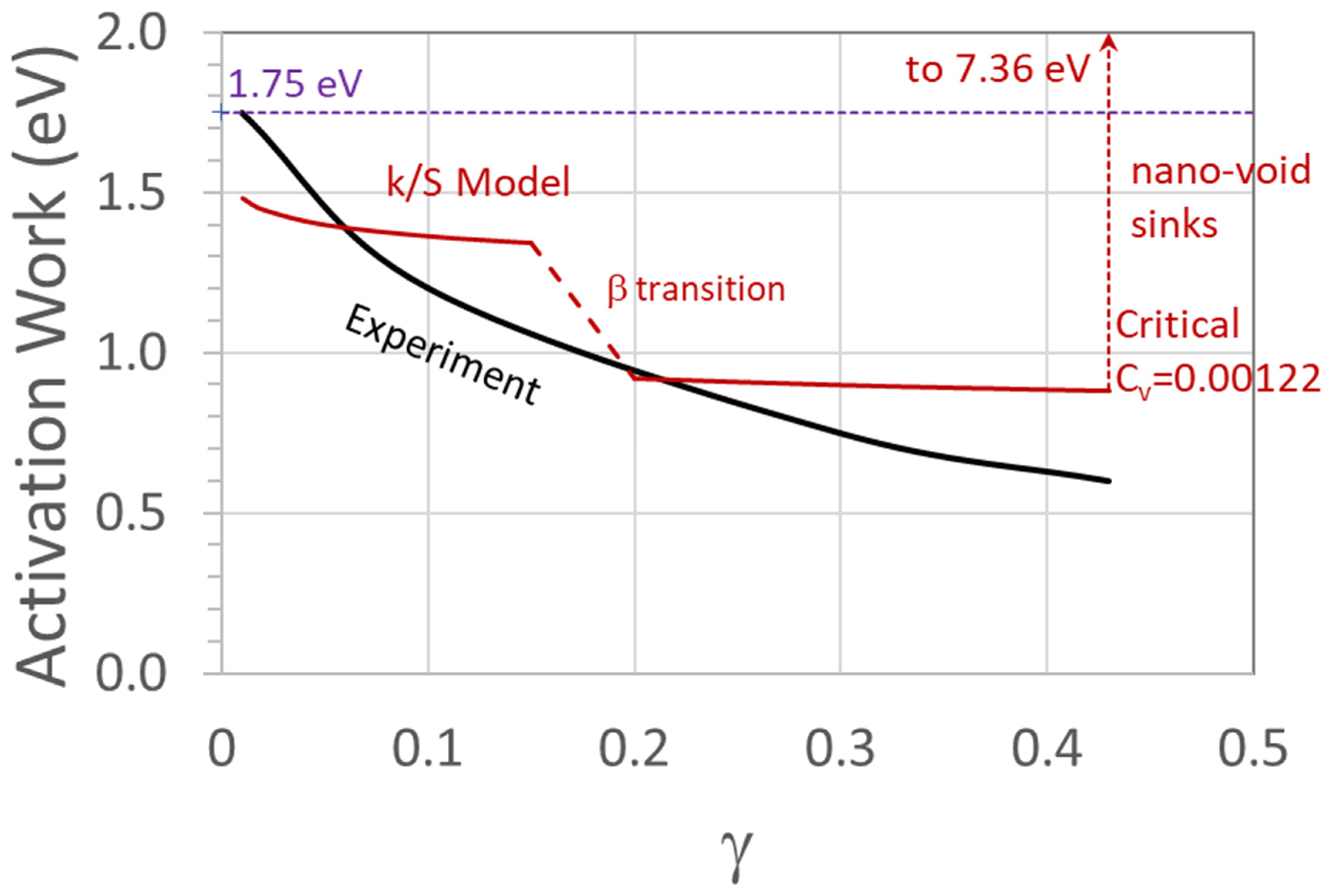
4.3. Correlation of Vacancy Supersaturation to Activation Work
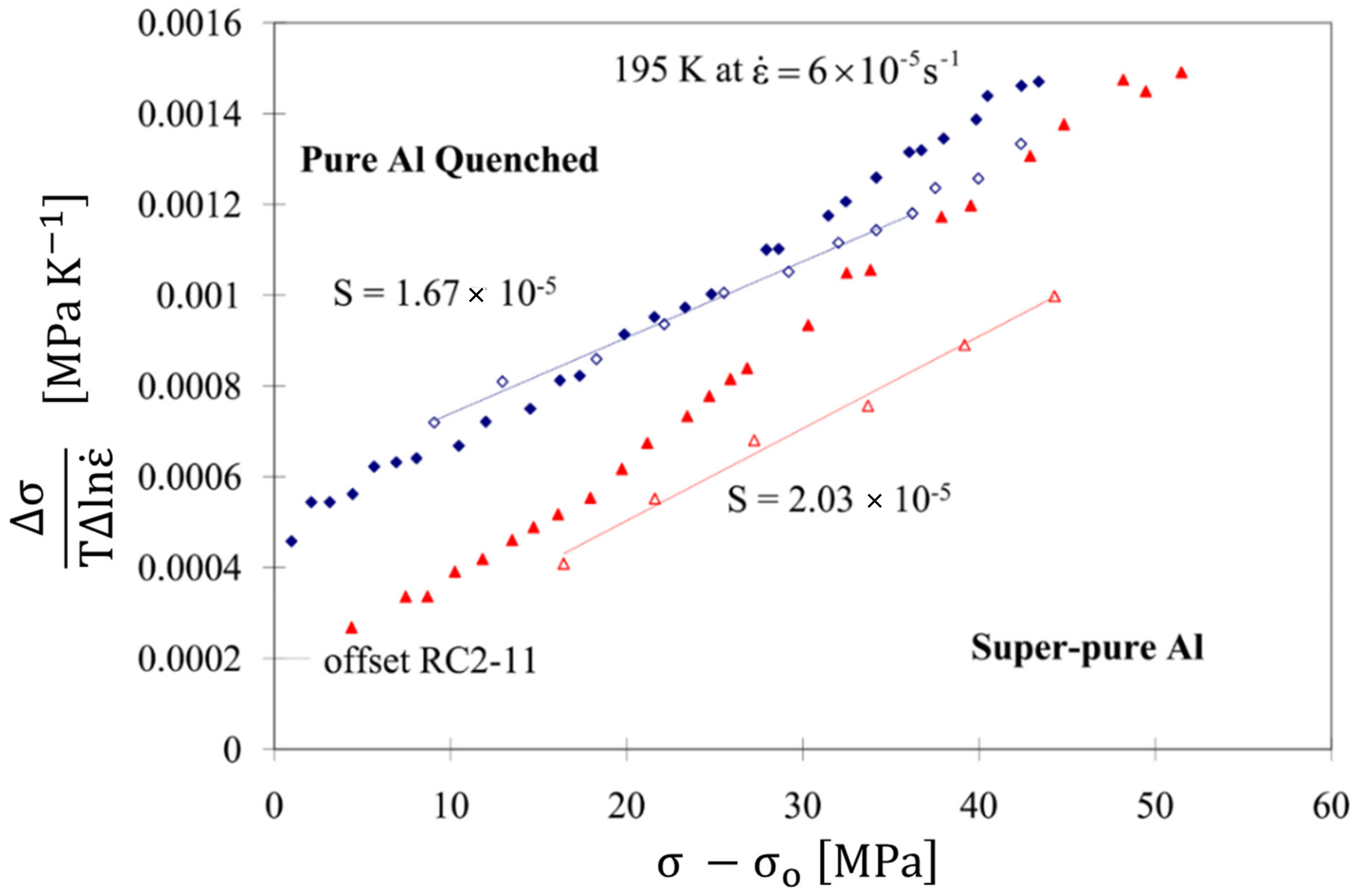
4.4. Derived Sfor and Determination of Sdebris from the Constant Haasen Slopes of Sup and Sdown
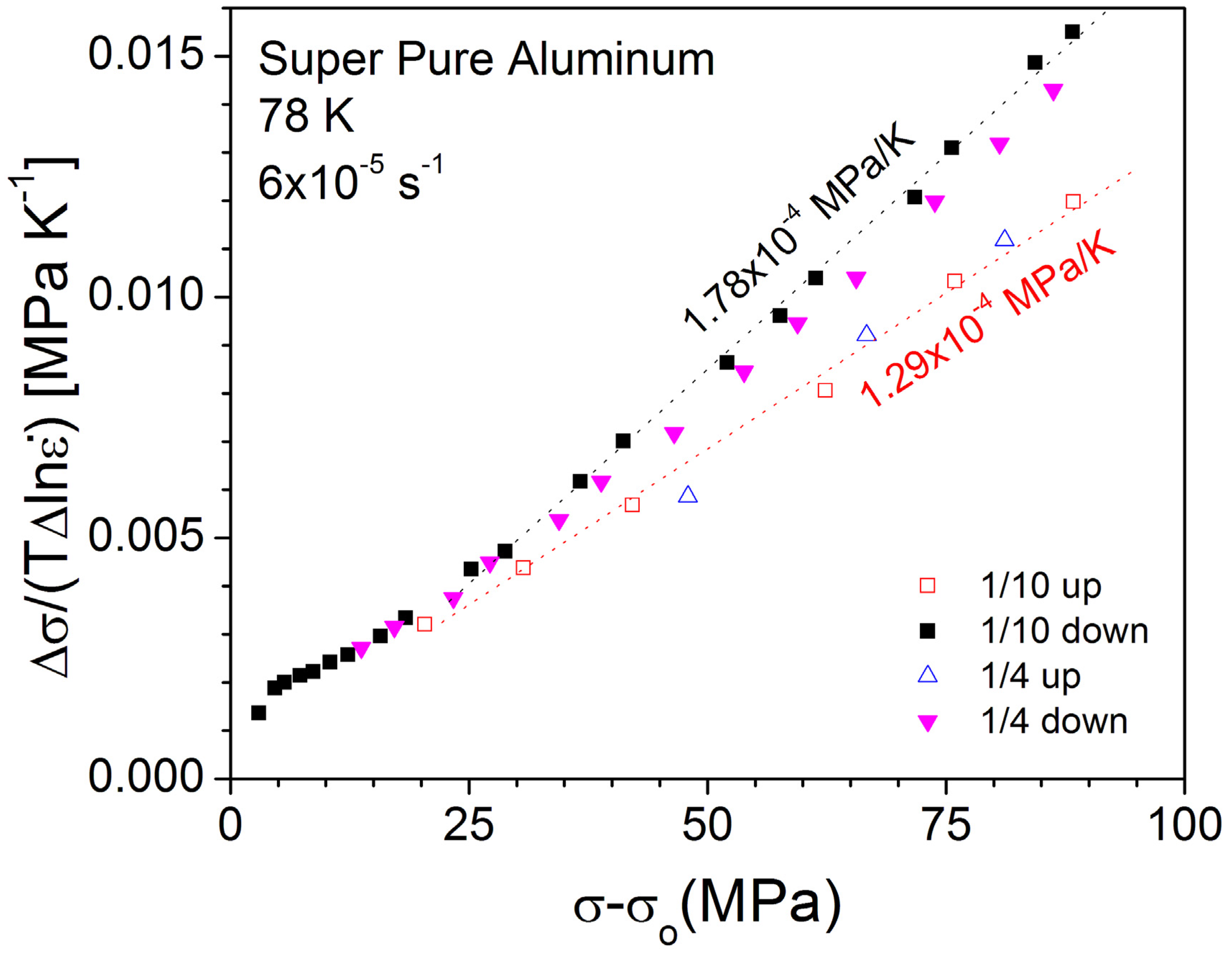
4.4.1. Haasen Plot for Super-Pure Al
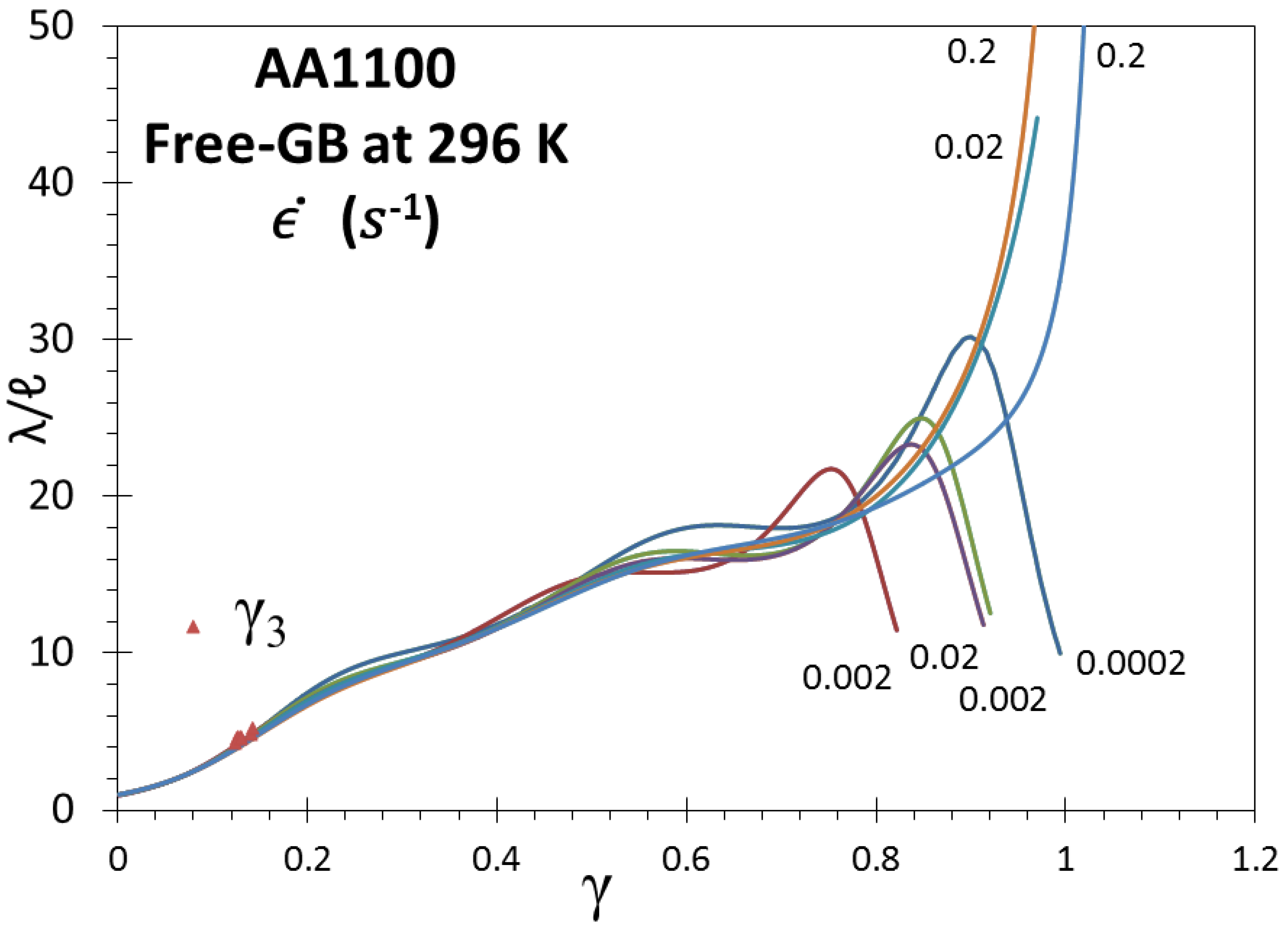
4.4.2. Derivation of Sfor and Sdebris for Free-GB Aluminum
5. Discussion
5.1. Synopsis of Forensic Survey of Vacancy Creation at Dislocation Intersections in Aluminum
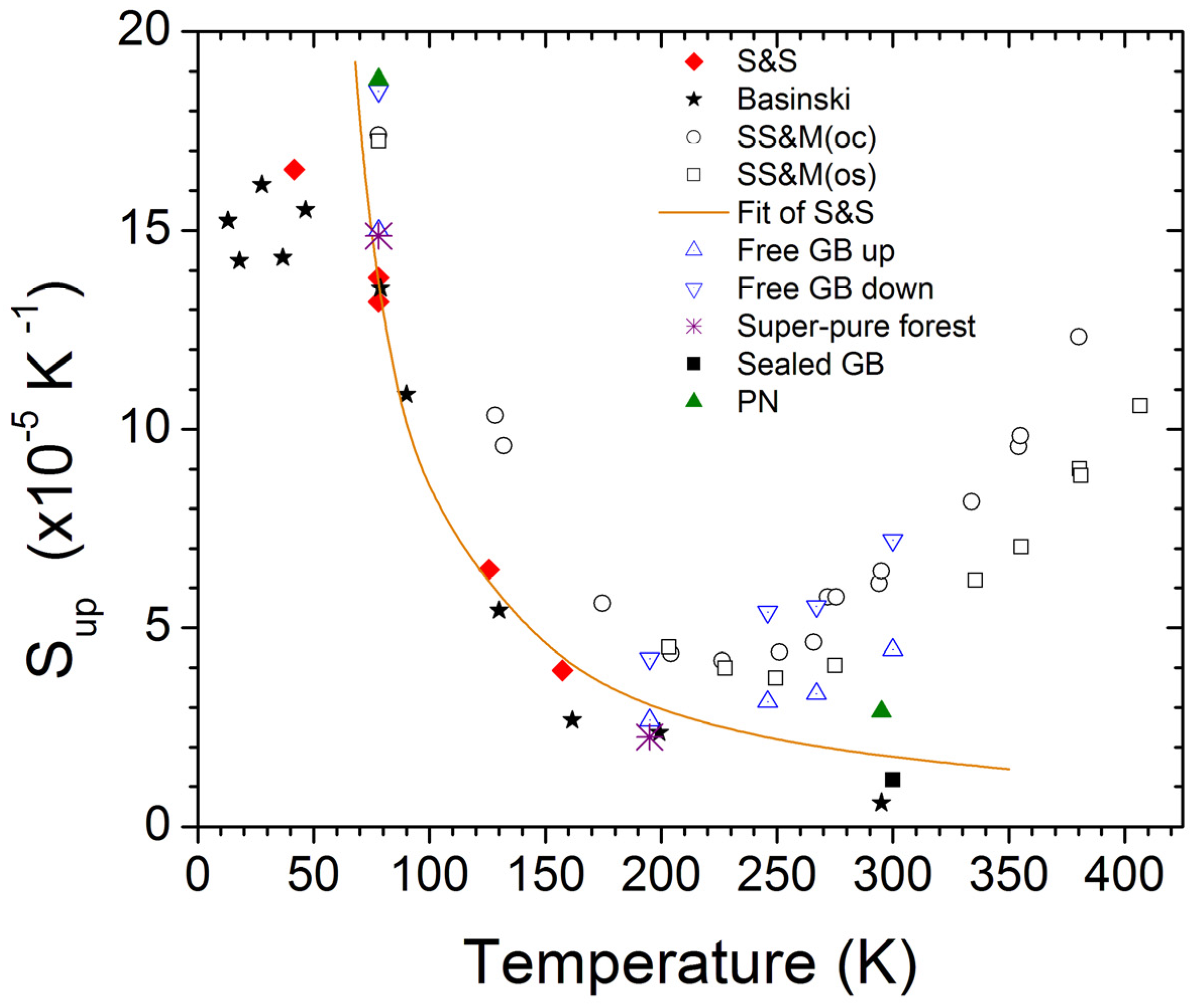
5.2. Overview Listing of Current Strain Rate Sensitivity (S) Results
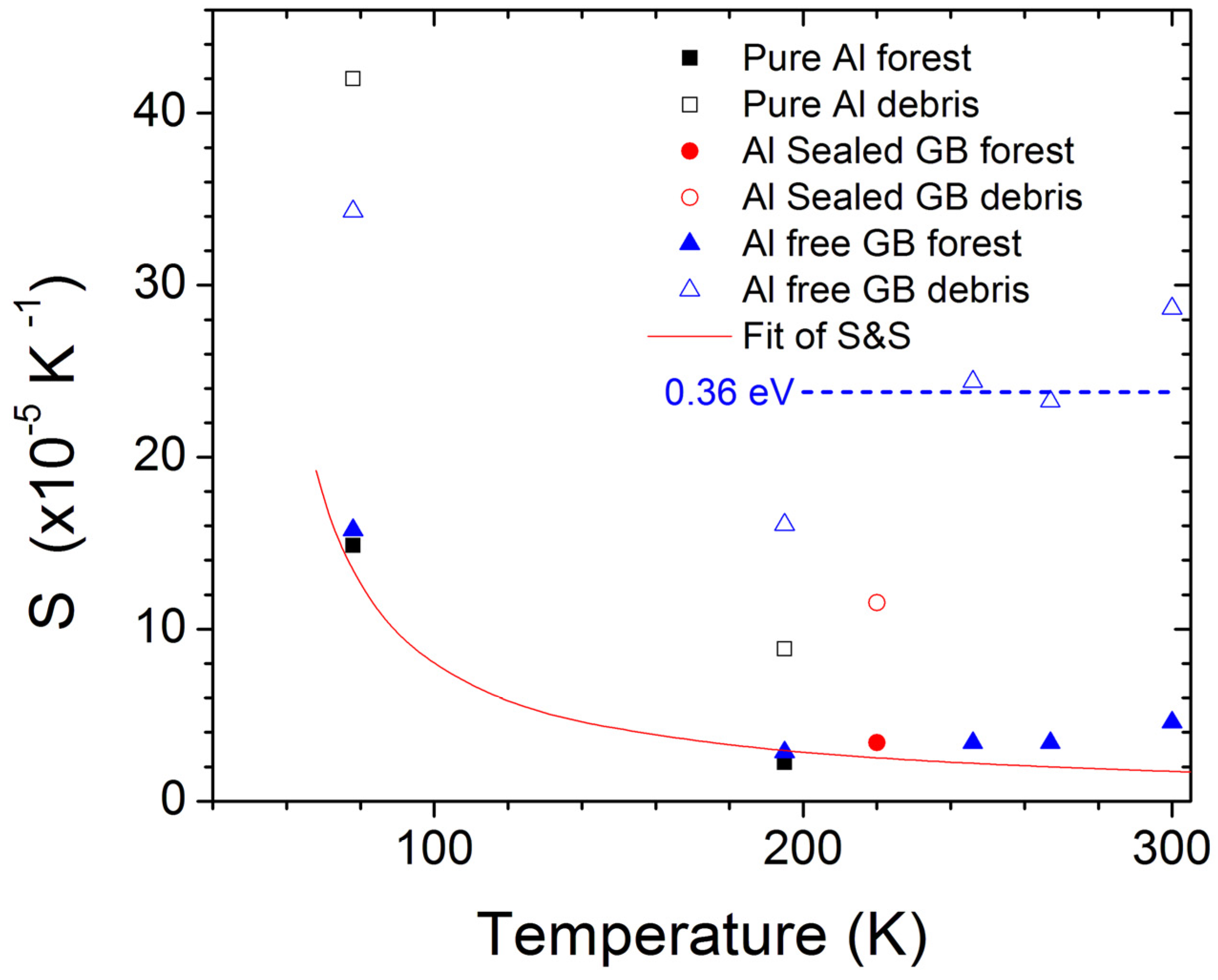
5.3. Categorization of Debris for Lattice Defect Identification
5.4. Characterization of Activation Work for Super-Pure Al at 78 K and 195 K
5.5. Characterization of Activation Work for Free-GB Al at 78, 195, 246, 267 and 300 K
5.6. Jog Dragging Due to Repulsive and Attractive Forest Intersections
5.7. Role of Repulsive Intersection on Nano-Void Formation and Recovery
5.8. Role of Attractive Junctions in Work-Hardening
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Activation Work-Based Derivation of Flow Stress as Function of Strain-Rate
Appendix B. Thermodynamic Description of Instantaneous Strain-Rate Change
References
- Saimoto, S. Determination of Different Combinations of Slip Systems in Face-Centred Cubic Lattice, in Appendix IV of Low Temperature Deformation of Copper Single Crystals Oriented for Multiple Slip. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1964. [Google Scholar]
- Taylor, G.I. Plastic strain in metals. J. Inst. Metals 1938, LXII, 307–324. [Google Scholar]
- Taylor, G.I. Analysis of plastic strain in a cubic crystal. In Stephen Timoshenko 60th Anniversary Volume; Macmillan Co.: New York, NY, USA, 1938; pp. 218–224. [Google Scholar]
- Asaro, R.J.; Needleman, A. Overview 42. Texture development and strain-hardening in rate dependant polycrystals. Acta Mater. 1985, 33, 923–953. [Google Scholar] [CrossRef]
- Brahme, A.P.; Inal, K.; Mishra, R.K.; Saimoto, S. A new stain hardening model for rate dependent crystal plasticity. Comput. Mater. Sci. 2011, 49, 2898–2908. [Google Scholar] [CrossRef]
- Saimoto, S.; Van Houtte, P. Constitutive relation based on Taylor slip analysis to replicate work-hardening evolution. Acta Mater. 2011, 59, 602–612. [Google Scholar] [CrossRef]
- Basinski, Z.S. Thermally activated glide in FCC metals and its application to the theory of strain hardening. Philos. Mag. 1959, 4, 393–432. [Google Scholar] [CrossRef]
- Diak, B.; Upadhyaya, K.; Saimoto, S. Characterization of thermodynamic response by materials testing. Prog. Mater. Sci. 1998, 43, 223–363. [Google Scholar] [CrossRef]
- Proville, L.; Rodney, D.; Brechet, Y.; Martin, G. Atomic-scale study of dislocation glide in a model solid solution. Philos. Mag. 2006, 86, 3893–3920. [Google Scholar] [CrossRef] [Green Version]
- Saimoto, S. Deformation kinetics and constitutive relation analyses of bifurcation in work-hardening of face-centred cubic metals at cryogenic temperatures. Acta Mater. 2019, 174, 43–52. [Google Scholar] [CrossRef]
- Saimoto, S.; Sang, H. A re-examination of the cottrell-stokes relation based on precision measurements of the activation volume. Acta Met. 1983, 31, 1873–1881. [Google Scholar] [CrossRef]
- Saimoto, S.; Diak, B.J.; Kula, A.; Niewczas, M. Assimilated model of work-hardening for FCC metals and its application to devolution of stored work. Mater. Today Commun. 2022, 105115. [Google Scholar] [CrossRef]
- Li, J.C.M. Kinetics and dynamics in dislocation plasticity. In Dislocation Dynamics; Rosenfield, A.R., Hahn, G.T., Bement, A.l., Jr., Jaffee, R.I., Eds.; McGraw-Hill Co.: New York, NY, USA, 1967; pp. 87–116. [Google Scholar]
- Cottrell, A.H.; Stokes, R.J. Effects of temperature on the plastic properties of aluminum crystals. Proc. R. Soc. Lond. A 1955, 17–34. [Google Scholar]
- Nabarro, F. Cottrell-stokes law and activation theory. Acta Met. Mater. 1990, 38, 161–164. [Google Scholar] [CrossRef]
- Dorn, J.E.; Goldberg, A.; Tietz, T.E. The effect of thermal-mechanical history on the strain hardening of metals. Trans. AIME 1949, 180, 205–224. [Google Scholar]
- Adams, M.A.; Cottrell, A.H. Effect of temperature on the flow stress of work-hardened copper crystals. Philos. Mag. 1955, 46, 1187–1193. [Google Scholar] [CrossRef]
- Seeger, A. The generation of lattice defects by moving dislocations and its application to the temperature dependence of the flow stress of FCC crystals. Philos. Mag. A 1955, 46, 1521–1546. [Google Scholar] [CrossRef]
- Makin, M.J. The temperature dependence of the flow stress in copper single crystals. Philos. Mag. 1958, 309–311. [Google Scholar] [CrossRef]
- Saimoto, S. Dynamic dislocation-defect analysis. Philos. Mag. 2006, 87, 4213–4233. [Google Scholar] [CrossRef]
- Basinski, Z.S.; Sahoo, M.; Saimoto, S. Resistivity change with deformation of high purity Cu crystals and its subsequent recovery. Acta Metall. 1977, 25, 657–665. [Google Scholar] [CrossRef]
- Saimoto, S.; Diak, B.J. Advanced method for the structure-strength-ductility assessment of dispersion-strengthened FCC metals using activation work, mean slip distance and constitutive relation analyses. Mater. Sci. Eng. A 2021, 828, 142119. [Google Scholar] [CrossRef]
- Foreman, A.J.E.; Makin, M.J. Dislocation movement through random arrays of obstacles. Philos. Mag. 1966, 14, 911–924. [Google Scholar] [CrossRef]
- Foreman, A.J.E.; Makin, M.J. Dislocation movement through random arrays of obstacles. Can. J. Phys. 1967, 45, 511–517. [Google Scholar] [CrossRef]
- Basinski, Z.S.; Saimoto, S. Resistivity of deformed crystals. Can. J. Phys. 1967, 45, 1161–1176. [Google Scholar] [CrossRef]
- Saimoto, S.; Jin, H.O. Effects of Solubility Limit and the Presence of Ultra-Fine Al6Fe on the Kinetics of Grain Growth in Dilute Al-Fe Alloys. Mater. Sci. Forum 2007, 550, 339–344. [Google Scholar] [CrossRef]
- Saimoto, S. Detection of nano-particles by dynamic dislocation-defect analysis. J. Phys. Conf. Ser. 2010, 240, 012031. [Google Scholar] [CrossRef]
- Langelaan, G.; Saimoto, S. Thermal expansion measurement of pure aluminum using a very low thermal expansion heating stage for X-ray diffraction experiments. Rev. Sci. Instrum. 1999, 70, 3413–3417. [Google Scholar] [CrossRef]
- Heller, H.; Stakhorst, J.; Verbraak, T. The development of rolling and recrystallization textures in high purity aluminum. Z. Metallk. 1977, 68, 31–37. [Google Scholar]
- Mukouda, I.; Shimomura, Y.; Kiritani, M. Cryo-transfer TEM study of vacancy cluster formation in thin foils of aluminum and copper elongated at low temperature. Mater. Sci. A 2003, 350, 37–43. [Google Scholar] [CrossRef]
- Ogi, H.; Tsujimoto, A.; Nishimura, S.; Hirao, M. Acoustic study of kinetics of vacancy diffusion toward dislocations in aluminum. Acta Mater. 2005, 53, 513–517. [Google Scholar] [CrossRef]
- Brotzen, F.; Seeger, A. Diffusion near dislocations, dislocation arrays and tensile cracks. Acta Met. 1989, 37, 2985–2992. [Google Scholar] [CrossRef]
- Saimoto, S.; Cooley, J.; Larsen, H.; Scholler, C. Kinetic analysis of dynamic defect pinning in aluminum initiated by strain-rate changes. Philos. Mag. 2009, 87, 853–868. [Google Scholar] [CrossRef]
- Saimoto, S. Dynamic manifestation of point defects on flow stress and the role of grain boundaries as vacancy sinks. Mater. Sci. Eng. A 2008, 67–70, 483–484. [Google Scholar] [CrossRef]
- Westfall, L.; Diak, B.J.; Singh, M.A.; Saimoto, S. Some observations of nano-voids in aluminum alloys by dynamic dislocation defect analysis and SAXS. J. Eng. Mater. Technol. 2008, 130, 201. [Google Scholar] [CrossRef]
- Crone, J.C.; Munday, L.B.; Knap, J. Capturing the effects of free surface on void strengthening with dislocation dynamics. Acta Mater. 2015, 101, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Saimoto, S.; Diak, B.J.; Kula, A.; Niewczas, M. Forensic analyses of microstructure evolution of stage II & III: New assimilated model for work-hardening in FCC metals. Acta Mater. 2020, 198, 168–177. [Google Scholar]
- Saimoto, S.; Diak, B.J. Point defect generation, nano-void formation and growth: 1. Validation. Philos. Mag. 2012, 92, 1890–1914. [Google Scholar] [CrossRef]
- Wenner, S.; Marioara, C.D.; Nishimura, K.; Matsuda, K.; Lee, S.; Namiki, T.; Watanabe, I.; Matsuzaki, T.; Holmestad, R. Muon spin relaxation study of solute-vacancy interactions during natural ageing of Al-Mg-Si-Cu alloys. Metall. Mater. Trans A 2019, 50A, 3446–3451. [Google Scholar] [CrossRef]
- Wolverton, C. Solute-vacancy binding in aluminum. Acta Mater. 2007, 55, 5867–5872. [Google Scholar] [CrossRef] [Green Version]
- Balluffi, R.W. Vacancy defect mobilities and binding energies obtained from annealing studies. J. Nucl. Mater. 1978, 69–70, 240–263. [Google Scholar] [CrossRef]
- Saimoto, S.; Lloyd, D.J. A new analysis of yielding and work hardening in AA1100 and AA5754 at low temperatures. Acta Mater. 2012, 60, 6352–6361. [Google Scholar] [CrossRef]
- Andersen, P.M.; Hirth, J.P.; Lothe, J. Theory of Dislocations, 3rd ed.; Cambridge Press: Cambridge, UK, 2017. [Google Scholar]
- Singh, M.A.; Saimoto, S.; Langille, M.R.; Levesque, J.; Inal, K.; Woll, A.R. Small-angle X-ray scattering investigation of deformation-induced nano-voids in AA6063 aluminum alloy. Philos. Mag. 2017, 97, 2496–2513. [Google Scholar] [CrossRef]
- Saimoto, S.; Cooley, J.I.; Diak, B.J.; Jin, H.; Mishra, R.K. Recovery studies of cold-rolled aluminum sheet using X-ray line broadening and activation volume determinations. Acta Mater. 2009, 57, 4822–4834. [Google Scholar] [CrossRef]
- Saimoto, S.; Sang, H.; Morris, L.R. Microplastic bases for constitutive relations found tensile testing. Acta Metall. 1981, 29, 215–228. [Google Scholar] [CrossRef]
- Park, D.-Y.; Niewczas, M. Plastic deformation of Al and AA5754 between 4.2 K and 295 K. Mater. Sci. Eng. A 2008, A491, 88–102. [Google Scholar] [CrossRef]
- Saimoto, S.; Diak, B.J.; Lloyd, D.J. Point defect generation, nano-void formation and growth: II. Criterion for ductile failure. Philos. Mag. 2012, 92, 1915–1936. [Google Scholar] [CrossRef]
- Saimoto, S.; Niewczas, M.; Langille, M.; Diak, B.J. Specific resistivity of dislocations and vacancies for super-pure aluminum at 4.2 K determined in-situ and post-recovery deformation and correlated to flow stress. Philos. Mag. 2019, 99, 2770–2788. [Google Scholar] [CrossRef]
- Niewczas, M. Intermittent plastic flow of single crystals: Central problems in plasticity: A review. Mater. Sci. Technol. 2014, 739–757. [Google Scholar] [CrossRef]
- Wang, H.; Xu, D.S.; Yang, R.; Veyssiere, P. The formation of stacking fault tetrahedra in Al and Cu I. dipole annihilation and the nucleation stage. II. SFT growth by successive absorption of vacancies generated by dipole annihilation. Acta Mater. 2011, 59, 1–9, 10–18. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Glide of jogged dislocations. Can. J. Phys. 1967, 45, 809–826. [Google Scholar] [CrossRef]
- Osetsky, Y.N.; Rodney, D.; Bacon, D.J. Atomic-scale study of dislocation–stacking fault tetrahedron interactions. Part I: Mechanisms. Philos. Mag. 2006, 16, 2295–2313. [Google Scholar] [CrossRef]
- Niewczas, M.; Hoagland, R.G. Molecular dynamic studies of the interaction of a/6 <112> Shockley dislocations with stacking fault tetrahedra in copper. Part 1. Intersection of SFT by an isolated Shockley. Philos. Mag. 2009, 89, 623–640. [Google Scholar] [CrossRef]
- Wang, H.; Xu, D.; Veyssière, P.; Yang, R. Interstitial loop strengthening upon deformation in aluminum via molecular dynamics simulations. Acta Mater. 2013, 61, 3499–3508. [Google Scholar] [CrossRef]
- Hirsch, P.B. Extended jogs in dislocations in face-centred cubic metals. Philos. Mag. 1962, 7, 67–93. [Google Scholar] [CrossRef]
- Cottrell, A.H. The intersection of gliding screw dislocations. In Dislocations and Mechanical Properties of Crystals; Fisher, J.C., Johnston, W.G., Thomson, R., Vreeland, T., Jr., Eds.; John Wiley: London, UK, 1957; pp. 509–512. [Google Scholar]
- Nabarro, F.R.N.; Brown, L.M. The enumeration and transformation of dislocation dipoles: 1. The dipole strengths of closed and open dislocation arrays. Philos. Mag. 2004, 84, 429–439. [Google Scholar] [CrossRef]
- Fujita, H. Continuous observation of dynamic behaviour of dislocations in aluminum. J. Phys. Soc. Jpn. 1967, 23, 1349–1361. [Google Scholar] [CrossRef]
- Bonneville, J.; Escaig, B.; Martin, J. A study of cross-slip activation parameters in pure copper. Acta Met. 1988, 36, 1989–2002. [Google Scholar] [CrossRef]
- Davies, C.K.L.; Sagar, V.; Stevens, R.N. Thermally activated dislocation intersection in face-centred cubic metals. Phys. Stat. Sol. 1973, 20, 201–210. [Google Scholar] [CrossRef]



| Super-Pure Al | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Temp. K | σ MPa | σ0 MPa | σ0.2% MPa | σ3 MPa | k/νYield × 10−4 MPa K−1 | k/νUp × 10−4 MPa K−1 | k/νDown × 10−4 MPa K−1 | SDown × 10−5 K−1 | SUp ×10−5 K−1 |
| 78 | 80.0 | 15.0 | 20.0 | 18.0 | 10.0 | 108.6 | 140.4 | 17.8 | 12.9 |
| 195 | 50.0 | 13.7 | 17.0 | 8.2 | 1.71 | 11.14 | 15.43 | 3.07 | 2.03 |
| Temp. K | Derived SFor × 10−5 K−1 | Derived SDebris × 10−5 K−1 | Δσ MPa | fDebris | Derived SDown × 10−5 K−1 | Expt. SDown × 10−5 K−1 | τνFor = k/S eV | τνdebris = k/S eV | τνFor/τνdebris ratio |
| 78 | 14.86 | 42..0 | 7.56 | 0.122 | 18.2 | 17.8 | 0.58 | 0.205 | 2.83 |
| 195 | 2.25 | 8.86 | 4.84 | 0.115 | 3.01 | 3.07 | 3.83 | 0.973 | 3.95 |
| NV = 5 | |||||||||
| Free-GB | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Temp. K | σ MPa | σ0 MPa | σ0.2% MPa | σ3 MPa | k/νYield × 10−4 MPa/K | k/νUp × 10−4 MPa/K | k/νDown × 10−4 MPa/K | SDown × 10−5 K−1 | SUp × 10−5 K−1 |
| 78 | 160.0 | 31.7 | 47.4 | 72.5 | 24. | 192. | 222. | 18.50 | 15.00 |
| 195 | 100.0 | 25.8 | 39.2 | 31.0 | 3.1 | 25.8 | 36.9 | 4.23 | 2.68 |
| 246 | 80 | 24.6 | 31.0 | 33.7 | 3.2 | 24.6 | 35.9 | 5.4 | 3.15 |
| 267 | 80.0 | 15.0 | 18.9 | 37.0 | 3. | 25.2 | 34.8 | 5.54 | 3.35 |
| 300 | 70 | 20.5 | 34.0 | 34.2 | 4.3 | 29.7 | 40.0 | 7.21 | 4.45 |
| Temp. K | Derived SFor × 10−5 K−1 | Derived SDebris × 10−5 K−1 | Δσ MPa | fDebris | Derived SDown × 10−5 K−1 | Expt. SDown × 10−5 K−1 | τνFor = k/S eV | τνdebris = k/S eV | τνFor/τνdebris ratio |
| 78 | 15.76 | 34.3 | 8.75 | 0.1 * | 17.6 | 18.5 | 0.55 | 0.25 | 2.2 |
| NV = 0 | |||||||||
| 195 | 2.85 | 16.08 | 6.9 | 0.1 * | 4.17 | 4.23 | 3.02 | 0.54 | 5.6 |
| NV = 4 | |||||||||
| 246 | 3.40 | 24.4 | 4.63 | 0.10 * | 5.50 | 5.4 | 2.58 | 0.353 | 7.3 |
| NV = 3 | |||||||||
| 267 | 3.40 | 23.25 | 4.3 | 0.10 * | 5.53 | 5.54 | 2.53 | 0.37 | 6.83 |
| NV = 3 | |||||||||
| 300 | 4.583 | 28.65 | 3.58 | 0.10 * | 7.00 | 7.21 | 1.88 | 0.30 | 6.26 |
| NV = 2 | |||||||||
| Sealed-GB | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Temp. K | σ MPa | σ0 MPa | σ0.2% MPa | σ3 MPa | k/νYield × 10−4 MPa/K | k/νUp × 10−4 MPa/K | k/νDown × 10−4 MPa/K | SDown × 10−5 K−1 | SUp × 10−5 K−1 |
| 220 | 100 | 18.1 | 30.3 | 32.0 | 1.5 | 28.8 | 36.7 | 4.26 | 3.11 |
| Temp. K | Derived SFor × 10−5 K−1 | Derived SDebris × 10−5 K−1 | Δσ MPa | fDebris | Derived SDown × 10−5 K−1 | Expt. SDown 10−5 | τνFor = k/S eV | τνdebris = k/S eV | τνFor/τνdebris ratio |
| 220 | 3.406 | 11.53 | 6.85 | 0.10 | 4.22 | 4.26 | 2.53 | 0.747 | 3.38 |
| NV = 3 | |||||||||
| Super-Pure Al | |||||||
| Temp. K | µ MPa | Derived Sfor × 10−5 K−1 | α (d/b) = τ ν/(µb3) | d/b if α = 0.4 | Derived Sdebris × 10−5 K−1 | α (d/b) = τ ν/(µb3) | d/b if α = 0.1 |
| 78 | 36,522 | 14.86 | 0.108 | 0.27 | 42.0 | 0.0383 | 0.383 |
| 195 | 34,125 | 2.25 | 0.766 | 1.91 | 8.86 | 0.194 | 1.94 |
| Free-GB | |||||||
| Temp. K | µ MPa | Derived Sfor × 10−5 K−1 | α (d/b) = τ ν/(µb3) | d/b if α = 0.4 | Derived Sdebris × 10−5 K−1 | α (d/b) = τ ν/(µb3) | d/b if α = 0.1 |
| 78 | 36,522 | 15.76 | 0.102 | 0.255 | 34.3 | 0.0469 | 0.469 |
| 195 | 34,125 | 2.85 | 0.605 | 1.512 | 16.08 | 0.1072 | 1.072 |
| 246 | 33,106 | 3.40 | 0.522 | 1.305 | 24.4 | 0.0728 | 0.728 |
| 267 | 32,649 | 3.40 | 0.535 | 1.337 | 23.25 | 0.0782 | 0.782 |
| 300 | 31.968 | 4.58 | 0.401 | 1.002 | 28.65 | 0.0642 | 0.642 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saimoto, S.; Diak, B.J.; Niewczas, M. Rate-Controlling Microplastic Processes during Plastic Flow in FCC Metals: Origin of the Variation of Strain Rate Sensitivity in Aluminum from 78 to 300 K. Crystals 2022, 12, 1811. https://doi.org/10.3390/cryst12121811
Saimoto S, Diak BJ, Niewczas M. Rate-Controlling Microplastic Processes during Plastic Flow in FCC Metals: Origin of the Variation of Strain Rate Sensitivity in Aluminum from 78 to 300 K. Crystals. 2022; 12(12):1811. https://doi.org/10.3390/cryst12121811
Chicago/Turabian StyleSaimoto, Shigeo, Bradley J. Diak, and Marek Niewczas. 2022. "Rate-Controlling Microplastic Processes during Plastic Flow in FCC Metals: Origin of the Variation of Strain Rate Sensitivity in Aluminum from 78 to 300 K" Crystals 12, no. 12: 1811. https://doi.org/10.3390/cryst12121811
APA StyleSaimoto, S., Diak, B. J., & Niewczas, M. (2022). Rate-Controlling Microplastic Processes during Plastic Flow in FCC Metals: Origin of the Variation of Strain Rate Sensitivity in Aluminum from 78 to 300 K. Crystals, 12(12), 1811. https://doi.org/10.3390/cryst12121811






