Two-Temperature Semiconductor Model Photomechanical and Thermal Wave Responses with Moisture Diffusivity Process
Abstract
1. Introduction
2. Basic Equations
3. Formulation of the Problem
4. Harmonic Wave Analysis
5. Applications
6. Numerical Results and Discussions
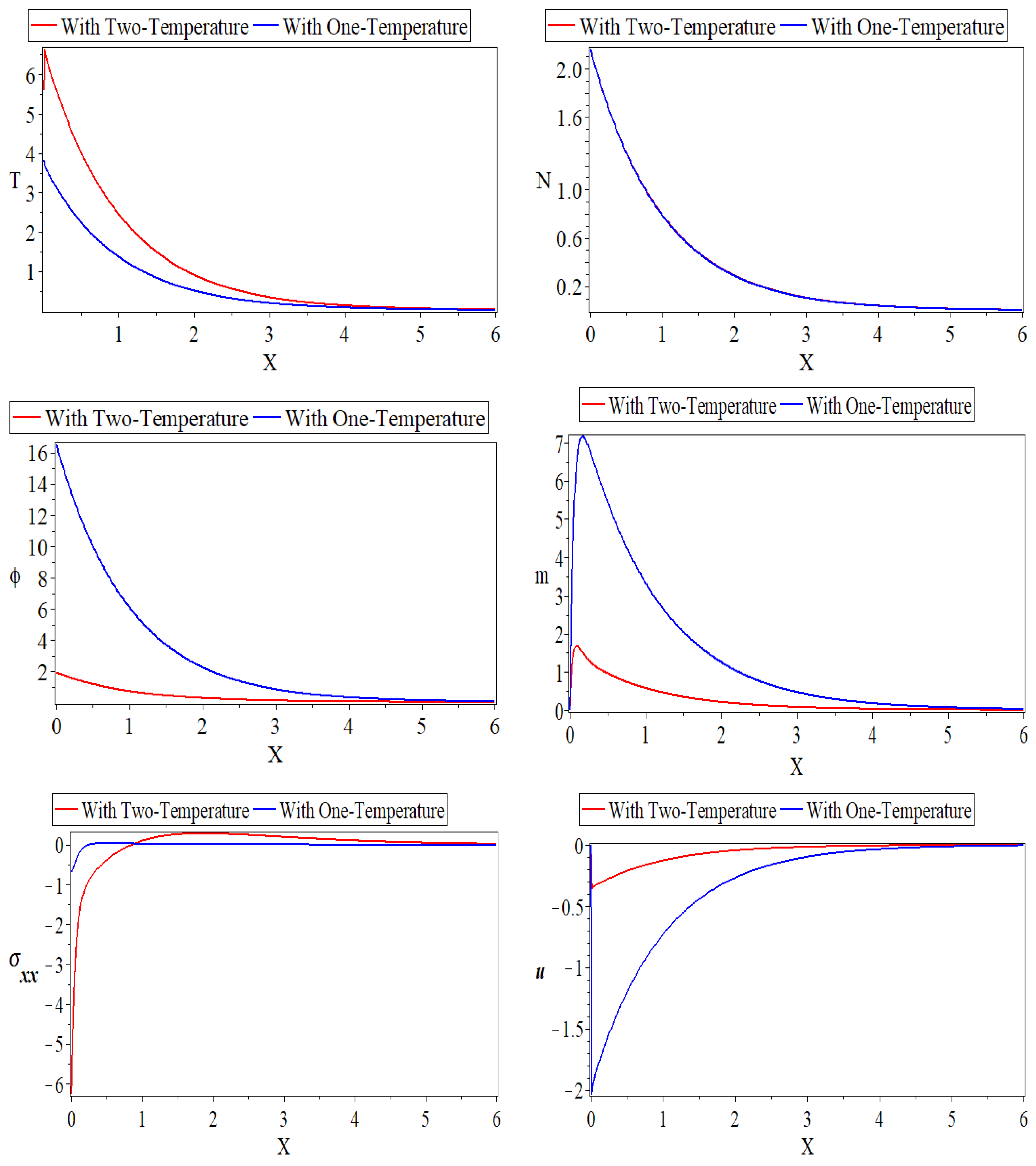
6.1. The Effect of Two-Temperature Parameter
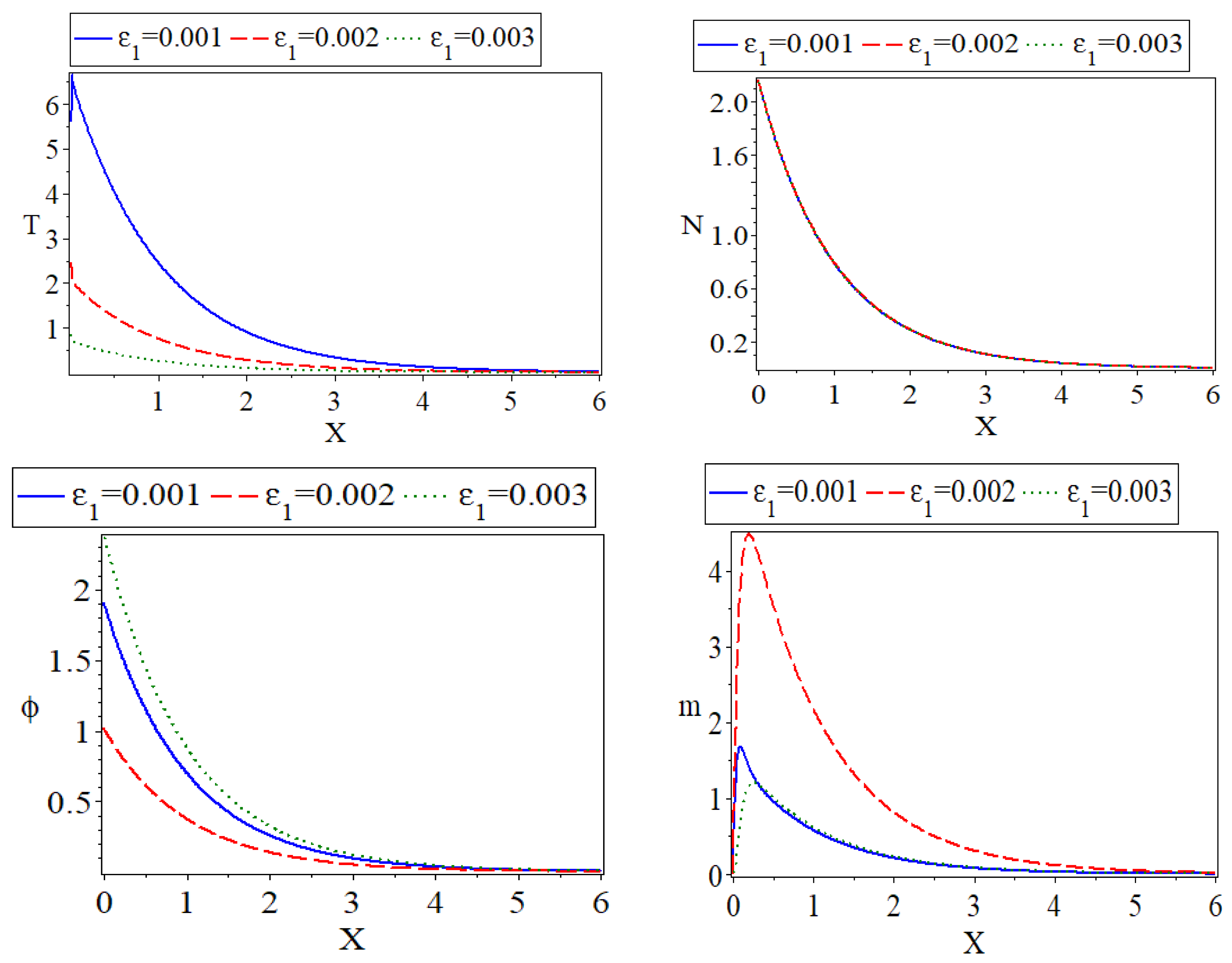
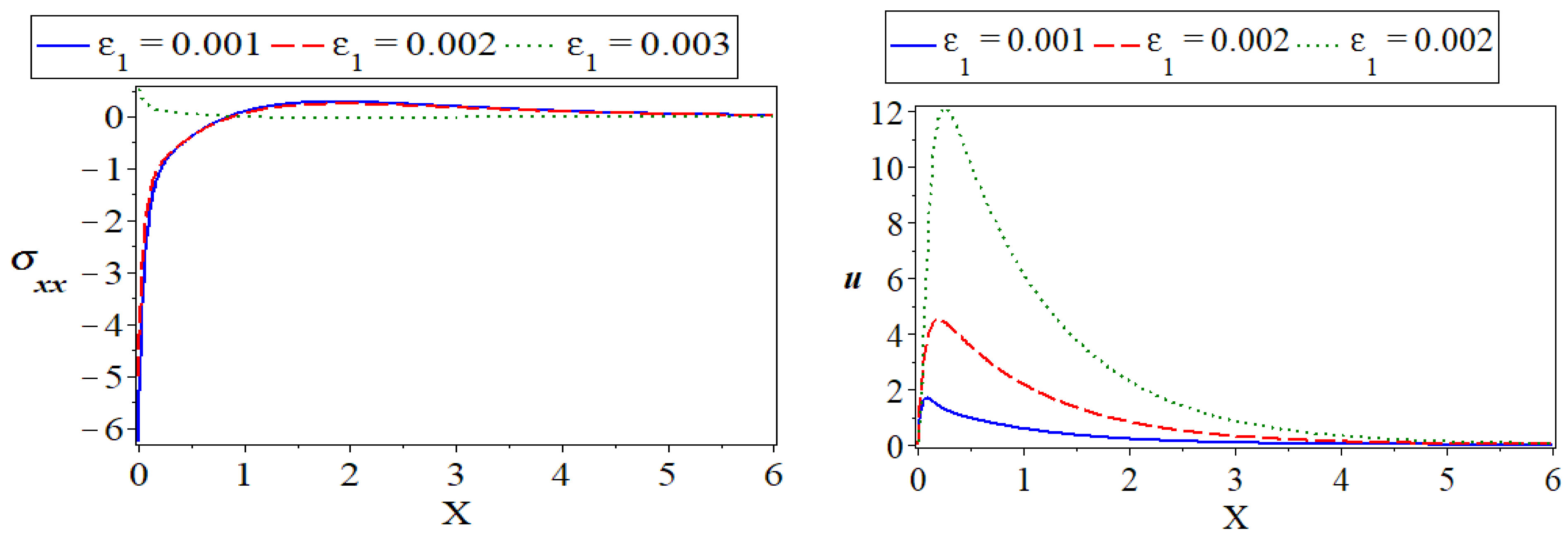
6.2. The Impact of Thermoelastic Coupling Parameter
 ) represent the case when , the dashed lines (
) represent the case when , the dashed lines ( ) express the case at , and the dotted lines (
) express the case at , and the dotted lines ( ) show the case at . The thermodynamic temperature distribution () is shown in the first subfigure along with how the distance affects the dimensionless thermoelastic coupling parameters. Starting from a positive minimum temperature that satisfies the thermally insulated requirement, the thermodynamic temperature rises rapidly in the first range until it reaches the maximum peak temperature close to the surface due to photo-excitation and moisture diffusivity. The distribution, on the other hand, shrinks in the second range to arrive at the minimum value distant from the surface. The electronic diffusive distribution is shown against the distance in variation values of the thermoelastic parameters in the second subfigure. However, the carrier density, which exhibits a similar quality characteristic, is not significantly affected by a slight change in the thermoelastic coupling parameters. The fourth subfigure describes the moisture concentration distribution versus the horizontal distance , while the third subfigure depicts the conductive temperature, which exhibits the same behavior as the first subfigure. For all three cases, the distribution of moisture content starts at zero. The distribution adopts an exponential pattern with smooth decrementing with . On the other hand, due to moisture diffusivity, when and the distribution of moisture concentration dramatically declines in the first range, and it adopts exponential propagation behavior until it reaches a minimum value close to the zero line. The fifth subfigure shows how the amplitude of the stress force is increasing as a result of the mechanical loads’ tendency to raise the thermoelastic coupling parameters’ values. The displacement distribution with horizontal distance caused by moisture diffusivity and the thermal impact of photothermal stimulation for the rough surface is shown in the sixth subfigure. For all three thermoelastic coupling parameter scenarios, the displacement distribution begins at zero and climbs to maximum values close to the surface before decreasing exponentially until it approaches a minimum value close to the zero line [41]. These results are in agreement with what has been observed through practical experiments [42,43].
) show the case at . The thermodynamic temperature distribution () is shown in the first subfigure along with how the distance affects the dimensionless thermoelastic coupling parameters. Starting from a positive minimum temperature that satisfies the thermally insulated requirement, the thermodynamic temperature rises rapidly in the first range until it reaches the maximum peak temperature close to the surface due to photo-excitation and moisture diffusivity. The distribution, on the other hand, shrinks in the second range to arrive at the minimum value distant from the surface. The electronic diffusive distribution is shown against the distance in variation values of the thermoelastic parameters in the second subfigure. However, the carrier density, which exhibits a similar quality characteristic, is not significantly affected by a slight change in the thermoelastic coupling parameters. The fourth subfigure describes the moisture concentration distribution versus the horizontal distance , while the third subfigure depicts the conductive temperature, which exhibits the same behavior as the first subfigure. For all three cases, the distribution of moisture content starts at zero. The distribution adopts an exponential pattern with smooth decrementing with . On the other hand, due to moisture diffusivity, when and the distribution of moisture concentration dramatically declines in the first range, and it adopts exponential propagation behavior until it reaches a minimum value close to the zero line. The fifth subfigure shows how the amplitude of the stress force is increasing as a result of the mechanical loads’ tendency to raise the thermoelastic coupling parameters’ values. The displacement distribution with horizontal distance caused by moisture diffusivity and the thermal impact of photothermal stimulation for the rough surface is shown in the sixth subfigure. For all three thermoelastic coupling parameter scenarios, the displacement distribution begins at zero and climbs to maximum values close to the surface before decreasing exponentially until it approaches a minimum value close to the zero line [41]. These results are in agreement with what has been observed through practical experiments [42,43].6.3. The Effect of the Thermoelectric Coupling Parameter
 ) represent the case when , the dashed lines (
) represent the case when , the dashed lines ( ) express the case at , and the dotted lines (
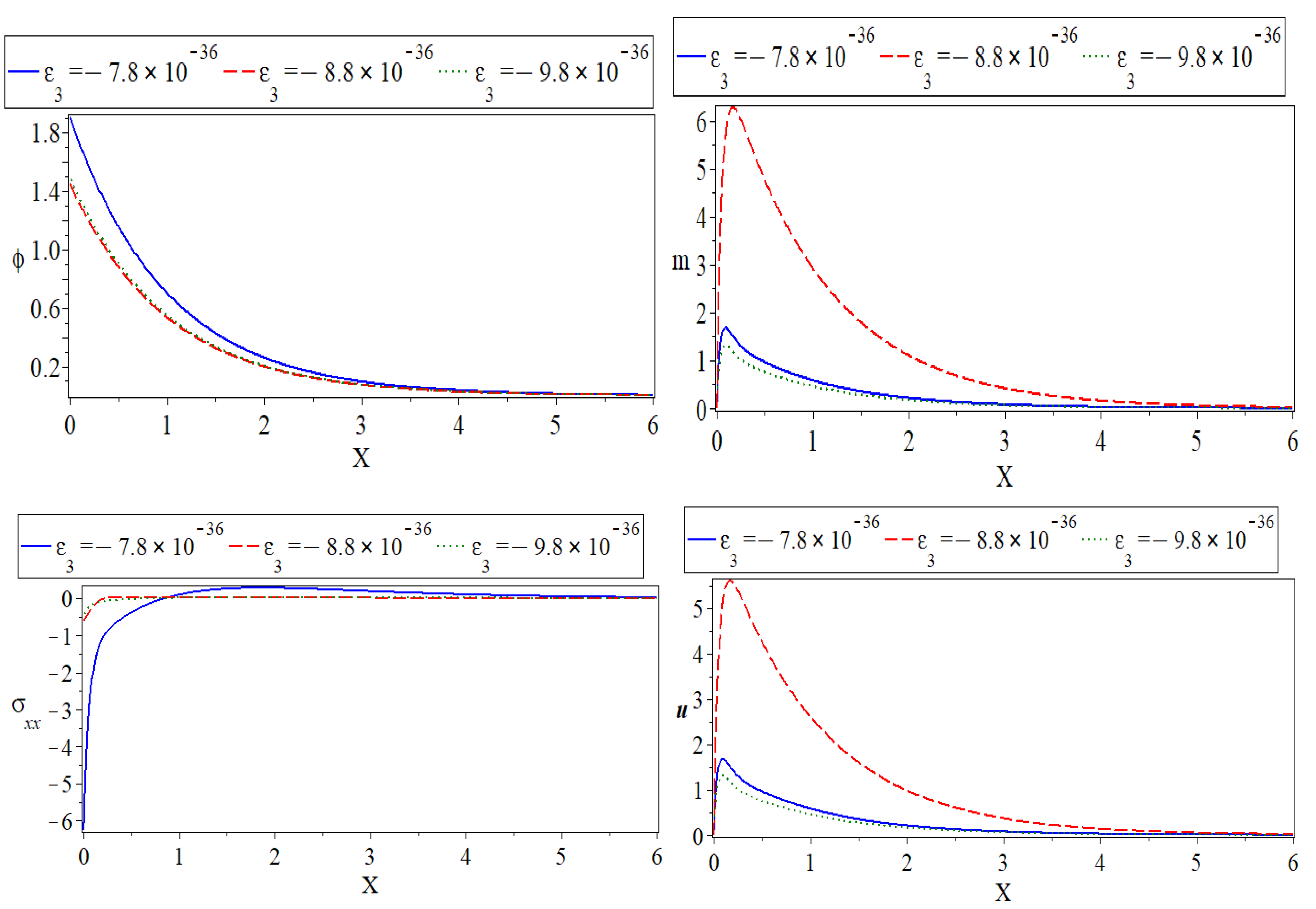
) express the case at , and the dotted lines ( ) show the case at . The thermo-dynamical temperature distribution with variation in the dimensionless thermoelectric coupling parameters with distance is shown in the first subfigure. Starting at a positive minimum value that satisfies the thermally insulated requirement, the thermodynamic temperature rises quickly in the first range until it reaches the peak maximum value close to the surface because of photo-excitation and moisture diffusivity. The distribution, on the other hand, contracts in the second range to approach the minimum value far from the surface. The carrier density distribution is shown against the distance in variation values of the thermoelastic parameters in the second subfigure. However, the carrier density, which exhibits a similar quality characteristic, is not significantly affected by a slight change in the thermoelastic coupling parameters. The conductive temperature, which behaves similarly to the dynamical temperature, is depicted in the third subfigure. The distribution of moisture concentration against horizontal distance is shown in the fourth subfigure. For each of the three scenarios, the moisture concentration distribution starts from a positive value for all three cases. In the case of , the distribution takes the exponential behavior with smooth decreasing. Still, on the other hand, when and , the distribution of moisture concentration decreases sharply near the surface, and it takes an exponential propagation behavior until it reaches a minimum value near the zero line due to moisture diffusivity. The fifth subfigure shows how the mechanical loads that tend to raise the value of the thermoelectric coupling parameters enhance the stress force amplitude. The displacement distribution with horizontal distance caused by moisture diffusivity and the thermal impact of photothermal stimulation for the rough surface is shown in the sixth subfigure. For each of the three thermoelectric coupling parameter situations, the displacement distribution begins at zero, climbs to maximum values near the surface, and then decreases in an exponential propagation pattern until it reaches a minimum value close to the zero line.
) show the case at . The thermo-dynamical temperature distribution with variation in the dimensionless thermoelectric coupling parameters with distance is shown in the first subfigure. Starting at a positive minimum value that satisfies the thermally insulated requirement, the thermodynamic temperature rises quickly in the first range until it reaches the peak maximum value close to the surface because of photo-excitation and moisture diffusivity. The distribution, on the other hand, contracts in the second range to approach the minimum value far from the surface. The carrier density distribution is shown against the distance in variation values of the thermoelastic parameters in the second subfigure. However, the carrier density, which exhibits a similar quality characteristic, is not significantly affected by a slight change in the thermoelastic coupling parameters. The conductive temperature, which behaves similarly to the dynamical temperature, is depicted in the third subfigure. The distribution of moisture concentration against horizontal distance is shown in the fourth subfigure. For each of the three scenarios, the moisture concentration distribution starts from a positive value for all three cases. In the case of , the distribution takes the exponential behavior with smooth decreasing. Still, on the other hand, when and , the distribution of moisture concentration decreases sharply near the surface, and it takes an exponential propagation behavior until it reaches a minimum value near the zero line due to moisture diffusivity. The fifth subfigure shows how the mechanical loads that tend to raise the value of the thermoelectric coupling parameters enhance the stress force amplitude. The displacement distribution with horizontal distance caused by moisture diffusivity and the thermal impact of photothermal stimulation for the rough surface is shown in the sixth subfigure. For each of the three thermoelectric coupling parameter situations, the displacement distribution begins at zero, climbs to maximum values near the surface, and then decreases in an exponential propagation pattern until it reaches a minimum value close to the zero line.6.4. Influence of Reference Moisture
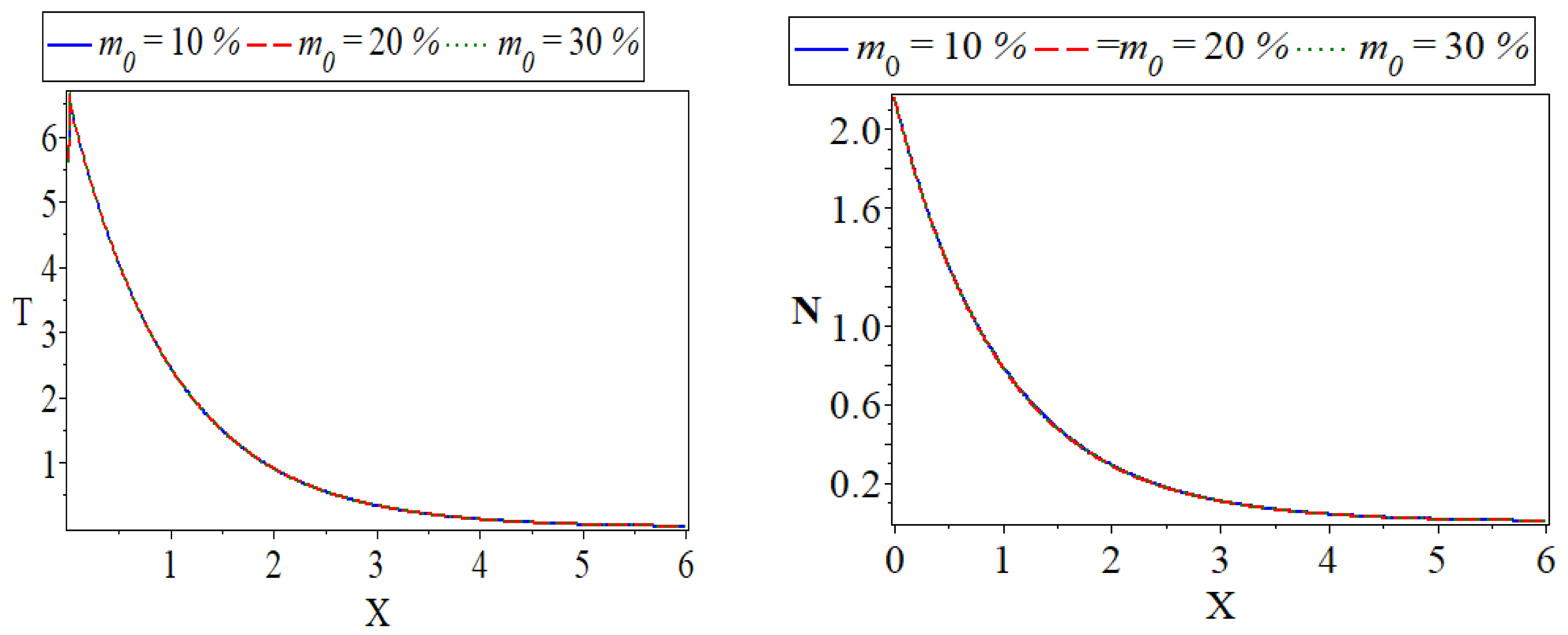
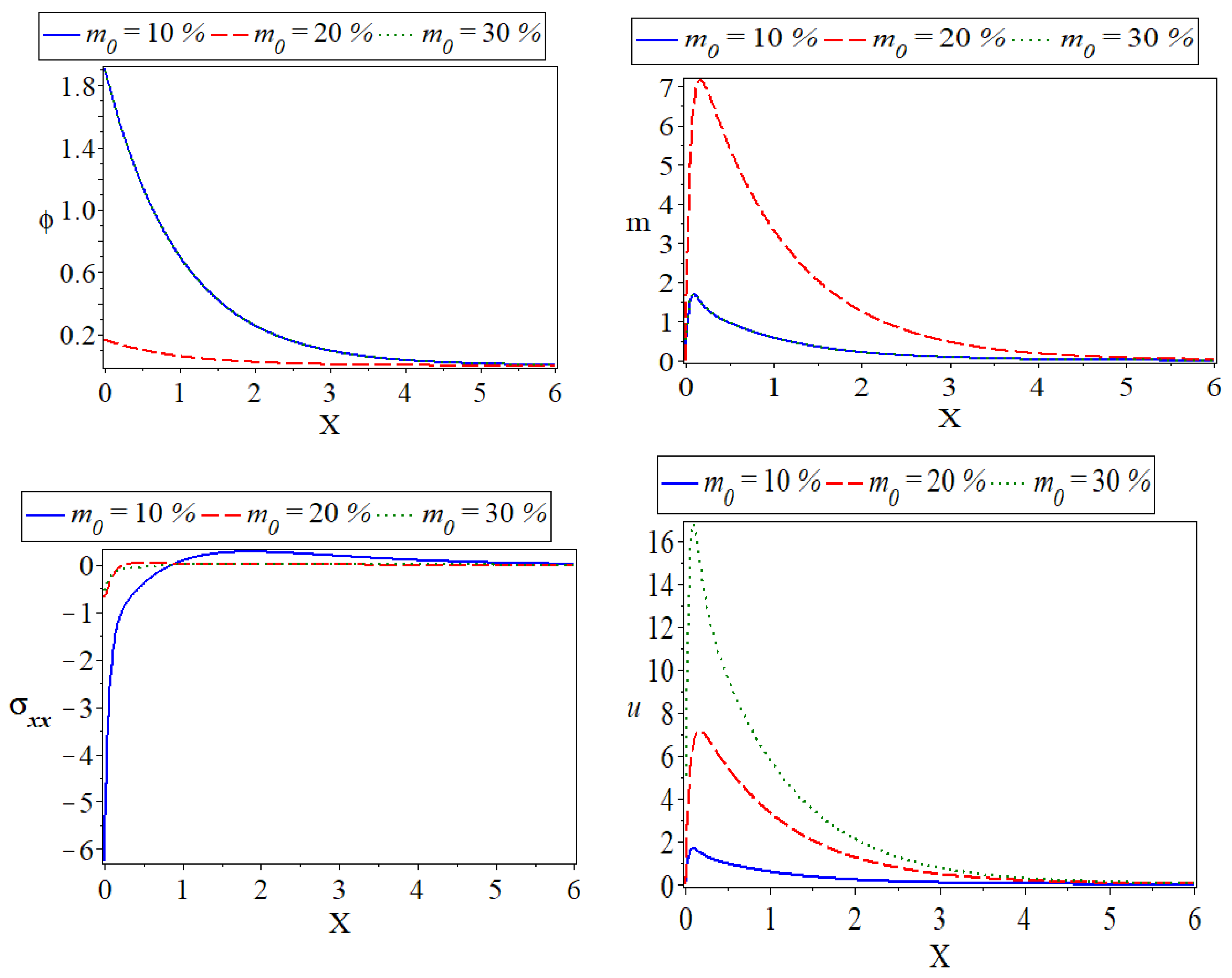
 ), the second case of reference moisture field when (
), the second case of reference moisture field when ( ), and the third case of reference moisture field when (
), and the third case of reference moisture field when ( ). All evaluations are made in the moisture field when and . From this figure, it is clear that the moisture field affects the wave propagation behavior of displacement, moisture concentration, stress force, temperature distributions, and carrier density distribution, but carrier density does not affect it.
). All evaluations are made in the moisture field when and . From this figure, it is clear that the moisture field affects the wave propagation behavior of displacement, moisture concentration, stress force, temperature distributions, and carrier density distribution, but carrier density does not affect it. 6.5. The Comparison between Si and Ge Materials
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lord, H.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Dhaliwal, R.S.; Sherief, H.H. Generalized thermoelasticity for anisotropic media. Q. Appl. Math. 1980, 38, 1–8. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P. A re-examination of the basic postulates of thermomechanics. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1991, 432, 171–194. [Google Scholar]
- Green, A.E.; Naghdi, P. On undamped heat waves in an elastic solid. J. Therm. Stress. 1992, 15, 253–264. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E. On a theory of heat conduction involving two temperatures. Z. Angew. Math. Und Phys. ZAMP 1968, 19, 614–627. [Google Scholar] [CrossRef]
- Chen, P.J.; Williams, W.O. A note on non-simple heat conduction. Z. Angew. Math. Und Phys. ZAMP 1968, 19, 969–970. [Google Scholar] [CrossRef]
- Warren, W.E.; Chen, P.J. Wave propagation in the two temperature theory of thermoelasticity. Acta Mech. 1973, 16, 21–33. [Google Scholar] [CrossRef]
- Singh, M.; Kumari, S. Influence of gravity and initial stress on Rayleigh wave propagation in magneto-thermoelastic medium. J. Math. Comput. Sci. 2021, 11, 2681–2698. [Google Scholar]
- Youssef, H.M. Theory of two-temperature-generalized thermoelasticity. IMA J. Appl. Math. 2006, 71, 383–390. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Karamany, A.S.; Ezzat, S.M. Two-temperature theory in magneto-thermoelasticity with fractional order dual-phase-lag heat transfer. Nucl. Eng. Des. 2012, 252, 267–277. [Google Scholar] [CrossRef]
- Shivay, O.N.; Mukhopadhyay, S. On the temperature-rate dependent two-temperature thermoelasticity theory. J. Heat Transf. 2020, 142, 022102. [Google Scholar] [CrossRef]
- Bajpai, A.; Kumar, R.; Sharma, P.K. Analysis of wave motion and deformation in elastic plate based on two temperature theory of thermoelasticity. Waves Random Complex Media 2021, 1–22. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Alanazi, R. Fractional Moore-Gibson-Thompson heat transfer model with two-temperature and non-singular kernels for 3D thermoelastic solid. J. Ocean. Eng. Sci. 2022, in press. [CrossRef]
- Sharma, J.N.; Sharma, Y.D.; Sharma, P.K. On the propagation of elasto-thermodiffusive surface waves in heat-conducting materials. J. Sound Vib. 2008, 315, 927–938. [Google Scholar] [CrossRef]
- Aouadi, M.; Moulahi, T. Asymptotic analysis of a nonsimple thermoelastic rod. Discret. Contin. Dyn. Syst.-S 2016, 9, 1475. [Google Scholar] [CrossRef][Green Version]
- Lotfy, K.; Hassan, W. Normal mode method for two-temperature generalized thermoelasticity under thermal shock problem. J. Therm. Stress. 2014, 37, 545–560. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, V. Wave propagation at the boundary surface of an elastic and thermoelastic diffusion media with fractional order derivative. Appl. Math. Model. 2015, 39, 1674–1688. [Google Scholar] [CrossRef]
- Kumar, R.; Kansal, T. Propagation of Rayleigh waves on free surface of transversely isotropic generalized thermoelastic diffusion. Appl. Math. Mech. 2008, 29, 1451–1462. [Google Scholar] [CrossRef]
- Kumar, R.; Kansal, T. Effect of rotation on Rayleigh waves in an isotropic generalized thermoelastic diffusive half-space. Arch. Mech. 2008, 60, 421–443. [Google Scholar]
- Kumar, R.; Kansal, T. Dynamic problem of generalized thermoelastic diffusive medium. J. Mech. Sci. Technol. 2010, 24, 337–342. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, V. Problem of Rayleigh Wave Propagation in Thermoelastic Diffusion. J. Solid Mech. 2016, 8, 602–613. [Google Scholar]
- Ezzat, M.A.; Abd Elall, M.Z. Generalized magneto-thermoelasticity with modified Ohm’s law. Mech. Adv. Mater. Struct. 2010, 17, 74–84. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Lotfy, K. On the Plane Waves in Generalized Thermomicrostretch Elastic Half-space. Int. Commun. Heat Mass Transf. 2010, 37, 192–200. [Google Scholar] [CrossRef]
- Othman, M.I.; Lotfy, K.; Farouk, R. Generalized thermo-microstretch elastic medium with temperature dependent properties for different theories. Eng. Anal. Bound. Elem. 2010, 34, 229–237. [Google Scholar] [CrossRef]
- Lotfy, K.; Othman, M. The effect of rotation on plane waves in generalized thermo-microstretch elastic solid with one relaxation time for a mode-I crack problem. Chin. Phys. B 2011, 20, 074601. [Google Scholar] [CrossRef]
- Lotfy, K. Mode-I crack in a two-dimensional fibre-reinforced generalized thermoelastic problem. Chin. Phys. B 2012, 21, 014209. [Google Scholar] [CrossRef]
- Othman, M.; Lotfy, K. The effect of magnetic field and rotation of the 2D problem of a fiber-reinforced thermoelastic under three theories with influence of gravity. Mech. Mater. 2013, 60, 120–143. [Google Scholar] [CrossRef]
- Lotfy, K.; Hassan, W.; El-Bary, A.; Kadry, M. Response of electromagnetic and Thomson effect of semiconductor mediu due to laser pulses and thermal memories during photothermal excitation. Results Phys. 2020, 16, 102877. [Google Scholar] [CrossRef]
- Youssef, H.; El-Bary, A. Theory of hyperbolic two-temperature generalized thermoelasticity. Mater. Phys. Mechs. 2018, 40, 158–171. [Google Scholar]
- Fahmy, M.A. Boundary element modeling of 3T nonlinear transient magneto-thermoviscoelastic wave propagation problems in anisotropic circular cylindrical shells. Compos. Struct. 2021, 27, 114655. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Almehmadi, M.M.; Subhi, F.M.; Sohail, A. Fractional boundary element solution of three-temperature thermoelectric problems. Sci. Rep. 2022, 2, 6760. [Google Scholar] [CrossRef]
- Fahmy, M.A. 3D Boundary Element Model for Ultrasonic Wave Propagation Fractional Order Boundary Value Problems of Functionally Graded Anisotropic Fiber-Reinforced Plates. Fractal Fract. 2022, 6, 247. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Alsulami, M.O. Boundary Element and Sensitivity Analysis of Anisotropic Thermoelastic Metal and Alloy Discs with Holes. Materials 2022, 15, 1828. [Google Scholar] [CrossRef] [PubMed]
- Fahmy, M.A. Boundary element modeling of fractional nonlinear generalized photothermal stress wave propagation problems in FG anisotropic smart semiconductors. Eng. Anal. Bound. Elem. 2022, 134, 665–679. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Sladek, J.; Sladek, V. Application of meshless local integral equations to two dimensional analysis of coupled non-Fick diffusionelasticity. Eng. Anal. Bound. Elem. 2013, 37, 603–615. [Google Scholar] [CrossRef]
- Abo-Dahab, S.; Lotfy, K. Two-temperature plane strain problem in a semiconducting medium under photothermal theory. Waves Random Complex Media 2017, 27, 67–91. [Google Scholar] [CrossRef]
- Lotfy, K.; Sarkar, N. Memory-dependent derivatives for photothermal semiconducting medium in generalized thermoelasticity with two- Temperature. Mech. Time-Depend. Mater. 2017, 21, 519–534. [Google Scholar] [CrossRef]
- Lotfy, K.; Elidy, E.S.; Tantawi, R.S. Photothermal Excitation Process during Hyperbolic Two-Temperature Theory for Magneto-Thermo-Elastic Semiconducting Medium. Silicon 2021, 13, 2275–2288. [Google Scholar] [CrossRef]
- Lotfy, K.; Elidy, E.S.; Tantawi, R.S. Piezo-photo-thermoelasticity transport process for hyperbolic two-temperature theory of semiconductor material. Int. J. Mod. Phys. C 2021, 32, 2150088. [Google Scholar] [CrossRef]
- Xiao, Y.; Shen, C.; Zhang, W.B. Screening and prediction of metal-doped α-borophene monolayer for nitric oxide elimination. Mater. Today Chem. 2022, 25, 100958. [Google Scholar] [CrossRef]
- Liu, J.; Han, M.; Wang, R.; Xu, S.; Wang, X. Photothermal phenomenon: Extended ideas for thermophysical properties characterization. J. Appl. Phys. 2022, 131, 065107. [Google Scholar] [CrossRef]
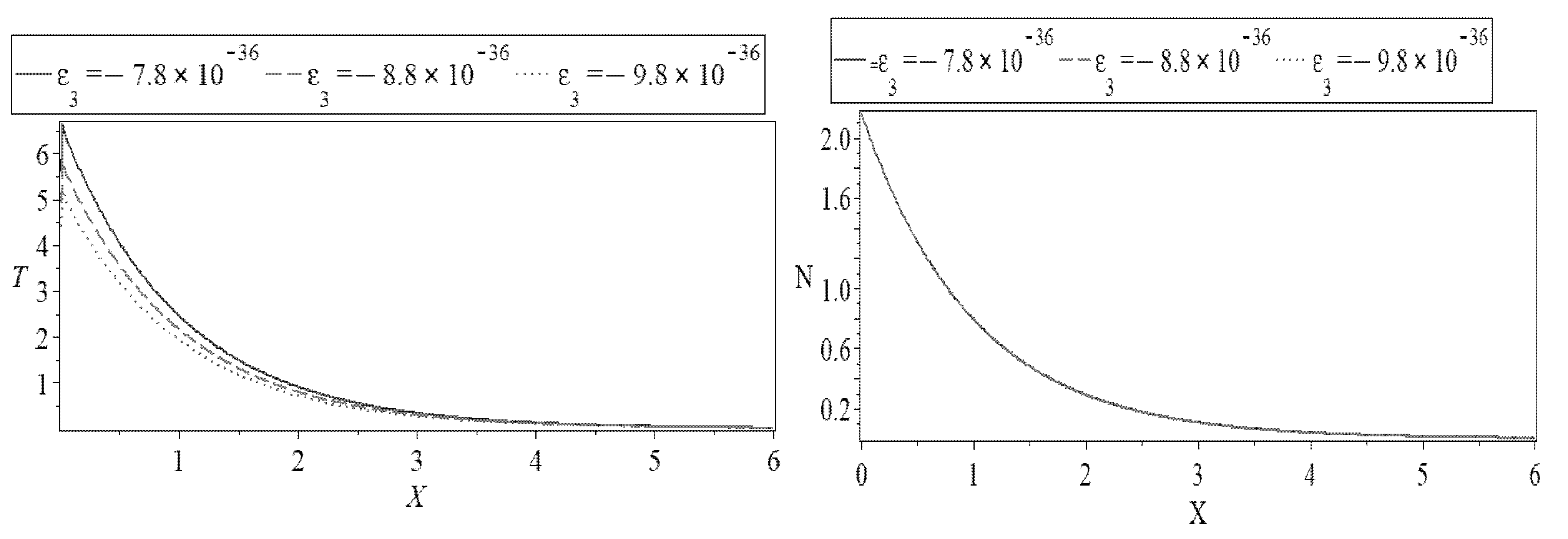

| Units | Symbol | Si | Ge |
|---|---|---|---|
| Reference moisture | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhashash, A.; Elidy, E.S.; El-Bary, A.A.; Tantawi, R.S.; Lotfy, K. Two-Temperature Semiconductor Model Photomechanical and Thermal Wave Responses with Moisture Diffusivity Process. Crystals 2022, 12, 1770. https://doi.org/10.3390/cryst12121770
Alhashash A, Elidy ES, El-Bary AA, Tantawi RS, Lotfy K. Two-Temperature Semiconductor Model Photomechanical and Thermal Wave Responses with Moisture Diffusivity Process. Crystals. 2022; 12(12):1770. https://doi.org/10.3390/cryst12121770
Chicago/Turabian StyleAlhashash, Abeer, E. S. Elidy, A. A. El-Bary, Ramdan S. Tantawi, and Khaled Lotfy. 2022. "Two-Temperature Semiconductor Model Photomechanical and Thermal Wave Responses with Moisture Diffusivity Process" Crystals 12, no. 12: 1770. https://doi.org/10.3390/cryst12121770
APA StyleAlhashash, A., Elidy, E. S., El-Bary, A. A., Tantawi, R. S., & Lotfy, K. (2022). Two-Temperature Semiconductor Model Photomechanical and Thermal Wave Responses with Moisture Diffusivity Process. Crystals, 12(12), 1770. https://doi.org/10.3390/cryst12121770








