A Fast, Low-Cost and Simple Method for Predicting Atomic/Inter-Atomic Properties by Combining a Low Dimensional Deep Learning Model with a Fragment Based Graph Convolutional Network

Abstract

Calculations with high accuracy for atomic and inter-atomic properties, such as nuclear magnetic resonance (NMR) spectroscopy and bond dissociation energies (BDEs) are valuable for pharmaceutical molecule structural analysis, drug exploration, and screening. It is important that these calculations should include relativistic effects, which are computationally expensive to treat. Non-relativistic calculations are less expensive but their results are less accurate. In this study, we present a computational framework for predicting atomic and inter-atomic properties by using machine-learning in a non-relativistic but accurate and computationally inexpensive framework. The accurate atomic and inter-atomic properties are obtained with a low dimensional deep neural network (DNN) embedded in a fragment-based graph convolutional neural network (F-GCN). The F-GCN acts as an atomic fingerprint generator that converts the atomistic local environments into data for the DNN, which improves the learning ability, resulting in accurate results as compared to experiments. Using this framework, the ${}^{13}$C/${}^1$H NMR chemical shifts of Nevirapine and phenol O–H BDEs are predicted to be in good agreement with experimental measurement.

1. Introduction

Accurate descriptions of inter-atomic information are increasingly important for chemical research [1,2,3,4,5,6,7]. For example, bond disassociation energies (BDEs) describe the energy difference that is caused by a change of bonding environment. Such metrics are relevant to reaction kinetics and can provide important chemical insights. In addition, the magnitudes of NMR chemical shifts can accurately reflect the atomic environment, and NMR measurements are important for structure determination. Accurate predictions of such metrics with affordable computation cost will be helpful for experimental researchers [8]. Over the past decades, density functional theory (DFT) has become a standard tool used by computational chemists [9,10,11,12,13]. Wave function based methods can be more accurate, but usually require a higher computational cost, and their use tends to be limited to small molecules. One way to improve the accuracy of DFT without significantly increasing the computational cost is to use data-driven methods.

Recently, artificial intelligence (AI) tools have been successfully applied in chemical and physical research, and through them, various kinds of expensive calculations, including atomic simulations, adsorptions, photocatalysis, etc, can be done with substantially reduced cost [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Moreover, with the development of graph convolutional neural networks (GCNs), accurate and efficient predictions of molecular and atomic properties have also become feasible [31,32,33,34,35]. Using molecular graphs, structural information can be systematically mapped to predicted properties within the framework of GCNs. However, using molecular graphs alone, it is difficult for GCNs to extract atomic and inter-atomic information; the reason behind this lies in the fact that the chemical environment cannot be effectively differentiated at the atomic level. To improve structure-function predictions, novel architectures can be exploited.

To successfully extract the local information in molecules, the fragment-based graph convolutional network (F-GCN) that is able to utilise multiple-level fragmentary graphs to accurately solve the chemical environment at the atomic level, will be helpful [36]. Unlike message-passing based approaches [37,38,39], the F-GCN doesn’t require large amounts of molecular information. For more accurate predictions that require the assistance of extra chemical knowledge, however, our original architecture needs to be revised. In this study, we combine our original F-GCN with a low dimensional DNN. The added DNN is able to reduce the risk of over-fitting during incorporation of numerical descriptors; such a combination architecture is suitable for few-shot learning, as it is more focused on atomic or inter-atomic sites within molecular graphs. To further improve the prediction accuracy and efficiency of this tool, we will make revisions of the original architecture and include some selective descriptors that are numerically correlated with the target property. Specifically, there is a numerical correlation between the experimental NMR chemical shifts and DFT calculated isotropic shielding constants [9,10,11,33]; the experimental BDEs can be approximated from QM computations. First, we employed a low dimensional DNN to approximate target properties with respect to the added QM descriptors; then, a high dimensional F-GCN was applied to refine the results of the DNN within the multiple-level molecular graphs. We find that the errors of the DFT calculations due to complicated chemical environments can be mitigated with the assistance of our molecular graph based calculation.

2. Computational Details

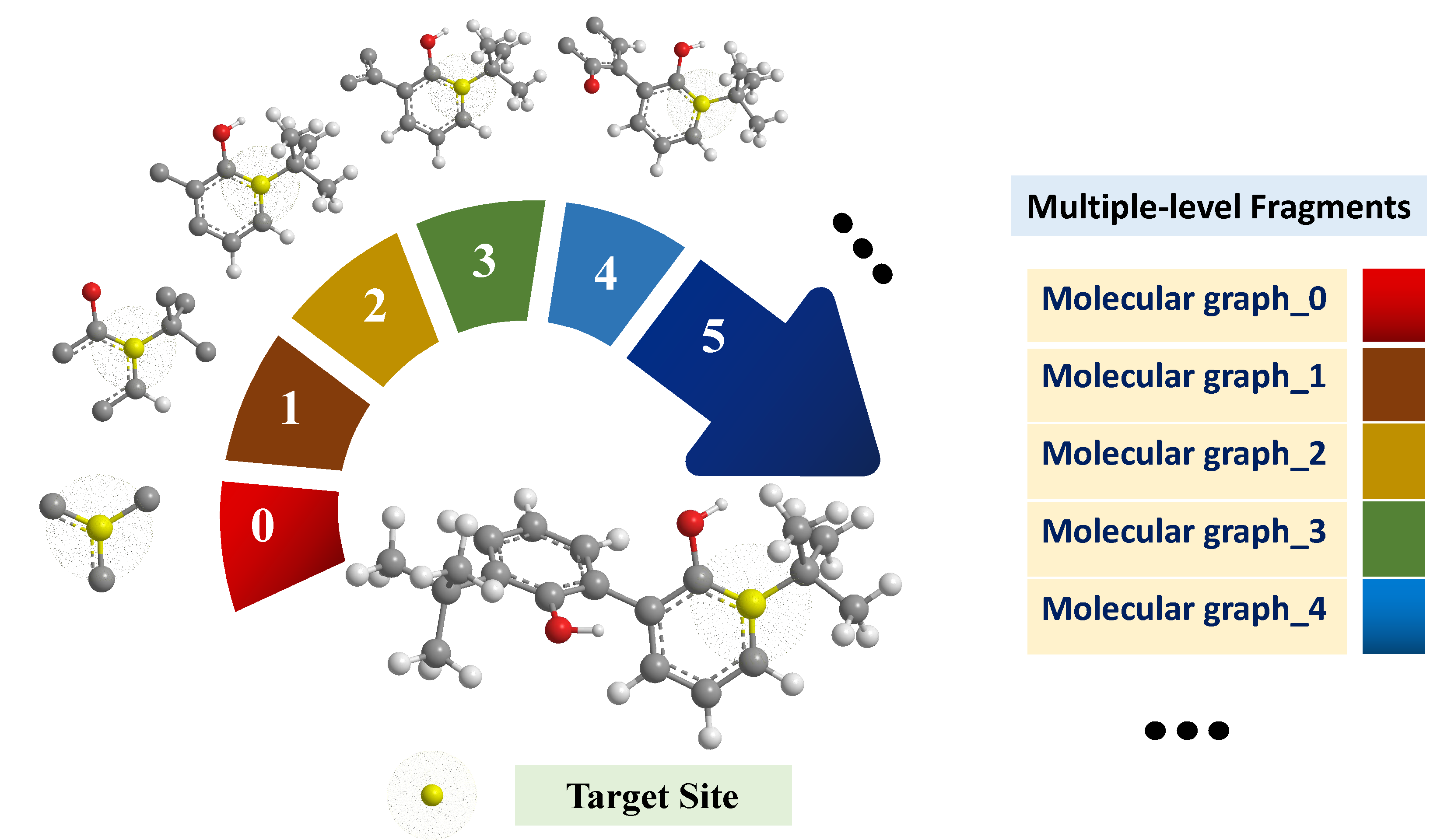
2.1. Structure of the F-GCN

In our previous study, we reported a F-GCN architecture [36], which utilises multiple-level molecular fragments to describe atomic environments. The workflow is as follows: starting from a target site, fragmentary graphs at different levels are generated systematically; then all fragments are described by independent GCNs for information extraction. The scheme of our fragment generation is shown in Figure 1; the overall workflow can be seen in Figure 2.

Once the multiple-level fragments are generated, the GCN is able to utilise them for information extraction. Within the DGL library, the input molecular and fragmentary graphs were transformed into nodes and edges that correspond to atoms and bonds, respectively [40,41]. At the radial basis function (RBF) layer, the bonding data are recorded in a distance tensor. Additionally, continuous-filter convolution layers were applied to describe the atomic environment. The evolution of the $i^{\mathrm{th}}$ atom at the $k+1$ layer can be expressed as:

$$a_i^{k+1}=\sum _{j=0}^N{a}_j^k\circ {\omega }^k\left(D_{ij}\right)$$

(1)

where, ${\omega }^k$ represents the filter-generation, and ∘ indicates element-wise multiplication. To control the overall optimisation accuracy, a Gaussian function, $g_k$, is applied as

$$g_l\left(D_{ij}\right)=exp(-\alpha {(D_{ij}-{\beta }_l)}^2)$$

(2)

in which, ${\beta }_l$ is the magnitude of cutoff, and $D_{ij}$ represents the connection between the $i^{\mathrm{th}}$ and $j^{\mathrm{th}}$ atom. We applied a default value of $\alpha =0.1$ in this study [31].

Moreover, for any chemical site, a loss function that takes an experimental value ($P{r}^{\prime }$) as reference is applied to control the accuracy of the predicted property ($Pr$).

$$L(Pr,P{r}^{\prime })={(Pr-P{r}^{\prime })}^2$$

(3)

To include extra chemical knowledge for more accurate predictions, modifications of this architecture are required.

2.2. Utilisation of QM Descriptors by a Low Dimensional DNN

To first approximate atomic/inter-atomic properties with respect to QM calculated descriptors, an independent DNN is employed, which is based on a polynomial fit to process the added descriptors, T${}_{\mathrm{QM}}$,

$$T=a_0+a_1{T}_{\mathrm{QM}}+a_2{\left(T_{\mathrm{QM}}\right)}^2+a_3{\left(T_{\mathrm{QM}}\right)}^3+a_4{\left(T_{\mathrm{QM}}\right)}^4.$$

(4)

If the included descriptors that numerically correlate with the target values are directly input into the GCN, there is a risk of over-fitting, especially when using few-shot learning, as the QM calculated values cannot be fully utilised; this can be attributed to the original architecture of graph based neural networks, as the actual prediction accuracy is highly associated with the sampling probability P${}_{\mathrm{model}}$

$${\theta }_{\mathrm{model}}=argmax\left(\theta \right)\sum _{k=1}{P}_{\mathrm{model}}(x^k,y^k;\theta ).$$

(5)

With numerical corrections by the independent DNN, however, the QM calculated results can be approximately calibrated with experimental values, and the difference between these two values can be input into the next GCN stage. The accuracy of such a methodology had been well verified by previous study [33]. Then, the range of the target values’ distribution becomes narrower (see the ${}^1$H NMR chemical shifts in Figure 3) where the risk of over-fitting is reduced, as shown in Figure 4, and the performance of the GCN is improved.

In this study, we focused on few-shot learning cases, and made a trial to combine QM calculations with molecular graphs for experimental NMR chemical shifts and BDEs predictions. Within molecules, for the $i^{\mathrm{th}}$ nucleus, ${\upsilon }_i$, the NMR frequency can be expressed as

$${\upsilon }_i=({\gamma }_i/2\pi )B_1=({\gamma }_i/2\pi )B_0(1-{\sigma }_i)$$

(6)

where ${\gamma }_i$ represents the gyromagnetic ratio of the $i^{\mathrm{th}}$ nucleus, which is approximately a constant value, and ${\sigma }_i$ is the isotropic shielding constant, which is calculated with the DFT/GIAO approach [12]. The accuracy of the QM calculations depends on many factors [11] including $B_1$, the strength of the induced field which is proportional to the strength of the uniformed external field along z-axis, and the value of the chemical shift, ${\delta }_i$ (in ppm), which can be obtained as

$${\delta }_i={10}^6({\upsilon }_i-{\upsilon }_0)/{\upsilon }_0$$

(7)

where ${\upsilon }_0$ is the resonance frequency of the referenced nucleus [42,43,44].

There is a quasi-linear relationship between the experimental chemical shifts (${\delta }_i$) and the QM calculated isotropic shielding constants (${\sigma }_i$) [11,45]. In previous studies, scaling factors have been applied to approximate NMR chemical shifts [11,45,46], using

$${\delta }_i=-(\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}-{\sigma }_i)/\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}.$$

(8)

It is worth noting, however, that for complex bonding environments, the approximate chemical shifts may deviate nonlinearly from the experimental values [11,12]. Within the F-GCN framework the structural information extracted can efficiently correct the approximate results of the DNN. First, we tested this refined F-GCN on ${}^{13}$C and ${}^1$H NMR chemical shift predictions with inclusion of the DFT calculated isotropic shielding constants [11]. To obtain such a descriptor, we first conducted geometry optimisation of the molecules to locate the minimum of the potential energy surface. The isotropic shielding constants were calculated with the GIAO approach; in this step, the SMD implicit solvent model [47] was adopted. In this study, we employed the M062X/6-31+G(d,p) level of theory for geometry optimisation, and mPW1PW91/6-311+G(2d,p) for the NMR GIAO calculations. The geometries with lowest energy were adopted. All the calculations were performed within the Gaussian 09 software package [48].

We also applied the proposed F-GCN for the experimental BDEs predictions with inclusion of DFT calculated bonding energies for C-H, O-H and C-C bonds [49]; and in this part, all the DFT calculations were performed at the M062X/def2-TZVP level, with the formula AB → A· + B·.

3. Results and Discussion

3.1. Performance of the QM Augmented F-GCN in NMR Chemical Shift Predictions

The prediction results for ${}^{13}$C and ${}^1$H NMR chemical shifts are presented in Figure 5; for the original data set, the ratio of the number of training to test molecules is set to 9:1. We can see that the architecture of the F-GCN is able to calibrate the DFT calculation results with respect to experimental values via inclusion of a low dimensional DNN network to numerically process the DFT calculated information. The reason behind this lies in the fact that the magnitudes of the chemical shifts are largely determined by the atomic environment; for complicated bonding environments, the heavily asymmetric distribution of electron density may make the DFT calculated isotropic shielding constants deviate non-linearly from the experimental NMR chemical shifts, leading to numerical errors. Such errors cannot be simply overcome by merely improving the level of QM theory. This combination F-GCN has natural advantages of accurately describing the chemical environment at the atomic level, and thus can effectively correct the DFT errors. At the same time, different from other models that merely rely on RDKit generated descriptors to extract structural information [33], the architecture of F-GCN is more efficient, due to the fact that it directly uses multiple-level fragments for information extraction. Additionally, with the inclusion of DFT calculated isotropic shielding constants that are processed by the mentioned DNN model, the augmented F-GCN becomes suitable for few-shot learning with a lower risk of over-fitting.

3.2. Performance of the QM Augmented F-GCN in BDE Predictions

To improve the performance of F-GCN on experimental inter-atomic properties predictions, inclusion of DFT calculated bonding energy descriptors may be helpful [33]. Thus, we revised the architecture of F-GCN to include both molecular graphs and QM calculated bond dissociation energy, and tested it for predictions at experimental level. The performance is summarised in Figure 6. We can clearly see that the prediction error is largely reduced, compared to that produced by the F-GCN model [36], due to the fact that F-GCN can describe the inter-atomic environment within molecular graphs through the calibration of DFT calculated BDEs. In summary, we can reasonably conclude that the inclusion of QM descriptors is helpful to enhance the overall performance of graph convolutional network. However, it is still worth noting that running a large number of DFT calculations may be computationally expensive, to handle this, more general quantitative structure-property relationship (QSPR) protocols still remain to be explored. Additionally, in the cases of complicated bonding structures, the calculated bonding energy may significantly deviate from the experimental value due to the deficiency of QM calculations, thus the performance of graph based approaches may also be negatively influenced.

It is understandable that the performance of the F-GCN in atomic/inter-atomic properties predictions is largely dependent on molecular coverage of the original data sets, as there always exists an imperfect mapping between the accuracy of DFT calculations and solution degree of molecular graphs; the prediction precision is positively correlated with the actual consistency between these two items. That is to say, to systematically overcome the hurdles of graph based approaches and make the proposed architecture more flexible for specific applications, in one aspect, it is helpful to enlarge the training data set selectively to enhance molecular diversity, thus their differentiation capability among various molecular graphs can be subsequently enhanced. In another aspect, identification of correlated yet affordable QM descriptors, is also of great significance, the ones that contain important chemical knowledge can positively influence the prediction accuracy within the framework of GCN.

3.3. Nevirapine Structure Elucidation by the QM Augmented F-GCN Architecture

Nevirapine is an important inhibitor for HIV reverse transcriptase, its structure is shown in Figure 7. Unfortunately, there exist multiple possible structures, and for experimental researchers, accurate structure elucidation still remains to be a challenging goal. In addition, due to the lower solubility of this compound, NMR spectra are difficult to obtain. Thus, a good consistence in NMR chemical shifts between computational predictions and experimental measurement will be of great significance for studies of this compound. We applied our proposed F-GCN for ${}^{13}$C/${}^1$H chemical shifts predictions for this complex structure. The results are summarised in

Table 1. Predicted and experimental ${}^{13}$C NMR chemical shifts (in ppm) of Nevirapine.

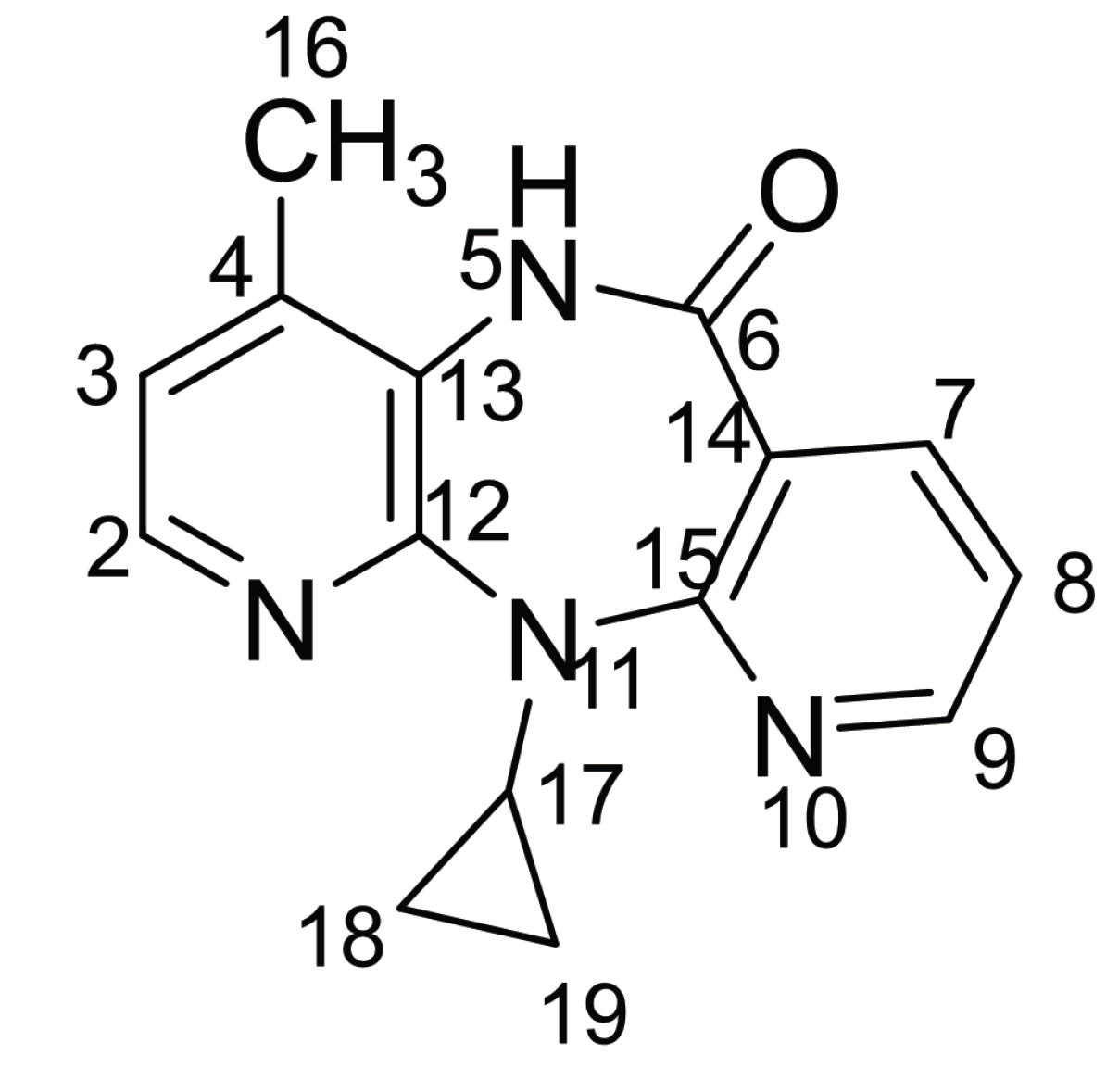
Position ${}^{\left(\mathit{a}\right)}$	Exptl.	Pred. ${}^{\left(\mathit{b}\right)}$	Error
2	140.36	143.33	2.97
3	120.35	122.41	2.06
4	139.52	137.42	2.10
6	169.06	165.45	3.61
7	144.47	138.38	6.09
8	118.99	119.93	0.94
9	152.15	155.36	3.21
12	154.17	152.68	1.49
13	124.97	126.29	1.32
14	122.13	120.39	1.74
15	160.73	159.95	0.78
16	17.86	20.39	2.53
17	29.65	32.49	2.84
18	8.88	9.07	0.19
19	9.15	9.45	0.30

^(a) Positions for the carbon atoms of interest. ^(b) The predicted ¹³C NMR chemical shifts via the trained QM augmented F-GCN architecture.

and

Table 2. Predicted and experimental ${}^1$H NMR chemical shifts (in ppm) of Nevirapine.

Position ${}^{\left(\mathit{a}\right)}$	Exptl.	Pred. ${}^{\left(\mathit{b}\right)}$	Error
2	8.08	7.80	0.28
3	7.07	6.71	0.36
7	8.02	7.93	0.09
8	7.20	6.77	0.43
9	8.51	8.25	0.26
16	2.34	2.25	0.09
17	3.62	3.60	0.02
18	0.35	0.51	0.16
19	0.88	0.87	0.01

^(a) Positions for the hydrogen atoms of interest. ^(b) The predicted ¹H NMR chemical shifts via the trained QM augmented F-GCN architecture.

; we can clearly see that the predicted results match well with the experimental values, indicating the applicability of this QM augmented F-GCN in challenging structure assignments.

3.4. Calculations of Phenol O-H BDEs by the QM Augmented F-GCN Architecture

Phenol inhibitors can efficiently retard the oxidation of polymers; for this class of compounds, the phenol O-H bonds are usually first attacked by the peroxyl based radicals. That is to say, the O-H BDE can serve as a demonstrative metric to characterise the performance of phenol inhibitors [50]. Currently, due to the operational complexity and time required for experimental measurements that are based on kinetic analysis, the number and types of referable O-H BDE values are limited and remain to be enlarged. Within the framework of F-GCN, by inclusion of QM descriptors, accurate calculations of phenol O-H BDEs can be realised. In Figure 8, we present the experimental and predicted O-H BDEs for a series of phenol compounds. It is notable that with F-GCN, the prediction results were all at experimental level, demonstrating its promising prospect for this kind of predictions. In addition, the DFT calculation results were found to be largely calibrated with the assistance of molecular graphs.

4. Conclusions

To sum up, through modification of the original architecture of F-GCN, the prediction performance in both atomic and inter-atomic properties are enhanced. The inclusion of QM descriptors within a separated neural network calibrate the prediction results, making it suitable for few-shot learning cases; the proposed F-GCN is shown to be more powerful for chemical environment description at the atomic level. The prediction results of NMR chemical shifts and BDEs are comparable to experimental measurement. Moreover, the proposed architecture is flexible to include other useful descriptors, thus can be applicable for various kinds of challenging structural assignments. The success of F-GCN indicates a promising direction for incorporating advanced AI technologies into physical and chemical research; however, purely QM calculations are time expensive, and cannot be conducted in large scales, thus reasonable identification of alternative yet affordable calculations will be expected. In the future, we expect that more scientific insights can be provided with assistance of novel yet functional data-driven approaches.