Numerical Simulation of Species Segregation and 2D Distribution in the Floating Zone Silicon Crystals
Abstract
:1. Introduction
2. Numerical Model
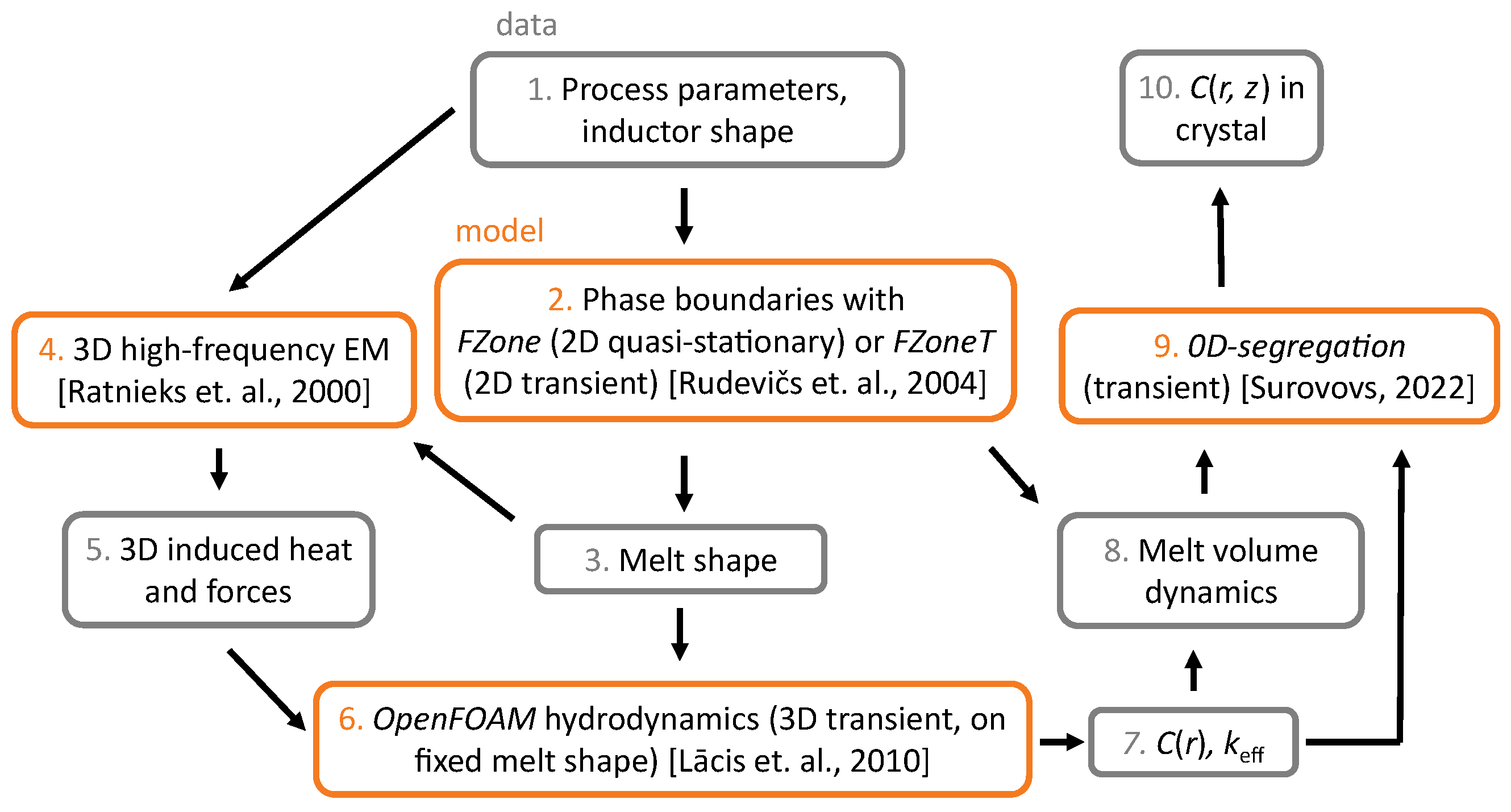
2.1. Overview of Modelling Scheme
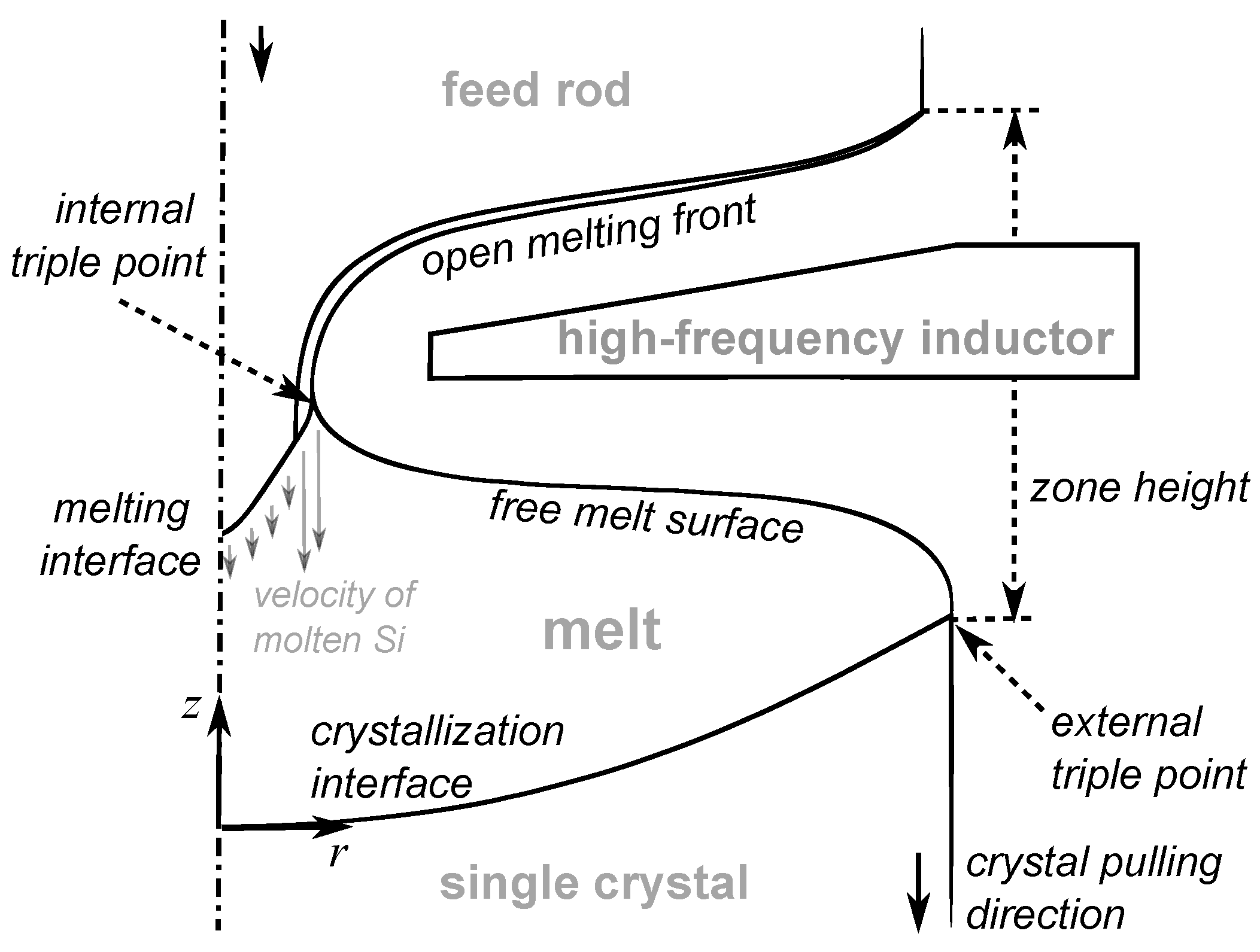
2.2. Phase Boundaries
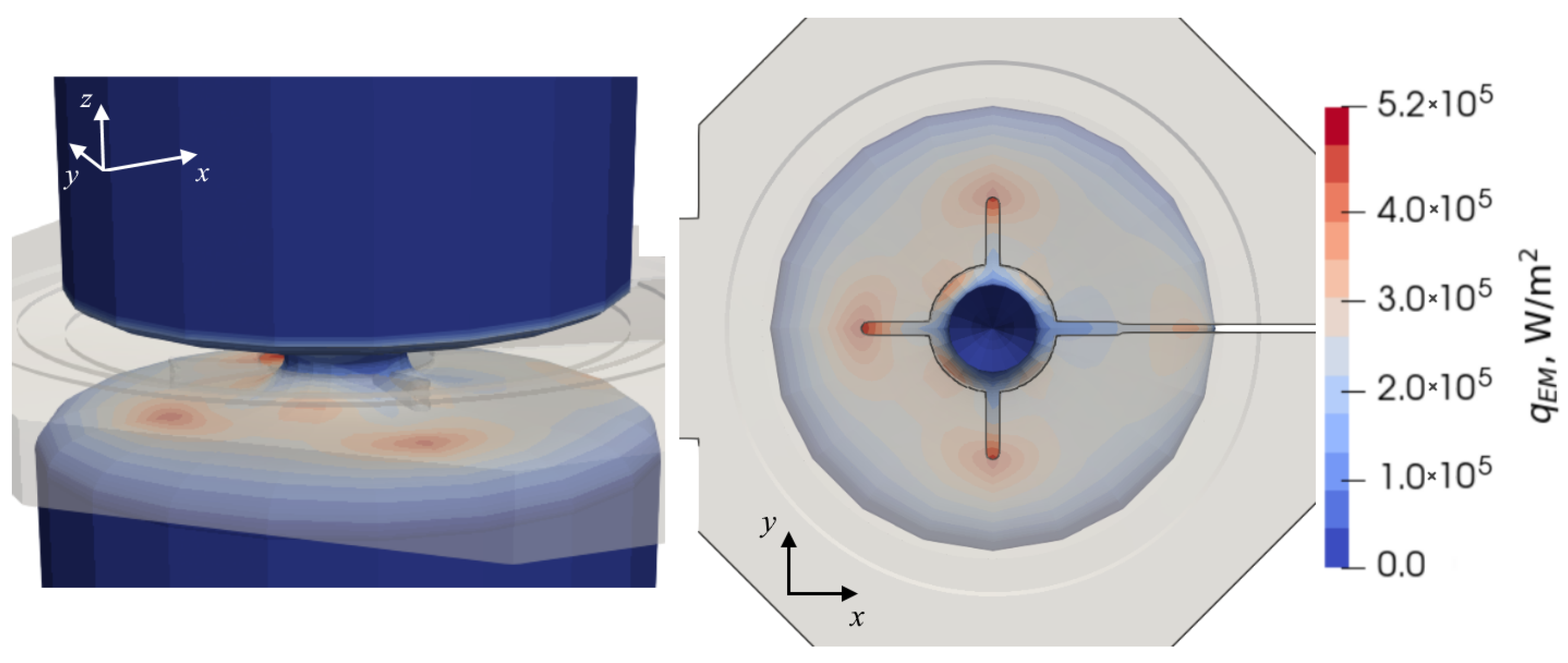
2.2.1. Electromagnetic Field
2.3. Species Transport in Melt
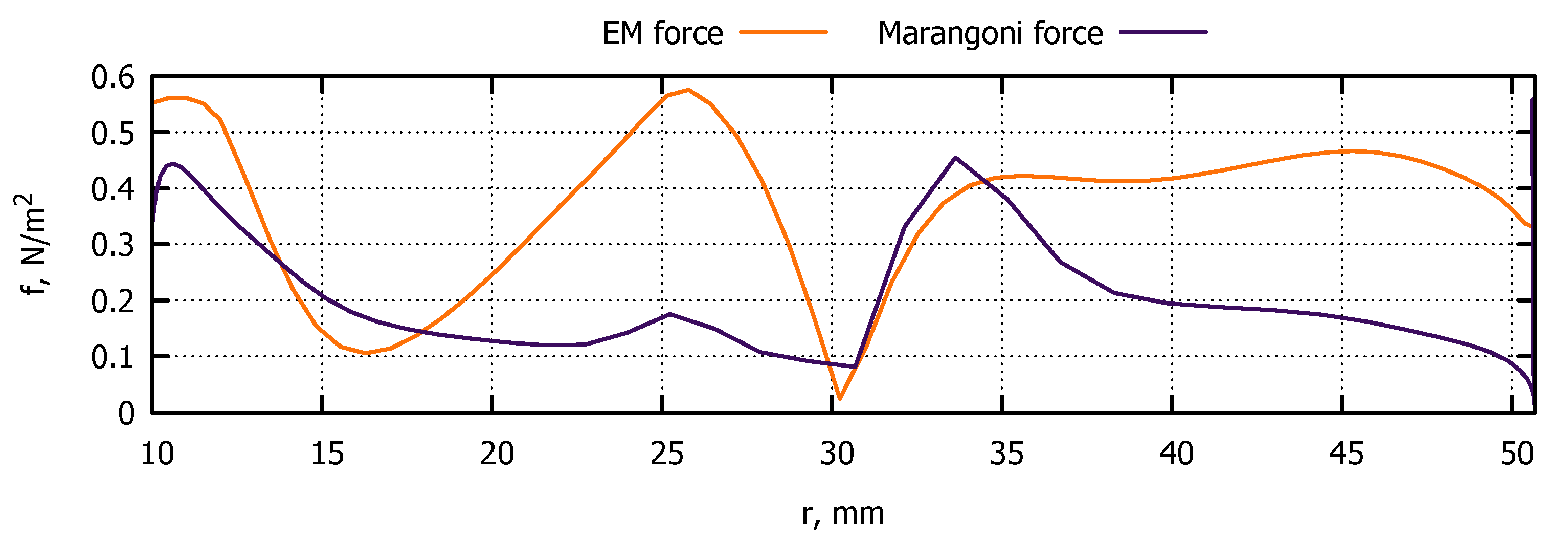
- Marangoni force and the EM force are applied on the free melt surface.
- Fixed velocity (crystal pulling speed and rotation)—on the crystallization interface.
- On the crystallization interface: where n is the normal coordinate, is the segregation coefficient, and is the the angle between the horizontal plane and the interface normal vector.
- On the melt free surface: due to the assumption of a pure gas atmosphere and lack of evaporation [24].
- On the melting interface: arb.u., i.e., the species concentration is normalized to the initial concentration in the feed rod, which is assumed to be homogeneous.
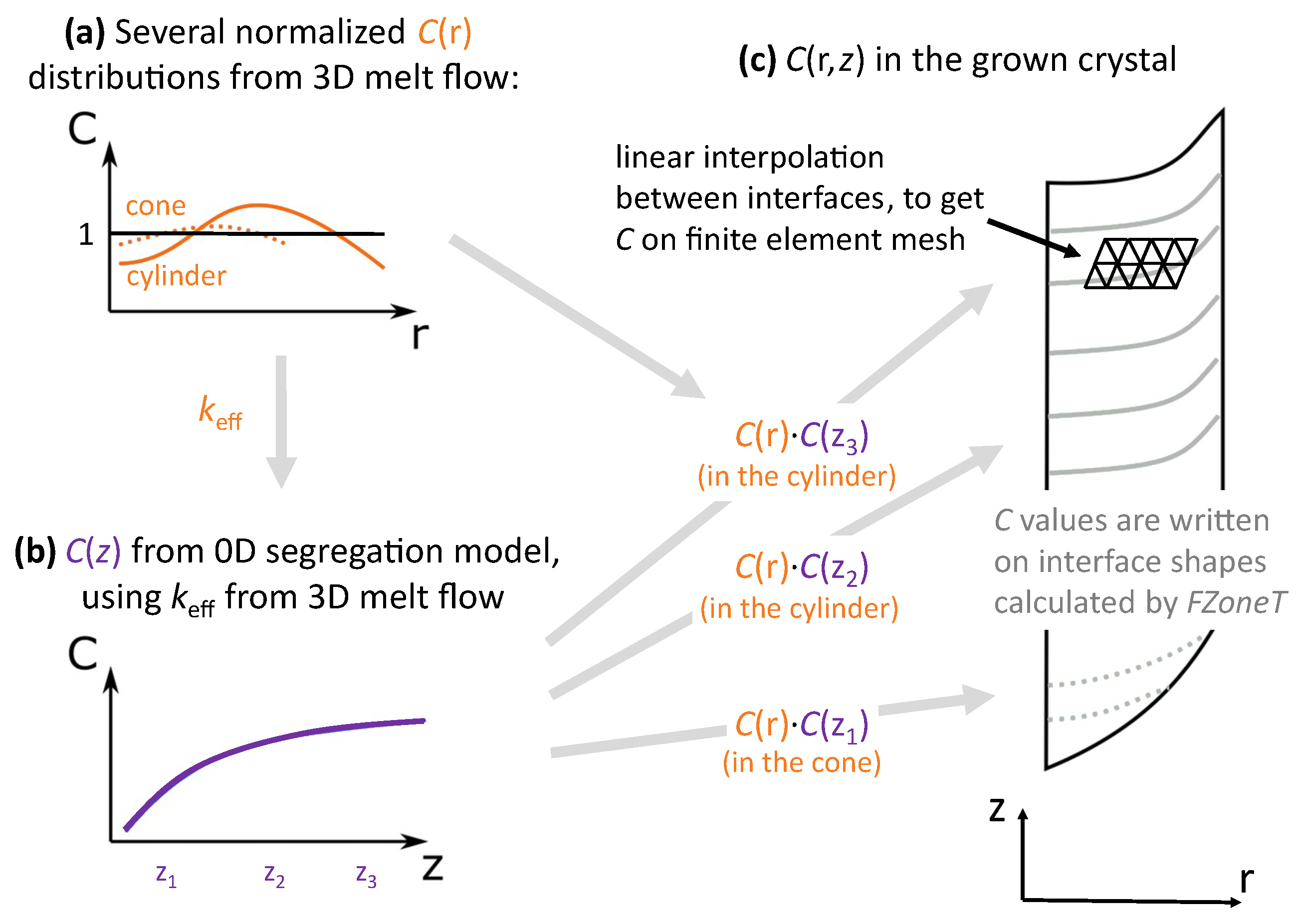
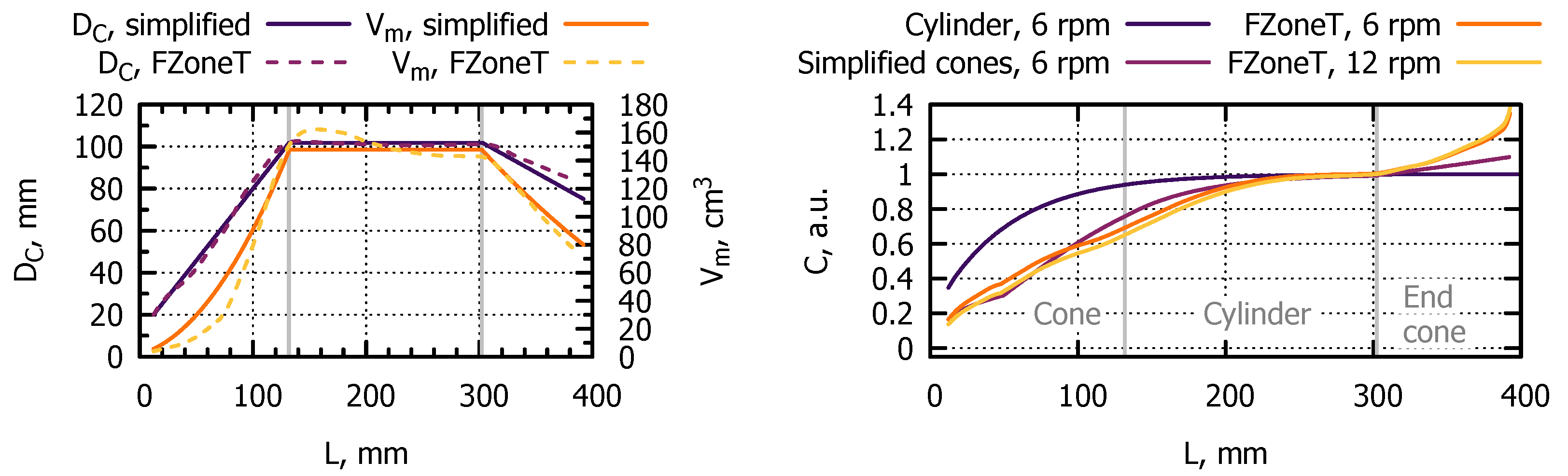
2.4. 2D Species Distribution in Crystal
- Importing the data about process dynamics (time-dependent , , and ) from transient phase boundary simulations with FZoneT.
- Creating an approximate description of the cone phase based only on the simplified crystal shape described as , where L is the crystal length:
- Due to the assumption of constant pulling velocity, .
- Cone surfaces are approximated as having constant slope, and thus .
- The free surface height above the external triple point is assumed to be constant even during the cone phases because it is impossible to predict its evolution for an arbitrary crystal shape (without experimental data); therefore, .
- The crystallized volume is proportional to the crystal cross-section: , where is the crystal pulling velocity, and is the crystal cross-section area. Therefore, .
- Due to silicon mass conservation, .
3. Results
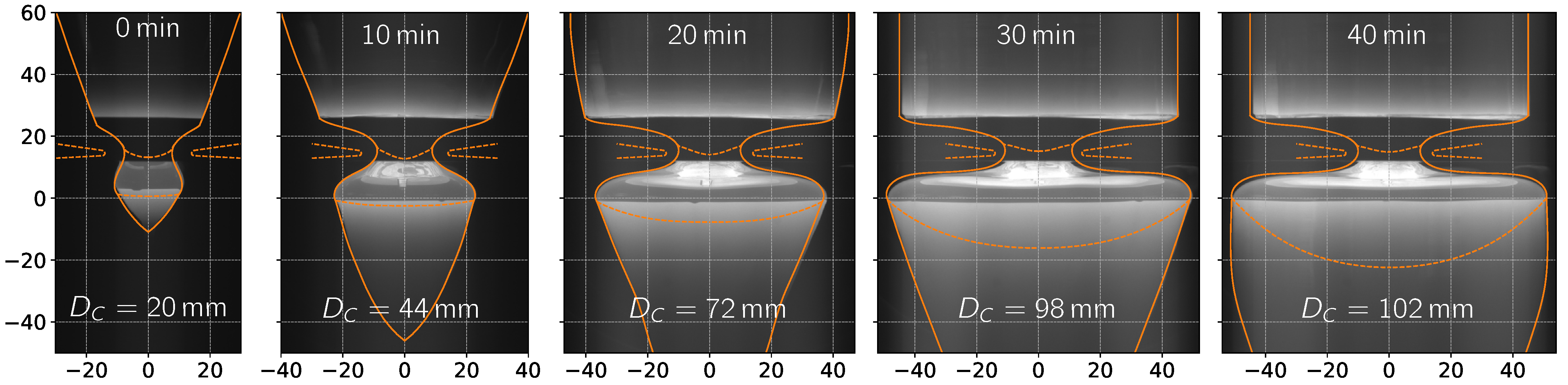
3.1. Description of the Experiment
3.2. Phase Boundaries
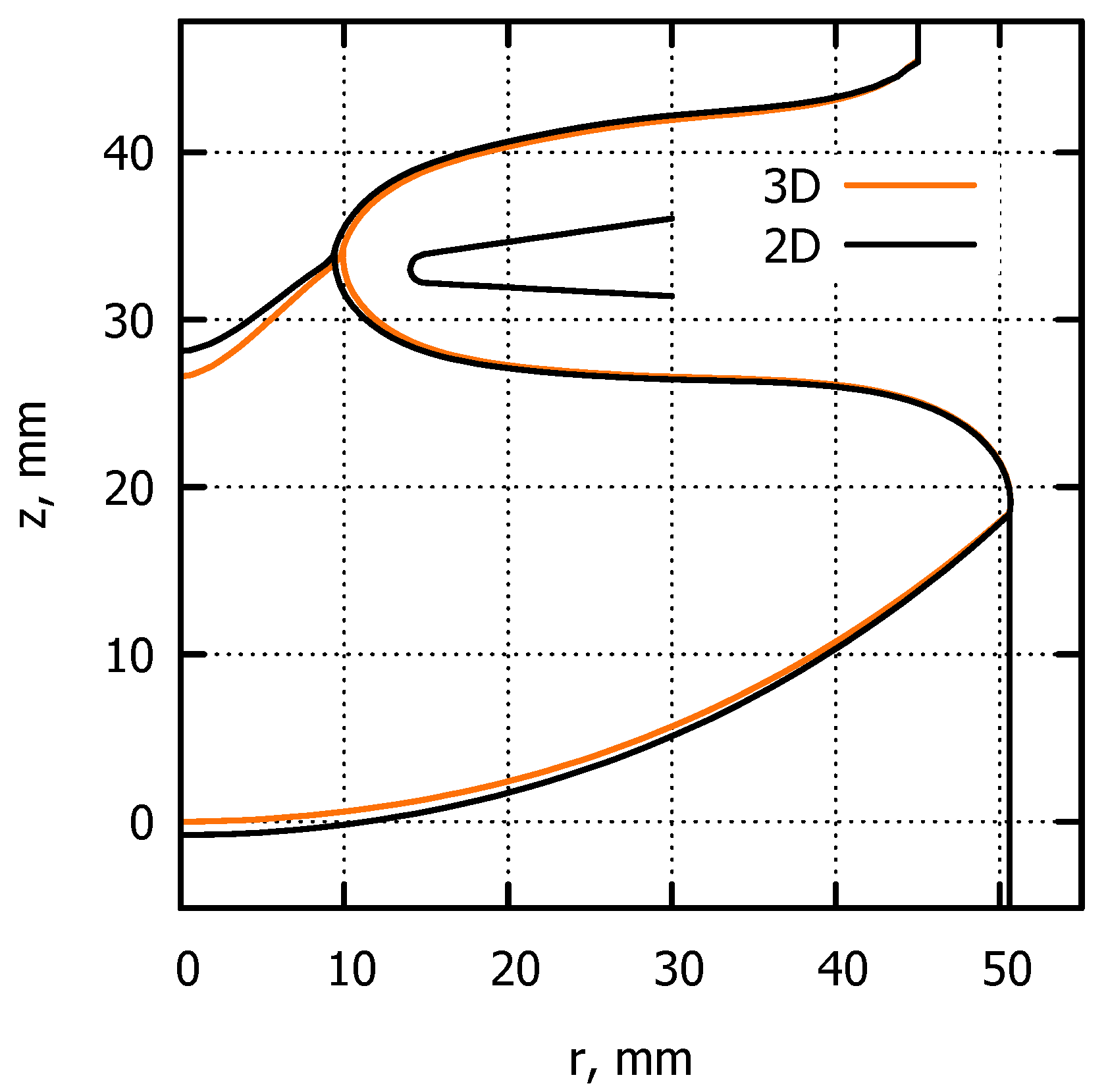
3.2.1. Quasi-Stationary Simulations
3.2.2. Influence of Three-Dimensionality of the EM Field
3.2.3. Transient Simulations
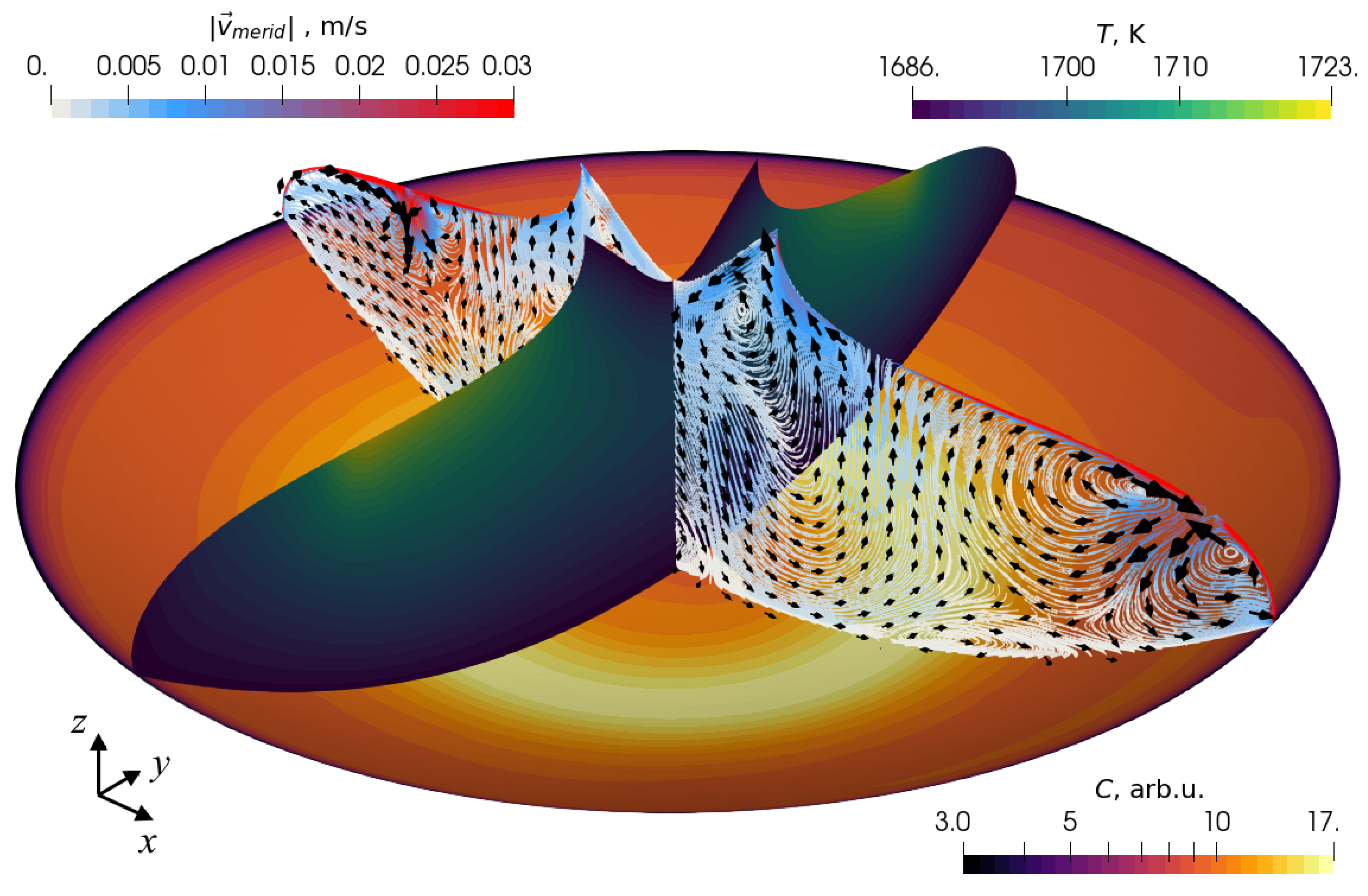
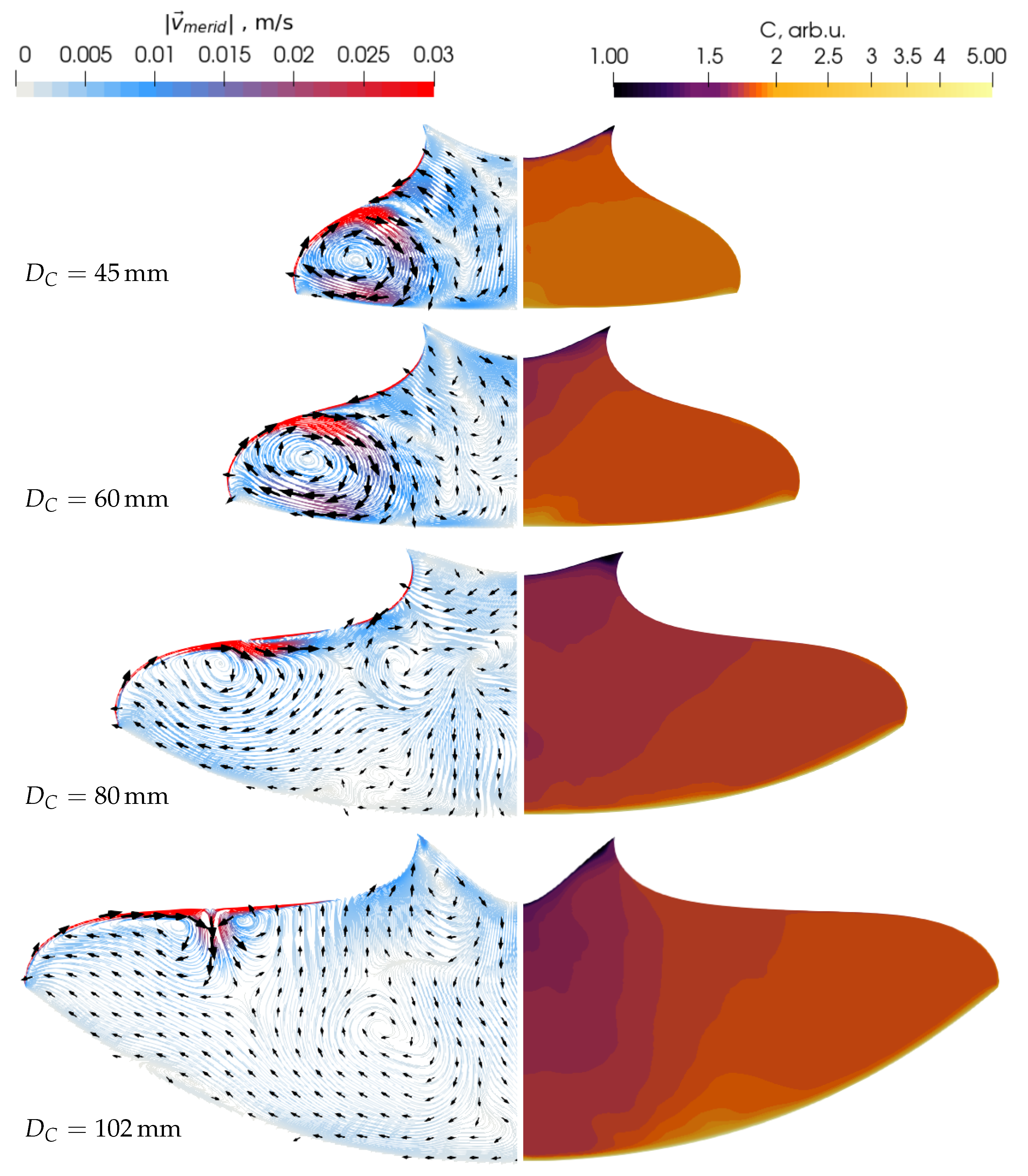
3.3. Species Transport in Melt
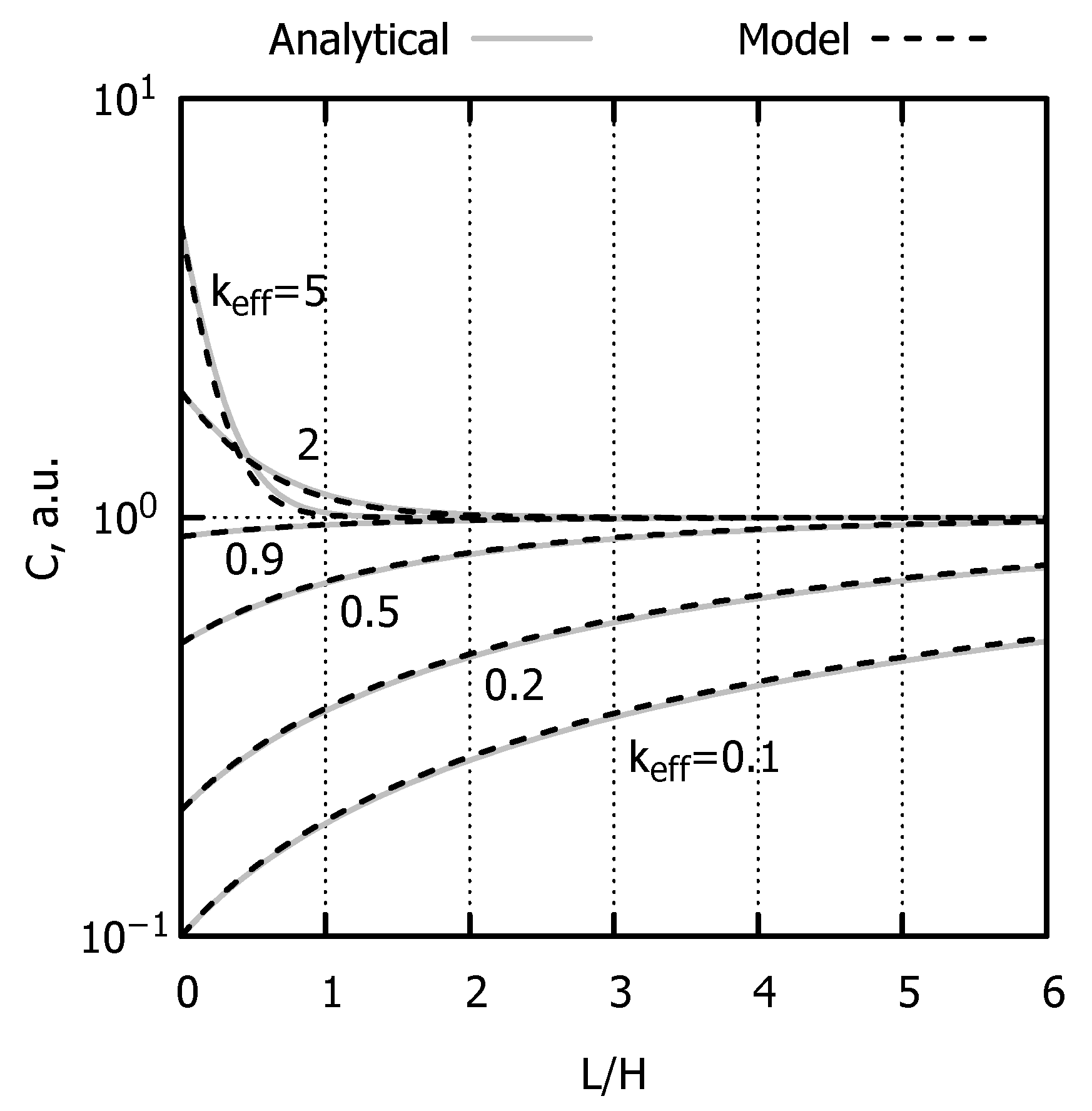
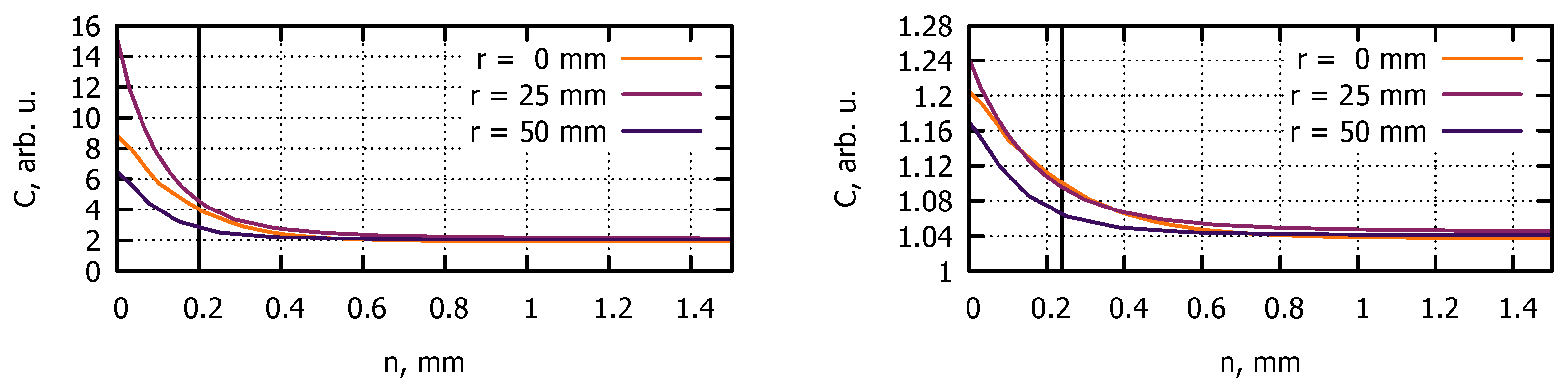
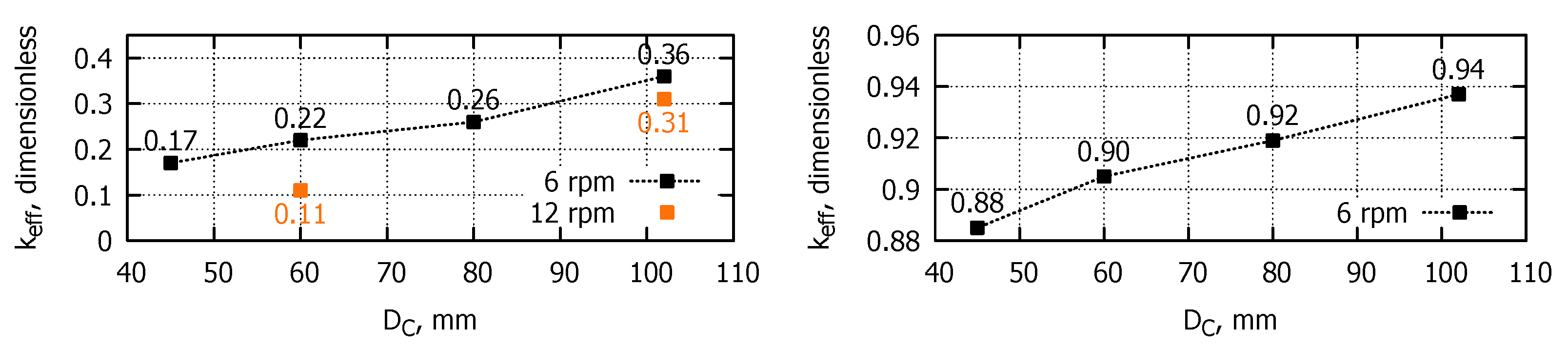
3.3.1. Effective Segregation Coefficient
3.3.2. Increased Crystal Rotation Rate
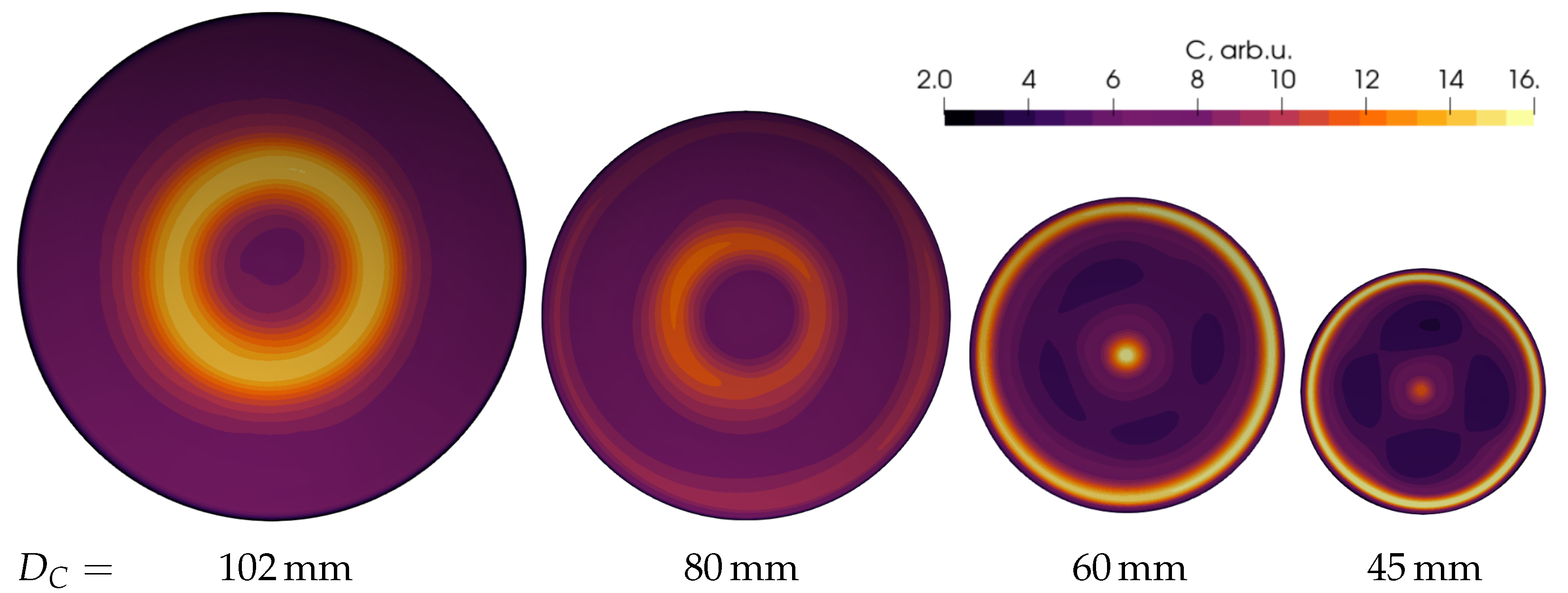
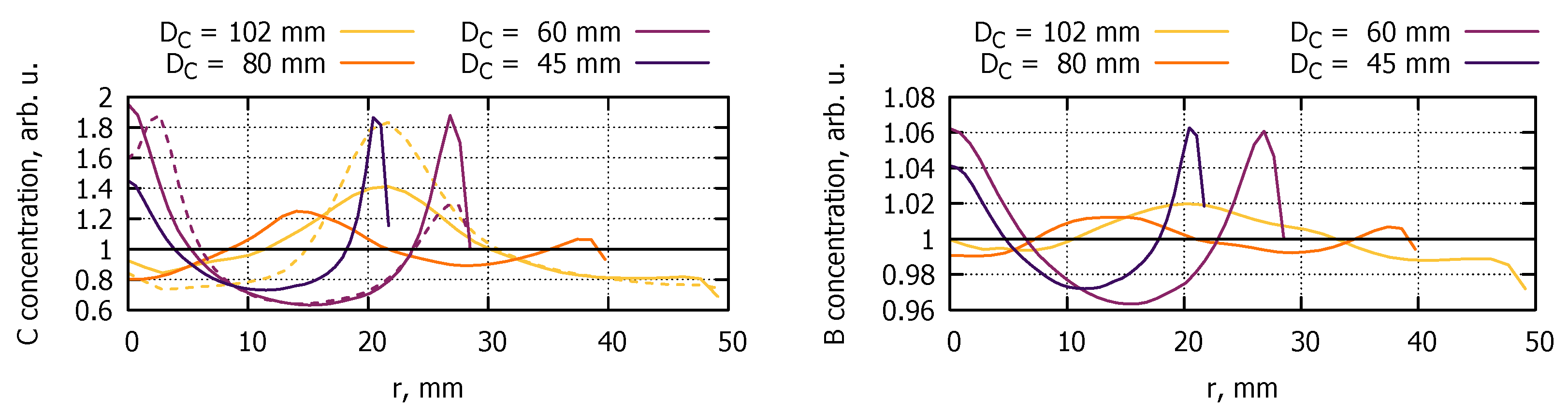
3.4. Species Distribution in Crystal
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
References
- Mühlbauer, A.; Muiznieks, A.; Raming, G.; Riemann, H.; Lüdge, A. Numerical modelling of the microscopic inhomogeneities during FZ silicon growth. J. Cryst. Growth 1999, 198, 107–113. [Google Scholar] [CrossRef]
- Abrosimov, N.V.; Aref’ev, D.G.; Becker, P.; Bettin, H.; Bulanov, A.D.; Churbanov, M.F.; Filimonov, S.V.; Gavva, V.A.; Godisov, O.N.; Gusev, A.V.; et al. A new generation of 99.999% enriched 28Si single crystals for the determination of Avogadro’s constant. Metrologia 2017, 54, 599–609. [Google Scholar] [CrossRef]
- Sze, S.; Lee, M. Semiconductor Devices: Physics and Technology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; p. 361. [Google Scholar]
- Burton, J.A.; Prim, R.C.; Slichter, W.P. The distribution of solute in crystals grown from the melt. Part I. Theoretical. J. Chem. Phys. 1953, 21, 1987–1991. [Google Scholar] [CrossRef]
- Priede, J.; Gerbeth, G. Breakdown of Burton-Prim-Slichter approach and lateral solute segregation in radially converging flows. J. Cryst. Growth 2005, 285, 261–269. [Google Scholar] [CrossRef] [Green Version]
- Wilson, L.O. Analysis of microsegregation in crystals. J. Cryst. Growth 1980, 48, 363–366. [Google Scholar] [CrossRef]
- Mühlbauer, A.; Muižnieks, A.; Virbulis, J. Analysis of the dopant segregation effects at the floating zone growth of large silicon crystals. J. Cryst. Growth 1997, 180, 372–380. [Google Scholar] [CrossRef]
- Lācis, K.; Muižnieks, A.; Jēkabsons, N.; Rudevičs, A.; Nacke, B. Unsteady 3D and analytical analysis of segregation process in floating zone silicon single crystal growth. Magnetohydrodynamics 2009, 45, 549–556. [Google Scholar] [CrossRef]
- Han, X.F.; Liu, X.; Nakano, S.; Kakimoto, K. Numerical analysis of dopant concentration in 200 mm (8 inch) floating zone silicon. J. Cryst. Growth 2020, 545, 125752. [Google Scholar] [CrossRef]
- Sim, B.C.; Kim, K.H.; Lee, H.W. Boron segregation control in silicon crystal ingots grown in Czochralski process. J. Cryst. Growth 2006, 290, 665–669. [Google Scholar] [CrossRef]
- Hong, Y.H.; Sim, B.C.; Shim, K.B. Distribution coefficient of boron in Si crystal ingots grown in cusp-magnetic Czochralski process. J. Cryst. Growth 2008, 310, 83–90. [Google Scholar] [CrossRef]
- Mei, P.R.; Moreira, S.P.; Cortes, A.D.S.; Cardoso, E.; Marques, F.C. Determination of the effective distribution coefficient (K) for silicon impurities. J. Renew. Sustain. Energy 2012, 4, 043118. [Google Scholar] [CrossRef]
- Series, R.W.; Hurle, D.T.; Barraclough, K.G. Effective distribution coefficient of silicon dopants during magnetic Czochralski Growth. IMA J. Appl. Math. 1985, 35, 195–203. [Google Scholar] [CrossRef]
- Jeon, H.J.; Park, H.; Koyyada, G.; Alhammadi, S.; Jung, J.H. Optimal cooling system design for increasing the crystal growth rate of single-crystal silicon ingots in the Czochralski process using the crystal growth simulation. Processes 2020, 8, 1077. [Google Scholar] [CrossRef]
- Ding, J.; Li, Y.; Liu, L. Effect of cusp magnetic field on the turbulent melt flow and crystal/melt interface during large-size Czochralski silicon crystal growth. Int. J. Therm. Sci. 2021, 170, 107137. [Google Scholar] [CrossRef]
- Ratnieks, G.; Muižnieks, A.; Mühlbauer, A. Modelling of phase boundaries for large industrial FZ silicon crystal growth with the needle-eye technique. J. Cryst. Growth 2003, 255, 227–240. [Google Scholar] [CrossRef]
- Rudevičs, A.; Muižnieks, A.; Ratnieks, G.; Mühlbauer, A.; Wetzel, T. Numerical study of transient behaviour of molten zone during industrial FZ process for large silicon crystal growth. J. Cryst. Growth 2004, 266, 54–59. [Google Scholar] [CrossRef]
- Lācis, K.; Muižnieks, A.; Rudevičs, A.; Sabanskis, A. Influence of DC and AC magnetic fields on melt motion in FZ large Si crystal growth. Magnetohydrodynamics 2010, 46, 199–218. [Google Scholar]
- Ratnieks, G.; Muiznieks, A.; Buligins, L.; Raming, G.; Mühlbauer, A.; Lüdge, A.; Riemann, H. Influence of the three dimensionality of the HF electromagnetic field on resistivity variations in Si single crystals during FZ growth. J. Cryst. Growth 2000, 216, 204–219. [Google Scholar] [CrossRef]
- Surovovs, K. A Program for Calculating Dopant Concentration Distribution in a Crystal Grown in Float-Zone Process. Available online: https://git.lu.lv/ks10172/zero-d (accessed on 30 September 2022).
- Muižnieks, A.; Rudevics, A.; Riemann, H.; Lacis, U. Comparison between 2D and 3D modelling of HF electromagnetic field in FZ silicon crystal growth process. In Proceedings of the International Scientific Colloquium Modelling for Material Processing, Riga, Latvia, 16–17 September 2010; pp. 61–65. [Google Scholar]
- Muižnieks, A.; Lacis, K.; Nacke, B. 3D unsteady modelling of the melt flow in the FZ silicon crystal growth process. Magnetohydrodynamics 2007, 43, 377–386. [Google Scholar] [CrossRef]
- Sabanskis, A.; Surovovs, K.; Virbulis, J. 3D modeling of doping from the atmosphere in floating zone silicon crystal growth. J. Cryst. Growth 2017, 457, 65–71. [Google Scholar] [CrossRef]
- Ribeyron, P.; Durand, F. Oxygen and carbon transfer during solidification of semiconductor grade silicon in different processes. J. Cryst. Growth 2000, 210, 541–553. [Google Scholar] [CrossRef]
- Rost, H.J.; Menzel, R.; Luedge, A.; Riemann, H. Float-Zone silicon crystal growth at reduced RF frequencies. J. Cryst. Growth 2012, 360, 43–46. [Google Scholar] [CrossRef]
- Surovovs, K.; Muiznieks, A.; Sabanskis, A.; Virbulis, J. Hydrodynamical aspects of the floating zone silicon crystal growth process. J. Cryst. Growth 2014, 401, 120–123. [Google Scholar] [CrossRef]
- Mills, C.; Courtney, L. Thermophysical Properties of Silicon. ISIJ Int. 2000, 40, 130–138. [Google Scholar] [CrossRef]
- Eremenko, V.N.; Gnesin, G.G.; Churakov, M.M. Dissolution of polycrystalline silicon carbide in liquid silicon. Test Methods Prop. Mater. 1972, 11, 471–474. [Google Scholar] [CrossRef]
- Garandet, J.P. New determinations of diffusion coefficients for various dopants in liquid silicon. Int. J. Thermophys. 2007, 28, 1285–1303. [Google Scholar] [CrossRef]
- Kolbesen, B.O.; Mühlbauer, A. Carbon in silicon: Properties and impact on devices. Solid-State Electron. 1982, 25, 759–775. [Google Scholar] [CrossRef]
- Menzel, R. Growth Conditions for Large Diameter FZ Si Single Crystals. Ph.D. Thesis, Technischen Universität, Berlin, Germany, 2013. [Google Scholar]
- Milliken, K.S. Simplification of a molten zone refining formula. J. Met. 1955, 7, 838. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Crystal diameter | 102 mm (cylinder phase) |
| Feed rod diameter | 90 mm |
| Crystal pulling rate | 3.5 mm/min |
| Feed rod push rate | 4.5 mm/min (cylinder phase) |
| Crystal rotation rate | 6 rpm |
| Feed rod rotation rate | −0.8 rpm |
| Zone height | 27 mm (cylinder phase) |
| Inductor frequency f | 3 MHz |
| Parameter | Value |
|---|---|
| Silicon density | |
| Silicon viscosity | |
| Silicon heat conductivity | |
| Silicon specific heat capacity | |
| Silicon thermal expansion coefficient | |
| Marangoni coefficient M | [26] |
| Carbon diffusion coefficient D | [28] |
| Carbon segregation coefficient | 0.07 [3] |
| Boron diffusion coefficient | [29] |
| Boron segregation coefficient | 0.8 [29] |
| Total number of mesh elements | 614,000 |
| Largest element size | 0.8–1.4 mm (inside the melt) |
| Smallest element thickness | 0.02–0.03 mm (at the crystallization interface) |
| Time step | 2 ms |
| Total simulation time | 350–500 s |
| Averaging interval for | 100 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Surovovs, K.; Surovovs, M.; Sabanskis, A.; Virbulis, J.; Dadzis, K.; Menzel, R.; Abrosimov, N. Numerical Simulation of Species Segregation and 2D Distribution in the Floating Zone Silicon Crystals. Crystals 2022, 12, 1718. https://doi.org/10.3390/cryst12121718
Surovovs K, Surovovs M, Sabanskis A, Virbulis J, Dadzis K, Menzel R, Abrosimov N. Numerical Simulation of Species Segregation and 2D Distribution in the Floating Zone Silicon Crystals. Crystals. 2022; 12(12):1718. https://doi.org/10.3390/cryst12121718
Chicago/Turabian StyleSurovovs, Kirils, Maksims Surovovs, Andrejs Sabanskis, Jānis Virbulis, Kaspars Dadzis, Robert Menzel, and Nikolay Abrosimov. 2022. "Numerical Simulation of Species Segregation and 2D Distribution in the Floating Zone Silicon Crystals" Crystals 12, no. 12: 1718. https://doi.org/10.3390/cryst12121718
APA StyleSurovovs, K., Surovovs, M., Sabanskis, A., Virbulis, J., Dadzis, K., Menzel, R., & Abrosimov, N. (2022). Numerical Simulation of Species Segregation and 2D Distribution in the Floating Zone Silicon Crystals. Crystals, 12(12), 1718. https://doi.org/10.3390/cryst12121718











