STM/STS Study of the Density of States and Contrast Behavior at the Boundary between (7 × 7)_N and (8 × 8) Structures in the SiN/Si(111) System

Abstract

The origin of the contrast appearing in STM images at the boundary between diverse ordered structures is studied using the example of two structures, (7 × 7)_N and (8 × 8), formed in the system of a two-dimensional silicon nitride layer on the Si(111) surface during ammonia nitridation. A significant dependence of the contrast between these structures on the voltage applied to the tunnel gap was found and studied both experimentally and theoretically. Variations in the contrast were quantitatively studied in the range from −3 V to +3 V, and they were studied in more detail for the positive biases on the sample from +1 V to +2.5 V, where the contrast was changed more than 2 times. Within the one-dimensional Wentzel–Kramers–Brillouin (WKB) model for the tunnel current, a comparatively simple procedure is proposed for the correction of the experimental STS-spectra of differential conductivity to identify the adequate (feasible) density of electron states (DOS). It is shown that the (8 × 8) structure DOS corresponds to a graphene-like layer of silicon nitride structure. The proposed correction procedure of the empirical differential conductivity spectra measured by STS will be useful for the quantitative determination of the DOS of new two-dimensional materials and surface structures.

1. Introduction

1.1. The STM Technique and the Tunneling Current Nature

The study of the atomic and electronic structure of solid surfaces is a problem of current interest for the development of a new post-silicon generation of electronic and optoelectronic devices, including the problem of the combination of nanosized components of diverse substances on a single surface. These studies are even more relevant with respect to the development of technologies for the synthesis or functionalization of two-dimensional (2D) materials, such as graphene, silicene and many other new graphene-like materials on solid surfaces and, in particular, on semiconductor surfaces. At present, new 2D materials attract great attention and are being actively studied, and that can be confirmed by becoming acquainted with, for example, recent reviews [1,2] and references in them. One of the most informative tools for the experimental investigation of the materials is scanning tunneling microscopy/spectroscopy (STM/STS), which provides unique opportunities to study in real space both the atomic and electronic structures [3,4] of new materials simultaneously. Now, STM is employed not only in its traditional application as a tool for studying the surface of new crystalline materials such as topological insulators [5,6] or charge density wave 2D materials [7], but also in a variety of modern chemistry and physical chemistry problems, such as studying adsorption processes with submolecular-resolution imaging [8,9], investigating the role of van der Waals dispersion force in organic molecule adsorption [10] and fabrication and characterization of self-assembling nanosystems with halogen bonds [11]. The data obtained with the help of the STM technique require a correct interpretation, namely the determination of the contributions to the formation of the STM image of both the morphological features on the surface and the density of states of the systems under study.

Obviously, in the STM technique, the information about a surface or a two-dimensional layer is associated with measuring the tunneling current between the probe and the sample. The tunneling occurs through a vacuum gap of a nanometer scale (~1–2 nm). It is well known that this technique provides a very high spatial resolution, up to the resolution of individual atoms, as well as the opportunity of studying the density of electronic states, which are located relatively close to the Fermi level of the sample for both filled and empty states.

To date, the physical foundations of electron tunneling in the STM are well understood. Bardeen, in 1961, a few years before the invention of STM, proposed a description of the tunneling current in the metal–dielectric–metal system based on the perturbation theory, where the initial unperturbed state is the equilibrium electronic states of both metals before the tunnel contact is set [12]. It turned out that the model is also well suited for the case of a tunneling current between the probe and the sample in STM [3]. Since then, a large number of contributions have been devoted to the theory of electron tunneling in the STM [13,14,15,16,17].

Tersoff and Hamann developed one of the earliest theories [13] describing the STM image as a manifestation of the lateral distribution of local density of states (LDOS) at the Fermi level. This approach is well suited for the scanning conditions, where low voltage is applied to the tunnel gap. The high STM resolution, down to the atomic level, was theoretically demonstrated by Lang [14,15,16]. The wave function of an individual atom obtained from ab initio calculations was used, while such an individual atom was assumed to be adsorbed on the substance surface described by the jelly model [14,15,16]. Moreover, this kind of model was used to describe both the probe and the sample. On the basis of Bardeen formulas and numerical integration, Lang showed that the STM operation principle can be understood in terms of the tunneling between one atom at the probe tip and one atom at the sample surface. Lang considered the spatial distribution of the tunneling current density in the gap between the probe and the sample, as well as the formation of an apparent image of individual adsorbed atoms. The characteristic features in the STS data of chemically different atoms adsorbed on the surface were investigated. The author demonstrated that the peak positions (resonances), in the differential dI/dV conductivity dependence on the voltage across the tunneling gap, show a good agreement with the positions of the maxima in the density of states of both the sample and the probe.

Feenstra et al. [17] studied the Si(111)-(2 × 1) surface structure using STM/STS and discussed various aspects of tunneling, for example, current–voltage characteristics (I–V) depending on the probe–sample separation, as well as oscillating the dependence of tip–sample separation versus voltage at the constant tunneling current arising from barrier resonances. The contribution of the states with a surface parallel wave-vector to the tunneling current was also discussed. The authors proposed using the normalized differential conductivity d(lnI)/d(lnV) = (dI/dV)/(I/V) to obtain information on the density of states in the framework of the one-dimensional WKB model. A number of methods for normalizing the differential conductivity were proposed to more accurately determine the density of states spectrum [18,19,20,21], requiring additional measurements, for example, at several voltages across the tunnel gap or at various spacings between the probe and the sample.

1.2. Image Contrast in the STM Technique: The Role of Topography and Density of States

Despite the fact that the theory of tunneling current in STM has already been developed very well, problems arise in the practical study of objects with lateral nanometer dimensions that differ in their composition or structure from the surrounding material. In this case, the contrast is observed in STM images and is interpreted in different ways, and different image contrast interpretations may contradict each other. The topographical approach is often used; in this approach, the contrast is interpreted directly as the height of morphological features (steps, hillocks or pits, etc.). For example, when islands or nuclei of a new material appear on an alien substrate, the island height is directly compared with the crystal lattice parameters of the particular corresponding material [22,23,24,25,26,27,28,29]. On the other hand, ideas according to which the STM contrast can be associated with a change in the density of electronic states of the surface are developed, although the STM contrast manifests itself in STM images through the apparent “height”. Sautet theoretically studied the contrast formed in the STM images due to the local electronic states of adsorbed atoms [30]. Specific forms of apparent “height profiles” were experimentally observed in the STM studies of individual adsorbed atoms on a metal surface by Spurgeon et al. [31]. The contrast arising in the presence of material islands on the foreign substrate was also explained by the difference in the densities of electronic states of the materials in several contributions [32,33]. In [33], the authors discussed the nature of the contrast arising in the STM for a thin layer of material with a wide bandgap on the top of a conducting substrate. These authors studied how the electronic states of a thin dielectric layer show up in images at low biases, i.e., when the Fermi level falls into the dielectric layer bandgap. At first sight, it seems that, under low biases, the dielectric layer simply contributes to the tunnel barrier thickness. However, the authors showed that there is a more complex phenomenon of states mixing near the Fermi level of the conducting substrate with the insulating layer band states on their interface, while the mixed states propagate with fading to the surface and contributing to the STM image.

To elucidate the nature of the contrast in the STM, i.e., to determine the origin of the contrast from the topography or density of states, as a rule, additional investigations are required. One way to reveal the nature of the contrast is to vary the voltage applied to the tunnel gap [34,35,36,37].

1.3. STM Contrast in the SiN/Si(111) System

An example of a system in which the interpretation of an STM contrast image is still controversial is a thin layer of silicon nitride on silicon, SiN/Si(111), despite the fact that it has been actively studied for more than 50 years. Now it seems the topographical approach is dominant [26,27,28]. According to modern generally accepted concepts, during the initial steps of the silicon surface nitridation process, an (8 × 8) structure arises, which is considered as a thin layer of the β-Si₃N₄ silicon nitride crystalline phase, covered by an ordered adsorbed nitrogen layer. Such a model of the (8 × 8) structure was first proposed by Ahn et al. [38]. Gangopadhyay used STM to investigate the formation kinetics of the (8 × 8) structure islands, which appear as dark triangles in the STM images [28]. The appearance of triangles was interpreted as the formation of the nuclei of β-Si₃N₄ crystalline silicon nitride in etched pits on the silicon substrate surface, which arise due to the surface silicon atom interaction with active nitrogen. The location of β-Si₃N₄ nuclei below the surrounding surface level, according to the authors, results in a darker tone of the triangles. The theoretical work of Petrenko et al. [39] also supports the idea of etching the silicon surface by active nitrogen precursors (for example, NH₃) along with the epitaxial growth of β-Si₃N₄ layers.

Gwo et al. [29] also follow a topographical approach. The authors measured by STM a step height of 3.3 Å for the (8 × 8) island, with respect to the surrounding area, and found that this value is greater than the expected value of 2.9 Å for β-Si₃N₄ (it is the lattice constant in the normal direction to the (0001) surface) and even greater than the distance between the bilayers for silicon (~3.13 Å). The authors did not give an exact explanation for the increased step height: there is only an assumption that, apparently, some kind of relaxation of the stressed nitride layer that nucleated on the silicon surface occurs. In the work of Wu et al. [27], devoted to the study of the (8 × 8) structure using STM/STS, the authors focused on the STS spectra, and the I–V curves were presented on a logarithmic scale. Note that it was not the logarithmic differential conductivity, which is mentioned above, but the tunneling current itself as a function of voltage that was presented. The data given by Wu et al. [27] demonstrated that the (8 × 8) nitride conduction band edge is located at +2.5 eV, which, in the authors’ opinion, is a consequence of the rather large β-Si₃N₄ bandgap (5.3 eV). Consequently, if this layer is scanned at low biases, below the value of +2.5 V, then the β-Si₃N₄ dielectric islands, as it seems, should not show up in the STM images sharply. In contrast to that, it is expected that the β-Si₃N₄ has to show up in the STM images as an additional contrast at biases higher than +2.5 V, as was described in [37]. However, looking ahead it can be noted that, in the present work, completely different behavior of the contrast, as a function of tunnel bias at the boundaries between the (8 × 8) islands and the surrounding (7 × 7)_N structure, was experimentally observed.

1.4. Purposes of the Present Work

Recently, we studied the evolution of the atomic and electronic structure of the nitride layer formed during the silicon surface nitridation process under the ammonia flux at a high temperature [40,41]. One of the results was the following: the dependence of contrast at the boundaries between structures (7 × 7)_N and (8 × 8), as a function of bias, was revealed. In ref. [40], we proposed a qualitative explanation of the effect based on a preliminary estimation of the expected change in the tunneling current because of different DOS values for both structures.

In the present work, we focused on a more thorough analysis of the scanning parameters affecting the contrast of STM images on a silicon surface with the (8 × 8) structure nuclei that appeared, after a high-temperature nitridation (~1000 °C) of the Si(111) surface under the ammonia flux, and quantitatively determined the density of states of the (8 × 8) structure. Special attention is paid to the experimental study and quantitative description of the contrast dependence on the tunnel bias, based on the one-dimensional WKB model. The contrast variation at the boundary of the (7 × 7)_N and (8 × 8) structures, as a function of bias, was observed. Hence, this contrast is not determined by distinctive morphological features, but by the density of electron states on the surface. As it turned out, the density of states suitable for calculating the contrast of the STM images and a direct comparison with the experimentally observed contrast is not known, in fact, at a necessary accuracy. It is clear that to determine the density of surface states, there are two main approaches: in the first case, the spectrum is determined by ab initio calculations; in the second case, the spectrum is determined by means of experimental studies.

For the first approach, the correspondence of the calculated spectrum and real density of states is not always obvious, because, firstly, different calculations often demonstrate significantly contradictory results: for example, the bandgap can vary markedly. So, in the article by Guo et al. [42], two different DFT calculations for the g-Si₃N₃ layer showed different bandgap values. Secondly, there are situations when it is difficult to carry out an ab initio calculation, since the true atomic structure of the surface under study is not known, and, apparently, it is most difficult to perform calculations from the first principles in the cases when the atomic structure of an investigated surface is disordered, such as in the case of the (7 × 7)_N structure. As was shown earlier [40,41], there is a disordered Si-enriched silicon nitride layer on the (7 × 7)_N structure. In turn, for the (8 × 8) structure, a new atomic model (not β-Si₃N₄) [41] has been recently proposed, and the density of states spectrum for the structure requires a detailed experimental study, as well as a comparison with the ab initio calculation carried out by Guo [42].

Another approach suggests relying on the experimentally obtained spectra of differential normalized conductivity. It is known that these spectra are proportional to the density of states of the surface [17]. However, the quantitative relation between the differential conductivity and the density of states still needs to be refined in each particular case. In most contributions dealing with STM/STS, the differential conductivity spectra are given in arbitrary units and these differential conductivity spectra are compared with each other rather qualitatively than quantitatively. In many cases, the focus is on the energy positions of the peaks instead of the exact quantitative knowledge of the density of states in the required spectral range.

In this work, the second approach based on the experimental differential conductivity spectra (dI/dV)/(I/V) is used. A relatively simple procedure for correcting the obtained experimental STS-spectra of the (8 × 8) structure based on the one-dimensional WKB model is proposed. Here, the normalized spectra are used to calculate the contrast of images at the boundary between (8 × 8) and (7 × 7)_N structures. This calculated contrast is quantitatively compared with the experimental STM data on the contrast variation, while the bias applied to the tunnel gap is varied. A good agreement between calculations and the experimental data was reached.

This work is structured as follows: In Section 3.1, a study of the effect of scanning parameters on the contrast of STM images of a clean Si(111)-(7 × 7) surface is presented. It is shown that, even for the simple case of a single-component surface, the STM image contrast appears somewhat more complex than the morphological features. In Section 3.2, a comparison of the behavior of the contrast, as a function of bias that arises on a morphological step and on the boundary (7 × 7)_N/(8 × 8), is carried out. Then, in Section 3.3, the I–V characteristics originating from structures (7 × 7)_N and (8 × 8) are compared. Next, in Section 3.4, the relation between the differential conductivity spectrum (dσ_n) and the density of states in the one-dimensional WKB model and the problem of the dσ_n correction are discussed. In Section 3.5, expected differences in the tunnel currents for the (7 × 7)_N and (8 × 8) structures, as a function of the bias based on the normalized DOS of these structures and calculated while the tunnel gap is fixed, are presented. Finally, in Section 3.6, the vertical displacement of the probe to compensate for the expected tunnel current variation is calculated, and that allows simulating the feedback through the tunneling current during the scanning in the STM. A comparison with the experimental data is also presented.

2. Experimental Section

Ultrathin silicon nitride layer samples for the studies by scanning tunneling microscopy/spectroscopy (STM/STS) were prepared on a conducting n-type Si(111) substrate with the resistivity of 0.3 Ω·cm in an ultrahigh-vacuum AFM/STM/STS analysis machine from Omicron (currently Scienta Omicron GmbH, Taunusstein, Germany). The machine is equipped with an ammonia gas source and a high-energy reflective electron diffraction (RHEED) system with the primary electron beam energy of 10 keV. The experiments were carried out using Si(111) substrates manufactured by Sil’tronix Silicon Technologies (Archamps, France) and special purity ammonia 99.9999% (manufacturer—Company “HORST” (Moscow, Russia)), additionally purified by an Entegris mechanical filter with a purification rate of 99.999999%.

The preparation of a clean silicon surface for experiments was carried out in two stages. First, the surface was annealed in a preparation chamber at 600 °C for 2 h. The silicon surface was finally cleaned in an analytical chamber at 1250 °C for 30 s. The high Si surface purity was confirmed by the appearance of the superstructure (7 × 7) after a cooling down below 830 °C. The STM images and STS spectra of the clean or nitridated silicon surface were recorded at room temperature, that is, after the samples had been cooled for 2 h. An electrochemically sharpened tungsten needle was used as a probe. Scanning was carried out in the feedback mode on a constant tunneling current, as well as in the current-imaging tunneling spectroscopy (CITS) mode [43] to determine the current–voltage (I–V) characteristics simultaneously with the conventional scanning on a selected surface area. Typical current values did not exceed 0.1 nA, and the typical tunneling current used was 0.025 nA; the bias voltage (V_bias) relative to the probe potential was applied to the silicon sample in the range of ±5 V. The differential conductivity (dI/d V_bias)/(I/V_bias) dependence on the voltage in the tunnel gap (V_bias) was determined by the numerical differentiation of the measured I–V dependences.

The nitridation procedure of a clean silicon surface in an ammonia flux and the variation of surface coverage by the (8 × 8) structure versus ammonia treatment doses were described elsewhere [40]. The procedure for calibrating measurements of the vertical probe displacements by the well-known monolayer step value on a clean Si(111) surface is also described in [40]. In the present work, the same coefficient as in the previous work was used to normalize the measured STM height profiles.

3. Results and Discussion

The scanning of a certain surface area in STM to record an image is often performed using the tunneling current feedback mode. Usually, to obtain a single image, it is necessary to set specific scanning parameters: scanning area, as well as such important parameters as operating voltage—U_sc (voltage across the tunnel gap) and operating tunnel current I_sc. The joint choice of these two parameters can be called the choice of “working or operating point” for the scanning. The value of the tunnel gap between the probe and sample is not measured in many cases and it is not known exactly, or otherwise, an independent measurement of this parameter is additionally required. During a single scan, the voltage is usually kept unchanged, and the tunneling current is supported at the constant value by means of feedback which properly regulates the probe spacing, with respect to the sample surface. During the lateral movement of the probe from point to point along the surface, the tunneling current may change due to the surface morphology (i.e., a change in the tunnel gap) or a change in the density of electronic states involved — due to the tunneling, because of, say, a composition variation at different points on the surface. The feedback returns the current to the set value due to the compensating vertical probe displacement, with respect to the surface: if the current drops, then the probe tip approaches the surface, if the current increases, then the probe moves away from the surface. Both parameters current and voltage, or in other words, this one or that choice of the operating point, affect the image contrast but in different ways. Take a closer look at the examples of how these parameters can affect the contrast observed in the STM image.

3.1. Testing the Influence of the Scanning Parameters on the STM Image Contrast for the Clean Silicon Surface with the (7 × 7) Superstructure

In the scanning of a clean silicon surface with a well-known (7 × 7) superstructure, it is assumed that only a slight change in the density of states is possible when the probe is moved laterally from point to point (or from a small area to the next similar area) along the surface since this is a pure single-component material with the same reconstruction on the terraces. Examples of spectra at different points of the (7 × 7) structure can be found in [41]. In this case, obviously, one should expect the formation of an image contrast that adequately reflects the surface morphology. The contrast on the Si(111) bilayer step was measured previously [40]. However, even in this seemingly simple case, there are certain features.

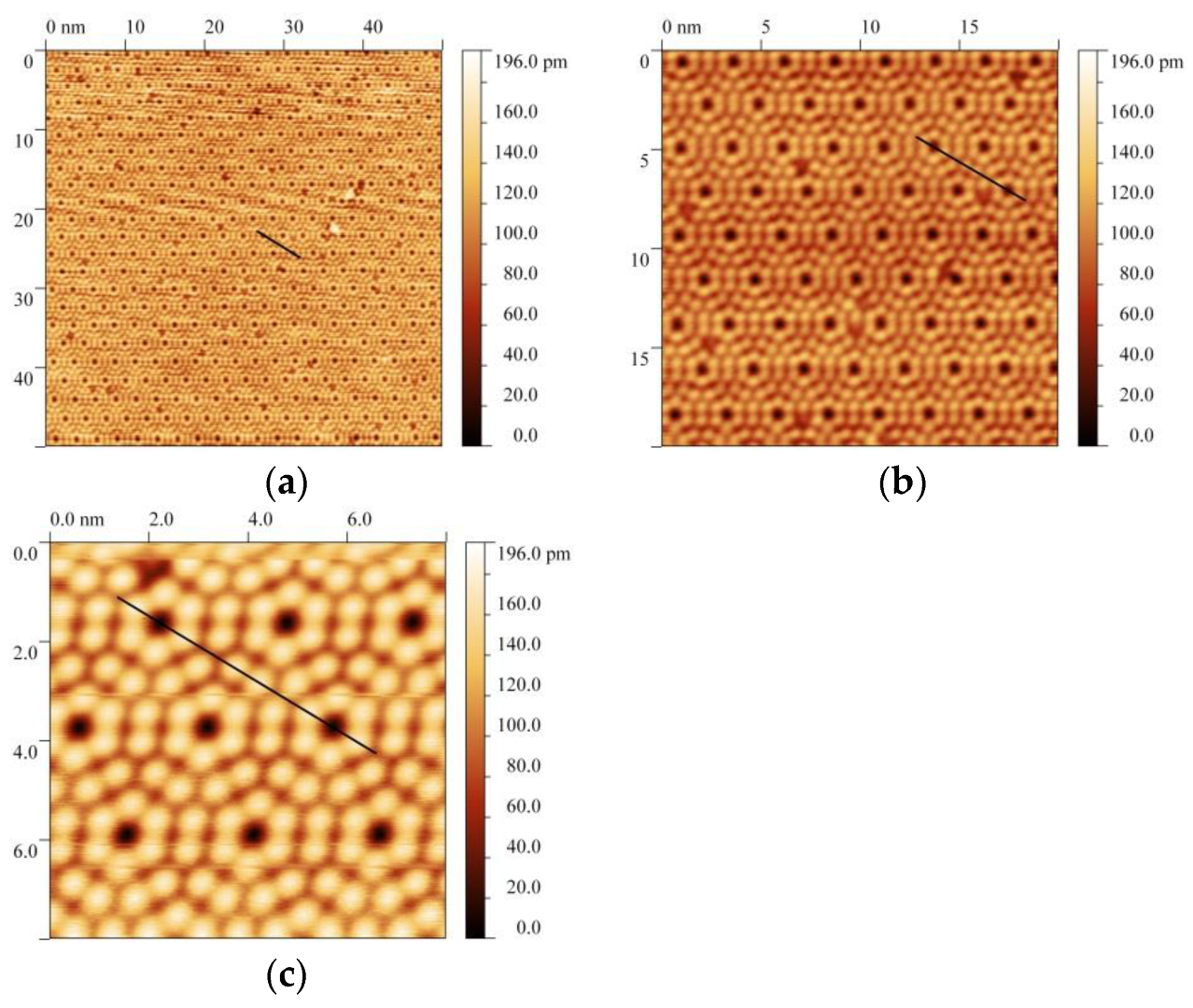
Figure 1 presents the STM images of several successive scans of the same Si(111)-(7 × 7) surface, obtained by varying only one parameter, namely the scan area, which is accompanied by a corresponding improvement in the lateral resolution with a decrease in the scan area, since the number of recorded points of 400 × 400 was not changed.

In this case, the same operating point was used to obtain all the presented images—the tunnel current was 0.025 nA and the voltage was +1.5 V. In general, it is obvious that the main visible features are light adatoms and dark corner holes, and the images look almost the same. Note that the pseudocolor scale was deliberately chosen to be the same for a more adequate comparison of the images. However, the differences in the contrast of light adatoms and dark corner holes in the presented images with different scan area sizes cannot be visually determined, despite the fact that adatoms and corner holes are clearly visible and differ sharply in color. If we compare the respective height profiles, the difference becomes apparent. The measured height profiles along the lines indicated in Figure 1 are shown in Figure 2. The profile registration line crosses two corner holes along the long diagonal of the elementary diamond cell of the (7 × 7) structure.

It is clearly shown in Figure 2 that, as the scan area decreases, the height difference between the adatom and the corner hole increases, and it can be measured quantitatively. The blue profile corresponding to Figure 1a has a height difference of 0.053 nm; the red profile from Figure 1b has a height difference of 0.08 nm and the black profile from Figure 1c has a height difference of 0.13 nm. This means that the contrast of the images increases accordingly. Note that this effect cannot be explained by the changes occurring on the surface or by a variation in the probe dimensions (for example, due to its degradation), since the contrast and height profiles are reproduced when a certain area is rescanned after a scanning area was changed in any way.

It should be noticed that it is very easy to bring all the images in Figure 1 to the same visible contrast or rescale the intensity difference from maximum to minimum and, hence, to distort the real change of the contrast. Moreover, many pieces of the STM/AFM measuring software perform this correction automatically. In this case, the contrast change in the image may not be recognized at all if the intensity scale color is not presented. This simplest notice is given here not only to emphasize the importance of accompanying any STM image with a scale that relates the pseudocolor (or gray scale) to the z-coordinate normal to the surface, i.e., to the height–depth coordinate. This would help to avoid possible ambiguities in the perception and interpretation of the pseudocolor. What is more important is that it is for pointing out one simple but not so obvious feature. Images with a noticeably higher lateral resolution of the (7 × 7) structure than that shown here in Figure 1 and Figure 2 can be found in the literature [44]. Indeed, high-resolution images show that, in the vertical direction, the difference in the heights of the adatoms and the corner hole in the experimental images and the corresponding contrast reaches 0.23 nm (see Figure 3c) in the referenced paper [44]. However, it is necessary to pay attention to the fact that this value is almost 2 times less than the vertical geometric distance from adatoms to the bottom in the center of the corner hole, which should be about 0.4 nm (i.e., 4 Å) according to the generally accepted dimer–adatom–stacking fault (DAS) model [45]. A detailed diagram of the DAS model indicating the vertical distances between different atoms is given, for example, in the recent work by Demuth [46]. In this case, we are interested in the vertical distance from the adatoms to the corner hole bottom. The authors of [44] explained the difference between the experimental profile and the DAS model by the effect of the probe size, which seems to be the most obvious explanation. However, using ab initio calculations of STM images even for an ideal probe with a zero tip radius, the authors obtained a height difference of about 0.35 nm or 3.5 Å, i.e., still less than the expected 3.98 Å for the DAS model. This fact indicates the existence of additional reasons for a discrepancy, such as the influence of the spatial tunneling current distribution, besides the sensitivity of the lateral and vertical resolution to the probe tip dimensions.

The observed effect of the contrast dependence on the scanning area could be explained, for example, by a simple dependence of the vertical resolution on the lateral one, that is, by a decrease in the number of measured points per scanning length unit. It is also likely that there are certain spatial tunneling current integration effects here due to the finite area involved in the tunneling. An additional uncontrolled contribution, probably not too much, may originate from the probe displacement relative to the surface (such as random deviation and/or drift) during the measurement process at each surface point with an increase in lateral displacements during the scanning of increased area.

The images obtained by varying the working tunnel current when two other parameters, namely the scanning area and the operating voltage, were fixed are shown in Figure 3. The image obtained at the current of 0.035 nA (Figure 3a) with the scanning area of 20 × 20 nm² should be compared with a similar image with a tunnel current of 0.025 nA, which is shown in Figure 1b above, and a comparison of the height profiles at these currents is shown in Figure 3b.

It is shown in Figure 3b that as the operating current increases, the profile depth increases. Obviously, the morphological features of the surface have not been changed, since the contrast is reproduced when the working tunneling current is reproduced. However, it should still be noted that, sometimes, changes in the probe state (because of possible events of some atoms jumping from the surface to the STM probe or vice versa, or due to the probe tip shape changing, caused by a strong electrical field applied between the probe and the surface as well as the high tunneling current density during the scanning along the surface) are possible, which can lead to an uncontrolled change in the contrast. In the absence of these random processes, the observed current variation effect is that the average tip-to-sample distance decreases as the operating current increases, and an increased feedback response is required to compensate for the increased current changes during the surface scanning. Again, it should be noted that the contrast here is not determined unambiguously by the surface morphology itself, but is associated with the features of the tunnel current formation and measurement and the feedback operation.

In the high-resolution images, the change in contrast while the tunneling current is varied appears to be much more pronounced (see Figure 3c,d). In Figure 3d, the profiles for the STM images obtained at 0.035 nA and 0.025 nA shown in Figure 1c and Figure 3c, respectively, are compared. One can see that the height difference between the adatoms and corner holes reaches the value of 2.8 Å. It should be noted that the range of the pseudocolor scale in Figure 3c is deliberately increased, from 0 to 340 pm, in comparison with other images in order to reflect the increased contrast adequately.

The variation of another operating parameter, the voltage, from +1.5 V to +2.0 V with a fixed scanning area, in this case 50 × 50 nm², and fixed operating current 0.025 nA does not lead to noticeable contrast changes. Here, the images in Figure 1a and Figure 4a are compared, along with the corresponding profiles shown in Figure 4b.

It is shown in Figure 4b that the profiles along the cell diagonal almost coincide; only the elementary cell orientation changed (it is rotated by 180 degrees). The difference between the halves of the elementary cell (faulted and unfaulted halves) of the (7 × 7) structure turns out to be noticeable, which is a well-known fact following from the DAS model of (7 × 7). An increase in the voltage at a fixed operating current captures a wider range of the spectrum of electronic states involved in the tunneling current formation (which is discussed below in detail). In this case, the voltage variation did not affect the image contrast (depth profile), since the spectra at different points on the surface of one material change synchronously.

Thus, even for the case of a clean surface of a single-component material, in our case, silicon, the contrast dependence on the scanning parameters can show a more complex nature of the tunneling current formation than just an unambiguous presentation of the surface morphology.

3.2. The Contrast Dependence on the Voltage on the Nitridated Silicon Surface. Simultaneous Observation of the Contrast Behavior on the Morphological Step and on the (7 × 7)_N/(8 × 8) Boundary as a Function of Tunnel Bias

A more interesting behavior of the contrast appears when the voltage is varied on scanning the nitridated silicon surface Si(111), in contrast to a clean surface. In this work, the contrast dependence on the operating voltage applied to the tunnel gap on the samples treated with a relatively small dose of ammonia was experimentally observed. To prepare the samples, a clean silicon surface was treated under ammonia flux p = 3 × 10⁻⁷ Torr at T = 1000 °C for several tens of seconds (10–30 s), and the corresponding nitridation dose was 3–10 Langmuir (L) (1 L corresponds to an exposition of 1 s at pressure 1 × 10⁻⁶ Torr). As a result of such treatment, the main part of the surface is covered by the (7 × 7)_N structure; along with this, islands of the (8 × 8) structure are also formed on the surface. We attributed the appearance of such an (8 × 8) structure to the graphene-like layer formation of silicon nitride g-Si₃N₃ [40,41].

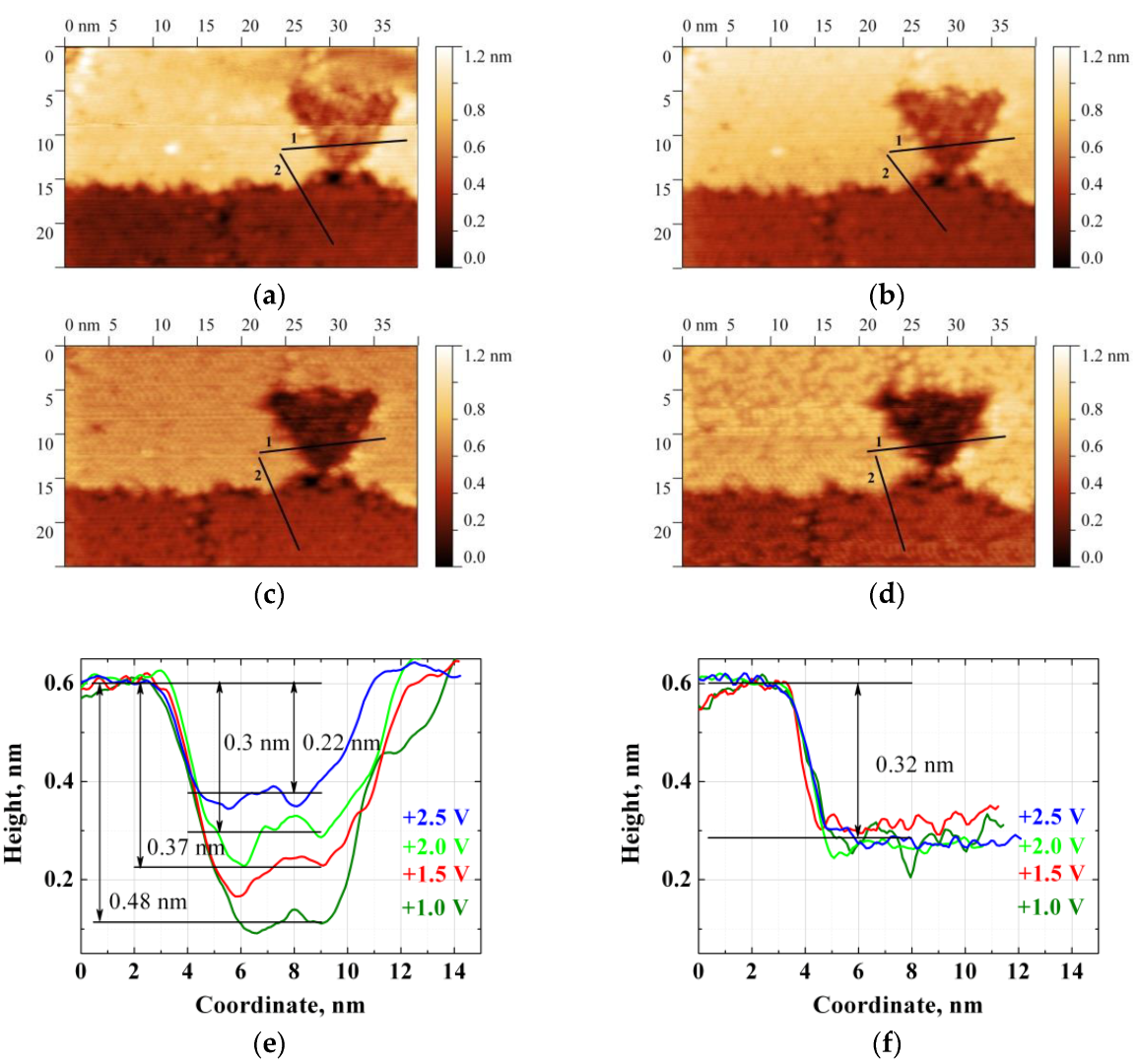
The images of the same nitridated sample area recorded sequentially with a decrease in the operating voltage from +2.5 V to +1.0 V are shown in Figure 5a–d.

On the STM images of Figure 5a–d, an extended one-dimensional (1D) morphological feature, i.e., a step, as well as a triangular island associated with the formation of the (8 × 8) structure, is observed. Somewhat lighter and darker backgrounds on the terraces on both step sides are observed, and the terraces are covered by the (7 × 7)_N structure. This fact was established in the STM images with a higher resolution. Characteristic images of the (7 × 7)_N structure with a high resolution were presented earlier [40], and this structure also becomes noticeable, for example, in the image of Figure 5d, where the characteristic dark trenches appear. This image was taken at the scan voltage of +1 V. It was shown that, at a low voltage, the characteristic contrast of the central and corner adatoms of the (7 × 7)_N images is more pronounced. On the other hand, for the triangular island in this image, as well as for other similar triangular islands observed on this surface, higher resolution images show the (8 × 8) structure. High-resolution images of the (8 × 8) structure were also presented earlier in [40,41]. In the images in Figure 5a–d, it is possible to observe simultaneously the contrast behavior at the morphological step and at the (7 × 7)_N/(8 × 8) interface with a varying voltage. It is shown in Figure 5 that the contrast does not depend on the voltage at the morphological step and that at the boundaries of these two structures ((7 × 7)_N and (8 × 8)), the contrast is decreased with the increase in operating voltage.

Figure 5e,f present the height profiles along the lines indicated in images a–d, where image e presents a profile along line #1 crossing the island of the (8 × 8) structure, and f presents a profile along line #2 crossing the morphological step. The profiles more clearly show the different behavior of the contrast or apparent “depth” at the morphological step and at the boundaries of the structures as a function of bias. The color contrast depth and the corresponding height of the morphological step do not change, despite the presence of random noise and a certain “shift” of the color tone of both terraces being observed. The “shift” is associated with a change in the contrast on the (7 × 7)_N structure itself [40]. The morphological step height was determined as ≈0.32 nm (≈3.2 Å) after the profile normalization, as described in [40], which is quite close to the normal well-known distance between the atomic bilayers of 3.14 Å for bulk silicon in the [111] direction. In turn, one can clearly see the apparent decrease in the depth of the “etch pit” (8 × 8) with the increasing voltage. In a previous work, we related this effect to the difference in the density of states for these two structures and gave a qualitative explanation of how such a difference in the DOS can manifest itself in the image contrast. Below, we will take a closer look and quantify the changes in the contrast within a simple empirical model based on the 1D WKB approximation.

The experimentally observed results do not agree with the expected behavior based on the generally accepted (8 × 8) structure model. In ref. [28] and other articles devoted to the island formation of the (8 × 8) structure, two main points were assumed. First, the (8 × 8) structure is formed in arising etch pits because the ammonia or another nitrogen-containing active component is supposed to chemically etch the silicon surface. The etched pits are the reason for the darker contrast of the islands in the STM images. Second, the (8 × 8) structure is connected with the crystalline phase formation of β-Si₃N₄ silicon nitride. It is known that this crystalline modification of silicon nitride is a good insulator with a bandgap of about 5.3 eV [27,47]. Then, one could expect a sharp variation in the contrast of the images or even the appearance of “new objects” associated with the β-Si₃N₄ dielectric islands when the voltage on the tunnel gap reaches and crosses the edge of the conduction band of the β-Si₃N₄ dielectric, i.e., at a voltage of about +2.5 eV. However, in our case, as can be seen in Figure 5, there is a smooth change in the image contrast: the contrast of (7 × 7)_N/(8 × 8) images systematically changes with voltages in the energy range below +2.5 V, which indicates the presence of a nonzero electron DOS in the voltage range that would be within the β-Si₃N₄ bandgap. Consequently, the (8 × 8) structure bandgap is smaller than that of the crystalline phase of silicon nitride β-Si₃N₄, as was already demonstrated earlier in [40]. This behavior of the contrast in STM images is in qualitative agreement with the experimental data of direct measurements of the STS spectra of the DOS (8 × 8) structure [41].

In order to understand in more detail the nature of this contrast and the observed voltage dependence, we will further consider and compare the STS data for areas with (7 × 7)_N and (8 × 8) structures.

3.3. Comparison of the Current–Voltage Characteristics of (7 × 7)_N and (8 × 8) Structures

Figure 6a presents the current–voltage (I–V) characteristics measured in the areas covered by the (7 × 7)_N and (8 × 8) structures. The scanning image was obtained in the current-imaging tunneling spectroscopy (CITS) mode, and a fragment of the image is shown in the inset in Figure 6a. The operating current at the scan voltage of −3 V was −0.025 nA, the image size was 20 × 20 nm² and the number of scan points was 400 × 400. I–V characteristics were measured at the nodes of the 80 × 80 grid points when the scanning was stopped at each of these points, the probe–sample spacing was fixed and the feedback was turned off. The current was measured while the voltage was varied in the range from −3.0 V to +3.0 V. After that, the operating voltage and current were returned, the feedback was turned on and obtaining the scanning image was continued.

To measure the I–V characteristics, the typical regions of both structures were selected, as shown in the upper inset of Figure 6a; as an example, an image with the coexistence of (7 × 7)_N and (8 × 8) structures in higher resolution (scanned at tunneling current 0.025 nA and bias −3 V) with marked (7 × 7)_N, (8 × 8) and (8/3 × 8/3) unit cells is shown in Figure 6b. The tunnel current was averaged over the region area corresponding to the sum of the selected rectangles on each of the structures. This helps to reduce the noise of the experimental I–V curves. The “locality degree” of the measurements, in this case, is set by an operator selecting the sites for the analysis. It can be seen in Figure 6a that the I–V characteristics measured on the (7 × 7)_N and (8 × 8) structures differ markedly. For the purposes of this work, it is important to know the DOS for these structures. As mentioned above, the DOS is related to the value dσ_n = (dI/dV)/(I/V) measured in the experiment.

It is clear that, for these experimental current–voltage characteristics, the curves necessarily coincide, at least, at two voltage points, regardless of how the local surface composition (and, accordingly, the local density of states) or surface morphology are varied. Namely, there is a match at V = 0, where the tunneling current is zero (this is the equilibrium point of the probe and the sample), and also at V_sc—the operating scanning voltage, where the operating tunnel current always coincides owing to the feedback. In this case, the operating point V_sc can and should be used to normalize the spectra dσ_n(V) in order to ensure a proper determination of the empirical densities of states. The details of the proposed procedure are described below. Meantime, let us note that the attempt to estimate the tunneling current directly by numerical integration in the frames of 1D WKB approximation using the obtained dσ_n(V) curves “as is”, which are shown in the bottom inset of Figure 6a, results in a failure. The curves shown in the inset were obtained by the numerical differentiation using the free software WSxM program for the STM image analysis [48]. In fact, these dependences do not even allow one to reproduce the coincidence of currents at the operating point V_sc for the compared structures.

3.4. Tunnel Current Model

The probe and the sample, as well as the emerging potential barrier in the tunnel gap between it at two voltage values +1.0 V and +2.5 V, are schematically shown in Figure 7a,b, respectively. Shown are a tungsten probe (left), the sample surface (right) and a tunnel gap between them. The diagram also shows the Fermi level positions of the probe and sample, the potential barrier in the tunnel gap, and the spectra of the density of states for the surface areas with the (7 × 7)_N and (8 × 8) structures. The green and blue colors indicate the energy range in which the tunneling occurs. Here the work functions are denoted as WF_{(7×7)N/(8×8)} for the sample and WF_W for the tungsten probe (WF—work function).

We describe the tunneling current behavior quantitatively in the framework of the classical model based on the one-dimensional WKB approximation [17]:

$$I(V,z)=A{\displaystyle \underset{0}{\overset{V}{\int }}{\rho }_s(E)\cdot {\rho }_t(E-eV)\cdot T}\left(E,eV,z\right)dE$$

(1)

$$T(E,eV,z)=\exp \left[-\sqrt{\alpha \cdot \left(\phi +\frac{eV}{2}-E\right)}\cdot z\right]$$

(2)

where A is the normalizing factor, φ is the average tunnel barrier height at zero voltage and α = 8m/h², z is the distance from the probe to the surface, or the tunnel gap, and E is the integration variable that covers the energy range corresponding to the difference between the Fermi levels of the probe and the sample. The function T(E,V,z) describes the transmission coefficient of the tunneling barrier, and it was assumed that the barrier has the shape of a trapezoid; ρ_s(E) is the sample density of states. The tungsten probe tip density of states ρ_t(E–V) in some works, for example [49], is taken into account, but it is usually considered as a smooth slowly changing function that can be replaced by a constant [17,50]. In ref. [50], the density of states is given for a tungsten surface near the Fermi level (Figure 3b in [50]), which demonstrates the acceptability of the substitution by a constant for the voltage range from −3 V to +3 V. Thus, in the present paper, the probe density of states is assumed to be a constant.

Using Equations (1) and (2), one can compare the calculated contrast with the experiment in two stages: first, an estimate of the expected tunneling currents at a given operating voltage for both structures (7 × 7)_N and (8 × 8) coexisting on the surface; then, an evaluation of the contrast change with a varying voltage. First, assume that the structures (7 × 7)_N and (8 × 8) are geometrically located on the surface at the same level, i.e., the tunnel gap (z₀) remains unchanged during the scanning. Then, at a given voltage value V_sc, the function describing the transmission coefficient becomes a function of the only variable E; that is, T(E,eV_sc,z₀) = f(E). Changes in the tunneling current in the selected surface areas are determined by the integral (over the E variable) of the product of the transmission function and the local DOS T(E) × ρ_s(E) within the integration range from 0 to the operating voltage V.

The density of states in the system under study is proposed to be determined based on the experimental dependence of the differential conductivity dσ_n = (dI/dV)/(I/V) on voltage. This allows determining the density of states originating from the entire system participating in the tunneling, i.e., from all layers arising during the nitridation process on the conducting Si(111) substrate surface.

For the one-dimensional WKB approximation, the formula describing the relation between the density of states and the logarithmic derivative of conductivity, which is presented in the work of Feenstra et al. [17] (see Equation (3)), can be rewritten as follows:

$${\rho }_{\mathrm{s}}\left(E\right)=a\cdot \mathrm{d}{\sigma }_{\mathrm{n}}+b$$

(3)

where

$$a(V)=\frac{1}{eV}{\displaystyle \underset{\mathrm{o}}{\overset{V}{\int }}{\rho }_{\mathrm{s}}(E)\frac{T(E,eV)}{T(eV,eV)}}\mathrm{d}E$$

(4)

and

$$b(V)={\displaystyle \underset{\mathrm{o}}{\overset{V}{\int }}\frac{{\rho }_{\mathrm{s}}(E) }{T(eV,eV)}}\frac{\mathrm{d}}{\mathrm{d}(eV)}\left[T(E,eV)\right]\mathrm{d}E$$

(5)

It is fair to say that the relation between ρ_s(E) and dσ_n(E) becomes a simple linear function if we assume that the parameters a and b are the numerical coefficients independent of voltage V. An even simpler relation, namely the proportionality of ρ_s(E)~dσ_n(E) is usually assumed, but in the general case, as can be seen from the above equations, this is not necessarily true. The constants a and b can be chosen in such a way that, after the numerical integration of the product T(E) × ρ_s(E) to calculate the tunnel current, two conditions are satisfied. The first condition is to obtain the same tunnel current for both structures (7 × 7)_N and (8 × 8) at the operating point at −3 V, as shown in Figure 6a. The second condition is to reach the contrast values or the tunnel gap (Δz) variation for the (7 × 7)_N and (8 × 8) structures at different scanning voltages to be close to the experiment. In this case, the spectrum dσ_n(E) for the (8 × 8) structure will be corrected using a linear transformation, and the spectrum of the (7 × 7)_N structure will be assumed to be the reference one. Then both spectra are normalized at the operating point to match the experimental operating current.

3.5. Correction Results of the Differential Conductivity Spectrum and Tunneling Current Estimation

The densities of states and the integrand of Equation (1), that is, of the product T(E) × ρ_s(E), for (7 × 7)_N and (8 × 8) structures as a function of energy are shown in Figure 8a. The curves in Figure 8b were calculated with the following parameters for the transmission coefficient T(E): z₀ = 15 Å, φ = 4.5 eV and V = −3 V. In this work, to correct the (8 × 8) structure spectrum, the coefficients a = 0.565 and b = 0.4 were found; as is shown further, these coefficients satisfy the two formulated criteria.

A comparison of the density of states for the (8 × 8) structure, obtained empirically in this work, and the DOS calculated in [42] is shown in Figure 8c. In both cases, it is assumed that the atomic structure of this array is based on a two-dimensional graphene-like g-Si₃N₃ layer. To compare the total DOS, we summarized the partial DOS given in [42].

It is clear in Figure 8c that the calculated and empirical DOS values are not identical, although there is a certain similarity in the spectra. The difference manifested itself despite the assumption that we are dealing with the same basis for the atomic structures of (8 × 8) and graphene-like g-Si₃N₃. Anyway, based on the presented graphs, it can be argued that the experimental and calculated bandgaps agree quite well, taking a value of about 2.3 eV. According to this fact and strong discrepancy with the expected β-Si₃N₄ bandgap of 5.3 eV, the graphene-like nature of the (8 × 8) structure became clearer, as follows from the better agreement between the experimental spectrum and the calculation of Guo at al. [42]. In contrast, if one sticks to the generally accepted model of the (8 × 8) structure as a thin β-Si₃N₄ layer, then one would expect an increase in the bandgap, in comparison with the bulk value of silicon nitride (>5.3 eV), due to the quantum confinement effect, as was shown, for example, in [51,52,53]. In turn, there may be several reasons for the detected discrepancies between the ab initio calculation of g-Si₃N₃ and the experimental spectra in Figure 8c. One of the main reasons, in our opinion, is as follows: the authors [42] considered the perfect isolated (not interacting with anything) two-dimensional layer when calculating from the first principles, and in our case, a similar layer (but, of course, nonperfect) is located on the silicon surface; moreover, the g-Si₃N₃ graphene-like layer is covered by an adsorption silicon layer [41]. In other words, in the STM experiment, a more complex nonperfect structure is studied, and there is the graphene-like g-Si₃N₃ layer interaction with the silicon substrate and the adsorption layer. Basically, between the layers, there should be van der Waals interactions (if some kinds of defects are neglected), although they are supposed to be weak, distorting the spectrum of an isolated g-Si₃N₃ layer. It is also possible that there is a certain “mixing” of the states of all these layers as was mentioned in the model considered in [33]. In addition, the states of the silicon substrate and the adsorption layer, immediately, in accordance with its geometric arrangement relative to the probe, are also more or less involved in the tunneling current formation. Another significant reason for the discrepancy may be related to the finite energy and spatial resolution of the scanning microscope, which usually reduces the amplitude and broadens the initially narrow peaks in the perfect spectra. It should be also noted that, in ab initio calculations, in one or another approximation and according to the chosen basis, a certain underestimation of the density of states in the region of unoccupied electronic states, that is, for the states lying above the Fermi level, may appear.

The changes in the expected tunneling current for the (7 × 7)_N and (8 × 8) structures obtained by the integration of T(E) × ρ_s(E), based on the corrected DOS of the (8 × 8) structure, as well as keeping the function T(E,eV,z) without variations, are shown in Figure 9.

To avoid possible ambiguities, it is necessary to make the following clarification: The calculated current values shown in Figure 9 do not correspond to the attempt at an accurate reproduction of the experimental I–V characteristics (how it might seem from the comparison with Figure 6a), even despite the coincidence of currents for both structures at the operating point of −3 V, for which the correction of the differential conductivity spectra was actually carried out. The meaning of the points presented in Figure 9 is estimating the hypothetically possible change in current ΔI, while the probe is laterally displaced from the structure (7 × 7)_N to (8 × 8) (or in the opposite direction) during the scanning at the fixed tunnel gap for the selected operating voltage. In this case, the current can be changed only due to the difference in the density of states of these structures. The empirical I–V characteristics of the structures shown in Figure 6a were actually measured at different tunnel gaps. Let us recall one more time that a change in the tunnel current usually does not occur during the real scanning of the surface at selected operating conditions (i.e., at selected voltage and current values), since the scanning is carried out with the feedback on the tunnel current.

3.6. Estimation of the Vertical Probe Offset Compensating the ΔI Value. Current Feedback Simulation

The necessary vertical displacement of the probe (offset) to compensate for the expected current changes during the lateral displacement from the surface region with the (7 × 7)_N structure to the region with the (8 × 8) structure is estimated: that is, this time, we are going to vary the only value of tunnel gap z which will change only the function T(E, eV, z), keeping the corrected DOS value without any variations, to reach the equalization of the tunnel currents in the areas for both structures. To be more precise, we determine the required vertical probe offset on the (8 × 8) structure to return to the same current that was calculated on the (7 × 7)_N structure at the given bias. In other words, one needs to eliminate the ΔI value calculated above by means of variation of T(E,eV,z), i.e., z₀ is replaced by z₀ + Δz when calculating this function, and it is necessary to determine a suitable Δz. All other parameters (except for variable Δz) used to calculate the function T(E,eV,z) were presented above and were kept constant, and suitable normalization parameters for DOS were found (as presented above). A comparison of the experimental data and calculation results for Δz at various biases is shown in Figure 10.

The black solid dots and the dotted line show the experimental contrast versus voltage (see Figure 5e), and the red blank dots present the estimation of the necessary probe offset Δz to compensate for the expected change in the current. It can be seen that as the voltage across the tunnel gap decreases, the required vertical probe offset increases, which corresponds qualitatively and quantitatively to the empirical behavior of the contrast versus voltage.

Thus, it is proposed to use the procedure for correcting the STS spectra of differential conductivity to match the behavior of the STM image contrast, as a function of bias, which helps to solve the problem of quantitative determination of DOS by the STM/STS technique. In this work, the (7 × 7)_N structure state spectrum was assumed to be known, and the correction of the (8 × 8) structure spectrum, according to the contrast behavior with the bias variation, turned out to be quite effective, since it made it possible to reproduce the empirical behavior of the contrast at the boundary between these two structures in the calculations. Then, the result shown in Figure 10 allows us to put forward a more general speculation. The proposed procedure for correcting the STS spectra dσ_n(V) = (dI/dV)/(I/V) can be actually useful for the STM studies of systems comprising surface boundaries between regions with a well-known DOS value and regions covered by poorly known structures or materials, the DOS values of which should be determined. The empirical determination of the differential conductance spectrum of this material from the STS measurements and the simple linear adjustment of this spectrum makes it possible to quantify the DOS. This approach is applicable to the study of a wide range of materials, both conductive and dielectric ones. In addition, this approach allows distinguishing the contrast associated with the density of states from the topographical contrast in STM images and a more adequate determination of the height of topographic surface features.

4. Conclusions

In this work, the influence of lateral variations in the local density of states on the contrast in STM images arising from the areas with different compositions and/or structures was studied both experimentally and theoretically. This kind of contrast frequently depends on the voltage applied to the tunnel gap. It is proposed to use the bias dependence of the contrast to make a correction of the differential conductivity spectrum in the STS in order to determine the local density of states. The studies were carried out on the example of the SiN/Si(111) system, where the behavior of the contrast near the lateral boundary between the (7 × 7)_N and (8 × 8) structures was studied as a function of tunnel bias. These structures were formed on the Si(111) silicon surface during its nitridation in the ammonia flux at the temperature of 1000 °C at small doses (3–10 L). In this system, a significant dependence of the contrast on the bias was found in the voltage range from −3 V to +3 V, and it was studied in more detail in the range of positive biases on the sample from +1 V to +2.5 V.

A comparatively simple procedure is proposed for the correction of the experimental STS-spectra of differential conductivity values to identify the corresponding DOS. The procedure is developed in the framework of the one-dimensional WKB model for the tunnel current. The procedure consists of two stages: (1) estimation of the expected change in the tunneling current due to the variation of local DOS when the probe moves from a region with one structure to a region with another structure during the scanning process; (2) calculation of the required tunnel gap variation (i.e., vertical probe offset) to compensate for the expected change in the current. The last step allows one to simulate the feedback operation on the tunneling current in the STM. The agreement between the calculations and the empirical behavior of the contrast on the voltage for the boundary between (7 × 7)_N and (8 × 8) structures is reached.

The proposed procedure for the correction of the differential conductivity spectra by matching the contrast behavior will be useful for the research and development of the technology for the formation of thin layers of a wide range of new materials (conductive and dielectric) and nanostructures, for example, for the synthesis of new two-dimensional materials and/or their functionalization. The proposed approach of spectral correction is expected to be particularly effective in situations on the surface where a lateral boundary is formed between a material with a well-known electronic state density spectrum and a new material whose spectrum has not yet been established. It will also allow avoiding ambiguities when distinguishing the contrast originating from lateral DOS variation against the topological contrast.