Step Bunches, Nanowires and Other Vicinal “Creatures”—Ehrlich–Schwoebel Effect by Cellular Automata
Abstract
:1. Introduction
2. Model
3. Pattern Formation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Table of Cellular Automaton Rules
| Crystal seed Rule(1,1,1,1,0) = 1 Rule(1,1,0,1,1) = 1 Rule(1,1,1,1,1) = 1 Adsorption at step Rule(1,0,0,1,2) = 1 Rule(1,0,0,2,1) = 1 Rule(1,0,1,2,0) = 1 Rule(1,1,2,0,0) = 1 Rule(1,2,1,0,0) = 1 Rule(1,2,0,0,1) = 1 Rule(1,0,1,1,2) = 1 Rule(1,0,1,2,1) = 1 Rule(1,0,2,1,1) = 1 Rule(1,1,0,1,2) = 1 Rule(1,1,0,2,1) = 1 Rule(1,1,1,0,2) = 1 Rule(1,1,1,2,0) = 1 Rule(1,1,2,0,1) = 1 Rule(1,1,2,1,0) = 1 Rule(1,2,0,1,1) = 1 Rule(1,2,1,0,1) = 1 Rule(1,2,1,1,0) = 1 Rule(1,1,1,1,2) = 1 Rule(1,1,1,2,1) = 1 Rule(1,1,2,1,1) = 1 Rule(1,2,1,1,1) = 1 Rule(1,0,2,1,0) = 1 Rule(1,1,0,0,2) = 1 | Adsorption at kink Rule(1,0,0,2,2) = 1 Rule(1,0,2,2,0) = 1 Rule(1,2,0,0,2) = 1 Rule(1,2,2,0,0) = 1 Rule(1,0,1,2,2) = 1 Rule(1,0,2,1,2) = 1 Rule(1,0,2,2,1) = 1 Rule(1,1,0,2,2) = 1 Rule(1,1,2,0,2) = 1 Rule(1,1,2,2,0) = 1 Rule(1,2,0,1,2) = 1 Rule(1,2,0,2,1) = 1 Rule(1,2,1,0,2) = 1 Rule(1,2,1,2,0) = 1 Rule(1,2,2,0,1) = 1 Rule(1,2,2,1,0) = 1 Rule(1,0,2,2,2) = 1 Rule(1,2,0,2,2) = 1 Rule(1,2,2,0,2) = 1 Rule(1,2,2,2,0) = 1 Rule(1,1,1,2,2) = 1 Rule(1,1,2,1,2) = 1 Rule(1,1,2,2,1) = 1 Rule(1,2,1,1,2) = 1 Rule(1,2,1,2,1) = 1 Rule(1,2,2,1,1) = 1 Rule(1,1,2,2,2) = 1 Rule(1,2,1,2,2) = 1 Rule(1,2,2,1,2) = 1 Rule(1,2,2,2,1) = 1 Rule(1,2,2,2,2) = 1 | Filling voids Rule(0,1,1,1,1) = 1 No Adsorption Rule(1,0,0,0,0) = 0 Rule(1,0,0,0,1) = 0 Rule(1,0,0,1,0) = 0 Rule(1,0,1,0,0) = 0 Rule(1,1,0,0,0) = 0 Rule(1,0,0,1,1) = 0 Rule(1,0,1,0,1) = 0 Rule(1,0,1,1,0) = 0 Rule(1,0,0,1,1) = 0 Rule(1,1,0,1,0) = 0 Rule(1,1,0,0,1) = 0 Rule(1,1,1,0,1) = 0 Rule(1,0,1,1,1) = 0 Rule(1,0,0,0,2) = 0 Rule(1,0,0,2,0) = 0 Rule(1,0,2,0,0) = 0 Rule(1,2,0,0,0) = 0 Rule(1,0,1,0,2) = 0 Rule(1,0,2,0,1) = 0 Rule(1,1,0,2,0) = 0 Rule(1,2,0,1,0) = 0 Rule(1,0,2,0,2) = 0 Rule(1,2,0,2,0) = 0 Rule(0,*,*,*,*) = 0 |
References
- Oreg, Y.; Refael, G.; von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef] [Green Version]
- Lutchyn, R.M.; Sau, J.D.; Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef] [Green Version]
- Mourik, V.; Zuo, K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.a.M.; Kouwenhoven, L.P. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science 2012, 336, 1003–1007. [Google Scholar] [CrossRef] [Green Version]
- Grünberg, P.; Schreiber, R.; Pang, Y.; Brodsky, M.B.; Sowers, H. Layered Magnetic Structures: Evidence for Antiferromagnetic Coupling of Fe Layers across Cr Interlayers. Phys. Rev. Lett. 1986, 57, 2442. [Google Scholar] [CrossRef] [PubMed]
- Baibich, M.N.; Broto, J.M.; Fert, A.; Nguyen, V.D.F.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 1988, 61, 2472. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fermon, C.; Pannetier-Lecoeur, M. Noise in GMR and TMR Sensors. In Giant Magnetoresistance (GMR) Sensors. Smart Sensors, Measurement and Instrumentation; Reig, C., Cardoso, S., Mukhopadhyay, S.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 6, pp. 47–70. [Google Scholar]
- Zheludev, N. The life and times of the LED—A 100-year history. Nat. Photonics 2007, 1, 189–192. [Google Scholar] [CrossRef]
- Isobe, Y.; Iida, D.; Sakakibara, T.; Iwaya, M.; Takeuchi, T.; Kamiyama, S.; Akasaki, I.; Amano, H.; Imade, M.; Kitaoka, Y.; et al. Growth of AlGaN/GaN heterostructure on vicinal m-plane free-standing GaN substrates prepared by the Na flux method. Phys. Status Solidi (A) Appl. Mater. Sci. 2011, 208, 1191–1194. [Google Scholar] [CrossRef]
- Amano, H.; Sawaki, N.; Akasaki, I. Metalorganic vapor phase epitaxial growth of a high quality GaN film using an AlN buffer layer. Appl. Phys. Lett. 1986, 48, 353. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.J.; Pickett, M.D.; Li, X.; Ohlberg, D.A.A.; Stewart, D.R.; Williams, R.S. Memristive switching mechanism for metal/oxide/metal nanodevices. Nat. Nanotechnol. 2008, 3, 429–433. [Google Scholar] [CrossRef]
- Yang, J.J.; Strukov, D.B.; Stewart, D.R. Memristive Devices for Computing. Nat. Nanotechnol. 2013, 8, 13–24. [Google Scholar] [CrossRef]
- Ehrlich, G.; Hudda, F.G. Atomic view of surface self-diffusion—Tungsten on tungsten. J. Chem. Phys. 1966, 44, 1039. [Google Scholar] [CrossRef]
- Schwoebel, R.L.; Shipsey, E.J. Step motion on crystal surfaces. J. Appl. Phys. 1966, 37, 3682. [Google Scholar] [CrossRef]
- Misbah, C.; Pierre-Louis, O.; Saito, Y. Crystal surfaces in and out of equilibrium: A modern view. Rev. Mod. Phys. 2010, 82, 981. [Google Scholar] [CrossRef]
- Saúl, A.; Métois, J.-J.; Ranguis, A. Experimental evidence for an Ehrlich-Schwoebel effect on Si(111). Phys. Rev. B 2001, 65, 075409. [Google Scholar] [CrossRef]
- Rogilo, D.I.; Fedina, L.I.; Kosolobov, S.S.; Ranguelov, B.S.; Latyshev, A.V. Critical Terrace Width for Two-Dimensional Nucleation during Si Growth on Si(111)-(7 × 7) Surface. Phys. Rev. Lett. 2013, 111, 036105. [Google Scholar] [CrossRef]
- De Theije, F.K.; Schermer, J.J.; Van Enckevort, W.J.P. Effects of nitrogen impurities on the CVD growth of diamond: Step bunching in theory and experiment. Diam. Relat. Mater. 2000, 9, 1439–1449. [Google Scholar] [CrossRef]
- Xie, M.H.; Cheung, S.H.; Zheng, L.X.; Ng, Y.F.; Wu, H.; Ohtani, N.; Tong, S.Y. Step bunching of vicinal GaN(0001) surfaces during molecular beam epitaxy. Phys. Rev. B Condens. Matter Mater. Phys. 2000, 61, 9983–9985. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.; Xie, M.H.; Wu, H.S.; Xue, Q.K. Kinetic energy barriers on the GaN (0001) surface: A nucleation study by scanning tunneling microscopy. Phys. Rev. B 2008, 77, 045303. [Google Scholar] [CrossRef]
- Gianfrancesco, A.G.; Tselev, A.; Baddorf, A.P.; Kalinin, S.V.; Vasudevan, R.K. The Ehrlich–Schwoebel barrier on an oxidesurface: A combined Monte-Carlo and in situ scanning tunneling microscopy approach. Nanotechnology 2015, 26, 455705. [Google Scholar] [CrossRef]
- Sarma, D.S.; Punyindu, P.; Toroczkai, Z. Non-universal mound formation in non-equilibrium surface growth Z. Surf. Sci. 2000, 457, L369–L375. [Google Scholar] [CrossRef] [Green Version]
- Leal, F.F.; Ferreira, S.C.; Ferreira, S.O. Modelling of epitaxial film growth with an Ehrlich–Schwoebel barrier dependent on the step height. J. Phys. Condens. Matter. 2011, 23, 292201. [Google Scholar] [CrossRef] [Green Version]
- Palczynski, K.; Herrmann, P.; Heimel, G.; Dzubiella, J. Characterization of step-edge barrier crossing of para-sexiphenyl on the ZnO (101 [combining macron] 0) surface. J. Phys. Chem. Chem. Phys. 2016, 18, 25329. [Google Scholar] [CrossRef]
- Xiang, S.K.; Huang, H. Ab initio determination of Ehrlich–Schwoebel barriers on Cu {111}. Appl. Phys. Lett. 2008, 92, 101923. [Google Scholar] [CrossRef]
- Hao, J.; Zhang, L. Strongly reduced Ehrlich–Schwoebel barriers at the Cu (111) stepped surface with In and Pb surfactants. Surf. Sci. 2018, 667, 13–16. [Google Scholar] [CrossRef]
- Xie, M.H.; Leung, S.Y.; Tong, S.Y. What causes step bunching-negative Ehrlich-Schwoebel barrier versus positive incorporation barrier. Surf. Sci. 2002, 515, L459–L463. [Google Scholar] [CrossRef]
- Krzyżewski, F.; Załuska–Kotur, M.A. Coexistence of bunching and meandering instability in simulated growth of 4H-SiC (0001) surface. J. Appl. Phys. 2014, 115, 213517. [Google Scholar] [CrossRef] [Green Version]
- Krzyżewski, F.; Załuska-Kotur, M.A. Stability diagrams for the surface patterns of GaN (0001¯) as a function of Schwoebel barrier height. J. Cryst. Growth 2017, 457, 80–84. [Google Scholar] [CrossRef]
- Krasteva, A.; Popova, H.; Krzyżewski, F.; Załuska-Kotur, M.; Tonchev, V. Unstable vicinal crystal growth from cellular automata. AIP Conf. Proc. 2016, 1722, 220014. [Google Scholar]
- Krzyżewski, F.; Załuska-Kotur, M.A.; Krasteva, A.; Popova, H.; Tonchev, V. Step bunching and macrostep formation in 1D atomistic scale model of unstable vicinal crystal growth. J. Cryst. Growth 2017, 474, 135–139. [Google Scholar] [CrossRef] [Green Version]
- Krzyżewski, F.; Załuska-Kotur, M.A.; Krasteva, A.; Popova, H.; Tonchev, V. Scaling and Dynamic Stability of Model Vicinal Surfaces. Cryst. Growth Des. 2019, 19, 821–831. [Google Scholar] [CrossRef]
- Toktarbaiuly, O.; Usov, V.O.; Coileáin, C.; Siewierska, K.; Krasnikov, S.; Norton, E.; Bozhko, S.I.; Semenov, V.N.; Chaika, A.N.; Murphy, B.E.; et al. Step bunching with both directions of the current: Vicinal W(110) surfaces versus atomistic-scale model. Phys. Rev. B Condens. Matter Mater. Phys. 2018, 97, 035436. [Google Scholar] [CrossRef] [Green Version]
- Popova, H.; Krzyżewski, F.; Załuska-Kotur, M.A.; Tonchev, V. Quantifying the Effect of Step–Step Exclusion on Dynamically Unstable Vicinal Surfaces: Step Bunching without Macrostep Formation. Cryst. Growth Des. 2020, 20, 7246–7259. [Google Scholar] [CrossRef]
- Turski, H.; Krzyżewski, F.; Feduniewicz-Żmuda, A.; Wolny, P.; Siekacz, M.; Muziol, G.; Cheze, C. Nowakowski-Szukudlarek Krzesimir, Xing Huili Grace, Jena Debdeep, Załuska-Kotur Magdalena, Skierbiszewski Czesław, Unusual step meandering due to Ehrlich-Schwoebel barrier in GaN epitaxy on the N-polar Surface. Appl. Surf. Sci. 2019, 484, 771–780. [Google Scholar] [CrossRef] [Green Version]
- Sato, M.; Uwaha, M. Growth law of step bunches induced by the Ehrlich-Schwoebel effect in growth. Surf. Sci. 2001, 493, 494–498. [Google Scholar] [CrossRef]



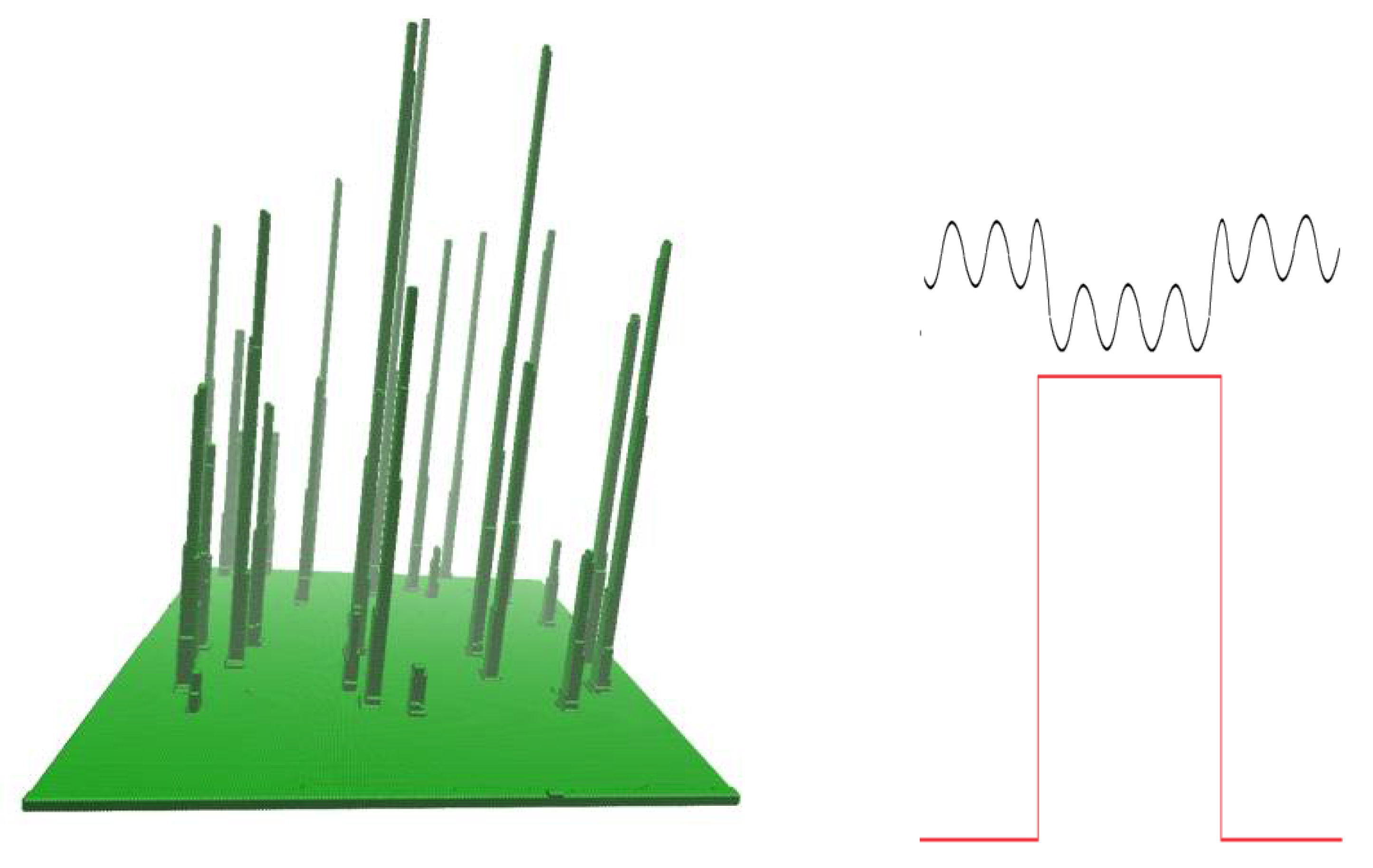
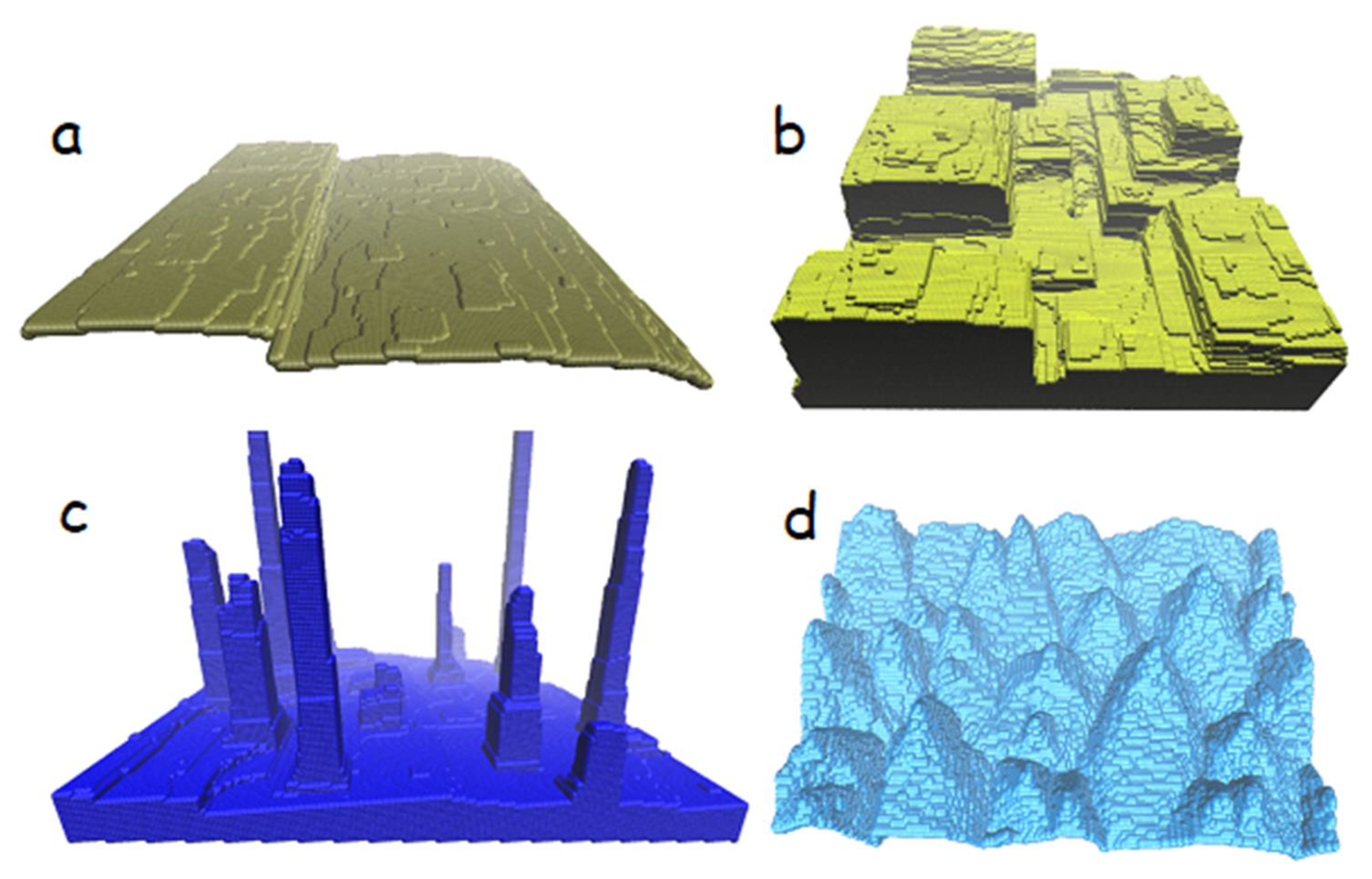
 describes regular step ordering,
describes regular step ordering,  means bunches,
means bunches,  bunches with antibunches,
bunches with antibunches,  describe nanopillars,
describe nanopillars,  nanowires,
nanowires,  pyramids, and
pyramids, and  is specific (0, 0) point.
is specific (0, 0) point.
 describes regular step ordering,
describes regular step ordering,  means bunches,
means bunches,  bunches with antibunches,
bunches with antibunches,  describe nanopillars,
describe nanopillars,  nanowires,
nanowires,  pyramids, and
pyramids, and  is specific (0, 0) point.
is specific (0, 0) point.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Załuska-Kotur, M.; Popova, H.; Tonchev, V. Step Bunches, Nanowires and Other Vicinal “Creatures”—Ehrlich–Schwoebel Effect by Cellular Automata. Crystals 2021, 11, 1135. https://doi.org/10.3390/cryst11091135
Załuska-Kotur M, Popova H, Tonchev V. Step Bunches, Nanowires and Other Vicinal “Creatures”—Ehrlich–Schwoebel Effect by Cellular Automata. Crystals. 2021; 11(9):1135. https://doi.org/10.3390/cryst11091135
Chicago/Turabian StyleZałuska-Kotur, Magdalena, Hristina Popova, and Vesselin Tonchev. 2021. "Step Bunches, Nanowires and Other Vicinal “Creatures”—Ehrlich–Schwoebel Effect by Cellular Automata" Crystals 11, no. 9: 1135. https://doi.org/10.3390/cryst11091135
APA StyleZałuska-Kotur, M., Popova, H., & Tonchev, V. (2021). Step Bunches, Nanowires and Other Vicinal “Creatures”—Ehrlich–Schwoebel Effect by Cellular Automata. Crystals, 11(9), 1135. https://doi.org/10.3390/cryst11091135






