Abstract
In the past decade, much evidence has been provided for an unusually low cost for bend deformations in the nematic phase of bent-core mesogens and bimesogens (liquid crystal dimers) having a bent shape on average. Recently, an analogous effect was observed for the splay mode of bent-core mesogens with an acute apical angle. Here, we present a systematic computational investigation of the Frank elastic constants of nematics made of V-shaped particles, with bend angles ranging from acute to obtuse. We show that by tuning this angle, the elastic behavior switches from bend dominated () to splay dominated (), with anomalously low values of the splay and the bend constant, respectively. This is related to a change in the shape polarity of particles, which is associated with the emergence of polar order, longitudinal for splay and transversal for bend deformations. Crucial to this study is the use of a recently developed microscopic elastic theory, able to account for the interplay of mesogen morphology and director deformations.
1. Introduction
Breaking of the continuous rotational symmetry, in liquid crystals, brings about the existence of a director field , which locally corresponds to the average molecular orientation. The ground state of conventional nematics is characterized by a uniform director field, and deformations have a cost, which is described in terms of the Oseen–Frank deformation free energy density [1,2]:
Here, are the so-called bulk elastic constants for splay (), twist () and bend () deformations. The recent discoveries of a variety of modulated nematic phases and of unconventional elastic behavior challenge this well-established picture. A different perspective is emerging, one novel aspect being a distinct role of polar order in the presence of splay and bend deformations [3]. The director field polarity, longitudinal for splay and transversal for bend deformations, can induce the polar order of mesogens if these have a suitable symmetry. This affects the free energy and subsequently the cost for director deformations.
There were early claims of the coupling between splay or bend deformations and molecular polarity, intended either as an electrostatic (hence the involvement of “flexoelectricity”) [4,5] or a steric interaction [6,7], but they remained mostly disregarded. Only recently, the observation of very low bend elastic constants in liquid crystal materials comprised of bent-shaped molecules, whether bent-core mesogens or bimesogens (liquid crystal dimers) having a bent shape on average [8,9,10,11,12,13,14,15,16,17], together with the discovery of novel modulated nematic phases [18,19,20,21,22,23,24], prompted renewed interest in this topic. Theory played a major role in solving the controversy concerning the origin of the observed softening of the bend elastic constant [11,12,13]. Both mesoscopic and microscopic approaches were used. In the former, the key point was the introduction of a flexoelectric contribution into a phenomenological expression for the deformation free energy [25]. At the microscopic level [26,27,28,29], what turned out to be crucial was the relaxation of the assumption, common to classical theories, that the orientational distribution of particles remains unperturbed when director distortions are present. Bent particles with an obtuse bend angle preferentially align their long axis to the nematic director, and a bend deformation introduces a bias in the orientation of their transversal (short) axes: orientations with the particle convexity in accordance with that of the director field or in opposition to it have a different probability, so a transversal polar order is induced. Since this allows better packing than in a uniaxial environment, the result is a decrease in the cost for bend deformations. In agreement with experiments, a subtle dependence of the bend elastic constant on the bend angle of molecules was demonstrated both by generic models [29] and by detailed modeling of the molecular structure [30,31,32].
The elasticity of nematics made of wedge-shaped mesogens has attracted less attention by far. In principle, analogous considerations for (obtuse angle) bent molecules can be made, with the difference that an effect on the splay mode is expected, since in this case, the polarity of particles is parallel to the axis that aligns to the director, rather than perpendicular [33]. Indeed, in a couple of theoretical studies a very low splay elastic constant, lower than the twist constant, was predicted for conical rods [28,34]. Only recently, an experimental observation of this behavior was reported for a mesogen with a 1,7-naphthalene central core, which features an acute apical angle [35,36]. The uniaxial nematic phase is followed, at low temperature, by a modulated phase, which has not yet been fully characterized.
Here, we present a comprehensive analysis of the elastic properties of nematics made of V-shaped mesogens of symmetry. These represent paradigmatic systems where a geometric parameter, the bend angle, can be identified as an appropriate descriptor to connect the molecular structure and macroscopic behavior. We extend previous studies to a wide range of bend angles, including acute ones. Our work relies on a recently proposed microscopic approach [37,38], which generalizes the Straley theory for rod-like mesogens [39] to particles of arbitrary shape. We use a generic model of particles, made by a rigid chain of tangent hard spheres, which allows us to explore general effects, without pretending to perform a punctual comparison with experimental data. We show how the bend angle can be used to tune the relative cost for splay and bend deformation, and we relate this change in behavior to the capability of nematics made of bent particles to respond to splay and bend deformations with an induced polar order [37,38].
The paper is organized as follows. The next section gives a brief overview of the theory and of the numerical methods, together with a description of the particle models used. Then, in the third section we report and discuss numerical results, and finally, the fourth section contains the conclusions.
2. Materials and Methods
2.1. Theoretical Framework
Our description of the nematic phase is based on Onsager second virial theory [40] with modified Parsons–Lee correction [41,42,43] for particles experiencing hard-core repulsion. In such a perspective, the free energy density F of a uniform nematic system made up by N particles at temperature T, contained in the volume V, is a functional of the single particle orientational distribution function (ODF) , where are the angles defining the particle orientation and can be expressed as a sum of an ideal, , and an excess term, . The former includes the ideal gas free energy density, , and a contribution that accounts for the decrease of orientational entropy with respect to the isotropic phase:
whereas the excess free energy density is approximated by the second virial expression:
In these equations is the Boltzmann constant; is the number density of particles; is a vector joining the centers of mass of a pair of particles (A and B), whose orientations are given by and , respectively; and is the Mayer function [44], which in turn is defined in terms of the pair potential as . The particle orientation is defined by the set of Euler angles , which rotate the laboratory fixed reference frame into the molecular frame attached to the particle (see Figure 1). Finally, is the modified Parsons–Lee factor [41,42,43], which approximately accounts for virial terms higher than the second:
where represents the effective volume of a particle (vide infra).
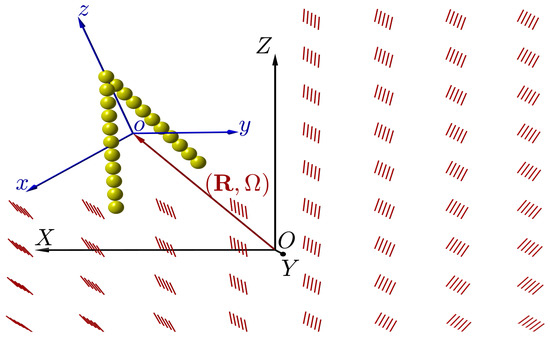
Figure 1.
Sketch of the laboratory frame of reference and of the particle frame of reference . is the vector position of the center of mass of the particle in the laboratory frame, and is the set of Euler angles that rotate into . The red segments represent the director field with a splay distortion of wavenumber .
In the presence of a non-uniform director field , the ODF becomes a function of the spatial position of the particle and crucial for our study is the use of a form that is sensitive to both the molecular shape and the director field configuration. We have recently proposed a non-local form [37,38] based on the general consideration that each part of a molecule experiences the director at its specific location. Considering a model particle that can be described as a chain of M segments and assuming the simplest form compatible with the local nematic symmetry, we use the following ansatz:
where is the position of the particle’s center of mass, is a unit vector parallel to the jth segment and is a unit vector parallel to the director at the position of the segment, . Here a is an adimensional parameter that measures the orienting strength: it jumps from 0 in the isotropic phase to a finite positive value in the (calamitic) nematic phase. The non-locality of this form of the ODF brings about the interplay between the particle morphology and the deformation field. This is the main difference from classical microscopic elastic theories [39,45,46], in which a molecule is assumed to interact with the director field at the position of its center of mass, and therefore, the ODF depends on the local orientation of the director, but it is not sensitive to spatial gradients of the latter. In other words, the ODF is assumed to rotate to follow the director field, without changing its profile. A simple form for a local ODF is the one-segment equivalent of Equation (5):
where is a unit vector parallel to the molecular axis that preferentially aligns with the nematic director. For rod-like, and in general for axially symmetric particles, the definition of this vector is obvious; for arbitrarily shaped particles, in the calculations reported in the following, we have taken parallel to the major principal axis of the tensor of gyration.
Using Equation (5) in Equations (2) and (3) with an appropriate form of the director field, , the free energy density in the presence of a specific deformation is obtained. The deformation free energy density is then calculated as the difference with respect to the uniform nematic state. It is therefore possible to estimate the elastic constants for splay, , twist, , and bend, , deformations. More specifically, we use the following form for [46]:
where and are unit vectors parallel to the X and Z axis of the laboratory fixed reference frame, and the angle between the director in a generic position and the director at the origin, , is defined as
The parameter q is the wavenumber of the deformation and is equal to 0 in the undeformed state. Then, using the Taylor expansion of the ODF, , in Equations (2) and (3), the elastic constants are obtained from the parabolic coefficients in q of the deformation free energy density for the three modes:
2.2. Interaction Potential and Model Details
We model particles as rigid chains made up by tangent identical hard spheres of diameter . Beside V-shapes, some other particle geometries are examined for comparison (see Figure 2). In our calculations the unit vectors appearing in the definition of the ODF, Equation (5), are taken parallel to the sphere–sphere bonds and are placed in the middle of bonds. The hard-core interaction potential between pairs of particles labeled A and B is defined as
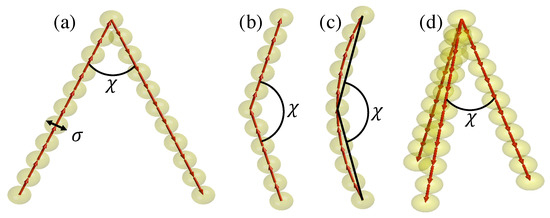
Figure 2.
Model particles considered in this work; is the hard sphere diameter, and is the bend angle, equal to in (a), in (b), in (c) and in (d).
The geometric volume of a particle, , used to calculate the packing fraction , is defined as the sum of the spheres’ volumes, from which, in the case of overlapping spheres, the intersection volume has to be subtracted. For non-convex shapes, the geometric volume is different from the effective volume appearing in the Parsons–Lee factor, Equation (4), which is defined as the portion of space in which any part of a particle cannot enter due to the presence of another particle [43]. We estimate as the volume enclosed by the tessellated surface defined by a sphere of radius equal to 0.5 rolling over the particle; a density of vertices on the surface equal to 1000 is assumed [47]. The values of and , as well as other geometric parameters for all the particles investigated in this work, are reported in Table 1.

Table 1.
Geometric parameters of the particles investigated in this work (number of segments M, bend angle , geometrical volume , effective volume); packing fractions at the isotropic-nematic coexistence, in the isotropic, , and in the nematic phase, .
2.3. Numerical Procedure
Given a specific geometry of particles, (i.e., the set of coordinates of the centers of hard spheres), we evaluate integrals such as Equation (3) over a 6-dimensional discrete grid of Euler angles , using Gauss–Legendre quadrature on azimuthal angles and Gauss–Chebyshev quadrature on polar angles [48]. The segmental ordering strength a is obtained for each number density of interest by minimizing the total free energy density, sum of Equations (2) and (3). Minimizations are performed by applying Nelder–Mead simplex algorithm [49] implemented in Matlab [50].
The packing fractions at the isotropic-nematic coexistence, in the isotropic, , and in the nematic phase, , are determined by equating the pressure P and the chemical potential of the two phases, which are calculated as
2.4. Frames of Reference
For all the systems studied in this work, we defined the particle frame of reference according to the following conventions: the origin o corresponds to the particle center of mass, the z-axis and x-axis are parallel to the eigenvectors of the particle’s gyration tensor corresponding to the largest eigenvalue and the second largest eigenvalue, respectively. This implies that for obtuse angle particles, the rotation axis is parallel to x, while for acute ones, the axis is parallel to z (see Figure 1).
The laboratory frame of reference in the undeformed nematic phase has the Z-axis parallel to the director, whereas X and Y can be arbitrarily taken. According to Equations (7) and (8), in presence of deformations, Z is parallel to the director at the origin O, and Y is perpendicular to the plane containing the splay and bend deformations, whereas for twist deformations, Y is parallel to the twist axis.
2.5. Orientational Order Parameters
We characterize the orientational order of particles in the undeformed uniaxial nematic phase by means of the nematic order parameter S and the biaxial parameter D [51], which are defined as
where , and are unit vectors parallel to the corresponding axes of the particle reference frame, and the symbol stands for the orientational average over the undeformed ODF (). S quantifies the degree of alignment of the particle’s long axis with the director, whereas D measures the difference in alignment with the director of the transversal axes of the particle. Both order parameters vanish in the isotropic phase, whereas in a perfectly ordered phase, and .
We also introduce two other order parameters to quantify the degree of polar order induced by splay or bend deformations:
where the symbol stands for the orientational average over the ODF in the presence of a splay or bend deformation of wavenumber q. quantifies the polar order of the particle’s transversal axis x with respect to the laboratory axis X, whereas does the same for the particle’s long axis z with respect to the laboratory Z axis. Both and vanish if the ODF does not have a polar character, as occurs for particles of any shape in the uniform nematic phase. In the presence of splay or bend deformations, or , respectively, can take a finite value, provided that particles have a polar symmetry. Of course, an ODF accounting for the polarity of the particle and of the director field, such as Equation (5), is needed for this purpose. It may be worth stressing that here, we speak of polarity in terms of symmetry; however, if molecules have an electric dipole, polar order implies the presence of electric polarization.
3. Results and Discussion
In the following, we report the results obtained for rigid V-shaped particles of symmetry, with different bend angles (see Figure 2a,b). The presentation is divided into two subsections, one on acute and the other on obtuse angle particles. The former have a longitudinal twofold symmetry axis; they are found to form a nematic calamitic phase where this axis is preferentially aligned to the director. On the contrary, obtuse angle particles, whose twofold symmetry axis is transversal, are predicted to form a nematic calamitic phase in which this axis is preferentially oriented perpendicular to the director. For intermediate values of the bend angle, no calamitic order is found. It may be worth mentioning that we describe the elastic properties of a potential nematic phase, which takes over from the isotropic beyond a certain density, but no comparison is made with other possible phases, e.g., smectic or twist-bend nematic, which might supersede the nematic in some cases [52].
In our calculations, we take as the unit of length and as the unit of energy. Since purely hard-core interactions are considered, systems are athermal; therefore, the results are reported as a function of the volume fraction. However, a comparison with thermotropic systems can be made through the order parameter.
3.1. Acute Angle Particles
Figure 3 shows the orientational order parameters S and D and the elastic constants calculated for V-shaped particles made of 21 hard spheres with an acute bend angle between 25 and 45, as a function of the volume fraction. In these particles, the reference system is defined with the z axis parallel to the twofold symmetry axis and the y axis perpendicular to the plane containing the two arms (see see Figure 1). The axial order parameter S, which quantifies the degree of quadrupolar order of the twofold symmetry axis of the particles, is generally high, decreases as the bend angle widens and, for a given particle, increases with increasing density. The biaxial order parameter D, which describes the different alignment with the director of two transversal axes, one parallel to the segment joining the centers of the terminal spheres and one perpendicular to the particle plane, is low and increases with increasing bend angle, as expected on the basis of the particle shape. It decreases with increasing density, with the only exception being the more biaxial particle (), for which a small growth of D with increasing density is found, just beyond the isotropic-nematic transition. A non-monotonic relationship between biaxial and uniaxial molecular order parameters is well known [53], but the initial increase of D cannot be observed if the isotropic-nematic transition occurs at a very high S value. We can also notice in Figure 3 that widening of the bend angle is associated with a shift of the isotropic-nematic transition at higher density, which can be ascribed to the increase in shape biaxiality.
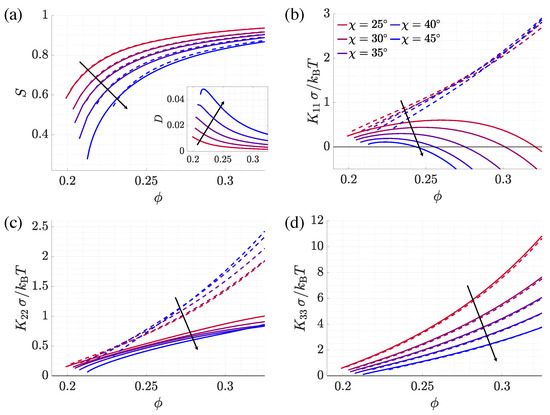
Figure 3.
(a) Order parameters S and D (inset), and (b) splay, (c) twist and (d) bend elastic constant, as a function of the volume fraction . Values obtained using the non-local form of the ODF, Equation (5) (solid lines), and the local uniaxial form, Equation (6) (dashed lines), for the nematic phase of acute angle V-shaped particles with different values of the bend angle.
As for the elastic constants, Figure 3b shows that the wedge shape has a dramatic impact on the splay mode: is anomalously low and exhibits a non-monotonic density dependence. The general trend is a small increase of the splay constant after the transition, which is followed by a decrease, until, at a certain density, vanishes. A strong sensitivity on the bend angle can be noticed, with the range of positive values that becomes very small for wider angles. This behavior is reminiscent of that reported for the bend elastic constant of bent particles with an obtuse bend angle [26,27,28,29]. As discussed in that context, negative values of bulk elastic constants are incompatible with the stability of the uniform nematic phase [54]; however, systems can rearrange into other phases, such as the twist bend nematic [18,19,20,21,22,23,24]. For the sake of comparison, we also report in Figure 3 the results obtained using the local form of ODF, Equation (6). In such calculations, the structure of particles is partially accounted for; in fact, elastic constants are determined using expressions, derived from Equation (3), containing generalized excluded volume integrals [38], which are evaluated for pairs of particles by explicitly taking into account their shape. However, the ODF appearing in such integrals is that of an effective rod-like particle, which interacts with the director at the position of its center of mass, and it maintains its profile irrespective of the presence of a deformation. In Figure 3b–d, we can see that the use of the local ODF has a dramatic effect on the splay constant, which exhibits the typical monotonic increase with density, analogous to that of rod-like particles. What makes the ODF defined in Equation (5) different from that defined in Equation (6) is that the former is able to acquire a polar character in the presence of a polar symmetry of the environment.
The induced polar order can be quantified by the order parameter defined in Equation (15). Figure 4a shows as a function of the deformation wavenumber q for V-shaped particles with bend angle at different values of the packing fraction. is equal to zero in the uniform nematic phase, but it then exhibits a linear increase (in absolute value) with the wavenumber q of the splay deformation. For a given splay deformation, takes a finite value at the isotropic-nematic transition and then increases upon moving to higher density. The slope of at , which can be seen as a kind of ’flexopolar’ coefficient [24], is a parameter that quantifies the capability of the material to acquire polar order in response to a splay deformation. Figure 4b shows the slope of at for V-shaped particles with different bend angles, as a function of the volume fraction, and we can see that this capability increases as the bend angle widens.
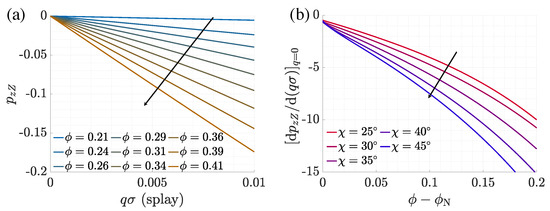
Figure 4.
(a) Polar longitudinal order parameter for V-shaped particles with bend angle in the presence of a splay deformation, as a function of the deformation wavenumber q, at different values of the packing fraction . (b) Slope of the longitudinal polar order parameter induced by a splay deformation, , calculated at , as a function of the volume fraction difference , for acute angle V-shaped particles with different values of the bend angle. is the packing fraction in the nematic phase at the nematic-isotropic boundary. Negative values mean that the apex of a V-shaped particle preferentially points towards the center of the splay deformation (see Figure 1).
It is interesting to observe that the bend elastic constants, shown in Figure 3d, are not affected by the form of the ODF and exhibit the usual trend typical of rod-like particles, characterized by a steep increase with increasing density. seems to be essentially determined by the aspect ratio of the acute angle V-shaped particles. For the twist elastic constant, on the contrary, we can see in Figure 3c that there are some differences between the results obtained using the local and the non-local form of the ODF. In particular, the values calculated using Equation (5) are smaller, exhibit a much weaker density dependence and tend to flatten at high order. Here it is no longer a matter of symmetry, but other geometrical features of particles, such as the biaxiality, can come into play. A role of biaxiality is confirmed by the results obtained for a tripodal particle, which are shown in Figure 5. We can see that for this particle, which has polar symmetry but uniaxial order (), the twist elastic constant does not change if either the non-local or the local form of the ODF. It may be worth pointing out the difference between the polar and biaxial order of particles with respect to elastic constants. Polar order is incompatible with the uniform nematic phase but can be induced by a deformation of polar symmetry. As we have shown, it can be accounted for by an ODF that changes in the presence of director deformations, in a way that depends on the particle shape. On the contrary, the biaxial order of mesogens is compatible with the symmetry of the uniform nematic phase. Therefore, it can be accounted for even by classical microscopic theories of elasticity, provided that a form of the ODF that is more general than Equation (6) and able to describe the different ordering of the two transversal axes of particles is used [53]. As for the non-local ODF that we have proposed, Equation (5), by construction, it takes into account the biaxiality as well as other geometrical features of the particles considered.
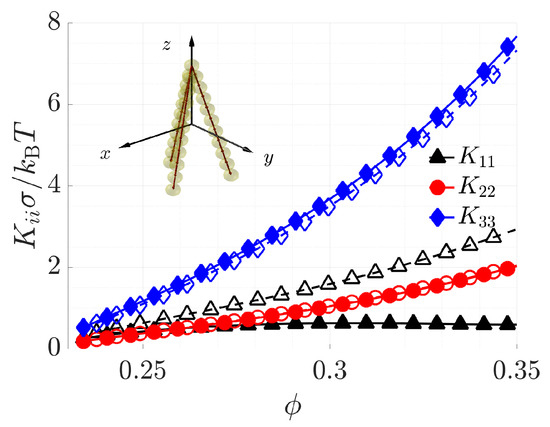
Finally, Figure 6 collects the three Frank elastic constants of particles with bend angle , which is close to the value of the apical angle in the molecules with 1,7-naphthalene central core investigated in Reference [36]. A strict comparison with experimental results is beyond the scope of this work, since the model used here (rigid particles interacting though a purely repulsive potential) lacks important elements for a proper description of thermotropic nematics made of flexible molecules. Nevertheless, it is interesting to see that for S around , which appears reasonable for thermotropic systems, the anomalous order is found, which is in line with the experimental trend reported in [36], and the relative values of the three elastic constants are also comparable to the measured quantities.
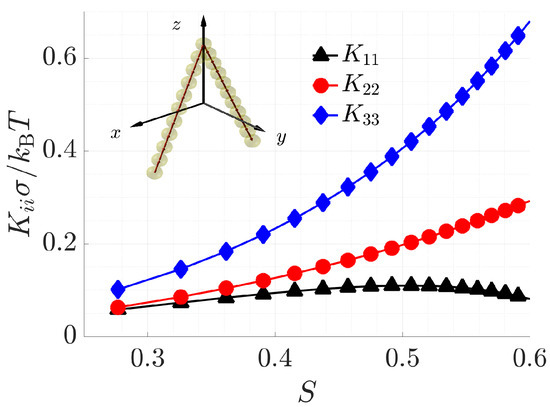
Figure 6.
Elastic constants calculated for acute angle V-shaped with a bend angle (see inset), as a function of the order parameter S.
3.2. Obtuse Angle Particles
Figure 7 shows order parameters and elastic constants for obtuse angle V-shaped particles made of 11 hard spheres, with bend angles in the range from to . The latter case is that of rod-like particles and is taken as a benchmark. In obtuse angle particles the reference system is defined with the x axis parallel to the twofold symmetry axis and y perpendicular to the plane containing the two arms. Thus, the order parameter S describes the orientational order for the direction parallel to the segment joining the terminal spheres, whereas D quantifies the different alignment with the director of the twofold symmetry axis and of the axis perpendicular to the particle plane. Compared with the acute angle systems examined in the previous section, obtuse angle particles have a behavior closer to the rod-like reference; indeed, they present generally higher values of the axial order parameter S, together with lower values of the biaxial order parameter D.
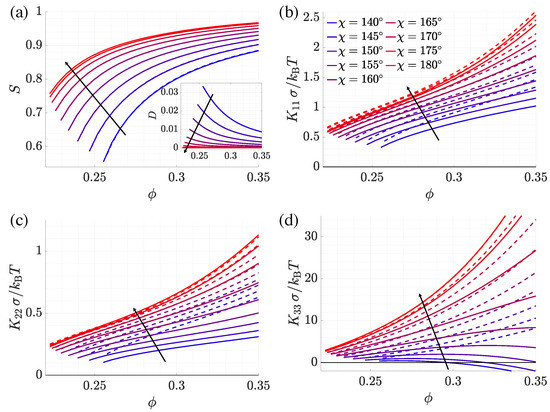
Figure 7.
(a) Order parameters S and D (inset), and (b) splay, (c) twist and (d) bend elastic constant, as a function of the volume fraction . Values obtained using the non-local form of the ODF, Equation (5) (solid lines), and the local uniaxial form, Equation (6) (dashed lines), for the nematic phase of obtuse angle V-shaped particles with different values of the bend angle.
Figure 7b–d shows the elastic constants, and, as for the case of acute angle particles, we also report the results obtained using the local ODF form, Equation (6). Of course, the curves coincide for the rod-like particle, i.e., . As the bend angle narrows, the isotropic-nematic transition shifts to higher density, and the calculated elastic constants exhibit a continuous decrease from the values for a straight rod. Such effects are also predicted by the local ODF model; they can, at least partly, be ascribed to the lowering of the particle aspect ratio as the bend angle narrows. With decreasing , the differences between the predictions of the local and the non-local ODF model also increase. This can be related to the increase in particle biaxiality, which is naturally accounted for by Equation (5). However, this is not sufficient for the bend elastic constant, where a distinctive behavior appears when the non-local form of the ODF is used: below a certain bend angle, it exhibits a non-monotonic density dependence, analogous to that reported in the previous section for the splay elastic constant of acute angle V-shaped particles. The unconventional bend elasticity of bent particles with an obtuse angle was already investigated using different models [26,27,29], and there is agreement on its origin being related to the emergence of polar order. Unlike the case of acute angle particles, examined in the previous subsection, here, the polar order is transversal, being related to the non-equivalence of particle orientations with the apex pointing either towards the center of the bend deformation or in the opposite direction. A suitable quantity to describe this is the order parameter , defined in Equation (14). For the linear particle (), the order parameter is equal to zero, but for particles of symmetry (), it is found to increase linearly with the wavenumber q of the bend deformation upon moving away from the uniform nematic state, . Figure 8 shows the slope of at , and we can see that it increases with the narrowing of the bend angle, which means an increasing polar response to bend deformations. For a given bend angle, the slope of takes a finite value at the isotropic-nematic transition, and it is subsequently an increasing function of density, i.e., of orientational order.
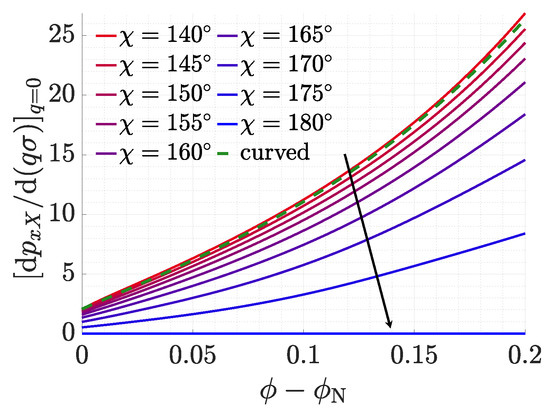
Figure 8.
Slope of the transversal polar order parameter induced by a bend deformation, , calculated at , as a function of the packing fraction difference , for acute angle V-shaped particles with different values of the bend angle. is the packing fraction in the nematic phase at the nematic-isotropic boundary. The dashed line shows the results for the curved particle shown in Figure 2c. Positive values mean that the apex of a V-shaped particle preferentially points to the opposite direction of the center of a bend deformation.
Before finishing this subsection, we will compare the elastic constants of the nematic phase of V-shaped particles with those for the curved particle shown in Figure 2c. This model was already investigated [28,37,55] and is used here to explore the role of some more subtle geometric parameters, rather than simply the shape polarity. A V-shaped particle with bend angle (slightly smaller than the value of defined in Figure 2c using a purely geometric criterion) is taken for this comparison, because it is found to be equivalent to the curved particle, as far as the splay and twist constants are concerned (see Figure 9). However, there are some differences between the bend elastic constants of the two types of particles: for both, exhibits a non-monotonic density dependence, but the range of positive values is significantly narrower for the curved particle. This can be related to a stronger tendency of nematics made of curved particles to acquire transverse polar order in the presence of a bend deformation, as described by the slope of at , reported in Figure 8. This comparison illustrates the high sensitivity of the bend elastic constant of slightly bent particles to morphological details. Interestingly, an analogous sensitivity was observed in the phase diagram: using theory and simulations, curved particles were found to form the twist-bend nematic phase [55], which is characterized by a heliconical deformation of the director field, whereas such a phase was not found for V-shaped particles [52,56]. Furthermore, experimentally, there are several examples of the twist-bend nematic phase for the so-called liquid crystal dimers, which are made up by two mesogens linked by a flexible chain and have on average a smoothly bent shape [24]. However, there are only very few examples of the twist-bend nematic phase in bent-core liquid crystals, which have a rigid core roughly comparable to a V-shaped particle [21].
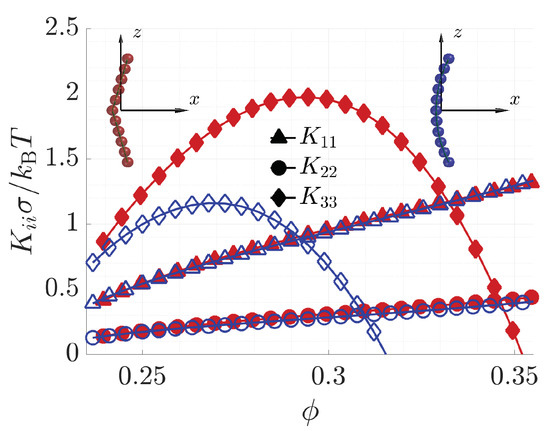
Figure 9.
Elastic constants as a function of the volume fraction , for a nematic phase formed by obtuse angle V-shaped particles with a bend angle , red full symbols, and by the curved particles as shown in Figure 2c, blue empty symbols. (For the latter system, the scale is different from the one in Figure 1a of [37], since in that case, the volume fraction was calculated as .)
4. Conclusions
We have used a recently developed approach to investigate the elastic properties of nematics made of rigid V-shaped particles. This is a minimal model, which allows us to probe different behaviors as a function of a single geometric parameter, the bend angle. Real liquid crystal molecules are characterized by a flexible structure; therefore, in general, it is not possible to uniquely evaluate the bend angle. Conformational changes can significantly modify the molecular geometry, and this has to be taken into account for accurate prediction of elastic properties. However, this is not the objective of our study, which is rather aimed at identifying general trends and correlations between molecular structure and macroscopic properties. Our analysis demonstrates that, by tuning the bend angle, the elastic behavior can be switched from bend dominated () for acute angles to splay dominated () for obtuse angles, with anomalously low values of the splay and bend elastic constant, respectively. Throughout the past decade, experimental examples of the latter behavior were reported in bent-core nematics and in the so-called liquid crystal dimers, and theory was crucial to relate the softening of the bend mode to the transversal shape polarity. Here, we have presented a systematic investigation of obtuse angle systems, and we have extended the study to acute angle particles, which are less investigated by far. We have identified analogous features for the two types of particles, with the difference that the latter, due to the presence of a longitudinal polar axis, affect the splay, rather than the bend mode. This change of behavior is in agreement with very recent findings for acute angle bent-core mesogens. We can relate the softening of Frank constants to the ability of a nematic system to acquire polar order, transversal or longitudinal, in the presence of a bend or splay deformation, respectively; this is a material property determined by the molecular structure and the thermodynamic state.
It is well known that liquid crystals have the ability to translate molecular chirality into a chiral deformation of the director field on a length scale that is larger by orders of magnitude, by a helical deformation of the director field. The effect of the molecular shape polarity on the splay and bend elastic constants, which we have illustrated here, can be seen as another example of this ability. In this case, the result cannot be uniformly splayed or bent phases, due to the incompatibility of these deformation modes with the Euclidean geometry of the 3D space [3]. However, the influence of the molecular shape polarity on the elastic anisotropy can have an impact on the mesoscale, e.g., through the control of the interaction between defects or embedded colloids and nanoparticles [57,58]. Interestingly, a change of behavior from splay to bend-dominated has been observed in active nematics as a consequence of changes of shape induced by activity [59].
A final comment regards microscopic theories of nematic elasticity. The results reported here show the inability of classical theories to capture the significant effects of the particle morphology on elastic constants. Their major fault is the neglect of changes in the orientational distribution function in the presence of deformations. Usually, this neglect is justified by the large size of director deformations on the molecular scale. However, our results show that the coupling between the symmetry of molecules and that of the director field can lead to a considerable relief of the energetic cost for elastic deformations.
Author Contributions
Conceptualization, D.R. and A.F.; writing—original draft preparation, D.R.; writing—review and editing, A.F.; supervision, A.F.; investigation and software, D.R. All authors have read and agreed to the published version of the manuscript.
Funding
D.R. gratefully acknowledges Fondazione CARIPARO for funding his PhD scholarship.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Oseen, C.W. The theory of liquid crystals. Trans. Faraday Soc. 1933, 29, 883–899. [Google Scholar] [CrossRef]
- Frank, F.C. I. Liquid crystals. On the theory of liquid crystals. Discuss. Faraday Soc. 1958, 25, 19–28. [Google Scholar] [CrossRef]
- Selinger, J.V. Director Deformations, Geometric Frustration, and Modulated Phases in Liquid Crystals. arXiv 2021, arXiv:2103.03803. [Google Scholar]
- Helfrich, W. Inherent Bounds to the Elasticity and Flexoelectricity of Liquid Crystals. Molec. Cryst. Liq. Cryst. 1971, 26, 1–5. [Google Scholar] [CrossRef]
- Meyer, R.B. Structural Problems in Liquid Crystal Physics. In Molecular Fluids (Les Houches Summer School in Theoretical Physics, 1973); R. Balian, G.W., Ed.; Gordon and Breach: New York, NY, USA, 1976; pp. 271–343. [Google Scholar]
- Gruler, H. Elastic properties of the nematic phase influenced by molecular properties. J. Chem. Phys. 1975, 61, 5408–5412. [Google Scholar] [CrossRef]
- Dozov, I. On the spontaneous symmetry breaking in the mesophases of achiral banana-shaped molecules. Europhys. Lett. 2001, 56, 247–253. [Google Scholar] [CrossRef]
- DiLisi, G.; Rosenblatt, C.; Griffin, A. Bend elastic modulus of a bent and a straight dimeric liquid crystal. J. Phys. II (France) 1992, 3, 1065–1071. [Google Scholar] [CrossRef][Green Version]
- Dodge, M.R.; Rosenblatt, C.; Petschek, R.G.; Neubert, M.E.; Walsh, M.E. Bend elasticity of mixtures of V-shaped molecules in ordinary nematogens. Phys. Rev. E 2000, 62, 5056–5063. [Google Scholar] [CrossRef]
- Kundu, B.; Pratibha, R.; Madhusudana, N.V. Anomalous temperature dependence of elastic constants in the nematic phase of binary mixtures made of rodlike and bent-core molecules. Phys. Rev. Lett. 2007, 99, 247802. [Google Scholar] [CrossRef]
- Sathyanarayana, P.; Mathew, M.; Li, Q.; Sastry, V.S.S.; Kundu, B.; Le, K.V.; Takezoe, H.; Dhara, S. Splay bend elasticity of a bent-core nematic liquid crystal. Phys. Rev. E 2010, 81, 050701(R). [Google Scholar] [CrossRef]
- Tadapatri, P.; Hiremath, U.S.; Yelamaggad, C.V.; Krishnamurthy, K.S. Permittivity, Conductivity, Elasticity, and Viscosity Measurements in the Nematic Phase of a Bent-Core Liquid Crystal. J. Phys. Chem. B 2010, 2010, 1745–1750. [Google Scholar] [CrossRef]
- Majumdar, M.; Salamon, P.; Jaakli, A.; Gleeson, J.T.; Sprunt, S. Elastic constants and orientational viscosities of a bent-core nematic liquid crystal. Phys. Rev. E 2011, 83, 031701. [Google Scholar] [CrossRef]
- Salter, P.S.; Tschierske, C.; Elston, S.J.; Raynes, E.P. Flexoelectric measurements of a bent-core nematic liquid crystal. Phys. Rev. E 2011, 84, 031708. [Google Scholar] [CrossRef]
- Adlem, K.; Copic, M.; Luckhurst, G.R.; Mertelj, A.; Parri, O.; Richardson, R.M.; Snow, B.D.; Timimi, B.A.; Tuffin, R.P.; Wilkes, D. Chemically induced twiat-bend nematic liquid crystals, liquid crystal dimers, and negative elastic constants. Phys. Rev. E 2013, 81, 022503. [Google Scholar] [CrossRef]
- Balachandran, R.; Panov, V.; Vij, J.; Kocot, A.; Tamba, M.; Kohlmeier, A.; Mehl, G. Elastic properties of bimesogenic liquid crystals. Liq. Cryst. 2013, 40, 681–688. [Google Scholar] [CrossRef]
- Babakhanova, G.; Parsouzi, Z.; Paladugu, S.; Wang, H.; Nastishin, Y.A.; Shiyanovskii, S.V.; Sprunt, S.; Lavrentovich, O.D. Elastic and viscous properties of the nematic dimer CB7CB. Phys. Rev. E 2017, 96, 062704. [Google Scholar] [CrossRef] [PubMed]
- Cestari, M.; Frezza, E.; Ferrarini, A.; Luckhurst, G.R. Crucial role of molecular curvature for the bend elastic and exoelectric properties of liquid crystals: Mesogenic dimers as a case study. J. Mater. Chem. 2011, 21, 12303–12308. [Google Scholar] [CrossRef]
- Borshch, V.; Kim, Y.K.; Xiang, J.; Gao, M.; Jakli, A.; Panov, V.P.; Vij, J.K.; Imrie, C.T.; Tamba, M.G.; Mehl, G.H.; et al. Nematic twist-bend phase with nanoscale modulation of molecular orientation. Nat. Commun. 2013, 4, 2635. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Porada, J.H.; Hooper, J.B.; Klittnick, A.; Shen, Y.; Tuchband, M.R.; Korblova, E.; Bedrov, D.; Walba, D.M.; Glaser, M.A.; et al. Chiral heliconical ground state of nanoscale pitch in a nematic liquid crystal of achiral molecular dimers. Proc. Natl. Acad. Sci. USA 2013, 113, 15931–15936. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Nakata, M.; Shao, R.; Tuchband, M.R.; Shuai, M.; Baumeister, U.; Weissflog, W.; Walba, D.M.; Glaser, M.A.; Maclennan, J.E.; et al. Twist-bend heliconical chiral nematic liquid crystal phase of an achiral rigid bent-core mesogen. Phys. Rev. E 2014, 89, 022506. [Google Scholar] [CrossRef] [PubMed]
- Meyer, C.; Blanc, C.; Luckhurst, G.R.; Davidson, P.; Dozov, I. Biaxiality-driven twist-bend to splay-bend nematic phase transition induced by an electric field. Sci. Adv. 2020, 6, eabb8212. [Google Scholar] [CrossRef]
- Fernández-Rico, C.; Chiappini, M.; Yanagishima, T.; de Sousa, H.; Aarts, D.G.A.L.; Dijkstra, M.; Dullens, R.P.A. Shaping colloidal bananas to reveal biaxial, splay-bend nematic, and smectic phases. Science 2020, 369, 950. [Google Scholar] [CrossRef]
- Jákli, A.; Lavrentovich, O.D.; Selinger, J.V. Physics of liquid crystals of bent-shaped molecules. Rev. Mod. Phys. 2018, 90, 045004. [Google Scholar] [CrossRef]
- Shamid, S.M.; Dhakal, S.; Selinger, J.V. Statistical mechanics of bend flexoelectricity and the twist-bend phase in bent-core liquid crystals. Phys. Rev. E 2013, 87, 052503. [Google Scholar] [CrossRef]
- Cestari, M.; Diez-Berart, S.; Dunmur, D.A.; Ferrarini, A.; de la Fuente, M.R.; Jackson, D.J.B.; Lopez, D.O.; Luckhurst, G.R.; Perez-Jubindo, M.A.; Richardson, R.M.; et al. Phase behavior and properties of the liquid-crystal dimer 1”,7”-bis(4-cyano- biphenyl-4’-yl) heptane: A twist-bend nematic liquid crystal. Phys. Rev. E 2011, 84, 031704. [Google Scholar] [CrossRef] [PubMed]
- Greco, C.; Marini, A.; Frezza, E.; Ferrarini, A. From the Molecular Structure to Spectroscopic and Material Properties: Computational Investigation of a Bent-Core Nematic Liquid Crystal. ChemPhysChem 2014, 15, 1336–1344. [Google Scholar] [CrossRef] [PubMed]
- De Gregorio, P.; Frezza, E.; Greco, C.; Ferrarini, A. Density functional theory of nematic elasticity: Softening from the polar order. Soft Matter 2016, 12, 5188–5198. [Google Scholar] [CrossRef]
- Osipov, M.; Pajak, G. Effect of polar intermolecular interactions on the elastic constants of bent-core nematics and the origin of the twist-bend phase. Eur. Phys. J. E 2016, 39, 45. [Google Scholar] [CrossRef] [PubMed]
- Kaur, S.; Liu, H.; Addis, J.; Greco, C.; Ferrarini, A.; Goertz, V.; Goodby, J.W.; Gleeson, H.F. The influence of structure on the elastic, optical and dielectric properties of nematic phases formed from bent-core molecules. J. Mater. Chem. C 2013, 1, 6667–66676. [Google Scholar] [CrossRef][Green Version]
- Kaur, S.; Tian, L.; Liu, H.; Greco, C.; Ferrarini, A.; Seltmann, J.; Lehmann, M.; Gleeson, H.F. The elastic and optical properties of a bent-core thiadiazole nematic liquid crystal: The role of the bend angle. J. Mater. Chem. C 2013, 1, 2416–2425. [Google Scholar] [CrossRef]
- Srigengan, S.; Nagaraj, M.; Ferrarini, A.; Mandle, R.; Cowling, S.J.; Osipov, M.A.; Pajak, G.; Goodby, J.W.; Gleeson, H.F. Anomalously low twist and bend elastic constants in an oxadiazole—based bent—Core nematic liquid crystal and its mixtures; contributions of spontaneous chirality and polarity. J. Mater. Chem. C 2018, 6, 980–988. [Google Scholar] [CrossRef]
- Dhakal, S.; Selinger, J.V. Statistical mechanics of splay flexoelectricity in nematic liquid crystals. Phys. Rev. E 2010, 81, 031704. [Google Scholar] [CrossRef]
- Somoza, A.M.; Tarazona, P. Density functional theory of the elastic constants of a nematic liquid crystal. Molec. Phys. 1991, 72, 911–926. [Google Scholar] [CrossRef]
- Kang, S.; Lee, E.W.; Li, T.; Liang, X.; Tokita, M.; Nakajima, K.; Watanabe, J. Two-Dimensional Skyrmion Lattice Formation in a Nematic Liquid Crystal Consisting of Highly Bent Banana Molecules. Angew. Chem. Int. Ed. 2016, 55, 11552–11556. [Google Scholar] [CrossRef]
- Li, B.X.; Nastishin, Y.A.; Gao, H.W.M.; Paladugu, S.; Li, R.; Fukuto, M.; Li, Q.; Shiyanovskii, S.V.; Lavrentovich, O.D. Liquid crystal phases with unusual structures and physical properties formed by acute-angle bent core molecules. Phys. Rev. Res. 2020, 2, 033371. [Google Scholar] [CrossRef]
- Revignas, D.; Ferrarini, A. Interplay of Particle Morphology and Director Distortions in Nematic Fluids. Phys. Rev. Lett. 2020, 125, 267802. [Google Scholar] [CrossRef] [PubMed]
- Revignas, D.; Ferrarini, A. Microscopic modelling of nematic elastic constants beyond Straley theory. J. Chem. Phys. 2021. submitted. [Google Scholar]
- Straley, J. Frank elastic constants of the hard-rod liquid crystal. Phys. Rev. A 1973, 8, 2181. [Google Scholar] [CrossRef]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Parsons, J.D. Nematic ordering in a system of rods. Phys. Rev. A 1979, 19, 1225–1230. [Google Scholar] [CrossRef]
- Lee, S.D. A numerical investigation of nematic ordering based on a simple hard-rod model. J. Chem. Phys. 1987, 87, 4972–4974. [Google Scholar] [CrossRef]
- Varga, S.; Szalai, I. Modified parsons-lee theory for fluids of linear fused hard sphere chains. Mol. Phys. 2000, 98, 693–698. [Google Scholar] [CrossRef]
- McQuarrie, D.A. Statistical Mechanics; Harper & Row: New York, NY, USA, 1976. [Google Scholar]
- Priest, R.G. Theory of the Frank Elastic Constants of Nematic Liquid Crystals. Phys. Rev. A 1973, 7, 720–729. [Google Scholar] [CrossRef]
- Gelbart, W.M.; Ben-Shaul, A. Molecular theory of curvature elasticity in nematic liquids. J. Chem. Phys. 1982, 77, 916–933. [Google Scholar] [CrossRef]
- Sanner, M.F.; Olson, A.J.; Spehner, J.C. Reduced surface: An efficient way to compute molecular surfaces. Biopolymers 1996, 38, 305–320. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder–Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- MATLAB. 9.2.0.538062 (R2017a); The MathWorks Inc.: Natick, MA, USA, 2017. [Google Scholar]
- Luckhurst, G.R.; Sluckin, T.J. Biaxial Nematic Liquid Crystals; John Wiley & Sons Ltd.: Chichester, UK, 2015. [Google Scholar]
- Chiappini, M.; Drwenski, T.; van Roij, R.; Dijkstra, M. Biaxial, Twist-bend, and Splay-bend Nematic Phases of Banana-shaped Particles Revealed by Lifting the “Smectic Blanket”. Phys. Rev. Lett. 2019, 123, 068001. [Google Scholar] [CrossRef] [PubMed]
- Luckhurst, G.R.; Zannoni, C.; Nordio, P.L.; Segre, U. A molecular field theory for uniaxial nematic liquid crystals formed by non-cylindrically symmetric molecules. Molec. Phys. 1975, 30, 1345–1358. [Google Scholar] [CrossRef]
- Ericksen, J.L. Inequalities in Liquid Crystal Theory. Phys. Fluids 1966, 9, 1205–1207. [Google Scholar] [CrossRef]
- Greco, C.; Ferrarini, A. Entropy-Driven Chiral Order in a System of Achiral Bent Particles. Phys. Rev. Lett. 2015, 115, 147801. [Google Scholar] [CrossRef]
- Lansac, Y.; Maiti, P.K.; Clark, N.A.; Glaser, M.A. Phase behavior of bent-core molecules. Phys. Rev. E 2003, 67, 011703. [Google Scholar] [CrossRef]
- Musevic, I. Liquid Crystal Colloids; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Smalyukh, I. Review: Knots and other new topological effects in liquid crystals and colloids. Rep. Prog. Phys. 2020, 83, 106601. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Zhang, R.; De Pablo, J.J.; Gardel, M.L. Tunable structure and dynamics of active liquid crystals. Sci. Adv. 2018, 4, eaat7779. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).