Measuring the Anisotropy in Interfacial Tension of Nematic Liquid Crystals
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Solution Preparation
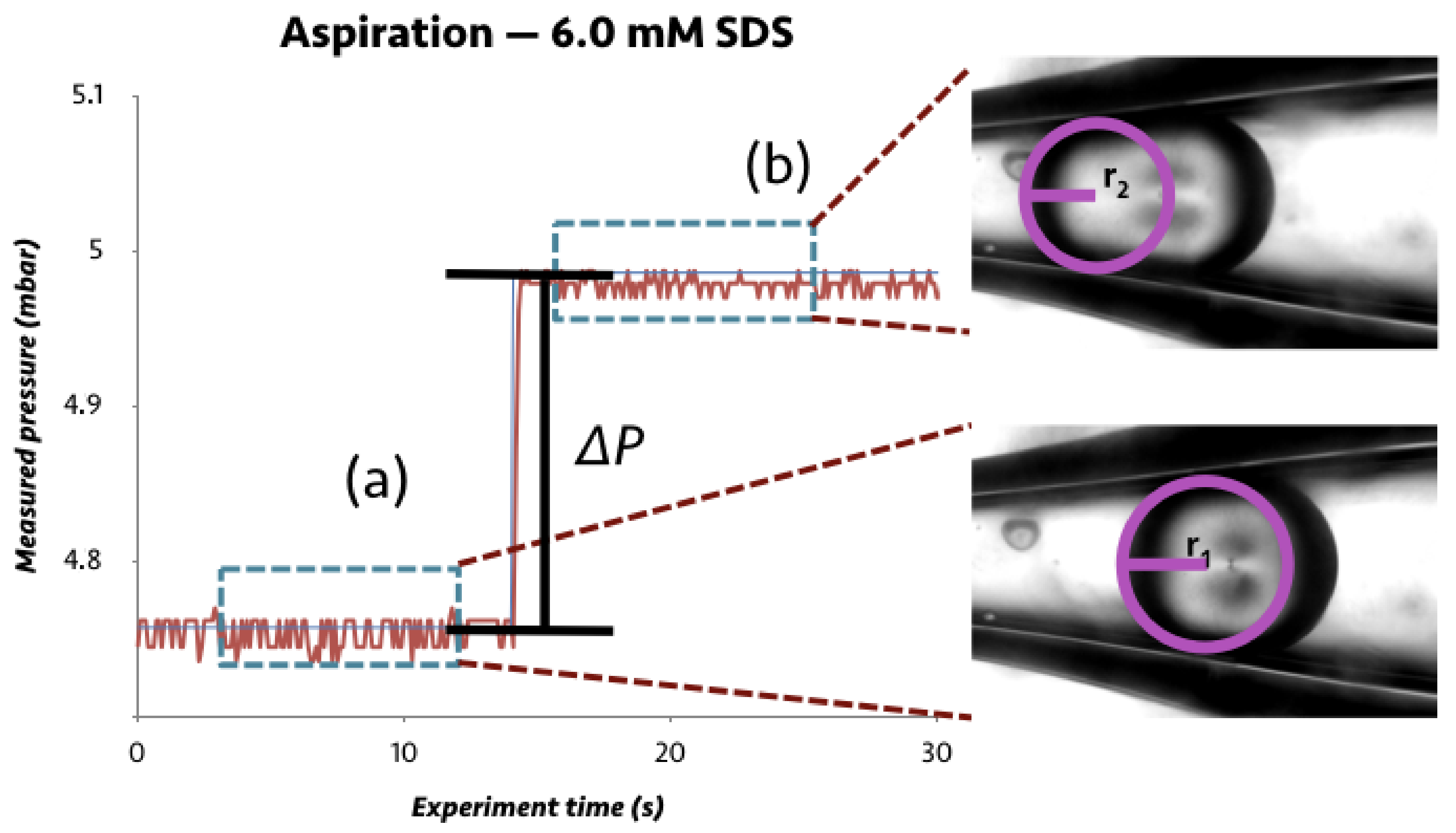
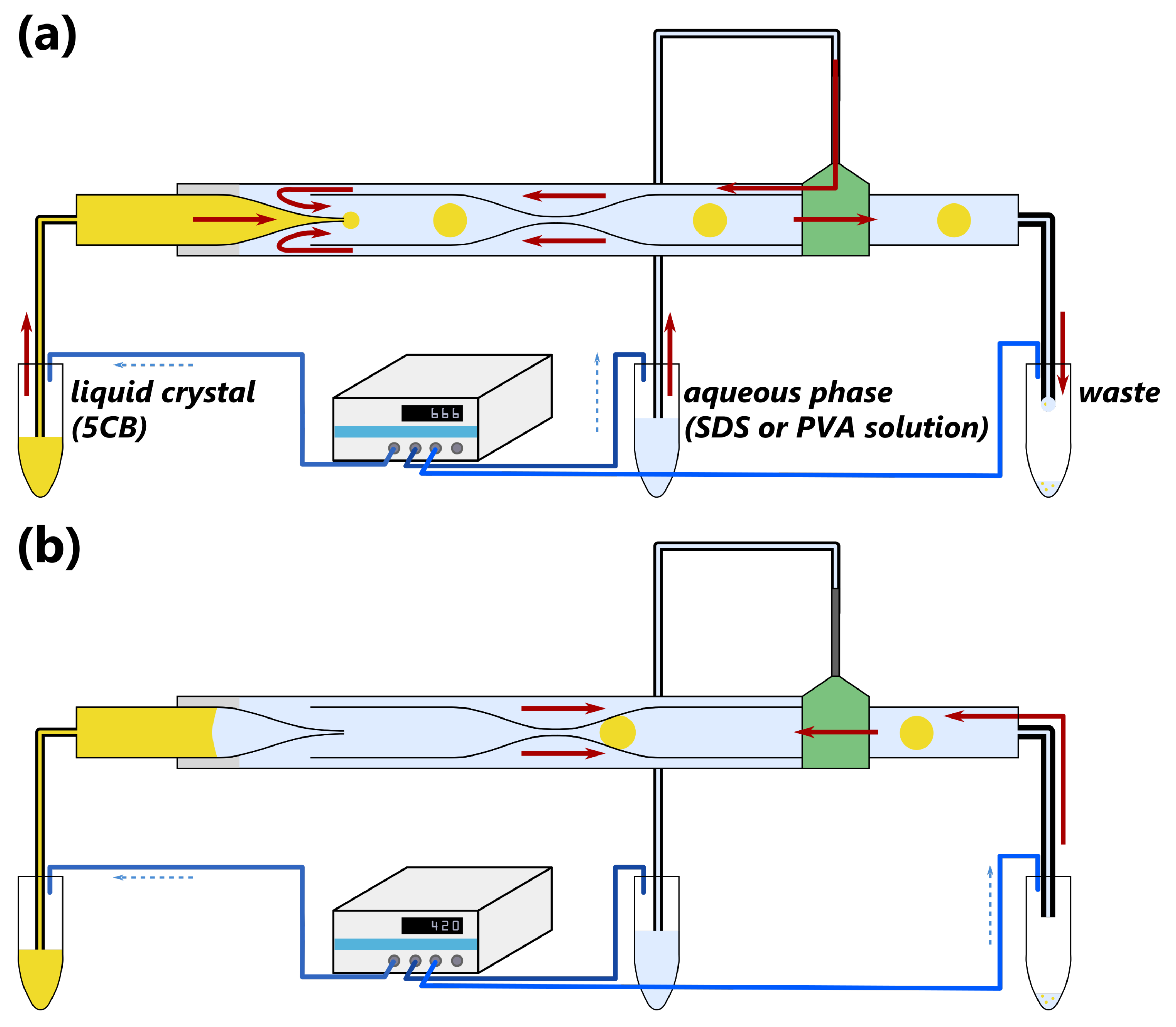
2.3. Microfluidic Droplet Aspiration
2.3.1. Device Assembly and Experimental Set-Up
2.3.2. Experimental Procedure
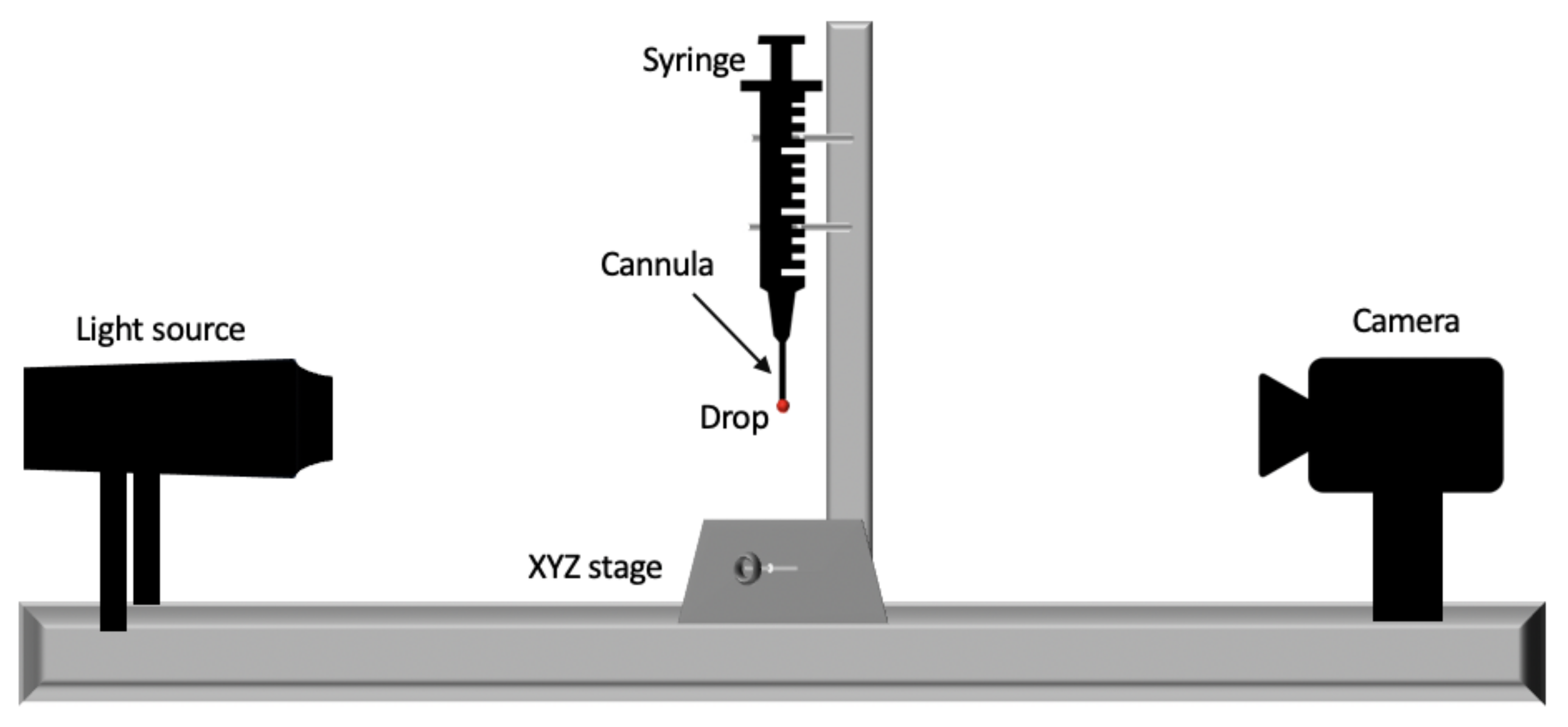
2.4. Pendant Drops
3. Results
3.1. Microfluidic Droplet Aspiration
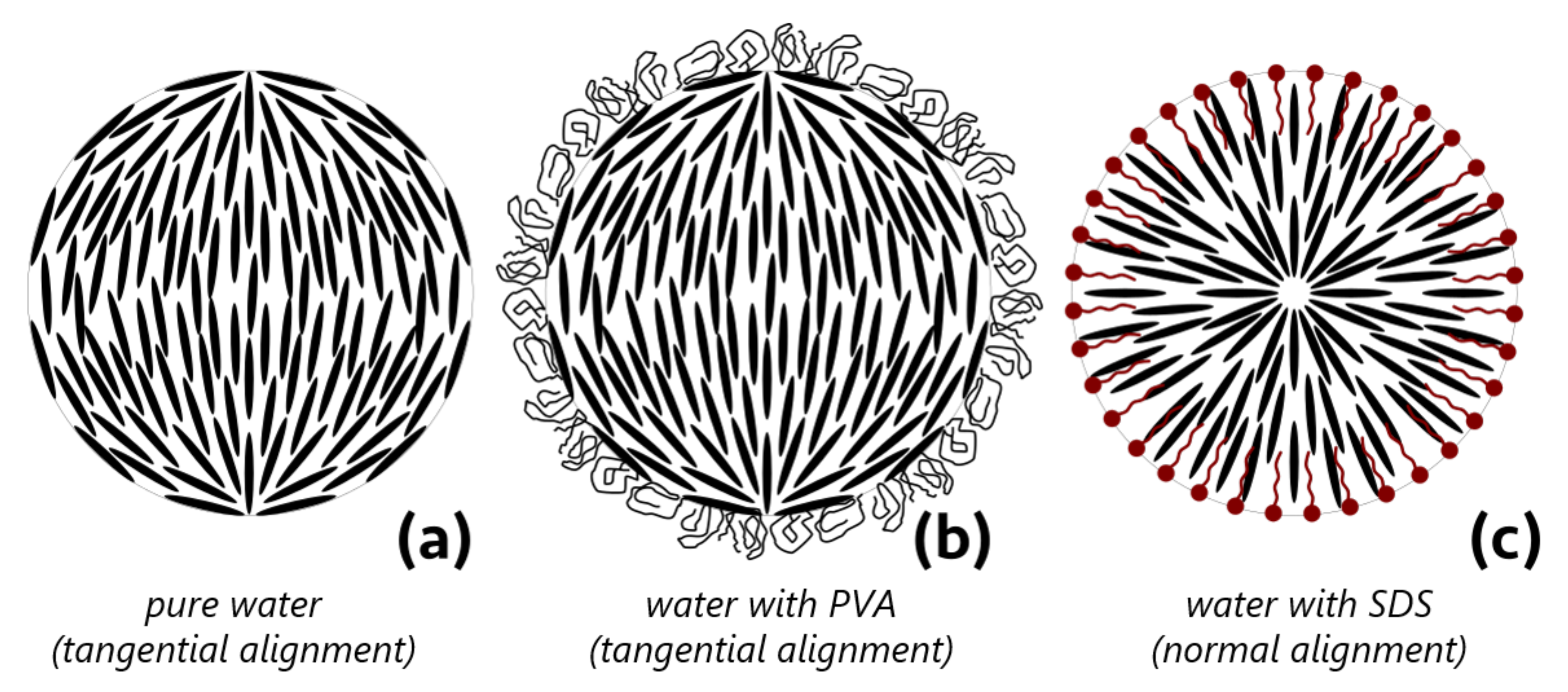
3.1.1. Normal Anchoring with Surfactant
3.1.2. Tangential Anchoring with and without Polymer Stabilizer
3.2. Pendant Drop Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 5CB | 4-cyano-4′-pentylbiphenyl |
| SDS | sodium dodecyl sulfate |
| PVA | poly(vinyl alcohol) |
| DMOAP | dimethyloctadecyl[3(trimethoxy-silyl)propyl]ammonium chloride |
| LC | liquid crystal |
References
- Gannon, M.G.; Faber, T.E. The surface tension of nematic liquid crystals. Philos. Mag. Phys. Condens. Matter Struct. Defects Mech. Prop. 1978, 37, 117–135. [Google Scholar] [CrossRef]
- Moll, C.J.; Meister, K.; Kirschner, J.; Bakker, H.J. Surface Structure of Solutions of Poly(vinyl alcohol) in Water. J. Phys. Chem. B 2018, 122, 10722–10727. [Google Scholar] [CrossRef]
- Lecomte du Noüy, P. An interfacial tensiometer for universal use. J. Gen. Physiol. 1925, 7, 625–632. [Google Scholar] [CrossRef]
- Kim, J.W.; Kim, H.; Lee, M.; Magda, J.J. Interfacial tension of a nematic liquid crystal/water interface with homeotropic surface alignment. Langmuir 2004, 20, 8110–8113. [Google Scholar] [CrossRef]
- Boyce, J.; Schürch, S.; Rotenberg, Y.; Neumann, A.W. The Measurement of Surface and Interfacial Tension by the Axisymmetric Drop Technique. Colloids Surf. 1984, 9, 307–317. [Google Scholar] [CrossRef]
- Del Río, O.I.; Neumann, A.W. Axisymmetric drop shape analysis: Computational methods for the measurement of interfacial properties from the shape and dimensions of pendant and sessile drops. J. Colloid Interface Sci. 1997, 196, 136–147. [Google Scholar] [CrossRef]
- Saad, S.M.I.; Policova, Z.; Neumann, A.W. Design and accuracy of pendant drop methods for surface tension measurement. Colloids Surf. A Physicochem. Eng. Asp. 2011, 384, 442–452. [Google Scholar] [CrossRef]
- Popov, P.; Honaker, L.W.; Mirheydari, M.; Mann, E.K.; Jákli, A. Chiral nematic liquid crystal microlenses. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Tintaru, M.; Moldovan, R.; Beica, T.; Frunza, S. Surface tension of some liquid crystals in the cyanobiphenyl series. Liq. Cryst. 2001, 28, 37–41. [Google Scholar] [CrossRef]
- Brosseau, Q.; Vrignon, J.; Baret, J.C. Microfluidic Dynamic Interfacial Tensiometry (μDIT). Soft Matter 2014, 10, 3066–3076. [Google Scholar] [CrossRef] [PubMed]
- Harth, K.; Stannarius, R. Measurement of the interface tension of smectic membranes in water. Phys. Chem. Chem. Phys. 2013, 15, 7204–7209. [Google Scholar] [CrossRef]
- Harth, K.; Shepherd, L.M.; Honaker, J.; Stannarius, R. Dynamic interface tension of a smectic liquid crystal in anionic surfactant solutions. Phys. Chem. Chem. Phys. 2015, 17, 26198–26206. [Google Scholar] [CrossRef][Green Version]
- Oweimreen, G.A.; Shihab, A.K.; Halhouli, K.; Sikander, S.F. Density Measurements in the Nematic and Isotropic Phases of 5CB and Dilute Solutions of Tetraethylmethane in 5CB. Mol. Cryst. Liq. Cryst. 1986, 138, 327–338. [Google Scholar] [CrossRef]
- Bao, P.; Paterson, D.A.; Harrison, P.L.; Miller, K.; Peyman, S.; Jones, J.C.; Sandoe, J.; Evans, S.D.; Bushby, R.J.; Gleeson, H.F. Lipid coated liquid crystal droplets for the on-chip detection of antimicrobial peptides. Lab Chip 2019, 19, 1082–1089. [Google Scholar] [CrossRef]
- Orlova, T.; Aßhoff, S.J.; Yamaguchi, T.; Katsonis, N.; Brasselet, E. Creation and manipulation of topological states in chiral nematic microspheres. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef]
- Peddireddy, K.; Čopar, S.; Le, K.V.; Muševič, I.; Bahr, C.; Jampani, V.S.R. Self-shaping liquid crystal droplets by balancing bulk elasticity and interfacial tension. Proc. Natl. Acad. Sci. USA 2021, 118, 1–7. [Google Scholar] [CrossRef]
- Sleczkowski, P.; Zhou, Y.; Iamsaard, S.; De Pablo, J.J.; Katsonis, N.; Lacaze, E. Light-activated helical inversion in cholesteric liquid crystal microdroplets. Proc. Natl. Acad. Sci. USA 2018, 115, 4334–4339. [Google Scholar] [CrossRef] [PubMed]
- Hochmuth, R.M. Micropipette aspiration of living cells. J. Biomech. 2000, 33, 15–22. [Google Scholar] [CrossRef]
- Lee, S.; Kim, D.H.; Needham, D. Equilibrium and Dynamic Interfacial Tension Measurements at Microscopic Interfaces Using a Micropipet Technique. 1. A New Method for Determination of Interfacial Tension. Langmuir 2001, 17, 5537–5543. [Google Scholar] [CrossRef]
- Lee, S.; Kim, D.H.; Needham, D. Equilibrium and Dynamic Interfacial Tension Measurements at Microscopic Interfaces Using a Micropipet Technique. 2. Dynamics of Phospholipid Monolayer Formation and Equilibrium Tensions at the Water-Air Interface. Langmuir 2001, 17, 5544–5550. [Google Scholar] [CrossRef]
- Honaker, L.W.; Lagerwall, J.P.F.; Jampani, V.S.R. Microfluidic Tensiometry Technique for the Characterization of the Interfacial Tension between Immiscible Liquids. Langmuir 2018, 34, 2403–2409. [Google Scholar] [CrossRef]
- Stephen, M.J.; Straley, J.P. Physics of liquid crystals. Rev. Mod. Phys. 1974, 46, 617–704. [Google Scholar] [CrossRef]
- Abe, K.; Usami, A.; Ishida, K.; Fukushima, Y.; Shigenari, T. Dielectric and fluorescence study on phase transitions in liquid crystal 5CB and 8CB. J. Korean Phys. Soc. 2005, 46, 220–223. [Google Scholar]
- Cui, M.; Kelly, J.R. Temperature Dependence of Visco-Elastic Properties of 5CB. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1999, 331, 49–57. [Google Scholar] [CrossRef]
- Jérôme, B. Surface effects and anchoring in liquid crystals. Rep. Prog. Phys. 1999, 54, 391–451. [Google Scholar] [CrossRef]
- Yokoyama, H. Surface Anchoring of Nematic Liquid Crystals. Mol. Cryst. Liq. Cryst. 1988, 165, 265–316. [Google Scholar] [CrossRef]
- Noh, J.; Reguengo de Sousa, K.; Lagerwall, J.P.F. Influence of interface stabilisers and surrounding aqueous phases on nematic liquid crystal shells. Soft Matter 2015, 12, 367–372. [Google Scholar] [CrossRef] [PubMed]
- Urbanski, M.; Reyes, C.G.; Noh, J.; Sharma, A.; Geng, Y.; Subba Rao Jampani, V.; Lagerwall, J.P.F. Liquid crystals in micron-scale droplets, shells and fibers. J. Phys. Condens. Matter 2017, 29, 1–53. [Google Scholar] [CrossRef] [PubMed]
- Squillace, O.; Fong, R.; Shepherd, O.; Hind, J.; Tellam, J.; Steinke, N.J.; Thompson, R.L. Influence of PVAc/PVA hydrolysis on additive surface activity. Polymers 2020, 12, 205. [Google Scholar] [CrossRef] [PubMed]
- Zhmud, B.V.; Tiberg, F.; Kizling, J. Dynamic surface tension in concentrated solutions of CnEm surfactants: A comparison between the theory and experiment. Langmuir 2000, 16, 2557–2565. [Google Scholar] [CrossRef]
- Barnaba, C.; García-Alvarado, M.A.; Tejero-Andrade, J.M.; Medina-Meza, I.G. Langmuir adsorption isotherms for different organic solutions of cholesterol. Rev. Mex. Ing. Qumica 2013, 12, 283–292. [Google Scholar]
- Bąk, A.; Podgórska, W. Interfacial and surface tensions of toluene/water and air/water systems with nonionic surfactants Tween 20 and Tween 80. Colloids Surf. Physicochem. Eng. Asp. 2016, 504, 414–425. [Google Scholar] [CrossRef]
- Schanen, A. Microfluidics for Measuring the Interfacial Tension of Liquid Crystals. Master’s Thesis, University of Luxembourg, Luxembourg, 2019. [Google Scholar]
- Honaker, L.W. Liquid Metals and Liquid Crystals Subject to Flow: From Fundamental Fluid Physics to Functional Fibers. Ph.D. Thesis, University of Luxembourg, Luxembourg, 2019. [Google Scholar]
- Proust, J.E.; Perez, E.; Ter-Minassian-Saraga, L. Films minces de cristal liquide nématique sur support liquide. Colloid Polym. Sci. Kolloid Z. Z. Polym. 1978, 256, 666–681. [Google Scholar] [CrossRef]
- Carboni, C.; Al-Ruzaiqi, S.; Al-Siyabi, A.; Al-Harthi, S.; George, A.; Sluckin, T. The behaviour of the interfacial surface tension of liquid-crystal materials in the vicinity of the nematic-isotropic phase transition. Mol. Cryst. Liq. Cryst. 2008, 494, 114–126. [Google Scholar] [CrossRef]
- Popov, N.; Smirnova, A.; Popov, P.; Usol’tseva, N. Determination of Concentrations of Surface-Active Materials in Aqueous Solutions at Different pH Values Using Liquid Crystals. Liq. Cryst. Their Appl. 2017, 17, 34–42. [Google Scholar] [CrossRef]
- Noh, J.H.; Wang, Y.; Liang, H.L.; Jampani, V.S.R.; Majumdar, A.; Lagerwall, J.P.F. Dynamic tuning of the director field in liquid crystal shells using block copolymers. Phys. Rev. Res. 2020, 2, 33160. [Google Scholar] [CrossRef]
- Popov, N.; Honaker, L.W.; Popova, M.; Usol’tseva, N.; Mann, E.K.; Jákli, A.; Popov, P.; Popov, P. Thermotropic Liquid Crystal-Assisted Chemical and Biological Sensors. Materials 2018, 11, 20. [Google Scholar] [CrossRef] [PubMed]


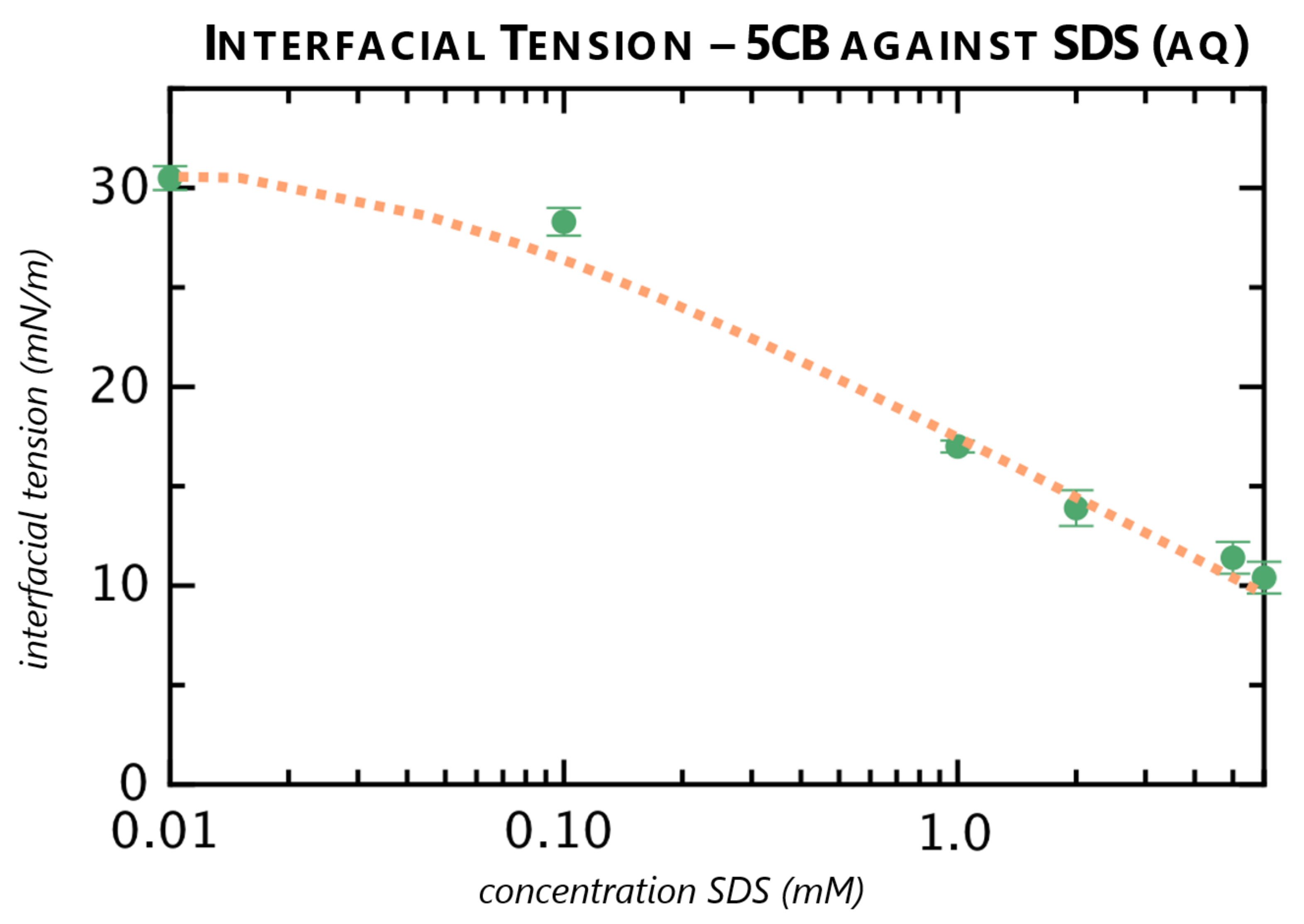
| Concentration SDS (aq), mM | Interfacial Tension, mN·m |
|---|---|
| 6.0 | 10.4 ± 0.8 |
| 5.0 | 11.4 ± 0.8 |
| 2.0 | 13.9 ± 0.9 |
| 1.0 | 17.0 ± 0.3 |
| 0.10 | 28.3 ± 0.7 |
| 0.010 | 30.5 ± 0.6 |
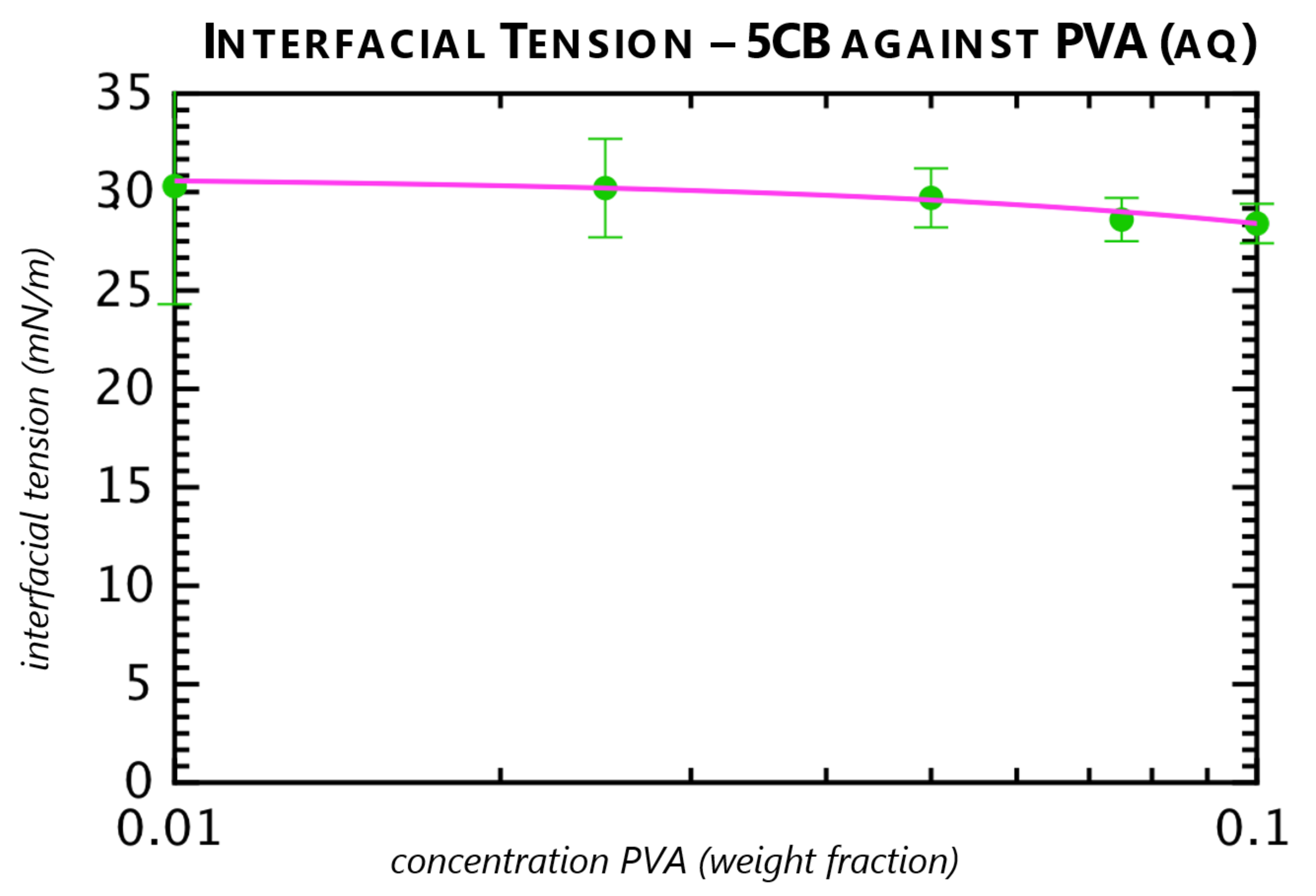
| Concentration PVA (aq), % w/w | Concentration Molar Equivalent | Interfacial Tension, mN·m |
|---|---|---|
| 1.0 | 0.44–0.78 mM | 30.3 ± 6.0 |
| 2.50 | 1.12–1.97 mM | 30.2 ± 2.5 |
| 5.0 | 2.29–4.05 mM | 29.7 ± 1.5 |
| 7.50 | 3.53–6.24 mM | 28.6 ± 1.1 |
| 10.0 | 4.83–8.55 mM | 28.4 ± 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Honaker, L.W.; Sharma, A.; Schanen, A.; Lagerwall, J.P.F. Measuring the Anisotropy in Interfacial Tension of Nematic Liquid Crystals. Crystals 2021, 11, 687. https://doi.org/10.3390/cryst11060687
Honaker LW, Sharma A, Schanen A, Lagerwall JPF. Measuring the Anisotropy in Interfacial Tension of Nematic Liquid Crystals. Crystals. 2021; 11(6):687. https://doi.org/10.3390/cryst11060687
Chicago/Turabian StyleHonaker, Lawrence W., Anjali Sharma, Andy Schanen, and Jan P. F. Lagerwall. 2021. "Measuring the Anisotropy in Interfacial Tension of Nematic Liquid Crystals" Crystals 11, no. 6: 687. https://doi.org/10.3390/cryst11060687
APA StyleHonaker, L. W., Sharma, A., Schanen, A., & Lagerwall, J. P. F. (2021). Measuring the Anisotropy in Interfacial Tension of Nematic Liquid Crystals. Crystals, 11(6), 687. https://doi.org/10.3390/cryst11060687






