Hugoniot States and Mie–Grüneisen Equation of State of Iron Estimated Using Molecular Dynamics
Abstract
:1. Introduction
2. Methodology
2.1. Hugoniot Pressure (PH) and Internal Energy (EH)
2.2. Cold Pressure (Pc) and Cold Energy (Ec)
2.3. Grüneisen Coefficient γ
2.4. Melting Temperature (Tm)
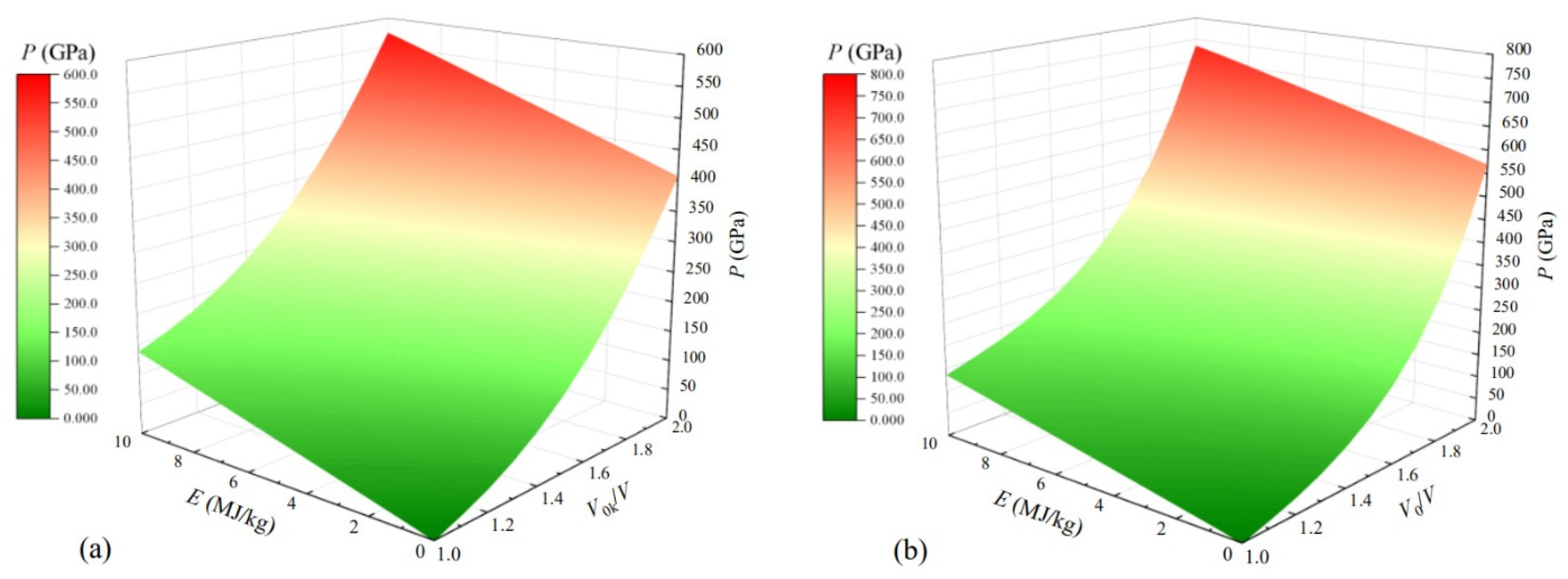
2.5. Mie–Grüneisen Equation of State
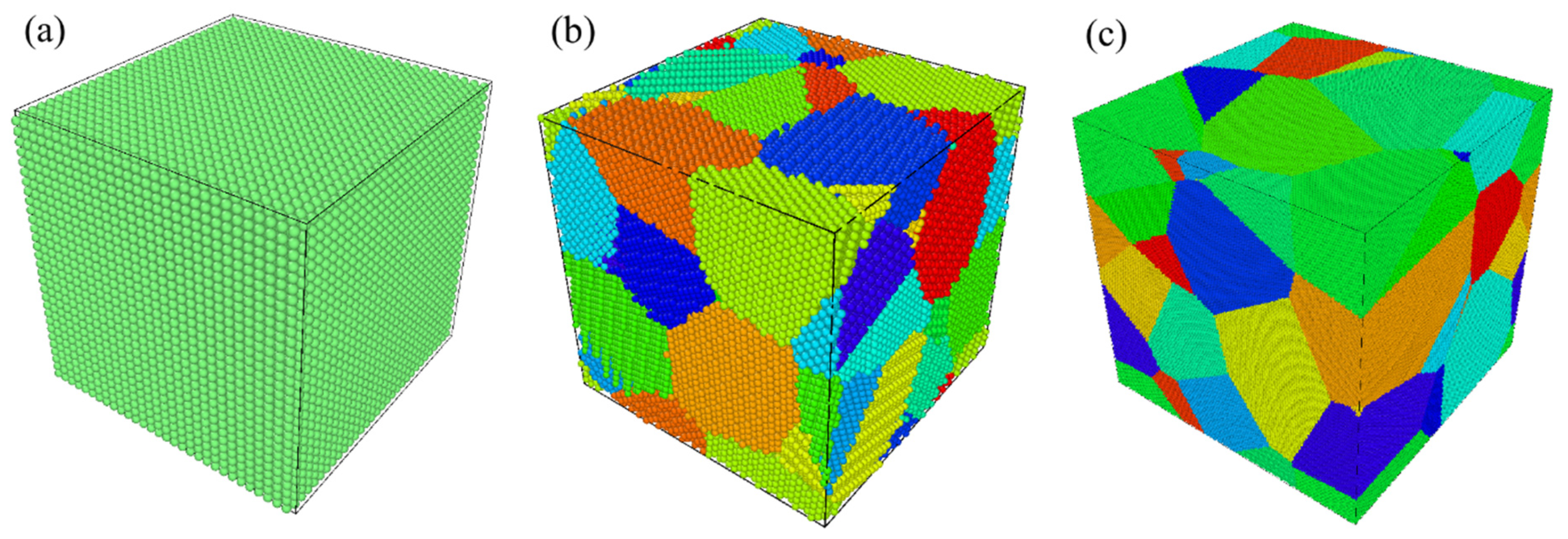
3. MD Simulation
4. Results and Discussion
4.1. Shock Hugoniot Pressure and Internal Energy
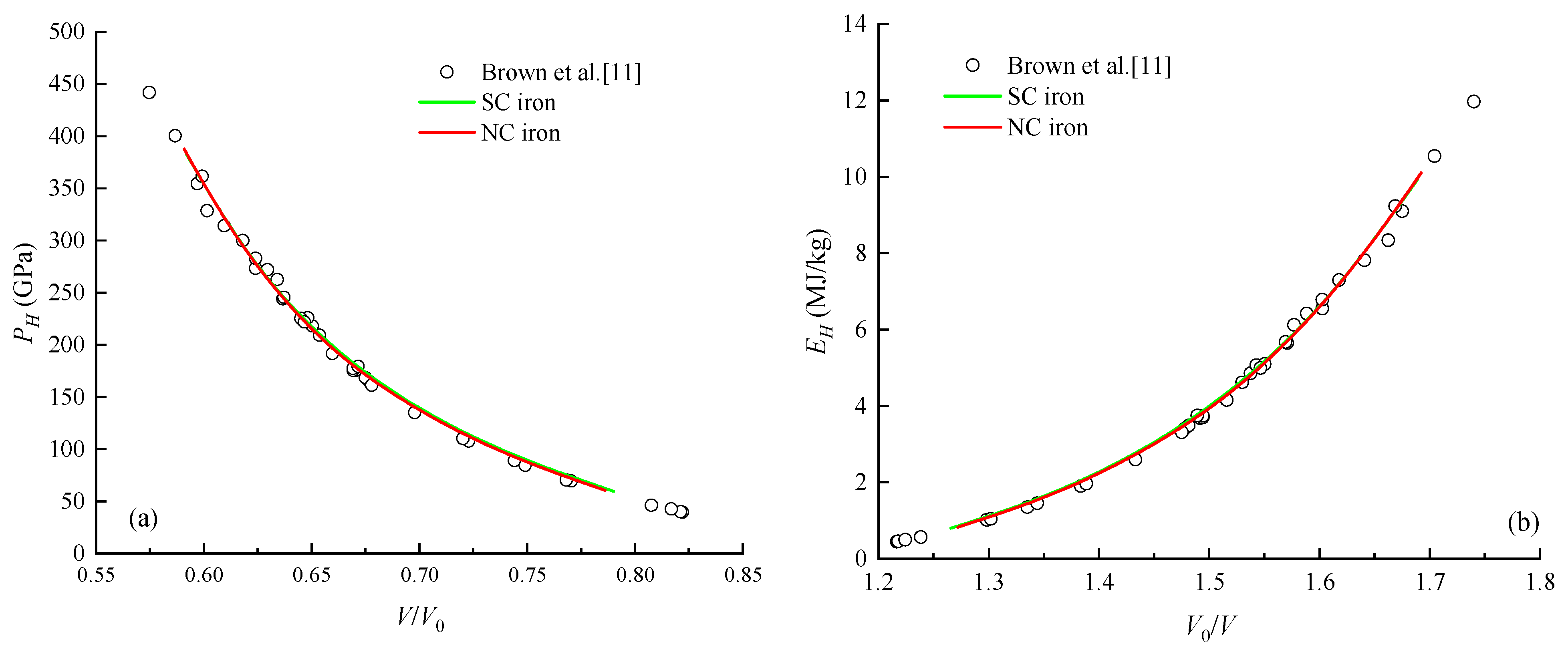
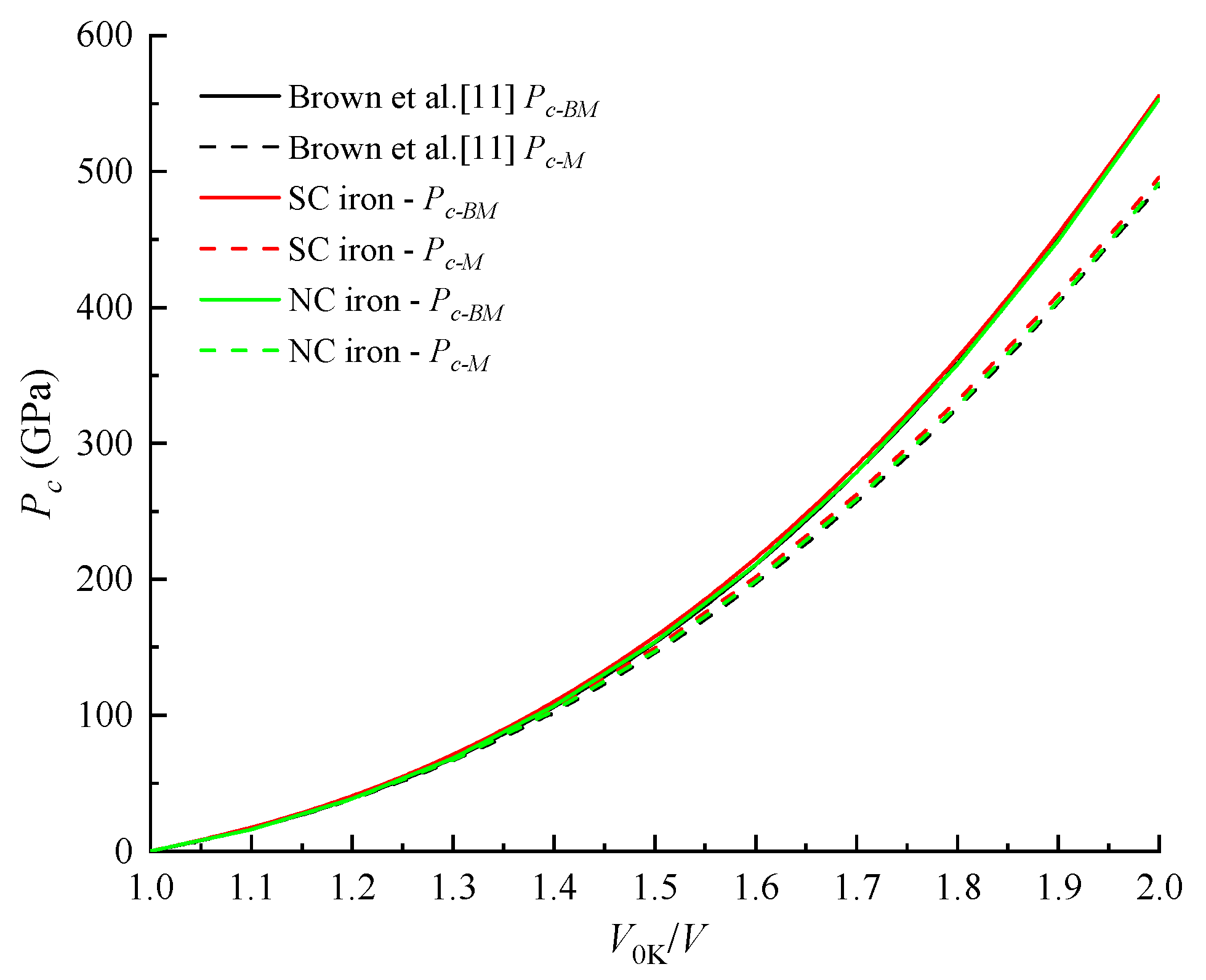
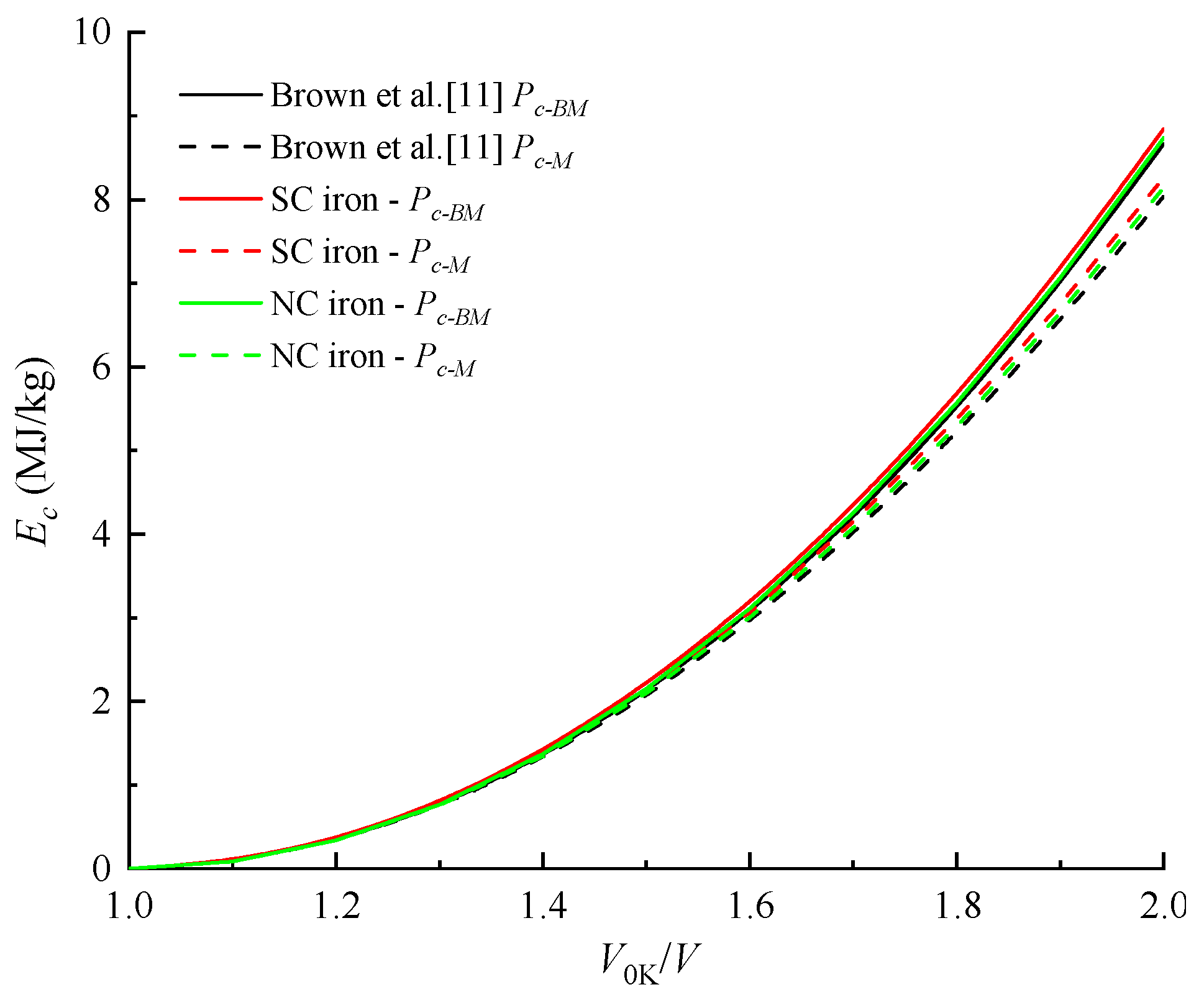
4.2. Cold Pressure and Cold Energy
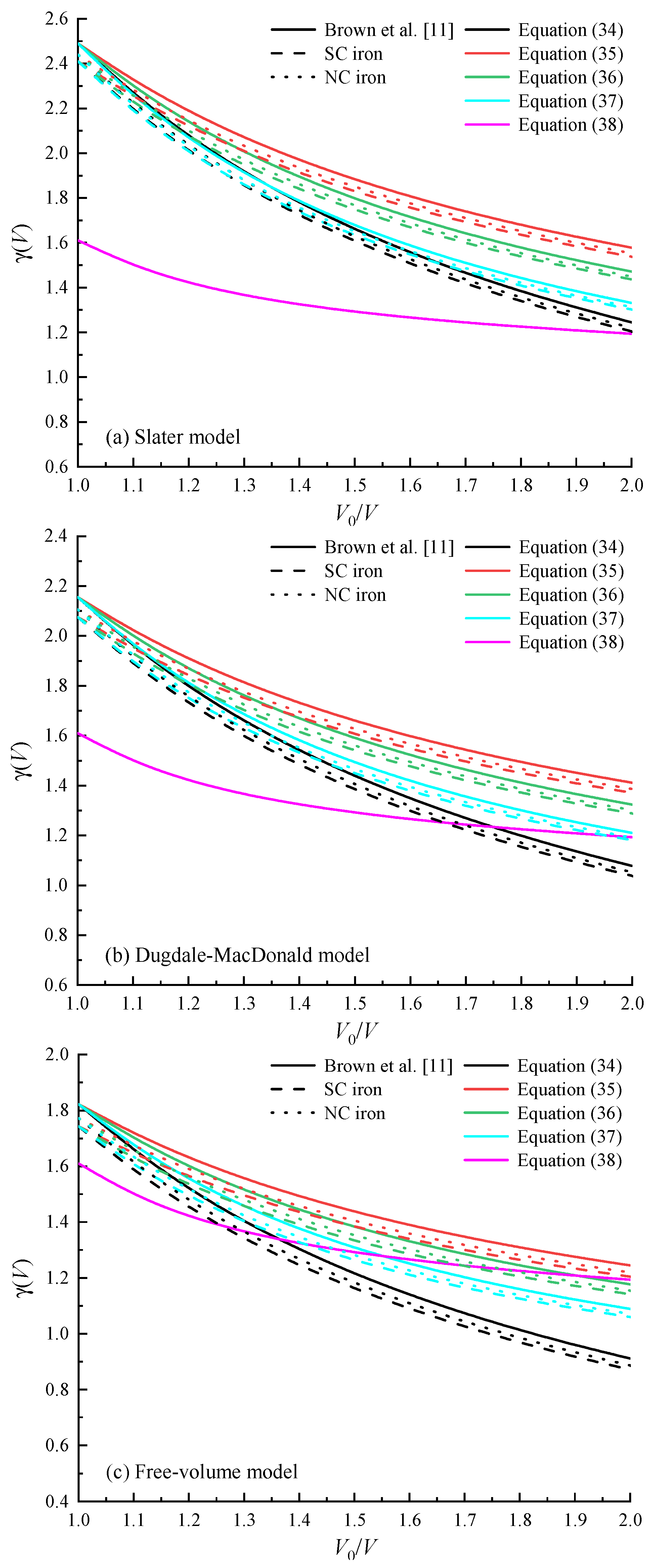
4.3. Grüneisen Coefficient
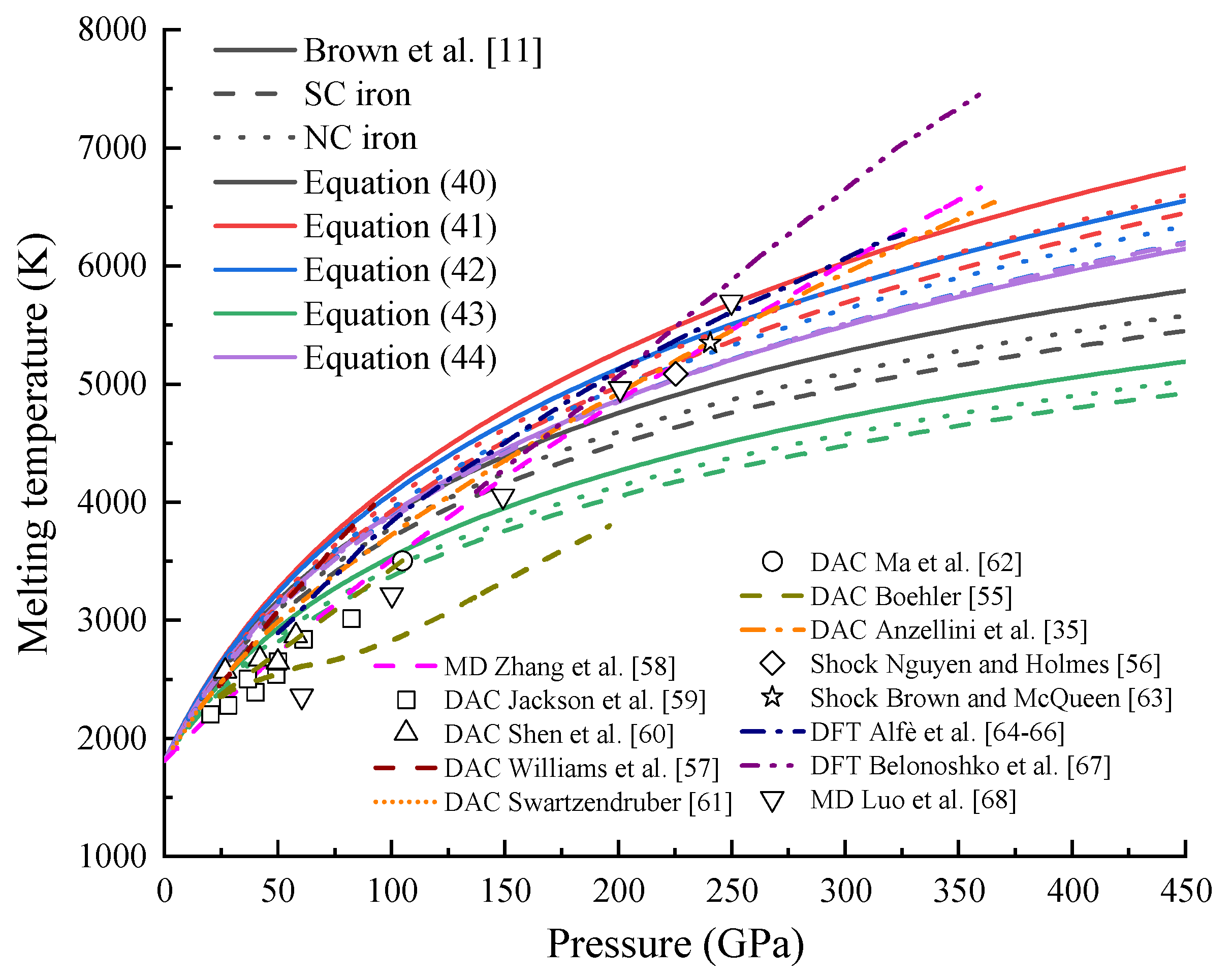
4.4. Melting Temperature
4.5. Mie–Grüneisen Equation of State
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Batani, D.; Morelli, A.; Tomasini, M.; Benuzzi-Mounaix, A.; Philippe, F.; Koenig, M.; Marchet, B.; Masclet, I.; Rabec, M.; Reverdin, C.; et al. Equation of state data for iron at pressures beyond 10 Mbar. Phys. Rev. Lett. 2002, 88, 235502. [Google Scholar] [CrossRef]
- Hai-Jun, H.; Fu-Qian, J.; Ling-Cang, C.; Yan, B. Grüneisen Parameter along Hugoniot and Melting Temperature of ε-Iron: A Result from Thermodynamic Calculations. Chin. Phys. Lett. 2005, 22, 836. [Google Scholar] [CrossRef]
- Dorogokupets, P.I.; Dymshits, A.M.; Litasov, K.D.; Sokolova, T.S. Thermodynamics and Equations of State of Iron to 350 GPa and 6000 K. Sci. Rep. 2017, 7, 41863. [Google Scholar] [CrossRef] [Green Version]
- Joshi, R.H.; Bhatt, N.K.; Thakore, B.Y.; Vyas, P.R.; Jani, A.R. Grüneisen parameter and equations of states for copper–High pressure study. Comput. Condens. Matter 2018, 15, 79–84. [Google Scholar] [CrossRef]
- Yang, X.; Zeng, X.; Pu, C.; Chen, W.; Chen, H.; Wang, F. Molecular dynamics modeling of the Hugoniot states of aluminum. AIP Adv. 2018, 8, 105212. [Google Scholar] [CrossRef] [Green Version]
- Shao, J.L.; He, A.M.; Wang, P. Atomistic simulations on the dynamic properties of shock and release melting in single crystal Al. Comput. Mater. Sci. 2018, 151, 240–245. [Google Scholar] [CrossRef]
- Nagayama, K. Extended Rice-Walsh equation of state for metals based on shock Hugoniot data for porous samples. J. Appl. Phys. 2017, 121, 175902. [Google Scholar] [CrossRef]
- Barker, L.M. Alpha-phase Hugoniot of iron. J. Appl. Phys. 1975, 46, 2544–2547. [Google Scholar] [CrossRef]
- Thomas, S.A.; Hawkins, M.C.; Matthes, M.K.; Gray, G.T., III; Hixson, R.S. Dynamic strength properties and alpha-phase shock Hugoniot of iron and steel. J. Appl. Phys. 2018, 123, 175902. [Google Scholar] [CrossRef] [Green Version]
- Kadau, K.; Germann, T.C.; Lomdahl, P.S.; Holian, B.L. Microscopic view of structural phase transitions induced by shock waves. Science 2002, 296, 1681–1684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, J.M.; Fritz, J.N.; Hixson, R.S. Hugoniot data for iron. J. Appl. Phys. 2000, 88, 5496–5498. [Google Scholar] [CrossRef]
- Zaretsky, E.B. Shock response of iron between 143 and 1275 K. J. Appl. Phys. 2009, 106, 023510. [Google Scholar] [CrossRef]
- Liu, X.; Mashimo, T.; Kawai, N.; Sano, T.; Zhou, X. Isotropic phase transition of single-crystal iron (Fe) under shock compression. J. Appl. Phys. 2018, 124, 215101. [Google Scholar] [CrossRef]
- Sjostrom, T.; Crockett, S. Quantum molecular dynamics of warm dense iron and a five-phase equation of state. Phys. Rev. E 2018, 97, 053209. [Google Scholar] [CrossRef] [Green Version]
- Kadau, K.; Germann, T.C.; Lomdahl, P.S.; Holian, B.L. Atomistic simulations of shock-induced transformations and their orientation dependence in bcc Fe single crystals. Phys. Rev. B 2005, 72, 064120. [Google Scholar] [CrossRef]
- Kadau, K.; Germann, T.C.; Lomdahl, P.S.; Albers, R.C.; Wark, J.S.; Higginbotham, A.; Holian, B.L. Shock waves in polycrystalline iron. Phys. Rev. Lett. 2007, 98, 135701. [Google Scholar] [CrossRef] [Green Version]
- Belkheeva, R.K. Equation of state for a highly porous material. High Temp. 2015, 53, 348–357. [Google Scholar] [CrossRef]
- Khishchenko, K.V. Equation of state of sodium for modeling of shock-wave processes at high pressures. Math. Montisnigri 2017, 40, 140–147. [Google Scholar]
- Maevskii, K.K.; Kinelovskii, S.A. Numerical simulation of thermodynamic parameters of high-porosity copper. Tech. Phys. 2019, 64, 1090–1095. [Google Scholar] [CrossRef]
- Hallajisany, M.; Zamani, J.; Albelda Vitoria, J. Numerical and theoretical determination of various materials Hugoniot relations based on the equation of state in high-temperature shock loading. High Press. Res. 2019, 39, 666–690. [Google Scholar] [CrossRef]
- Maevskii, K.K.; Kinelovskii, S.A. Modeling of High-Porosity Copper-Based Mixtures under Shock Loading. J. Appl. Mech. Tech. Phys. 2019, 60, 612–619. [Google Scholar] [CrossRef]
- Khishchenko, K.V. Equation of state for niobium at high pressures. Math. Montisnigri 2020, 47, 119–123. [Google Scholar] [CrossRef]
- Gilev, S.D. Low-parametric equation of state of aluminum. High Temp. 2020, 58, 166–172. [Google Scholar] [CrossRef]
- Heuzé, O. General form of the Mie–Grüneisen equation of state. C. R. Mec. 2012, 340, 679–687. [Google Scholar] [CrossRef]
- Zhang, X.F.; Qiao, L.; Shi, A.S.; Zhang, J.; Guan, Z.W. A cold energy mixture theory for the equation of state in solid and porous metal mixtures. J. Appl. Phys. 2011, 110, 013506. [Google Scholar] [CrossRef]
- Patel, N.N.; Sunder, M. High pressure melting curve of osmium up to 35 GPa. J. Appl. Phys. 2019, 125, 055902. [Google Scholar] [CrossRef]
- Slater, J.C. Introduction to Chemical Physics; Chapter XIII; McGraw-Hill: New York, NY, USA, 1939. [Google Scholar]
- Dugdale, J.S.; MacDonald, D.K.C. The thermal expansion of solids. Phys. Rev. 1953, 89, 832. [Google Scholar] [CrossRef]
- Vashchenko, V.Y.; Zubarev, V.N. Concerning the Grüneisen constant. Fiz. Tverd. Tela 1963, 5, 886–890. [Google Scholar]
- Al’tshuler, L.V. Use of shock waves in high-pressure physics. Phys. Uspekhi 1965, 8, 52–91. [Google Scholar] [CrossRef]
- Cui, G.; Yu, R. Volume and pressure dependence of Grüneisen parameter γ for solids at high temperatures. Phys. B Condens. Matter 2007, 390, 220–224. [Google Scholar] [CrossRef]
- Sha, X.; Cohen, R.E. Lattice dynamics and thermodynamics of bcc iron under pressure: First-principles linear response study. Phys. Rev. B 2006, 73, 104303. [Google Scholar] [CrossRef] [Green Version]
- Xi-Jun, L.; Xian-Ming, Z.; Fan-Hou, W.; Fu-Qian, J. Restudy of Grüneisen Parameter of Iron in the Pressure Range of 90–160 GPa. Chin. Phys. Lett. 2001, 18, 85. [Google Scholar] [CrossRef]
- Errandonea, D. High-pressure melting curves of the transition metals Cu, Ni, Pd, and Pt. Phys. Rev. B 2013, 87, 054108. [Google Scholar] [CrossRef]
- Anzellini, S.; Dewaele, A.; Mezouar, M.; Loubeyre, P.; Morard, G. Melting of iron at Earth’s inner core boundary based on fast X-ray diffraction. Science 2013, 340, 464–466. [Google Scholar] [CrossRef]
- Bouchet, J.; Mazevet, S.; Morard, G.; Guyot, F.; Musella, R. Ab initio equation of state of iron up to 1500 GPa. Phys. Rev. B 2013, 87, 094102. [Google Scholar] [CrossRef]
- Barton, M.A.; Stacey, F.D. The Grüneisen parameter at high pressure: A molecular dynamical study. Phys. Earth Planet. Inter. 1985, 39, 167–177. [Google Scholar] [CrossRef]
- Maillet, J.B.; Mareschal, M.; Soulard, L.; Ravelo, R.; Lomdahl, P.S.; Germann, T.C.; Holian, B.L. Uniaxial Hugoniostat: A method for atomistic simulations of shocked materials. Phys. Rev. E 2000, 63, 016121. [Google Scholar] [CrossRef]
- Vočadlo, L.; Dobson, D.P.; Wood, I.G. An ab initio study of nickel substitution into iron. Earth Planet. Sci. Lett. 2006, 248, 147–152. [Google Scholar] [CrossRef]
- Reed, E.J.; Fried, L.E.; Joannopoulos, J.D. A method for tractable dynamical studies of single and double shock compression. Phys. Rev. Lett. 2003, 90, 235503. [Google Scholar] [CrossRef] [Green Version]
- Wen, P.; Demaske, B.; Spearot, D.E.; Phillpot, S.R.; Tao, G. Effect of the initial temperature on the shock response of Cu50Zr50 bulk metallic glass by molecular dynamics simulation. J. Appl. Phys. 2021, 129, 165103. [Google Scholar] [CrossRef]
- Dewapriya, M.A.N.; Miller, R.E. Energy absorption mechanisms of nanoscopic multilayer structures under ballistic impact loading. Comput. Mater. Sci. 2021, 195, 110504. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W.; Chen, S.; Zhou, G.; Zhang, T. Shock Hugoniot and Mie-Grüneisen EOS of TiAl alloy: A molecular dynamics approach. Comput. Mater. Sci. 2020, 174, 109495. [Google Scholar] [CrossRef]
- Born, M.; Mayer, J.E. Zur Gittertheorie der Ionenkristalle. Z. Phys. 1932, 75, 1–18. [Google Scholar] [CrossRef]
- Morse, P.M. Diatomic molecules according to the wave mechanics. II. Vibrational levels. Phys. Rev. 1929, 34, 57. [Google Scholar] [CrossRef]
- Eliezer, S.; Ghatak, A.; Hora, H. Fundamentals of Equations of State; World Scientific: Singapore, 2002; pp. 197–207. [Google Scholar]
- Segletes, S.B.; Walters, W.P. On theories of the Grüneisen parameter. J. Phys. Chem. Solids 1998, 59, 425–433. [Google Scholar] [CrossRef]
- Jacobs, M.H.G.; Schmid-Fetzer, R. Thermodynamic properties and equation of state of fcc aluminum and bcc iron, derived from a lattice vibrational method. Phys. Chem. Miner. 2010, 37, 721–739. [Google Scholar] [CrossRef]
- Burakovsky, L.; Preston, D.L. An analytic model of the Grüneisen parameter all densities. J. Phys. Chem. Solids 2004, 65, 1581–1587. [Google Scholar] [CrossRef] [Green Version]
- Ross, M. Generalized Lindemann melting law. Phys. Rev. 1969, 184, 233. [Google Scholar] [CrossRef]
- Haynes, W.M. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Prieto, F.E.; Renero, C. Equation for the Shock Adiabat. J. Appl. Phys. 1970, 41, 3876–3883. [Google Scholar] [CrossRef]
- Boehler, R. Temperatures in the Earth’s core from melting-point measurements of iron at high static pressures. Nature 1993, 363, 534–536. [Google Scholar] [CrossRef]
- Nguyen, J.H.; Holmes, N.C. Melting of iron at the physical conditions of the Earth’s core. Nature 2004, 427, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Williams, Q.; Jeanloz, R.; Bass, J.; Svendsen, B.; Ahrens, T.J. The melting curve of iron to 250 gigapascals: A constraint on the temperature at Earth’s center. Science 1987, 236, 181–182. [Google Scholar] [CrossRef]
- Zhang, W.J.; Liu, Z.Y.; Liu, Z.L.; Cai, L.C. Melting curves and entropy of melting of iron under Earth’s core condi-tions. Phys. Earth Planet. Inter. 2015, 244, 69–77. [Google Scholar] [CrossRef]
- Jackson, J.M.; Sturhahn, W.; Lerche, M.; Zhao, J.; Toellner, T.S.; Alp, E.E.; Sinogeikin, S.V.; Bass, J.D.; Murphy, C.A.; Wicks, J.K. Melting of compressed iron by monitoring atomic dynamics. Earth Planet. Sci. Lett. 2013, 362, 143–150. [Google Scholar] [CrossRef]
- Shen, G.; Prakapenka, V.B.; Rivers, M.L.; Sutton, S.R. Structure of liquid iron at pressures up to 58 GPa. Phys. Rev. Lett. 2004, 92, 185701. [Google Scholar] [CrossRef]
- Swartzendruber, L.J. The Fe (Iron) system. Bull. Alloy Phase Diagr. 1982, 3, 161–165. [Google Scholar] [CrossRef]
- Ma, Y.; Somayazulu, M.; Shen, G.; Mao, H.K.; Shu, J.; Hemley, R.J. In situ X-ray diffraction studies of iron to Earth-core conditions. Phys. Earth Planet. Inter. 2004, 143–144, 455–467. [Google Scholar] [CrossRef]
- Brown, J.M.; McQueen, R.G. Phase transitions, Grüneisen parameter, and elasticity for shocked iron between 77 GPa and 400 GPa. J. Geophys. Res. 1986, 91, 7485–7494. [Google Scholar] [CrossRef]
- Alfè, D. Temperature of the inner-core boundary of the Earth: Melting of iron at high pressure from first-principles coexistence simulations. Phys. Rev. B 2009, 79, 060101. [Google Scholar] [CrossRef] [Green Version]
- Alfè, D.; Cazorla, C.; Gillan, M.J. The kinetics of homogeneous melting beyond the limit of superheating. J. Chem. Phys. 2011, 135, 024102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alfè, D.; Price, G.; Gillan, M. Iron under Earth’s core conditions: Liquid-state thermodynamics and high-pressure melting curve from ab initio calculations. Phys. Rev. B 2002, 65, 165118. [Google Scholar] [CrossRef] [Green Version]
- Belonoshko, A.B.; Ahuja, R.; Johansson, B. Quasi–ab initio molecular dynamic study of Fe melting. Phys. Rev. Lett. 2000, 84, 3638–3641. [Google Scholar] [CrossRef]
- Luo, F.; Cheng, Y.; Chen, X.R.; Cai, L.C.; Jing, F.Q. The melting curves and entropy of iron under high pressure. J. Chem. Eng. Data 2011, 56, 2063–2070. [Google Scholar] [CrossRef]
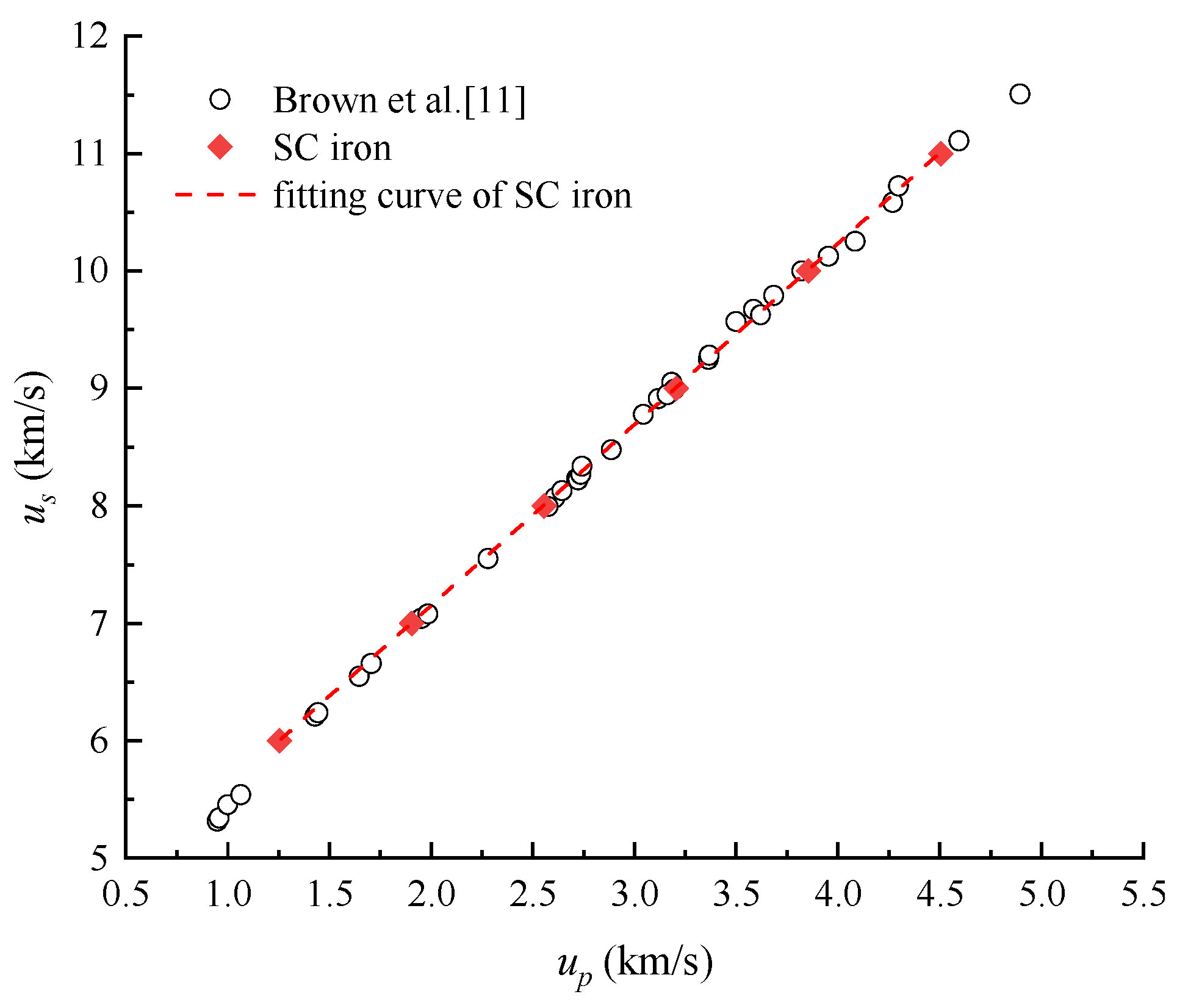
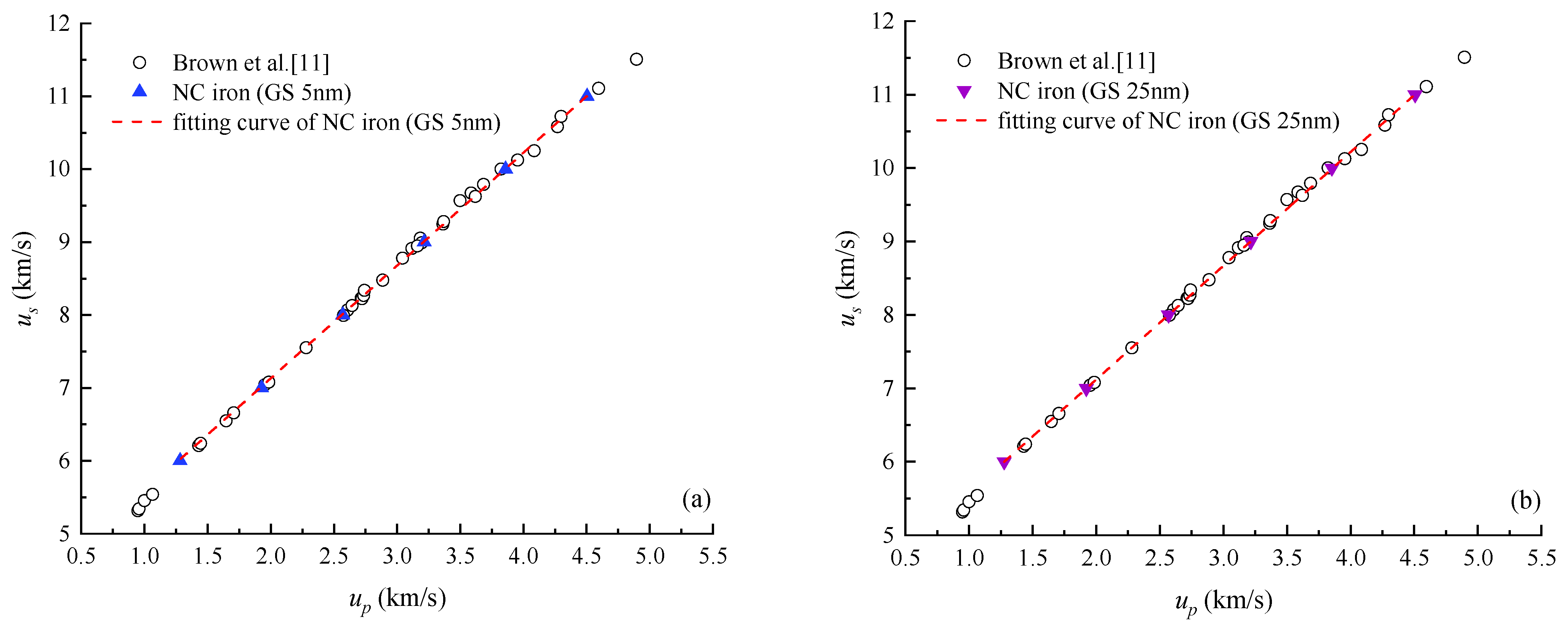
| Material | up (km/s) | us (km/s) | P (GPa) | ρ (g/cm3) |
|---|---|---|---|---|
| SC iron | 1.25 | 6.00 | 60.84 | 9.92 |
| 1.90 | 7.00 | 102.92 | 10.78 | |
| 2.55 | 8.00 | 158.50 | 11.53 | |
| 3.20 | 9.00 | 224.72 | 12.19 | |
| 3.85 | 10.00 | 301.71 | 12.77 | |
| 4.50 | 11.00 | 389.62 | 13.29 | |
| NC iron (GS 5 nm) | 1.27 | 6.00 | 62.36 | 9.98 |
| 1.92 | 7.00 | 105.82 | 10.82 | |
| 2.57 | 8.00 | 161.41 | 11.56 | |
| 3.21 | 9.00 | 227.10 | 12.21 | |
| 3.85 | 10.00 | 302.92 | 12.78 | |
| 4.50 | 11.00 | 388.85 | 13.29 | |
| NC iron (GS 25 nm) | 1.28 | 6.00 | 62.34 | 9.98 |
| 1.92 | 7.00 | 105.74 | 10.82 | |
| 2.56 | 8.00 | 161.22 | 11.56 | |
| 3.21 | 9.00 | 226.75 | 12.20 | |
| 3.85 | 10.00 | 302.34 | 12.77 | |
| 4.50 | 11.00 | 387.98 | 13.28 |
| Material | Shock Velocity | C0 (km/s) | λ | Relative Error | Reference | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| SC | NC (GS 5 nm) | NC (GS 25 nm) | ||||||||
| C0 | λ | C0 | λ | C0 | λ | |||||
| Commercial iron | 5.3–11.5 km/s | 3.935 | 1.578 | 3.34% | 2.60% | 1.89% | 1.67% | 1.87% | 1.61% | [11] |
| SC | 6–11 km/s | 4.071 | 1.538 | - | - | 1.49% | 0.90% | 1.50% | 0.96% | This work |
| NC (GS 5 nm) | 6–11 km/s | 4.011 | 1.552 | 1.49% | 0.90% | - | - | 0.02% | 0.06% | This work |
| NC (GS 25 nm) | 6–11 km/s | 4.010 | 1.553 | 1.50% | 0.96% | 0.02% | 0.06% | - | - | This work |
| Material Constants | V0 (g/cm3) | λ′ | Q (GPa) | q | A (GPa) | B | |
|---|---|---|---|---|---|---|---|
| Experiment | 0.127 | 4.010 | 1.581 | 41.245 | 11.192 | 87.662 | 4.325 |
| SC iron | 0.127 | 4.094 | 1.540 | 46.473 | 10.716 | 97.319 | 4.162 |
| NC iron | 0.127 | 4.093 | 1.541 | 44.238 | 10.894 | 93.170 | 4.223 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zeng, X.; Chen, H.; Yang, X.; Wang, F.; Ding, J. Hugoniot States and Mie–Grüneisen Equation of State of Iron Estimated Using Molecular Dynamics. Crystals 2021, 11, 664. https://doi.org/10.3390/cryst11060664
Wang Y, Zeng X, Chen H, Yang X, Wang F, Ding J. Hugoniot States and Mie–Grüneisen Equation of State of Iron Estimated Using Molecular Dynamics. Crystals. 2021; 11(6):664. https://doi.org/10.3390/cryst11060664
Chicago/Turabian StyleWang, Yuntian, Xiangguo Zeng, Huayan Chen, Xin Yang, Fang Wang, and Jun Ding. 2021. "Hugoniot States and Mie–Grüneisen Equation of State of Iron Estimated Using Molecular Dynamics" Crystals 11, no. 6: 664. https://doi.org/10.3390/cryst11060664
APA StyleWang, Y., Zeng, X., Chen, H., Yang, X., Wang, F., & Ding, J. (2021). Hugoniot States and Mie–Grüneisen Equation of State of Iron Estimated Using Molecular Dynamics. Crystals, 11(6), 664. https://doi.org/10.3390/cryst11060664





