1. Introduction
Lithium niobate (LiNbO
, LN) is a transparent ferroelectric solid that is extensively used in optical technologies due to its advantageous combination of functional properties and commercial availability. In particular, its large piezoelectric, electro-optical, acousto-optical, and nonlinear optical coefficients make it an ideal material for a wide range of optical devices, such as optical modulators [
1], waveguides [
2], optical sensors [
3], holographic storage [
4], and integrated photonics [
5]. By doping with other elements or by manipulating the sample geometry or crystal structure, for example by periodic poling of the ferroelectric domains, the properties of LN can be tailored for specific purposes [
6]. To achieve optimal results, it is important to understand how structural details at the atomic scale influence the observable electronic and optical properties of the material.
The nominal composition of LiNbO
involves an equal number of lithium and niobium atoms, and although it is possible to produce high-quality stoichiometric LN samples by various methods [
7], these are not viable for large-scale fabrication. Instead, the Czochralski technique that is typically used to grow LN single crystals for commercial applications from a congruent melt leads to a Li:Nb ratio of about 48.5:51.5 [
8]. Even without external doping, this relative surplus of Nb in congruent LN crystals implies a high concentration of intrinsic defects, whose nature has long been a matter of debate, as different conceivable defect models are compatible with the observed nonstoichiometric composition [
9]. Nowadays, it is widely accepted that Nb
antisite defects, where extra niobium atoms are inserted on regular lithium sites, play a central role in explaining this imbalance. As the two atomic species have different charge states, the resulting excess charge must be compensated by other defect types, such as cationic vacancies, however. In the prevalent Li-vacancy model, originally proposed by Lerner et al. [
10], each Nb
antisite defect is compensated by four Li vacancies, denoted as V
. However, interstitial Nb
atoms placed at empty cationic sites in the crystal lattice could also contribute to the surplus of niobium [
11]. As we showed recently, these models may be partially reconciled, because a Nb
–V
defect pair consisting of an interstitial niobium atom and a lithium vacancy can be regarded as a metastable variant of the Nb
antisite defect, where the antisite niobium atom overcomes a modest energy barrier and migrates to a neighboring empty cationic site [
12].
An important consequence of the high defect concentration in LN is the ubiquitous occurrence of different types of polarons [
13]. These arise when mobile electrons or holes interact with the ionic lattice to create a local distortion, leading to an attractive effective potential. If the resulting potential well is sufficiently deep, then the charge carrier is trapped and immobilized. The quasiparticle consisting of the self-trapped electron or hole together with the surrounding spatially localized lattice distortion is called polaron or, more specifically, small polaron if the coupling is so strong that the charge carriers are essentially confined to a single lattice site. In LN, three polaron-related optical absorption bands are experimentally observed at 0.9 eV [
14], 1.6 eV [
15], and 2.5 eV [
16]. Based on circumstantial evidence, these are usually attributed to the free electron polaron trapped at a regular Nb lattice site (Nb
), the bound polaron formed by a single localized electron at a Nb
antisite defect, and the bipolaron formed by a pair of bound electrons, one at a Nb
antisite defect and the other at the neighboring regular Nb
atom, respectively, [
13]. In particular, the temperature dependence of the relative strengths of the absorption bands at 1.6 eV and 2.5 eV are consistent with the thermal [
16] or optical [
17] dissociation of bipolarons into single bound polarons, and the band at 0.9 eV could only be observed in reduced samples with a high dopant concentration of Mg ions, which inhibit the formation of Nb
antisite defects, leaving free polarons as a natural explanation [
14]. On the other hand, the assignment to particular defect types rests chiefly on the correlation with electron-paramagnetic-resonance (EPR) signals believed to originate from Nb
antisite defects [
13], but as the actual spatial distribution of the polaron cannot be imaged directly in experiments, the precise relation between the antisite defect and the localized charge accumulation ultimately remains open. In this situation, first-principles simulations of the defect structures and their EPR parameters [
12] as well as their optical spectroscopic properties provide valuable further insight.
In an early theoretical study, Donnerberg et al. [
18] employed a semiempirical shell model to investigate intrinsic defects in LN. Their results, as well as other subsequent atomistic simulations with improved interaction potentials [
19], lent support to the Li-vacancy model and indicated the stability of small electron polarons and bipolarons, but neither the electronic energy levels nor the corresponding orbitals appear explicitly in this approach. Later, first-principles calculations based on density-functional theory yielded accurate quantitative values for the formation energies of several possible intrinsic defects and confirmed the Li-vacancy scenario as the dominant mechanism for the deviation from stoichiometry [
20,
21]. Furthermore, the localized wavefunctions of the bound polaron and the bipolaron at the Nb
antisite defect are accessible in this framework [
22]. As density-functional theory systematically underestimates the band gap of insulators like LN, the position of the defect levels inside the band gap cannot be obtained reliably in this way, however, precluding a quantitative comparison with the experimentally observed absorption bands. In a first step, the band-gap problem can be solved by including quasiparticle corrections within the
approximation for the electronic self-energy [
23,
24], the zero-point renormalization due to lattice vibrations [
25], and spin-orbit coupling, which altogether raise the band gap of LN by about 2 eV compared to standard density-functional theory [
26]. Second, the optical absorption spectrum is strongly influenced by electron-hole attraction effects, which give rise to excitonic resonances. In principle, these can be treated within time-dependent density-functional theory. Numerical results reported by Friedrich et al. for intrinsic [
27] and extrinsic [
28] defects in LN were in good quantitative agreement with the experimental data, but the uncertainty due to empirical corrections, which are necessary to countervail limitations of standard approximations in time-dependent density-functional theory [
29], still precluded a reliable discrimination between competing defect configurations involving antisite or interstitial niobium atoms. As an alternative, we adopt the Bethe–Salpeter equation (BSE), which requires no such empirical corrections, to determine the optical response in this work. Owing to the much higher computational expense, a full solution of the BSE was initially limited to stoichiometric LN [
23,
30], but we recently succeeded in extending this approach to congruent LN [
12], which requires a larger supercell to accommodate the defect.
The aim of this paper is twofold. First, we present a detailed description of the geometric and electronic structure of electron polarons in LN, with special focus on the quasi-Jahn-Teller distortion that breaks the threefold rotational symmetry in the case of free and bound polarons. The resulting tilted configurations were only very recently revealed as the true ground states [
12] and are hence not yet widely discussed in the literature, as previous theoretical studies [
21,
22] were based on simpler, axially symmetric structure models instead. Second, we analyze the contribution of polarons to the dielectric function, which is related to the optical absorption spectrum. Going beyond our previous work [
12], we also investigate polaron signatures in other optical coefficients like the reflectivity or the electron-energy-loss function, which can be measured directly in experiments.
This paper is organized as follows. In
Section 2, we present the different structure models for free polarons, bound polarons, and bipolarons, and we explain our computational methods. Subsequently, we discuss our results for the polaron-induced lattice deformation in
Section 3.1, for the electronic structure in
Section 3.2, and for the dielectric function and optical coefficients in
Section 3.3. Finally,
Section 4 summarizes our conclusions.
2. Models and Methods
Lithium niobate belongs to the trigonal crystal system with the space group
[
8]. Its crystal structure consists of octahedral cages formed by oxygen atoms. The cationic sites inside the oxygen cages can either be occupied by a lithium or niobium ion, or remain empty. For defect-free stoichiometric lithium niobate (SLN), the stacking order along the threefold symmetry axis is a periodic repetition of the sequence Li–Nb–vacancy as illustrated in
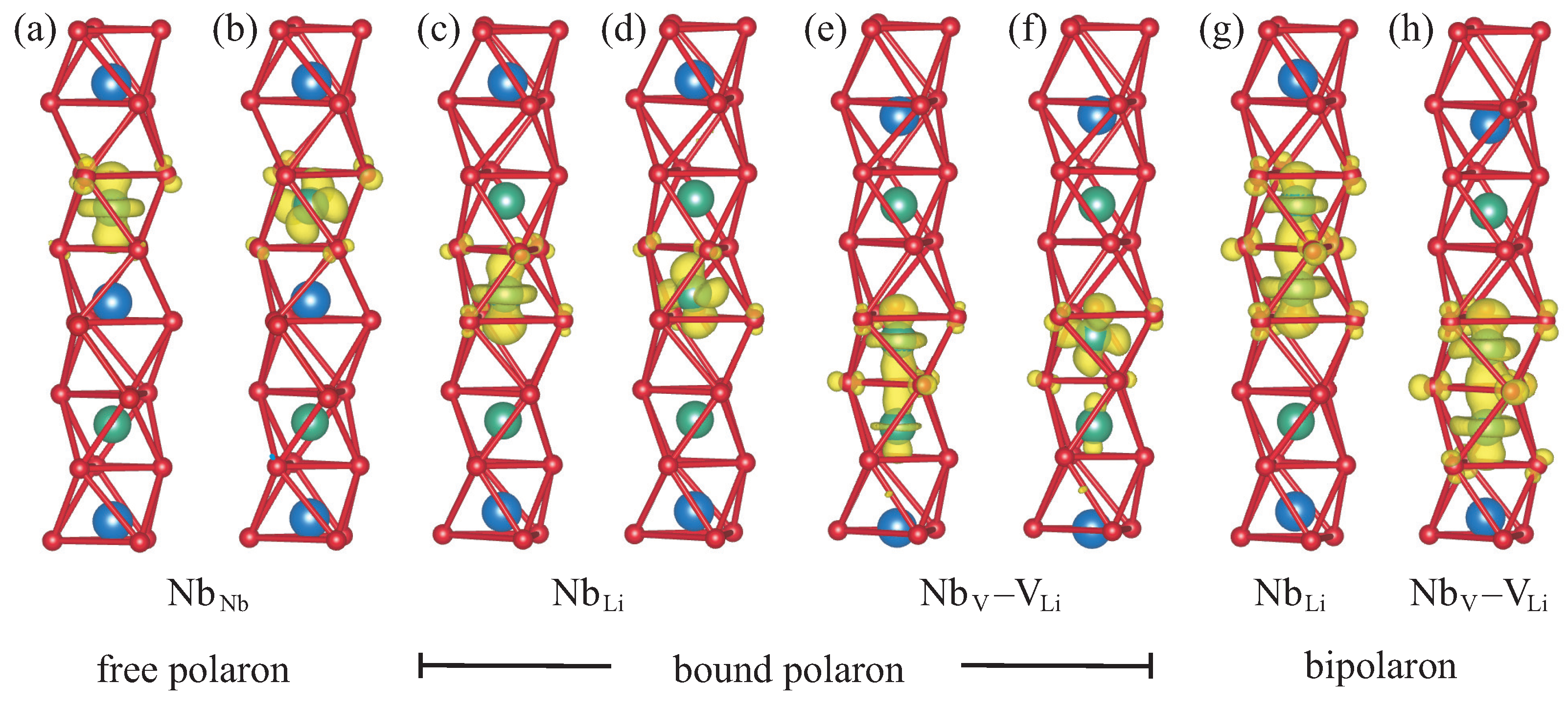
Figure 1a. Due to the ferroelectric distortion, which breaks the inversion symmetry, the cations do not reside in the geometric center of the oxygen cages but are slightly displaced in the vertical direction. To highlight point defects in LN, which can be characterized by a modified occupancy of the cationic sites, we use a schematic representation where each square symbolizes a filled or empty oxygen octahedron.
In the absence of defects, an additional electron introduced into the material will localize at one of the regular Nb
atoms, as indicated by the red square in
Figure 1b. Together with the resulting lattice relaxation, this gives rise to the free polaron. Congruent LN, on the other hand, features a high concentration of Nb
antisite defects. In this scenario, an additional electron will localize at the defect site instead, creating a bound polaron as in
Figure 1c. The Nb
antisite atom can also migrate into the next empty oxygen octahedron, producing a Nb
–V
defect pair. This configuration can likewise host a bound polaron, depicted in
Figure 1d. If not one but two electrons are added to the system, then a bipolaron forms either at the antisite,
Figure 1e, or the defect pair,
Figure 1f. All defect structures illustrated in
Figure 1 are considered in this work.
The primitive rhombohedral unit cell of stoichiometric LN contains two formula units of LiNbO
, amounting to 10 atoms. For the investigation of point defects, we choose a periodically repeated 2 × 2 × 2 supercell with 80 atoms, in which one defect is embedded. The same supercell geometry was used in [
21,
22]. An explicit comparison of different supercells containing between 80 and 270 atoms found that the formation energies of the defect types considered here remain stable for all supercell sizes, with merely slight numerical variations [
20]. This is in agreement with our own test calculations for a larger 3 × 3 × 3 supercell containing 270 atoms, reported previously in [
27], which also confirmed that the relaxed interatomic distances in the immediate vicinity of the defect are almost identical and that the resonances in the imaginary part of the dielectric function align nicely for both supercell sizes, except for a variation in intensity that reflects the different defect concentrations. The present choice is hence justified and serves to limit the computational cost associated with the solution of the BSE, but it will also be validated a posteriori in this work. Incidentally, we note that it is possible to avoid supercells altogether by using perturbation theory and describing the properties of polarons in leading order in terms of the electronic structure of the pristine stoichiometric crystal [
31], which is advantageous for materials featuring large polarons, but as electron polarons in LN are known to be small [
13], the nonperturbative supercell approach seems appropriate here.
All external and internal degrees of freedom are relaxed within density-functional theory (DFT) using the Quantum ESPRESSO [
32] package. We use norm-conserving pseudopotentials and the PBEsol functional [
33] to describe electronic exchange-correlation effects. Compared to other common parametrizations, the PBEsol functional yields more reliable lattice parameters for LN [
25] and closely related materials [
34,
35,
36]. The oxygen
and
orbitals as well as the lithium
orbitals are treated explicitly as valence states. The pseudopotential of niobium is optimized for the Nb
cation configuration, which emerges on regular lattice sites in LN, in order to increase the numerical stability and to allow for smaller cutoff radii; in this case, the
,
,
, and
orbitals are treated as valence states. This leads to 256 valence bands for the free-polaron system in stoichiometric LN and 260 valence bands for all models of bound polarons and bipolarons, where one Li
cation is substituted by a Nb
ion. We select a kinetic-energy cutoff of 85 Ry for the plane-wave basis set and a shifted Monkhorst-Pack mesh with 2 × 2 × 2
points for the Brillouin-zone integration during the self-consistency cycle, equivalent to 4 × 4 × 4
points in the larger Brillouin zone corresponding to the primitive unit cell. The convergence thresholds for energies and forces during the relaxation are set to
Ry and
Ry/Bohr, respectively. For an accurate description of the Nb
orbitals, we employ the DFT +
U scheme [
37]. The values for the Hubbard
U parameter are determined self-consistently as 5.2 eV for the Nb
antisite and Nb
interstitial atoms and 4.7 eV for regular Nb
atoms, including the one hosting the free polaron [
12]. For free and bound polarons, which feature a single unpaired electron, we perform spin-polarized calculations; for bipolarons, this is not necessary, because they comprise two electrons with opposite spin orientations.
From the one-particle energies
and the associated wavefunctions
, we obtain the projected density of states
which provides important information about the electronic structure of the material. The summation over
n includes 800 bands, sufficient to cover an energy interval up to 10 eV above the valence-band maximum, and the wavevector
runs over all points of a shifted 4 × 4 × 4 mesh. A Gaussian function
g with a broadening of 0.05 eV is applied to compensate for the discrete
-point mesh. The operator
P projects the one-particle wavefunctions onto orthogonalized atomic orbitals corresponding to the selected pseudopotentials; the total density of states (DOS) is obtained by setting
.
The frequency-dependent dielectric function, from which the absorption spectrum and other optical coefficients may be derived, is constructed at different levels of theory in this work. Within the independent-particle approximation (IPA), the tensor elements in the long-wavelength limit are
where
denotes the spatial direction. We follow the usual convention where the threefold symmetry axis is identified with the
z direction, while the
x direction is perpendicular to the
z direction and lies in the plane spanned by the threefold symmetry axis and one of the three equivalent basis vectors of the primitive rhombohedral unit cell. For the numerical evaluation of the dielectric function, we employ the Yambo package [
38]. The first sum in Equation (
2) runs over all combinations of valence (
v) and conduction (
c) bands, the second over the set of wavevectors inside the Brillouin zone. The transition dipole moments include the commutator
with the nonlocal part of the pseudopotentials,
is the volume of the supercell, and the broadening
again compensates for the finite
-point mesh.
For a better quantitative description, we replace the Kohn–Sham eigenvalues
in a first step by the proper quasiparticle energies
calculated within the
approximation, which not only opens the band gap by about 2 eV, in agreement with experimental measurements, but also modifies the dispersion [
26]. Within this independent-quasiparticle approximation (IQA), the transition energies between valence and conduction bands are larger than in the IPA, reflecting the widened band gap, but there is no interaction between the created electrons and holes. For the numerical evaluation of the exchange-correlation self-energy, we employ a plasmon-pole approximation for the dynamical screening function as implemented in the Yambo package.
In a second step, we then incorporate the electron-hole interaction by solving the BSE, again with the Yambo package. In this scheme, the macroscopic dielectric function is constructed as
where
approaches zero in the direction
. The energies
of the interacting electron-hole pairs and the expansion coefficients
of the resulting exciton states in the basis of one-particle wavefunctions are given by the eigenvalues and eigenvectors of the two-particle Hamiltonian
The first, diagonal term, which equals the transition energies between quasiparticle states in the valence and conduction bands, corresponds to the IQA. The second, nondiagonal term, the kernel of the BSE, is composed of the electron-hole exchange part and the electron-hole attraction W. The latter describes the formation of excitons, i.e., bound electron-hole pairs, which strongly influence the shape of the dielectric function.
From the real and imaginary parts of the complex dielectric function, obtained by solving the BSE, various optical coefficients with a direct relation to experimental measurements may subsequently be derived. In particular, the refractive index
and the extinction coefficient
are given by
From these, we may obtain the reflectivity
and the absorption coefficient
according to
where
c denotes the speed of light. Finally, the electron-energy-loss function equals
4. Conclusions
Using first-principles calculations based on density-functional theory, we performed a detailed analysis of electron polarons in LN, taking free polarons, bound polarons, and bipolarons into account. In contrast to earlier studies [
21,
22], we not only considered electron polarons bound to Nb
antisite atoms but also to another defect compatible with the Li-vacancy model, namely the Nb
–V
defect pair, which arises when an antisite niobium atom migrates to a neighboring empty oxygen octahedron. Furthermore, we did not restrict ourselves to axially symmetric structure models but performed a full unconstrained relaxation, which leads to lower-energy tilted configurations where the threefold rotational symmetry is broken. Our results show that the distortion lowers the energy of the occupied defect level inside the band gap and thereby stabilizes the tilted configurations for free and bound polarons, which feature a single unpaired electron. On the other hand, it reduces the hybridization between the orbitals of neighboring niobium atoms along the threefold symmetry axis, which is essential for the formation of bipolarons. Therefore, bipolarons at both defect types relax to an axially symmetric geometry instead. An examination of the charge densities and the projected densities of states reveals that for all configurations, about one third of the trapped electronic charge is not actually localized at the niobium atoms hosting the polaron but distributed over the oxygen atoms that form the octahedral cage enclosing the defect site, well within the limits of the supercell used in this work. The lattice distortion associated with the polaron formation extends farther, especially for bipolarons at Nb
–V
defect pairs, but it is not necessary to include its full spatial extent outside the localized charge distribution in calculations of the electronic and optical properties of polarons in LN. This justifies the use of a smaller supercell, which in turn allows us to apply sophisticated many-body techniques that would otherwise be prohibitively expensive.
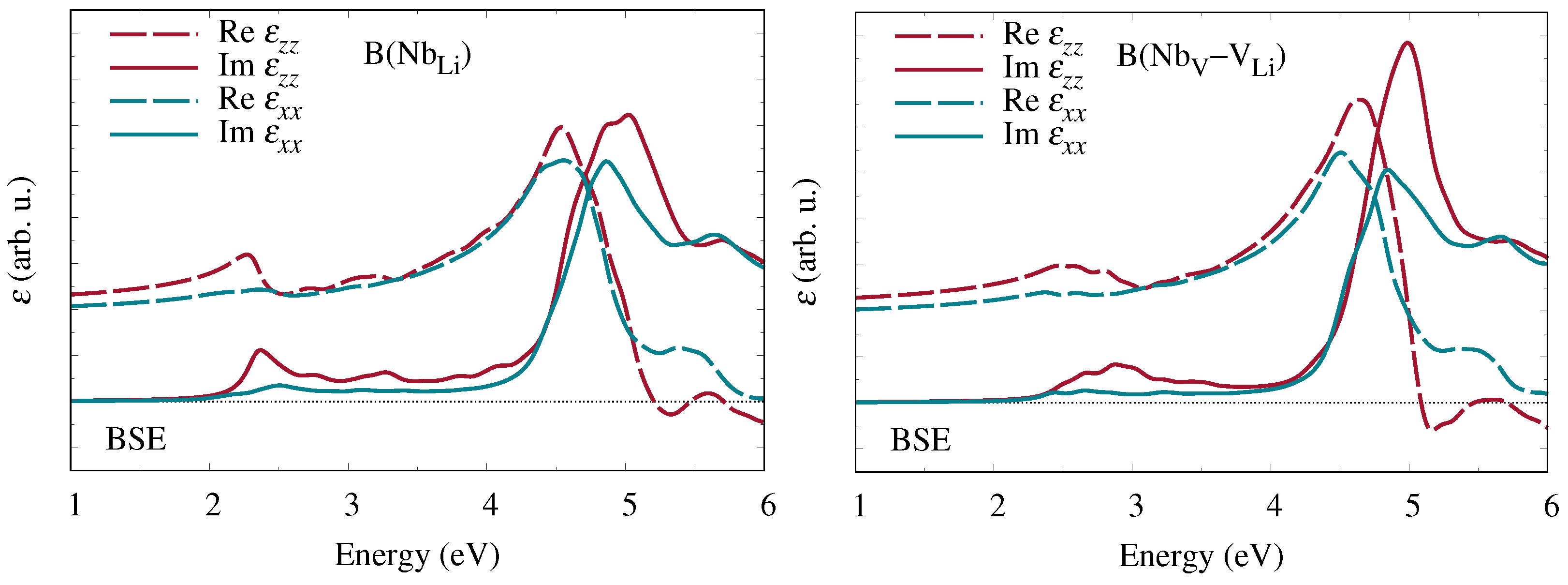
Hereupon we performed state-of-the-art first-principles calculations of the frequency-dependent complex dielectric function and related optical coefficients. Starting from the independent-particle approximation, we additionally included quasiparticle corrections within the
approximation for the electronic self-energy as well as excitonic contributions obtained from the Bethe–Salpeter equation. Our results for bipolarons at Nb
antisite defects and Nb
–V
defect pairs show clear signatures at low photon energies in all optical coefficients that are characteristic of the specific defect type. A quantitative comparison of the calculated absorption spectra with experimental measurements of the absorption band attributed to bipolarons [
12,
13] suggests that at least some of the antisite niobium atoms indeed migrate to neighboring oxygen octahedra and form interstitial-vacancy pairs.
Finally, the structure models established in this work constitute a basis for further theoretical studies. Besides the linear optical properties already addressed here and in previous works [
12,
27,
28,
30], the nonlinear response is of particular interest, because it is central to the performance of LN as a key material in many optical technologies. Due to the enormous computational cost [
41], significant challenges must still be overcome in order to facilitate accurate quantitative calculations of the polaron contribution to the nonlinear optical coefficients of congruent LN, however.