Determination of the Exact Orientation of Single-Crystal X-ray Optics from Its Glitch Spectrum and Modeling of Glitches for an Arbitrary Configuration
Abstract
1. Introduction
2. Materials and Methods
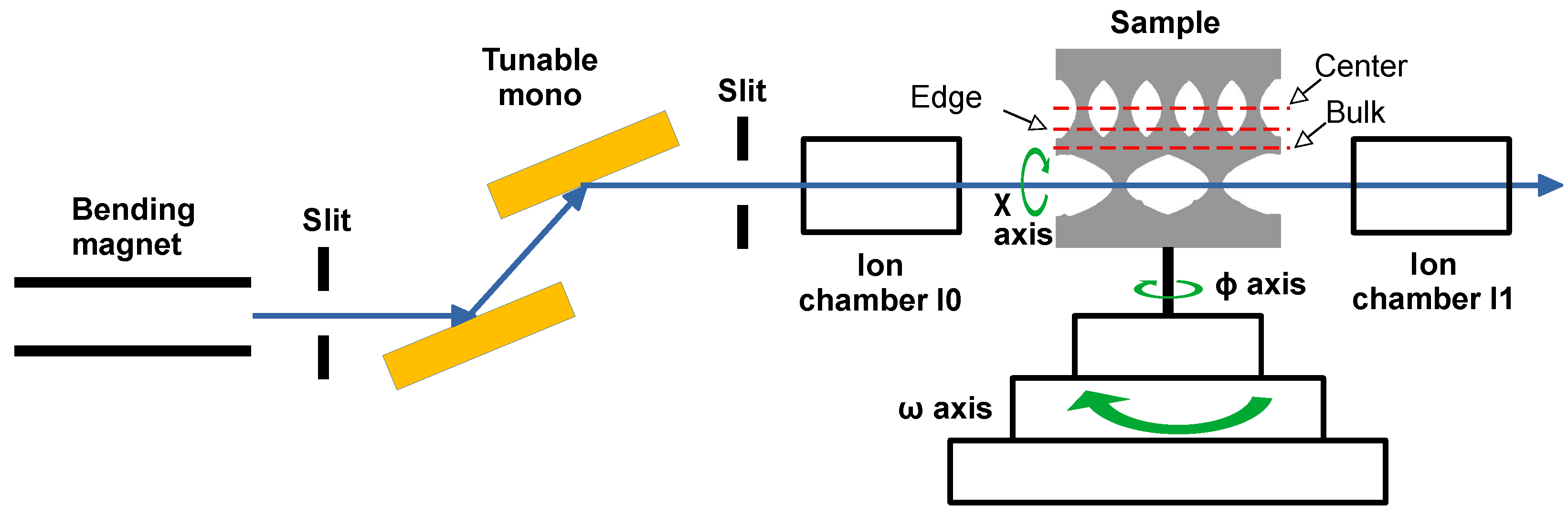
2.1. Experiment Description
- No profiling plate, supplied by Element Six Ltd., Santa Clara, CA (USA) [22];
- One-dimensional CRL, which consists of three sets of compound refractive lenses, manufactured in Saint Petersburg, Russia by New Diamond Technology (NDT) [25];
- Two-dimensional lens, grown at the Technological Institute for Superhard and Novel Carbon Materials (TISNCM), Troitsk, Russia [26].
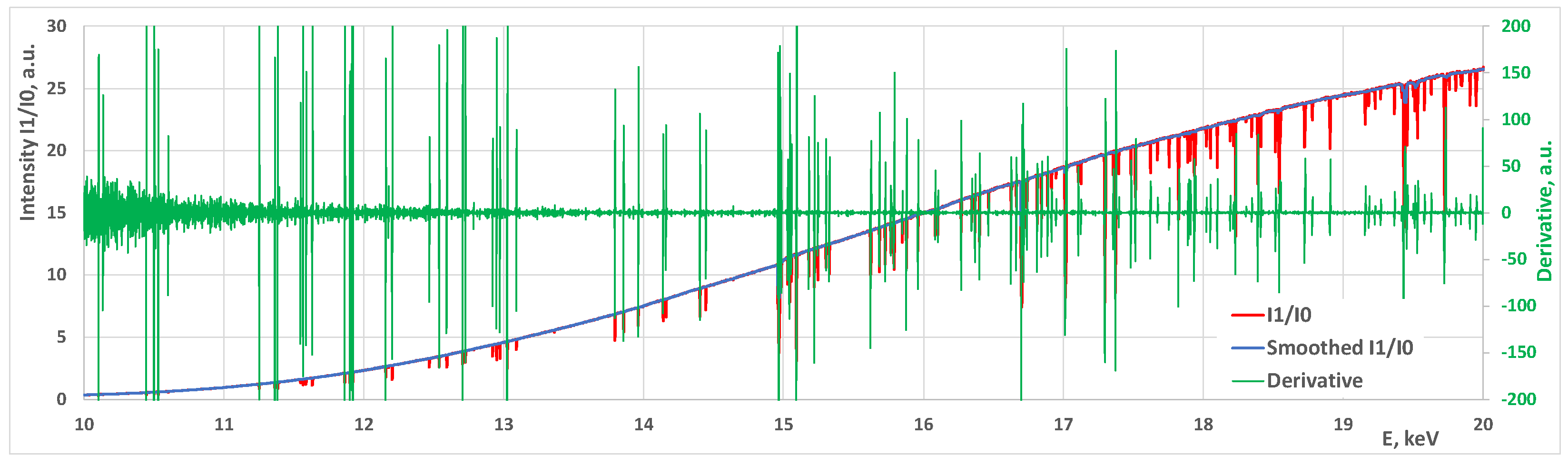
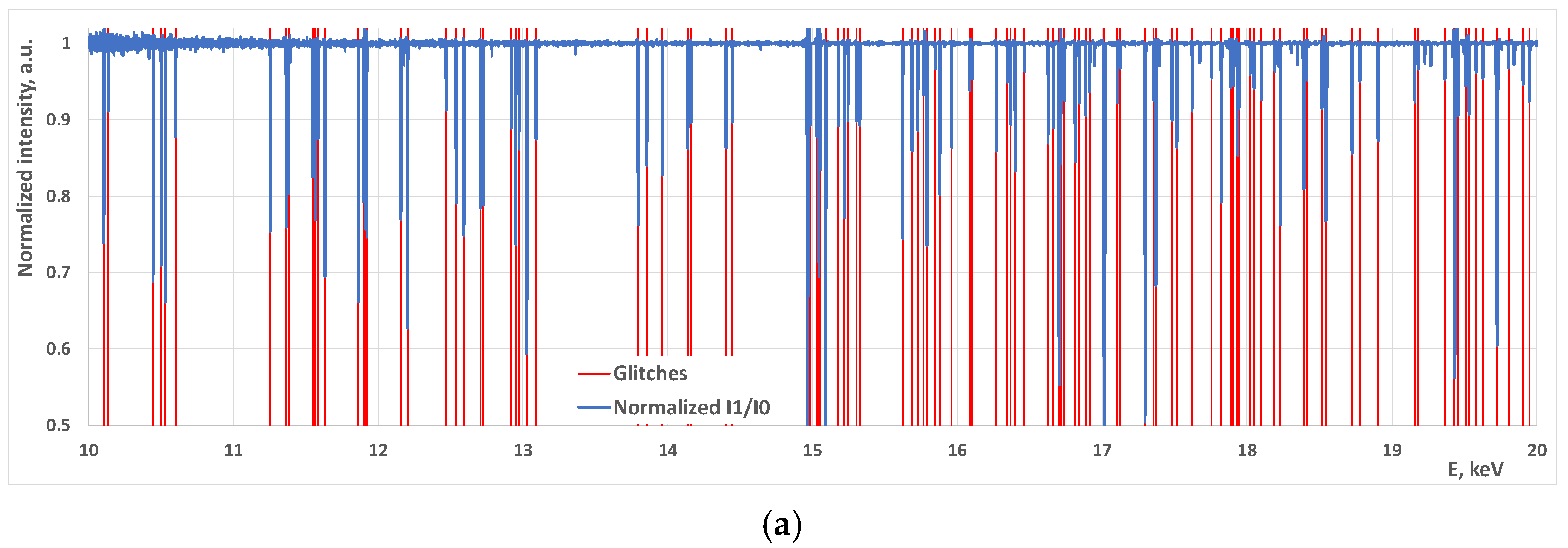
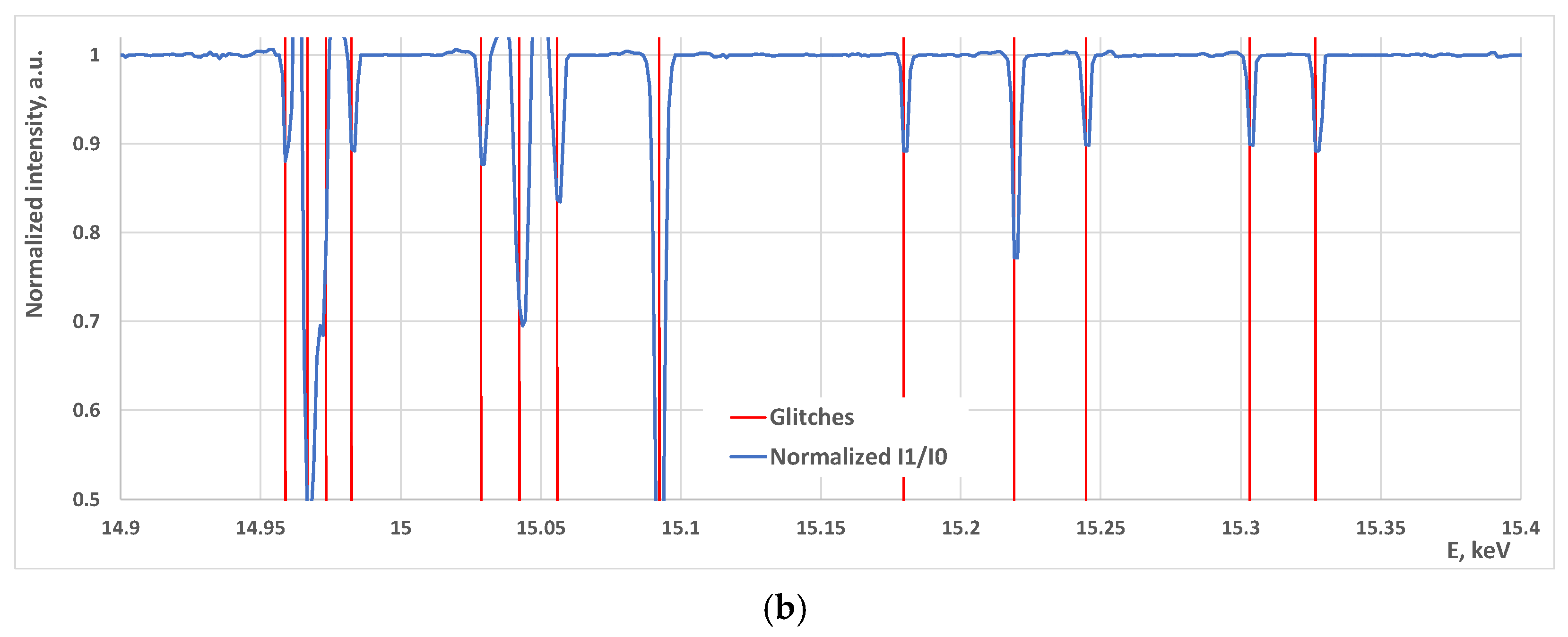
2.2. Extracting Glitches from the Experimental Data
- Divide I1/I0 to get normalized spectrum;
- Make a smoothed version of the curve (running median with 15 pixels window);
- Divide the normalized curve by the smoothed one;
- Smooth the resulting curve a little (running median with 3 pixels window);
- Calculate the derivative of the resulting curve;
- Select regions with intensities smaller than some threshold (like 0.97) as potential glitches;
- Analyze derivatives in the preselected regions. If the derivative changes the sign from “−” to “+” and has some reasonable amplitude (usually 1–5), declare this as a glitch.
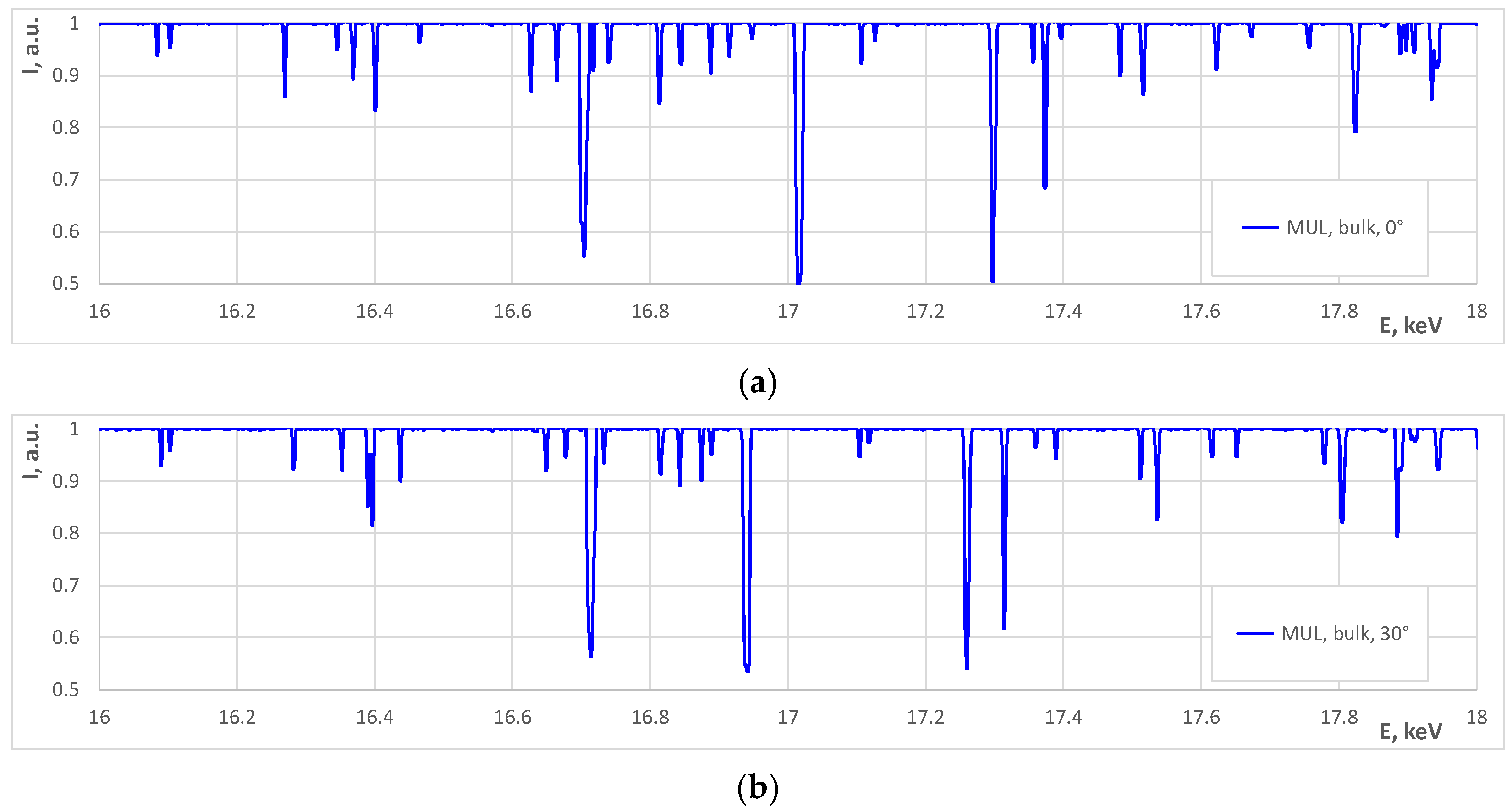
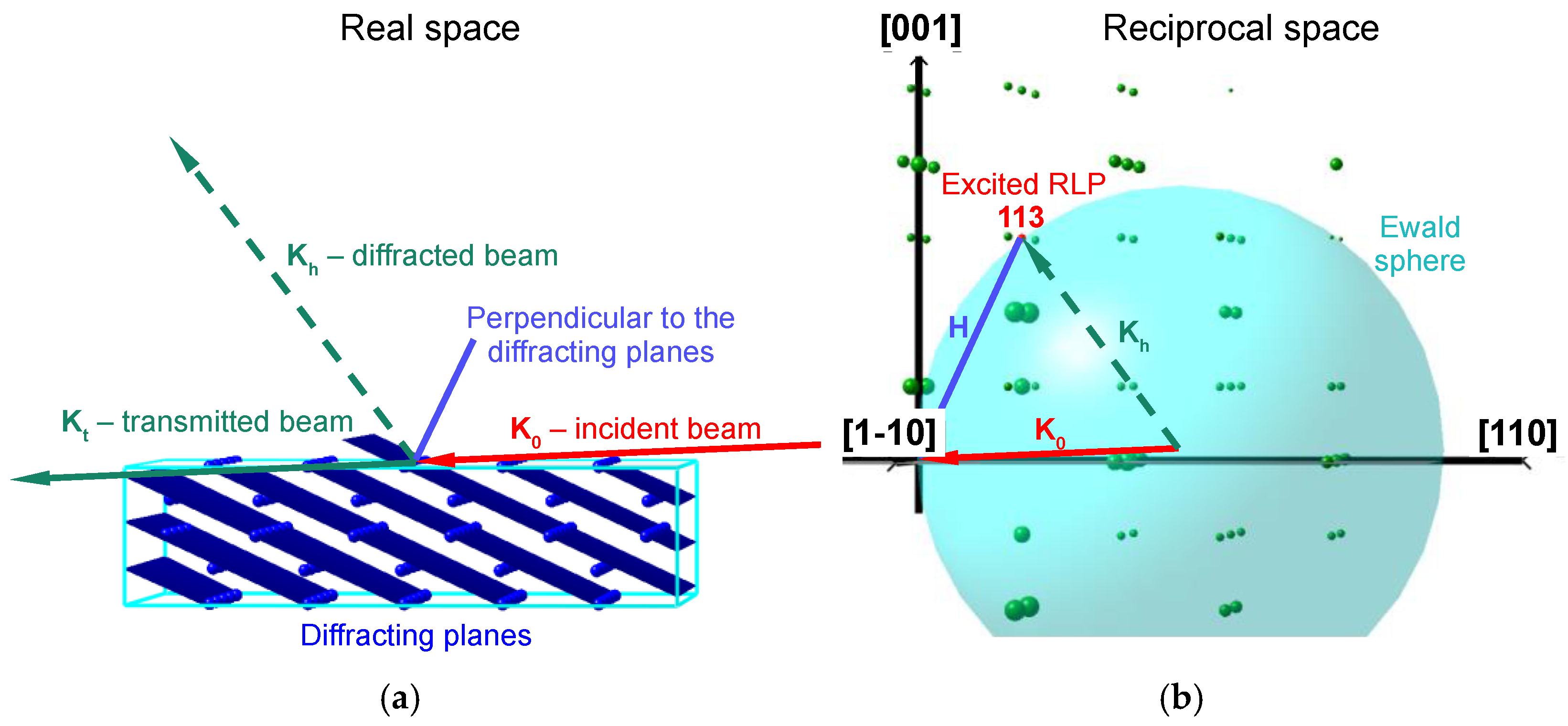
2.3. Explanation of Glitches
2.4. Extracting Glitches from the Experimental Data
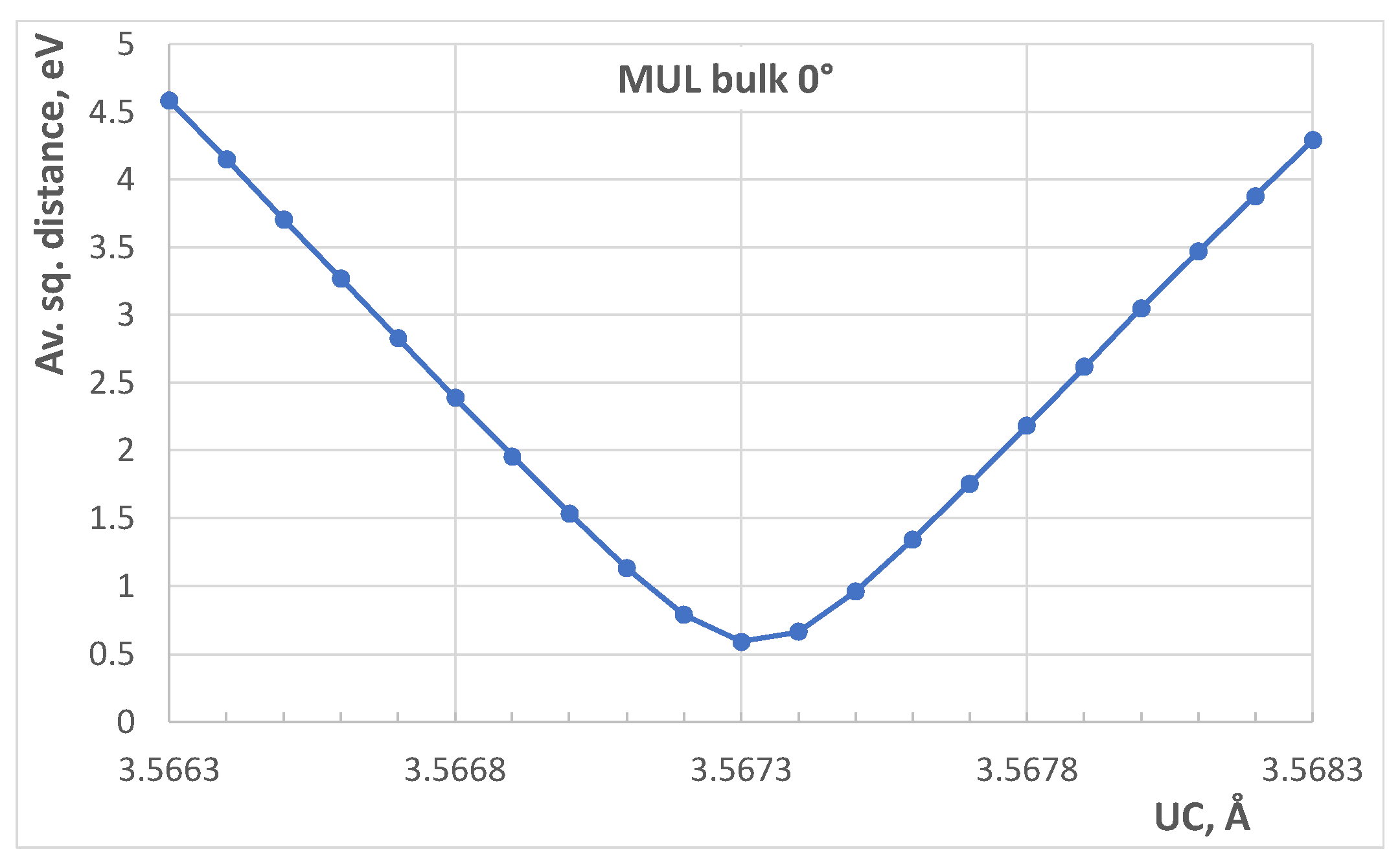
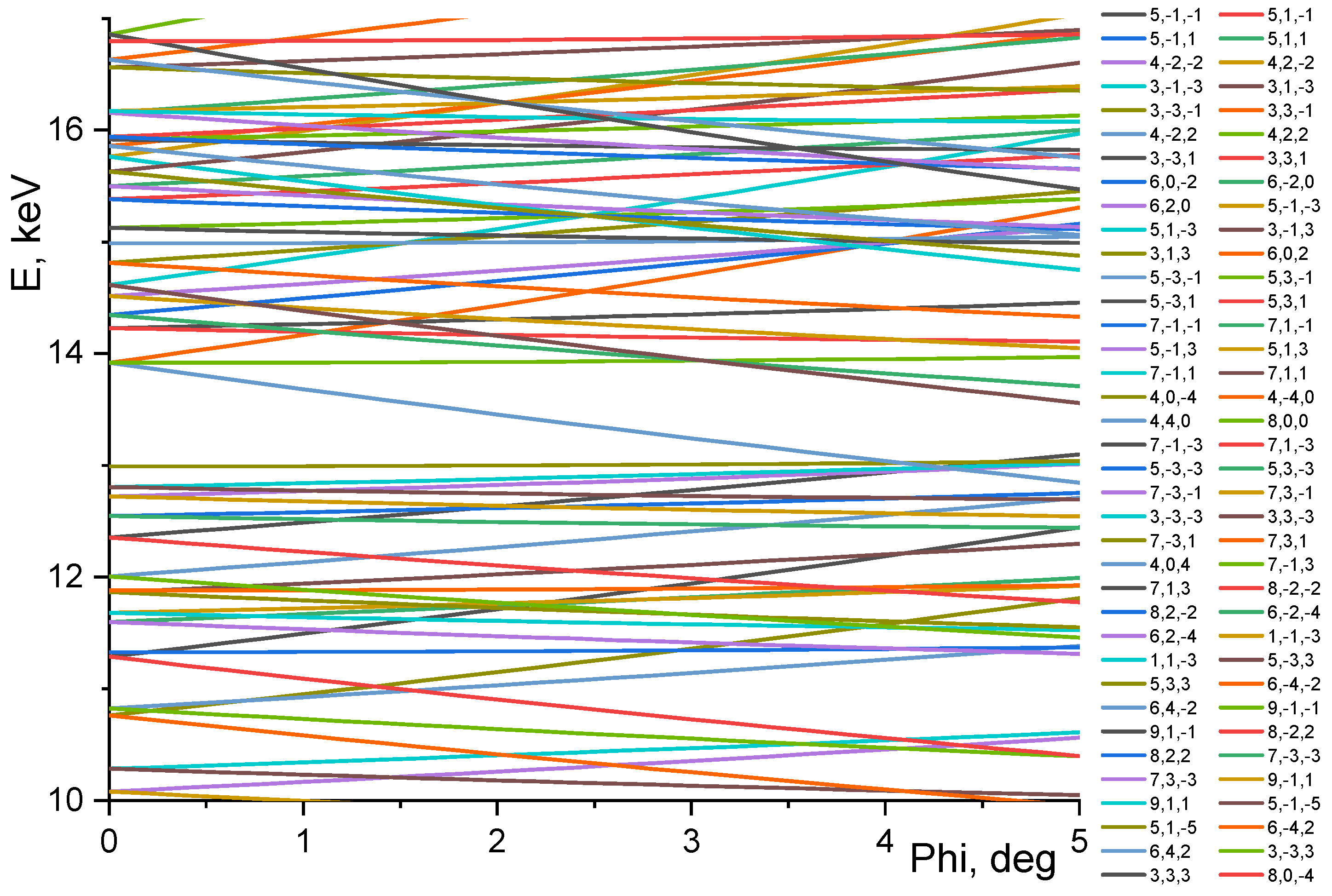
2.5. Finding Approximate Orientation and Indexing Glitches
- (a)
- Search of the UC, ω, ϕ (in some range with fixed step size), while minimizing the average square distance between found and predicted glitches;
- (b)
- Repeating the first step 1–2 times narrowing the windows and minimizing the step of search parameters (UC, ω, ϕ);
- (c)
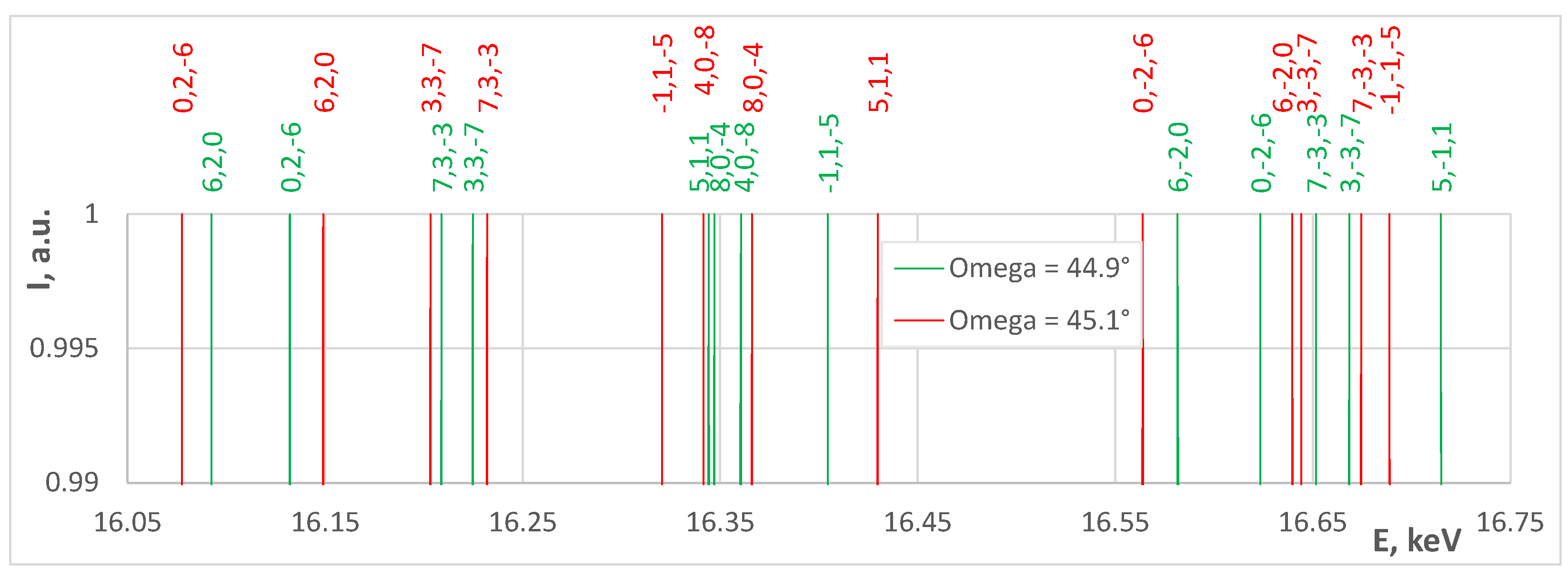
- Indexing the measured spectra by assigning to each glitch the Miller indexes of the closest predicted Bragg peak.
2.6. Determining the Exact Orientation and Cell Parameters
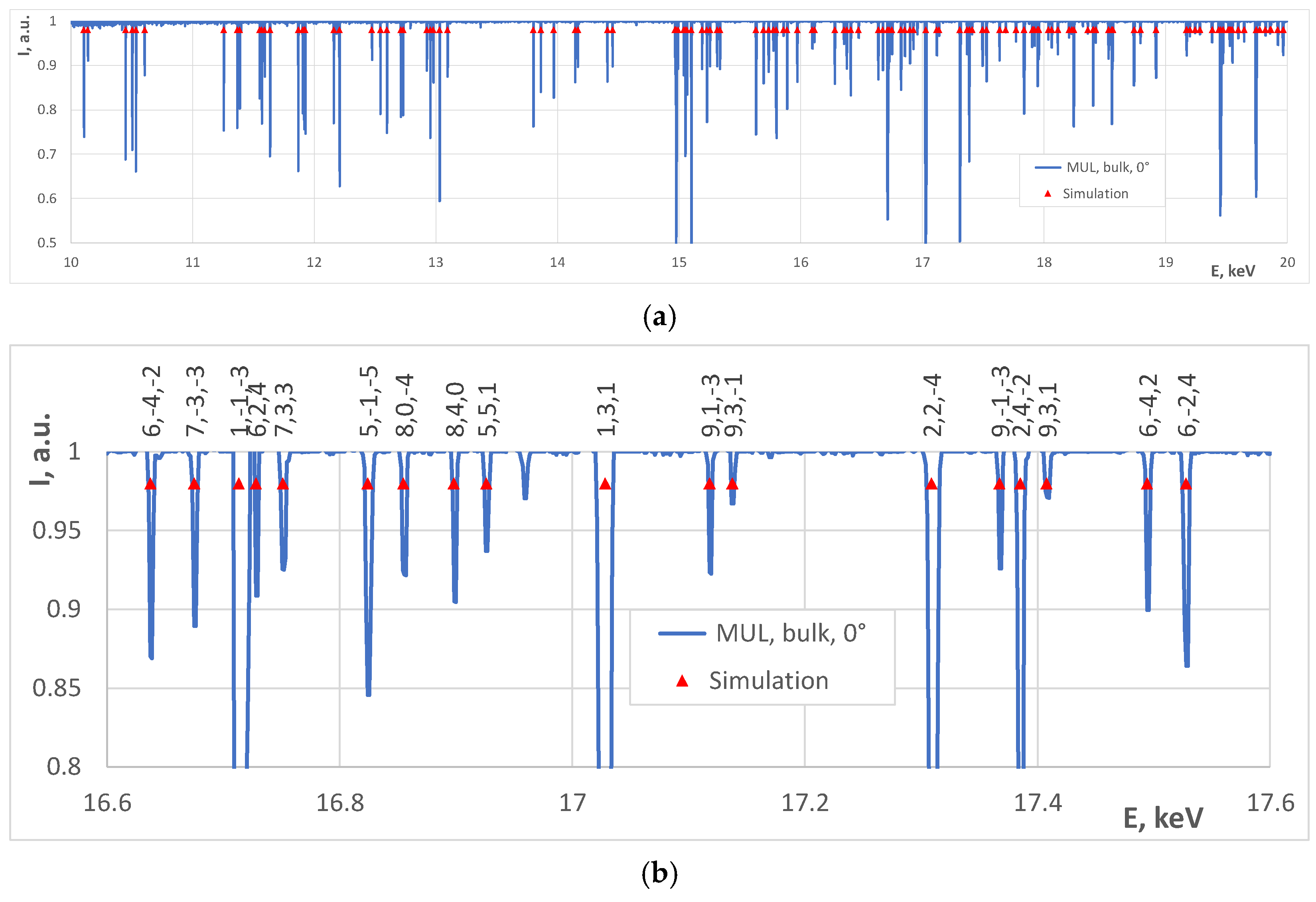
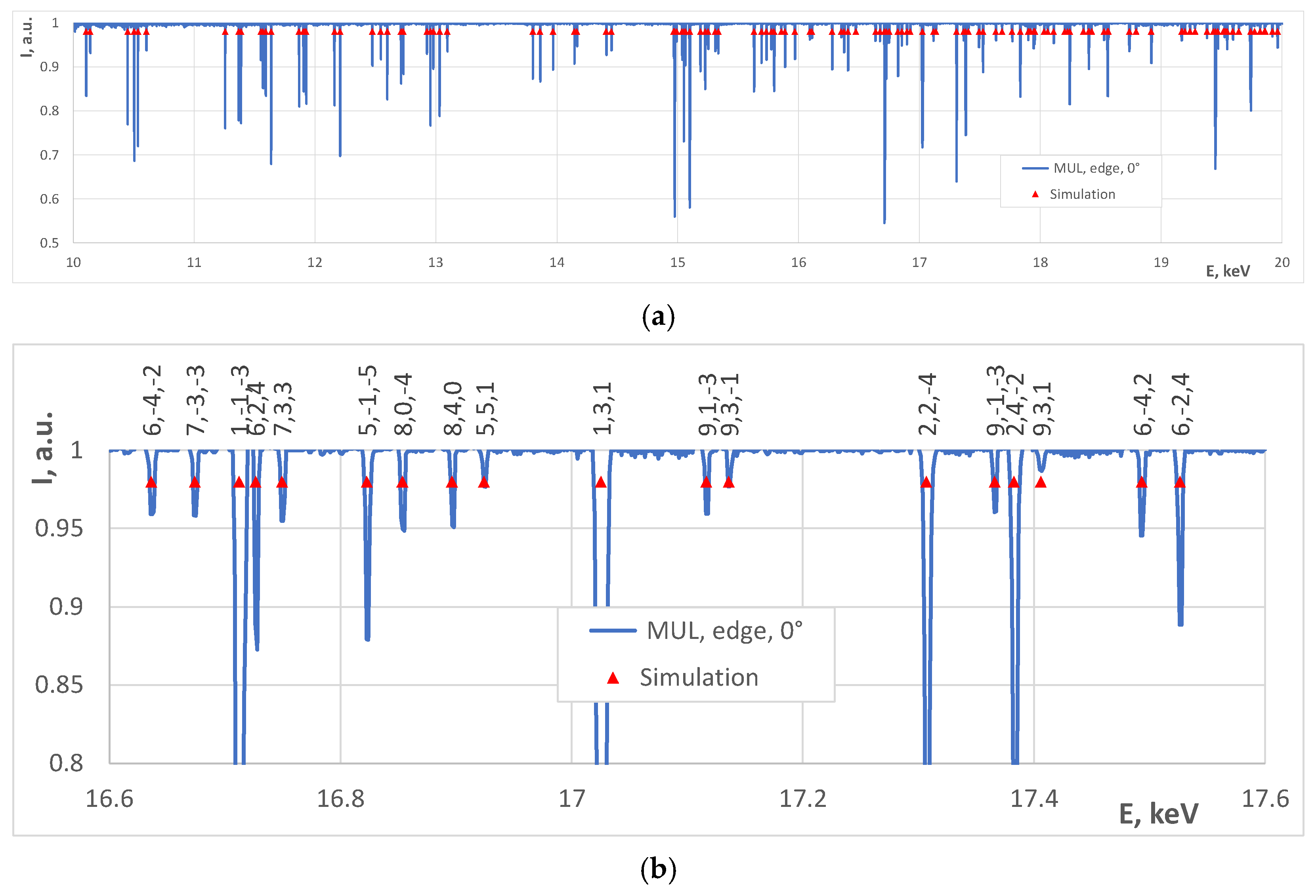
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Snigirev, A.; Kohn, V.; Snigireva, I.; Lengeler, B. A compound refractive lens for focusing high-energy X-rays. Nature 1996, 384, 49–51. [Google Scholar] [CrossRef]
- Polikarpov, M.; Emerich, H.; Klimova, N.; Snigireva, I.; Savin, V.; Snigirev, A. Spectral X-Ray Glitches in Monocrystalline Diamond Refractive Lenses. Phys. Status Solidi B 2018, 255, 1700229. [Google Scholar] [CrossRef]
- Konigsberger, D.S.; Prins, R. X-ray Absorption: Principles, Applications, Techniques of Exafs, Sexafs and Xanes (Chemical Analysis); A Wiley-Interscience Publication: New York, NY, USA, 1987. [Google Scholar]
- Bunker, G. Introduction to XAFS: A Practical Guide to X-ray Absorption Fine Structure Spectroscopy; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Van Zuylen, P.; Van Der Hoek, M.J. Some Considerations on Glitches and The Design Of a Double Crystal Monochromator With Bent Crystals. In Soft X-ray Optics and Technology; International Society for Optics and Photonics: Bellingham, WA, USA, 1986; Volume 733, pp. 248–253. [Google Scholar] [CrossRef]
- Van Der Laan, G.; Thole, B.T. Determination of glitches in soft X-ray monochromator crystals. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1988, 263, 515–521. [Google Scholar] [CrossRef]
- Bauchspiess, K.R.; Crozier, E.D. Crystal Glitches of X-Ray Monochromators. In EXAFS and Near Edge Structure III, 2nd ed.; Springer Proceedings in Physics; Hodgson, K.O., Hedman, B., Hahn, J.E., Eds.; Springer: Berlin/Heidelberg, Germany, 1984; Volume 2, pp. 514–516. [Google Scholar]
- Li, G.; Bridges, F.; Wang, X. Monochromator-induced glitches in EXAFS data II. Test of the model for a pinhole sample. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1994, 340, 420–426. [Google Scholar] [CrossRef]
- Nöhammer, B.; Hoszowska, J.; Freund, A.K.; David, C. Diamond planar refractive lenses for third- and fourth-generation X-ray sources. J. Synchrotron Radiat. 2003, 10, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Kononenko, T.V.; Ralchenko, V.G.; Ashkinazi, E.E.; Polikarpov, M.; Ershov, P.; Kuznetsov, S.; Yunkin, V.; Snigireva, I.; Konov, V.I. Fabrication of polycrystalline diamond refractive X-ray lens by femtosecond laser processing. Appl. Phys. A 2016, 122, 1–6. [Google Scholar] [CrossRef]
- Fox, O.J.L.; Alianelli, L.; Malik, A.M.; Pape, I.; May, P.W.; Sawhney, K.J.S. Nanofocusing optics for synchrotron radiation made from polycrystalline diamond. Opt. Express 2014, 22, 7657–7668. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, C.; Beretta, S.; Rotunno, E.; Korytár, D.; Zaprazny, Z. Compressive strain formation in surface-damaged crystals. J. Appl. Crystallogr. 2020, 53, 629–634. [Google Scholar] [CrossRef] [PubMed]
- Martinson, M.; Samadi, N.; Shi, X.; Liu, Z.; Assoufid, L.; Chapman, D. Characterization of a bent Laue double-crystal beam-expanding monochromator. J. Synchrotron Radiat. 2017, 24, 1146–1151. [Google Scholar] [CrossRef] [PubMed]
- Dobson, B.R.; Hasnain, S.S.; Morrell, C.; Konigsberger, D.C.; Pandya, K.; Kampers, F.; Van Zuylen, P.; Van Der Hoek, M.J. Non-normalization behavior of crystal glitches in an EXAFS spectrum: Is it possible to remove crystal glitches? Rev. Sci. Instrum. 1989, 60, 2511–2514. [Google Scholar] [CrossRef]
- Rowen, M.; Wong, J.; Tanaka, T. Suppression of Positive Glitches in the Transmission Function of YB66 Monochromator. J. Phys. IV France 1997, 7, C2-315. [Google Scholar] [CrossRef]
- Tang, Z.; Zheng, L.; Chu, S.; Wu, M.; An, P.; Zhang, L.; Hu, T. Optimal azimuthal orientation for Si(111) double-crystal monochromators to achieve the least amount of glitches in the hard X-ray region. J. Synchrotron Radiat. 2015, 22, 1147–1150. [Google Scholar] [CrossRef] [PubMed]
- Sutter, J.P.; Boada, R.; Bowron, D.T.; Stepanov, S.A.; Díaz-Moreno, S. Rotation of X-ray polarization in the glitches of a silicon crystal monochromator. J. Appl. Crystallogr. 2016, 49, 1209–1222. [Google Scholar] [CrossRef] [PubMed]
- Abe, H.; Aquilanti, G.; Boada, R.; Bunker, B.; Glatzel, P.; Nachtegaal, M.; Pascarelli, S. Improving the quality of XAFS data. J. Synchrotron Radiat. 2018, 25, 972–980. [Google Scholar] [CrossRef] [PubMed]
- Monochromator Crystal Glitch Library. Available online: https://www-ssrl.slac.stanford.edu/~xas/glitch/glitch.html (accessed on 16 March 2021).
- Wallace, S.M.; Alsina, M.A.; Gaillard, J.F. An algorithm for the automatic deglitching of X-ray absorption spectroscopy data. arXiv 2020, arXiv:2011.14467. [Google Scholar]
- ALBA Synchrotron. Laue Spots Identification in Channel Cut Monochromators. Available online: https://intranet.cells.es/Beamlines/MSPD/Laue_spots_ccm/index (accessed on 16 March 2021).
- Element Six Ltd. Available online: https://www.e6.com/ (accessed on 16 March 2021).
- Micro Usinage Laser. Available online: http://micro-usinage-laser.com/ (accessed on 16 March 2021).
- Polikarpov, M.; Snigireva, I.; Morse, J.; Yunkin, V.; Kuznetsov, S.; Snigirev, A. Large-acceptance diamond planar refractive lenses manufactured by laser cutting. J. Synchrotron Radiat. 2015, 22, 23–28. [Google Scholar] [CrossRef] [PubMed]
- New Diamond Technology. Available online: http://ndtcompany.com/ (accessed on 16 March 2021).
- Terentyev, S.; Blank, V.; Polyakov, S.; Zholudev, S.; Snigirev, A.; Polikarpov, M.; Kolodziej, T.; Qian, J.; Zhou, H.; Shvyd’Ko, Y. Parabolic single-crystal diamond lenses for coherent x-ray imaging. Appl. Phys. Lett. 2015, 107, 111108. [Google Scholar] [CrossRef]
- Zhang, Q.; Polikarpov, M.; Klimova, N.; Larsen, H.B.; Mathiesen, R.; Emerich, H.; Thorkildsen, G.; Snigireva, I.; Snigirev, A. Investigation of glitches induced by single-crystal diamond compound refractive lenses based on crystal orientation. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2054, p. 060007. [Google Scholar] [CrossRef]
- Zhang, Q.; Polikarpov, M.; Klimova, N.; Larsen, H.B.; Mathiesen, R.; Emerich, H.; Thorkildsen, G.; Snigireva, I.; Snigirev, A. Investigation of ‘glitches’ in the energy spectrum induced by single-crystal diamond compound X-ray refractive lenses. J. Synchrotron Radiat. 2019, 26, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Programs to Calculate Glitches in Single-Crystal X-ray Optics. Available online: https://github.com/XrayViz/Glitches (accessed on 15 March 2021).
- Klimova, N.; Yefanov, O.; Snigirev, A. Predicting glitches of intensity in single-crystal diamond CRLs. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2020; Volume 2299, p. 060016. [Google Scholar] [CrossRef]
- Yefanov, O.; Kladko, V.; Slobodyan, M.; Polischuk, Y. XVis: An educational open-source program for demonstration of reciprocal-space construction and diffraction principles. J. Appl. Cryst. 2008, 41, 647–652. [Google Scholar] [CrossRef]
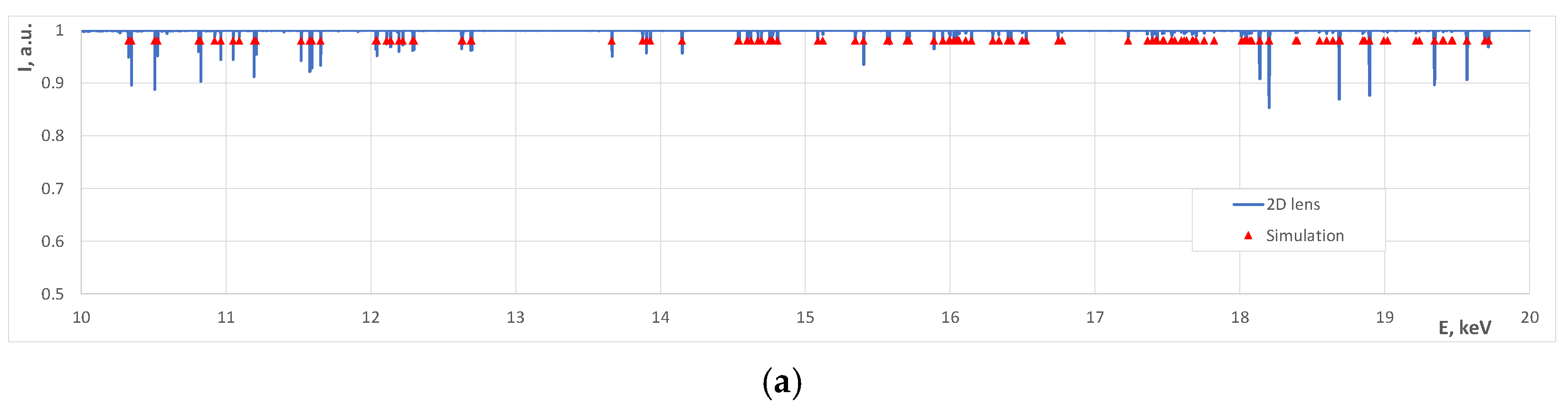
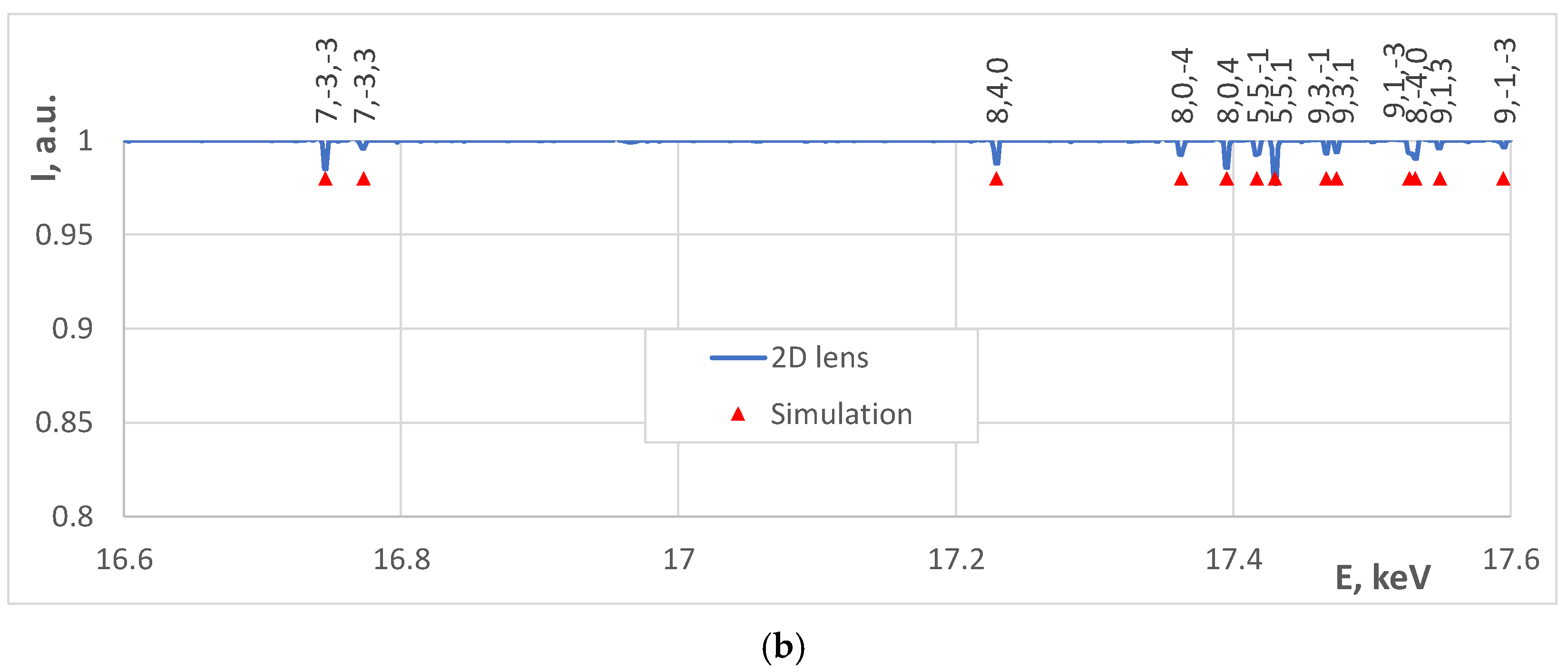
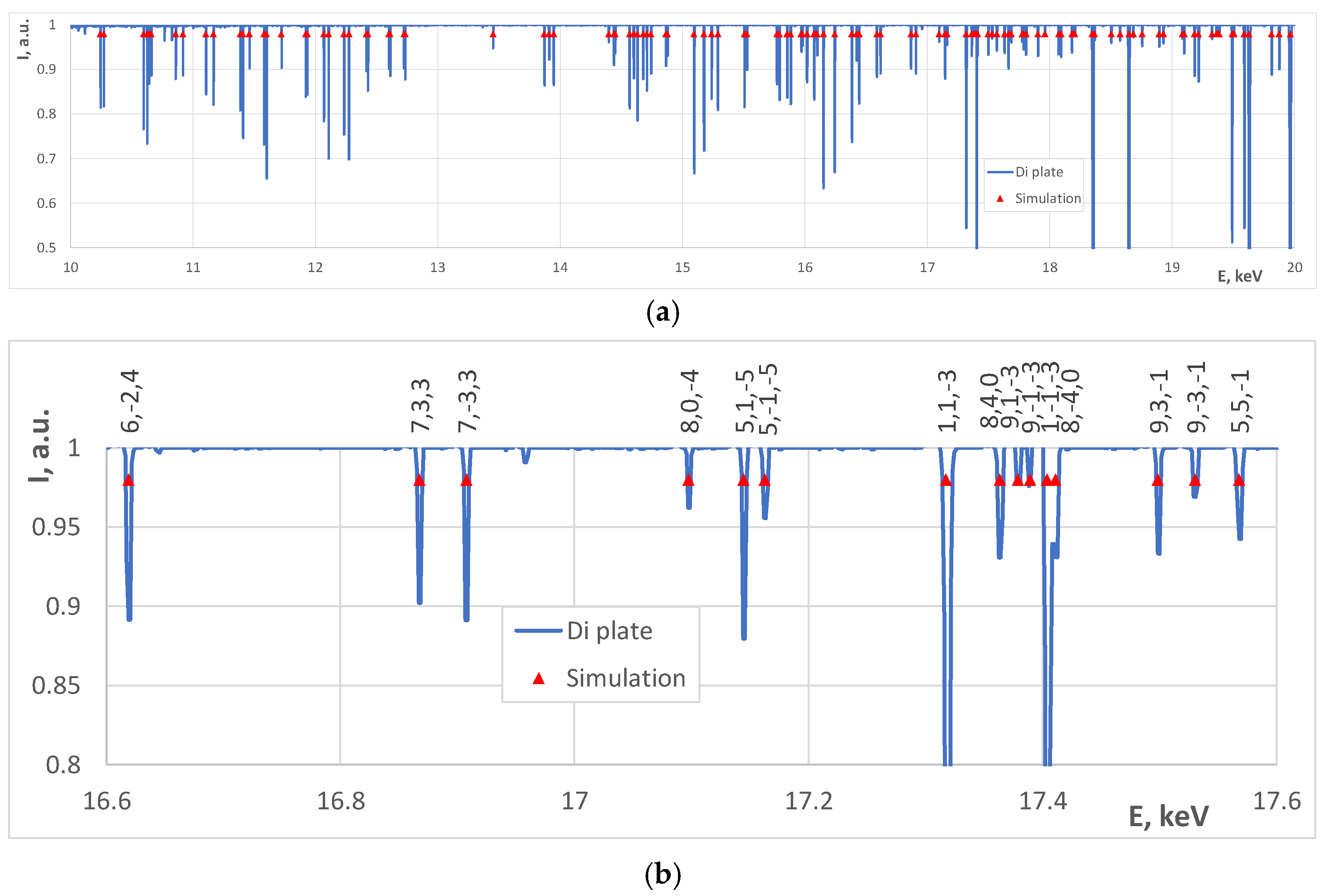
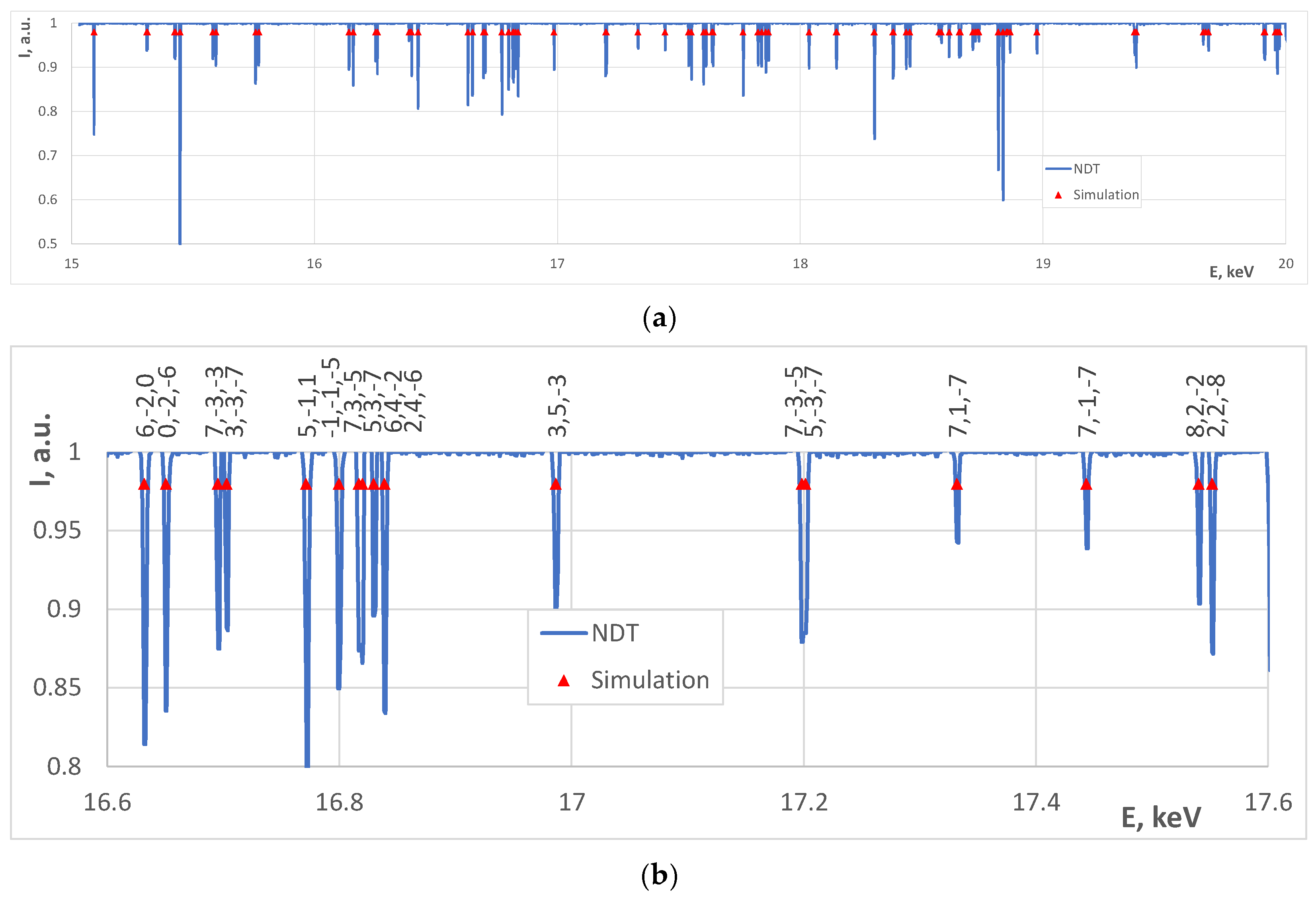
| Object | E Range, keV | χ, ° | UC, Å | ω, ° | ϕ, ° | Error, eV |
|---|---|---|---|---|---|---|
| Plate | 10–20 | 0 | 3.56743 | 1.9414 | 0.1567 | 0.461 |
| NDT | 15–20 | 0 | 3.56729 | 44.9394 | 2.5680 | 0.512 |
| 2D | 10–20 | 0 | 3.56762 | 0.1086 | 0.9965 | 0.496 |
| MUL bulk | 10–20 | 0 | 3.56730 | 4.1069 | 3.8129 | 0.589 |
| 10–20 10–20 | 15 30 | 3.56741 3.56728 | 4.1266 4.1331 | 3.8668 3.9229 | 0.494 0.690 | |
| MUL edge | 10–20 10–20 10–20 | 0 10 20 | 3.56760 3.56756 3.56755 | 4.1069 3.8393 3.8765 | 3.8148 4.1318 4.1414 | 0.671 0.529 0.626 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimova, N.; Yefanov, O.; Snigireva, I.; Snigirev, A. Determination of the Exact Orientation of Single-Crystal X-ray Optics from Its Glitch Spectrum and Modeling of Glitches for an Arbitrary Configuration. Crystals 2021, 11, 504. https://doi.org/10.3390/cryst11050504
Klimova N, Yefanov O, Snigireva I, Snigirev A. Determination of the Exact Orientation of Single-Crystal X-ray Optics from Its Glitch Spectrum and Modeling of Glitches for an Arbitrary Configuration. Crystals. 2021; 11(5):504. https://doi.org/10.3390/cryst11050504
Chicago/Turabian StyleKlimova, Nataliya, Oleksandr Yefanov, Irina Snigireva, and Anatoly Snigirev. 2021. "Determination of the Exact Orientation of Single-Crystal X-ray Optics from Its Glitch Spectrum and Modeling of Glitches for an Arbitrary Configuration" Crystals 11, no. 5: 504. https://doi.org/10.3390/cryst11050504
APA StyleKlimova, N., Yefanov, O., Snigireva, I., & Snigirev, A. (2021). Determination of the Exact Orientation of Single-Crystal X-ray Optics from Its Glitch Spectrum and Modeling of Glitches for an Arbitrary Configuration. Crystals, 11(5), 504. https://doi.org/10.3390/cryst11050504







