Concepts of Nucleation in Polymer Crystallization
Abstract
1. What Makes Nucleation of Polymer Crystals so Difficult?
2. Beyond Thermodynamic Concepts
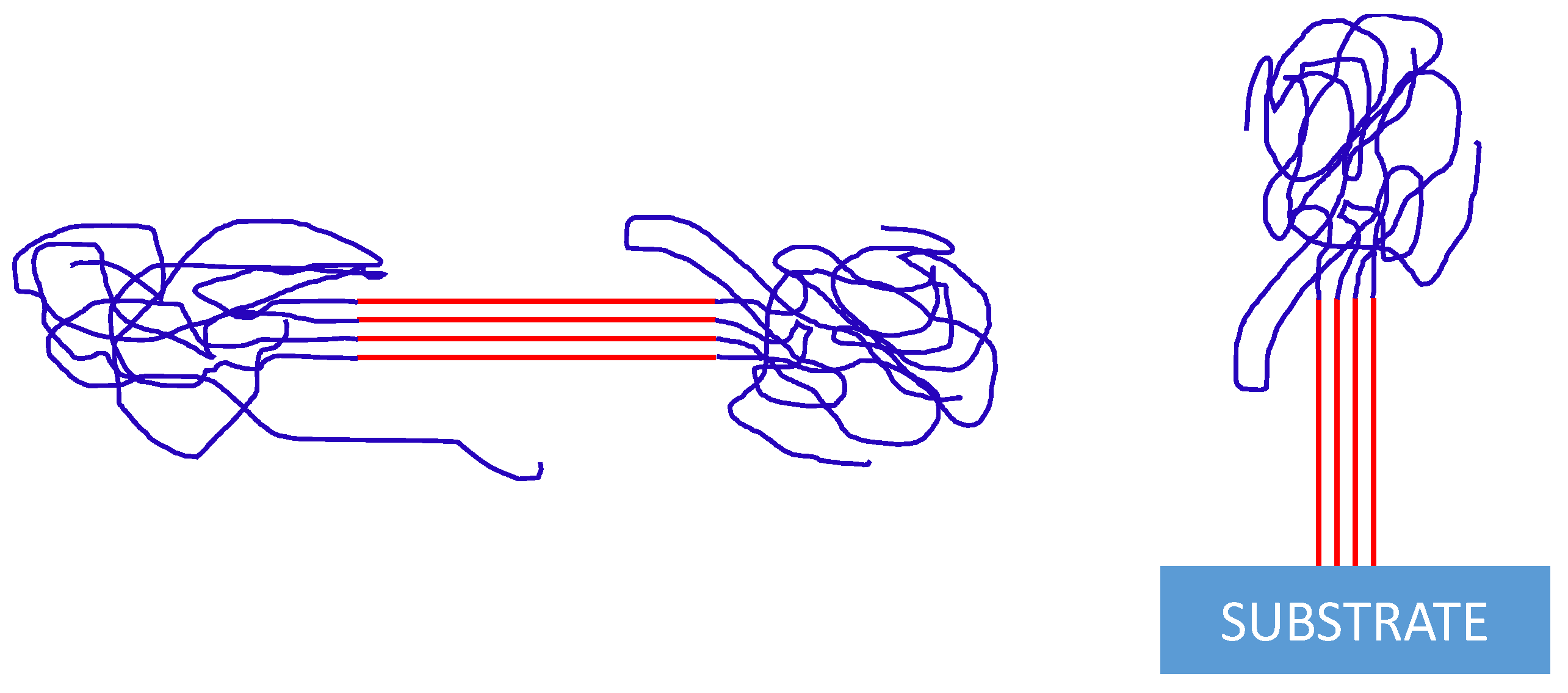
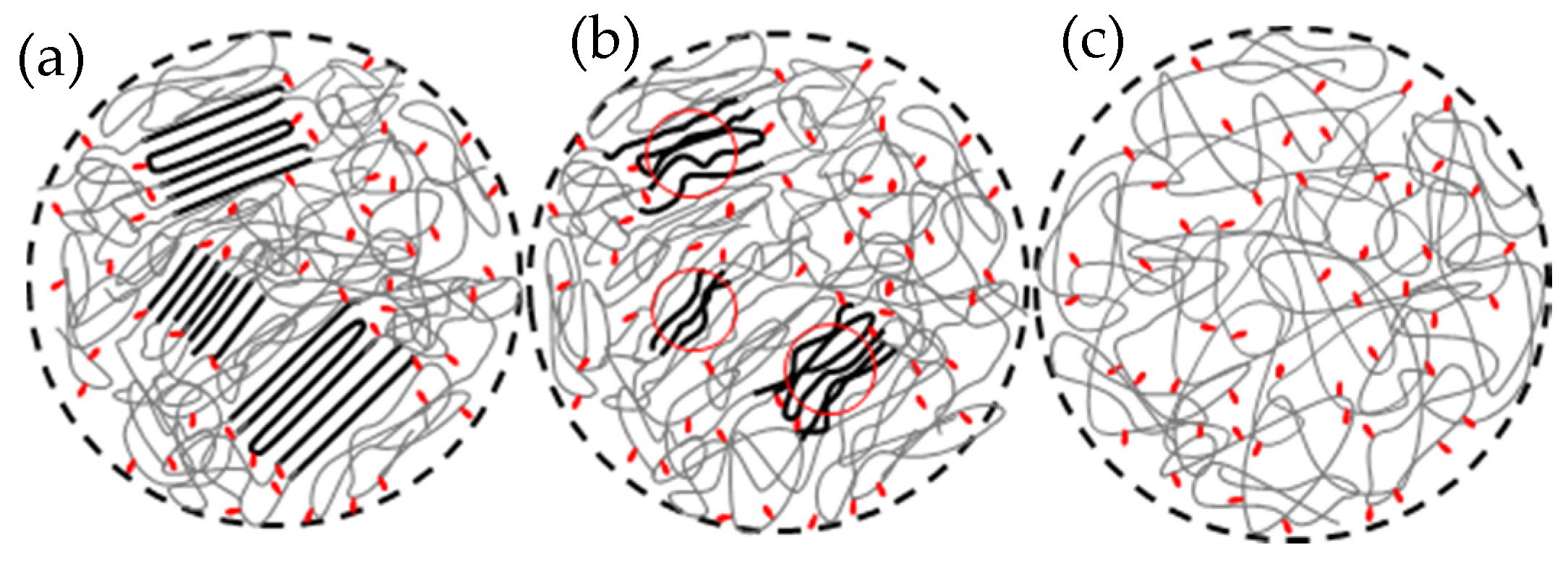
3. Nucleation from Non-Equilibrated Melts
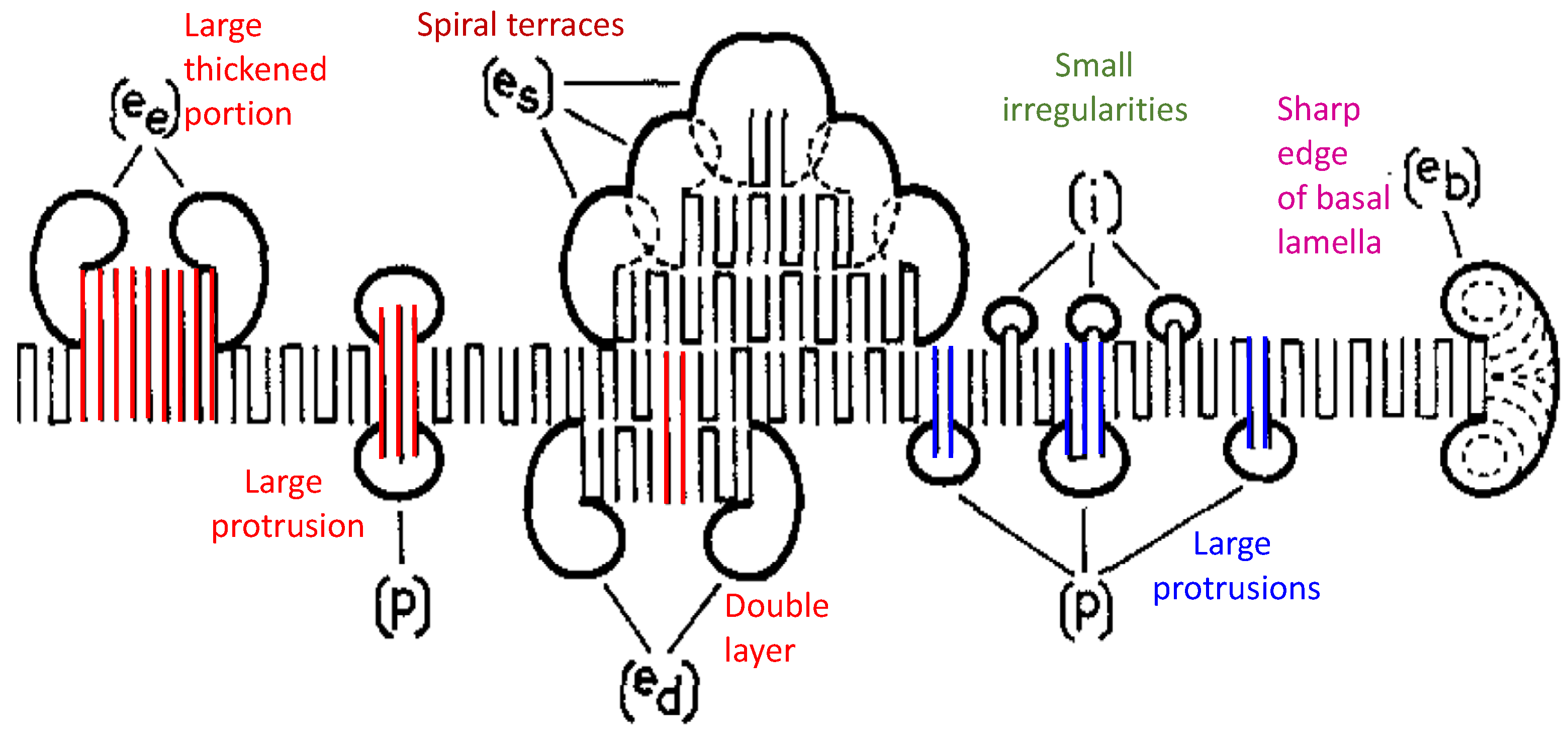
4. Nucleation on the Fold Surface of Polymer Lamellar Single Crystals
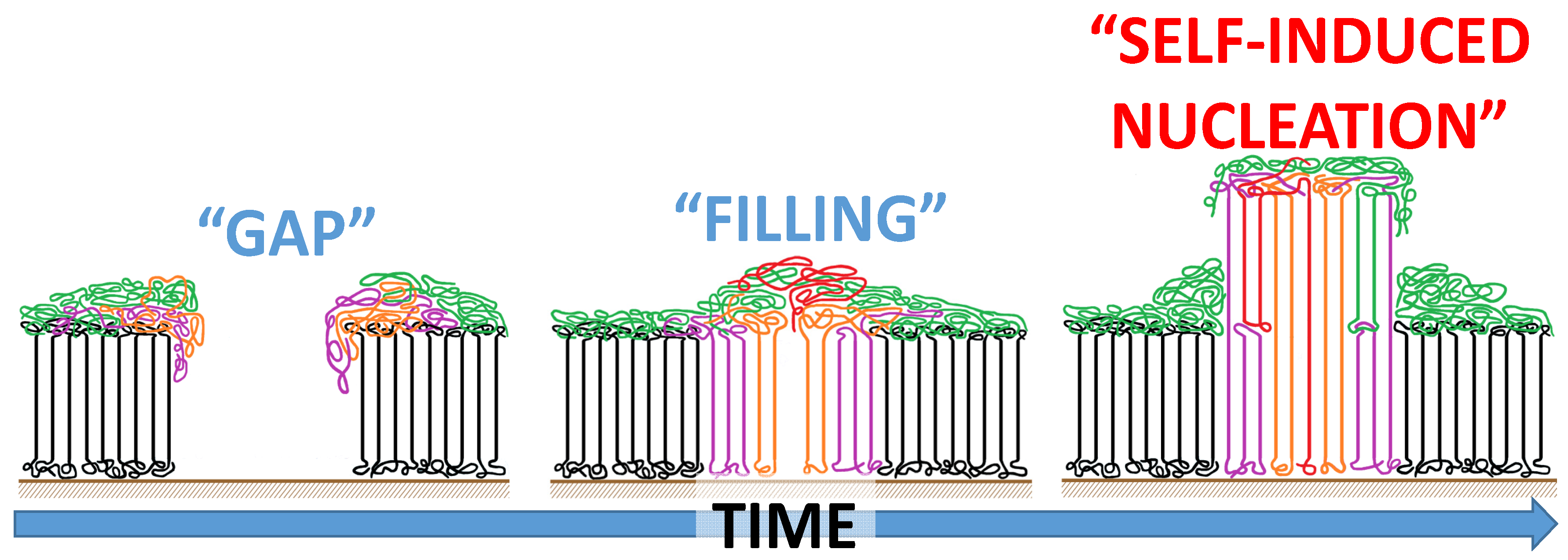
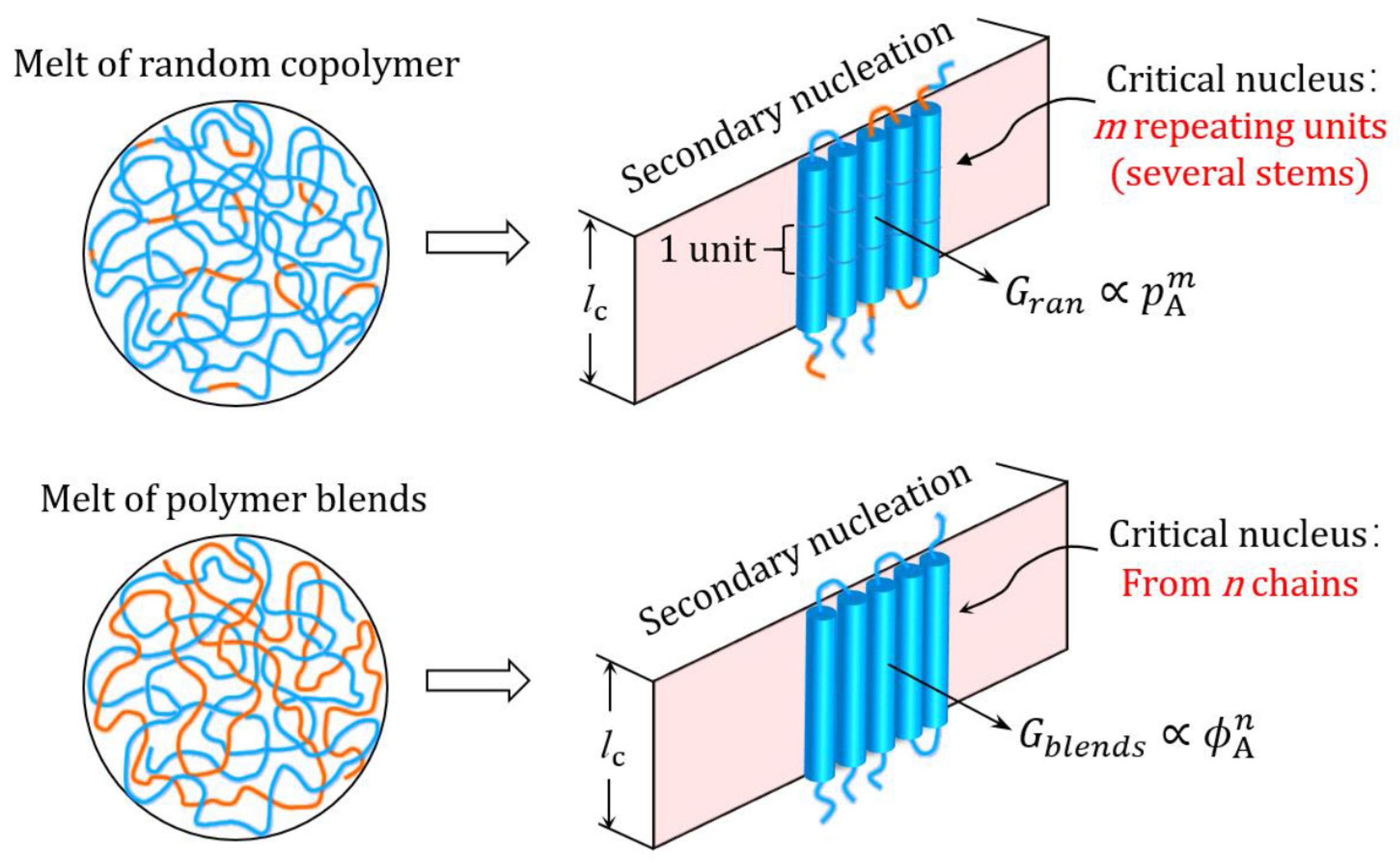
5. Secondary Nucleation on the Lateral Growth Front of Polymer Lamellar Crystals
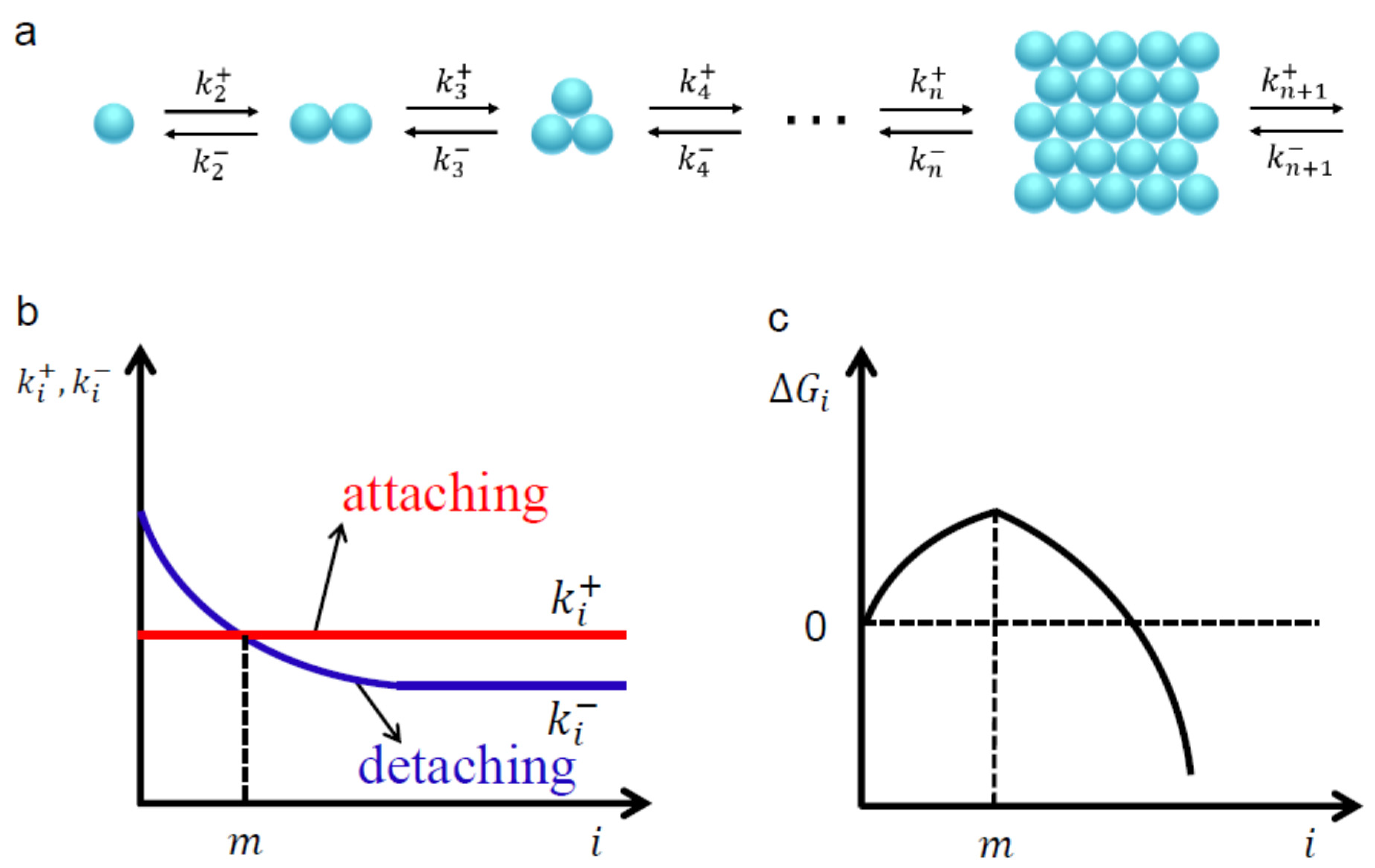
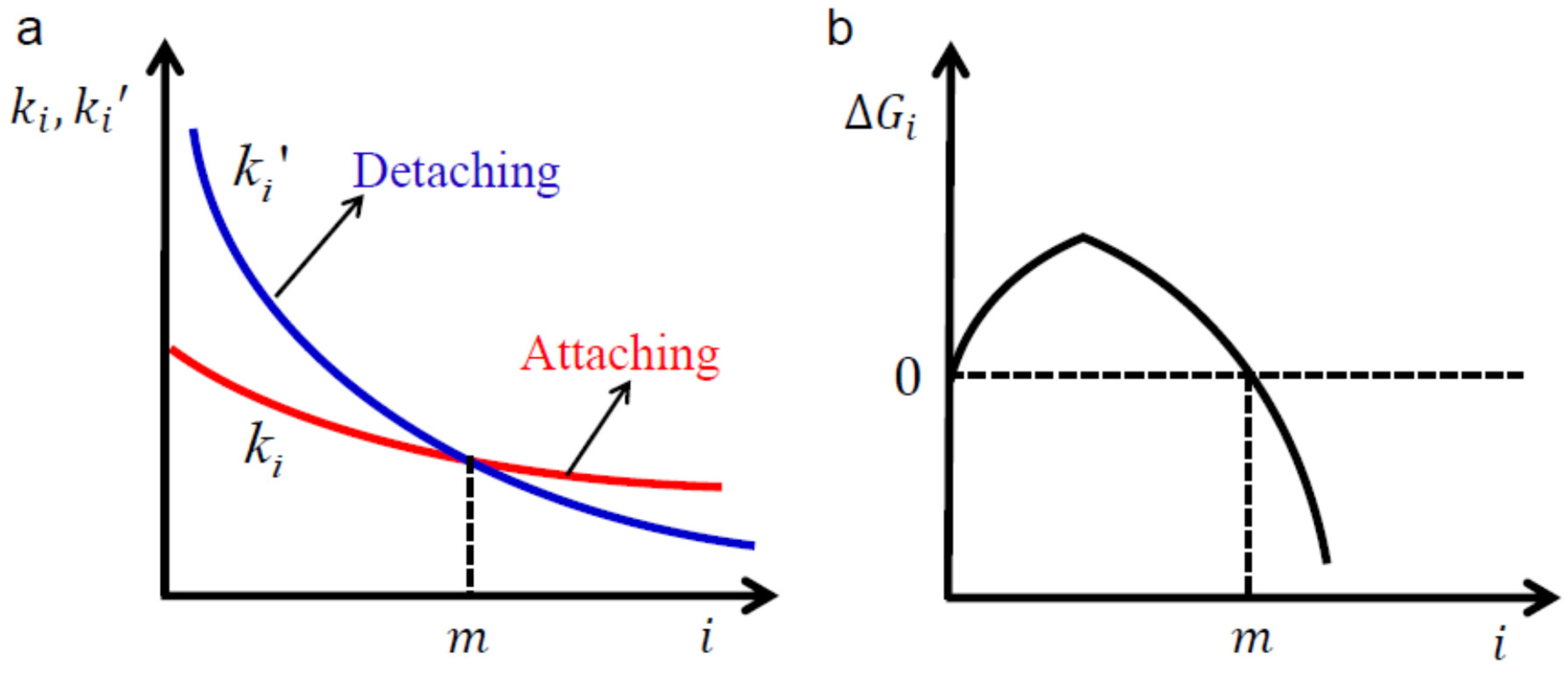
6. Kinetics of Molecular Processes Involved in Nucleation of Crystals
7. Differences in the Kinetics of Nucleation for Polymer Lamellar Crystals and for Small Molecular Crystals
8. Metastability of Polymer Crystals
9. Structural Changes during Nucleation
10. Interesting Observations and its Implications
11. Effect of Nucleation on the Semicrystalline Structure and Final Properties of Polymers
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wittmann, J.C.; Lotz, B. Epitaxial crystallization of polyethylene on organic substrates: A reappraisal of the mode of action of selected nucleating agents. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 1837–1851. [Google Scholar] [CrossRef]
- Vidotto, G.; Levy, D.; Kovacs, A.J. Crystallization and fusion of self-seeding polymers. I. Poly-1-butene, polyethylene and polyoxyethylene of high molecular weight. Kolloid-Z. Z. Polym. 1969, 230, 289–305. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Y.; Hu, W.; Rehahn, M.; Reiter, G. Cloning polymer single crystals through self-seeding. Nat. Mater. 2009, 8, 348–353. [Google Scholar] [CrossRef] [PubMed]
- Mauritz, K.A.; Baer, E.; Hopfinger, A.J. The epitaxial crystallization of macromolecules. J. Polym. Sci. Macromol. Rev. 1978, 13, 1–61. [Google Scholar] [CrossRef]
- Xin, R.; Zhang, J.; Sun, X.; Li, H.; Qiu, Z.; Yan, S. Epitaxial Effects on Polymer Crystallization. Adv. Polym. Sci. 2015, 277, 55–94. [Google Scholar] [CrossRef]
- Miller, R.L. Flow-Induced Crystallization in Polymer Systems; Gordon and Breach Science: New York, NY, USA, 1977. [Google Scholar]
- Li, L.; De Jeu, W.H. Flow-induced mesophases in crystallizable polymers. Interphases and Mesophases in Polymer Crystalli-zation II. Adv. Polym. Sci. 2005, 181, 75–120. [Google Scholar]
- Su, Z.; Dong, M.; Guo, Z.; Yu, J. Study of Polystyrene and Acrylonitrile-Styrene Copolymer as Special β-Nucleating Agents to Induce the Crystallization of Isotactic Polypropylene. Macromolecules 2007, 40, 4217–4224. [Google Scholar] [CrossRef]
- Fillon, B.; Wittmann, J.C.; Lotz, B.; Thierry, A. Self-nucleation and recrystallization of isotactic polypropylene (α phase) investigated by differential scanning calorimetry. J. Polym. Sci. Part B Polym. Phys. 1993, 31, 1383–1393. [Google Scholar] [CrossRef]
- Reid, B.O.; Vadlamudi, M.; Mamun, A.; Janani, H.; Gao, H.; Hu, W.; Alamo, R.G. Strong memory effect of crystallization above the equilibrium melting point of random copolymers. Macromolecules 2013, 46, 6485–6497. [Google Scholar] [CrossRef]
- Mamun, A.; Chen, X.; Alamo, R.G. Interplay between a strong memory effect of crystallization and liquid-liquid phase sepa-ration in melts of broadly distributed ethylene-1-alkene copolymers. Macromolecules 2014, 47, 7958–7970. [Google Scholar] [CrossRef]
- Sangroniz, L.; Cavallo, D.; Santamaria, A.; Müller, A.J.; Alamo, R.G. Thermo-rheologically complex self-seeded melts of pro-pylene-ethylene copolymers. Macromolecules 2017, 50, 642–651. [Google Scholar] [CrossRef]
- Sangroniz, L.; Cavallo, D.; Müller, A.J. Self-Nucleation Effects on Polymer Crystallization. Macromolecules 2020, 53, 4581–4604. [Google Scholar] [CrossRef]
- Fischer, E.W.; Schmidt, G.F. Long Periods in Drawn Polyethylene. Angew. Chem. Int. Ed. 1962, 1, 488–499. [Google Scholar] [CrossRef]
- Chen, X.; Qu, C.; Alamo, R.G. Effect of annealing time and molecular weight on melt memory of random ethylene 1-butene copolymers. Polym. Int. 2019, 68, 248–256. [Google Scholar] [CrossRef]
- Chen, X.; Mamun, A.; Alamo, R.G. Effect of level of crystallinity on melt memory above the equilibrium melting temperature in a random ethylene 1-butene copolymer. Macromol. Chem. Phys. 2015, 216, 1220–1226. [Google Scholar] [CrossRef]
- Kovacs, A.J.; Gonthier, A. Crystallization and fusion of self-seeded polymers. 2. Growth-rate, morphology and isothermal thickening of single-crystals of low molecular-weight poly(ethylene-oxide) fractions. Kolloid-Z. Z. Polym. 1972, 250, 530–551. [Google Scholar] [CrossRef]
- Keith, H.; Chen, W. On the origins of giant screw dislocations in polymer lamellae. Polymer 2002, 43, 6263–6272. [Google Scholar] [CrossRef]
- Kaner, P.; Ruiz-Orta, C.; Boz, E.; Wagener, K.B.; Tasaki, M.; Tashiro, K.; Alamo, R.G. Kinetic Control of Chlorine Packing in Crystals of a Precisely Substituted Polyethylene. Toward Advanced Polyolefin Materials. Macromolecules 2013, 47, 236–245. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, M.; Zhang, B.; Reiter, R.; Vielhauer, M.; Mülhaupt, R.; Xu, J.; Reiter, G. Correlating Polymer Crystals via Self-Induced Nucleation. Phys. Rev. Lett. 2014, 112, 237801. [Google Scholar] [CrossRef]
- Majumder, S.; Reiter, R.; Xu, J.; Reiter, G. Controlling the Growth of Stacks of Correlated Lamellar Crystals of a Block Copolymer. Macromolecules 2019, 52, 9665–9671. [Google Scholar] [CrossRef]
- Majumder, S.; Poudel, P.; Zhang, H.; Xu, J.; Reiter, G. A nucleation mechanism leading to stacking of lamellar crystals in polymer thin films. Polym. Int. 2020, 69, 1058–1065. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Phase Separation in Polymer Solutions under Extension. Polym. Sci. Ser. C 2018, 60, 106–117. [Google Scholar] [CrossRef]
- Alfonso, G.C.; Ziabicki, A. Memory effects in isothermal crystallization II. Isotactic polypropylene. Colloid Polym. Sci. 1995, 273, 317–323. [Google Scholar] [CrossRef]
- Zhang, Y.-S.; Zhong, L.-W.; Yang, S.; Liang, D.-H.; Chen, E.-Q. Memory effect on solution crystallization of high molecular weight poly (ethylene oxide). Polymer 2012, 53, 3621–3628. [Google Scholar] [CrossRef]
- Mamun, A.; Umemoto, S.; Okui, N.; Ishihara, N. Self-Seeding Effect on Primary Nucleation of Isotactic Polystyrene. Macromolecules 2007, 40, 6296–6303. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Arnal, M.L.; Sanchez, J.J.; Müller, A.J. Effect of annealing time on the self-nucleation behavior of semicrystal-line polymers. J. Polym. Sci. B Polym. Phys. 2006, 44, 1738–1750. [Google Scholar] [CrossRef]
- Häfele, A.; Heck, B.; Hippler, T.; Kawai, T.; Kohn, P.; Strobl, G. Crystallization of poly(ethylene-co-octene): II Melt memory effects on first order kinetics. Eur. Phys. J. E 2005, 16, 217–224. [Google Scholar] [CrossRef]
- Ergoz, E.; Fatou, J.G.; Mandelkern, L. Molecular Weight Dependence of the Crystallization Kinetics of Linear Polyethylene. I. Experimental Results. Macromolecules 1972, 5, 147–157. [Google Scholar] [CrossRef]
- Supaphol, P.; Spruiell, J.E. Crystalline memory effects in isothermal crystallization of syndiotactic polypropylene. J. Appl. Polym. Sci. 2000, 75, 337–346. [Google Scholar] [CrossRef]
- Hu, W.; Mathot, V.B.F.; Alamo, R.G.; Gao, H.; Chen, X. Crystallization of Statistical Copolymers. Adv. Polym. Sci. 2016, 276, 1–43. [Google Scholar] [CrossRef]
- Gao, H.; Vadlamudi, M.; Alamo, R.G.; Hu, W. Monte Carlo simulations of strong memory effect of crystallization in random copolymers. Macromolecules 2013, 46, 6498–6506. [Google Scholar] [CrossRef]
- Fernández-D’Arlas, B.; Balko, J.; Baumann, R.P.; Pöselt, E.; Dabbous, R.; Eling, B.; Thurn-Albrecht, T.; Müller, A.J. Tailoring the morphology and melting points of segmented thermoplastic polyurethanes by self-nucleation. Macromolecules 2016, 49, 7952–7964. [Google Scholar] [CrossRef]
- Luo, C.; Sommer, J.-U. Frozen topology: Entanglements control nucleation and crystallization in polymers. Phys. Rev. Lett. 2014, 112, 195702. [Google Scholar] [CrossRef]
- Maus, A.; Hempel, E.; Thurn-Albrecht, T.; Saalwaechter, K. Memory effect in isothermal crystallization of syndiotactic poly-propylene Role of melt structure and dynamics? Eur. Phys. J. E 2007, 23, 91–101. [Google Scholar] [CrossRef]
- Hamad, F.G.; Colby, R.H.; Milner, S.T. Lifetime of Flow-Induced Precursors in Isotactic Polypropylene. Macromolecules 2015, 48, 7286–7299. [Google Scholar] [CrossRef]
- Schamme, B.; Dargent, E.; Fernandez-Ballester, L. Effect of random ethylene comonomer on relaxation of flow-induced pre-cursors in isotactic polypropylene. Macromolecules 2017, 50, 6396–6403. [Google Scholar] [CrossRef]
- Klein, J.; Briscoe, B.J. The diffusion of long-chain molecules through bulk polyethelene. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1979, 365, 53–73. [Google Scholar] [CrossRef]
- Bartels, C.R.; Crist, B.; Graessley, W.W. Self-diffusion coefficient in melts of linear polymers: Chain length and temperature dependence for hydrogenated polybutadiene. Macromolecules 1984, 17, 2702–2708. [Google Scholar] [CrossRef]
- Schuman, T.; Stepanov, E.V.; Nazarenko, S.; Capaccio, G.; Hiltner, A.; Baer, E. Interdiffusion of linear and branched poly-ethylene in microlayers studied via melting behavior. Macromolecules 1998, 31, 4551–4561. [Google Scholar] [CrossRef]
- Tao, H.; Lodge, T.P.; Von Meerwall, E.D. Diffusivity and Viscosity of Concentrated Hydrogenated Polybutadiene Solutions. Macromolecules 2000, 33, 1747–1758. [Google Scholar] [CrossRef]
- Muthukumar, M. Communication: Theory of melt-memory in polymer crystallization. J. Chem. Phys. 2016, 145, 031105. [Google Scholar] [CrossRef]
- Mandelkern, L. Crystalline-amorphous interphase in polymeric systems. Chemtracts-Macromol. Chem. 1992, 3, 347. [Google Scholar]
- Reiter, G. ChemInform Abstract: Some Unique Features of Polymer Crystallization. Chem. Soc. Rev. 2014, 45, 2055–2065. [Google Scholar] [CrossRef]
- Wunderlich, B. Macromolecular Physics, Volume 1: Crystal Structure, Morphology, Defects; Academic Press: Mishawaka, IN, USA, 1973. [Google Scholar]
- Geil, P.H.; Reneker, D.H. Morphology of dendritic polyethylene crystals. J. Polym. Sci. 1961, 51, 569–582. [Google Scholar] [CrossRef]
- Geil, P.H. Polymer Single Crystals; Interscience: New York, NY, USA, 1963. [Google Scholar]
- Wang, Y.; Chan, C.-M.; Ng, K.-M.; Jiang, Y.; Li, L. Real-Time Observation of Lamellar Branching Induced by an AFM Tip and the Stability of Induced Nuclei. Langmuir 2004, 20, 8220–8223. [Google Scholar] [CrossRef] [PubMed]
- Voigt-Martin, I.G.; Mandelkern, L. A quantitative electron microscopic study of the crystallite structure of molecular weight fractions of linear polyethylene. J. Polym. Sci. Polym. Phys. Ed. 1984, 22, 1901–1917. [Google Scholar] [CrossRef]
- Lauritzen, J.I.; Hoffman, J.D. Theory of formation of polymer crystals with folded chains in dilute solution. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1960, 64, 73–102. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, J.D.; Lauritzen, J.I., Jr. Crystallization of bulk polymers with chain folding: Theory of growth of lamellar spherulites. J. Res. Natl. Bur. Stand. A 1961, 65, 297–336. [Google Scholar] [CrossRef]
- Sadler, D.; Gilmer, G. A model for chain folding in polymer crystals: Rough growth faces are consistent with the observed growth rates. Polymer 1984, 25, 1446–1452. [Google Scholar] [CrossRef]
- Sadler, D.M.; Gilmer, G.H. Rate-Theory Model of Polymer Crystallization. Phys. Rev. Lett. 1986, 56, 2708–2711. [Google Scholar] [CrossRef]
- Wunderlich, B.; Mehta, A. Macromolecular nucleation. J. Polym. Sci. Polym. Phys. Ed. 1974, 12, 255–263. [Google Scholar] [CrossRef]
- Wunderlich, B. Molecular nucleation and segregation. Faraday Discuss. Chem. Soc. 1979, 68, 239–243. [Google Scholar] [CrossRef]
- Hu, W.; Frenkel, D.; Mathot, V.B.F. Intramolecular Nucleation Model for Polymer Crystallization. Macromolecules 2003, 36, 8178–8183. [Google Scholar] [CrossRef]
- Kundagrami, A.; Muthukumar, M. Continuum theory of polymer crystallization. J. Chem. Phys. 2007, 126, 144901. [Google Scholar] [CrossRef]
- Strobl, G. From the melt via mesomorphic and granular crystalline layers to lamellar crystallites: A major route followed in polymer crystallization? Eur. Phys. J. E 2000, 3, 165–183. [Google Scholar] [CrossRef]
- Strobl, G. Colloquium: Laws controlling crystallization and melting in bulk polymers. Rev. Mod. Phys. 2009, 81, 1287–1300. [Google Scholar] [CrossRef]
- Alamo, R.G.; Viers, B.D.; Mandelkern, L. A Re-examination of the Relation between the Melting Temperature and the Crys-tallization Temperature: Linear Polyethylene. Macromolecules 1995, 28, 3205–3213. [Google Scholar] [CrossRef]
- Xu, J.; Heck, B.; Ye, H.-M.; Jiang, J.; Tang, Y.-R.; Liu, J.; Guo, B.-H.; Reiter, R.; Zhou, D.-S.; Reiter, G. Stabilization of Nuclei of Lamellar Polymer Crystals: Insights from a Comparison of the Hoffman-Weeks Line with the Crystallization Line. Macromolecules 2016, 49, 2206–2215. [Google Scholar] [CrossRef]
- Zhang, S.; Han, J.; Gao, Y.; Guo, B.; Reiter, G.; Xu, J. Determination of the Critical Size of Secondary Nuclei on the Lateral Growth Front of Lamellar Polymer Crystals. Macromolecules 2019, 52, 7439–7447. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, B.; Reiter, G.; Xu, J. Estimation of the Size of Critical Secondary Nuclei of Melt-Grown Poly(l-lactide) Lamellar Crystals. Macromolecules 2020, 53, 3482–3492. [Google Scholar] [CrossRef]
- Volmer, M.; Weber, A. Nucleus Formation in Supersaturated Systems. Z. Phys. Chem. 1926, 119, 277–301. [Google Scholar]
- Becker, R.; Döring, W. Kinetische behandlung der keimbildung in übersättigten dämpfen. Ann. Phys. 1935, 416, 719–752. [Google Scholar] [CrossRef]
- Turnbull, D.; Fisher, J.C. Rate of Nucleation in Condensed Systems. J. Chem. Phys. 1949, 17, 71–73. [Google Scholar] [CrossRef]
- Lauritzen, J.I.; Hoffman, J.D. Extension of theory of growth of chain-folded polymer crystals to large undercoolings. J. Appl. Phys. 1973, 44, 4340–4352. [Google Scholar] [CrossRef]
- Stamm, M. Influence of the conformation of polyethylene on wide-angle neutron scattering patterns. J. Polym. Sci. Polym. Phys. Ed. 1982, 20, 235–244. [Google Scholar] [CrossRef]
- Fischer, E.W. Neutron Scattering Studies on the Crystallization of Polymers. Polym. J. 1985, 17, 307–320. [Google Scholar] [CrossRef]
- Hong, Y.-L.; Miyoshi, T. Chain-Folding Structure of a Semicrystalline Polymer in Bulk Crystals Determined by13C-13C Double Quantum NMR. ACS Macro Lett. 2013, 2, 501–505. [Google Scholar] [CrossRef]
- Hong, Y.; Koga, T.; Miyoshi, T. Chain trajectory and crystallization mechanism of a semicrystalline polymer in melt-and so-lution-grown crystals as studied using 13C-13C double quantum NMR. Macromolecules 2015, 48, 3282–3293. [Google Scholar] [CrossRef]
- Ma, Z.; Yang, P.; Zhang, X.; Jiang, K.; Song, Y.; Zhang, W. Quantifying the chain folding in polymer single crystals by single-molecule force spectroscopy. ACS Macro Lett. 2019, 8, 1194–1199. [Google Scholar] [CrossRef]
- Muthukumar, M. Nucleation in Polymer Crystallization. Adv. Chem. Phys. 2004, 128, 1–63. [Google Scholar] [CrossRef]
- Yokota, H.; Kawakatsu, T. Nucleation theory of polymer crystallization with conformation entropy. Polymer 2020, 186, 121975. [Google Scholar] [CrossRef]
- Marand, H.; Huang, Z. Isothermal Lamellar Thickening in Linear Polyethylene: Correlation between the Evolution of the Degree of Crystallinity and the Melting Temperature. Macromolecules 2004, 37, 6492–6497. [Google Scholar] [CrossRef]
- Toda, A.; Androsch, R.; Schick, C. Insights into polymer crystallization and melting from fast scanning chip calorimetry. Polymer 2016, 91, 239–263. [Google Scholar] [CrossRef]
- Xie, Z.-N.; Ye, H.-M.; Chen, T.; Zheng, T.-Z.; Xu, J.; Guo, B.-H. Melting and Annealing Peak Temperatures of Poly (butylene succinate) on the Same Hoffman-Weeks Plot Parallel to Tm = Tc Line. Chin. J. Polym. Sci. 2020. [Google Scholar] [CrossRef]
- Alamo, R.G.; Chan, E.K.M.; Mandelkern, L.; Voigt-Martin, I.G. Influence of molecular weight on the melting and phase structure of random copolymers of ethylene. Macromolecules 1992, 25, 6381–6394. [Google Scholar] [CrossRef]
- Kim, M.H.; Phillips, P.J.; Lin, J.S. The equilibrium melting points of random ethylene-octene copolymers: A test of the Flory and Sanchez-Eby theories. J. Polym. Sci. Part B Polym. Phys. 2000, 38, 154–170. [Google Scholar] [CrossRef]
- Furushima, Y.; Toda, A.; Rousseaux, V.; Bailly, C.; Zhuravlev, E.; Schick, C. Quantitative understanding of two distinct melting kinetics of an isothermally crystallized poly (ether ether ketone). Polymer 2016, 99, 97–104. [Google Scholar] [CrossRef]
- Jariyavidyanont, K.; Androsch, R.; Schick, C. Crystal reorganization of poly (butylene terephthalate). Polymer 2017, 124, 274–283. [Google Scholar] [CrossRef]
- Toda, A.; Taguchi, K.; Nozaki, K.; Guan, X.; Hu, W.; Furushima, Y.; Schick, C. Crystallization and melting of poly (butylene terephthalate) and poly (ethylene terephthalate) investigated by fast-scan chip calorimetry and small angle X-ray scattering. Polymer 2020, 192, 122303. [Google Scholar] [CrossRef]
- Broadhurst, M.G. An analysis of the solid phase behavior of the normal paraffins. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1962, 66, 241. [Google Scholar] [CrossRef]
- Mandelkern, L.; Prasad, A.; Alamo, R.G.; Stack, G.M. Melting temperature of the n-alkanes and the linear polyethylenes. Macromolecules 1990, 23, 3696–3700. [Google Scholar] [CrossRef]
- Ye, H.-M.; Chen, X.-T.; Liu, P.; Wu, S.-Y.; Jiang, Z.; Xiong, B.; Xu, J. Preparation of poly (butylene succinate) crystals with ex-ceptionally high melting point and crystallinity from its inclusion complex. Macromolecules 2017, 50, 5425–5433. [Google Scholar] [CrossRef]
- Ye, H.-M.; Chen, X.-T.; Li, H.-F.; Zhang, P.; Ma, W.; Li, B.; Xu, J. Industrializable and sustainable approach for preparing extended-chain crystals of biodegradable poly (butylene succinate) and their applications. Polymer 2019, 160, 93–98. [Google Scholar] [CrossRef]
- Tang, X.; Chen, W.; Li, L. The Tough Journey of Polymer Crystallization: Battling with Chain Flexibility and Connectivity. Macromolecules 2019, 52, 3575–3591. [Google Scholar] [CrossRef]
- Jaric, M.V. Long-Range Icosahedral Orientational Order and Quasicrystals. Phys. Rev. Lett. 1985, 55, 607–610. [Google Scholar] [CrossRef]
- Tang, X.; Yang, J.; Xu, T.; Tian, F.; Xie, C.; Li, L. Local structure order assisted two-step crystal nucleation in polyethylene. Phys. Rev. Mater. 2017, 1, 073401. [Google Scholar] [CrossRef]
- Stolte, I.; Androsch, R.; Di Lorenzo, M.L.; Schick, C. Effect of Aging the Glass of Isotactic Polybutene-1 on Form II Nucleation and Cold Crystallization. J. Phys. Chem. B 2013, 117, 15196–15203. [Google Scholar] [CrossRef] [PubMed]
- Vekilov, P.G. Dense Liquid Precursor for the Nucleation of Ordered Solid Phases from Solution. Cryst. Growth Des. 2004, 4, 671–685. [Google Scholar] [CrossRef]
- Erdemir, D.; Lee, A.Y.; Myerson, A.S. Nucleation of Crystals from Solution: Classical and Two-Step Models. Acc. Chem. Res. 2009, 42, 621–629. [Google Scholar] [CrossRef] [PubMed]
- Gebauer, D.; Kellermeier, M.; Gale, J.D.; Bergström, L.; Cölfen, H. Pre-nucleation clusters as solute precursors in crystallization. Chem. Soc. Rev. 2014, 43, 2348–2371. [Google Scholar] [CrossRef]
- Kimura, T.; Ezure, H.; Tanaka, S.; Ito, E. In situ FTIR spectroscopic study on crystallization process of isotactic polystyrene. J. Polym. Sci. Part B Polym. Phys. 1998, 36, 1227–1233. [Google Scholar] [CrossRef]
- Zhu, X.; Yan, D.; Fang, Y. In Situ FTIR Spectroscopic Study of the Conformational Change of Isotactic Polypropylene during the Crystallization Process. J. Phys. Chem. B 2001, 105, 12461–12463. [Google Scholar] [CrossRef]
- An, H.; Zhao, B.; Ma, Z.; Shao, C.; Wang, X.; Fang, Y.; Li, L.; Li, Z. Shear-Induced Conformational Ordering in the Melt of Isotactic Polypropylene. Macromolecules 2007, 40, 4740–4743. [Google Scholar] [CrossRef]
- Yan, C.; Li, H.; Zhang, J.; Ozaki, Y.; Shen, D.; Yan, D.; Shi, A.C.; Yan, S. Surface-induced anisotropic chain ordering of poly-carprolactone onoriented polyethylene substrate: Epitaxy and soft epitaxy. Macromolecules 2006, 39, 8041–8048. [Google Scholar] [CrossRef]
- Cong, Y.; Hong, Z.; Qi, Z.; Zhou, W.; Li, H.; Liu, H.; Chen, W.; Wang, X.; Li, L. Conformational Ordering in Growing Spherulites of Isotactic Polypropylene. Macromolecules 2010, 43, 9859–9864. [Google Scholar] [CrossRef]
- Ruiz-Orta, C.; Fernandez-Blazquez, J.; Pereira, E.; Alamo, R. Time-resolved FTIR spectroscopic study of the evolution of helical structure during isothermal crystallization of propylene 1-hexene copolymers. Identification of regularity bands associated with the trigonal polymorph. Polymer 2011, 52, 2856–2868. [Google Scholar] [CrossRef]
- Panine, P.; Di Cola, E.; Sztucki, M.; Narayanan, T. Early stages of polymer melt crystallization. Polymer 2008, 49, 676–680. [Google Scholar] [CrossRef]
- Androsch, R.; Schick, C. Interplay between the Relaxation of the Glass of Random l/d-Lactide Copolymers and Homogeneous Crystal Nucleation: Evidence for Segregation of Chain Defects. J. Phys. Chem. B 2016, 120, 4522–4528. [Google Scholar] [CrossRef]
- Androsch, R.; Di Lorenzo, M.L.; Schick, C. Crystal nucleation in random l/d-lactide copolymers. Eur. Polym. J. 2016, 75, 474–485. [Google Scholar] [CrossRef]
- Löhmann, A.-K.; Henze, T.; Thurn-Albrecht, T. Direct observation of prefreezing at the interface melt-solid in polymer crystallization. Proc. Natl. Acad. Sci. USA 2014, 111, 17368–17372. [Google Scholar] [CrossRef] [PubMed]
- Flieger, A.-K.; Schulz, M.; Thurn-Albrecht, T. Interface-Induced Crystallization of Polycaprolactone on Graphite via First-Order Prewetting of the Crystalline Phase. Macromolecules 2017, 51, 189–194. [Google Scholar] [CrossRef]
- Dolynchuk, O.; Tariq, M.; Thurn-Albrecht, T. Phenomenological Theory of First-Order Prefreezing. J. Phys. Chem. Lett. 2019, 10, 1942–1946. [Google Scholar] [CrossRef]
- Chang, H.; Zhang, J.; Li, L.; Wang, Z.; Yang, C.; Takahashi, I.; Ozaki, Y.; Yan, S. A Study on the Epitaxial Ordering Process of the Polycaprolactone on the Highly Oriented Polyethylene Substrate. Macromolecules 2010, 43, 362–366. [Google Scholar] [CrossRef]
- Anzai, T.; Kawauchi, M.; Kawauchi, T.; Kumaki, J. Crystallization Behavior of Single Isotactic Poly (methyl methacrylate) Chains Visualized by Atomic Force Microscopy. J. Phys. Chem. B 2015, 119, 338–347. [Google Scholar] [CrossRef] [PubMed]
- Ono, Y.; Kumaki, J. In Situ Real-Time Observation of Polymer Folded-Chain Crystallization by Atomic Force Microscopy at the Molecular Level. Macromolecules 2018, 51, 7629–7636. [Google Scholar] [CrossRef]
- Razavi, M.; Wang, S.-Q. Why is Crystalline Poly (lactic acid) Brittle at Room Temperature? Macromolecules 2019, 52, 5429–5441. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, S.; Guo, B. Insights from polymer crystallization: Chirality, recognition and competition. Chin. Chem. Lett. 2017, 28, 2092–2098. [Google Scholar] [CrossRef]
- Lai, Y.; Men, Y. Polymorph selection during crystallization of random copolymers. Eur. Polym. J. 2018, 101, 218–224. [Google Scholar] [CrossRef]
- Zhang, X.; Santonja-Blasco, L.; Wagener, K.B.; Boz, E.; Tasaki, M.; Tashiro, K.; Alamo, R.G. Infrared Spectroscopy and X-ray Diffraction Characterization of Dimorphic Crystalline Structures of Polyethylenes with Halogens Placed at Equal Distance along the Backbone. J. Phys. Chem. B 2017, 121, 10166–10179. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W.; Wagener, K.B.; Boz, E.; Alamo, R.G. Effect of Self-Poisoning on Crystallization Kinetics of Dimorphic Precision Polyethylenes with Bromine. Macromolecules 2018, 51, 1386–1397. [Google Scholar] [CrossRef]
- Marxsen, S.F.; Alamo, R.G. Melt-memory of polyethylenes with halogen substitution: Random vs. precise placement. Polymer 2019, 168, 168–177. [Google Scholar] [CrossRef]
- Zhang, X.; Marxsen, S.F.; Ortmann, P.; Mecking, S.; Alamo, R.G. Crystallization of Long-Spaced Precision Polyacetals II: Effect of Polymorphism on Isothermal Crystallization Kinetics. Macromolecules 2020, 53, 7899–7913. [Google Scholar] [CrossRef]
- Zheng, Y.; Pan, P. Crystallization of biodegradable and biobased polyesters: Polymorphism, cocrystallization, and structure-property relationship. Prog. Polym. Sci. 2020, 109, 101291. [Google Scholar] [CrossRef]
- Powers, J.; Hoffman, J.D.; Weeks, J.J.; Quinn, F.A. Crystallization kinetics and polymorphic transformations in polybutene-1. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1965, 69, 335–345. [Google Scholar] [CrossRef]
- Xin, R.; Guo, Z.; Li, Y.; Sun, X.; Xue, M.; Zhang, J.; Yan, S. Morphological Evidence for the Two-Step II-I Phase Transition of Isotactic Polybutene-1. Macromolecules 2019, 52, 7175–7182. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Liu, J.; Duan, Y.; Jiang, S.; Yan, S. On the α → β transition of carbon-coated highly oriented PVDF ultrathin film induced by melt recrystallization. J. Am. Chem. Soc. 2003, 125, 1496–1497. [Google Scholar] [CrossRef]
- Qi, H.; Zhou, H.; Tang, Q.; Lee, J.Y.; Fan, Z.; Kim, S.; Staub, M.C.; Zhou, T.; Mei, S.; Han, L.; et al. Block copolymer crystalsomes with an ultrathin shell to extend blood circulation time. Nat. Commun. 2018, 9, 1–10. [Google Scholar] [CrossRef]
- Mei, S.; Staub, M.; Li, C.Y. Directed nanoparticle assembly through polymer crystallization. Chem. Eur. J. 2020, 26, 349–361. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Chen, J.; Shen, C.; Reiter, G.; Zhang, B. Relation between charge transport and the number of interconnected lamellar poly (3-hexylthiophene) crystals. Macromolecules 2019, 52, 6088–6096. [Google Scholar] [CrossRef]
- Wu, T.; Pfohl, T.; Chandran, S.; Sommer, M.; Reiter, G. Formation of needle-like poly (3-hexylthiophene) crystals from meta-stable solutions. Macromolecules 2020, 53, 8303–8312. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Reiter, G.; Alamo, R.G. Concepts of Nucleation in Polymer Crystallization. Crystals 2021, 11, 304. https://doi.org/10.3390/cryst11030304
Xu J, Reiter G, Alamo RG. Concepts of Nucleation in Polymer Crystallization. Crystals. 2021; 11(3):304. https://doi.org/10.3390/cryst11030304
Chicago/Turabian StyleXu, Jun, Günter Reiter, and Rufina G. Alamo. 2021. "Concepts of Nucleation in Polymer Crystallization" Crystals 11, no. 3: 304. https://doi.org/10.3390/cryst11030304
APA StyleXu, J., Reiter, G., & Alamo, R. G. (2021). Concepts of Nucleation in Polymer Crystallization. Crystals, 11(3), 304. https://doi.org/10.3390/cryst11030304







