Abstract
Ultrafast supercontinuum generation crucially depends on the dispersive properties of the underlying waveguide. This strong dependency allows for tailoring nonlinear frequency conversion and is particularly relevant in the context of waveguides that include geometry-induced resonances. Here, we experimentally uncovered the impact of the relative spectral distance between the pump and the bandgap edge on the supercontinuum generation and in particular on the dispersive wave formation on the example of a liquid strand-based photonic bandgap fiber. In contrast to its air-hole-based counterpart, a bandgap fiber shows a dispersion landscape that varies greatly with wavelength. Particularly due to the strong dispersion variation close to the bandgap edges, nanometer adjustments of the pump wavelength result in a dramatic change of the dispersive wave generation (wavelength and threshold). Phase-matching considerations confirm these observations, additionally revealing the relevance of third order dispersion for interband energy transfer. The present study provides additional insights into the nonlinear frequency conversion of resonance-enhanced waveguide systems which will be relevant for both understanding nonlinear processes as well as for tailoring the spectral output of nonlinear fiber sources.
1. Introduction
Photonic crystal fibers (PCFs) [1,2] represent a sophisticated type of silica microstructured optical fibers that consist of air holes running along the fiber axis and are widely used for supercontinuum generation (SCG) [3,4,5]. In case the cylindrical inclusions forming the periodic lattice in the cladding include a material with a refractive index higher than that of glass (established by fluids [6,7], or solids [8,9]) a photonic bandgap (PBG) structure can form, which allows for light guidance in the low index core in selected spectral domains, which are subsequently referred to as transmission bands. The wavelengths corresponding to minimal core mode transmission (i.e., high loss peaks), named here as resonance wavelength, can be estimated by the condition [10]:
λm = 2 × Dstrand/(m + 0.5) × (nliquid2 − ncore2)0.5 (m = 1,2,3,…)
Here, Dstrand is the diameter of the cylindrical strands. Due to the strong wavelength dependence of this interference effect, PBG fibers (PBGFs) are highly suitable for the spectral filtering of multiple selected wavelengths, with extinction ratios as high as 60 dB/cm [9], or for ultrahigh sensitivity sensors to measure temperature [11] or strain [12]. In addition, the inclusion of resonances into the waveguiding system imposes a unique dispersion landscape [13] that strongly differs from its non-resonant counterpart [14,15] and that for instance leads to a massive increase in the group velocity dispersion (GVD) in close proximity to the edge of the transmission bands. This allowed for the observation of sophisticated nonlinear optical effects in PBGFs, examples of which include the extreme deceleration of the soliton self-frequency shift (SSFS) or the cancellation of the SSFS at the long-wavelength edge of the bandgap regions [16,17]. Within this context another interesting phenomenon is the phase-matched dispersive wave (DW) generation across high attenuation regions between adjacent transmission bands, which for instance has been recently observed in gas-filled anti-resonant fibers [18]. In PBGFs established by high-index fluids [19,20] or high-index germanium-doped inclusions [21], it has been experimentally shown that it is not possible to extend the supercontinuum (SC) bandwidth beyond the bandgap, irrespective of the pump wavelength or power. In a hybrid PCF [22,23] combining the total internal reflection and the bandgap effect, however, DWs can be generated across the resonance in a different transmission band, which was numerically demonstrated [24]. Despite the great success of the reported results, there has been no detailed study on how the wavelength difference between the pump and resonance changes the SCG in PBGFs.
In this work, the impact of the relative spectral distance between the pump and resonance on nonlinear pulse propagation was experimentally demonstrated by using a carbon disulfide (CS2)-based PBGF. Moreover, the influence of third order dispersion on energy transfer between different bandgaps is discussed. This experimental result and discussion could be used for PBGF design to develop characteristic wavelength converters and enhance the flexibility of SCG in the future.
2. Optical Properties of Liquid Strand Bandgap Fiber
The PBGF used in this work was established by a regular air-hole-based endlessly single mode PCF that has been filled by CS2, which has a refractive index substantially higher than that of silica. The used PCF (LMA-5, NKT photonics A/S, Blokken, Birkerød, Denmark, Figure 1a) has a pure silica core (core diameter approx. 5.4 μm, refractive index 1.46 @ 0.7 μm) surrounded by six rings of CS2 strands (diameter Dstrand = 1.44 μm, pitch Λ = 3.6 μm, refractive index 1.61 @ 0.7 μm) that are arranged in a hexagonal lattice with the central strand omitted, forming the defect core region. Since the CS2-filled strands in the cladding have a higher refractive index than the silica core, the fiber shows the PBG effect, i.e., yields spectral regions of high and low transmission. Three PBGs can be identified in the range of 500 nm < λ < 1200 nm from the measured loss spectrum of the fundamental core mode (Figure 1b, filled area with green, cyan and yellow colors). The modal loss of the core mode is determined through spectrally monitoring the filling process, i.e., by selectively taking output spectra during filling process, defining a cutback-like method. Specifically, white light from a broadband source (450–2400 nm, SuperK COMPACT, NKT photonics, Blokken, Birkerød, Denmark) is launched into the empty fiber (length 12 cm) mounted onto optofluidic mounts on both sides, and the transmitted signal is fed to an optical spectrum analyzer (OSA). After coupling and optimizing the transmission through the empty fiber, the optofluidic mount on the output side is filled with CS2 leading to dynamically extending PBG-section starting at the output side with the bandgap loss becoming more and more significant. During the filling process, selected transmitted spectra are acquired via a LabVIEW (National Instruments, Austin, TX, USA) routine. Taking into account the well-known viscosity of CS2 [25] and the strand diameter (Dstrand = 1.44 μm), Washburn’s equation [26] allows determining the filling length from the file’s timestamp. As a consequence, the acquired spectra can be correlated to a particular length of the PBG section and the modal loss can be retrieved via a linear fitting of the transmission (in log scale)/filled length dependency for each wavelength. Here, the data (Figure 1b) are smoothed by a 10 nm moving average for better visualization. The propagation loss of the PCF is neglected here and the scanning speed of the grating of the OSA is not accounted for.
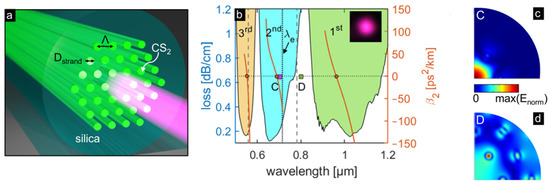
Figure 1.
(a) Sketch of the CS2- photonic bandgap fiber (PBGF) (green: hexagonal array of high-index CS2 strands with diameter Dstrand = 1.44 μm and pitch Λ = 3.6 μm; semitransparent dark green: silica; pink: light emitted from the silica core); (b) measured loss spectrum of the fundamental mode (filled areas with green, cyan and yellow colors, left axis) and the corresponding simulated group velocity dispersion (GVD) parameter β2 (orange, right axis). The orange dots indicate three zero dispersion wavelengths (ZDWs). The two grey dashed vertical lines indicate the calculated resonance wavelengths from Equation (1) with m = 2 and 3. The black dotted line indicates the bandgap edge (−5 dB) at 715 nm of the second order PBG. The inset in (b) is the output beam profile captured by the CCD camera (image extension 265 µm: 50 pixels with each pixel size 5.3 µm). The mode field patterns shown in (c,d) refer to the simulated mode profiles inside a selected transmission band ((c) λ = 700 nm, purple square in (b) labeled C) and inside a resonance region ((d) λ = 800 nm, green square in (b) labeled D).
In our nonlinear experiment, the pump laser wavelength (695–710 nm) located in the second order PBG and its long-wavelength edge (−5 dB) at 715 nm is named λe in the following. As mentioned in the introduction, the resonant nature of the waveguiding mechanism in PBGFs gives rise to very sophisticated dispersion properties. The dispersion of the fundamental core mode (examples of mode patterns within and outside the transmission bands are given in Figure 1c,d) has been simulated using finite-element modeling (COMSOL Multiphysics, COMSOL Inc., Burlington, MA, USA) including material dispersion but neglecting material loss for both silica and CS2 (the material dispersion of CS2 has been taken from Reference [27]). Figure 1b shows the spectral distribution of the GVD parameter β2 = ∂2β/∂ω2 (with the propagation constant β = neff(ω) × ω/c, effective refractive index neff, angular frequency ω, and speed of light in vacuum c) in three transmission bands, which is essential for the SCG process and shows a characteristic evolution within each band with a different sign of β2. This type of behavior is in qualitative accordance with the dispersion of anti-resonance hollow-core fibers [15,28] suggesting a conceptual similarity that results from the general concept of including resonances into the waveguide system for dispersion manipulation, which was also recently demonstrated on the example of dielectric nano-films located on the core of an exposed core fiber [13]. In the present case, the zero dispersion wavelengths (ZDWs) are 553, 689 and 962 nm within these three transmission bands.
3. Nonlinear Experiments—DW Generation
The experimental setup used for the nonlinear experiments is shown in Figure 2. Here, a wavelength-tunable Ti:Sapphire laser system (Chameleon-VIS laser, Coherent, Santa Clara, CA, USA, repetition rate 80 MHz, pulse duration 100 fs) acted as an excitation laser allowing for adjusting the central pump wavelength between 695 nm < λP < 710 nm and thus enabling the investigation of the SCG process as a function of spectral distance between the pump and bandgap edge of PBG Δλ = λe − λP. Note that even though the tuning range of the laser is starting at 690 nm, the laser does not stably operates at this wavelength, thus the investigation starts at 695 nm. Via a combination of a thin-film polarizer and a half-wave plate inserted after the polarized pump laser, the input power launched into the fiber was controlled. The beam was coupled into the core area of the CS2-PBGF (length 0.5 m) using an anti-reflection coated lens (A375-B, Thorlabs, Newton, NJ, USA, focal length 7.5 cm, NA 0.3). A transmission efficiency of 40% (ratio of average output power from the objective and input power before the lens) was achieved. This value was kept constant for different pump wavelengths by slightly adjusting the position of the input lens. The output beam from the fiber was collimated by a 10× objective and guided by a multimode fiber to the spectrometer (AQ-6315A, Ando Electric, Kanagawa, Japan). To monitor the pattern of the mode, a small fraction of the beam was reflected by a wedge and monitored by a CCD camera (Thorlabs, Newton, NJ, USA).
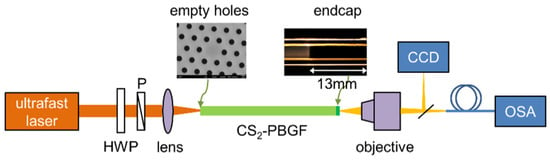
Figure 2.
Sketch of the ultrafast experimental setup to characterize the supercontinuum generation process in the CS2-PBGF (HWP: half-wave plate; P: polarizer; OSA: optical spectrum analyzer). The left top image is the SEM picture of the used PCF without fluid inside. The right top image shows a microscopic image of the spliced endcap (the green part at the end of the CS2-PBGF, details in the main text).
Note that the input side of the CS2-PBGF remains open to the environment, while the output side is blocked by a home-made endcap. The endcap is a short piece of single mode fiber (780-HP, Nufern, CT, USA, length 13 mm), spliced to the output side of the CS2-PBGF to prevent the liquid from evaporating. The reason why there is no endcap at the input side is that the damage of the fiber was observed at low input power in the experiment when the CS2-PBGF was blocked by endcaps at both sides. We also want to stress that mounting the fiber into optofluidic mounts on both sides [29] was not appropriate for this case. After exposure to short pulses, some debris was observed on the surface of the solid core, which caused the coupling efficiency to dramatically drop when the input power was increased. We attribute this damage to the liquid–solid interface within the focal spot: the liquid burns more easily on this interface compared to liquid–core fibers which show only a transition from bulk liquid to liquid core. Therefore, from the practical perspective, we leave the input side of the fiber open to the environment to prevent a liquid–solid interface. This increases the damage threshold of the CS2-PBGF at the expense of fluid evaporation. The evaporating rate of CS2 is measured and the effective sample length is calibrated accordingly (see Appendix A Figure A1 for details). Although the damage threshold can be increased effectively using the present method (the input side left free and the output side blocked by an endcap), fiber damage is still observed at peak powers around 2.5 kW (pulse energy 0.25 nJ).
In our previous numerical simulation work [30], we revealed that the spectral distance between our pump and resonance plays a crucial role in the SCG process of PBGF. In the present work, this impact is studied from the experimental perspective. Figure 3a–e show the nonlinear dynamics of SCG process with an increasing pulse energy for different spectral distances Δλ = λe − λp between the pump λp and the bandgap edge λe of second order PBG. The spectral distance Δλ has important influence on the formation of a DW, which is emitted in the normal dispersion (ND) regime by a soliton that is formed from the input pulse after initial self-phase modulation (SPM). When Δλ is decreased from 20 to 10 nm (Figure 3a–d), the generated DW blue shifts (spectral distance between the pump and DW (ΔλDW = λp – λDW) increases). This is accompanied by a higher threshold for DW generation (Figure 3f), which is associated with the increasing spectral distance between soliton and DW [31]. For the case Δλ = 5 nm, the pump energy is not high enough to generate DW radiation. These experimental results can be supported by simulations of nonlinear pulse propagation based on the generalized nonlinear Schrödinger equation (GNLSE) [32] (see Appendix A Figure A2 for details).
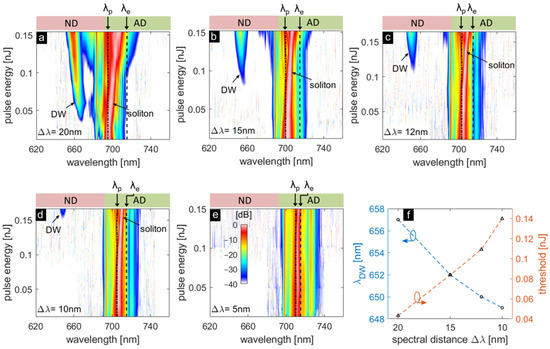
Figure 3.
(a–e) Measured energy/spectral evolutions of the supercontinuum generation (SCG) process in the CS2-PBGF for various spectral distances Δλ= λe − λp between the pump λp and bandgap edge λe of second order PBG ((a–e) Δλ = 20, 15, 12, 10 and 5 nm). The black dashed line indicates λe and the black dash-dotted line indicates λp; (f) dispersive wave (DW) wavelength λDW and threshold of the generated DW both as functions of Δλ.
The significantly different nonlinear pulse evolution for various values of Δλ is caused by the strongly changed dispersion landscape in the vicinity of the bandgap edge. The behavior of DW can be explained particularly by the phase-matching (PM) condition of soliton and DW as outlined in the following. DW generation results from the fission of a higher order soliton into its fundamental counterparts, which release the excess energy to DW. DW generation is most effective at the wavelength that fulfills the PM condition defined by the following equation [4,31]:
ΔβDW(ω) = β(ω) − [β(ωsol) + (ω − ωsol)β1,sol + ½ × γ × Psol]
Here, ω and ωsol are the frequencies of DW and soliton, respectively, β1,sol = ∂β/∂ω|ωsol is the inverse group velocity at ωsol, Psol is the peak power of the assumed first soliton (with input peak power P0 and soliton number N, Psol = (2 − 1/N)2 × P0) [31], and γ = ωsol × n2/c/Aeff is the nonlinear coefficient (Aeff is the effective mode area and n2 is the nonlinear refractive index). The condition ΔβDW = 0 determines the phase-matched spectral location of DW (λDW) in the case the soliton wavelength (λsol) is given or vice versa. Note that in the experiments the observed λsol is located in close proximity to or inside the resonant (high-loss) region and thus this wavelength cannot be unambiguously determined, whilst λDW is clearly visible in the energy/spectral evolutions (Figure 3a–d). Therefore, the λsol is calculated from the measured spectral position and the threshold of DW (taken from its creation position, 667 nm at 0.04 nJ, 657 nm at 0.08 nJ, 654 nm at 0.11 nJ, and 649 nm at 0.15 nJ corresponding to Figure 3a–d, respectively) via Equation (2) and is shown in Figure 4. It can be seen that the solitons are located between 704 nm < λ < 713 nm (marked as gray bar in Figure 4) for the cases of Δλ = 20, 15, 12 and 10 nm, which agrees well with the experimental results in Figure 3a–e. It should be noted that in the dispersion simulation, a small deviation in the hole diameter (2%) will cause a 10 nm deviation of ZDW and thus induce a significant discrepancy from the experimental results (see Appendix A Figure A3 and Table A1 for details). While such structural asymmetries may only have a minor effect on the transmission spectra of anti-resonant reflecting optical waveguide (ARROW) PCFs, it is quite likely that they greatly affect the higher-order dispersion terms that are important for ultrafast nonlinear frequency conversion.
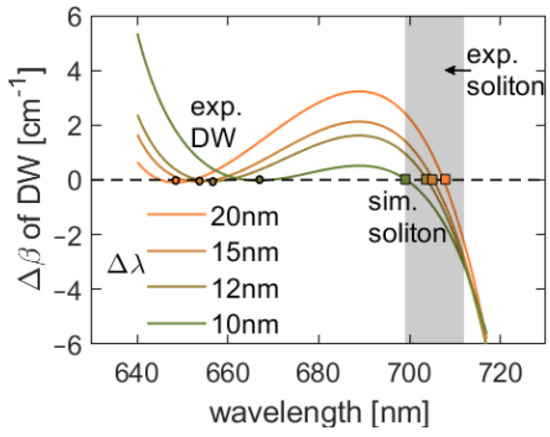
Figure 4.
The calculated phase-mismatching rate of DW generation ΔβDW in the same second order PBG as the pump for different spectral distances Δλ (γ = 6.5 W−1/km, pulse: 100 fs, 80 MHz) using Equation (2). The wavelengths of DWs are taken from the experiments and the Psol is calculated from the DW generation threshold. The corresponding soliton wavelengths are obtained by the crossing of the individual curves with the zero line (Δβ = 0), corresponding to DW-PM. The gray area means the soliton wavelengths taken from experiment.
To clearly demonstrate that filling the PCF with CS2 leads to a massive change of waveguide dispersion and thus to the nonlinear frequency conversion, Figure 5 shows the measured output spectra of the CS2-PBGF (blue) in comparison to the same PCF with air holes (orange) both at the same pump peak power (1.5 kW) and pump wavelength (λp = 700 nm). For the empty PCF, only SPM in close proximity to λp can be observed, whilst efficient DW generation is visible for the CS2-PBGF due to the entirely different dispersion landscape. Note that the ZDW of the air-hole based PCF is ~1400 nm, which is an unsuitable scenario for DW generation pumped at around 700 nm. The CS2-PBGF, however, shows a ZDW at 689 nm which is induced by the inclusion of the resonance and enables DW formation. The sharp spectral peak at around 690 nm which can be seen in Figure 3a–e and Figure 5 is a feature of the pump laser.
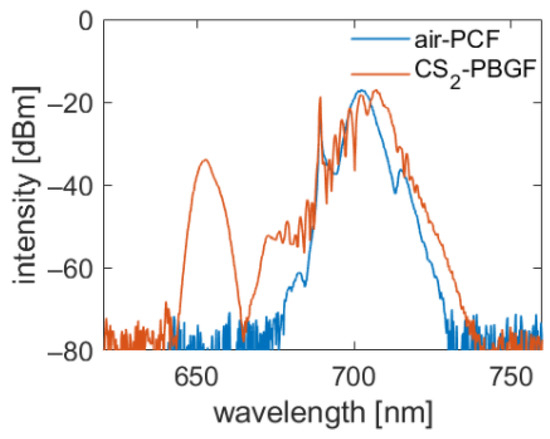
Figure 5.
Comparison of the measured nonlinear frequency conversion spectra in the CS2-PBGF (blue) and air-hole based photonic crystal fibers (PCF) (orange) both for the same pump peak power (1.5 kW) and pump wavelength (700 nm).
4. Discussion
To investigate the critical parameter that determines whether DWs can be generated across the resonances (i.e., high attenuation regions) between different PBGs, the propagation constant β(ω) is expanded into a Taylor series around the soliton frequency ωsol and is inserted into the DW-PM condition (Equation (2)). We neglect the nonlinear phase which only plays a minor role here because of the low pulse power (confirmed in Figure 6), leading to [23]:
where β2 = ∂2β/∂ω2|ωsol and β3 = ∂3β/∂ω3|ωsol are the group-velocity dispersion and third order dispersion at ωsol. Therefore, the estimated dispersive wave λDW, defined by the condition ΔβDW(λDW)=0, can be written as [23]
ΔβDW(λ) = 2 × (π × c/λsol)2 × (λsol/λ − 1)2 × β2 + 4/3 × (π × c/λsol)3 × (λsol/λ − 1)3 × β3
λDW = λsol/[1 − β2 × λsol/(2 × π × c × β3)]
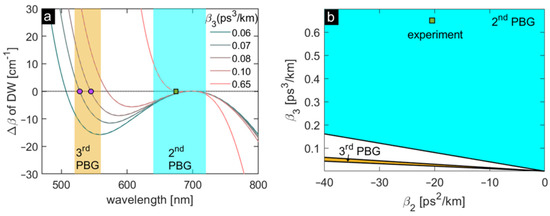
Figure 6.
(a) Analytical description of the phase-mismatching rate ΔβDW as a function of β3 in the second order PBG with β2 = −20.4 ps2/km corresponding to Δλ = 20 nm case. The solid lines indicate ΔβDW neglecting the nonlinear phase (Equation (3)) while the dashed lines indicate ΔβDW with the nonlinear phase (Equation (2), γ = 6.5 W−1/km, N = 1.6, Psol = 1 kW corresponding to DW generation threshold in Figure 3b). The cyan bar indicates the second order PBG and the yellow bar indicates the third order PBG of the sample. The green square corresponds to the Δλ = 20 nm case in Figure 3b. The purple dots indicate the DW generated across the resonance band; (b) the estimated DW wavelength for different combinations of β2 and β3 from Equation (4) (soliton wavelength λsol = 699 nm corresponding to the Δλ = 20 nm case). The cyan area indicates the second order PBG and the yellow area indicates third order PBG of the sample. The green square indicates the generated DW in the experiment for the Δλ = 20 nm case.
To demonstrate the critical impact of β3 and its interplay with β2 on the interband DW-generation, the DW-PM condition (including Equation (2) and the simplified one Equation (3)) and estimated DW wavelength from Equation (4) are shown in Figure 6, taking the parameters of Δλ = 20 nm case (soliton wavelength λsol = 699 nm). Figure 6a shows the DW-PM condition for different values of β3 with fixed β2 = −20.4 ps2/km corresponding to Δλ = 20 nm case. Only when β3 is within the range of 0.06–0.1 ps3/km, the PM condition can be satisfied for interband DW-generation. This can explain why no interband DW-generation was detected in the experiment (β3 = 0.65 ps3/km, see Table 1; the DW generated in the experiment is indicated as the green square in Figure 6a). To investigate the impact of β3 and its interplay with β2 on the interband DW-generation further and give some insights into the fiber design in the future to realize the interband DW-generation, the estimated DW for the different combination of β2 and β3 from Equation (4) is plotted in Figure 6b (cyan area: second order PBG; yellow area: third order PBG). It can be seen that only a small part of combinations of β2 and β3 can satisfy the PM condition to realize the interband energy transfer from the second to third PBG. The situation for the experiment conducted in this work (dispersion parameters β2 and β3 of the sample) is shown in Table 1 and for the Δλ = 20 nm case, the DW is indicated as a green square in Figure 6b, revealing that the established combinations of β2 and β3 prevent the interband DW-generation.

Table 1.
Dispersion parameters β2 and β3 (β(ω) come from the numerical simulation (COMSOL)) at soliton wavelengths (taken from the experiments, Figure 3a–e) for different spectral distances Δλ.
5. Conclusions
Understanding the impact of dispersion on nonlinear frequency conversion is particularly relevant within the context of ultrafast supercontinuum generation, which crucially depends on the dispersive properties of the underlying waveguide. This impact is particularly strong for optical waveguides that include geometry-induced resonances, leading to a significant modification of higher-order dispersion terms. Here, we experimentally unlocked the impact of the relative spectral distance between the pump and resonance on nonlinear pulse propagation through the example of a liquid-based PBGF. The PBGF shows a sophisticated dispersive landscape leading to dispersive wave generation on the short-wavelength side of the pump. Due to the dramatic change of the dispersion in close proximity to the bandgap edges, an adjustment of the pump wavelength by a few nanometers results in a different nonlinear pulse propagation situation, i.e., in the dispersive wave to be generated at a different wavelength. This behavior is explained by phase-matching considerations between the soliton and DW, additionally revealing the critical influence of third order dispersion for interband energy transfer. The present study gives additional insights into nonlinear frequency conversion of resonance-enhanced waveguide systems which will be relevant for both understanding nonlinear processes as well as for tailoring the spectral output of nonlinear fiber sources.
Author Contributions
Conceptualization, M.A.S.; methodology, X.Q., K.S., G.L. and M.A.S.; software, X.Q. and T.L.; validation, X.Q. and M.A.S.; formal analysis, X.Q. and M.A.S.; investigation, X.Q.; resources, K.S., S.J. and R.S.; data curation, X.Q.; writing—original draft preparation, X.Q.; writing—review and editing, K.S., S.J., R.S., T.L. and M.A.S.; visualization, X.Q., K.S. and T.L.; supervision, M.A.S.; project administration, M.A.S.; funding acquisition, M.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deutsche Forschungsgemeinschaft, grant number SCHM2655/11-1, SCHM2655/12-1, SCHM2655/8-1, 259607349/GRK2101; H2020 Marie Skłodowska-Curie Actions, grant number 713694.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available from the corresponding author on reasonable request.
Acknowledgments
The authors thank Tomas Cizmar and Sergey Turtaev for the support of Ti:Sapphire laser system. The authors acknowledge support by the German Research Foundation and the Open Access Publication Fund of the Thueringer Universitaets- und Landesbibliothek Jena Projekt-Nr. 433052568.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The evaporation rate of CS2 in PCF (NKT-5) at room temperature is measured with the help of an optical microscope (the other side of PCF is closed with an endcap, PCF length 40 cm). As shown in Figure A1, the evaporation rate is high at the beginning but drops dramatically after 50 min and stabilizes at 0.8 μm/s in 2 h. At the same time, the measured fiber length, in which CS2 has been evaporated, increases rapidly at first and then increases linearly at a lower rate. Since the nonlinear experiment in this paper is implemented in 2 h, the effective sample length can be calibrated by the original length minus 1 cm.
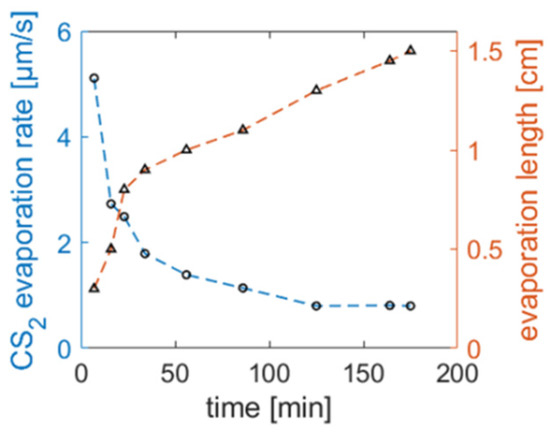
Figure A1.
Measured evaporation rate of CS2 in PCF (blue line) and the length of fiber in which CS2 has been evaporated (red line).
The simulated energy/spectral evolutions of the SCG process in the CS2-PBGF with Dstrand = 1.44 µm for various spectral distances Δλ= λe- λp between the pump λp and the bandgap edge λe of second order PBG (Δλ = 20, 15, 12, 10 and 5 nm) are shown in Figure A2a–e. The simulation results show great consistency with experimental ones (Figure 3a–e). These simulations of nonlinear pulse propagation are implemented based on the generalized nonlinear Schrödinger equation (GNLSE) [32] with the parameters: nonlinear coefficient γ = 6.5 W−1/km, pulse: 100 fs, 80 MHz, sample length L = 0.5 m. Note that the measured loss (Figure 1b) is included in the simulation.
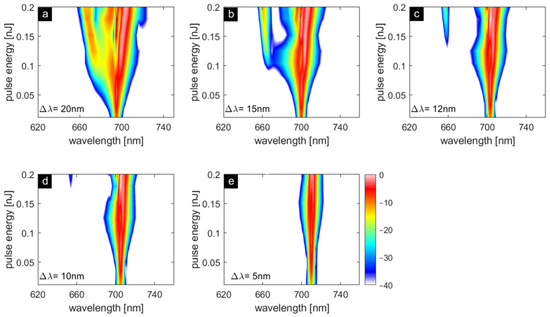
Figure A2.
(a–e) Simulated energy/spectral evolutions of the SCG process in the CS2-PBGF with Dstrand= 1.44 µm for various spectral distances Δ λ= λe − λp between the pump λp and bandgap edge λe of second order PBG (Δλ = 20, 15, 12, 10 and 5 nm). Parameters used: γ = 6.5 W−1/km, pulse: 100 fs, 80 MHz, sample length L = 0.5 m.
More details about the measurement error of strand diameters and the corresponding impact on the difference between the simulation and experimental results are discussed in the following. The measured diameter distribution of the air holes in the inner ring of the fiber cladding ranges from 1.462 to 1.497 µm, which we believe results from (i) measurement errors in the SEM imaging (the typical deviation in measuring lengths with our SEM instrument is at least 3%) and (ii) fabrication imperfections. It should be noted that a small deviation in strand diameter (e.g., 2%) will cause a strong change of ZDW and calculated soliton wavelength according to the DW phase-mismatching rate (Equation (2)), which are shown in Figure A3. To determine an average hole diameter required for the numerical calculations, we compared the results of nonlinear pulse propagation simulations for different air hole diameters with the experimental results, revealing that when Dstrand = 1.44 µm, simulations (Figure 4, Figure A2 and Figure A3b) match well with the experimental results.
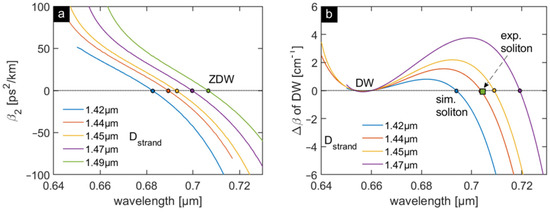
Figure A3.
(a) Simulated GVD parameter β2 and (b) calculated phase-mismatching rate of DW generation ΔβDW in the second order PBG for different strand diameters (γ = 6.5 W−1/km, pulse: 100 fs, 80 MHz) using Equation (2) of the manuscript. The wavelength of the DW (657 nm) and the Psol calculated from the DW generation threshold (0.08 nJ) are taken from the experiment (Figure 3b). The corresponding soliton wavelengths are obtained by the crossing of the individual curves with the zero line (). Note that the green square in (b) indicates the measured soliton wavelength in the experiment.

Table A1.
ZDWs and soliton wavelengths calculated by Equation (2) of CS2-PBGF assuming different strand diameters (the percentage indicates the deviation from Dstrand = 1.44 µm). The assumed diameters roughly correspond to the intrinsic range of strand diameter deviation of the PCF used that needs to be taken into account. Note that no soliton wavelength can be calculated for Dstrand = 1.49 µm as the pump pulse (700 nm) locates in the normal dispersion region.
Table A1.
ZDWs and soliton wavelengths calculated by Equation (2) of CS2-PBGF assuming different strand diameters (the percentage indicates the deviation from Dstrand = 1.44 µm). The assumed diameters roughly correspond to the intrinsic range of strand diameter deviation of the PCF used that needs to be taken into account. Note that no soliton wavelength can be calculated for Dstrand = 1.49 µm as the pump pulse (700 nm) locates in the normal dispersion region.
| Dstrand (µm) | 1.42 | 1.44 | 1.45 | 1.47 | 1.49 |
|---|---|---|---|---|---|
| Deviation from 1.44 µm | −1.4% | 0% | +0.7% | +2.1% | +3.5% |
| ZDW (nm) | 683 | 689 | 693 | 700 | 706 |
| Calculated λsol with Equation (2) (nm) | 694 | 704 | 709 | 719 | - |
References
- Russell, P. Photonic Crystal Fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef]
- Birks, T.A.; Knight, J.C.; Russell, P.S.J. Endlessly single-mode photonic crystal fiber. Opt. Lett. 1997, 22, 961–963. [Google Scholar] [CrossRef]
- Husakou, A.V.; Herrmann, J. Supercontinuum Generation of Higher-Order Solitons by Fission in Photonic Crystal Fibers. Phys. Rev. Lett. 2001, 87, 203901. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum Generation in Photonic Crystal Fibre. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Qi, X.; Chen, S.; Li, Z.; Liu, T.; Ou, Y.; Wang, N.; Hou, J. High-power visible-enhanced all-fiber supercontinuum generation in a seven-core photonic crystal fiber pumped at 1016 nm. Opt. Lett. 2018, 43, 1019. [Google Scholar] [CrossRef] [PubMed]
- Steinvurzel, P.; Eggleton, B.J.; de Sterke, C.M.; Steel, M.J. Continuously tunable bandpass filtering using high-index inclusion microstructured optical fibre. Electron. Lett. 2005, 41, 463. [Google Scholar] [CrossRef]
- Bise, R.T.; Windeler, R.; Kranz, K.S.; Kerbage, C.; Eggleton, B.J.; Trevor, D.J. Tunable photonic band gap fiber. In Proceedings of the Optical Fiber Communications Conference, Anaheim, CA, USA, 17–22 March 2002. [Google Scholar] [CrossRef]
- Schmidt, M.A.; Granzow, N.; Da, N.; Peng, M.; Wondraczek, L.; Russell, P.S.J. All-solid bandgap guiding in tellurite-filled silica photonic crystal fibers. Opt. Lett. 2009, 34, 1946. [Google Scholar] [CrossRef]
- Granzow, N.; Schmidt, M.A.; Tverjanovich, A.S.; Wondraczek, L.; Russell, P.S.J. Band-gap guidance in chalcogenide-silica photonic crystal fibers. Opt. Lett. 2011, 36, 2432–2434. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Dunn, S.C.; Steinvurzel, P.E.; Eggleton, B.J.; White, T.P.; McPhedran, R.C.; Martijn de Sterke, C. Application of an ARROW model for designing tunable photonic devices. Opt. Express 2004, 12, 1540. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Wu, J.J.; Hu, X.W.; Peng, J.G.; Yang, L.Y.; Dai, N.L.; Li, J.Y. Ultrahigh Temperature Sensitivity Using Photonic Bandgap Effect in Liquid-Filled Photonic Crystal Fibers. IEEE Photonics J. 2017, 9, 1–7. [Google Scholar] [CrossRef]
- Lin, C.; Wang, Y.; Huang, Y.; Liao, C.; Bai, Z.; Hou, M.; Li, Z.; Wang, A.Y. Liquid modified photonic crystal fiber for simultaneous temperature and strain measurement. Photonics Res. 2017, 5, 129–133. [Google Scholar] [CrossRef]
- Lühder, T.A.K.; Schaarschmidt, K.; Goerke, S.; Schartner, E.P.; Ebendorff-Heidepriem, H.; Schmidt, M.A. Resonance-Induced Dispersion Tuning for Tailoring Nonsolitonic Radiation via Nanofilms in Exposed Core Fibers. Laser Photonics Rev. 2020, 1900418. [Google Scholar] [CrossRef]
- Zeisberger, M.; Schmidt, M.A. Analytic model for the complex effective index of the leaky modes of tube-type anti-resonant hollow core fibers. Sci. Rep. 2017, 7, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Zeisberger, M.; Hartung, A.; Schmidt, M. Understanding Dispersion of Revolver-Type Anti-Resonant Hollow Core Fibers. Fibers 2018, 6, 68. [Google Scholar] [CrossRef]
- Bétourné, A.; Kudlinski, A.; Bouwmans, G.; Vanvincq, O.; Mussot, A.; Quiquempois, Y. Control of supercontinuum generation and soliton self-frequency shift in solid-core photonic bandgap fibers. Opt. Lett. 2009, 34, 3083. [Google Scholar] [CrossRef] [PubMed]
- Vanvincq, O.; Kudlinski, A.; Bétourné, A.; Mussot, A.; Quiquempois, Y.; Bouwmans, G. Manipulating the Propagation of Solitons with Solid-Core Photonic Bandgap Fibers. Int. J. Opt. 2012, 2012, 1–12. [Google Scholar] [CrossRef]
- Sollapur, R.; Kartashov, D.; Zürch, M.; Hoffmann, A.; Grigorova, T.; Sauer, G.; Hartung, A.; Schwuchow, A.; Bierlich, J.; Kobelke, J.; et al. Resonance-enhanced multi-octave supercontinuum generation in antiresonant hollow-core fibers. Light Sci. Appl. 2017, 6, e17124. [Google Scholar] [CrossRef]
- Fuerbach, A.; Steinvurzel, P.; Bolger, J.A.; Nulsen, A.; Eggleton, B.J. Nonlinear propagation effects in antiresonant high-index inclusion photonic crystal fibers. Opt. Lett. 2005, 30, 830. [Google Scholar] [CrossRef]
- Fuerbach, A.; Steinvurzel, P.; Bolger, J.A.; Eggleton, B.J. Nonlinear pulse propagation at zero dispersion wavelength in anti-resonant photonic crystal fibers. Opt. Express 2005, 13, 2977–2987. [Google Scholar] [CrossRef]
- Kibler, B.; Martynkien, T.; Szpulak, M.; Finot, C.; Fatome, J.; Wojcik, J.; Urbanczyk, W.; Wabnitz, S. Nonlinear femtosecond pulse propagation in an all-solid photonic bandgap fiber. Opt. Express 2009, 17, 10393. [Google Scholar] [CrossRef]
- Arismar Cerqueira, S., Jr.; Cordeiro, C.M.B.; Biancalana, F.; Roberts, P.J.; Hernandez-Figueroa, H.E.; Cruz, C.H.B. Nonlinear interaction between two different photonic bandgaps of a hybrid photonic crystal fiber. Opt. Lett. 2008, 33, 2080. [Google Scholar] [CrossRef]
- Arismar Cerqueira, S.; do Nascimento, A.R.; Bonomini, I.A.M.; Franco, M.A.R.; Serrão, V.A.; Cordeiro, C.M.B. Strong power transfer between photonic bandgaps of hybrid photonic crystal fibers. Opt. Fiber Technol. 2015, 22, 36–41. [Google Scholar] [CrossRef]
- Pureur, V.; Dudley, J.M. Nonlinear spectral broadening of femtosecond pulses in solid-core photonic bandgap fibers. Opt. Lett. 2010, 35, 2813. [Google Scholar] [CrossRef]
- Laesecke, A.; Muzny, C.D. Reference Correlation for the Viscosity of Carbon Dioxide. J. Phys. Chem. Ref. Data 2017, 46, 013107. [Google Scholar] [CrossRef] [PubMed]
- Washburn, E.W. The Dynamics of Capillary Flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef]
- Chemnitz, M.; Scheibinger, R.; Gaida, C.; Gebhardt, M.; Stutzki, F.; Pumpe, S.; Kobelke, J.; Tünnermann, A.; Limpert, J.; Schmidt, M.A. Thermodynamic control of soliton dynamics in liquid-core fibers. Optica 2018, 5, 695. [Google Scholar] [CrossRef]
- Grigorova, T.; Sollapur, R.; Hoffmann, A.; Hartung, A.; Schwuchow, A.; Bierlich, J.; Kobelke, J.; Schmidt, M.A.; Spielmann, C. Measurement of the Dispersion of an Antiresonant Hollow Core Fiber. IEEE Photonics J. 2018, 10. [Google Scholar] [CrossRef]
- Chemnitz, M.; Gaida, C.; Gebhardt, M.; Stutzki, F.; Kobelke, J.; Tünnermann, A.; Limpert, J.; Schmidt, M.A. Carbon chloride-core fibers for soliton mediated supercontinuum generation. Opt. Express 2018, 26, 3221. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.; Schaarschmidt, K.; Chemnitz, M.; Schmidt, M.A. Essentials of resonance-enhanced soliton-based supercontinuum generation. Opt. Express 2020, 28, 2557. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 5th ed.; Elsevier: Burlington, MA, USA, 2007; ISBN 9780123970237. [Google Scholar]
- Dudley, J.M.; Taylor, R. Supercontinuum Generation in Optical Fibers; Cambridge University Press: Cambridge, UK, 2010; ISBN 9780521514804. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).