Abstract
Photoinduced charge transport in lithium niobate for standard illumination, composition and temperature conditions occurs by means of small polaron hopping either on regular or defective lattice sites. Starting from Marcus-Holstein’s theory for polaron hopping frequency we draw a quantitative picture illustrating two underlying microscopic mechanisms besides experimental observations, namely direct trapping and migration-accelerated polaron trapping transport. Our observations will be referred to the typical outcomes of transient light induced absorption measurements, where the kinetics of a polaron population generated by a laser pulse then decaying towards deep trap sites is measured. Our results help to rationalize the observations beyond simple phenomenological models and may serve as a guide to design the material according to the desired specifications.
1. Introduction
Lithium Niobate (LN) stands out among other ferroelectric oxides for its large use in the realisation of acousto-optical, electro-optical and non-linear optical devices. Since its development in the ’60 s, this material has evidenced several light-induced effects that were recognized as a complex interplay between charge excitation and migration processes, such as photoconductivity, the bulk photovoltaic effect and ultimately photorefractivity. The interest in those phenomena is timely because they bear a high interest for practical applications: in the field of nonlinear and ultra-fast optics the photorefractive effect is a drawback that limits the use of LN for high intensity multiphoton processes [1], while in photorefractive holography this effect is used to record high quality gratings, optical memories and demonstrate low-intensity all-optical interactions [2]. Integrated optics as well needs to control those phenomena due to the high continuous-wave light intensities obtained in waveguiding regions [3]. Moreover, in analogous materials, charge excitation and transport play a key role in a number of important applications such as ferroelectric photovoltaics [4,5] and in oxide catalysis [6,7,8].
Thanks to many results obtained especially by O. Schirmer and co-workers [9,10,11,12,13,14], it is nowadays accepted that charge transport in LN and related materials must be understood in terms of small polarons hopping among regular and/or defective sites. In the initial stage of the process, some charge carriers are photo-generated from deep donor centers and emitted with a preferential direction in the conduction band. Subsequently those “hot” carriers lose energy by interaction with the lattice and finally condensate into a new state which is self-localized by a distortion of the local ionic environment. Under certain conditions the carrier, localized at a single lattice site, and the surrounding deformation can be thought as a quasi-particle that moves as a whole: the small polaron. Its motion takes place by thermally assisted hopping transitions among different sites, until a deep trap is encountered; the polaron is then stably trapped and ready to be photo-excited again [15].
Despite this understanding, it is still challenging to relate the macroscopic observations to basic polaron hopping processes. The technique of choice to investigate the transient decay of a polaron population is time-resolved Light Induced Absorption (LIA) spectroscopy ([1] and refs. therein) in which a polaron population is created in the material by a pulsed photo-excitation process and its decay towards deep trap centers is observed by means of time resolved absorption spectroscopy. One of the main problems of this technique is that the experimental decay curves are difficult to interpret from a microscopic point of view, being the result of the parallel relaxation of the different polarons through a variety of microscopic processes. For this reason experimental curves are generally analyzed phenomenologically with the help of suitable fitting functions such as the widely used Kohlrausch-William-Watts (KWW) stretched exponential law, without a true understanding of the microscopic mechanisms determining the decay.
In this paper we apply a Monte Carlo analysis to investigate the different processes responsible for the decay in the technologically important case of Fe-doped LN, with special focus on the role of deep () and shallow () defect centers where the polarons can be trapped. We will show how transient measurements can reveal different stages of the decay kinetics corresponding to different types of hopping processes separated by largely different time scales. Furthermore the effect of changing experimental constraints such as sample temperature and composition on the different hopping processes will be elucidated and some criteria will be given to establish a priori what is the regime one should expect on the basis of a given sample composition and temperature.
2. Small Polarons in Fe:LiNbO3
Polarons are quasiparticles made up of an electrical charge that, by interaction with the polar crystalline environment, is able to distort the neighbouring lattice creating a local potential well. As a net result, the particle becomes self-localized. If the confinement effect is strong, the charge is concentrated on a single lattice site (small strong-coupling polaron) and randomly moves by thermal-assisted hopping among different sites.
Standard LN crystals of congruent composition contain a high density of point defects either intrinsic (such as the substitutional “antisite” defect or the Li vacancy ), or extrinsic (dopants or impurities) [16]. Those defects constitute preferential sites for the formation of polarons, so that several types of small electron polarons are recognized in congruent LN [13]: the free polaron (F) forming on regular sites; the bound polaron (P) forming on antisite defects ; the bipolaron (BP) which is a combination of a free and a bound polaron on neighbouring sites , with the possible existence of some variants depending on the actual site occupied by the Nb interstitial, which in some cases could be either a vacant Li site, either an octahedral void naturally present in the LN structure [17]. LN may also host holes, created when energetic photons capable of band-to band excitation are involved. In this case, hole polarons (H) are formed. Finally, impurities with two or more valence states, such as the prototypical case of , have the possibility to capture an electron with a potential that is a mixture of Coulomb attraction and polaronic lattice deformation.
In LN, polarons can be seen as localized defect states in the band gap (Figure 1), which can absorb the light releasing the trapped charge to higher energy levels under the Franck-Condon principle [13]. In Figure 1 the electronic energy is referred to the uncoupled level instead of the bottom of the conduction band, being a more appropriate description when the electron-lattice coupling is strong. Values for and are calculated according to ref. [13] while the one for the according to ref. [18].
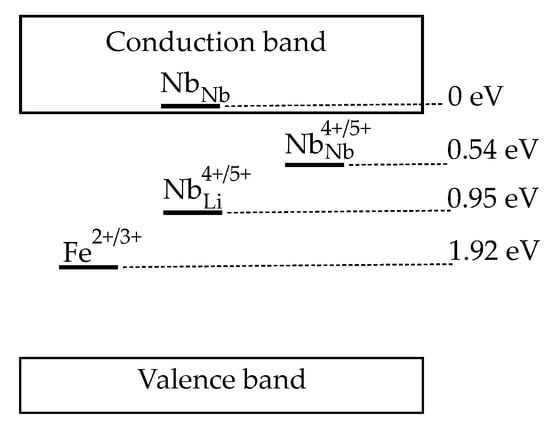
Figure 1.
Electronic energy of the different polaron centers in Fe:LiNbO with respect to the level in a rigid lattice (i.e., not considering the lowering in energy due to the local lattice distortion associated to the polaronic effect).
The typical experiment dealing with the relaxation of a suddenly-created polaron population is Light Induced Absorption (LIA) [19,20]. The sample is illuminated with a pulsed laser with a pulse duration of few ns and a maximum pulse energy of hundreds of mJ while one or more continuous-wave probe lasers record simultaneously the time evolution of the sample absorption at different wavelengths. The pump laser creates a polaron population by photo-excitation from charged defects (in this case ) and since polarons can absorb light, the probe beams detect an additional absorption signal that is proportional to the polaron concentration in the sample. In this way the decay of the polaron population as a function of time can be observed. Moreover, since the absorption cross section of the different polaron species is quite different at the different probe wavelengths [20], it is possible to reconstruct the decay kinetic of the different polaron species.
3. Monte Carlo Simulation of Polaron Hopping
According to the Marcus-Holstein polaron hopping model [15,21,22], the non-adiabatic hopping frequency for a () hop is:
with:
In Equation (1), r is the distance between initial and final sites, is the absolute temperature (in energy units) and is an orbital parameter describing the overlap between the electronic wavefunctions at sites i and f.
In ref. [18] we determined that it is reasonable to reduce the number of orbital parameters to two. The first one Å describing “trapping” transitions between F or P and . The second one Å describes electronic transfer of polaron migration, i.e., hopping between Nb ions whatever their positions is regular () or defective ().
In Equation (2) is the reorganization energy of Marcus’ theory corresponding to the energy paid to rearrange the lattice, here equal to the sum of the elastic energies of the two polarons.
The hopping barrier can be computed using the harmonic approximation of small polaron theory [23,24] as:
with and the binding energies of the electron at zero deformation. When the hop occurs between sites of the same type (), , recovering the standard result that the hopping activation energy is one half of the polaron stabilization energy [1,13,25]. The pre-exponential factor describes the intrinsic hopping rate between the two sites and is determined by the choice of the combination. By comparing the results of our simulations to experimental decay curves we estimated that a fair value for all the processes is . In this situation the non-adiabatic condition is always fulfilled for all polarons species, as discussed in ref. [24].
Those hopping frequencies are used in a dedicated Monte Carlo code based on a classical Gillespie algorithm. The LN structure is generated at the beginning of the code in a 80 × 80 × 80 super-cell with periodic boundary conditions. A given number of empty and Fe defects is then placed on a certain number of lattice sites in accordance to a specified sample composition. For sake of simplicity, we will restrict ourselves to the case in which the number of photo-generated polarons is small compared to the amount of antisites and Fe traps. This approximation is valid for antisites, which are present in large amount in standard LN crystals, but may not be so for Fe traps when the concentration of photo-excited donor centers is comparable to the one of traps e.g., in strongly reduced samples with a high ratio. In spite of the fact that this assumption may lead to an inaccurate modelling of the decay shape, our general results remain valid.
Under the assumption of weak concentration, we can perform two important simplifications. (i) The probability that two polarons may interact and/or form bipolaronic states is negligible. This is consistent with the fact that energy level of Fe traps is significantly lower than the bipolaron one ( eV with respect to eV, respectively [13]), so that migrating polarons tend to move to Fe traps instead of forming bipolarons. The absence of bipolarons in Fe:LN samples is also corroborated by the observation that in LIA experiments there is no evidence of an increased absorption in the blue spectral region, as it would be the case upon bipolaron formation [26]. (ii) Trap saturation effects are negligible, so that we can assume that the trap concentrations are constant.
Our simulation routine works as it follows: one polaron per time is placed on a randomly chosen starting site, either a regular or on an antisite defect according to the user’s choice. The program then computes the hopping frequencies towards all possible destination sites comprised in a suitably defined volume and finally chooses the actual destination site by a statistical procedure which weights the possible outcomes according to their respective hopping frequencies using a Gillespie algorithm. The higher the hop frequency towards a given site, the higher the probability that this site will be selected. Note that, according to Equation (1), this probability depends both on distance and on temperature as well as on the type of initial and destination site. This means that (i) long jumps beyond nearest neighbour are always allowed and, if proper conditions are met, may even be more probable than jumps within the first coordination sphere and (ii) the relative weight of the different processes may change according to temperature. The hopping routine is then repeated until a deep Fe trap is reached: in this situation the program records the final polaron position with respect to its original site, the number of different sites encountered during its walk and the time needed to reach the final site. The whole cycle is then repeated until a sufficient statistics is collected. Further details on the code may be found in refs. [18,26].
In the following, we will focus our attention on the decay kinetics of P polarons considering that in some suitably-chosen experimental conditions they are the predominant polaron species present in the sample [18]. In fact, few ns after the pulse, a dynamic equilibrium is established between P and F polarons but since the hopping rate of F polarons is much higher than the one of P polarons, the equilibrium is strongly displaced in favor of the latter ones. In particular we will consider that, in standard congruent samples at room temperature and below, free polarons eventually created by the pulse thermalize quickly to deep traps and to bound polarons, from which they can depart and migrate for short times due to thermal detrapping from charged antisite defects. This process corresponds in our code to a () hopping event.
Also, we assume that the excitation wavelength is chosen in such a way that the photo-excitation of electrons from the valence to the conduction band is disfavoured, in order to neglect the presence of hole polarons. Typically the wavelength is in the visible range (532 nm).
Under these conditions, the photo-generation process occurs when a photon is absorbed by a donor center. The electronic charge is ejected and subsequently thermalizes to form the polaron in the neighbourhood of its empty donor center. In this situation, all the created polarons would appear close to their respective generating Fe trap and would have a strong chance of being quickly retrapped and disappear from the system soon after the pulse has ended. However the experimentally studied LIA decays, which are the focus of our study, last for long times ranging to milliseconds or even seconds, depending on the experimental conditions. How is this possible? Since the bound polaron formation time (<1 ps, see ref. [27]) is much shorter than the pulse duration while their lifetime is generally much longer, we consider that already during the pulse a given bound polaron concentration is present within the sample. If the pulse energy density D is not too low, there is a fair chance that several polarons absorb additional photons which kicks them far away from the original center, helping to randomize their initial position. In fact, for typical values in the range of , [1,28,29] the average number of photons absorbed by the polaron is about , where is the absorption cross section of bound polarons and is the photon energy at 532 nm. On the basis of this reasoning, we consider that the polarons remaining after the pulse is ended are those which have absorbed more than one photon and that find themselves in a position completely uncorrelated with respect to their originating site. Accordingly, in our code the initial position of the walking polaron is randomly chosen on a site.
4. Direct Trapping versus Migration-Accelerated Trapping
In the top part of Figure 2 it is simulated the decay of a bound polaron population for a LN sample doped with 0.02 mol.% corresponding to a deep trap concentration of . On the bottom figure is reported the occurrence of and hops (hereby abbreviated as PP and FF) performed by the different polarons, sorted according to their lifetime. It can be seen that at short times the decay is due to polarons that do not perform any hop among antisites or regular sites and are therefore directly trapped by a Fe trap. At this stage, polarons born near the traps die in one hop, having a high probability of jumping directly to the Fe impurity center. We shall indicate this initial decay mode as direct trapping regime. After this stage, we encounter those polarons that live long enough so that the chance to hop on another transport site is not negligible and thus are able to perform a certain number of hops before meeting a Fe trap. This stage is indicated as migration-accelerated regime. We can define a characteristic time separating the two regimes. may be regarded as the average waiting time spent by the polaron on the initial site before hopping on another antisite and/or a regular Nb site. When the trapping processes require a time significantly longer than this, polaron migration has a chance to take place.
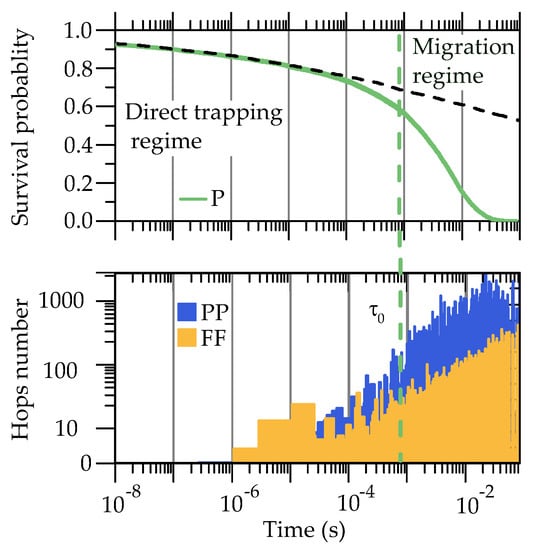
Figure 2.
(Top) Survival probability of P polarons as measured by a typical LIA experiment. The black dashed line shows the decay shape when polaron migration is prohibited. The green dashed line is placed at , as calculated from Equation (12). (Bottom) Number of PP and FF hopping processes performed by each polaron during its walk.
5. Estimation of the Escape Time
To perform some quantitative reasoning on we need to recall the concept of trapping radius already introduced in [18,24,26]. According to Equation (1), for a fixed temperature, fast trapping processes are the ones for which Fe traps are “near” to the starting site. We may therefore define a characteristic distance from a Fe trap at which a trapping process is as fast as the typical hopping rate.
To begin with, we consider a free polaron hopping only among regular sites that comes close to a Fe trap. The trapping radius for the process is defined as:
where is given by Equations (1) and (2) and is a geometric constant factor that depends only on the lattice positions of the sites. For the LN structure, summing up to the coordination shell of the Nb sublattice and using for the orbital parameter the value Å we get . From Equation (1) we get:
depends on the temperature through the term . For example, Å at room temperature, while Å at 200 K. We may now consider that any Fe trap is surrounded by a sphere of radius dependent on temperature and that whenever a F polaron finds itself inside this sphere it will almost surely be captured by direct transfer to the trap. Polarons spawning outside of these spheres must make a number of jumps before they can get close enough to any trap.
This concept can be readily extended to the case of free polarons captured by antisite shallow traps. In this case the trapping radius is:
Let us now consider one polaron starting its walk from a antisite, as it is customary to assume in standard LN samples. Let us assume that this starting site is far away from Fe traps. By thermally activated polaron hopping, the charge may leave this site in two possible ways: either hopping on another antisite nearby, either transforming into a free polaron and migrating away on the Nb sublattice. To estimate the first hopping rate (polarons jumping on the disordered antisite lattice) we use a result of percolation theory [30] to take into account the random positions of the sites, so that the expression for the waiting time reads:
where is a measure of the average distance between two antisites in a sample with antisite concentration given by:
The waiting time for the second process (conversion ) is slightly more difficult to compute. A priori, this kind of hop can occur towards a Nb site at any distance from the original Nb antisite. Moreover, since the Nb sites form a nearly-cubic lattice around the starting site, the probability for the polaron to escape is given by the sum of the frequency over all the destination sites, as in Equation (4). However, the sites contained within the antisite trapping sphere of radius (see Equation (6)) correspond to inefficient processes because if the polaron hops in one of them, it will almost surely go back to the origin instead of leaving the initial site. Therefore the (macroscopic) effective waiting time can be computed by summing over all the equivalent destination sites available out of the antisite trapping sphere:
By approximating the summation with an integral and substituting Equation (1) we get:
with:
where is the atomic density of the Nb sublattice and V is the volume of a spherical layer of thickness around a sphere of radius .
The effective waiting time on the antisite can now be estimated from the parallel between the two above-mentioned processes (Equations (7) and (10)):
From Equation (12) one can now specify what is the average waiting time on the site for a polaron about to leave either by hopping on an antisite nearby or by performing intermediate passages through the sites. In absence of deep traps, this can be understood as the effective hopping rate along the mixed and lattices since, in moving from one site to the other, the waiting time due the processes is negligible. Thus, Equation (12) can be used to compute a trapping radius for the capture process according to the usual equation:
which gives:
Note that expression (12) should not be confused with the emigration time, i.e., the average time required to leave the starting site without returning to it. A rigorous estimation of the former would require to specify correctly the probability that the moving polaron may be captured back considering all the possible trajectories. In other words, Equation (12) is not verifying the irreversibly of the migration process and must therefore be understood simply as an underestimation of the emigration time. In spite of its limitations, Equation (12) is nevertheless useful as it provides a qualitative understanding of the general behaviour of our system. In the following we shall explore the different properties of .
From Equations (6)–(8) and (10) it is clear that depends both on sample temperature and on the concentration of antisite defects (i.e., on the LN stoichiometry). The temperature dependence is illustrated in Figure 3a. Here it can be noticed that the first part of the decay corresponding to the direct trapping regime is not altered too much by the temperature changes, as the activation energy of the trapping process is very small ( eV, according to Equation (3) and ref. [26]) so that the effect of lowering the temperature is essentially to move to longer times, extending the direct trapping regime to a larger part of the decay curve. In particular, for sufficiently low temperatures, is pushed beyond the end of the decay curve so that a pure direct trapping regime is attained.
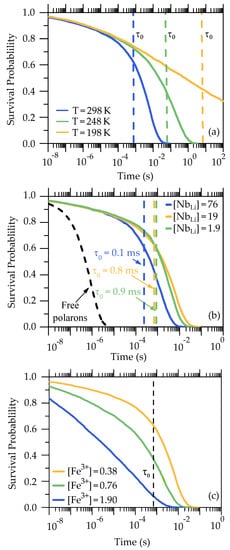
Figure 3.
(a) Survival probability of P polarons at 298 K, at 248 K and at 198 K in a congruent sample with the same composition as the one in Figure 2. The dashed lines indicate the value of as approximately determined by (12). (b) Survival probability for P polarons at room temperature in a sub-congruent (blue), congruent (green) and near-stoichiometric sample (yellow). The blackdashed line shows for comparison a decay of a population of F polarons in a fully stoichiometric sample. The numbers in the legend indicate the concentration in . (c) Survival probability for P polarons at room temperature in a congruent sample for increasing Fe concentrations. The dashed line indicates the hopping characteristic time . The numbers in the legend indicate the concentration in .
The composition effect is shown in Figure 3b. Here it can be seen that at room temperature, the first term in Equation (12) dominates only for high antisite concentrations, corresponding to a strongly Li-deficient, sub-congruent LN sample. In this situation the antisite concentration is so high that is determined essentially by the direct hopping process. By lowering the antisite concentration, the first term in Equation (12) becomes smaller while the second one, which is independent on the sample composition, remains constant. Interestingly, when the sample composition is close to the congruent one i.e., , the two terms become comparable at room temperature ( , hence . From this point on, a further reduction of the antisite concentration has a relatively small effect. In Figure 3b for example by decreasing of one order of magnitude the concentration it can be seen that barely changes. Note that in those examples we are always assuming the as starting site. The situation is however different in the case (experimentally difficult to realize, but not impossible) of null antisite concentration. In this case the starting site of the polaron must be a regular site, which makes a large difference because now the migration occurs solely on the regular pseudo-cubic Niobium sublattice. The new characteristic time in this situation is shifted to much smaller values so that the migration regime sets in very soon, leading to a high mobility and a short lifetime for the polarons (see for comparison the simulated decay of F polarons in Figure 3b). This is the ultimate reason for the well-known threshold dependence of the photorefractive effect upon the sample stoichiometry (see e.g. [16]): the photoconductive properties of LN are only weakly affected by the sample composition until virtually all antisite defects are eliminated.
Finally, in Figure 3c is shown the behaviour of the P polarons decay curve for increasing Fe trap concentrations, corresponding to faster initial decays. For sufficiently high trap concentrations the polaron lifetime eventually becomes shorter than and in this case the kinetic is purely determined by direct trapping processes. In this respect, increasing the Fe concentration brings to the same result as lowering the temperature, i.e., it makes the direct trapping processes predominant with respect to diffusive ones. In this respect it should however be stressed that expression (12) is a meaningful expression of the waiting time on the antisites only assuming that the Fe trap concentration is not too high. In this latter case, direct trapping dominates with its own specific kinetic mechanism and hopping on other sublattices becomes not relevant. In the following section we will explore in more details under which conditions this trapping regime is attained.
6. Pure Trapping Regimes
For practical applications it is useful to provide a criterion to determine at which temperature/composition combination one can consider that a sample is in a trapping or migration regime. As shown in the previous section, there is a characteristic time roughly given by separating the two situations. The direct trapping regime is defined by the condition that the trapping frequency is much larger than the inverse of the characteristic hopping time. In other words, for direct trapping processes, all the polarons leave their starting site hopping directly towards a deep Fe trap.
An equivalent way to visualize this condition is that, for a given temperature, the trapping spheres around the traps are so large that they start to overlap. Let us consider for instance a condition of pure trapping regime for free polarons in an undoped LN sample with varying concentration of antisite defects. Free polarons would be directly trapped if the antisite concentration satisfies:
where the strong inequality is required since the theoretical expression on the left hand side underestimates the concentration needed to achieve direct trapping, as a consequence of the fact that all the processes are considered irreversible.
The other simple situation involves an iron-doped sample containing no antisites (stoichiometric Fe:LN). In this case the free polarons will disappear by direct Fe trapping for trap concentrations satisfying the following criterion:
In the case of a mixed trap situation such as Fe:LN of varying composition (both deep and shallow traps), a criterion for the full trapping regime of free polarons is easily obtained by combining together Equations (5)–(15):
For reference, in the case of a congruent sample at room temperature, we have and .
Using Equation (14) we can also define a criterion on the Fe concentration for which bound polarons are directly trapped:
To check the above criteria, it is possible to use Monte Carlo simulations to quantify, for a given experimental situation, how much hops of a given type the polarons perform on average [26].
In Figure 4a it is reported the percentage of FF hops performed during the polaron walk as a function of the temperature and composition in an undoped LN crystal with varying antisite concentration, where the vertical dashed line at indicates the standard congruent composition. Along this line it can be seen that, as the temperature increases, the polaron walk is constituted by a larger fraction of FF hops. At temperatures around 400 K about one half of the hops occurs between regular Nb sites. Conversely, by lowering the temperature and/or increasing the antisite concentration, the diffusion process becomes less and less dependent on free polaron transport. The temperature-composition line corresponding to is visible in the bottom right part of the figure. Note that for the typical case of congruent LN, free polaron contribution is not negligible if not at very low temperatures (<200 K).
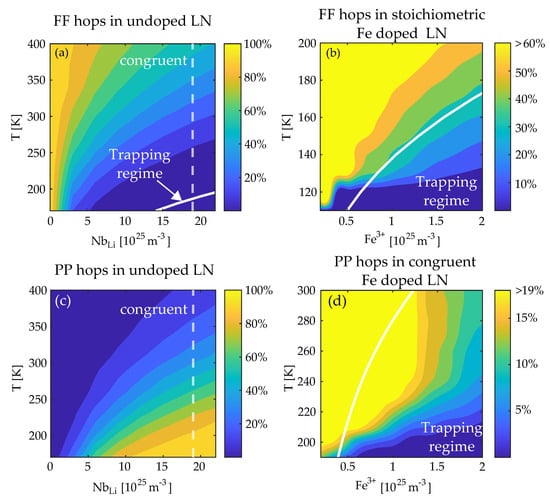
Figure 4.
(a) Fraction of hops as a free polaron as a function of temperature and concentration for an undoped sample ([Fe] = 0). (b) Fraction of hops as a free polaron as a function of the temperature and [Fe] concentration for a stoichiometric sample . The solid lines represent the theoretical boundary between the pure trapping regime calculated according to Equations (15) and (16). (c) as a function of temperature and concentration for an undoped sample ([Fe] = 0). (d) as a function of the temperature and [Fe] concentration for a congruent sample (). Note the different temperature range in the two plots.
Figure 4b shows, for the case of a stoichiometric sample (i.e., ) doped with Fe, the average value of the fraction of FF hops over the total that a free polaron performs before being trapped by a Fe trap. As expected, by cooling the sample and/or increasing the Fe concentration percentage of hops on the Nb sublattice gets smaller and smaller. Below a certain boundary the polaron enters in a direct trapping regime so that all the created polarons are likely to be immediately captured by a Fe trap. Again, the solid line shows the boundary below which it can be expected the disappearence of hops, according to the criterion (16). As it can be seen the simulation is in line with the theoretical estimate and in particular confirms that the pure trapping regime is attained for .
In Figure 4c are reported the simulation results for the case of P polarons. Here the behaviour is roughly complementary to the one of Figure 4a, so that by lowering the temperature and/or increasing the antisite concentration the fraction of bound-bound hops becomes predominant. In Figure 4d is shown the situation of a congruent sample () with varying Fe concentration. Again the direct trapping regime is attained for low temperatures and high Fe concentration, in agreement with the criterion (18). As expected, the condition indicated by a solid line in the figure provides an underestimation, i.e., at a given temperature, more Fe traps than expected are necessary to capture all the polarons. This is due to the fact that our calculations do not verify strictly the irreversibility condition, so that the time needed to truly leave the antisite is longer than . As a consequence the trapping radius in Equation (14) is an underestimation and a larger amount of Fe traps is necessary to achieve the trapping regime.
7. Conclusions
The outcome of a typical light-induced absorption experiment performed on iron-doped lithium niobate (Fe:LN) has been studied numerically with the help of a Monte Carlo simulation code based on the Marcus-Holstein model for polaron hopping.
Our analysis shows that in general, within the decay process of a polaron population induced by an impulsive illumination, we can distinguish at least two regimes. At short times the decay describes the direct trapping processes of those bound polarons that, at the beginning of the experimental time window, are located close to deep Fe traps and therefore are likely to disappear in a single hopping event due to their high trapping probability. At longer times, we can find those polarons that are located far away from the Fe traps, so that the waiting time on the initial site is comparable with the typical time required for the polarons to migrate away, hopping on other transport sites. The two regimes have a quite different behaviour. For example the direct trapping regime is practically independent on temperature due to the low activation energy of the trapping barrier, in agreement with the experimental data [26]. On the other hand the migration-accelerated regime is especially important when the photoconductive properties of the sample are considered, as this is the regime were significant charge transport takes place.
Under appropriate experimental conditions, it may happen that the transient decay of a polaron population (such as those produced in a time-resolved LIA experiment) is predominantly due to one of the two processes, resulting in a direct trapping or migration-accelerated regime. We determined a criterion on the antisite and/or on Fe concentration to consider the free polaron contribution negligible in the charge transport processes at a given temperature. In these specific cases the criterion reads:
where and are the trapping radiuses for the and trapping processes respectively, given by Equations (5)–(15).
On the other hand, for a bound polaron population in a Fe doped sample, the criterion to distinguish between one of the two regimes reads as follows:
where is a characteristic radius of a sphere of strong interaction surrounding the Fe traps. The quantities and are the hopping frequency pre-factor and the typical waiting time for the bound polarons hopping, described by Equations (2) and (12) respectively.
Our results are meaningful in the interpretation of experimental results obtained by time-resolved LIA as they allow a more physical reading of the decay curves. Besides this, they are of strong interest to crystal growers and experimenters to tailor the composition and/or the experimental conditions of a given sample in order to obtain a desired response. For example, a strong photorefractive effect is to be expected in a pure trapping regime, while a strong optical damage resistance is attained in conditions of free polaron diffusion. Further studies are now in progress to investigate, in the case of dominating diffusion conditions, the mobility of small and bound polarons, in order to determine an explicit expression for the sample photoconductivity according to the different regimes.
Author Contributions
Conceptualization, L.G., M.B. and S.F.; methodology, M.B.; software, L.V.; validation, M.B. and L.V.; formal analysis, L.G. and S.F.; investigation, L.V. and M.B.; resources, M.B.; data curation, L.V. and M.B.; writing—original draft preparation, M.B.; writing—review and editing, L.V., S.F. and L.G.; visualization, L.V.; supervision, M.B.; project administration, M.B.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Università degli Studi di Padova, grant number BIRD209412.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LN | Lithium Niobate |
| KWW | Kohlrausch Williams and Watts stretched exponential function |
| F | free polarons |
| P | bound polarons |
| LIA | Light Induced Absorption spectroscopy |
References
- Imlau, M.; Badorreck, H.; Merschjann, C. Optical nonlinearities of small polarons in lithium niobate. Appl. Phys. Rev. 2015, 2, 040606. [Google Scholar] [CrossRef]
- Günter, P.; Huignard, J.P. Photorefractive Materials and Their Applications 1; 0342-4111; Springer: New York, NY, USA, 2006; Volume 113. [Google Scholar]
- Bazzan, M.; Sada, C. Optical waveguides in lithium niobate: Recent developments and applications. Appl. Phys. Rev. 2015, 2, 040603. [Google Scholar] [CrossRef]
- He, J.; Franchini, C.; Rondinelli, J.M. Lithium Niobate-Type Oxides as Visible Light Photovoltaic Materials. Chem. Mater. 2016, 28, 25–29. [Google Scholar] [CrossRef]
- Tisdale, W.A.; Williams, K.J.; Timp, B.A.; Norris, D.J.; Aydil, E.S.; Zhu, X.Y. Hot-electron transfer from semiconductor nanocrystals. Science 2010, 328, 1543–1547. [Google Scholar] [CrossRef]
- Pelaez, M.; Nolan, N.T.; Pillai, S.C.; Seery, M.K.; Falaras, P.; Kontos, A.G.; Dunlop, P.S.; Hamilton, J.W.; Byrne, J.A.; O’shea, K.; et al. A review on the visible light active titanium dioxide photocatalysts for environmental applications. Appl. Catal. B Environ. 2012, 125, 331–349. [Google Scholar] [CrossRef]
- Migani, A.; Blancafort, L. Excitonic interfacial proton-coupled electron transfer mechanism in the photocatalytic oxidation of methanol to formaldehyde on TiO2 (110). J. Am. Chem. Soc. 2016, 138, 16165–16173. [Google Scholar] [CrossRef]
- Zhong, Y.; Trinh, M.T.; Chen, R.; Purdum, G.E.; Khlyabich, P.P.; Sezen, M.; Oh, S.; Zhu, H.; Fowler, B.; Zhang, B.; et al. Molecular helices as electron acceptors in high-performance bulk heterojunction solar cells. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Schirmer, O.F.; von der Linde, D. Two-photon- and x-ray-induced Nb4+ and O- small polarons in LiNbO3. Appl. Phys. Lett. 1978, 33, 35–38. [Google Scholar] [CrossRef]
- Schirmer, O.; Juppe, S.; Koppitz, J. Electron-spin-resonance, optical and photovoltaic studies of reduced undoped Fe:LiNbO3. Cryst. Lattice Defects Amorph. Mater. 1987, 16, 353–357. [Google Scholar]
- Schirmer, O.; Thiemann, O.; Wöhlecke, M. Defects in LiNbO3. experimental aspects. J. Phys. Chem. Solids 1991, 52, 185–200. [Google Scholar] [CrossRef]
- Schirmer, O.F. O- bound small polarons in oxide materials. J. Phys. Condens. Matter 2006, 18, R667. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Imlau, M.; Merschjann, C.; Schoke, B. Electron small polarons and bipolarons in LiNbO3. J. Phys. Condens. Matter 2009, 21, 123201. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Imlau, M.; Merschjann, C. Bulk photovoltaic effect of LiNbO3:Fe and its small-polaron-based microscopic interpretation. Phys. Rev. B 2011, 83, 165106. [Google Scholar] [CrossRef]
- Emin, D. Polarons; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Tatyana Volk, M.W. Lithium Niobate; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Schmidt, F.; Kozub, A.L.; Biktagirov, T.; Eigner, C.; Silberhorn, C.; Schindlmayr, A.; Schmidt, W.G.; Gerstmann, U. Free and defect-bound (bi)polarons in LiNbO3: Atomic structure and spectroscopic signatures from ab initio calculations. Phys. Rev. Res. 2020, 2, 043002. [Google Scholar] [CrossRef]
- Guilbert, L.; Vittadello, L.; Bazzan, M.; Mhaouech, I.; Messerschmidt, S.; Imlau, M. The elusive role of NbLi bound polaron energy in hopping charge transport in Fe: LiNbO3. J. Phys. Condens. Matter 2018, 30, 125701. [Google Scholar] [CrossRef] [PubMed]
- Merschjann, C. Optically Generated Small Polarons: Time-Resolved Pump-Multiprobe Experiments in Lithium Niobate vs. Random-Walk Charge-Transport Simulations in Oxide Crystals. Ph.D. Thesis, Fachbereich Physik, Univesitat Osnabrueck, Osnabrück, Germany, 2007. [Google Scholar]
- Merschjann, C.; Schoke, B.; Conradi, D.; Imlau, M.; Corradi, G.; Polgár, K. Absorption cross sections and number densities of electron and hole polarons in congruently melting LiNbO3. J. Phys. Condens. Matter 2009, 21, 015906. [Google Scholar] [CrossRef] [PubMed]
- Holstein, T. Studies of polaron motion. Ann. Phys. 1959, 8, 343–389. [Google Scholar] [CrossRef]
- Marcus, R.A. On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. I. J. Chem. Phys. 1956, 24, 966–978. [Google Scholar] [CrossRef]
- Zylbersztejn, A. Thermally activated trapping in Fe-doped LiNbO3. Appl. Phys. Lett. 1976, 29, 778–780. [Google Scholar] [CrossRef]
- Mhaouech, I.; Guilbert, L. Temperature dependence of small polaron population decays in iron-doped lithium niobate by Monte Carlo simulations. Solid State Sci. 2016, 60, 28–36. [Google Scholar] [CrossRef]
- Austin, I.G.; Mott, N.F. Polarons in crystalline and non-crystalline materials. Adv. Phys. 2001, 50, 757–812. [Google Scholar] [CrossRef]
- Vittadello, L.; Bazzan, M.; Messerschmidt, S.; Imlau, M. Small polaron hopping in Fe: LiNbO3 as a function of temperature and composition. Crystals 2018, 8, 294. [Google Scholar] [CrossRef]
- Beyer, O.; Maxein, D.; Woike, T.; Buse, K. Generation of small bound polarons in lithium niobate crystals on the subpicosecond time scale. Appl. Phys. B 2006, 83, 527–530. [Google Scholar] [CrossRef]
- Berben, D.; Buse, K.; Wevering, S.; Herth, P.; Imlau, M.; Woike, T. Lifetime of small polarons in iron-doped lithium niobate crystals. J. Appl. Phys. 2000, 87, 1034–1041. [Google Scholar] [CrossRef]
- Herth, P.; Granzow, T.; Schaniel, D.; Woike, T.; Imlau, M.; Krätzig, E. Evidence for Light-Induced Hole Polarons in LiNbO3. Phys. Rev. Lett. 2005, 95, 067404. [Google Scholar] [CrossRef] [PubMed]
- Shklovskii, B.I.; Efros, A.L. Electronic Properties of Doped Semiconductors; Springer Science & Business Media: New York, NY, USA, 2013; Volume 45. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).