Twisting Structures in Liquid Crystal Polarization Gratings and Lenses
Abstract
1. Introduction
2. Twisted LC with LCPG Structure
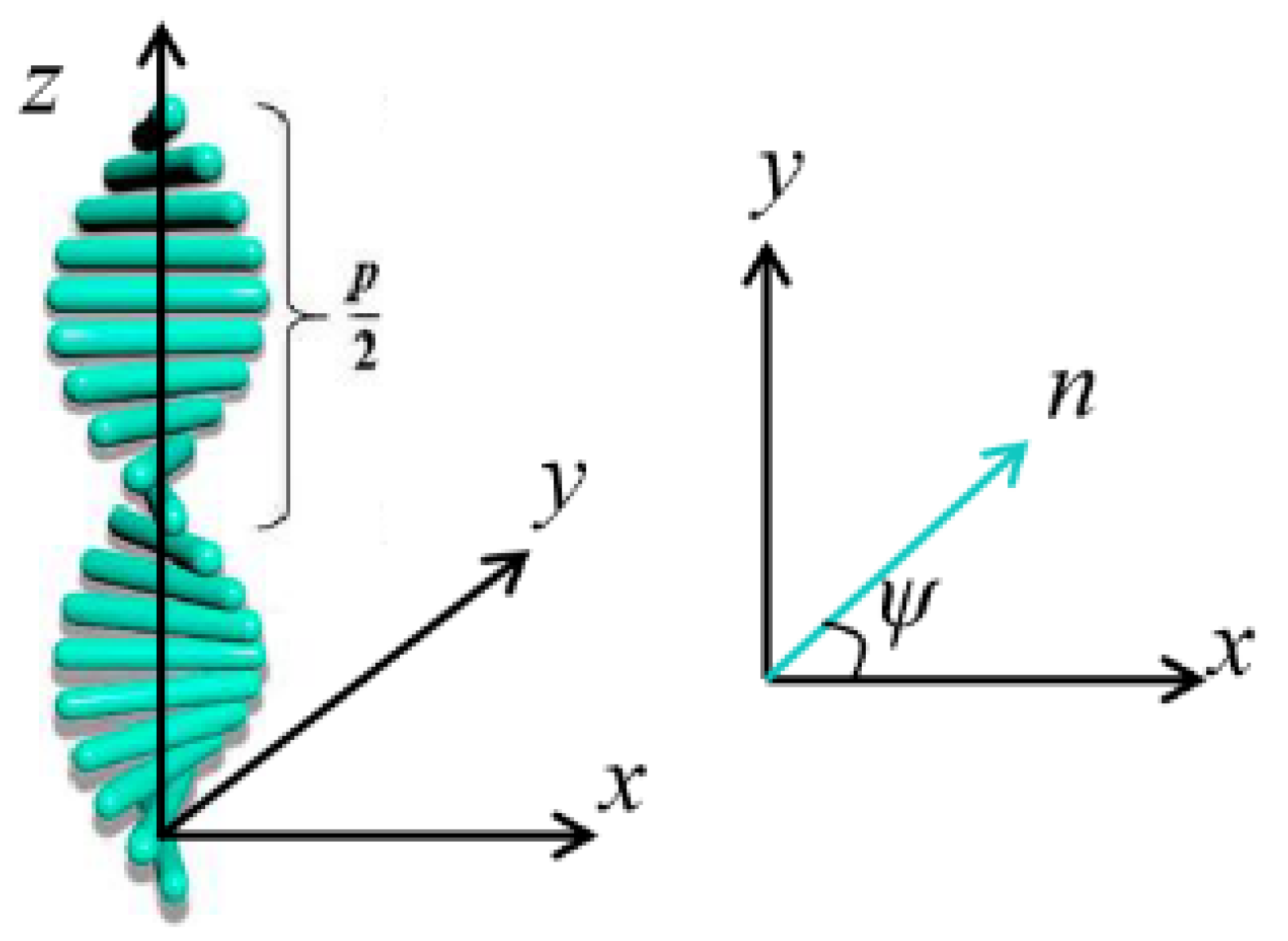
- Mauguin region: In this region (λ << 0.5ΔnP), the polarization ellipses of the eigenmodes have either near-infinite ellipticity with the long axis parallel or perpendicular to the local director, which could be approximated as a pair of orthogonal linear polarization states. As the eigenmodes propagate in the medium, the polarization axes will follow the twist of the local director, which is called waveguiding (or adiabatic following). TN-LCDs correspond to this situation [32];
- Short-wavelength circular birefringence region (SW-CBR): In this region (λ < P), the eigenmodes are elliptically polarized with the opposite handedness. As helical pitch decreases, the waveguiding phenomenon no longer holds. When the incident polarized light propagates in the LC layer, its polarization axis still rotates, but, usually, it will not remain parallel (or perpendicular) to the local LC director. Besides, its ellipticity will change along with the propagation distance. In essence, the Mauguin region is a limiting case of this region;
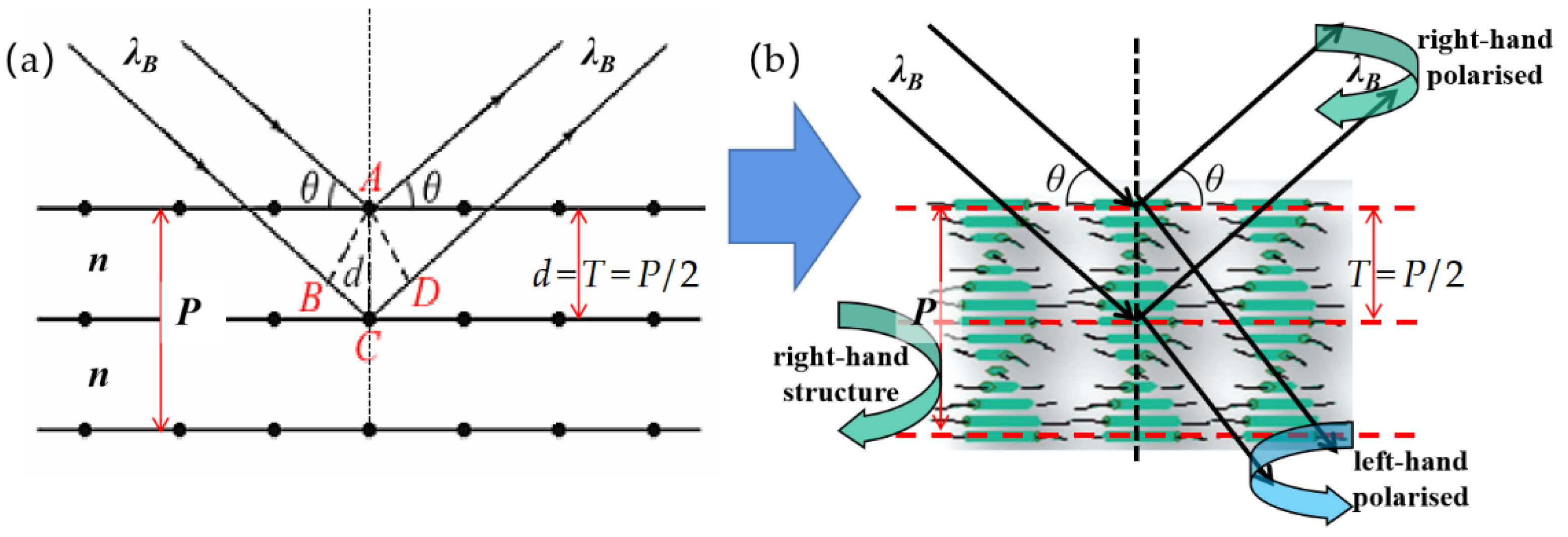
- Bragg region: In this region (noP < λ < neP), the liquid crystal layer will provide a strong selective circular reflection to the incident light, that is, a circular polarized incident light with the same rotation direction of the LC layer will be reflected, meanwhile the opposite one could propagate through. The twisting LC configuration produces a Bragg structure: its period T (T = 0.5P) could be regarded as a series of the crystal plane, shown in Figure 2. According to Equation (2), which is known as Bragg’s law:supposed that the medium within a period is homogeneous and provides an average refractive index , θ is the angle between the incident light and the “crystal plane”. For normal incidence (θ = 90°), the central wavelength of the reflection is , and the reflectance band is noP < λ < neP. For tilted incidence, the central wavelength of the reflection is .
- Long-wavelength circular birefringence region (LW-CBR): In this region (λ >> P), both eigenmodes are almost circularly polarized, and would pass through the LC layer. However, due to the difference in the wavenumber (refractive index), their propagation speeds are different, and the principal axes of their resultant, a beam of linearly polarized light, has a net rotation relative to the LC director at the exit plane.
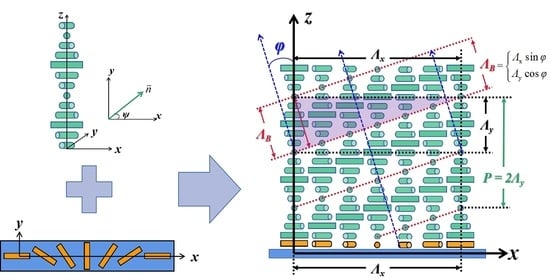
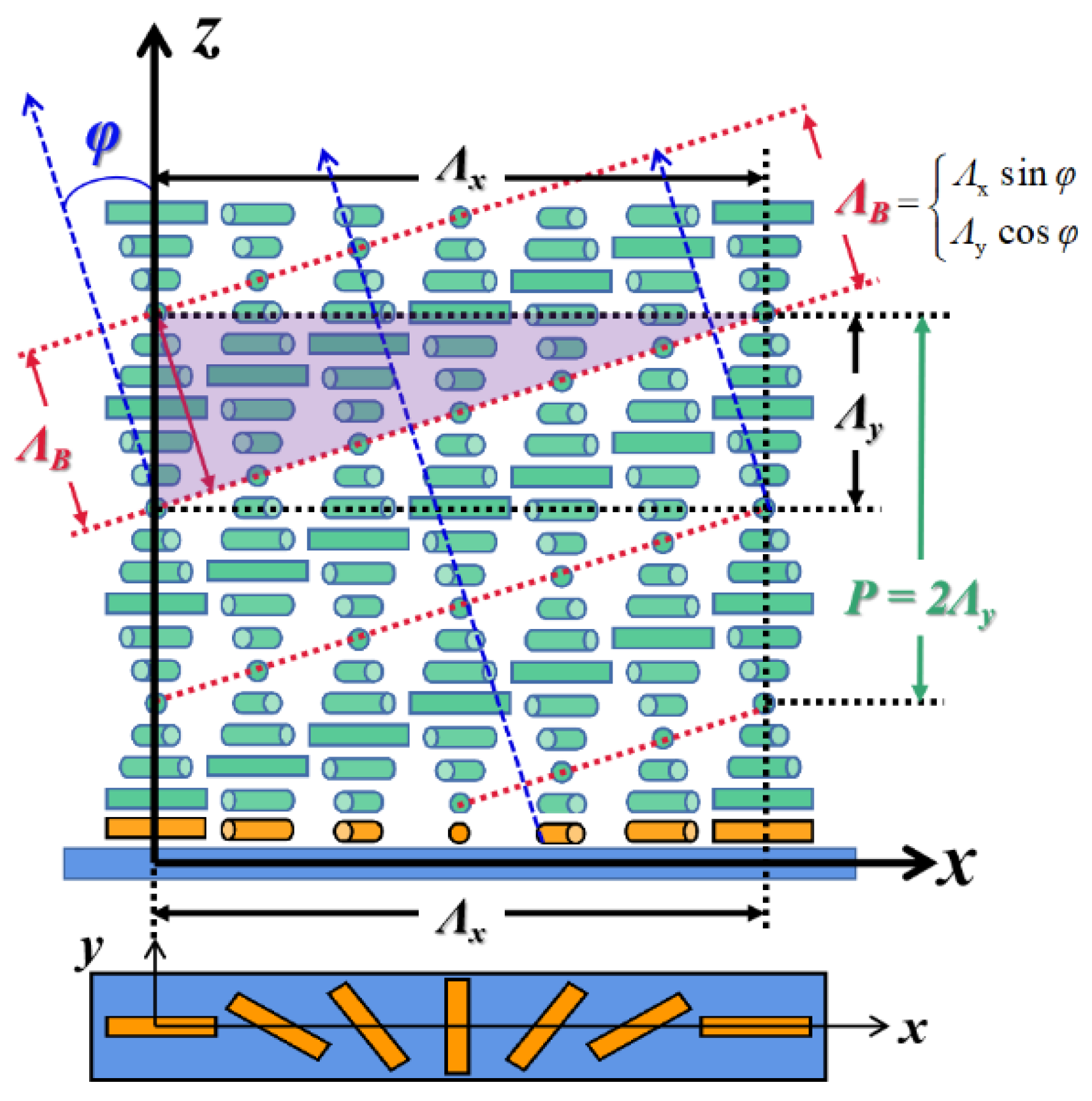
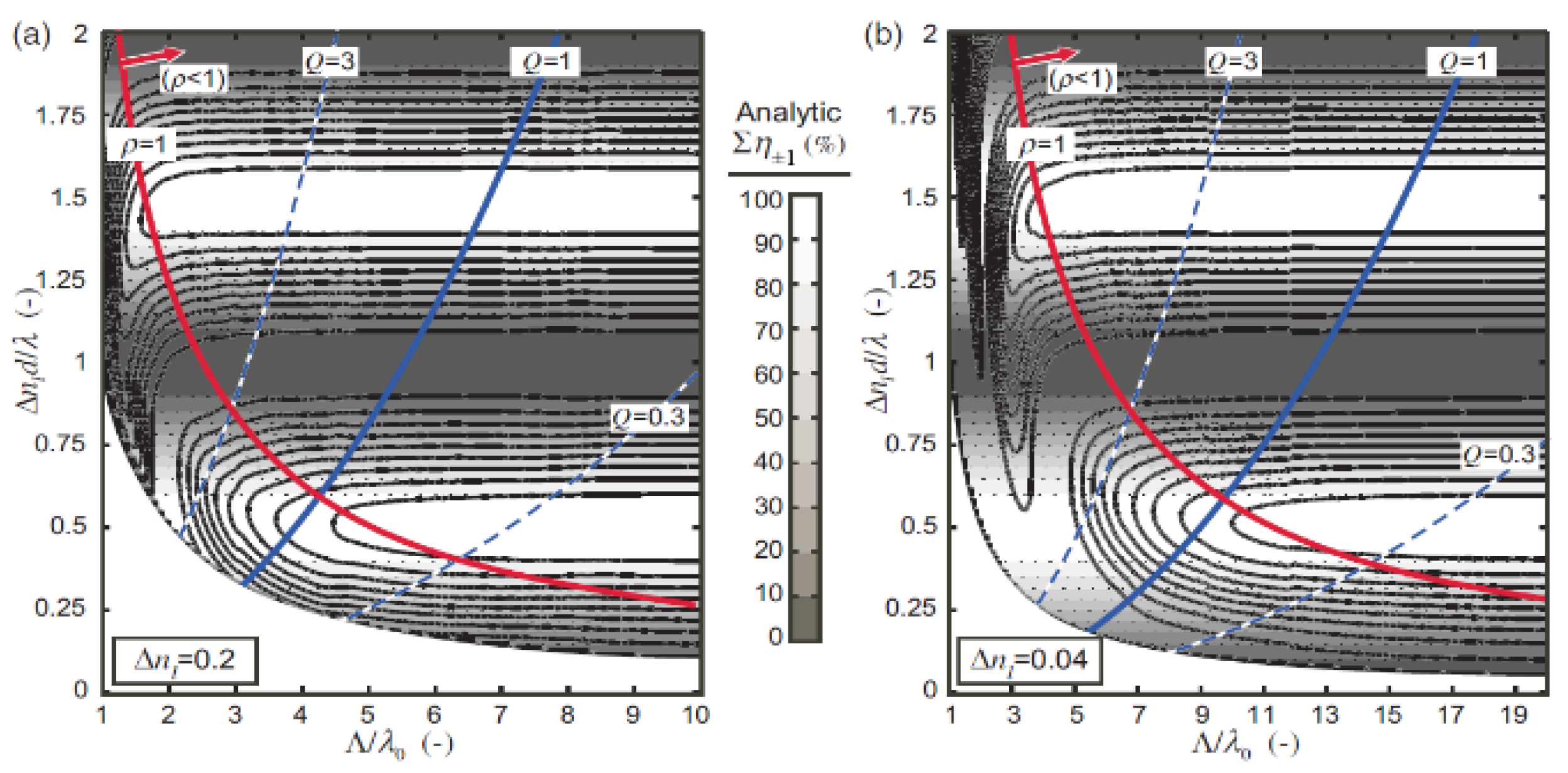
- Bragg diffraction can be established when ΛB meets the condition of the incident wavelength, according to Equation (2) (where d = ΛB, θ = π/2 − φ) and LC layer is thick enough to generate enough periodical refractive index planes. Then a large-angle diffraction with high efficiency can be achieved [7,28,30,33].
- When the pitch ΛB is much greater than that in the Bragg condition, the optical properties of the twisted LC itself (in short-wave circular birefringence region) is revealed. It has a potential to create a LCPG or LCPL with broadband and wide-view angle [22,23,26,34,35], by means of phase compensation.
3. Broadband and Wide-View Angle LCPGs and LCPLs—Based on Phase Compensation of Multi-Layer Twisted LC Structures
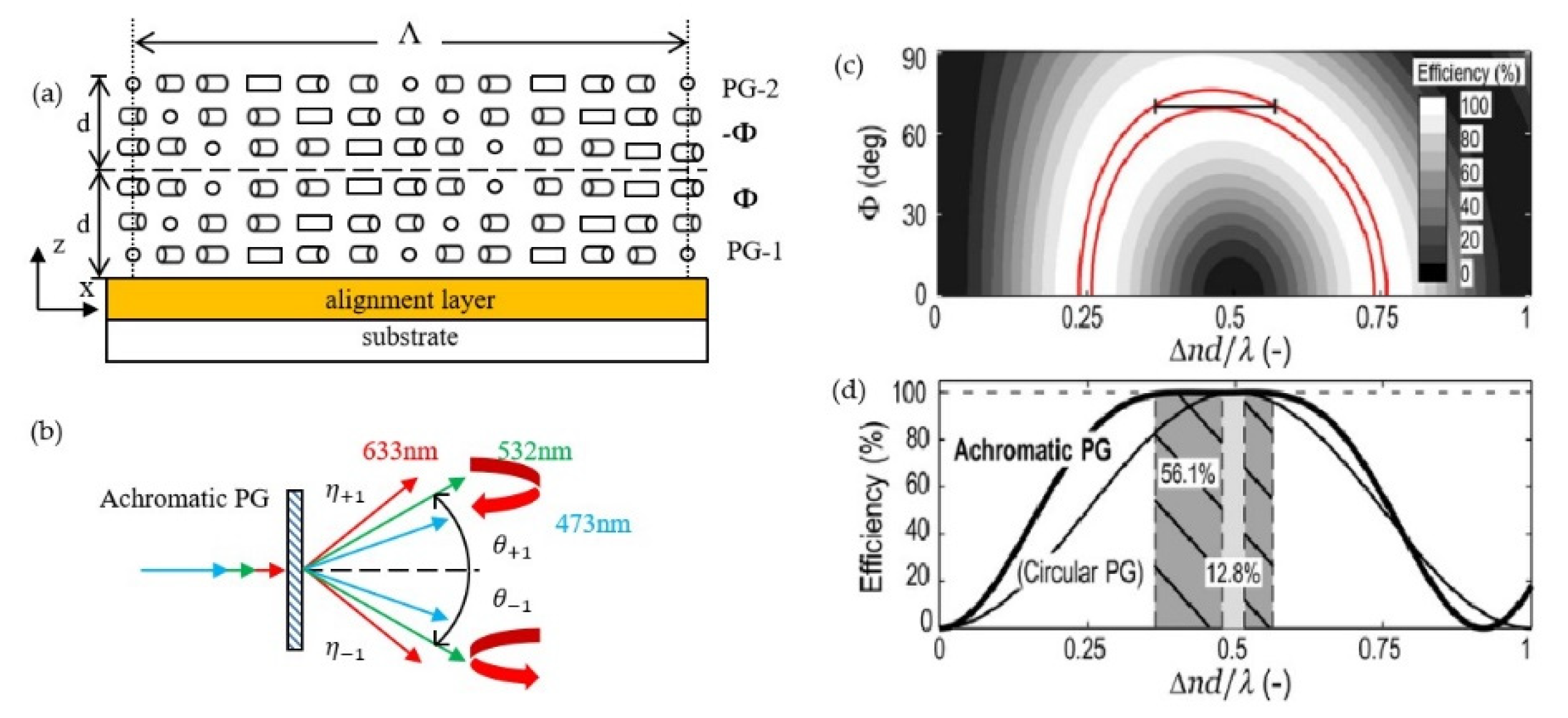
3.1. Dual-Layer Twisted PGs with Broadband and Wide-View Angle
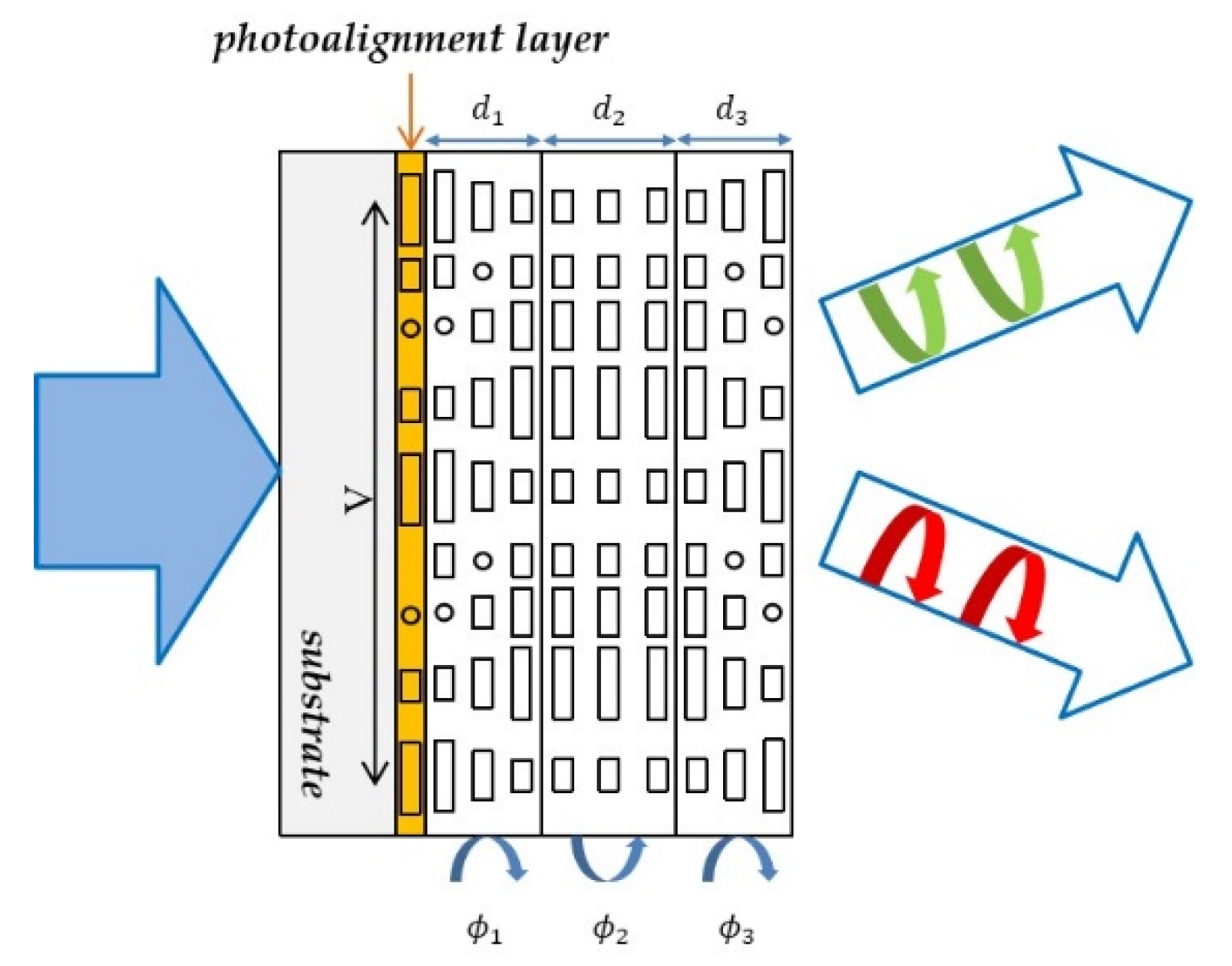
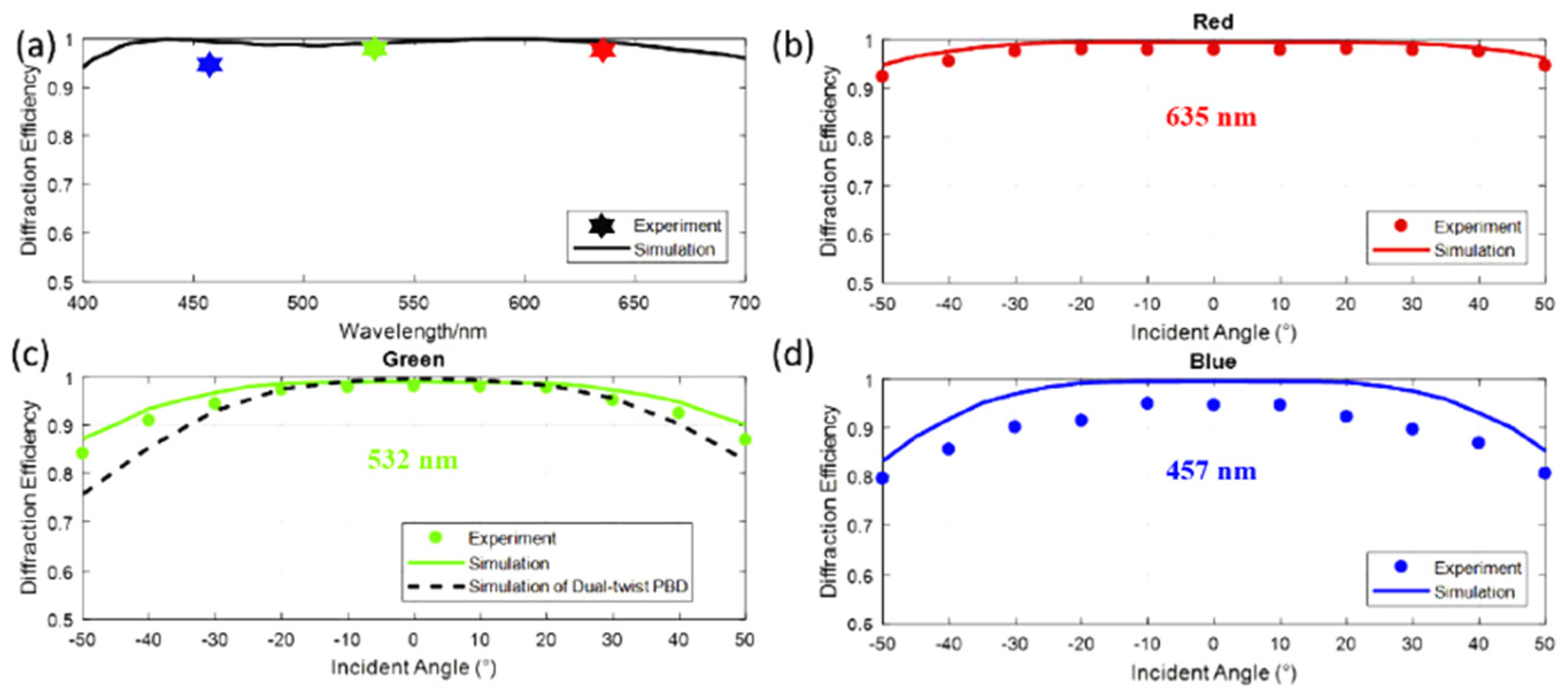
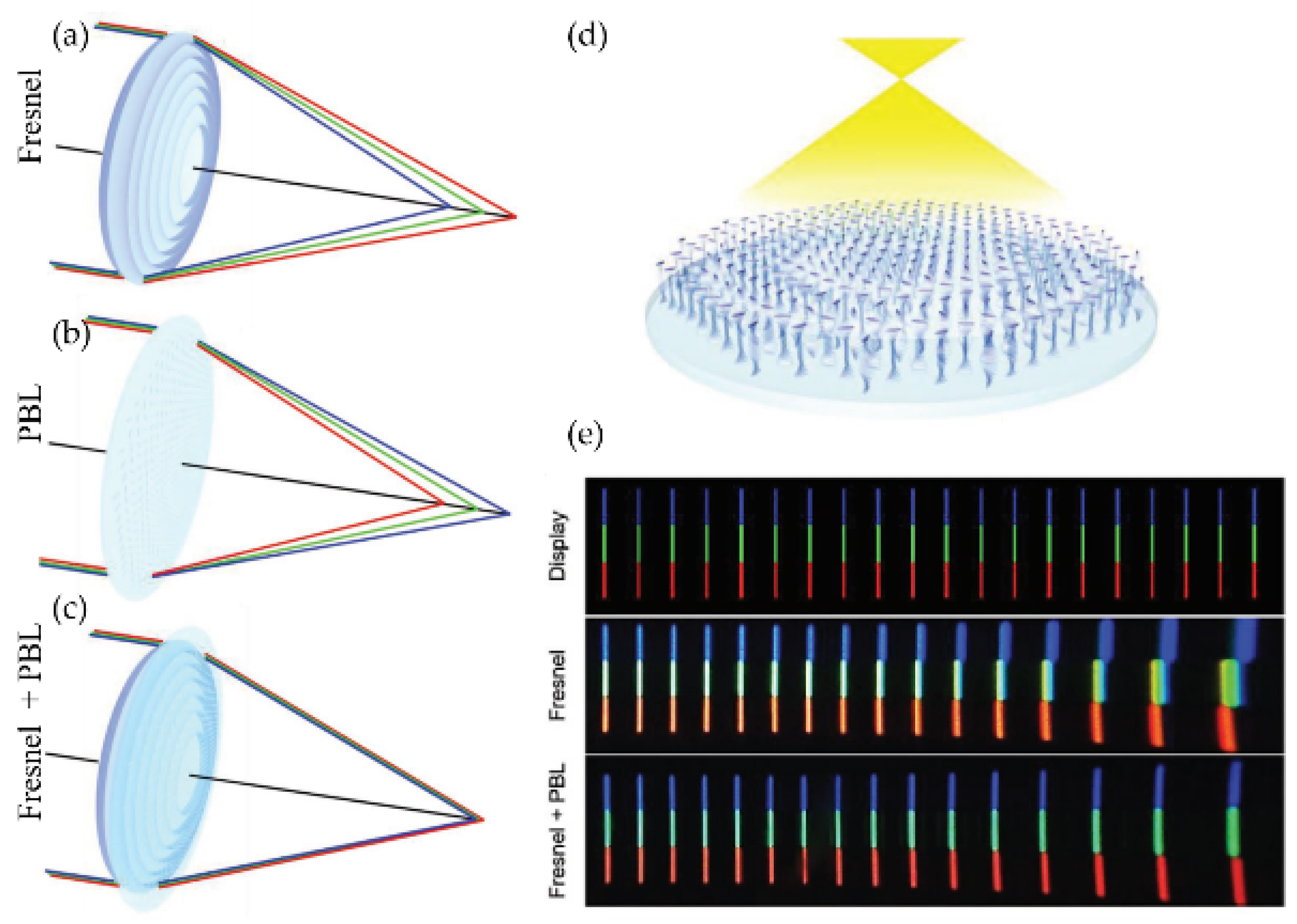
3.2. Three-Layer Multi-Twist PGs and PLs with Ultra-Broadband and Wide-View Angle
4. High Efficiency and Large-Angle Diffraction Gratings and Lenses—Based on Bragg Diffraction Generated by Twisted LC Structures
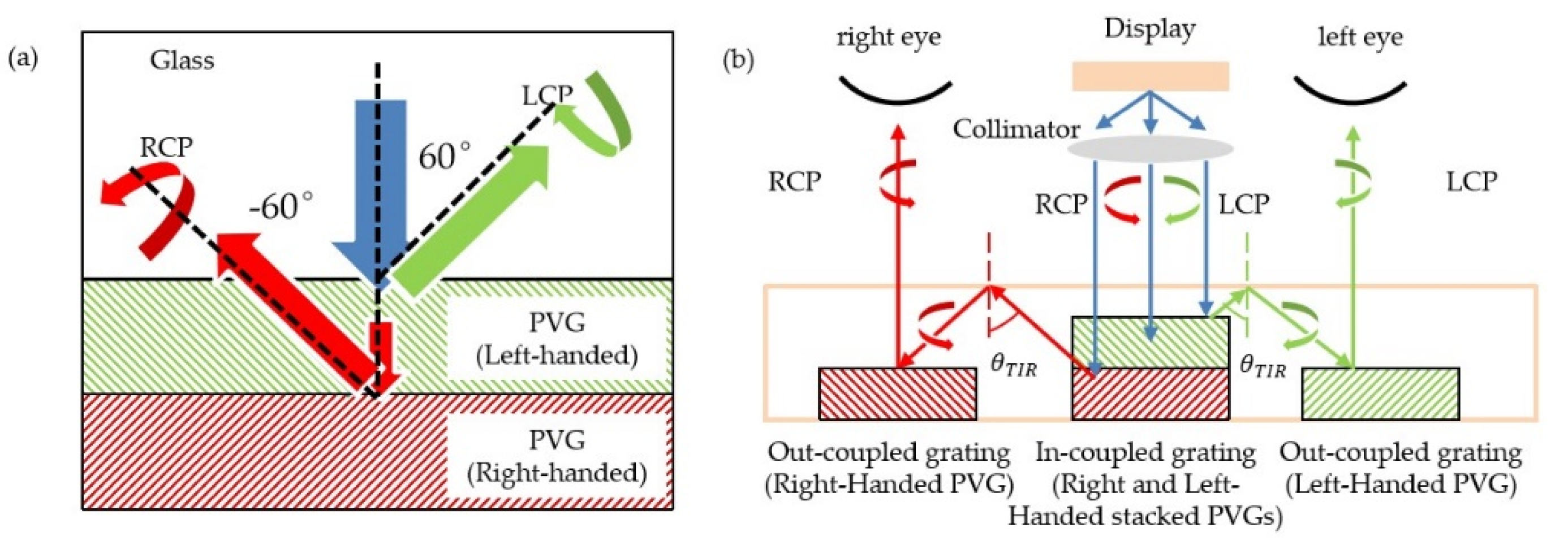
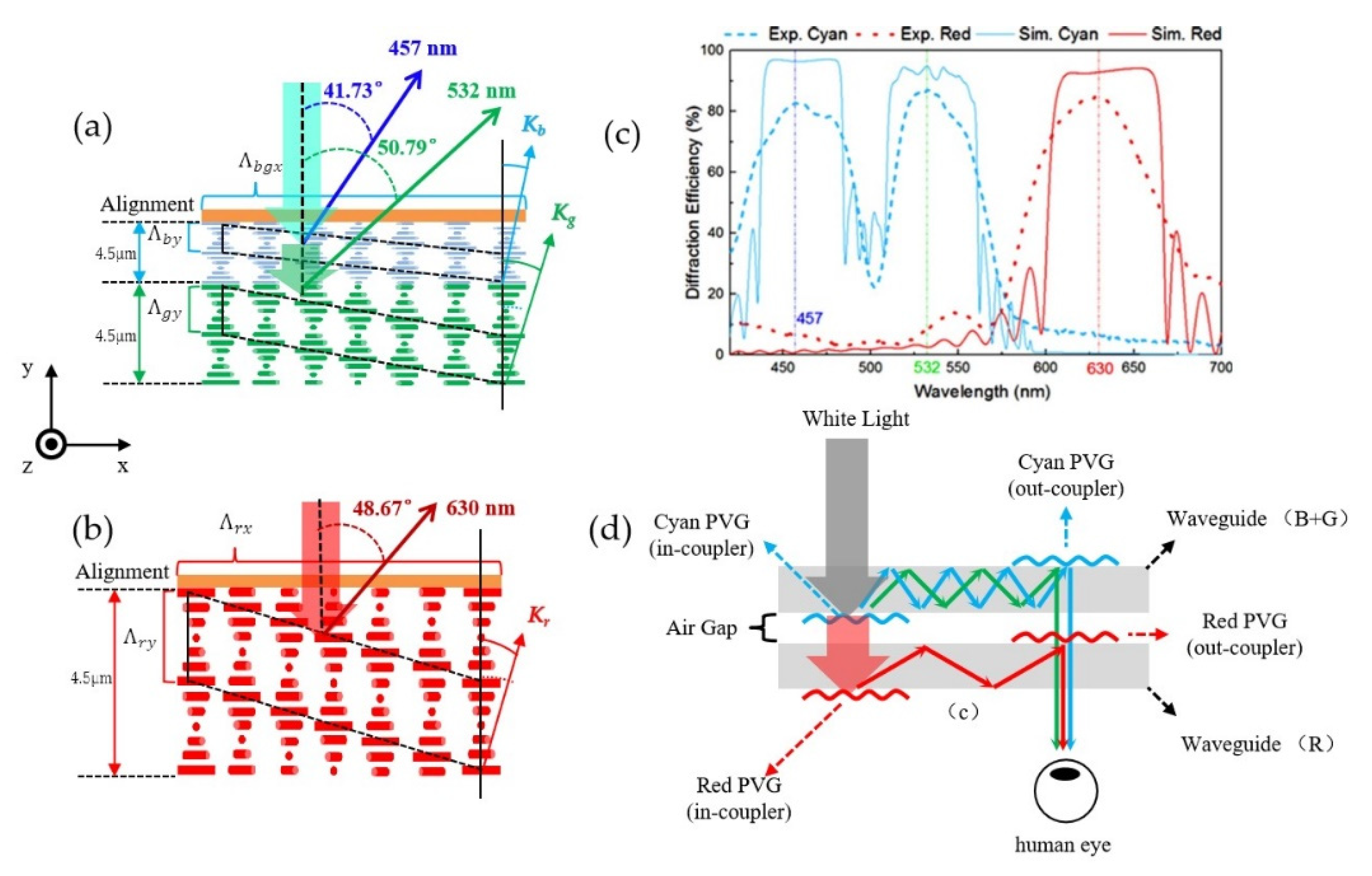
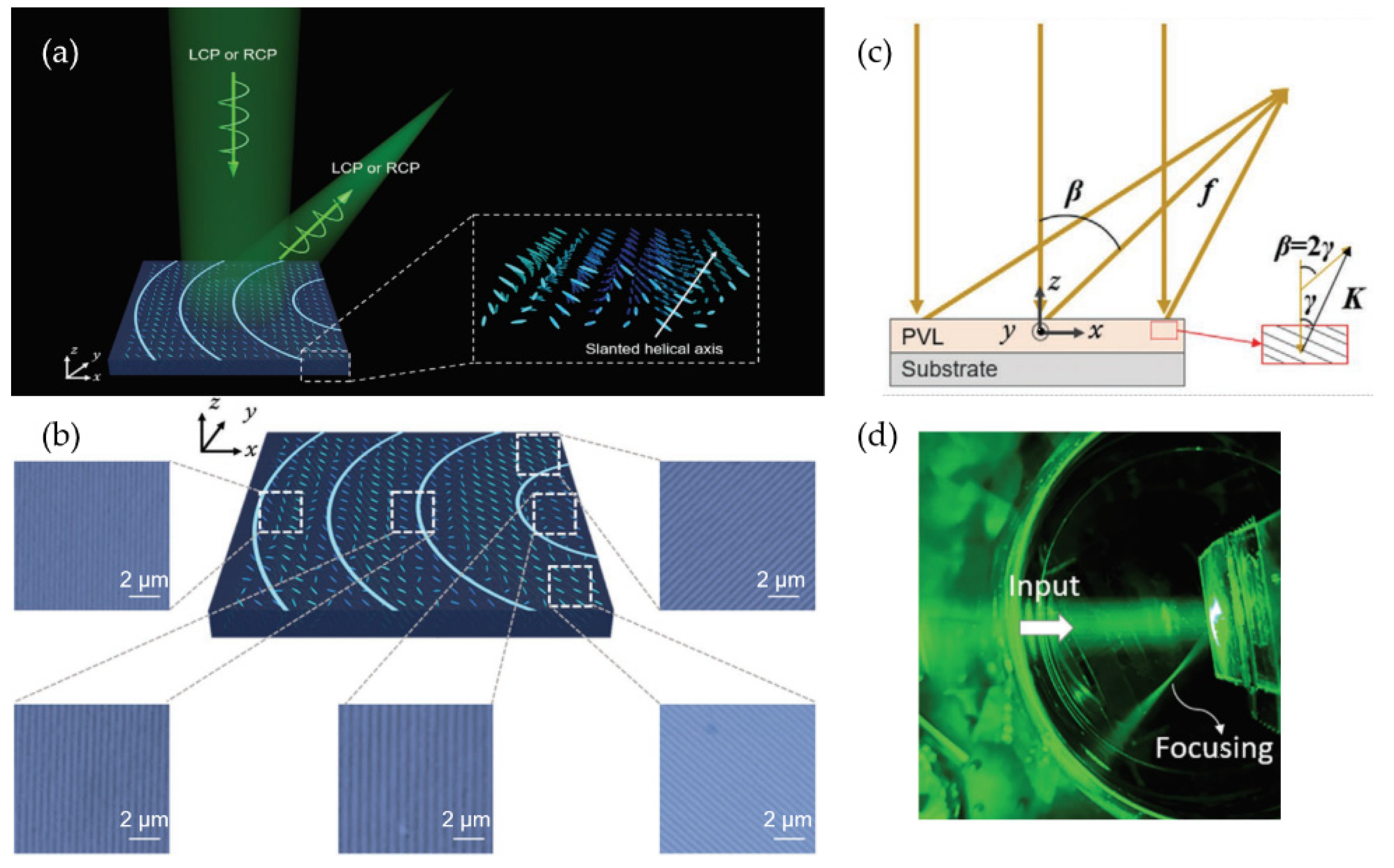
4.1. Reflective Bragg Volume Polarization Gratings (PVGs) and Lens (PVLs)
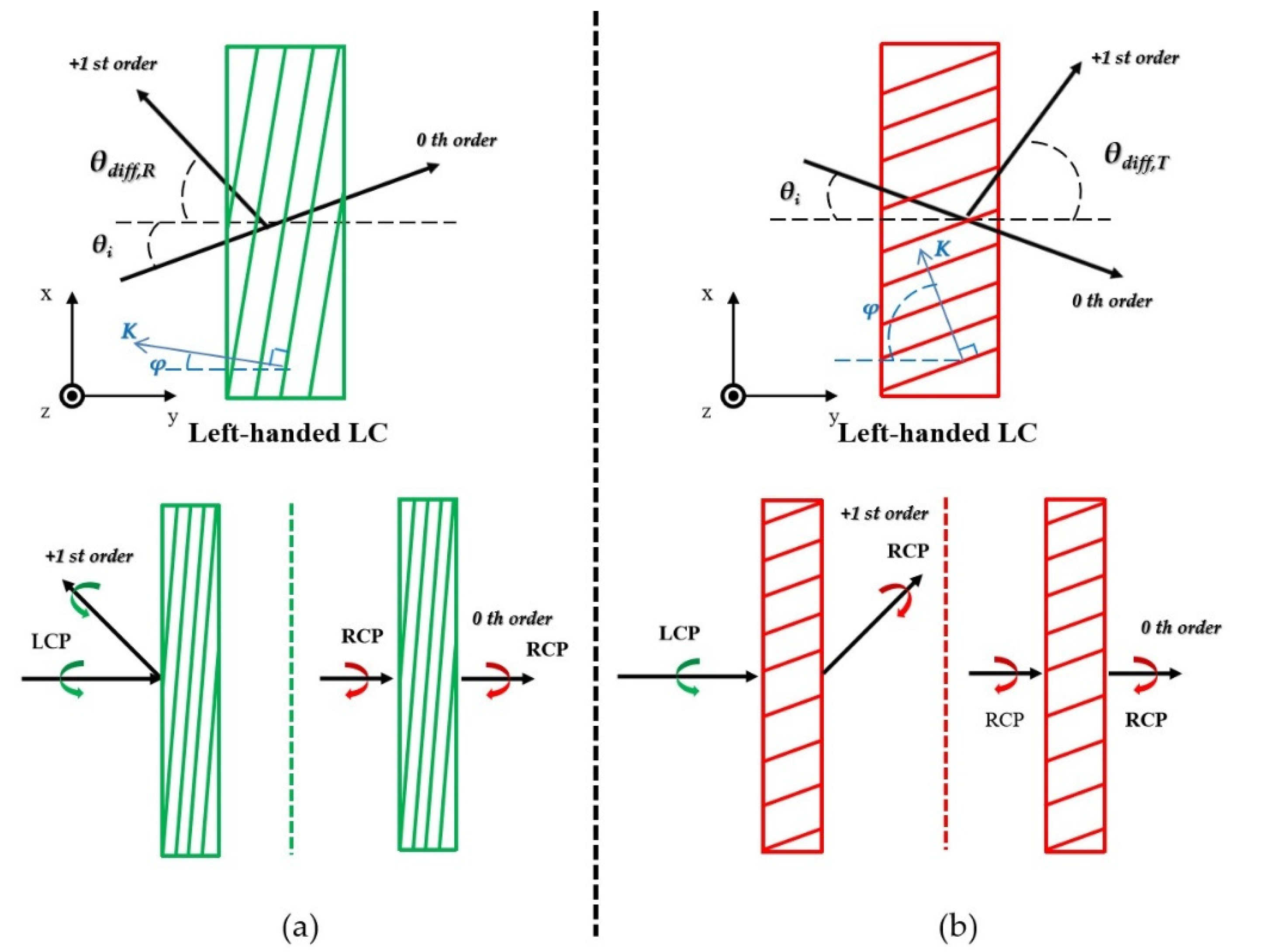
4.2. Transmissive Bragg PGs
5. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Ramachandran, G.N.; Ramaseshan, S. Magneto-optic rotation in birefringent media—Application of the Poincaré Sphere. J. Opt. Soc. Am. 1952, 42, 49–52. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C. Pancharatnam—Berry phase of optical systems. Opt. Lett. 2011, 36, 1143–1145. [Google Scholar] [CrossRef]
- Pancharatnam, S. Generalized Theory of Interference, and Its Applications. In Proceedings—Mathematical Sciences; Springer International Publishing: New York, NY, USA, 1956; Volume 44, pp. 247–262. [Google Scholar]
- Nicolescu, E.; Escuti, M.J. Polarization-independent tunable optical filters based on liquid crystal polarization gratings. Proc. SPIE 2007, 6654, 1–12. [Google Scholar] [CrossRef]
- Packham, C.; Escuti, M.; Ginn, J.; Oh, C.; Quijano, I.; Boreman, G. Polarization gratings: A novel polarimetric component for astronomical instruments. Publ. Astron. Soc. Pac. 2010, 122, 1471–1482. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, Z.; Wang, C.; Li, H.; Wei, R.; Zhang, S.; Peng, Z.; Liu, Y.; Wang, Q.; Mu, Q.; et al. Linear polarization grating combining a circular polarization grating with a special cycloidal diffractive quarter waveplate. Opt. Express 2019, 27, 33378–33390. [Google Scholar] [CrossRef]
- Weng, Y.; Xu, D.; Zhang, Y.; Li, X.; Wu, S.T. Polarization volume grating with high efficiency and large diffraction angle. Opt. Express 2016, 24, 17746–17759. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.H.; Yin, K.; Wu, S.T. Reflective polarization volume gratings for high efficiency waveguide-coupling augmented reality displays. Opt. Express 2017, 25, 27008–27014. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.; Zhang, Y.; Weng, Y.; Shen, Z.; Wang, B. Diffraction efficiency distribution of output grating in holographic waveguide display system. IEEE Photon. J. 2018, 10, 1–10. [Google Scholar] [CrossRef]
- Weng, Y.; Zhang, Y.; Cui, J.; Liu, A.; Shen, Z.; Li, X.; Wang, B. Liquid-crystal-based polarization volume grating applied for full-color waveguide displays. Opt. Lett. 2018, 43, 5773–5776. [Google Scholar] [CrossRef]
- Zhan, T.; Zou, J.; Xiong, J.; Liu, X.; Chen, H.; Yang, J.; Liu, S.; Dong, Y.; Wu, S.T. Practical chromatic aberration correction in virtual reality displays enabled by cost-effective ultra-broadband liquid crystal polymer lenses. Adv. Opt. Mater. 2019, 8, 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Zhan, T.; Wu, S.T. Flat cholesteric liquid crystal polymeric lens with low f-number. Opt. Express 2020, 28, 5875–5882. [Google Scholar] [CrossRef]
- Yin, K.; He, Z.; Wu, S.T. Reflective polarization volume lens with small f-number and large diffraction angle. Adv. Opt. Mater. 2020, 8, 1–7. [Google Scholar] [CrossRef]
- Yin, K.; Zhan, T.; Xiong, J.; He, Z.; Wu, S.T. Polarization volume gratings for near-eye displays and novel photonic devices. Crystals 2020, 10, 561. [Google Scholar] [CrossRef]
- Tan, L. Liquid Crystal Polarization Gratings and Their Applications. Ph.D. Thesis, Hong Kong University of Science and Technology, Hong Kong, China, 2013. [Google Scholar]
- Lin, Y.-H.; Wang, Y.-J.; Reshetnyak, V. Liquid crystal lenses with tunable focal length. Liq. Cryst. Rev. 2018, 5, 111–143. [Google Scholar] [CrossRef]
- Algorri, J.F.; Zografopoulos, D.C.; Urruchi, V.; Sánchez-Pena, J.M. Recent advances in adaptive liquid crystal lenses. Crystals 2019, 9, 272. [Google Scholar] [CrossRef]
- Oh, C.; Escuti, M.J. Numerical analysis of polarization gratings using the finite-difference time-domain method. Phys. Rev. A 2007, 76, 1–8. [Google Scholar] [CrossRef]
- Oh, C. Broadband Polarization Gratings for Efficient Liquid Crystal Display, Beam Steering, Spectropolarimetry, and Fresnel Zone Plate. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2009. [Google Scholar]
- Xiangjie, Z.; Jiazhu, D.; Dayong, Z.; Cangli, L.; Yongquan, L. Oblique incidence effect on steering efficiency of liquid crystal polarization gratings used for optical phased array beam steering amplification. Opt. Rev. 2016, 23, 713–722. [Google Scholar] [CrossRef]
- Cheng, H.H.; Bhowmik, A.K.; Bos, P.J. Concept for a transmissive, large angle, light steering device with high efficiency. Opt. Lett. 2015, 40, 2080–2083. [Google Scholar] [CrossRef]
- Oh, C.; Shaw, J.A.; Escuti, M.J.; Tyo, J.S. Achromatic polarization gratings as highly efficient thin-film polarizing beamsplitters for broadband light. Proc. SPIE 2007, 6682, 1–12. [Google Scholar] [CrossRef]
- Oh, C. Achromatic diffraction from polarization gratings with high efficiency. Opt. Lett. 2008, 33, 2287–2289. [Google Scholar] [CrossRef]
- Tan, L.; Ho, J.Y.; Kwok, H.S. Extended Jones matrix method for oblique incidence study of polarization gratings. Appl. Phys. Lett. 2012, 101, 1–4. [Google Scholar] [CrossRef]
- Tan, L.; Ho, J.Y.; Srivastava, A.K.; Kwok, H.S. A simplified model for the optimization of LC photonic elements. IEEE Photon. Technol. Lett. 2014, 26, 1096–1099. [Google Scholar] [CrossRef]
- Li, L.; Kim, J.; Shi, S.; Escuti, M.J.; Khoo, I.C. Color-selective geometric phase lens for apochromatic lens system. Proc. SPIE 2020, 11472, 1–15. [Google Scholar] [CrossRef]
- Xiang, X.; Escuti, M.J. Numerical analysis of Bragg regime polarization gratings by rigorous coupled-wave analysis. Proc. SPIE 2017, 10127, 1–7. [Google Scholar] [CrossRef]
- Xiang, X.; Kim, J.; Komanduri, R.; Escuti, M.J. Nanoscale liquid crystal polymer Bragg polarization gratings. Opt. Express 2017, 25, 19298–19308. [Google Scholar] [CrossRef]
- Xiang, X.; Kim, J.; Escuti, M.J. Bragg polarization gratings for wide angular bandwidth and high efficiency at steep deflection angles. Sci. Rep. 2018, 8, 1–6. [Google Scholar] [CrossRef]
- Xiang, X.; Escuti, M.J. Numerical analysis of Bragg polarization gratings. J. Opt. Soc. Am. B 2019, 36, D1–D8. [Google Scholar] [CrossRef]
- Yeh, P.; Gu, C. Optics of Liquid Crystal Displays, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2009; pp. 461–484. [Google Scholar]
- Yoon, K.C.; Yoon, H.C.; Kim, K.Y.; Cui, H.; Park, J.R.; Jang, W.; Park, O.O. Application of twisted retarders to a cholesteric liquid crystal polarizer for the control of output polarization states. Jpn. J. Appl. Phys. 2009, 48, 1–6. [Google Scholar] [CrossRef]
- Lee, Y.-H.; He, Z.; Wu, S.-T. Optical properties of reflective liquid crystal polarization volume gratings. J. Opt. Soc. Am. B 2019, 36, D9–D12. [Google Scholar] [CrossRef]
- Yousefzadeh, C.; Jamali, A.; McGinty, C.; Bos, P.J. “Achromatic limits” of Pancharatnam phase lenses. Appl. Opt. 2018, 57, 1151–1158. [Google Scholar] [CrossRef] [PubMed]
- Zou, J.; Zhan, T.; Xiong, J.; Wu, S.T. Broadband wide-view Pancharatnam-Berry phase deflector. Opt. Express 2020, 28, 4921–4927. [Google Scholar] [CrossRef]
- Wu, T.X.; Huang, Y.; Wu, S.-T. Design optimization of broadband linear polarization converter using twisted nematic liquid crystal. Jpn. J. Appl. Phys. 2003, 42, L39–L41. [Google Scholar] [CrossRef]
- Shen, S.; She, J.; Tao, T. Optimal design of achromatic true zero-order waveplates using twisted nematic liquid crystal. J. Opt. Soc. Am. A 2005, 22, 961–965. [Google Scholar] [CrossRef]
- Komanduri, R.K.; Lawler, K.F.; Escuti, M.J. Multi-twist retarders: Broadband retardation control using self-aligning reactive liquid crystal layers. Opt. Express 2013, 21, 404–420. [Google Scholar] [CrossRef]
- Bigelow, J.E.; Kashnow, R.A. Poincaré sphere analysis of liquid crystal optics. Appl. Opt. 1977, 16, 2090–2096. [Google Scholar] [CrossRef]
- Xiong, J.; Chen, R.; Wu, S.T. Device simulation of liquid crystal polarization gratings. Opt. Express 2019, 27, 18102–18112. [Google Scholar] [CrossRef] [PubMed]
- Xiang, X.; Escuti, M.J. Numerical modeling of polarization gratings by rigorous coupled wave analysis. Proc. SPIE 2016, 9769, 1–7. [Google Scholar] [CrossRef]
- Moharam, M.G.; Pommet, D.A.; Grann, E.B.; Gaylord, T.K. Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings: Enhanced transmittance matrix approach. J. Opt. Soc. Am. A 1995, 12, 1077–1086. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. A 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Kobashi, J.; Yoshida, H.; Ozaki, M. Planar optics with patterned chiral liquid crystals. Nat. Photon. 2016, 10, 389–392. [Google Scholar] [CrossRef]
- Gao, K.; McGinty, C.; Payson, H.; Berry, S.; Vornehm, J.; Finnemeyer, V.; Roberts, B.; Bos, P. High-efficiency large-angle Pancharatnam phase deflector based on dual-twist design. Opt. Express 2017, 25, 6283–6293. [Google Scholar] [CrossRef] [PubMed]
- Sakhno, O.; Gritsai, Y.; Sahm, H.; Stumpe, J. Fabrication and performance of efficient thin circular polarization gratings with Bragg properties using bulk photo-alignment of a liquid crystalline polymer. Appl. Phys. B 2018, 124, 1–10. [Google Scholar] [CrossRef]
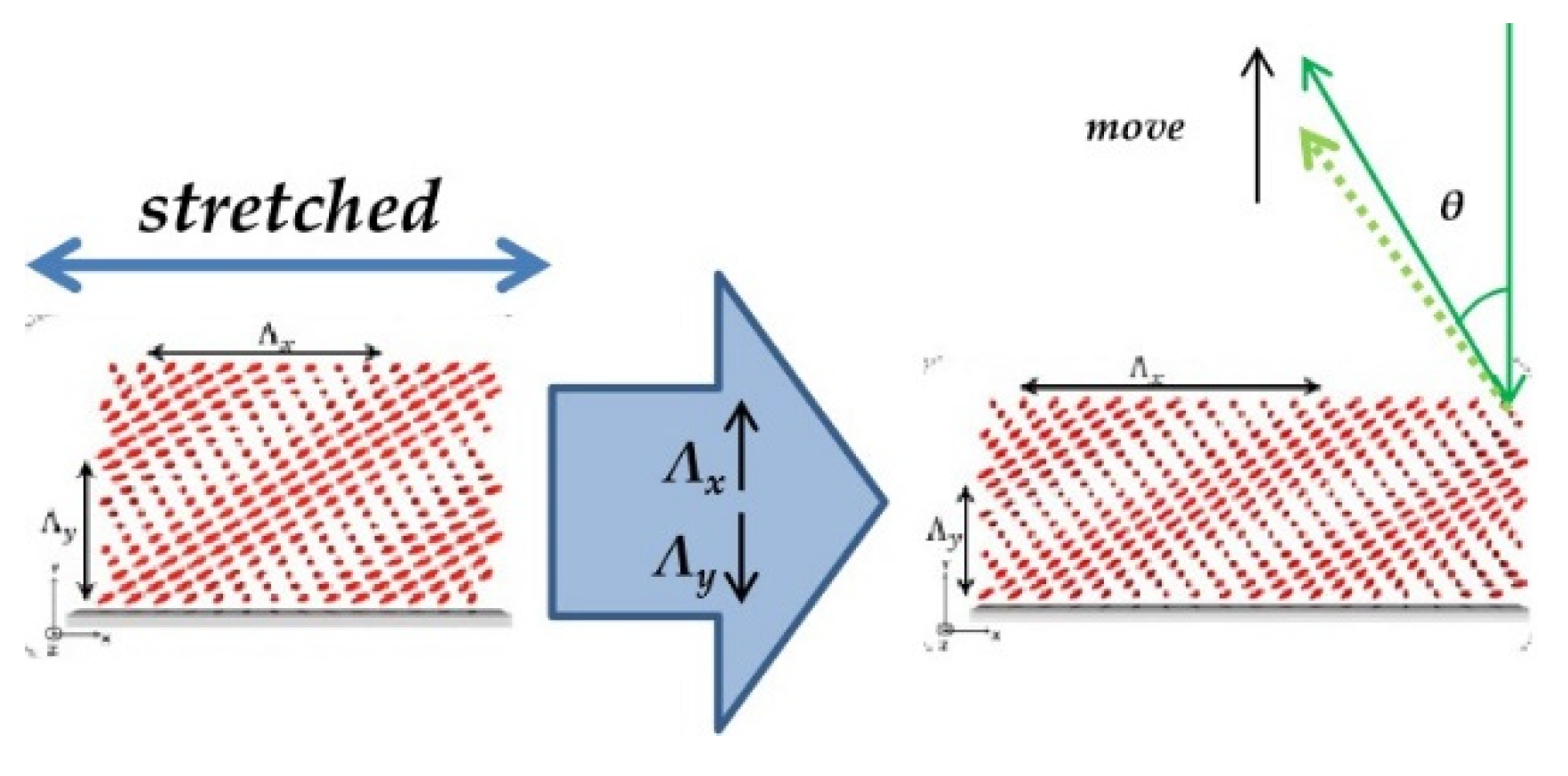
- Yin, K.; Lee, Y.H.; He, Z.; Wu, S.T. Stretchable, flexible, rollable, and adherable polarization volume grating film. Opt. Express 2019, 27, 5814–5823. [Google Scholar] [CrossRef]
- Cheng, H.; Bhowmik, A.K.; Bos, P.J. Analysis of a dual-twist Pancharatnam phase device with ultrahigh-efficiency large-angle optical beam steering. Appl. Opt. 2015, 54, 10035–10043. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Chen, W.; Yu, Y.; Wang, Q.; Mu, Q.; Li, S.; Chen, J. Twisting Structures in Liquid Crystal Polarization Gratings and Lenses. Crystals 2021, 11, 243. https://doi.org/10.3390/cryst11030243
Zhang S, Chen W, Yu Y, Wang Q, Mu Q, Li S, Chen J. Twisting Structures in Liquid Crystal Polarization Gratings and Lenses. Crystals. 2021; 11(3):243. https://doi.org/10.3390/cryst11030243
Chicago/Turabian StyleZhang, Shiyuan, Wan Chen, Yang Yu, Qidong Wang, Quanquan Mu, Shixiao Li, and Jin Chen. 2021. "Twisting Structures in Liquid Crystal Polarization Gratings and Lenses" Crystals 11, no. 3: 243. https://doi.org/10.3390/cryst11030243
APA StyleZhang, S., Chen, W., Yu, Y., Wang, Q., Mu, Q., Li, S., & Chen, J. (2021). Twisting Structures in Liquid Crystal Polarization Gratings and Lenses. Crystals, 11(3), 243. https://doi.org/10.3390/cryst11030243