Abstract
The additive manufacturing process of laser powder-bed fusion (L-PBF) is an increasingly popular approach for patient-specific production of dental frameworks made from Co-Cr alloys. Macroscopically, frameworks produced in this way exhibit high anisotropy especially in Young’s modulus, and are missing standardized requirements. Microscopically, pronounced texture and high residual stresses are characteristic. To reduce resulting detrimental effects, the as-built (AB) parts are heat treated. Dependent on the treatment temperature, effects like the transformation of the -phase matrix in the AB condition to -phase, precipitation, stress relief, and grain growth were observed. While the existence of these processes was established in the past, little is known about their kinetics. To fill this gap, these effects were studied with in-situ X-ray diffraction (XRD) methods in isothermal heat treatments (HTs) at four different sample surface temperatures reaching from to . Furthermore, room temperature ex situ XRD and SEM/EDS measurements completed the analysis. An evaluation of the datasets, with single peak fitting and QXRD methods, yielded the following results. In the HTs below a certain threshold, a -to- transformation was observed in the sample bulk and close to the sample surface. In the latter case, evidence for a partially strain-induced transformation related to oxide formation was present. Above this threshold and possibly slightly below, - and Laves-phase precipitated. Additionally, peak profile evolutions hinted at a drop of inter- and intragranular stresses within the first 30 to 60 min. Therefore, an HT of about 30 to 60 min slightly above the threshold is proposed as optimal for reducing residual stresses while retaining a predominantly single-phased microstructure, possibly superior in corrosion properties and likewise in bio-compatibility.
1. Introduction
Framework materials in biomedical applications have to fulfill requirements regarding biocompatibility, corrosion resistance, and load bearing capabilities [1]. In dentistry, with a special focus on the framework of porcelain fused to metal (PFM) and removable partial dentures (RPDs), these basic requirements are extended by application specific ones like tarnish resistance, burnishability, polishability, and aesthetics [2].
In the past, this extended catalogue of requirements was best fulfilled by noblemetal alloys [3]. Today, these are partially superseded by various cheaper metallic alloys on the basis of Ti, Ni-Cr, or Co-Cr [2].
In particular, Co-Cr alloys are a common choice, as they generally fulfill all stated requirements [3]. They even outperform noblemetal and partially Ti alloys in their mechanical performance regarding strength and Young’s modulus (E), enabling a filigree but still rigid design of dental frameworks [4]. Due to a strong Cr-rich passive layer, they additionally offer good corrosion resistance and biocompatibility, particularly in comparison to Ni-Cr alloys [4]. Nevertheless, there remain concerns about hypersensitive reactions and carcinogenic effects induced by the in-vivo release of Co and Cr ions, especially at unusual high corrosion rates or by the exposure to Co-Cr powders and dusts mainly present in manufacturing [1,3,5].
Usually, either or are added to Co-Cr alloys to further increase the mechanical performance via solid solution strengthening [6]. Subsequently, focusing on -containing alloys, is added to avoid embrittlement caused by precipitates of -phase type [7,8].
Conventionally, patient specific production of Co-Cr dental frameworks is based on investment casting [9], a labor-intensive manufacturing process, or CNC machining of blanks, involving high costs due to material wastage [10,11].
In recent years, additive manufacturing techniques have become a feasible alternative [12,13]. The most relevant approach for dental applications is based on laser powder-bed fusion (L-PBF) [11,12,14]. This method builds up a part layer-by-layer through recurrently coating thin layers of a desired metal powder, which is then locally fully melted with a focused laser beam moved in a hatching fashion in the zones of the part to be created [12,15]. Though L-PBF is a complex thermophysical process, once properly adjusted, predictable results with high geometrical accuracy ensure successful clinical outcomes at low costs in the long run [11,16].
The predominant phase in Co-Cr parts conventionally cast or as built (AB) with L-PBF is a metastable face-centered cubic (fcc) -phase with the constituent atoms of the alloy in solid solution [4,17]. This is known to transform to the equilibrium hexagonal close-packed (hcp) -phase during certain heat treatments (HTs) or via strain-induced transformation [8,18].
Though phase composition is similar between conventional and additive manufacturing methods in Co-Cr alloys, their microstructures and resulting part-properties differ fundamentally. Slow cooling rates typical for casting result in coarse-grained cellular dendritic microstructures susceptible to solidification segregation and interdendritic microporosity [4,14].
In contrast, the high cooling rates combined with the characteristic L-PBF build-process lead to a fine-grained, homogeneous, and largely dense microstructure resulting in mechanical properties generally superior to cast samples [17]. The AB condition is, however, also highly textured and bears residual stresses on the micro-scale [18,19]. On the macro-scale, this condition is anisotropic, especially regarding the Young’s modulus, which not even reaches the ISO 22674 type 5 criteria of in certain directions [10].
To address the detrimental effects present in the AB condition of samples produced with L-PBF, isothermal post production HTs are applied. On the macro-scale, these result in a homogenization and an increase in mechanical properties, in particular, the Young’s modulus [10]. On the micro-scale, multiple mechanisms like the -to- phase transformation, precipitation, recovery, residual stress relieve, recrystallization, and grain growth are activated by the HT [18,19,20]. Some of these mechanisms can affect the performance of dental frameworks adversely, which is the reason why the parameters of the HT have to be optimized with regard to the stated requirements. While the influence of temperature as a parameter was already partially covered, the influence of the treatment’s duration has not been thoroughly established yet [19].
Another open question is the link between the increase in Young’s modulus on the macro-scale and the mechanisms active on the micro-scale during HTs. A -to- transformation was ruled out by von Kobylinski et al., as it was absent from their applied experimental conditions [18]. While taking the phase fractions into consideration, they furthermore concluded that precipitates can only account for a contribution to the observed increases, but cannot be the sole mechanism. Additionally, an explanation based on the residual stress relieve was proposed, but could not be fully verified.
Therefore, the goals of this study are to investigate the kinetics of microstructural changes and phase transformations with primary importance, and also to further study the link between micro-effects and the increase of Young’s modulus on the macro-scale. To achieve these goals, samples were isothermally treated at four different temperatures, while observing microstructural changes with in-situ X-ray diffraction (XRD) methods. Ex-situ diffraction experiments, scanning electron microscopy (SEM), and energy-dispersive X-ray spectroscopy (EDS) studies complemented the research.
2. Materials and Methods
2.1. Sample Preparation
Feed stock for sample production was a Remanium star Cl (Dentaurum GmbH & Co. KG, Ispringen, Germany) alloy powder. The composition specification of this alloy is: Co Bal.; Cr 28; W 9; Si 1.5; Mn < 1; Fe < 1; Nb < 1; N < 1 wt.-% [21]. An MLab L-PBF printer (Concept Laser GmbH, Lichtenfels, Germany) equipped with an inert chamber was utilized to process the powder to a cylindrical rod (ø 7 mm × 55 mm). To average microstructural features induced by the L-PBF process, an angle of between the rod’s axis and the base plate’s surface, as illustrated in Figure 1, was selected. The rod was cut perpendicular to its axis by electrical discharge machining to four disk-shaped samples with diameter and thickness. Both top surfaces of the samples were sanded to with silicon carbide (SiC) paper and one of them was further sanded (SiC, up to ) and polished with diamond suspension up to grain sizes smaller than . Samples were finished by chamfering the polished surface of the disks. Another iteration of grinding and polishing was performed on the samples after HT to access bulk properties. Subsequently, this re-polished condition is referred to as the samples’ bulk, whereas the state of disks left untreated after HT is referred to as samples’ surface.
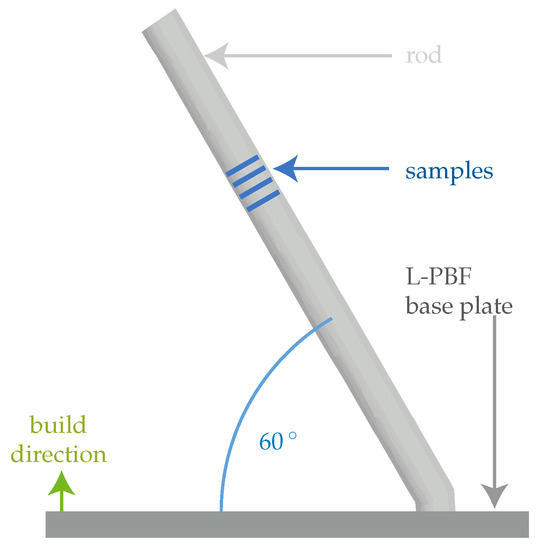
Figure 1.
Illustration of the orientation of the samples in the L-PBF process.
2.2. Heat Treatment and Hot Stage
On each sample, a separate isothermal HT was conducted with a Domed Hot Stage (DHS) 1100 (Anton Paar GmbH, Graz, Austria). An image of the stage is shown in Figure 2.

Figure 2.
Image of the Domed Hot Stage: (1) AlN base plate; (2) sample; (3) TiAl holders; (4) graphite dome; (5) ring with cooling air exhausts; (6) heat sink; (7) feed pipes.
The sample was placed with the unpolished side in contact with the stage’s heated AlN base plate during HT. To offer the best possible thermal contact and position accuracy, the specimen was clamped by TiAl holders acting on the bevels. A semispherical X-ray transmissible graphite dome was superimposed during HT to enclose the sample in a sealed cavity, which then was evacuated to pressures below with a short spike of about during the heat-up process.
The stage is temperature-controlled by measuring with an S-type thermocouple in contact with the conduction heating elements underneath the base plate. Heat-up and cool-down rates of the controller were set to a maximum of for all experiments [22]. Isothermal holding was performed at values of , , , and on samples 1, 2, 3, and 4, respectively, for .
Discrepancies between values and the sample surface temperature (relevant for XRD) are known to occur [23]. However, a direct quantification of the sample surface temperature during HT is restricted by the graphite dome. Hence, a comparative set-up, suited for short-period use only, was developed. It includes a PEEK-dome that is distinguished by an additional thermocouple feed-through. With this set-up and a K-type thermocouple spot-welded to the sample’s surface, could be measured simultaneously to for different steady states, see Table 1.

Table 1.
Recordings of the steady state temperatures measured in the reference set-up at the controller and the sample’s surface.
2.3. XRD
In-situ XRD datasets were acquired on a Bruker D8 advanced system (Bruker AXS GmbH, Karlsruhe, Germany) during each HT. At the expense of a dominant fluorescence background in the signal, an X-ray tube (operated at , ) with a Cu-target and a primary Ni -filter was selected for these experiments, as the characteristic Cu- radiation is transmitted through the dome in major fractions. The Cu-target was chosen since it allows a clearly visible separation of diffraction cones.
Diffracted radiation was recorded with a Bruker Vantec 500 microgap 2D detector (Bruker AXS GmbH, Karlsruhe, Germany) at a fixed detector position in multiple frames with a duration of . The sample was fully rotated about the surface normal and oscillated in-plane on an area >5 mm in each frame to reduce texture influence and to improve grain statistics. Preliminary studies with directly succeeding frames hinted at a drift in the detector’s gain. A possible explanation for this can be seen in charge-up effects occurring in gaseous detectors containing dielectric materials [24]. Due to this fact, exposure breaks of at least the measurement time were introduced between each frame to allow for a recovering process of the detector.
For the evaluation of in-situ datasets, software based on single-peak fitting of Voigt functions was developed. The Voigt function is a convolution of a Gaussian profile, modeling strain broadening, and a Lorentzian (or Cauchy) profile, capturing finite crystallite size [25,26]. In line with Mittemeijer and Welzel, the use of more advanced peak-profile analysis tools was rejected due to the complexity of parametrization in non-ambient conditions [25].
Prior to peak fitting, each frame of the in-situ dataset was pre-processed. In a first step, each 2D frame was integrated into 1D diffractograms along the -angle tracing the recorded sections of diffraction cones. Thereafter, for each diffractogram, a background model, based on Gaussian radial basis functions with a kernel size of , was fitted to manually classified peak-free segments with a support vector machine, see Figure 3. On top of that, another model, based on partially overlapping asymmetric Voigt functions, was fitted, this time with a weighted linear regression realized by Minuit [27], to the interfering defocused peaks of the graphite dome. Glancing angles at which sample peaks occur are omitted within this analysis. On top of these two models, the actual peak fitting was carried out in the same fashion as graphite peak fitting, though with symmetrical Voigt functions, as asymmetrical ones caused over-fitting behavior. This resulted in estimates for the integrated area of a peak as a measure for the peak intensity , the peak position , the full width at half maximum (FWHM) of the Gaussian component , and the FWHM of the Lorentzian component for each frame.
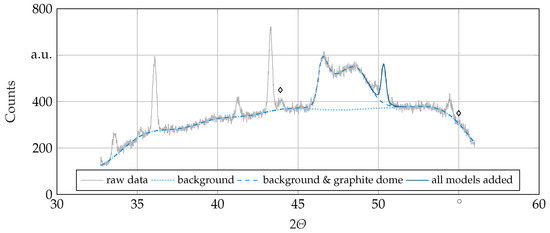
Figure 3.
Diffractogram of the last frame of the in-situ dataset from sample 4 at with graphs of the various models fitted to the raw data. Diamond markers: Possible peaks of a high temperature phase not present in ambient conditions.
Additionally, ex-situ datasets were recorded in ambient environments on a second system comprised of a Bruker D8 advanced instrument. This diffractometer was likewise equipped with a Cu-target X-ray tube (operated at , ), however using a graphite monochromator in the primary beam path, a conventional sample stage, and a Bruker Vantec 2000 (Bruker AXS GmbH, Karlsruhe, Germany) microgap 2D detector. This setup was used due to its higher angular resolution over the former one. Each ex-situ dataset consists of several frames with exposure times of in surface and in bulk measurements, each taken at incremented detector positions. For each dataset, the frames were merged to a diffractogram, and the background was subtracted with standard procedures implemented in Bruker’s DIFFRAC.EVA software. To access intensity estimations for further calculations, peak fitting as described above was applied on a selected frame for each ex-situ dataset.
2.4. QXRD
To access the kinetics of the metastable -phase to -phase transformation during HT, quantitative XRD (QXRD) methods were applied to measurements taken on samples 1 and 2, which were most relevant for this purpose. Of fundamental importance for QXRD is the following equation, first derived by Alexander and Klug [28], which was used in an adapted form:
This equation links the peak intensity to the weight fractions of the observed phase i at any point k in time t throughout the treatment, with . Equation (1) is based on the calibration constant , with the respective subscripts j for a certain peak and p for either the in- or ex-situ set-up. It should be noted that yet another subscript l was introduced to indicate differences due to the temperature dependence of the Debye–Waller factor implicitly incorporated in the calibration constant [29]. Additionally needed for a quantitative evaluation are values for the density of the respective phase assumed to be equal to for all matrix phases and the mass absorption coefficient of the sample calculated to be [21,30].
If is known, could be calculated with Equation (1) and the estimated peak intensities from the XRD measurements. Anticipating the results of further analysis and focusing on the beginning of the in-situ measurements, it can be assumed that there the amount of -phase is equal to 1. This results in the calibration constant for the -phase and hence in the respective weight fractions. Nevertheless, this type of analysis is highly dependent on estimates of peak intensities taken at certain points in time, e.g., at the beginning , especially when using in-situ datasets with low counting statistics. To be less prone to deviations, a model was fitted to all intensity values of one in-situ data set with weighted linear regression and the model’s value at a certain point, e.g., , was used for the calculation of the calibration constants instead.
To access the weight fractions of a second phase without the knowledge of the corresponding calibration constant in a two-phase system, as it is approximately valid for sample 1, the intensity Equation (1) can be complemented by the mass balance equation:
In the case of sample 2 and in addition to the two matrix phases, an oxide layer was observed. To account for the attenuation caused by the oxide layer, Equation (1) was expanded with the Beer–Lambert law according to the relation:
where describes the thickness, the density (), and the calculated mass absorption coefficient () of the oxide [30,31]. Deviating from Equation (1), the weight fraction relative to the sum of weight fractions from the sub volume of matrix phases diffracting under the oxide layer is used to simplify calculations. For this sub volume, another form of mass balance equation has to be applied:
With Equations (3) and (4), and the in-situ dataset of sample 2 alone, the system could not be solved. The direct exchange of already determined calibration constants between the in-situ measurements of samples 1 and 2 was also not possible due to temperature differences in the experiments. However, the ambient conditions and the constant setup of all ex-situ datasets allowed for transferring the calibration constants. With the additional assumption that the microstructure is approximately frozen at the time point of the treatments’ ends with no relevant changes occurring during cool-down and at room temperature, and the assumption that the weight fraction of possible precipitates is negligible, all relevant calibration constants can be accessed in the way outlined in Figure 4 and therefore the whole system becomes solvable. To increase the accuracy of the analysis, carry-over variables were calculated on the basis of model intensities too. As the calibration constant for the -phase in the in-situ dataset of sample 2 can be calculated for two points in time separately, this parameter was assumed to be linearly time dependent between these values and denoted as .

Figure 4.
Flow chart for the calculation of calibration constants for all phases present in samples 1 and 2.
2.5. SEM
Beyond XRD methods, scanning electron microscopy (SEM) using a Jeol JSM-7600F (JEOL (Germany) GmbH, Freising, Germany) instrument was employed on the gold-sputtered samples’ bulk after HT and on the cross section of samples 1 and 2 to determine oxide layer thickness. Additionally, energy-dispersive X-ray spectroscopy (EDS) was performed on these samples to identify chemical segregations.
3. Results
3.1. Phase Identification and Morphology
Diffractograms of as-built (AB) and post HT samples measured ex-situ on the samples’ surface together with reference patterns of identified phases are displayed in Figure 5. In the AB condition, all samples exhibited dominant amounts of the metastable fcc -phase. The small peak at is pointing towards the existence of very small fractions of the stable hcp -phase in the AB condition. Furthermore, peak positions indicate that both matrix phases contain the elements of the alloy in solid solution.
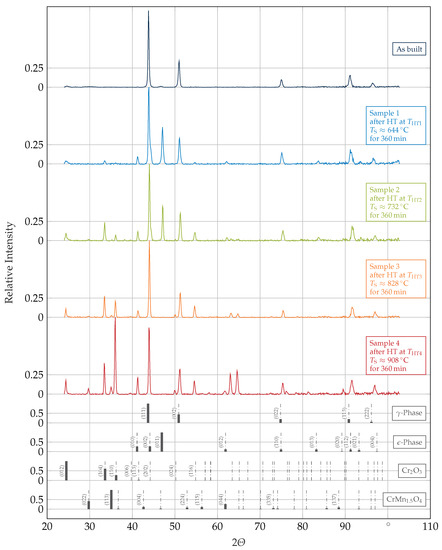
Figure 5.
In color: Ex-situ XRD diffractograms, with intensities normalized to the highest peak in the respective pattern, of samples composed of a Co-Cr-W alloy in states AB by L-PBF and after HTs measured on the samples’ surface. Additionally in grey: Stick reference pattern calculated with VESTA [32] of a solution of W in Co fcc -phase (COD:1524796 [33]), a solution of W in Co hcp -phase (COD:1524797 [33]), a oxide (COD:2104122 [34]), and a spinel (COD:7222202 [35]).
The diffractograms of the samples 1 and 2 post HT show peaks suiting the same aforementioned phases in alternated volume fractions and additionally a phase. Judging by the relative peak intensities, similar and substantial amounts of the -matrix transformed to -phase in both samples. Concerning the content of these samples, there is evidence of a trend towards increased phase fractions with increased HT temperatures. This is especially visible on the peak height of the - reflection. Additionally, yet barely visible, peaks around and appeared, matching reflections expected from a phase of the spinel type within the space group . A feasible reference with best fit within this space group is , although the content is rather low in our alloy [35].
In samples 3 and 4, treated at further increased HT temperatures, a threshold is surpassed, above which the -phase is completely absent from these samples. The trend of increasing fractions with rising HT temperatures is continued within these samples, accompanied by fractions of the spinel. In sample 4, the --peak is particularly apparent, possibly related to the formation of texture.
Comparing the diffractograms of Figure 5, taken at room temperature after HT, and of Figure 3, taken at at the end of HT, strong similarities were expected. Instead, additional peaks at and barely visible at clearly show the existence of a high temperature phase not perceived with applied cooling rates. A candidate for this phase, only present in sample 4, has the stoichiometry and a lattice within the space group (SS: , , , COD1524836 [36]). The fit was improved, compared to the literature reference, with the choice of a slightly smaller lattice parameter [36].
Diffractograms of the samples’ bulk are displayed in Figure 6. In these measurements, none of the samples exhibit a significant amount of oxide or spinel, proving that these are surface-related effects. Besides that, changes in the ratio of the -to--phase fraction for samples 1 and 2 are different to the previously displayed results (see Figure 5). Additionally, small amounts of -phase were detected in sample 3, which hint that the stability region of -phase could be close to . Another difference is the appearance of Laves-phase precipitates with a lattice (SS: , , [37]) in samples 3 and 4, and maybe also in sample 2, identifiable by the small side peaks near the --peak. An improved fit for this compound was achieved with manual refining to .
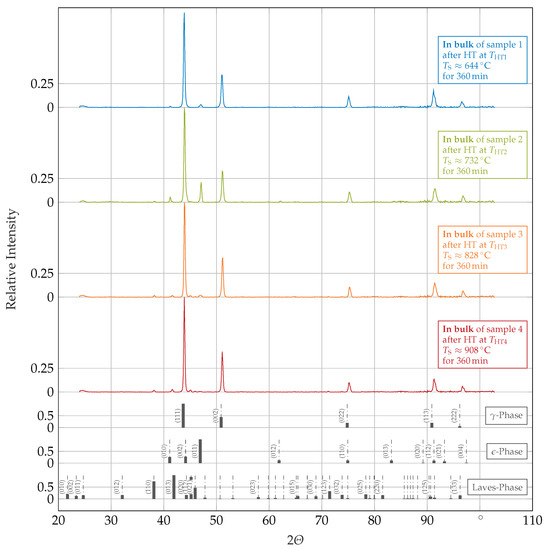
Figure 6.
In color: Ex-situ XRD diffractograms, with intensities normalized to the highest peak in the respective pattern, of samples composed of a Co-Cr-W alloy in states AB by L-PBF and after HTs measured on the samples’ bulk. Additionally in grey: Stick reference pattern calculated with VESTA [32] of a solution of W in Co fcc -phase (COD:1524796 [33]), a solution of W in Co hcp -phase (COD:1524797 [33]), and a Laves-phase [37].
To access the phase morphology of observed phases, SEM and EDS were utilized. The chemical composition of the matrix of all samples was fairly close to the specification of the alloy and almost homogeneous, although some diffuse areas with a diameter of , slightly enriched in and , were present in the element mappings of samples 1 and 2. The Laves-phase seemed to appear in a spotty fashion in the SE and BSE images of samples 2 to 4, as exemplary highlighted in Figure 7. In the SE image, additional light gray patches were present in sample 4 and also in sample 3, although less pronounced. This points to the existence of yet another phase, which was not detected in XRD measurements. Quantitative mappings show an enrichment of and and a depletion of in these patches. The overall appearance of this additional phase is comparable to the -phase identified by Yamanaka et al. in a similar alloy [8].

Figure 7.
SEM images, measured with secondary electron (SE) and backscattered electron (BSE) detectors, as well as quantitative maps acquired with EDS of the bulk in sample 4 after HT with (). Spotty dots: Laves-phase; Light gray patches: -phase.
3.2. Phase Transformation Kinetics
The -to- phase transformation in samples 1 and 2 is investigated in detail. The estimated peak intensities of the (002)-- and additionally the (011)--peak for sample 2 presented in Figure 8 are the basis for this analysis. These peaks were not overlapping with other relevant sample peaks in the observed range. To describe the intensity trend, linear models were preferred for their simplicity here over more complex ones based on higher order polynomials or the Johnson–Mehl–Avrami–Kolmogorov equation [38]. Nevertheless, no major violation of fit premises could be determined in residual analysis of the fitted model. Some data points, displayed with smaller markers, were excluded from the analyses due to problems during the measurement or for issues with error estimations near the hard border 0 of the previous peak-fitting algorithm.
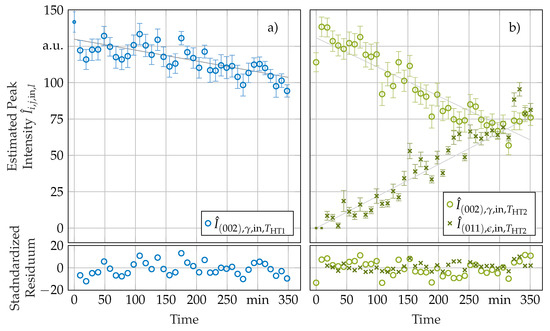
Figure 8.
Estimated peak intensities as acquired by fitting Voigt-functions to the in-situ datasets recorded during HT with XRD of (a) sample 1 at () and (b) sample 2 at (). Additionally given: Graph of the linear model fitted to the estimated peak intensities with smaller marks indicating datapoints excluded from the fit.
These data sets and models were evaluated with the procedure described in Section 2.4. The results of this analysis are shown in Figure 9 and Figure 10. Despite the difference in the treatment temperature between samples 1 and 2 after HT, both samples exhibited approximately 80% of -phase and 20% of -phase in the matrix. The oxide layer growth in sample 2 seems to follow a linear growth law with some scatter. The model-based calculation of yielded a thickness of after the treatment. This result is in good agreement with the measurement of an oxide layer thickness of determined by SEM on sample 2. An equivalent determination of the oxide layer thickness on sample 1 was not possible due to the absence of measurable amounts of oxide.
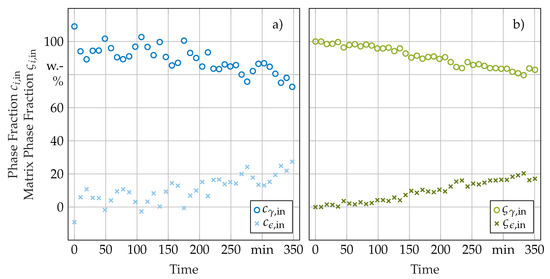
Figure 9.
Calculated weight fractions and weight fractions relative to the matrix phases over the time spent in the HT based on the in-situ XRD measurements for (a) sample 1 and (b) sample 2.
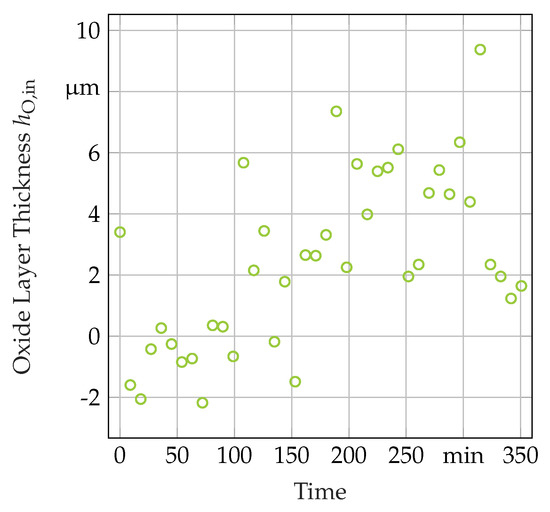
Figure 10.
Calculated oxide layer thickness over the time spent in the HT for sample 2 based on in-situ XRD measurements.
3.3. Secondary In-Situ Fit Variables
Beyond the peak intensities, the Voigt distribution, which was used as peak shape function, offered three further degrees of freedom for peak-fitting (, , and ).
One of these is peak position, which is plotted over time for the --peak in Figure 11 of all samples. The peak position shifts to higher angles after the start of the treatment, which is true for all specimens. This is equal to a shrinkage of lattice-spacing most likely indicating a compression of the -lattice perpendicular to the surface. Samples 3 and 4 show a counter trend leading to a maximum and afterwards a decline of or, in other words, an increase in lattice-spacing within the duration of the treatments. The velocity of the peak shift increases with increasing HT temperature.
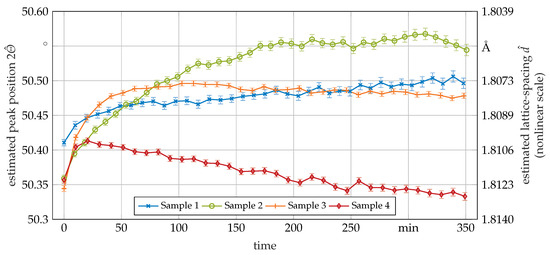
Figure 11.
XRD based estimation of peak positions of the --peak over the time spent in the HT measured in situ. The estimated lattice spacing was calculated using the Bragg equation. Error bars are related to the -scale.
The --peak is discussed here, since it is the only non-overlapping peak present in all data sets over the total time period of the HT. However, similar trends were also observed with a slightly smaller drop at the end of the HT for the - peak in samples 3 and 4.
Another degree of freedom is , which drops from about within 30 to 60 min after the start of the HT to a constant value of about for all samples. The third degree of freedom, namely , immediately becomes about with a slight rising tendency over the entire duration of the HT (results shown in Appendix A).
4. Discussion
At first, the identification and the kinetics of all phases, besides the matrix phases, are discussed.
The determined oxides and spinels are in line with findings from similar alloys [39]. Due to small amounts of present in the alloy and the existence of similar crystals containing , it is assumed that in the spinel is partly substituted by . Based on the evolution of oxide peaks as a measure for oxide layer thickness, a positive correlation between oxide layer growth kinetics and HT temperatures was evident, which was not evaluated in detail as the applied low-pressure environmental conditions are not representative for real applications.
Regarding the Laves-phase precipitates, findings are in line with Yamanaka et al. [8], but not with the results of von Kobylinski et al. [18]. Hence, the electron diffraction and XRD patterns presented by the latter were reevaluated, and a fit could be achieved for Laves-phase also in these results. Kinetics of Laves-phase precipitation could not be established in-situ as the relevant peaks seemed to be suppressed in measurements besides the bulk ones by the attenuation caused by the oxide layer especially dominant at low and medium glancing angles. The -phase determination is solely based on morphology and on chemical composition, therefore identification was not yet fully proven. The most reasonable explanation for the absence of this phase in XRD measurements is its low volume fractions coupled with X-ray micro-absorption on the particles.
The presence of both these precipitate phases could affect the corrosion performance and hence the biocompatibility of dental frameworks adversely, as the chemical potential between these phases and the matrix could create multiple localized corrosion cells. This would serve as an explanation for the enhanced ion release of post HT L-PBF samples as observed by Alifui-Segbaya et al. [40]. Regarding the mechanical properties, in particular, -phase is known to have a negative impact on the performance by causing embrittlement [8]. Therefore, it is mandatory to avoid a significant formation of such precipitates. As no precipitates were observed in the AB condition and increasing amounts were found at higher treatment temperatures, short or low-temperature HTs seem to be preferable in this regard.
For the detected high-temperature phase, -phase seems to be more likely according to thermodynamic assessments evaluated for an estimated equivalent composition than the assigned -phase [41,42]. Nevertheless, the fit to data, mainly based on the dominant peak, was better for the -reference, but identification is still believed to be faulty.
When focusing on the detected matrix phases, the finding of an almost pure -phase in the AB condition after L-PBF processing is in good agreement with previous results [14,18]. During the HTs, -phase can be transformed to an -phase. The investigations of the in-situ measurements taken during HTs on the surfaces of samples 1 and 2 showed no relevant differences in their transformation kinetics, which could be related to the respective HT temperatures being below and above a maximum in the transformation rate. In comparison to Co-Cr-Mo alloys, the kinetics would then be shifted to later times and lower temperatures [43]. This should be taken with caution as it is shown that some of the fundamental assumptions for kinetics calculations are violated. The affected assumptions are the existence of pure -phase in the AB condition, the absence of oxide on sample 1 and the absence of precipitates in sample 2. Nevertheless, the calculations were just off from the measured oxide layer thickness, indicating their applicability.
Between surface and bulk measurements, strong deviations in the -peak intensities and thus in the -to- phase fractions were observed in samples 1 and 2. This, on the one hand, could be attributed to temperature gradients within the samples between the likely cooler surface and the hotter bulk during HTs. Especially in these cooler areas, the recovery rate is lower and hence the dislocation density higher. With the -to- transformation model presented by Bauer et al., this could subsequently be seen as a reason for increasing transformation rates and thus higher -phase fractions close to the surface [44].
One the other hand, high temperature gradients are implausible within the small samples. However, Co-Cr-W alloys are also known for strain-induced phase transformation [18]. The mechanical driving forces for this phase transformation acting slightly below the sample surface could be stresses and strains imposed by the growing oxide onto the matrix.
This is based on the higher molar volume of the oxide in comparison to the matrix, indicated by the Pilling–Bedworth ratio [6], which was calculated to be approximately for the case paired with our alloy. Hence, the oxide in the surface plane would expand if it were not geometrically constrained by the matrix. As a result, proportional to the amount of oxide formed, the matrix is loaded in tension, hence stretched in the surface plane and compressed perpendicularly. This compression could also explain the decrease in lattice-spacing as displayed in Figure 11.
A second explanation for the decreasing lattice-spacing could be a drop in temperature induced by the set-up. However, in short-term temperature dynamic studies, the steady state value of was reached just after and remained constant for at least with only a slight increase, thus ruling out this explanation. An increase in temperature in the long run could, however, be responsible for the observed increases in lattice-spacing observed in samples 3 and 4 following the minimum. The long-term temperature rise could be related to changes in the heat flux caused by comparatively thick oxide layers acting as insulation. Therefore, average HT temperatures could be higher than the measured values, especially in samples 3 and 4.
A final explanation for the decrease of the lattice-spacing could be the shrinkage of the lattice due to the diffusion of , the element with the largest atomic radius present in relevant amounts in the alloy, between the -phase solid solution and the precipitates. Though this is likely to happen, the relative difference between the radii of the atoms of the matrix phases and is in the range of and with just about 3 at.-% of in the alloy composition, and this effect is too small to cause the observed peak shifts [45]. This argumentation is supported by the observations made in sample 1, for which no precipitation and no other major chemical segregation but a decrease of the lattice-spacing was observed.
Hence, the measured in-situ phase transformation kinetics is most likely influenced by surface-related effects. Therefore, no bulk kinetics for the -to--phase transformation could be established. Nevertheless, these findings could be relevant for dental frameworks as the metal surface is usually partially covered by a veneering ceramic in a burning process, and one of the relevant causes for failure of dentures is veneering chipping off at the material interface between the metallic framework and the ceramic [46,47].
With HT at temperatures above a threshold, the -matrix can also be retained instead of being transformed, which can be beneficial as the fcc lattice of the -phase is known for its good workability. This property is especially desirable in RPDs with filigree clamps where small plastic deformations are usually less critical than fracture. Therefore, HTs above the threshold are preferable.
In the analysis of the secondary in-situ fit variables, a reduction of strain broadening was also observed within the first 30 to in the HT, indicating a reduction of inter- and intragranular stresses in the -matrix. This supports the assumption by von Kobylinski et al., that for small macroscopic stress levels the Young’s modulus seems to be smaller in the AB condition compared to the HT condition, due to an early onset of plastic deformation assisted by local high residual stresses [18]. As and could be partially confused by the fitting algorithm and as changes in strain broadening are a volatile indicator for alterations in residual stresses in general, more evidence is needed to finally establish the explanation given by von Kobylinski et al. as the predominant effect. In this study, no further indicators for changes in Young’s modulus within HTs were found. Analysis of the secondary in-situ fit variables also hinted at a slight increase of over the HT duration. Steady grain growth could be an explanation for this observation.
Bringing together all findings, an isothermal HT for around 30 to at temperatures just above the -to- threshold is proposed to optimize the performance for L-PBF manufactured frameworks regarding dental requirements. This treatment seems to reduce residual stresses whilst retaining the favorable fcc -matrix without precipitating significant amounts of Laves-phase or -phase.
5. Conclusions
To study the kinetics of the microstructural change and the phase transformations in Co-Cr-W alloys manufactured with L-PBF, in-situ datasets were collected during HTs at four different temperatures. Based on single peak fitting and QXRD methods, these datasets were evaluated. Assisted by ambient condition XRD as well as SEM and EDS measurements, the following conclusions were drawn:
- The AB condition was mainly composed of an fcc -phase;
- HTs at temperatures below a certain threshold (probably close to ) induced a -to- matrix transformation, which was slightly below the surface likely assisted by the formation of an oxide imposing stresses and strains onto the matrix and thus, evoking a partially strain-induced transformation there;
- Increasing amounts of Laves-phase and of another phase, likely -phase, precipitated with increasing HT temperatures;
- Inter- and intragranular stresses seemed to be reduced within 30 to during HTs;
- The existence of a high-temperature phase, not present at room temperature and not distinctively assignable, was observed at the highest applied HT temperature ().
Based on this list, an HT of 30 to at temperatures just above the -to- threshold was proposed, specialized to optimize the performance of dental frameworks. This HT seemed sufficient for reducing residual stresses, whilst at the same time containing a mostly uniform -matrix without excessive precipitation.
Regarding precipitates, further investigations, based on small angle neutron scattering experiments, could verify the phase identification, with a special focus on the -phase, and establish the precipitation kinetics to fine-tune the HT or the alloys composition. In addition, studying the observed high-temperature phase, not retained in ambient conditions, with dedicated diffraction experiments is proposed to improve the phase assignment, in order to enhance the overall understanding of these alloys, and to exclude possible detrimental effects on the performance of dental frameworks. Finally, designing and executing a dedicated study of residual stress evolution during HTs is recommended, to verify the findings of this study and to further elaborate on the link between residual stresses and an apparent increase in Young’s modulus.
Author Contributions
Conceptualization, J.v.K. and L.H.; methodology, P.H.; software, P.H.; validation, J.v.K., L.H., C.K., and E.W.; formal analysis, P.H.; investigation, P.H. and J.v.K.; resources, C.K. and E.W.; data curation, P.H.; writing—original draft preparation, P.H.; writing—review and editing, P.H., L.H., C.K., and E.W.; visualization, P.H.; supervision, J.v.K., C.K. and E.W.; project administration, P.H.; funding acquisition, J.v.K., C.K., and E.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by DFG Grant No. 280883331.
Data Availability Statement
The data that support the findings of the study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors thank Carola Reiff and Zhonghua Wang for metallography and microscopy.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Abbreviated | Unabbreviated | ||
| fcc | Face-centered cubic | ||
| hcp | Hexagonal close-packed | ||
| AB | As built | ||
| AlN | Aluminiumnitride | ||
| BSE | Backscattered electron | ||
| CNC | Computerized numerical control | ||
| DHS | Domed hot stage | ||
| EDS | Energy-dispersive X-ray spectroscopy | ||
| FWHM | Full width at half maximum | ||
| HT | Heat treatment | ||
| L-PBF | Laser powder-bed fusion | ||
| PFM | Porcelain fused to metal | ||
| QXRD | Quantitative X-ray diffraction | ||
| RPD | Removable partial denture | ||
| SE | Secondary electron | ||
| SEM | Scanning electron microscopy | ||
| SiC | Silicon carbide | ||
| TiAl | Titaniumaluminide | ||
| XRD | X-ray diffraction | ||
| Symbol | Meaning | First | Unit |
| Use | |||
| First lattice parameter | Section 2.4 | ||
| Third lattice parameter | Section 2.4 | ||
| c | Weight fraction | Section 2.4 | w.-% |
| Model based weight fraction | Section 2.4 | w.-% | |
| Azimuthal angle of the diffraction cone | Section 2.3 | ||
| Measured lattice-spacing | Section 3.3 | ||
| E | Young’s modulus | Section 1 | |
| Measured FWHM of Gaussian component | Section 2.4 | ||
| Measured FWHM of Lorentzian component | Section 2.4 | ||
| Oxide layer thickness | Section 2.4 | ||
| Model based oxide layer thickness | Section 2.4 | ||
| i | Counting variable referring to observed phases | Section 2.4 | - |
| I | Peak intensity | Section 2.4 | |
| Measured peak intensity | Section 2.4 | ||
| Model based peak intensity | Section 2.4 | ||
| j | Counting variable referring to certain peaks | Section 2.4 | - |
| k | Point in time throughout the treatment | Section 2.4 | - |
| Calibration constant | Section 2.4 | ||
| l | Counting variable referring to a temperature | Section 2.4 | - |
| Average mass absorption coefficient of matrix phases | Section 2.4 | ||
| Mass absorption coefficient of | Section 2.4 | ||
| n | Number of all phases | Section 2.4 | - |
| p | Counting variable referring a setup | Section 2.4 | - |
| Average density of matrix phases | Section 2.4 | ||
| Density of the oxide | Section 2.4 | ||
| Weight fraction relative to matrix phases | Section 2.4 | w.-% | |
| Model based weight fraction relative to matrix phases | Section 2.4 | w.-% | |
| t | Time throughout the treatment | Section 2.4 | |
| Controller temperature of DHS | Section 2.2 | ||
| Sample surface temperature | Section 2.2 | ||
| Glancing angle or Bragg angle | Section 2.3 | ||
| Measured glancing angle | Section 2.3 |
Appendix A. Additional In-Situ XRD-Data
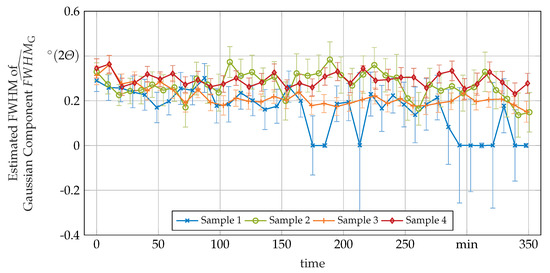
Figure A1.
Estimated FWHM of the Gaussian component of the used Voigt peak shape function fitted to the --peak over the time spent in the HT measured with in-situ XRD.
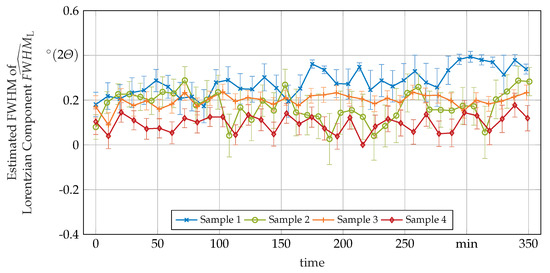
Figure A2.
Estimated FWHM of the Lorentzian component of the used Voigt peak shape function fitted to the --peak over the time spent in the HT measured with in-situ XRD.
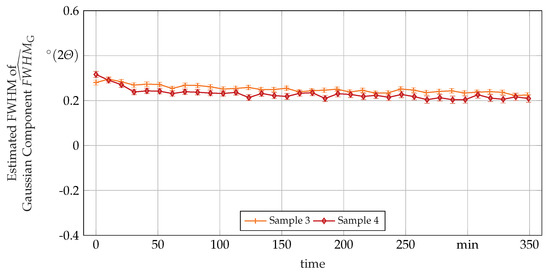
Figure A3.
Estimated FWHM of the Gaussian component of the used Voigt peak shape function fitted to the --peak over the time spent in the HT measured with in-situ XRD. Values for samples 1 and 2 could not be given due to peak overlap with --peak.
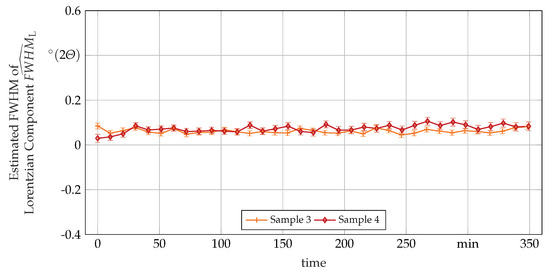
Figure A4.
Estimated FWHM of the Lorentzian component of the used Voigt peak shape function fitted to the --peak over the time spent in the HT measured with in-situ XRD. Values for samples 1 and 2 could not be given due to peak overlap with --peak.
References
- Helsen, J.A.; Missirlis, Y. Biomaterials; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Roberts, H.W.; Berzins, D.W.; Moore, B.K.; Charlton, D.G. Metal-Ceramic Alloys in Dentistry: A Review. J. Prosthodont. 2009, 18, 188–194. [Google Scholar] [CrossRef]
- Kassapidou, M.; Franke Stenport, V.; Hjalmarsson, L.; Johansson, C.B. Cobalt-Chromium Alloys in Fixed Prosthodontics in Sweden. Acta Biomater. Odontol. Scand. 2017, 3, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Al Jabbari, Y.S. Physico-mechanical Properties and Prosthodontic Applications of Co-Cr Dental Alloys: A Review of the Literature. J. Adv. Prosthodont. 2014, 6, 138–145. [Google Scholar] [CrossRef]
- Wataha, J.C. Biocompatibility of Dental Casting Alloys: A Review. J. Prosthet. Dent. 2000, 83, 223–234. [Google Scholar] [CrossRef]
- Bürgel, R.; Jürgen Maier, H.; Niendorf, T. Handbuch Hochtemperatur-Werkstofftechnik: Grundlagen, Werkstoffbeanspruchungen, Hochtemperaturlegierungen und-Beschichtungen, 4th ed.; Vieweg+Teubner Verlag: Wiesbaden, Germany, 2011. [Google Scholar]
- Karaali, A.; Mirouh, K.; Hamamda, S.; Guiraldenq, P. Microstructural Study of Tungsten Influence on Co–Cr Alloys. Mater. Sci. Eng. A-Struct. 2005, 390, 255–259. [Google Scholar] [CrossRef]
- Yamanaka, K.; Mori, M.; Kuramoto, K.; Chiba, A. Development of New Co–Cr–W-based Biomedical Alloys: Effects of Microalloying and Thermomechanical Processing on Microstructures and Mechanical Properties. Mater. Des. 2014, 55, 987–998. [Google Scholar] [CrossRef]
- Asgar, K. Casting Metals in Dentistry: Past-Present-Future. Adv. Dent. Res. 1988, 2, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Hitzler, L.; Alifui-Segbaya, F.; Williams, P.; Heine, B.; Heitzmann, M.; Hall, W.; Merkel, M.; Öchsner, A. Additive Manufacturing of Cobalt-based Dental Alloys: Analysis of Microstructure and Physicomechanical Properties. Adv. Mater. Sci. Eng. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Koutsoukis, T.; Zinelis, S.; Eliades, G.; Al-Wazzan, K.; Rifaiy, M.A.; Al Jabbari, Y.S. Selective Laser Melting Technique of Co-Cr Dental Alloys: A Review of Structure and Properties and Comparative Analysis with Other Available Techniques. J. Prosthodont. 2015, 24, 303–312. [Google Scholar] [CrossRef]
- Hitzler, L.; Merkel, M.; Hall, W.; Öchsner, A. A Review of Metal Fabricated with Laser- and Powder-Bed Based Additive Manufacturing Techniques: Process, Nomenclature, Materials, Achievable Properties, and its Utilization in the Medical Sector. Adv. Eng. Mater. 2018, 20, 1700658. [Google Scholar] [CrossRef]
- Hitzler, L. The Anisotropic and Inhomogeneous Nature of Additively Manufactured Metals, and the Application of Selective Laser Melting in Dentistry. Ph.D. Thesis, Griffith University, Gold Coast, Australia, 2018. [Google Scholar] [CrossRef]
- Takaichi, A.; Nakamoto, T.; Joko, N.; Nomura, N.; Tsutsumi, Y.; Migita, S.; Doi, H.; Kurosu, S.; Chiba, A.; Wakabayashi, N.; et al. Microstructures and Mechanical Properties of Co–29Cr–6Mo Alloy Fabricated by Selective Laser Melting Process for Dental Applications. J. Mech. Behav. Biomed. Mater. 2013, 21, 67–76. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure. VDI 3405: Additive Fertigungsverfahren - Grundlagen, Begriffe, Verfahrensbeschreibungen; Beuth Verlag: Berlin, Germany, 2014. [Google Scholar]
- Alifui-Segbaya, F.; Evans, J.; Eggbeer, D.; George, R. Clinical Relevance of Laser-Sintered Co-Cr Alloys for Prosthodontic Treatments: A Review. In Proceedings of the 1st International Conference on Progress in Additive Manufacturing, Singapore, 26–28 May 2014; Research Publishing Services: Singapore, 2014; pp. 115–120. [Google Scholar] [CrossRef]
- Kim, H.R.; Jang, S.H.; Kim, Y.K.; Son, J.S.; Min, B.K.; Kim, K.H.; Kwon, T.Y. Microstructures and Mechanical Properties of Co-Cr Dental Alloys Fabricated by Three CAD/CAM-Based Processing Techniques. Materials 2016, 9, 596. [Google Scholar] [CrossRef]
- von Kobylinski, J.; Hitzler, L.; Lawitzki, R.; Krempaszky, C.; Öchsner, A.; Werner, E. Relationship between Phase Fractions and Mechanical Properties in Heat–Treated Laser Powder–Bed Fused Co–based Dental Alloys. ISR J. Chem. 2020. [Google Scholar] [CrossRef]
- Kajima, Y.; Takaichi, A.; Kittikundecha, N.; Nakamoto, T.; Kimura, T.; Nomura, N.; Kawasaki, A.; Hanawa, T.; Takahashi, H.; Wakabayashi, N. Effect of Heat-treatment Temperature on Microstructures and Mechanical Properties of Co–Cr–Mo Alloys Fabricated by Selective Laser Melting. Mater. Sci. Eng. A-Struct. 2018, 726, 21–31. [Google Scholar] [CrossRef]
- Hitzler, L.; von Kobylinski, J.; Lawitzki, R.; Krempaszky, C.; Werner, E. Microstructural Development and Mechanical Properties of Selective Laser Melted Co–Cr–W Dental Alloy. In TMS 2020 149th Annual Meeting & Exhibition Supplemental Proceedings; The Minerals, Metals & Materials Series; Springer International Publishing: Cham, Switzerland, 2020; pp. 195–202. [Google Scholar] [CrossRef]
- Dentaurum: Remanium Star CL Powered by Dentaurum. Available online: https://www.dentaurum.de/files/1105_remaniumstarCL_Materialdatenblatt-10.pdf (accessed on 13 January 2021).
- Instruction Manual DHS 1100: Domed Hot Stage: Version PANalytical. Available online: https://pf18b.neocities.org/docu/Anton%20Paar%20DHS%201100.pdf (accessed on 15 January 2021).
- Resel, R.; Tamas, E.; Sonderegger, B.; Hofbauer, P.; Keckes, J. A Heating Stage up to 1173 K for X-Ray Diffraction Studies in the Whole Orientation Space. J. Appl. Crystallogr. 2003, 36, 80–85. [Google Scholar] [CrossRef]
- Samarati, J.; Iengo, P.; Longo, L.; Sekhniaidze, G.; Sidiropoulou, O.; Wotschack, J. Characterisation of the Charging Up Effect in Resistive Micromegas Detectors. J. Phys. Conf. Ser. 2020, 1498, 012030. [Google Scholar] [CrossRef]
- Mittemeijer, E.J.; Welzel, U. The “State of the Art” of the Diffraction Analysis of Crystallite Size and Lattice Strain. Z. Kristallogr. 2008, 223, 134. [Google Scholar] [CrossRef]
- Schreier, F. Optimized Implementations of Rational Approximations for the Voigt and Complex Error Function. J. Quant. Spectrosc. Radiat. 2011, 112, 1010–1025. [Google Scholar] [CrossRef]
- James, F. Minuit: Function Minimization and Error Analysis Reference Manual. Available online: https://cds.cern.ch/record/2296388/files/minuit.pdf (accessed on 13 January 2021).
- Alexander, L.; Klug, H.P. Basic Aspects of X-Ray Absorption in Quantitative Diffraction Analysis of Powder Mixtures. Anal. Chem. 1948, 20, 886–889. [Google Scholar] [CrossRef]
- Zevin, L.S.; Kimmel, G.; Mureinik, I. Quantitative X-ray Diffractometry; Springer US: New York, NY, USA, 1995. [Google Scholar]
- He, B.B. Two-Dimensional X-ray Diffraction; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Persson, K. Materials Data on Cr2O3 by Materials Project. Available online: https://materialsproject.org/materials/mp-19399/ (accessed on 13 January 2021).
- Momma, K.; Izumi, F. VESTA 3 for Three-dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Larikov, L.N.; Shmatko, O.A. Solubility of Tungsten in Cobalt in Solid Phase. Dopov. Akad. Nauk A 1967, 29, 540–541. [Google Scholar]
- Yang, J. Structural Analysis of Perovskite LaCr1-xNixO3 by Rietveld Refinement of X-Ray Powder Diffraction Data. Acta Crystallogr. B 2008, 64, 281–286. [Google Scholar] [CrossRef]
- Priebe, R.; Sabrowsky, H. Über einen Chrom-Mangan-Spinell mit Kationenmangelstruktur, CrMn1,5O4: About a Chromium Manganese Spinel with Cation Deficient Structure, CrMn1,5O4. Z. Naturforschung B 1979, 34, 1663–1665. [Google Scholar] [CrossRef]
- Magneli, A.; Westgren, A. Röntgenuntersuchung von Kobalt-Wolframlegierungen. Zeitschrift für Anorganische und Allgemeine Chemie 1938, 238, 268–272. [Google Scholar] [CrossRef]
- Villars, P.; Cenzual, K. W2Co3Si (WCo1.5Si0.5) Crystal Structure: Datasheet from “PAULING FILE Multinaries Edition-2012” in SpringerMaterials. Available online: https://materials.springer.com/isp/crystallographic/docs/sd_0539453 (accessed on 9 September 2020).
- Fanfoni, M.; Tomellini, M. The Johnson-Mehl- Avrami-Kohnogorov Model: A Brief Review. Il Nuovo Cimento D 1998, 20, 1171–1182. [Google Scholar] [CrossRef]
- Hanawa, T.; Hiromoto, S.; Asami, K. Characterization of the Surface Oxide Film of a Co–Cr–Mo Alloy after Being Located in Quasi-biological Environments Using XPS. Appl. Surf. Sci. 2001, 183, 68–75. [Google Scholar] [CrossRef]
- Alifui-Segbaya, F.; Lewis, J.; Eggbeer, D.; Williams, R.J. In Vitro Corrosion Analyses of Heat Treated Cobalt-Chromium Alloys Manufactured by Direct Metal Laser Sintering. Rapid Prototyp. J. 2015, 21, 111–116. [Google Scholar] [CrossRef]
- Peng, Y.; Du, Y.; Materials Science International Team (MSIT). Co-Cr-W Ternary Phase Diagram Evaluation: Phase Diagrams, Crystallographic and Thermodynamic Data: MSI Eureka in SpringerMaterials. Available online: https://materials.springer.com/msi/docs/sm_msi_r_10_017469_01 (accessed on 3 November 2019).
- Yang, S.Y.; Jiang, M.; Li, H.X.; Wang, L. Thermodynamic Assessment of Co-Cr-W Ternary System. Trans. Nonferr. Met. Soc. 2011, 21, 2270–2275. [Google Scholar] [CrossRef]
- Turrubiates-Estrada, R.; Salinas-Rodriguez, A.; Lopez, H.F. FCC to HCP Transformation Kinetics in a Co–27Cr–5Mo–0.23C Alloy. J. Mater. Sci. 2011, 46, 254–262. [Google Scholar] [CrossRef]
- Bauer, R.; Jägle, E.A.; Baumann, W.; Mittemeijer, E.J. Kinetics of the Allotropic hcp–fcc Phase Transformation in Cobalt. Philos. Mag. 2011, 91, 437–457. [Google Scholar] [CrossRef]
- Trömel, M.; Hübner, S. Metallradien und Ionenradien. Z. Krist. Cryst. Mater. 2000, 215. [Google Scholar] [CrossRef]
- Pjetursson, B.E.; Sailer, I.; Zwahlen, M.; Hämmerle, C.H.F. A Systematic Review of the Survival and Complication Rates of All-Ceramic and Metal-Ceramic Reconstructions after an Observation Period of at Least 3 Years. Part I: Single Crowns. Clin. Oral Implants Res. 2007, 18 (Suppl. 3), 73–85. [Google Scholar] [CrossRef] [PubMed]
- Sailer, I.; Pjetursson, B.E.; Zwahlen, M.; Hämmerle, C.H.F. A Systematic Review of the Survival and Complication Rates of All-ceramic and Metal-ceramic Reconstructions after an Observation Period of at Least 3 Years. Part II: Fixed Dental Prostheses. Clin. Oral Implants Res. 2007, 18 (Suppl. 3), 86–96. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).