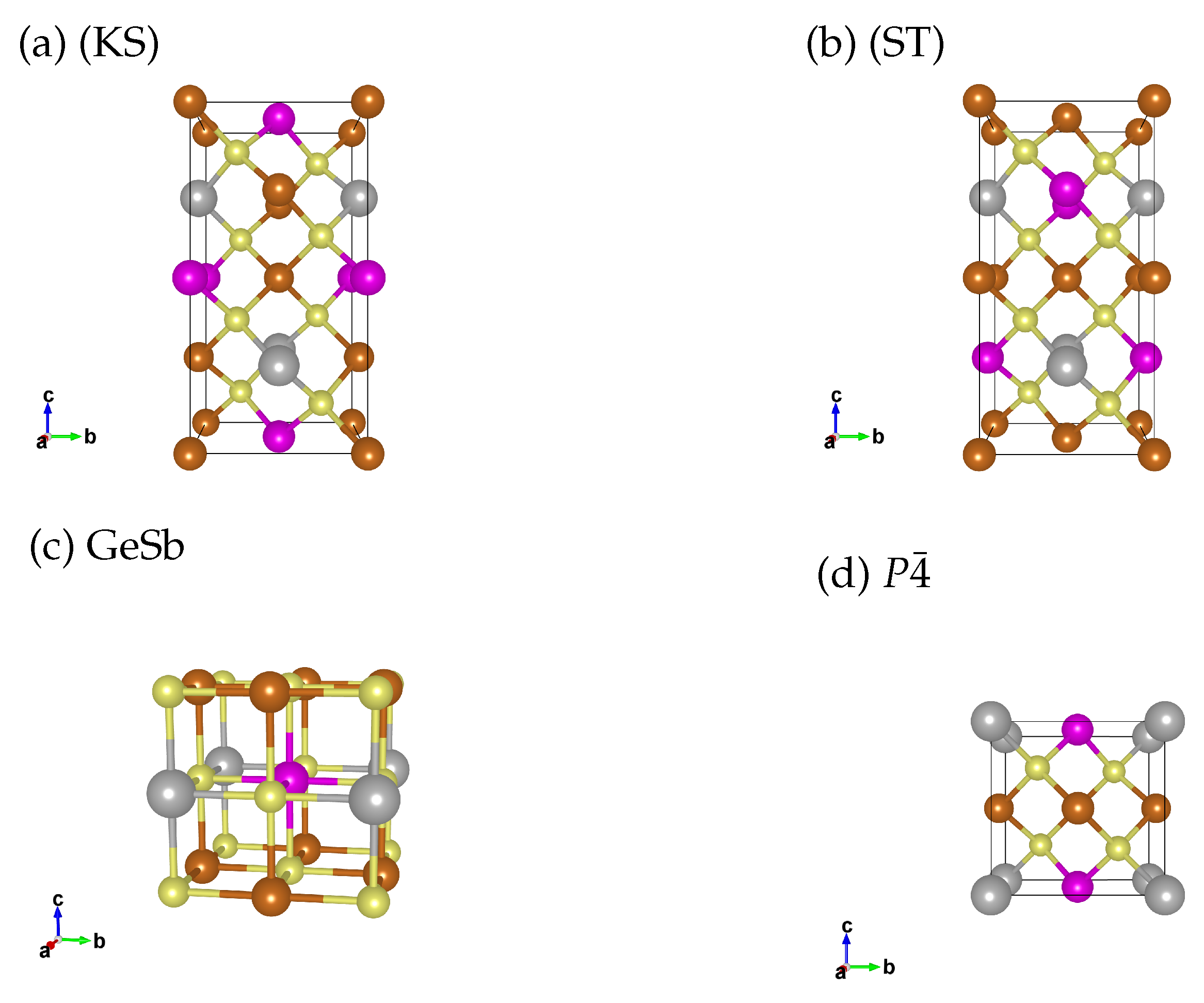
3.1. Equilibrium Structures
Before discussing the enthalpies we will review the equilibrium structures at zero pressure of Cu
2FeSnS
4 and Cu
2MnSnS
4, obtained at the PBE level (
Table 1) and compare to published crystal structures. XRD (X-ray diffraction) analysis by
Brockway dating back to 1934 revealed that natural Cu
2FeSnS
4 samples crystallise in ST structure [
28]. Those results where subsequently confirmed in the 1970s by Ganiel et al., they furthermore studied the magnetic ordering via
Mössbauer spectroscopy and found that it was anti-ferromagnetic [
29]. In 1972
Springer studied the solution series Cu
Fe
Zn
SnS
. Beyond
x = 0.4 and above 680
C he observed an ST crystal structure he labeled
-Cu
(Fe/Zn)SnS
. Below
x = 0.4 and 680
C he found another tetragonal phase he labeled
-Cu
(Fe/Zn)SnS
[
25,
30]. In 2000 pure
-Cu
FeSnS
was synthesised [
26]. After the solid state reaction of CuFeS
2 on SnS at 1323 K in sealed graphite crucible for 24 h the product was cooled slowly over 50 h. Through the slow cooling they obtained the thermodynamically most stable
-phase. Through XRD measurements the space group of the sample was determined to be
[
26]. Those results where confirmed by Rincon et al. who furthermore studied the magnetic susceptibility and revealed that also
-Cu
FeSnS
exhibits an anti-ferromagnetic ordering [
27].
Our PBE results for Cu
2FeSnS
4 agree very well with the experiments. We found the anti-ferromagnetic
(corresponding to
-Cu
FeSnS
) structure to be most stable (
Table 1). But it is only 22 meV more stable than the naturally occurring anti-ferromagnetic ST structure. The anti-ferromagnetic KS structure is another 100 meV above the anti-ferromagnetic ST structure. The small energy difference between ST and
may give an explanation why the
phase is hard to obtain in pure form. From the experimental results we conclude that the formation of the ST phase has to be kinetically favoured. This aspect dominates the crystallisation process if the samples are rapidly cooled. We expect the thermodynamic equilibrium to build up slowly based on the small energy difference between the
and ST structures, hence slow cooling is crucial to obtain
-Cu
FeSnS
. In agreement with the experimental data we find the anti-ferromagnetic ordering favoured over the ferromagnetic ordering by 82 meV and 152 meV, for ST and
, respectively. The PBE lattice parameter for both Cu
2FeSnS
4 phases agree reasonably well with the XRD experiments. The lattice parameters change only slightly between the magnetic phases and are within the error bars of the functional applied.
Our PBE prediction for the most stable structure for Cu
2MnSnS
4 does not agree with experimental results. Magnetisation and neutron-diffraction measurements have shown that Cu
2MnSnS
4 has an anti-ferromagnetic ST structure [
31]. We predict the anti-ferromagnetic KS structure to be 35 meV more stable (
Table 2). We also tested the
structure and found it to be the least stable anti-ferromagnetic and ferromagnetic structure. The anti-ferromagnetic
structure is 17 meV less stable than the anti-ferromagnetic ST phase at the PBE level. Our results on the relative KS and ST stability agree closely with PBEsol calculations by Scragg et al [
32]. The same group has also carried out HSE06 calculations and found the ST structure to be more stable than the KS structure. The difference is only 15 meV per unit cell. The error in the lattice constants of the PBE calculations is in the range of the differences between the structures and magnetic phases. The PBE lattice constants for Cu
2MnSnS
4 show subtle interplay between magnetism and structure but all of them are close to the experimental lattice parameter of ST (AM).
In contrast to the KS equilibrium structure of Cu
2ZnSnS
4, the compounds Cu
2FeSnS
4 and Cu
2MnSnS
4 experimentally favour a ST and/or
structure. The ST and
structures are group theoretically related, both structures exhibit similar cationic layers. We can rationalise the formation of ST and or
structures over KS by comparing the ionic crystal radii (defined according to
Fumi and
Tosi [
33]) of the substituted bivalent elements (Zn, Fe and Mn) in chalcogenides determinded by
Shannon [
34].
Cu2ZnSnS4 in the KS structure consists of Cu+-Zn2+ layers and Cu+-Sn4+ layers. The crystal radius of Zn2+ (rc = 0.60 Å) is identical to the crystal radius of Cu+ (rc = 0.60 Å), which allows them to fit in the same layer. If we replace Zn2+ with the larger Fe2+ (rc = 0.63 Å) or Mn2+ (rc = 0.66 Å), a ST or structure is formed. In those structures pure Cu+ layers alternate with Sn4+-Fe2+/Mn2+ layers. Like this the largest and the smallest ion (Sn4+, r = 0.55 Å) are paired in one layer. In a KS structure the large bivalent cation would have to be in the same layer as the second largest Cu+ ion. We suspect that this is the main reason which drives the formation of the ST and/or structures for the magnetic derivates.
In contrast to Cu
2FeSnS
4, we do not find the ST structure to be more stable than KS in our calculations for Cu
2MnSnS
4, although Mn
2+ has an even larger ionic crystal radius than Fe
2+. We found that PBE fails do describe the electron density around Mn
2+, the charge is more smeared out than for Fe
2+ which leads to larger positive charge at Mn (for details see
Table A3 in
Appendix A.1).
The PBE lattice parameter
a and
c of the ST and
structure (2
c for the
structure) for Cu
2FeSnS
4 differ by less than 0.1%. The differences in Cu
2MnSnS
4 of
a and
c between ST and KS are larger, particularly in
c where the difference is 2%. We think that the reason must be the different composition of the cationic layers. If we compare the ST structures of both materials, we find that the size of the lattice parameters corresponds to the crystal radius of the bivalent cation. All presented structures for Cu
2FeSnS
4 and Cu
2MnSnS
4 have lattice parameter within 2% of the values for the Cu
2MnSnS
4 KS (5.485 Å and 10.94 Å [
23]).
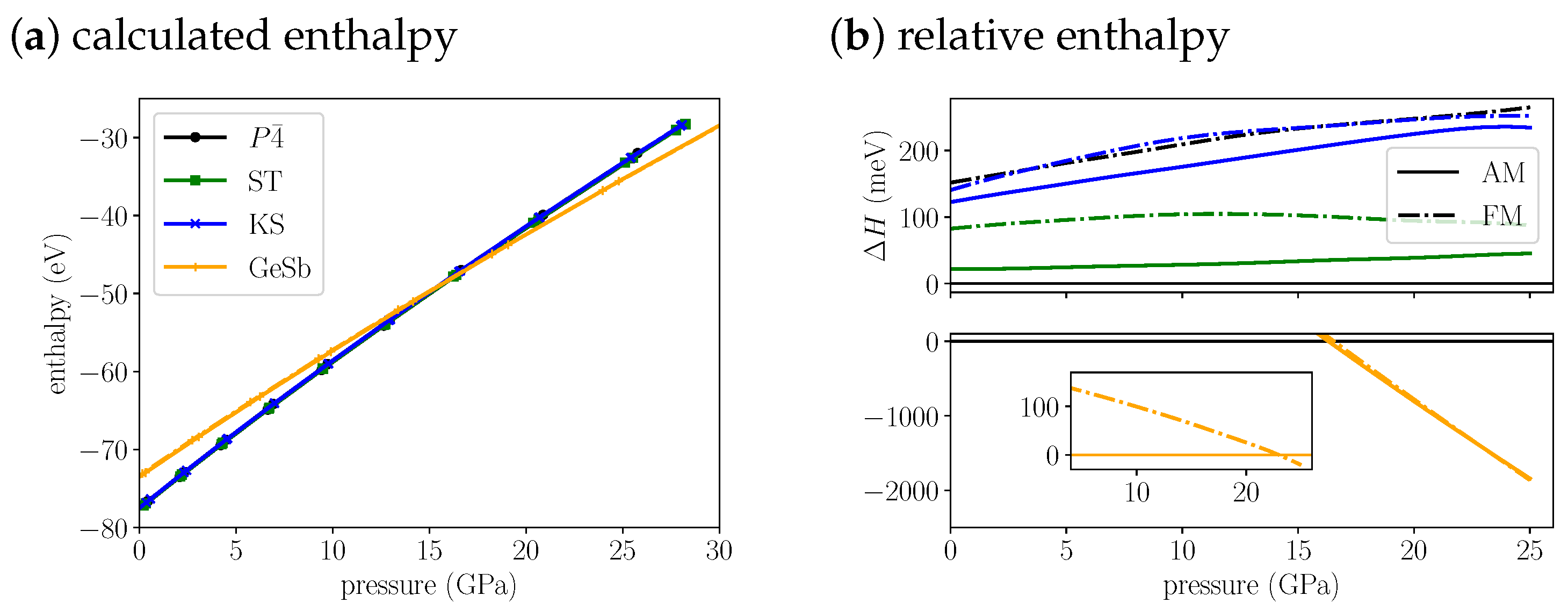
3.2. Pressure-Dependent Enthalpies
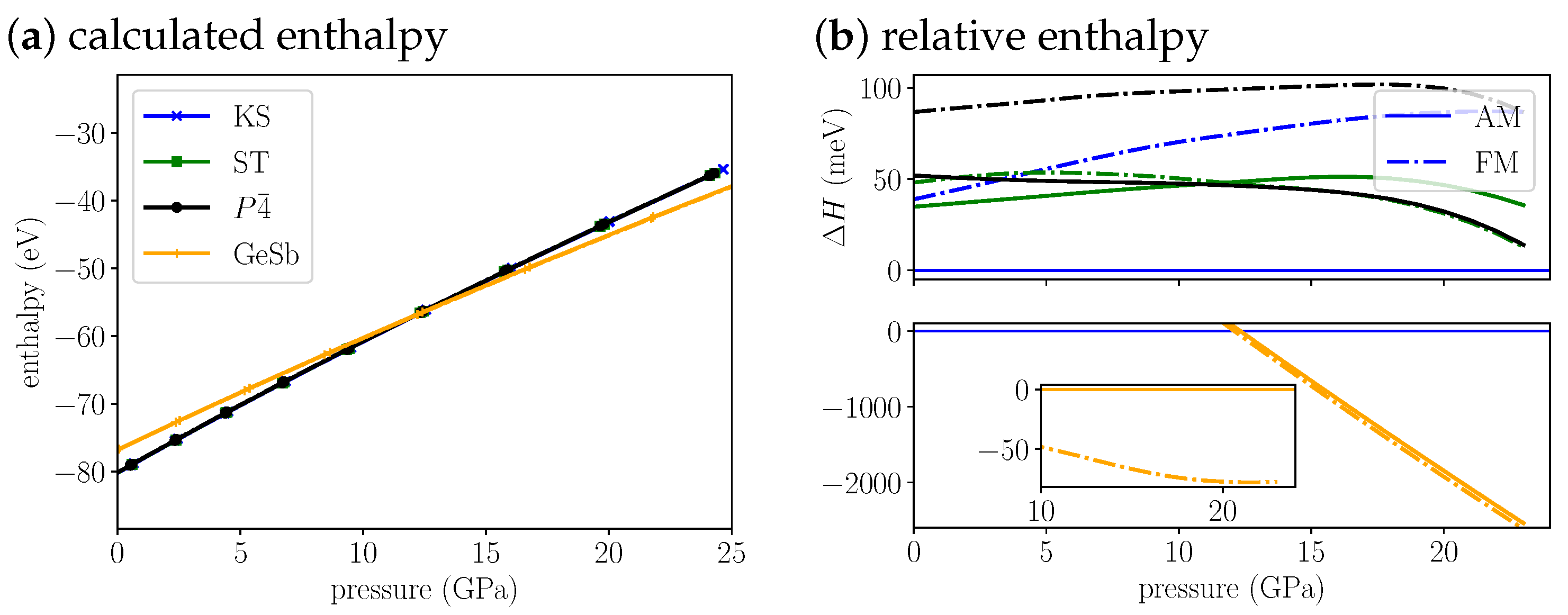
If we plot and compare the enthalpies for Cu
2FeSnS
4 (
Figure 2a,b) we find the anti-ferromagentic
structure to be most stable up to 16.3 GPa. Throughout this pressure range the anti-ferromagentic ST structures is only 22 to 40 meV less stable. The anti-ferromagentic KS structure is even less stable than the ferromagnetic ST structure which is about 100 meV above the
structure. The energy splitting between AM and FM increases from the KS over the ST to the
structure. As a consequence the ferromagnetic
structure is as unstable as the ferromagnetic KS structure in the investigated pressure range. At 16.3 GPa, we find a transition from the
structure to the GeSb structure. Its purely a structural transition, the magnetic phase remains anti-ferromagnetic. The cell volume decreases by 13% (
Table 3) through the transition. At 23.0 GPa we predict a magnetic phase transition of GeSb to ferromagnetic. The energy difference between the two different magnetic phases is very small, at the structural transition pressure it is 15 meV and decreases up to the magnetic transition pressure. Afterwards it increases again, but the difference remains small, at 25 GPa it amounts to 75 meV. The anti-ferromagnetic modification for KS and ST is more stable than the ferromagnetic modification over the whole pressure range. As pointed out for the equilibrium structures, the anti-ferromagnetic
structure and the ST structure can be observed experimentally, depending on the preparation method. Due to the small energy difference between both structures also at the transition pressure, we predict that an ST-to-GeSb transition would also appear at a very similar pressure as the
-to-GeSb transition.
The enthalpy for Cu
2MnSnS
4 (
Figure 3a,b) indicates that anti-ferromagnetic KS is most stable at ambient conditions and up to 12.1 GPa, where we predict a KS-to-GeSb phase transition. The structural phase transition is accompanied by a magnetic phase transition from anti-ferromagnetic to ferromagnetic. The cell volume decreases by 14% (
Table 3) through the transition. At the transition pressure the ferromagnetic GeSb modification is 66 meV more stable than the anti-ferromagnetic modification. With increasing pressure the difference is nearly constant, at 20 GPa it amounts to 73 meV. For the KS structure the anti-ferromagnetic modification remains more stable than the ferromagnetic modification by over 40 meV throughout the whole pressure range. For the ST structure the ferromagnetic modification becomes more stable around 12 GPa. The difference between both magnetic phases is much lower than for KS and remains below 20 meV throughout the whole pressure range. The anti-ferromagnetic
has a very similar stability as the ferromagnetic ST structure. The splitting between AM and FM is the largest, rendering the ferromagnetic
structure the least stable through the whole pressure range. As pointed out above, the relative stability of KS and ST is wrong at the PBE level. Over the whole pressure range the difference in energy between KS and ST stays below 50 meV. In comparison to the energy change induced by the structural phase transition (already 1 eV at 5 GPa above phase transition), this energy difference is small. That is why we think we can still predict a phase transition around 12 GPa. But experimentally we expect a ST(AM)-to-GeSb(FM) transition instead of the KS-to-GeSb phase transition our calculations suggest.
3.3. Electronic Structure
We investigated the electronic band structure for equilibrium and high-pressure structures for both compounds at the equilibrium and at the transition pressure with the HSE06 hybrid functional [
17].
For Cu
2FeSnS
4, we predicted the band gap of the anti-ferromagnetic ST structure to be 1.3 eV (
Table 4). Based on absorption spectra, the band gap was determined to be 1.6 eV [
35]. We think that the difference from our prediction is largely due to the fact that we only optimised our structures at the PBE level but also partly due to the error of the HSE06 functional in reproducing band gaps. In an earlier study within our group we obtained similar results for Cu
2ZnSnS
4 KS. Experimentally the Cu
2ZnSnS
4 KS band gap is determined to be 1.5 eV [
6]. The HSE06 band gap for the PBE optimised structure is 1.2 eV. Only if the structure is also optimised at the HSE06 level, we obtain the experimental band gap [
36]. The HSE06 band gap deviation for Cu
2ZnSnS
4 of the PBE structure is −0.3 eV. We expect it to have similar magnitude for Cu
2FeSnS
4 and Cu
2MnSnS
4.
The HSE06 band gap for the most stable anti-ferromagnetic structure of Cu2FeSnS4 is 1 eV. For and ST Cu2FeSnS4 the anti-ferromagnetic modification has an 0.2 and 0.3 eV larger band gap than the ferromagnetic modification.
For Cu
2MnSnS
4 we predicted an equilibrium band gap for ST of 1.1 eV (
Table 4). Experimental measurements by Raudsich et al. of Cu
2MnSnS
4 indicate a band gap of 1.42 to 1.79 eV. All measured samples contained Cu
2MnSn
3S
8 as a secondary phase. They also calculated the band gap at the HSE06 level which they reported to be 1.5 eV. Again the deviation to our result must be due to the fact that they also carried out the optimisation at the HSE06 level while we restricted ourselves to PBE optimisations.
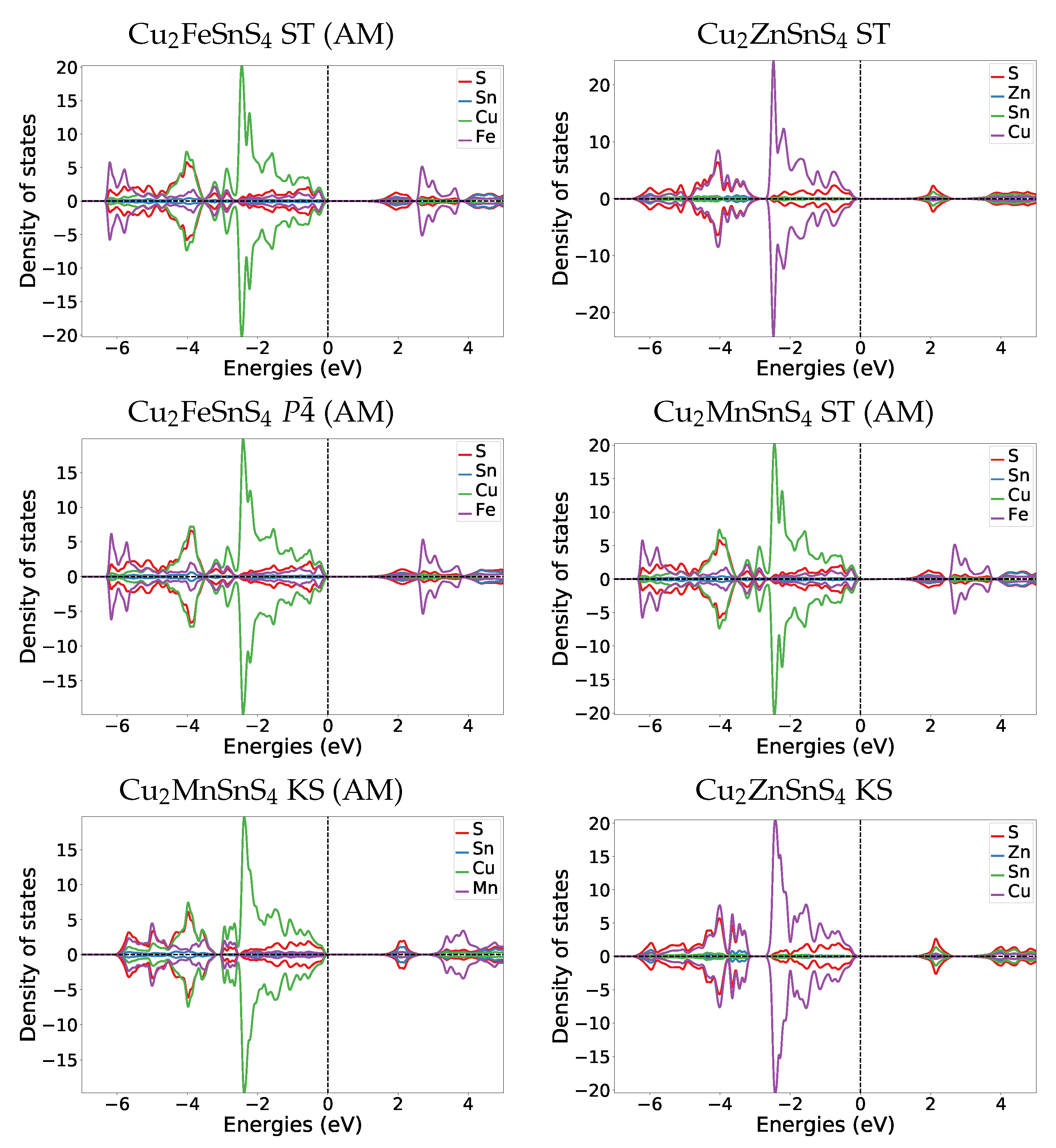
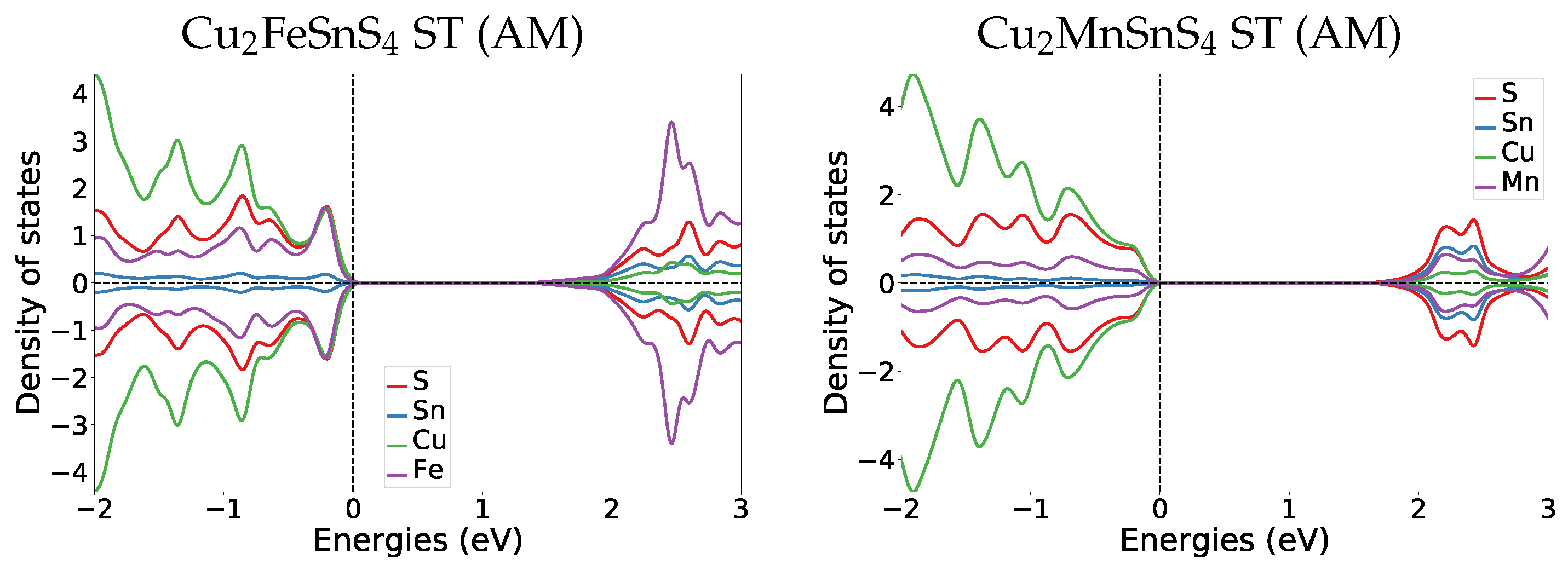
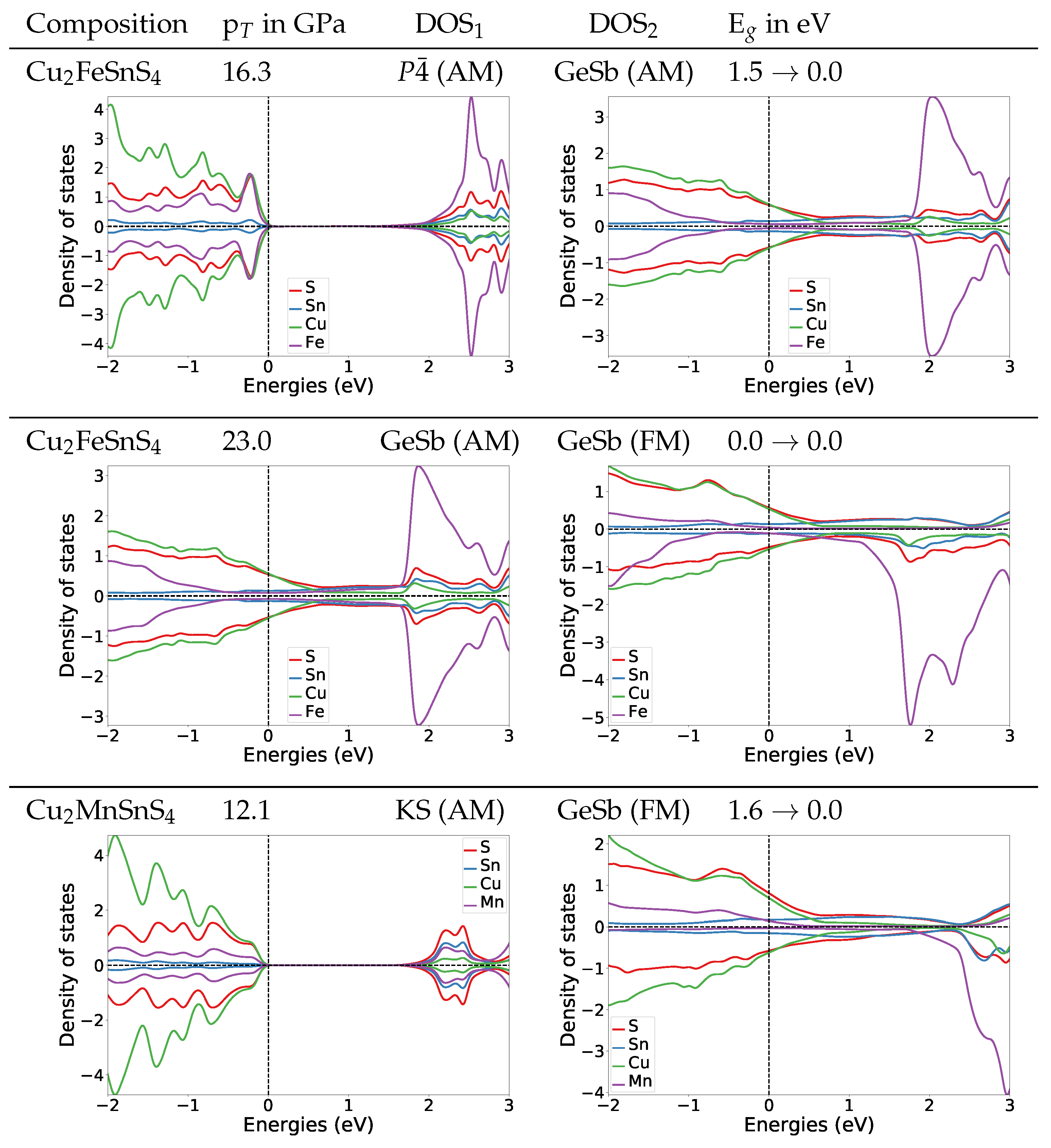
To understand the change of the electronic structures under pressure, we also calculated the DOS at the transition pressures for both systems. For the
structure of Cu
2FeSnS
4 at the transition pressure the band gap is widened to 1.4 eV (
Figure 4). For the naturally occurring ST structure (AM) the band gap is widened to 1.5 eV (for DOS see
Appendix A.4.2). After the transition to the anti-ferromagnetic GeSb structure the band gap closes completely. In the DOS plot for anti-ferromagnetic GeSb at the transition pressure we can see that all bands from the valence band now extend in the region from 0 eV to 1.5 eV which is the band gap region for the
structure. Thus we predict a change from semi-conducting to metallic behaviour. The band gap stays zero with the second magnetic transition from anti-ferromagnetic to ferromagnetic.
For Cu
2MnSnS
4 we find the same behaviour concerning the electronic structure at the transition pressure, a closing of the gap and a metallic character above the transition pressure (
Figure 4). During the structural transition, the magnetic structure changes from AM to FM. We are confident that this also holds for the ST (AM) to GeSb (FM) transition we expect based on the observation that the experimental equilibrium structure for Cu
2MnSnS
4 is the anti-ferromagnetic ST structure. To verify this assumption we also calculated the DOS for ST at the transition pressure, its band gap is 1.2 eV (for DOS see
Appendix A.4.2). This confirms that also for the ST (AM) to GeSb (FM) transition the electronic structure would change from semi-conducting to metallic.
Both materials show similar electronic structure changes at the transition pressure as Cu
2ZnSnS
4, which changes from semi-conducting to metallic at 16 GPa (for details see
Appendix A.4.2).
3.4. Mechanical Properties
Finally we want to analyse how the bulk modulus changes due to the phase transitions in the magnetic materials Cu2FeSnS4 and Cu2MnSnS4 and compare to Cu2ZnSnS4. In the used equation of states the equilibrium volume, the bulk modulus and its pressure dependence are fit parameters.
First of all it strikes that regardless of the composition all tetragonal anti-ferromagnetic structures (KS, ST or
) have very similar bulk moduli ranging within 2 GPa around the value for Cu
2ZnSnS
4 KS (
Table 5). The first derivative
shows larger differences, the values for Cu
2FeSnS
4 and Cu
2MnSnS
4 are 7% and 10% lower than for the KS Cu
2ZnSnS
4 material. Without an error analysis we can not determine whether the differences in
are significant. At zero pressure the
(AM) structure of Cu
2FeSnS
4 has a higher bulk modulus than the ST (AM) structure, but at higher pressures eventually it flips due to the larger first derivative for the ST (AM) structure. If we compare the same structure ST(AM) for all three materials, the bulk modulus of Mn over Zn to Fe are slightly increasing, but only in a range where it would not be measurable experimentally.
All bulk moduli for the anti-ferromagnetic GeSb structures are in the range of 77.8–85.8 GPa, thus each about 15% larger than their tetragonal counterparts. In all cases the phase transition leads to stiffer materials. The bulk modulus of GeSb is smallest for Cu2MnSnS4 (AM), followed by Cu2ZnSnS4 and largest for Cu2FeSnS4 (AM). This is the same ordering we observe for the ST (AM) phases.