The Relative Contribution of Solutal Marangoni Convection to Thermal Marangoni Flow Instabilities in a Liquid Bridge of Smaller Aspect Ratios under Zero Gravity
Abstract
1. Introduction
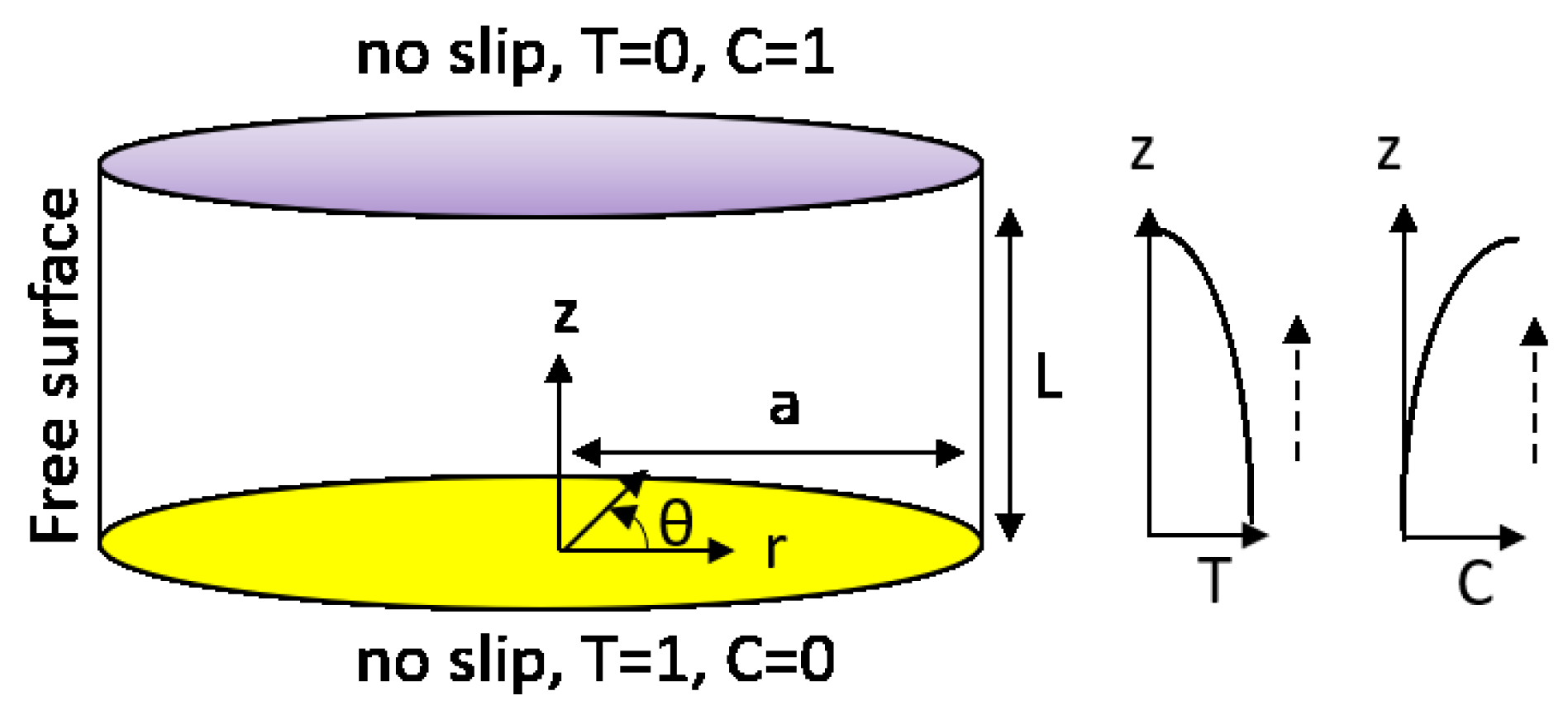
2. Numerical Method
2.1. Numerical Simulation
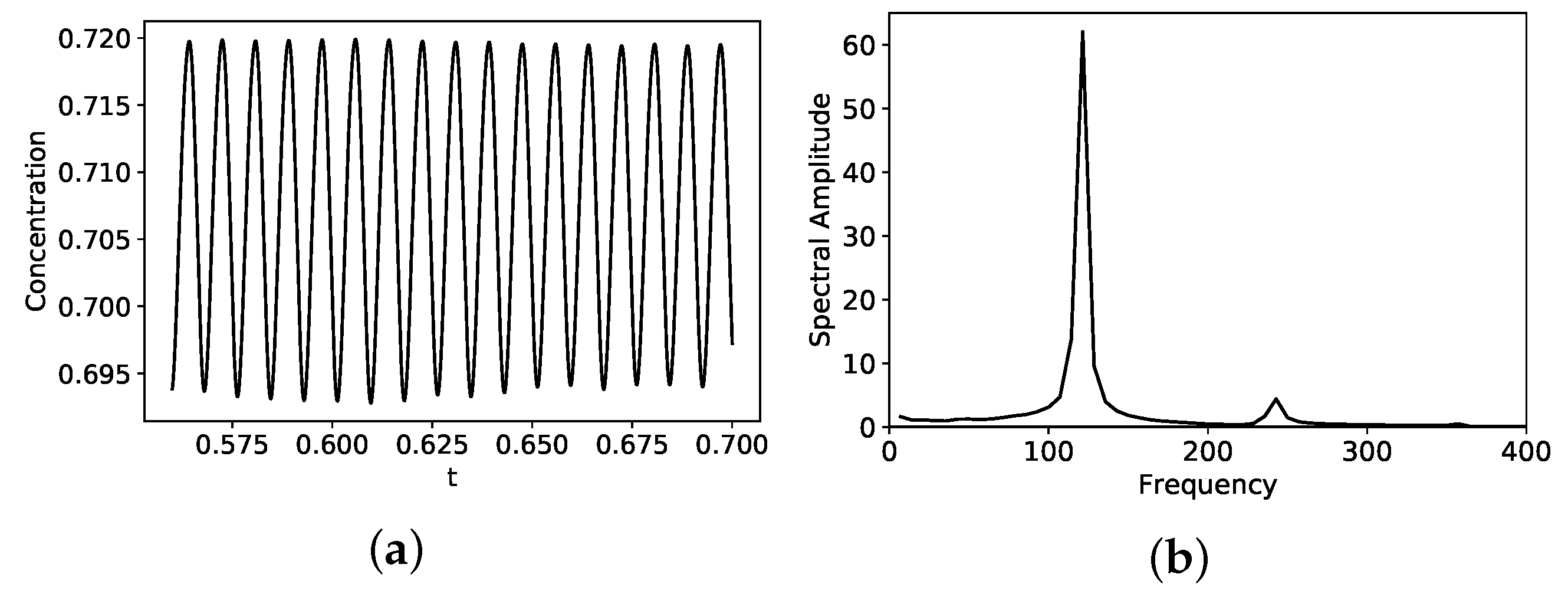
2.2. Dynamic Mode Decomposition (DMD)
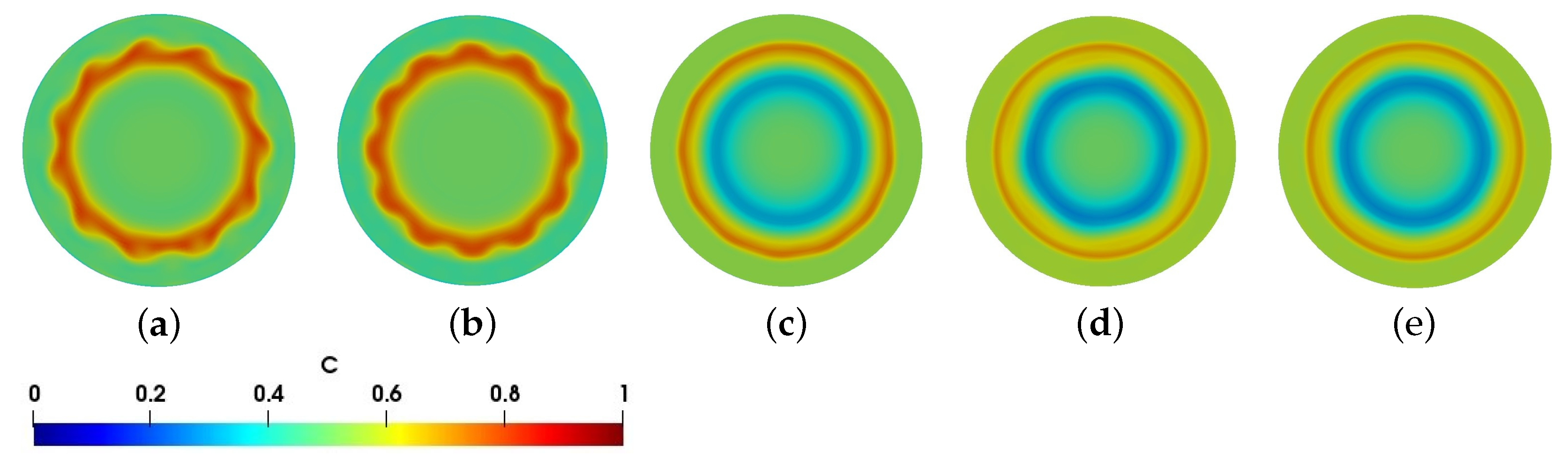
3. Results and Discussion
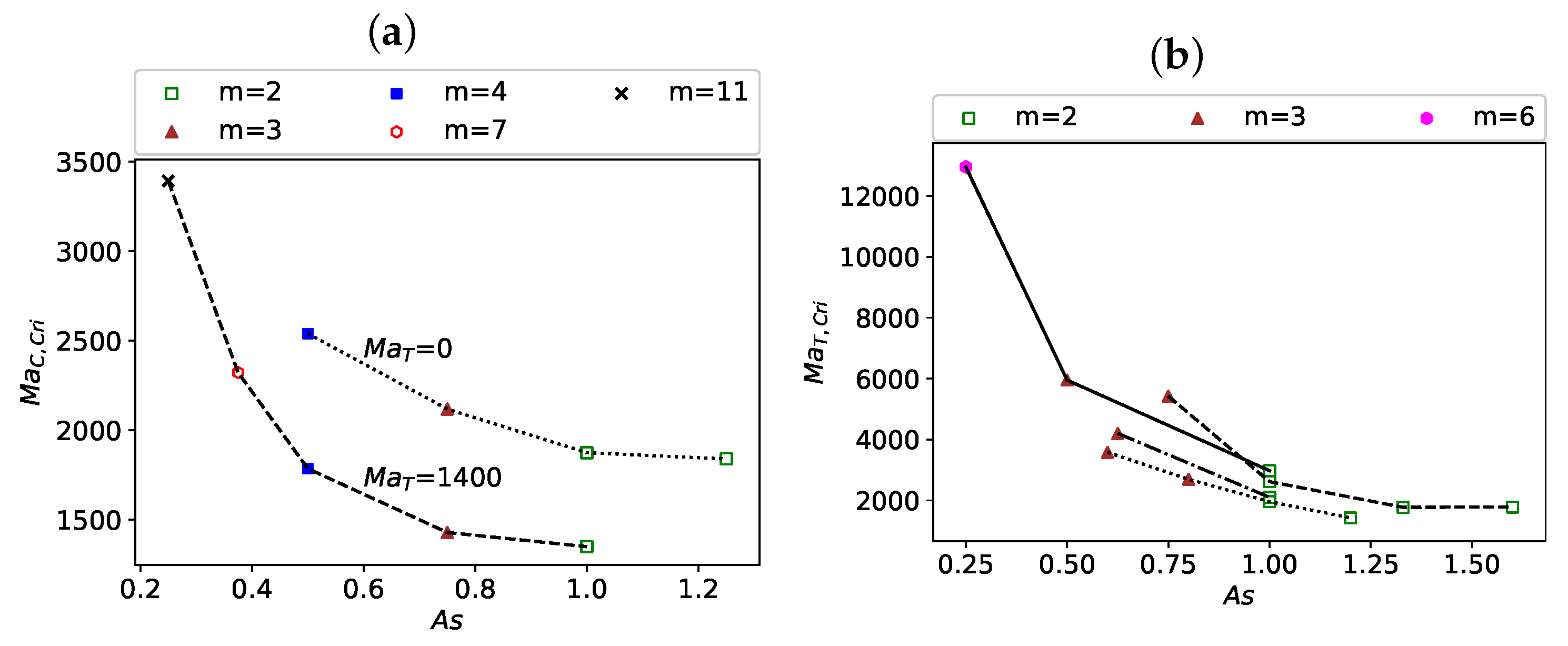
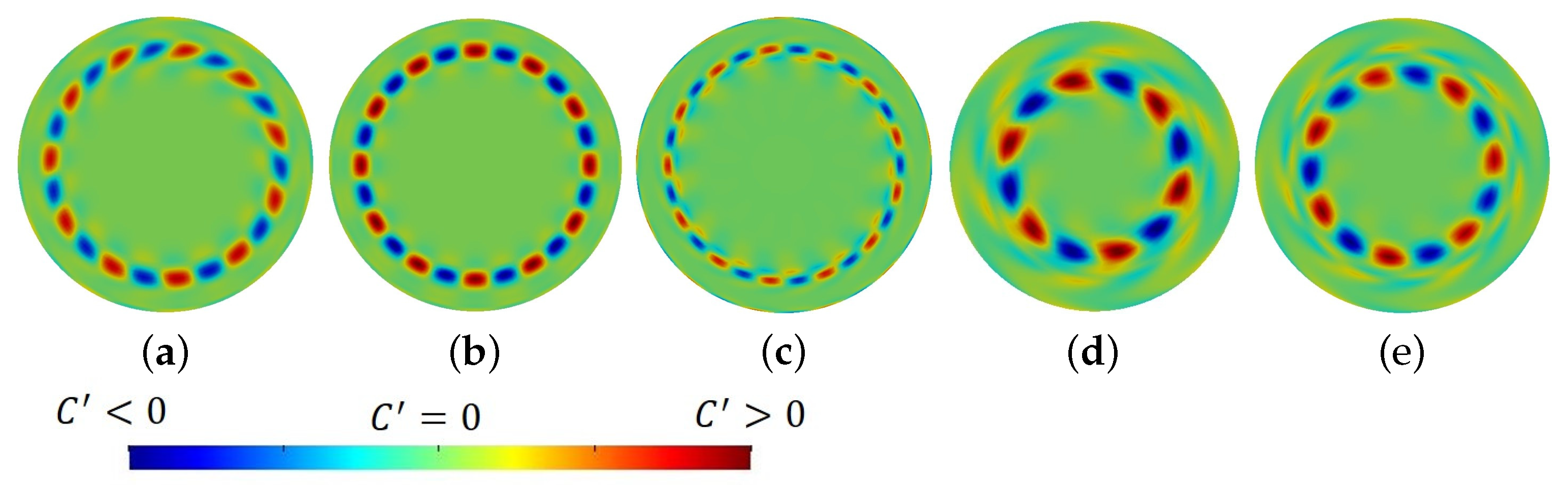
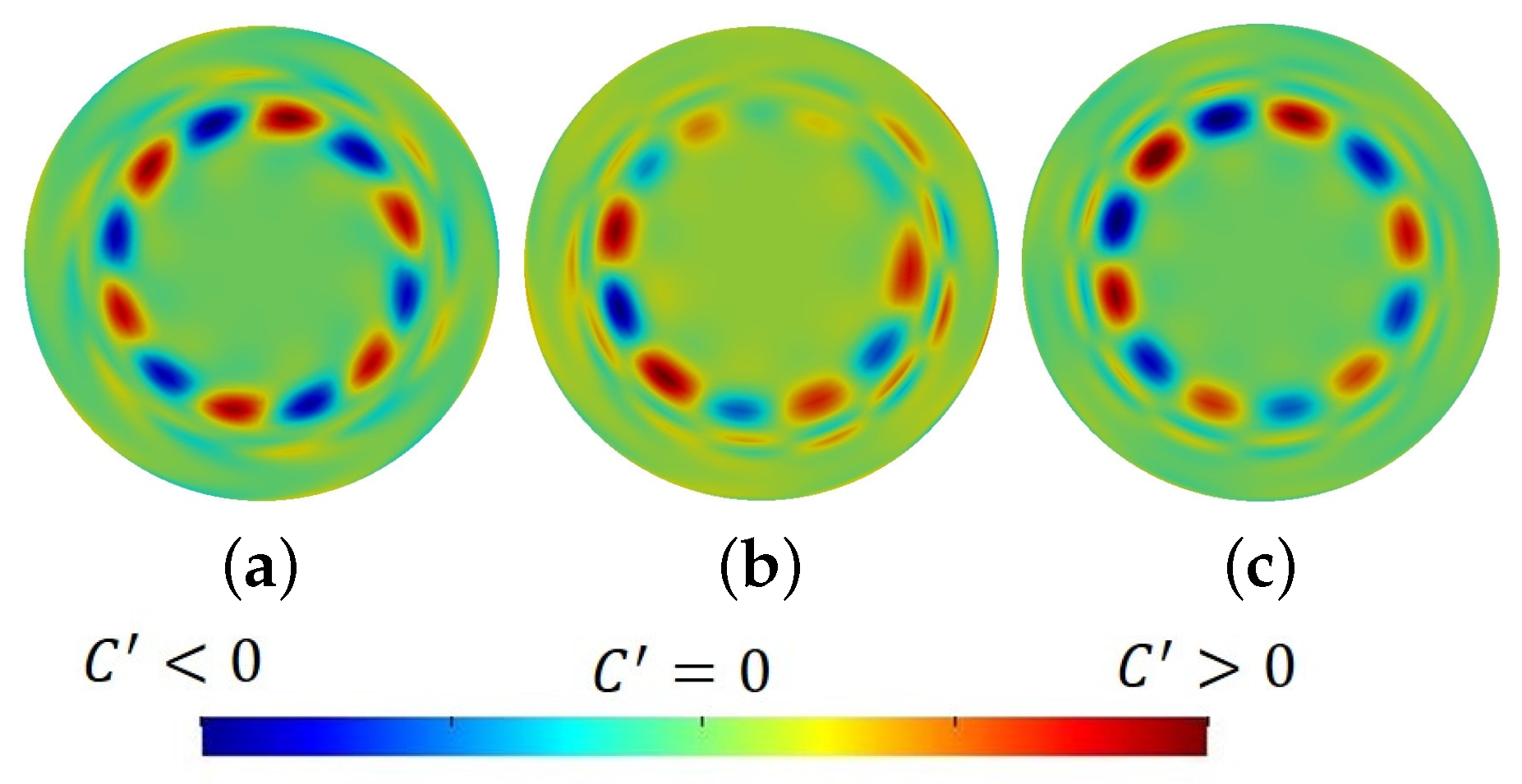
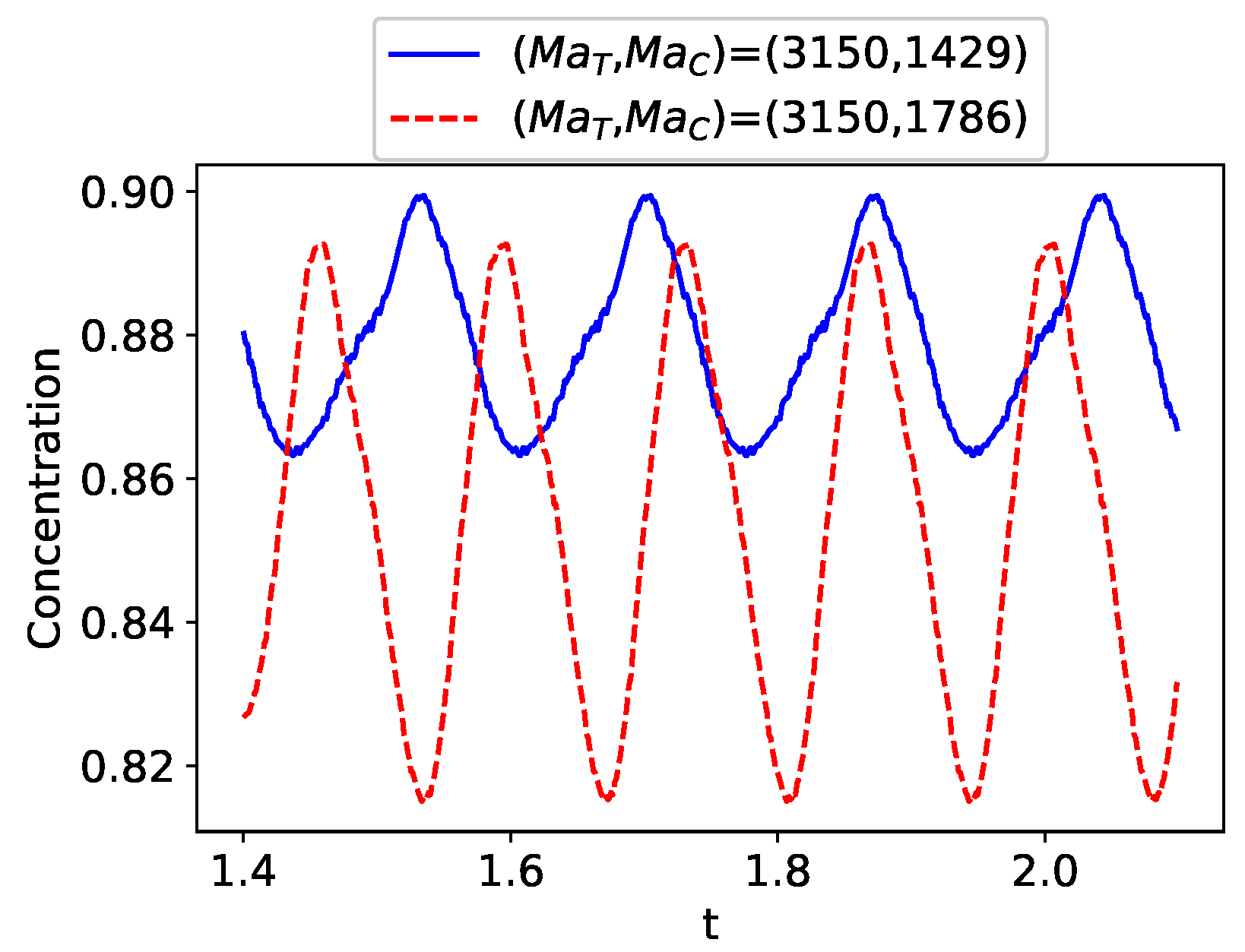
3.1. Critical at Small Thermal Marangoni Numbers,
3.2. Critical under a Weak Solutal Marangoni Convection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| LSA | Linear stability analysis |
| POD | Proper orthogonal decomposition |
| DMD | Dynamic mode decomposition |
References
- Lappa, M. CHAPTER 1—Space research. In Fluids, Materials and Microgravity; Lappa, M., Ed.; Elsevier: Oxford, UK, 2004; pp. 1–37. [Google Scholar] [CrossRef]
- Carotenuto, L.; Castagnolo, D.; Albanese, C.; Monti, R. Instability of thermocapillary convection in liquid bridges. Phys. Fluids 1998, 10, 555–565. [Google Scholar] [CrossRef]
- Yasuhiro, S.; Imaishi, N.; Kuhlmann, H.C.; Yoda, S. Numerical simulation of three-dimensional oscillatory thermocapillary flow in a half zone of Pr=l fluid. Adv. Space Res 1999, 24, 1385–1390. [Google Scholar] [CrossRef]
- Leypoldt, J.; Kuhlmann, H.C.; Rath, H.J. Three-dimensional numerical simulation of thermocapillary flows in cylindrical liquid bridges. J. Fluid Mech. 2000, 414, 285–314. [Google Scholar] [CrossRef]
- Rupp, R.; Müller, G.; Neumann, G. Three-dimensional time dependent modelling of the Marangoni convection in zone melting configurations for GaAs. J. Cryst. Growth 1989, 97, 34–41. [Google Scholar] [CrossRef]
- Chen, G.; Lizée, A.; Roux, B. Bifurcation Analysis of the thermocapillary convection in cylindrical Liquid Bridges. J. Cryst. Growth 1997, 180, 638–647. [Google Scholar] [CrossRef][Green Version]
- Wanschura, M.; Shevtsova, V.M.; Kuhlmann, H.C.; Rath, H.J. Convective instability mechanisms in thermocapillary liquid bridges. Phys. Fluids 1995, 7, 912–925. [Google Scholar] [CrossRef]
- Minakuchi, H.; Okano, Y.; Dost, S. A three-dimensional numerical simulation study of the Marangoni convection occurring in the crystal growth of SixGe1−x by the float-zone technique in zero gravity. J. Cryst. Growth 2004, 266, 140–144. [Google Scholar] [CrossRef]
- Minakuchi, H.; Okano, Y.; Dost, S. Effect of thermo-solutal Marangoni convection on the azimuthal wave number in a liquid bridge. J. Cryst. Growth 2017, 468, 502–505. [Google Scholar] [CrossRef]
- Minakuchi, H.; Okano, Y.; Dost, S. The Hysteresis Phenomena of Flow Patterns due to Thermal and Solutal Marangoni Convections in a Liquid Bridge under Zero Gravity. Fluid Mech. Res. Int. J. 2018, 2, 00018. [Google Scholar] [CrossRef]
- Agampodi Mendis, R.L.; Sekimoto, A.; Okano, Y.; Minakuchi, H.; Dost, S. Global Linear Stability Analysis of Thermo-solutal Marangoni Convection in a Liquid Bridge Under Zero Gravity. Microgravity Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Jin, C.; Sekimoto, A.; Okano, Y.; Minakuchi, H.; Dost, S. Characterization of the thermal and solutal Marangoni flows of opposite directions developing in a cylindrical liquid bridge under zero gravity. Phys. Fluids 2020, 32, 034104. [Google Scholar] [CrossRef]
- Lappa, M.; Savino, R.; Monti, R. Three-dimensional numerical simulation of Marangoni instabilities in liquid bridges: Influence of geometrical aspect ratio. Int. J. Numer. Methods Fluids 2001, 36, 53–90. [Google Scholar] [CrossRef]
- Preisser, F.; Schwabe, D.; Scharmann, A. Steady and oscillatory thermocapillary convection in liquid columns with free cylindrical surface. J. Fluid Mech. 1983, 126, 545–567. [Google Scholar] [CrossRef]
- Lappa, M. Three-dimensional numerical simulation of Marangoni flow instabilities in floating zones laterally heated by an equatorial ring. Phys. Fluids 2003, 15, 776–789. [Google Scholar] [CrossRef]
- Numerical investigation of the effect of rotation on the oscillatory thermocapillary convection and dopant transport in a silicon liquid bridge. J. Cryst. Growth 2019, 523. [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Rowley, C.W.; Mezi, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef]
- Imaishi, N.; Yasuhiro, S.; Akiyama, Y.; Yoda, S. Numerical simulation of oscillatory Marangoni flow in half-zone liquid bridge of low Prandtl number fluid. J. Cryst. Growth 2001, 230, 164–171. [Google Scholar] [CrossRef]
- Minakuchi, H.; Takagi, Y.; Okano, Y.; Mizoguchi, K.; Gima, S.; Dost, S. A grid refinement study of half-zone configuration of the Floating Zone growth system. J. Adv. Res. Phys. 2012, 3, 011201. [Google Scholar]
- Abbasoglu, S.; Sezai, I. Three-dimensional modelling of melt flow and segregation during Czochralski growth of GexSi1−x single crystals. Int. J. Therm. Sci. 2007, 46, 561–572. [Google Scholar] [CrossRef]
- Minakuchi, H.; Yoshino, T.; Okano, Y. The relative contributions and control of thermo-solutal Marangoni convections on flow patterns in a liquid bridge. J. Cryst. Growth 2014, 285, 61–65. (In Japanese) [Google Scholar] [CrossRef]
- Chun, C.H. Experiments on steady and oscillatory temperature distribution in a floating zone due to the Marangoni convection. Acta Astronaut. 1980, 7, 479–488. [Google Scholar] [CrossRef]





| Case | Eigenvalue () | Frequency | m | |||
|---|---|---|---|---|---|---|
| (i) | 0.25 | 14,000 | 1786 | 0.0002 | 19 | 6 |
| 13,300 | 1786 | 0.0002 | 33 | 7 | ||
| 2100 | 3572 | 0.0052 | 55 | 11 | ||
| 1400 | 3572 | 0.0219 | 50 | 12 | ||
| 9100 | 3572 | 0.00006 | 120 | 13 | ||
| (ii) | 1 | 3150 | 1490 | 0.006 | 6.19 | 2 |
| 3150 | 1786 | 0.0032 | 6.32 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agampodi Mendis, R.L.; Sekimoto, A.; Okano, Y.; Minakuchi, H.; Dost, S. The Relative Contribution of Solutal Marangoni Convection to Thermal Marangoni Flow Instabilities in a Liquid Bridge of Smaller Aspect Ratios under Zero Gravity. Crystals 2021, 11, 116. https://doi.org/10.3390/cryst11020116
Agampodi Mendis RL, Sekimoto A, Okano Y, Minakuchi H, Dost S. The Relative Contribution of Solutal Marangoni Convection to Thermal Marangoni Flow Instabilities in a Liquid Bridge of Smaller Aspect Ratios under Zero Gravity. Crystals. 2021; 11(2):116. https://doi.org/10.3390/cryst11020116
Chicago/Turabian StyleAgampodi Mendis, Radeesha Laknath, Atsushi Sekimoto, Yasunori Okano, Hisashi Minakuchi, and Sadik Dost. 2021. "The Relative Contribution of Solutal Marangoni Convection to Thermal Marangoni Flow Instabilities in a Liquid Bridge of Smaller Aspect Ratios under Zero Gravity" Crystals 11, no. 2: 116. https://doi.org/10.3390/cryst11020116
APA StyleAgampodi Mendis, R. L., Sekimoto, A., Okano, Y., Minakuchi, H., & Dost, S. (2021). The Relative Contribution of Solutal Marangoni Convection to Thermal Marangoni Flow Instabilities in a Liquid Bridge of Smaller Aspect Ratios under Zero Gravity. Crystals, 11(2), 116. https://doi.org/10.3390/cryst11020116






