The Influence of Supercooling and Hydrodynamics on the Mosaic and Radial Inhomogeneity of K₂Ni_XCo_(1–X)(SO₄)₂·6H₂O Mixed Crystal

Abstract

The mosaic and radial inhomogeneity of shaped mixed crystals of K₂Ni_xCo_(1–x)(SO₄)₂·6H₂O (KCNSH) were studied depending on the supercooling of solution, its velocity and its method of supply into the shaper. It was shown that mosaic inhomogeneity could be suppressed when solution is supercooled to about 2 °C. Peripheral supply of the solution (tangential to the wall of the shaper to create a “swirling” flow) with a rate of 55–135 cm/s provides better composition uniformity along the crystal surface in comparison with upright supply of the solution (flow is perpendicular to the crystal surface).

1. Introduction

The use of the UV-C range for diagnostics of different processes is interesting for many fields of science and technology. This is due to the extremely low level of background interference, since the solar radiation in this spectrum range is almost eliminated by the ozone layer of the Earth. The technology of detecting and recording radiation with a wavelength of 250–280 nm is called “solar-blind” one, and it has been intensively developing in the world. One basic element in the devices of solar-blind technology is an effective zone filter, which is transparent in the range of 250–280 nm and nontransparent in other ranges. One promising direction is the creation of an optical filter based on a mixed KCNSH crystal. Due to its optical characteristics and dehydration temperature, its application will allow the significant improvement of the quality and operational characteristics of devices [1,2].

Due to the peculiarities of the crystallization in multicomponent systems [3,4,5], the mixed crystals show higher inhomogeneity compared to single-component crystals. This is due to the larger number of degrees of freedom during crystallization and the difference in the distribution coefficients of isomorphic components occupying equivalent positions in the crystal. As a result, besides defects inherent to all water-soluble crystals, the mixed crystals contain specific examples of micro- inhomogeneity, such as mosaic and radial.

According to the Gibbs phase rule, at constant pressure, a three-component system consisting of a solvent (water) and two salts has two degrees of freedom (temperature and composition). This means that at a given temperature there is a continuous series of both saturated solutions and crystals whose compositions correspond to the equilibrium conditions with these solutions. Thus, during the growth of mixed crystals, a contact of the growing crystal with nonequilibrium solution should be expected. This mechanism of interaction is called the isomorphic substitution reaction and has been considered in detail in [4]. This is a complex phenomenon when oppositely directed processes of dissolution and growth of various crystalline phases occur simultaneously. This leads to the transformation of the crystal surface into a mosaic of randomly alternating areas of different compositions. As a result, a mosaic inhomogeneity is formed in the crystal bulk. This is a new type of inhomogeneity that occurs only in mixed crystals. It was first detected in (Pb,Ba)(NO₃)₂, K(Br,Cl) and (K,Rb)HC₈H₄O₄ crystals by X-ray microtomography [6,7,8,9], then it was confirmed by energy-dispersion analysis in KCNSH crystals [10,11]. As was shown by in situ laser interferometry, the mosaic inhomogeneity in these crystals can occur as a result of instability of the solution composition or solution velocity [12]. It was found that supercooling about and more 2 °C is required to suppress such inhomogeneity.

The radial inhomogeneity of mixed crystals is associated with the nonuniformity of the solution flow near the growing face [5,12,13]. Theoretical calculations carried out to simulate the growth process of mixed crystals in the shaper have showed that the distribution of isomorphic components in the solution at the crystallization front (and hence the value of radial inhomogeneity) is determined by the flow velocity of solution and the way in which it is fed into the shaper [13].

Despite the fact that the values of mosaic and radial inhomogeneities in mixed crystals are not so high, they can significantly affect the crack resistance of the crystal samples [14]. In our previous study, shaped KCNSH mixed crystals of high structural perfection were obtained by the temperature difference method [2], in which the supersaturation of the solution and the growth temperature are constant and feeding of the mother solution is continuous. However, despite the improved optical properties of the obtained crystals and their visual transparency, most of them turned out to be quite fragile during final processing. This may be due to mosaic and radial inhomogeneity. Therefore, in order to obtain less fragile crystals, it is necessary to choose growth conditions under which the above mentioned inhomogeneities will be minimal.

This article presents the results of studies of the values of mosaic and radial inhomogeneities in mixed KCNSH crystals depending on the growth conditions, the flow velocity of the solution and the way in which it is supplied into the shaper.

2. Experimental Section

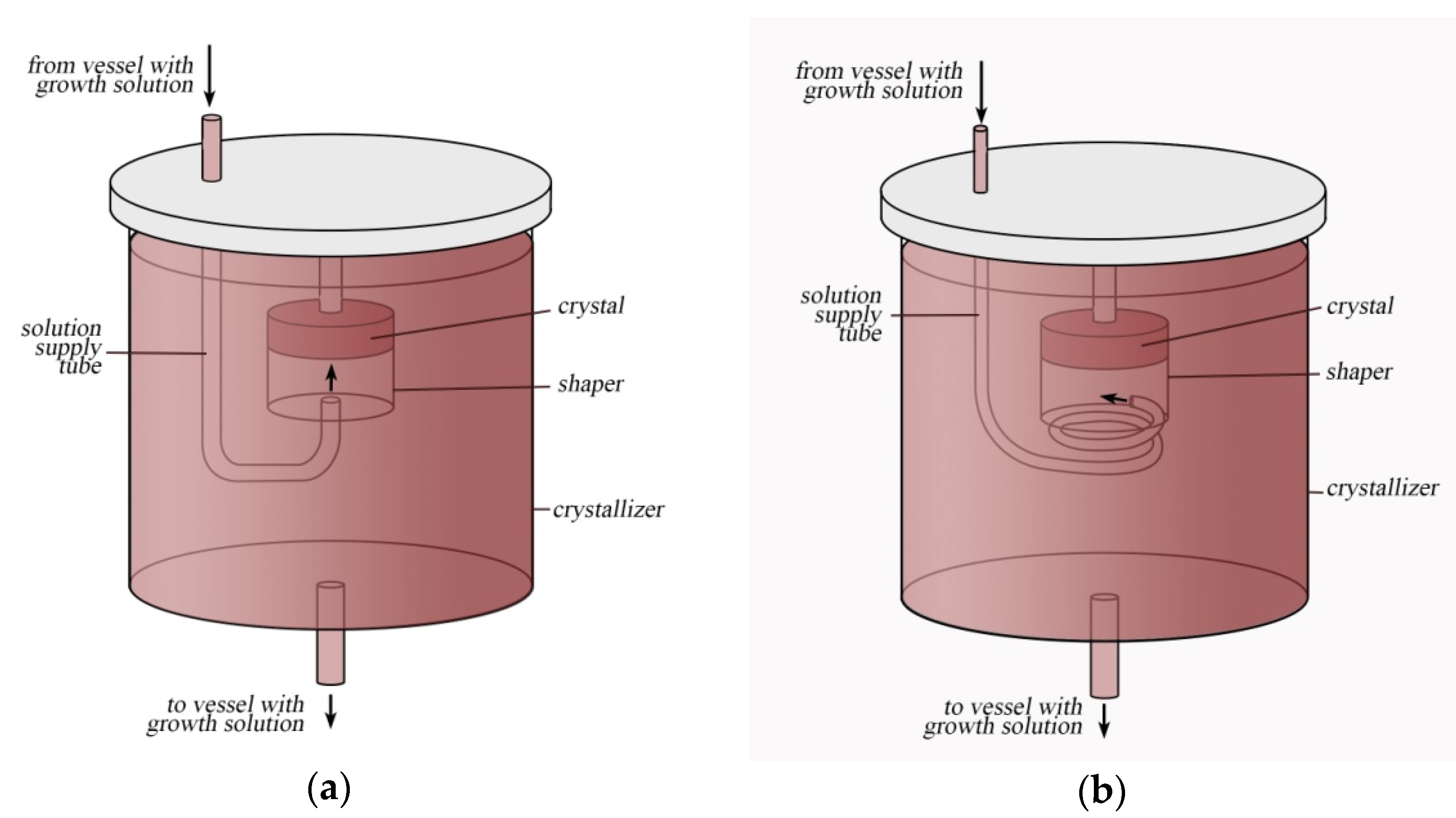
2.1. Growing of Shaped Mixed KCNSH Crystals

Mixed KCNSH crystals were obtained by the temperature difference method with the feeding of mother solution, as described in [2]. The solution feeding mode was calculated for two growth modes, taking into account the change in composition due to both the different distribution coefficients of isomorphic components during the stationary growth and the formation of a boundary diffusion layer at the initial transient mode of the growth. Round flat plates of mixed crystals of appropriate composition with a surface orientation (110) were used as seed crystals. The ratio of isomorphic salts in the solution was KCSH:KNSH = 1:2; the solutions were saturated at 42–44 °C, the supercooling varied from 0.3 to 2.5 °C and was constant during every experiment. The seed was mounted in a cylindrical shaper and the crystal was grown top down (Figure 1). The diameter of the shaper was 30 mm. The solution volume in crystallizer was 1 l, whole volume including solution in the vessel was 4.5 l. The solution was fed directly to the crystal surface through solution supply tube. According to the results of numerical simulation [11], in order to achieve a better uniformity of the crystal composition along the growing face, it is preferable to provide the peripheral supply of the solution to the shaper. To confirm these calculations, two modes of feeding the solution were implemented in our experiments: upright supply of the solution to the center of growing crystal surface (Figure 1a) and supply to periphery of crystal surface along the wall of the shaper (Figure 1b).

2.2. Study of the Composition of Mixed KCNSH Crystals by Energy-Dispersive Analysis

Studies of mosaic and radial inhomogeneities of the composition of mixed KCNSH crystals were carried out by energy-dispersion X-Ray spectrometer (EDS) (FEI, Hillsboro, OR, USA) established on FEI Quanta 200 3D scanning electron microscope (up to 30 kV). Cross sections of crystals cut along the growth direction made by a diamond wire saw were subjected to mechanical grinding and polishing. Polishing was carried out with a powder with a grain size of 1 μm. Then the samples were washed with absolutized ethanol.

To obtain data on the radial inhomogeneity, the elemental composition was measured in 9 “points” from the edge of the crystal to its geometric center with a step of 2 mm. To obtain an integral result, EDS measurements in each “point” were taken from an area of 300 × 200 μm at accelerating voltage 30 kV and beam current 0.67 nA in a low vacuum mode and water vapor system (to prevent sample charging effects) for 45 min. EDS maps of the element distribution for the analysis of mosaic inhomogeneity were built with exposure time 2000 ms (512 × 400 pixels) in each point. Scanning in 32 passes was performed within a 3 × 2 mm² area with a step of 5.9 μm horizontally and 5 μm vertically. At the same time, the detector’s count was in the range of 10–13 thousand cps. The concentrations were calculated using Kα lines of Ni and Co.

The processing of obtained maps was carried out as follows. At first, the contribution of the surface roughness to the intensity variations on the Ni distribution maps was excluded. That was done to exclude the contribution of surface roughness to the intensity variations due to the shielding of part of the outgoing X-ray radiation by the edges of the hollows. The contribution of the surface relief to the intensity variations was eliminated by subtracting the K distribution maps from the Ni distribution maps, since the concentration of K in the sample should be constant, and all intensity variations are due to the surface roughness. The obtained difference image was averaged over an area of 2 × 2 pixels to identify the mosaic structure of the sample and to reduce random fluctuations in intensity. Next, a statistical analysis of the obtained image was carried out, while the average absolute deviation |δ${\mathrm{x}}_{\mathrm{Ni}}$| was taken as a measure of the composition variations.

3. Results and Discussion

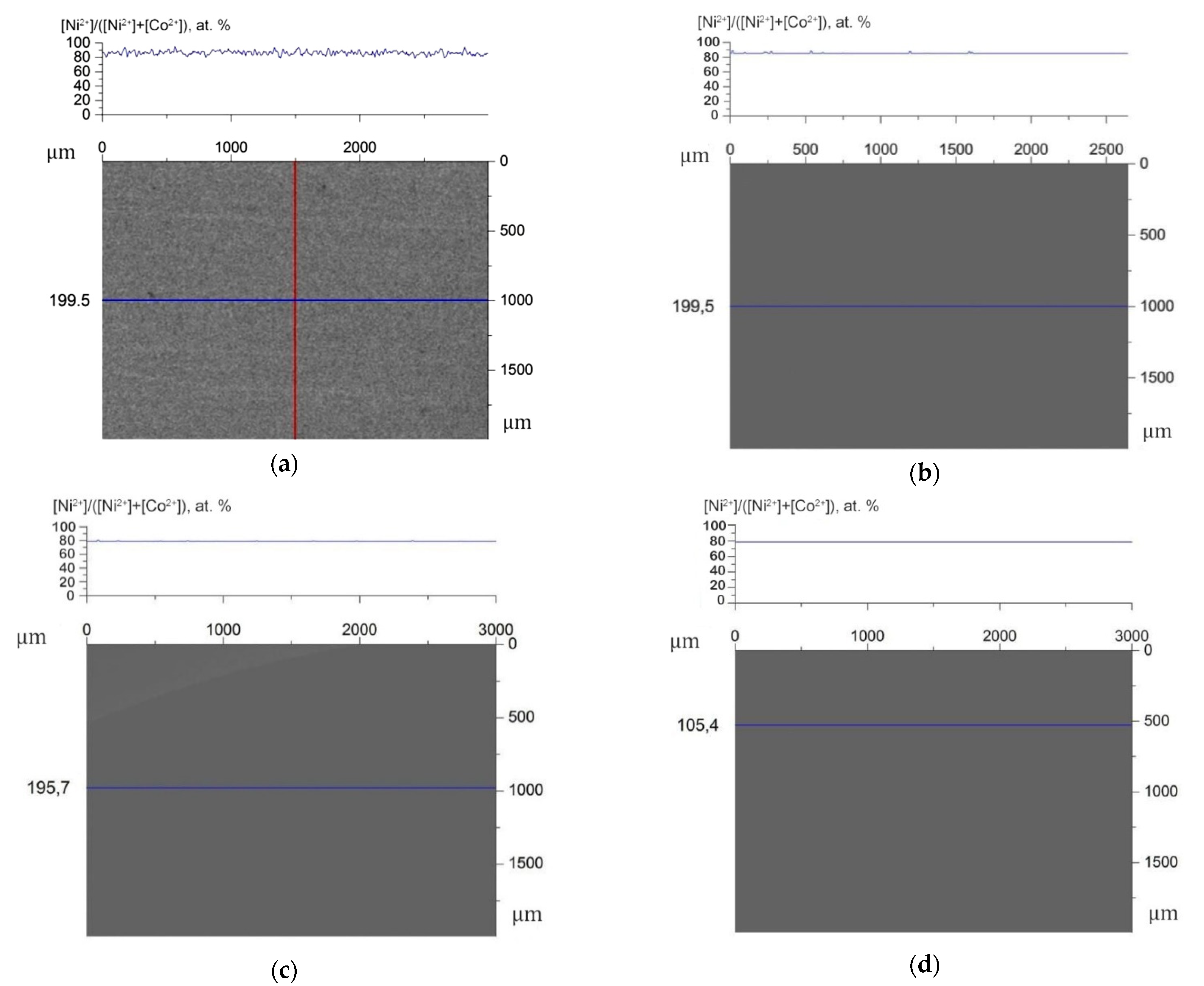
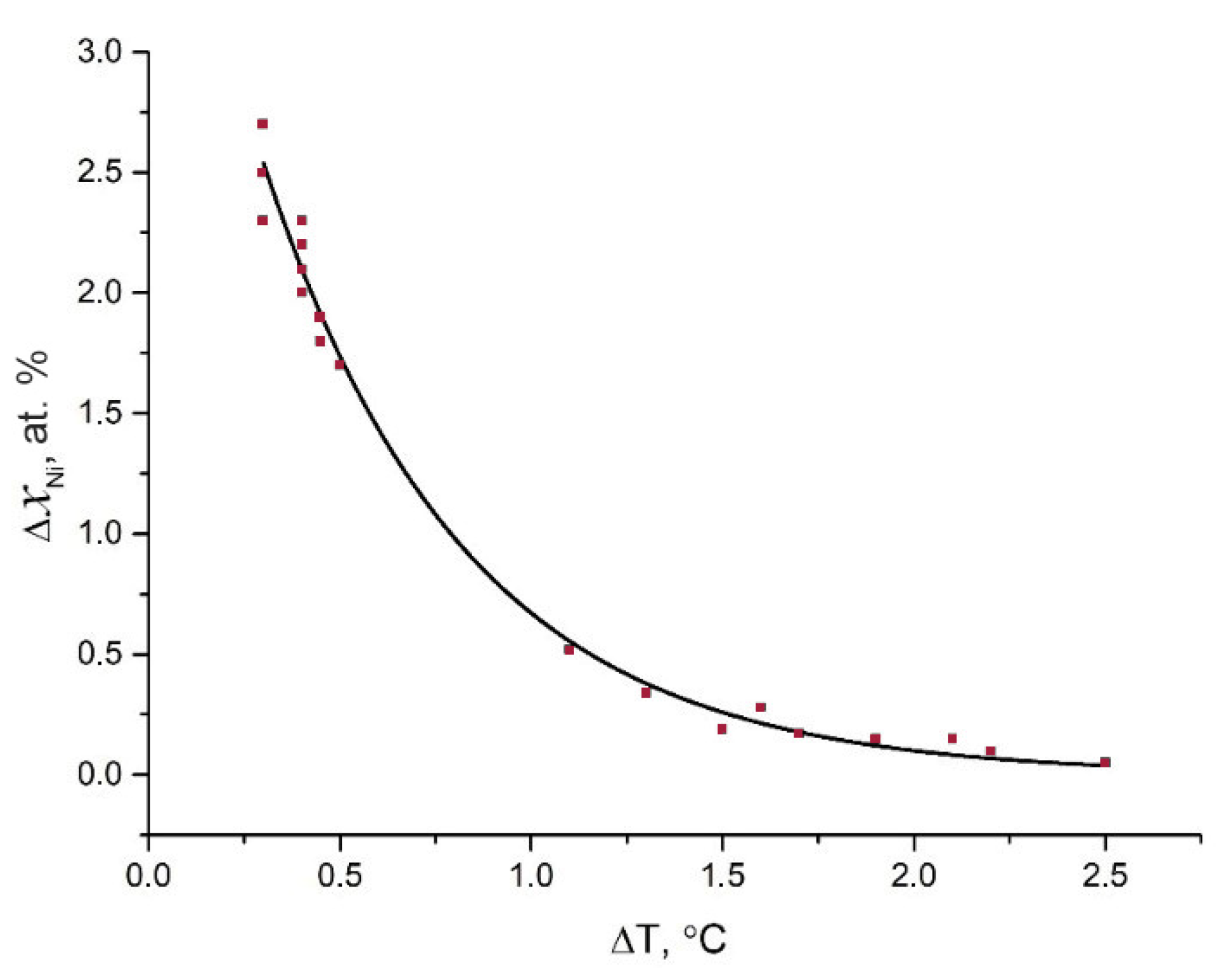
3.1. Study of Mosaic Inhomogeneity of Mixed KCNSH Crystals

The 15 mixed KCNSH crystals grown at various supercooling of the solution by the method of temperature difference with the solution feeding were analyzed during the study of mosaic inhomogeneity. As an example, the processed maps of the distribution of Ni in several samples are shown in Figure 2.

If our assumption that the mosaic inhomogeneity appears as a result of local acts of isomorphic substitution is correct, then it can be suppressed by bringing the value of supercooling of the solution to a certain critical value [3,4]. Figure 3 shows the obtained dependence of the mosaic inhomogeneity of KCNSH crystals on the supercooling of solution.

At low supercooling, the mosaic inhomogeneity can reach a rather significant value of ≥2 at. %. However, under supercooling ∆T ≥ 2 °C it nearly disappeared, and the observed insignificant variations in the composition were associated with both experimental error and local inhomogeneity of crystals due to the morphology of the surface: the presence of vicinal-sectorial and intervicinal boundaries, macrosteps, etc. This result is in good agreement with the results of the study of the stability of the surface of KCNSH crystals by laser interferometry [12] and shows the practical possibility of suppressing mosaic inhomogeneity in mixed crystals.

3.2. Study of the Radial Inhomogeneity of KCNSH Crystals

Since the conditions of experiments on the analysis of radial inhomogeneity of mixed KCNSH crystals were similar to the conditions for studying mosaic inhomogeneity, the radial inhomogeneity was measured using EDS on some of the same crystals as the mosaic one to summarizing and comparison of obtained results. The results are shown in Figure 4 and in

Table 1. Radial inhomogeneity of shaped KCNSH crystals.

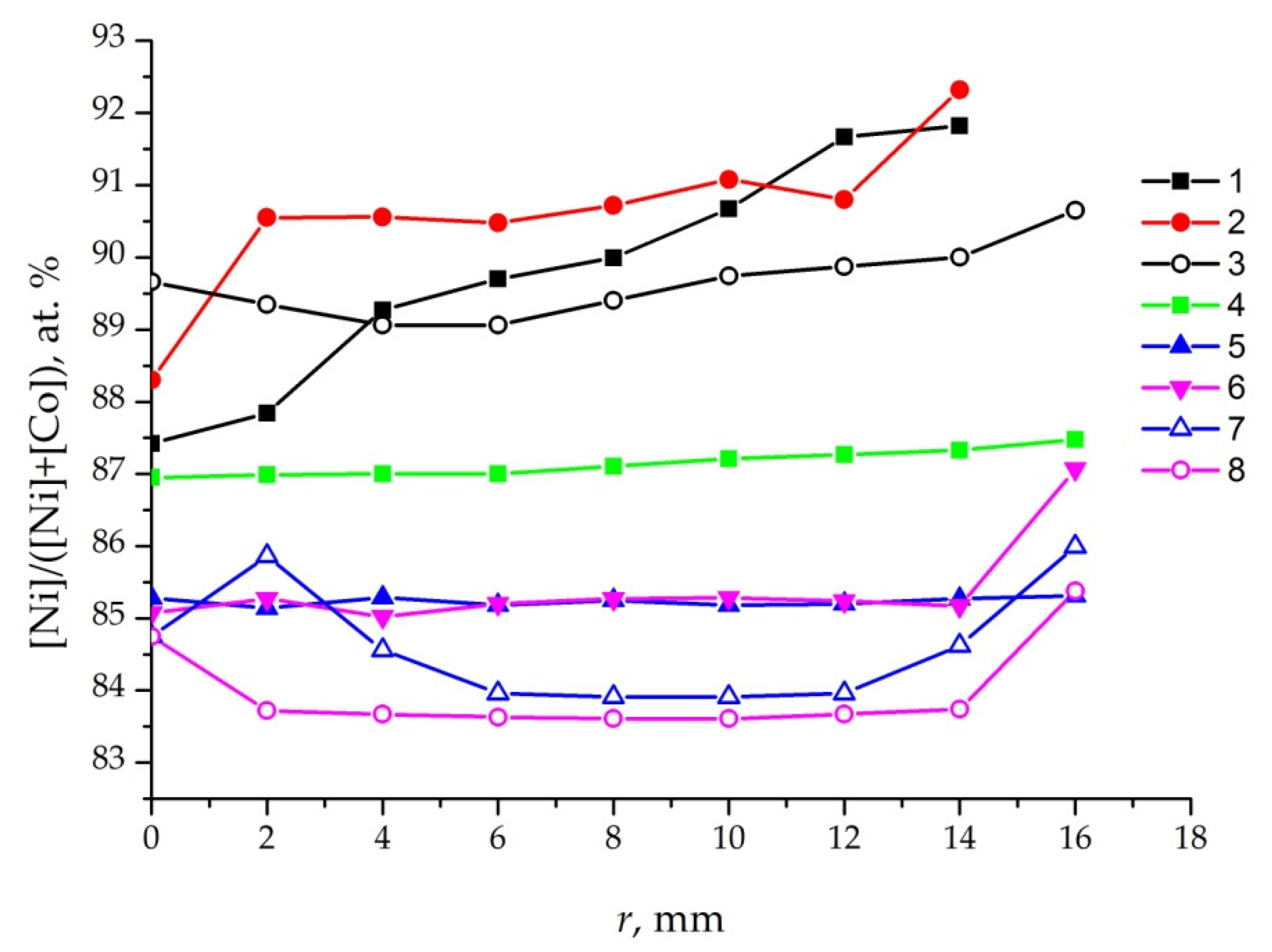
KCNSH Crystal	Supercooling ∆T, °C	Growth Rate, mm/day	Solution Velocity, cm/s	Solution Supply Mode	Radial Inhomogeneity, $\mathsf{\Delta }{\mathbf{x}}_{\mathbf{N}\mathbf{i}},\mathbf{at}.\%$
1	2.1	0.70	175	centre	4.4
2	1.6	0.33	85	centre	4.0
3	1.3	0.18	170	periphery	1.6
4	1.9	0.50	135	periphery	0.5
5	1.7	0.37	55	periphery	0.17
6	1.5	0.25	55	periphery	2.0
7	2.2	0.82	10	periphery	2.1
8	2.5	1.00	10	periphery	1.8

.

According to the results of numerical simulation [13], the peripheral supply of the solution to the shaper with a curling of the flow provides the more uniform radial distribution of the components, compared to the supply to the center of the crystal. Moreover, in accordance with the simulation data, an increase in the flow velocity from 10 cm/s to 55 cm/s results in a significantly more uniform distribution of Ni in case of the peripheral supply of the solution. However, with an increase in the velocity of the solution flow to 135 cm/s and then to 170 cm/s, the uniformity of the crystals decreases. Apparently, this may be due to the development of turbulence in the boundary layers of the flow.

High radial inhomogeneity of crystals at solution velocity of 10 cm/s could be explained by the fact that at such velocity the kinetic mode of KCNSH crystal growth has not yet been achieved [12]. Therefore, there is a rather extended diffusion layer near the surface. The thickness of this layer strongly depends on the value of the horizontal component of the flow velocity. Therefore, the greatest variations in the composition are observed in the center of the face and on the periphery of the crystal, where the flow changes its direction.

As was shown [12], the kinetic mode of KCNSH crystal growth is realized if the solution velocity is more than 37 cm/s. In this mode, the thickness of the boundary diffusion layer is negligible and the initial non-stationary transient mode of crystal growth does not manifest itself. Thus, only feeding for the stationary mode is needed to compensate for changes in the composition of the solution due to differences in the distribution coefficients of the components.

4. Conclusions

The mosaic and radial inhomogeneities in mixed KCNSH crystals grown with feeding by the temperature difference technique from solutions with the ratio of isomorphic components KCSH:KNSH = 1:2 were studied. The key parameters for obtaining highly homogeneous mixed KCNSH crystals were determined. As a proof of the earlier numerical modeling, it was shown that the peripheral supply of the solution (to periphery of crystal surface along the wall of the shaper to create a “curling” flow) with velocity from 55 cm/s to 135 cm/s provides the best radial uniformity of the crystal composition. In addition, at such solution velocities, there is no boundary diffusion layer, since the kinetic growth mode is realized, and no feeding is needed for the non-stationary growth mode. The mosaic inhomogeneity nearly disappeared when the solution supercooling was ∆T ≥ 2 °C, which is in a good agreement with earlier interferometric in situ observations [12] of exchange processes on the surface of mixed KCNSH crystals.