Abstract
Electronic, optical, and thermoelectric properties of germanium tellurides (GeTe) were investigated through a series of first-principles calculations of band structures, absorption coefficients, and thermoelectric transport coefficients. We consider bulk GeTe to consist of cubic and rhombohedral phases, while the two-dimensional (2D) GeTe monolayers can form as a 2D puckered or buckled honeycomb crystals. All of the GeTe variants in the bulk and monolayer shapes are excellent light absorbers in a wide frequency range: (1) bulk cubic GeTe in the near-infrared regime, (2) bulk rhombohedral GeTe and puckered monolayer GeTe in the visible-light regime, and (3) buckled monolayer GeTe in the ultraviolet regime. We also found specifically that the buckled monolayer GeTe exhibits remarkable thermoelectric performance compared to the other GeTe phases due to a combination of electronic band convergence, a moderately wide band gap, and unique 2D density of states from the quantum confinement effect.
1. Introduction
Growing worldwide demand for energy and environmental impact associated with conventional energy sources is at the base of a probable energy crisis soon. This situation is well known as the economy, energy, and environment (“3E”) trilemma [1]. Petroleum will become increasingly expensive and scarce, while we have felt the climatic effects of the massive use of all fossil fuels. At present, we should not abandon any existing energy sources, especially the renewable ones or wasted ones. Freely available solar energy in the environment and the waste heat given off by engines and machines are examples of energy sources that we can convert to electrical power. For such energy conversions, we need materials that are excellent at absorbing light [2] and also efficient in transforming heat directly to electricity [3].
Of many functional materials, group-IV-VI compounds have been used for a long time in optoelectronic and thermoelectric devices due to their optimal band gaps from narrow to moderate sizes. The most utilized group-VI element in the group-IV-VI compounds is tellurium (Te), which thus forms a class of group-IV tellurides, consisting of GeTe, SnTe, and PbTe. Bulk GeTe, in particular, is well-known for its ferroelectricity and phase-changing characteristics [4,5,6], where changing temperature can give a transition of GeTe from the rhombohedral lattice (in the literature also referred to as -GeTe) to the cubic lattice (-GeTe). The phase change affects the optical response so that GeTe can be used for optical data storage [7,8]. In addition to its excellent optical properties, under certain conditions and depending on sample quality, bulk GeTe has recently emerged as one of the world record holders for the most efficient thermoelectrics [9,10] with the figure of merit close to the commercial thermoelectric material Bi2Te3.
On the other hand, nanotechnology and miniaturization have become more popular in recent years, with the spirit of good-old Feynman’s quotes [11], “There is plenty of room at the bottom,” which have inspired generations of scientists to explore low-dimensional-materials for practical usages. Simply saying, when something gets smaller, its physical properties become distinct from the bulk one. The two-dimensional materials, in particular, attracted significant attention when Geim and Novoselov [12] successfully obtained graphene from the mechanical exfoliation of graphite in 2004 because many unique properties of graphene, such as high carrier mobility and quantum Hall effect [13,14], are not found in graphite. Since then, we have witnessed rapid developments of other two-dimensional (2D) materials, such as 2D phosphorene [15], 2D transition metal dichalcogenides (TMDs) [16], and 2D group-III monochalcogenides [17]. Therefore, it is natural to continue exploration of more 2D materials, especially in the class of group-IV tellurides which already have excellent properties in their bulk forms.
In this work, by using first-principles density functional theory (DFT) approach, we focus on investigating the electronic, optical, and thermoelectric properties of GeTe monolayers and compare the properties with those of bulk GeTe. All these GeTe phases are dynamically stable according to the literature, e.g., Reference [18] for cubic and rhombohedral GeTe, Reference [19] for puckered GeTe, and Reference [20] for buckled GeTe. There have also been earlier DFT calculations for the electronic band structures of GeTe monolayers in the puckered lattice [19,21,22,23] and buckled lattice [23,24], but the results seem to be inconsistent with a recent experiment [25]. In Reference [25], Zhang et al. only observed buckled GeTe thin films in argon and oxygen environments with band gaps of about – eV, while References [23,24] obtained band gaps of about eV. The eV difference is quite remarkable, and it may affect the other physical properties that are sensitive to the band gap. We decided to recalculate the electronic band structures and look for the best agreement with the available experimental data. From the reliable calculations of the band structures, we can confidently evaluate the optical and thermoelectric properties of GeTe in all of its possible phases without worrying about overrating these materials. Besides checking the consistency of the published literature, as a unique finding in this work, we show the potential of buckled GeTe monolayer as a thermoelectric material.
2. Computational Methods
We computed the electronic structures of bulk and monolayer GeTe using the input of optimized geometry from the DFT simulation as implemented in the Quantum ESPRESSO package [26]. Having the calculated data of electronic structures, which consist of the energy dispersion and wave functions, we could proceed to obtain the dielectric function within the independent particle and dipole approximation, from which we calculated the absorption coefficient. We finally calculated the thermoelectric transport coefficients, i.e., the Seebeck coefficient, electrical conductivity, and thermal conductivity, within the Boltzmann transport theory [27] and constant relaxation time approximation [28,29]. In the following subsections, we give a brief description of the parameters and formulas used in this study.
2.1. DFT Parameters
We show the lattice structures of bulk and monolayer GeTe in Figure 1. We considered bulk GeTe to form in two phases, i.e., the cubic and rhombohedral lattices as shown in Figure 1a, while monolayer GeTe may have formed as the puckered and buckled honeycomb lattices as shown in Figure 1b. From their top view, the puckered and buckled GeTe can be imagined as the reduction of cubic and rhombohedral lattices in two dimension, respectively. Note that although puckered and buckled GeTe are considered monolayers, they still have sizable thicknesses due to their buckling heights. From our calculations, the thicknesses of puckered and buckled GeTe are and , respectively. In Table 1, we list the optimized lattice constants for bulk and monolayer GeTe along with some reference data.
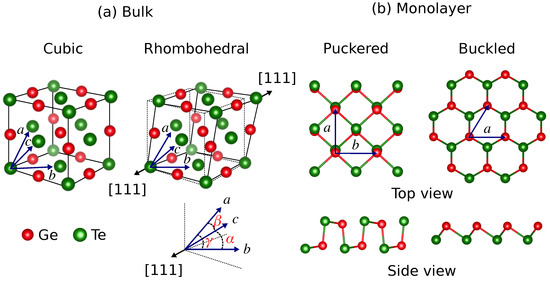
Figure 1.
Lattice structures of (a) bulk and (b) monolayer GeTe. Bulk GeTe consists of cubic and rhombohedral lattices, while monolayer GeTe consists of puckered and buckled honeycomb lattices. The structural models are visualized by using VESTA [30].

Table 1.
Lattice constants (in Å) of bulk and monolayer GeTe. The lattice constants (a, b, c) and angles (, , ) are in accordance to the illustrations in Figure 1.
To achieve the convergence in the DFT simulation while considering a reasonable calculation time, we set the kinetic energy cutoff for the wave function in this work to 50 Ry and the convergence threshold for successive iteration as low as Ry. The electronic wave vectors in the Brillouin zone are sampled using the Monkhorst-Pack scheme [35] with quite dense and -point grids for the bulk and monolayer GeTe, respectively. We employ the optimized norm-conserving Vanderbilt (ONCV) pseudopotentials [36,37] along with the generalized gradient approximation (GGA) [38] for the exchange-correlation energy functionals. We show later in Section 3.1 that such a choice of pseudopotentials and functionals can already approach experimental band gaps of bulk and monolayer GeTe [9,25]. For complementary information, we also checked the bandgap calculation using the commonly used Heyd-Scuseria-Ernzerhof (HSE) hybrid functional [39].
2.2. Optical Coefficients
The Quantum ESPRESSO package natively supports the less expensive (yet also less accurate) calculation of complex dielectric function, , within the independent particle and dipole approximation [40]. The calculation outputs are the real part and imaginary part of the dielectric function, where is the photon frequency. With the calculated results of and , the absorption coefficient can be obtained using the following formula [41]:
where c is the speed of light in vacuum. The absorption coefficient is generally direction dependent, and it can be expressed in terms of a second rank tensor, . In this work, we consider linearly polarized light with polarization direction along each axis of Cartesian coordinates, so that only the diagonal matrix elements (index , , and for the x-, y-, and z-axes, respectively) are discussed in Section 3.2.
It is worth noting that a more accurate (and computationally costly) approach to the optical spectra calculation is the GW method, which takes into account the electron-hole interaction [42]. However, since we are interested in the qualitative comparison between optical spectra of the bulk and monolayer GeTe to judge their possible absorption performance, it is sufficient to consider the independent particle and dipole approximation. For GeTe, the relative absorption coefficients calculated using this approach should not be much different from that calculated with the GW method [22].
2.3. Thermoelectric Transport Coefficients
Within the Boltzmann transport theory and constant relaxation time approximation, we can calculate the Seebeck coefficient S, electrical conductivity , and electronic part of thermal conductivity using the following formulas [28,29]:
and
where e is the fundamental electron charge, is the Fermi–Dirac distribution function, is the Fermi energy, and T is the absolute temperature. In Equations (2)–(4), is known as the thermoelectric integral related to the transport distribution function [27]. The integral is expressed as:
where is the DOS and is the relaxation time constant. The integration was performed numerically by considering that the energy dispersion E is a function of discrete electronic wave vectors from the DFT calculation. Moreover, in the above formulation, for simplicity, we already averaged the transport coefficients so that we no longer deal with the direction-dependent indices in the tensorial forms as in the case of absorption coefficient. In other words, the above formulation is equivalent to calculating one third of each trace of S, , and tensors. We noticed that GeTe may possess small anisotropic transport features [9,21,22], where a particular transport axis gives slightly larger coefficients than the others; however, we preferred to focus our attention to the average comparison of the thermoelectric properties of bulk and monolayer GeTe at certain temperatures to identify which form of GeTe has the best thermoelectric performance.
3. Results and Discussion
In this section, we firstly discuss the electronic band structures of bulk and monolayer GeTe by highlighting two approaches: the ONCV-GGA [36,37] and HSE [39] methods for the band gap calculations. We find that the use of ONCV pseudopotentials with GGA functionals already reasonably describes the experimental band gaps of GeTe. Therefore, we take the resulted energy dispersion and wave function data from the ONCV-GGA method as the main ingredient to obtain the optical and thermoelectric properties of GeTe.
3.1. Electronic Band Structures
We show the electronic band structures of bulk and monolayer GeTe in Figure 2 within the ONCV-GGA method. The energy dispersion is plotted along selected high-symmetry points in the Brillouin zone of each GeTe phase. All the phases exhibit semiconducting properties as indicated by the band gap values in Table 2.
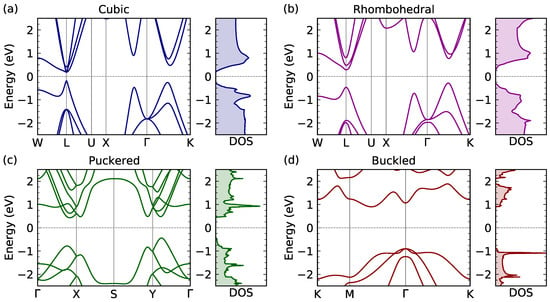
Figure 2.
Energy dispersion and density of states (DOS) of (a) bulk cubic, (b) bulk rhombohedral, (c) puckered monolayer, and (d) buckled monolayer GeTe. The DOS is expressed in arbitrary units for clarity since we do not need the details of the number of states per energy.

Table 2.
Calculated band gaps of bulk (cubic and rhombohedral) and monolayer (puckered and buckled) GeTe using the ONCV-GGA and HSE methods.
According to Figure 2a and Table 2 (within the ONCV-GGA method), we can see that cubic GeTe possesses a direct gap of about eV at the L point, while rhombohedral GeTe in Figure 1b is an indirect-gap semiconductor with a band gap of about eV and the valence band maximum located along the –M path. There have been various reports on the electronic properties of bulk GeTe [4,6,9,20,43,44,45], but the gaps calculated with the ONCV-GGA method reasonably agree with the literature values, which are about – eV for the cubic phase and of about – eV for the rhombohedral phase. It should be noted that bulk GeTe is well known as a phase-changing material with the transition temperature of about 700 K [6,9,10,19], below (above) which bulk GeTe assumes the rhombohedral (cubic) phase. Therefore, in Section 3.3, when discussing the thermoelectric performance, we will set temperatures below and above the transition temperature for the relevant phases of GeTe.
In the case of monolayer GeTe, as shown in Figure 2a,c, the puckered and buckled honeycomb lattices have different features of band structures. The puckered monolayer GeTe is characterized by about four conduction band minima along the –X–S–Y– path with very small energy difference among them and one valence band maximum on the Y– path. Accordingly, we carefully consider the puckered monolayer GeTe as an indirect- or a quasidirect-gap semiconductor with gap of eV, in good agreement with a previous study by the optPBE-vdW method, which is a kind of GGA variation [19]. Our calculations also suggest that buckled monolayer GeTe is an indirect-gap semiconductor with band gap of about eV, which is consistent with prior studies when they do not include the HSE correction [20,24,33,34]. The indirect gap for the buckled GeTe is due to the valence band maximum at the point and the conduction band minimum along the –M path. We also observe significant changes in the DOS from the bulk phases to the monolayers, in which typical 2D van Hove singularities emerge in the conduction band of puckered GeTe and valence band of buckled GeTe. In contrast to bulk GeTe, the experimental measurements for the band gaps of monolayer GeTe are still scarce. To date, we only found an experimental work by Zhang et al. [25] in 2020. Through X-ray photoelectron spectroscopy, they observed the band gap of buckled GeTe in the range of – eV and suggested the monolayer GeTe to be in the form of buckled lattice.
As shown in Table 2, we also found that the HSE method, which is actually intended to correct the exchange-correlation term [39], highly overestimates the band gaps of GeTe in all forms, whether bulk or monolayer. Although the use of the HSE method has recently become a trend in many papers of first-principles calculations, especially for obtaining optical spectra, we discourage its usage for the GeTe simulation. Unfortunately, some earlier first-principles studies on monolayer GeTe already used the HSE method for investigating the optical properties of buckled GeTe (e.g., Reference [24] in 2018) and for the thermoelectric properties of puckered GeTe (e.g., Reference [21] in 2020). Our present work takes this opportunity to emphasize that not all band gap values should be “corrected” by the HSE method if the calculated values by a less expensive method already reproduce the experimental data.
3.2. Absorption Spectra
In Figure 3, we show the absorption coefficients calculated using Equation (1). Although not so obvious from Figure 3a–c, we confirm that cubic GeTe is isotropic with . On the other hand, rhombohedral GeTe is anistropic with . This result is consistent with an earlier simulation by Singh [6] for optical properties of bulk cubic and rhombohedral GeTe. Both of Singh’s and present works indicate that bulk cubic GeTe is an excellent near-infrared light absorber, as is clear from the presence of a strong peak below eV, which is the lower boundary of the visible-light regime. On the other hand, reducing the symmetry to the rhombohedral phase at lower temperatures makes bulk GeTe better at absorbing higher-frequency light.
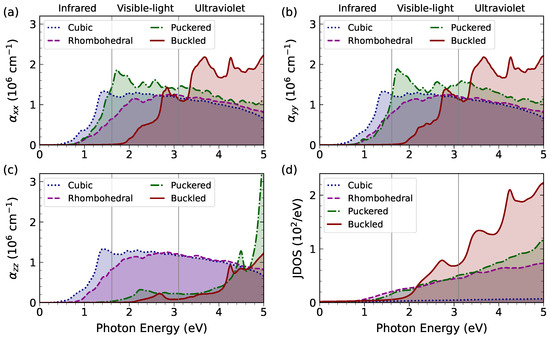
Figure 3.
Optical properties of bulk and monolayer GeTe. Panels (a–c) give the absorption coefficients for light polarization along the x-, y-, and z-axes. Panel (d) shows the joint density of states. Two vertical lines at eV and are the borders of the visible-light regime. Below eV (above eV) is the infrared (ultraviolet) regime.
In the present work, what is interesting is that when we transform GeTe to the monolayer phases, we observe multiple distinct peaks for puckered GeTe in the frequency range of visible light and for buckled GeTe in the frequency range of ultraviolet light. The values of absorption coefficients themselves are not much different, keeping the orders of magnitude as high as 106 cm−1, which is better than most of low-dimensional solar-cell materials for the visible light [46]. However, it is clear that either puckered or buckled GeTe has stronger absorption coefficient peaks than their bulk counterparts. We notice that, within the same approximation, the monolayer GeTe has better absorption than the celebrated monolayer transition metal dichalcogenides [47] in the visible-light regime by almost one order of magnitude. The monolayer phases also exhibit moderate anisotropy in absorption coefficients for the in-plane polarization direction. Regardless, in the near-infrared to the ultraviolet regime, the absorption coefficients for all of the GeTe variants in all directions of the linearly polarized light stay within 1–2 × 106 cm−1. Comparing the joint DOS in Figure 3d with the absorption coefficients, it is interesting to see that only in buckled GeTe, the JDOS contributes strongly to the absorption coefficient in the visible-light regime. This feature can be traced back to the presence of stronger van Hove singularity in buckled GeTe than in the puckered GeTe, while the bulk GeTe phases do not possess any van Hove singularity.
3.3. Thermoelectric Properties
Before discussing the thermoelectric transport coefficients of bulk and monolayer GeTe, we briefly explain the assessment of the performance of a thermoelectric material. The thermoelectric performance is usually assessed by two indicators: (1) power factor (PF), which is related to how much power the material outputs, and (2) dimensionless figure of merit (), which is related to the efficiency of thermoelectric energy conversion. The formulas for PF and are
and
where is the total thermal conductivity containing the electronic part and lattice part (originating from collective atomic motions known as phonons). According to Equations (2) and (3), with the help of Equation (5), we can scale both S and by the relaxation time constant . The choice of thus strongly determines the value of PF. Some researchers often deliberately set a “magic” s to justify that power factor of a material being larger or smaller than the others, but such an approach is actually too rough. We cannot evaluate PF properly unless we know the correct value of , which is usually obtained from electrical transport measurements. When we insist on discussing the overall performance of the thermoelectric performance without the knowledge of , it is better to omit the lattice thermal conductivity, i.e., , and define the most ideal that only contains the electronic thermal conductivity as follows:
In Figure 4, we show the thermoelectric transport coefficients along with of bulk and monolayer GeTe. By considering that in bulk GeTe we have a phase transition at around 700 K between the cubic and rhombohedral phases, we decided to use two different temperature values for evaluating the thermoelectric coefficients and performance. Since the cubic (rhombohedral) phase is stable above (below) the transition temperature [9,10], we set the evaluation temperature slightly far from 700 K. We conjecture that monolayer GeTe may also have such a phase transition. In this case, the buckled monolayer is expected to be present at higher temperature than the pucked monolayer due to the nature of the hexagonal lattice. Therefore, we set K for cubic GeTe and buckled GeTe, while for rhombohedral GeTe and puckered GeTe, we set K.
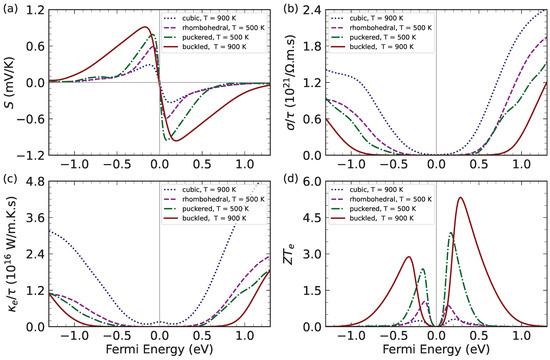
Figure 4.
Thermoelectric properties of bulk and monolayer GeTe calculated from band structure information: (a) Seebeck coefficient, (b) electrical conductivity, (c) electronic thermal conductivity, and (d) ideal figure of merit. Note that the electrical conductivity and electronic thermal conductivity are scaled by relaxation time constant . Considering a possible phase transition at K, we set two different values of temperature: K for bulk cubic and monolayer buckled GeTe; and K for bulk rhombohedral and monolayer puckered GeTe.
With the above consideration, we can compare thermoelectric properties of bulk GeTe and monolayer GeTe one by one according to the temperature groups. As shown in Figure 4a, at 900 K, the maximum Seebeck coefficient of bulk cubic GeTe is about mV/K, while the maximum Seebeck coefficient of the the puckered GeTe monolayer is about mV/K. Since the Seebeck coefficient is roughly proportional to the band gap, the huge increase in the maximum Seebeck coefficient from bulk cubic to puckered monolayer is expected for the increase in the band gap from to eV. We obtain a similar behavior for the comparison between Seebeck coefficients of the bulk rhombohedral and puckered monolayer at 500 K. The difference in Seebeck coefficients is now smaller because of the smaller difference between the rhombohedral gap ( eV) and puckered gap ( eV), as previously given in Table 2.
Next, in Figure 4b,c, we show the calculated results of electrical conductivity and electronic thermal conductivity, both of which are scaled by . Now, we see that the smaller gap materials generally have larger conductivities. Therefore, we can expect the peaks of to appear, as shown in Figure 4d, due to the trade off between the Seebeck coefficient and both electrical and (electronic) thermal conductivities. However, the tendency of the increase in as we increase the band gap (from bulk cubic to buckled monolayer) is similar to the increase in the Seebeck coefficient because we can see in Figure 2 for the energy dispersion relations that there are several conduction band minima and valence band maxima at different points that can contribute to the thermoelectric transport. This kind of “semidegenerate” bands are known as the phenomenon of band convergence, which is often beneficial for thermoelectrics [48,49]. Bulk GeTe, especially in the rhombohedral phase, has already been famous for possessing the band convergence [9,10], but probably almost none of the literature mention this possibility as the origin of the excellent thermoelectric performance of monolayer GeTe. In other words, the band convergence can still persist in monolayer GeTe.
It should also be noted that the GeTe monolayers (both puckered and buckled forms) have a larger maximum in the n-type doping area (more positive Fermi energy) than in the p-type regime (more negative Fermi energy), while the situations in bulk GeTe, especially in rhombohedral phase, are opposite. Again, the phenomena are related to the band convergence, whether it is more prominent in the valence bands or in the conduction bands. The buckled GeTe monolayer interestingly has the largest among others GeTe phases with the maximum of about in the n-type regime. To our knowledge, this striking thermoelectric performance of buckled GeTe monolayer is not yet reported in the literature. Although buckled GeTe is a realistic GeTe monolayer that has already been synthesized experimentally [25], another theoretical work calculated the thermoelectric properties of puckered GeTe instead [21]. Interestingly, Reference [21] seems to use the “full power” of Boltzmann transport theory to obtain not only the electronic structure-dependent thermoelectric properties but also the lattice thermal conductivity of a puckered GeTe monolayer. At K for puckered GeTe, Reference [21] reported the maximum (not ) of about , while the maximum (not ) at the same temperature from our calculation is about . We can thus use the the ratio of to the of the puckered GeTe monolayer to estimate the realistic maximum of the buckled GeTe monolayer as
which is very excellent for the high-temperature 2D thermoelectrics.
Furthermore, we can attribute the enhancement of ZT in the GeTe monolayers to the quantum confinement effect [50], especially by analyzing the confinement length L (of 2D materials) relative to the so-called thermal wavelength (of the bulk materials) [51]. The thermal wavelength is expressed as
where ℏ is the reduced Planck’s constant, is the Boltzmann’s constant, and is the effective mass around the band maxima or minima. Calculated using the available data of effective mass [9], we obtain of rhombohedral GeTe in the range of – nm, while of cubic GeTe in the range of – nm. The thicknesses, which correspond to L, of both puckered GeTe ( Å) and buckled GeTe ( Å) are already from one to two orders of magnitudes smaller than the thermal wavelength. Therefore, the strong enhancement in for the GeTe monolayers is well anticipated.
4. Conclusions
GeTe in the forms of cubic (bulk), rhombohedral (bulk), puckered (monolayer), and buckled (monolayer) lattices overall exhibits excellent absorption and thermoelectric performance. For the photon frequency in the near-infrared to the ultraviolet regime, the absorption coefficients for all directions of the linearly polarized light stay within 1–2 × 106 cm−1, which is better than the absorption in most solar-cell materials. The absorption coefficients for the in-plane direction of the GeTe monolayers, in particular, have larger values than those of the bulk GeTe phases. As for thermoelectric properties, the GeTe monolayers also give better performance than their bulk counterparts with theoretically due to the survival of the band convergence, larger band gaps (for larger Seebeck coefficients), and quantum confinement effect, which gives a unique DOS for providing more available states of electronic conduction.
Author Contributions
Conceptualization, S.A.W. and A.R.T.N.; methodology, S.A.W. and A.R.T.N.; validation, W.V.S., S.A.W., F.S.A. and N.T.H.; investigation, W.V.S. and S.A.W.; data curation, W.V.S. and S.A.W.; writing—original draft preparation, W.V.S. and A.R.T.N.; writing—review and editing, S.A.W., F.S.A., N.T.H. and A.R.T.N.; visualization, W.V.S., S.A.W. and A.R.T.N.; supervision, F.S.A. and A.R.T.N.; project administration, N.T.H. and A.R.T.N. All authors have read and agreed to the published version of the manuscript.
Funding
N.T.H. acknowledges JSPS KAKENHI Grant No. JP20K15178.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data files for this work are available publicly at the GitHub account of the corresponding author: https://github.com/artnugraha/GermaniumTellurides accessed on 24 September 2021.
Acknowledgments
W.V.S., S.A.W., and A.R.T.N. acknowledge Mahameru HPC for their high-performance computing facilities.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hamakawa, Y. Solar PV energy conversion and the 21st century’s civilization. Sol. Energy Mater. Sol. Cells 2002, 74, 13–23. [Google Scholar] [CrossRef]
- Becquerel, E. Memoire sur les effects electriques produits sous I’influence des rayons solaires. Comptes Rendus 1839, 9, 561–567. [Google Scholar]
- Seebeck, T.J. Magnetische Polarisation der Metalle und Erze Durch Temperatur-Differenz; Abhandlungen der Königlichen Akademie der Wissenschaften: Berlin, Germany, 1825; pp. 265–373. [Google Scholar]
- Lewis, J.E. Optical properties and energy gap of GeTe from reflectance studies. Phys. Status Solidi B 1973, 59, 367–377. [Google Scholar] [CrossRef]
- Chattopadhyay, T.; Boucherle, J.X.; vonSchnering, H.G. Neutron diffraction study on the structural phase transition in GeTe. J. Phys. C 1987, 20, 1431. [Google Scholar] [CrossRef]
- Singh, D.J. Optical properties of cubic and rhombohedral GeTe. J. Appl. Phys. 2013, 113, 203101. [Google Scholar] [CrossRef] [Green Version]
- Wuttig, M.; Yamada, N. Phase-change materials for rewriteable data storage. Nat. Mater. 2007, 6, 824–832. [Google Scholar] [CrossRef]
- Raoux, S. Phase Change Materials. Annu. Rev. Mater. Sci. 2009, 39, 25–48. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.; Zhang, X.; Sun, Y.; Yang, J.; Pei, Y. Electronic origin of the high thermoelectric performance of GeTe among the p-type group IV monotellurides. NPG Asia Mater. 2017, 9, e353. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhang, X.; Chen, Z.; Lin, S.; Li, W.; Shen, J.; Witting, I.T.; Faghaninia, A.; Chen, Y.; Jain, A.; et al. Low-Symmetry Rhombohedral GeTe Thermoelectrics. Joule 2018, 2, 976–987. [Google Scholar] [CrossRef]
- Feynman, R.P. There’s plenty of room at the bottom. Eng. Sci. Caltech Mag. 1960, 25, 22–36. [Google Scholar]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, Z.; Zhang, Y.; Morozov, S.V.; Stormer, H.L.; Zeitler, U.; Maan, J.C.; Boebinger, G.S.; Kim, P.; Geim, A.K. Room-temperature quantum Hall effect in graphene. Science 2007, 315, 1379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An unexplored 2D semiconductor with a high hole mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bandurin, D.A.; Tyurnina, A.V.; Yu, G.L.; Mishchenko, A.; Zólyomi, V.; Morozov, S.V.; Kumar, R.K.; Gorbachev, R.V.; Kudrynskyi, Z.R.; Pezzini, S.; et al. High electron mobility, quantum Hall effect and anomalous optical response in atomically thin InSe. Nat. Nanotechnol. 2017, 12, 223–227. [Google Scholar] [CrossRef]
- Wdowik, U.D.; Parlinski, K.; Rols, S.; Chatterji, T. Soft-phonon mediated structural phase transition in GeTe. Phys. Rev. B 2014, 89, 224306. [Google Scholar] [CrossRef]
- Wan, W.; Liu, C.; Xiao, W.; Yao, Y. Promising ferroelectricity in 2D group IV tellurides: A first-principles study. Appl. Phys. Lett. 2017, 111, 132904. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Zhao, F.; Long, P.; Wang, Y.; Yue, Y.; Liu, X.; Feng, Y.; Li, R.; Hu, W.; Li, Y.; et al. Sonication-assisted liquid-phase exfoliated α-GeTe: A two-dimensional material with high Fe3+ sensitivity. Nanoscale 2018, 10, 15989–15997. [Google Scholar] [CrossRef]
- Zhang, D.; Hu, S.; Sun, Y.; Liu, X.; Wang, H.; Wang, H.; Chen, Y.; Ni, Y. XTe (X = Ge, Sn, Pb) monolayers: Promising thermoelectric materials with ultralow lattice thermal conductivity and high-power factor. ES Energy Environ. 2020, 10, 59–65. [Google Scholar]
- Wang, Q.; Wu, L.; Urban, A.; Cao, H.; Lu, P. Anisotropic to Isotropic Transition in Monolayer Group-IV Tellurides. Materials 2021, 14, 4495. [Google Scholar] [CrossRef]
- Ge, G.; Zhang, Y.; Yan, H.; Yang, J.; Zhou, L.; Sui, X. Complexly electronic structure induced largely tunable anisotropic mobility for monolayer GeTe by uniaxial strain. Appl. Surf. Sci. 2021, 538, 148009. [Google Scholar] [CrossRef]
- Qiao, M.; Chen, Y.; Wang, Y.; Li, Y. The germanium telluride monolayer: A two dimensional semiconductor with high carrier mobility for photocatalytic water splitting. J. Mater. Chem. A 2018, 6, 4119–4125. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, F.; Wang, Y.; Liang, X.; Zhang, Z.; Feng, Y.; Li, Y.; Tang, L.; Feng, W. Two-Dimensional GeTe: Air Stability and Photocatalytic Performance for Hydrogen Evolution. ACS Appl. Mater. Interfaces 2020, 12, 37108–37115. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer: Berlin, Germay, 2010. [Google Scholar]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef] [Green Version]
- Madsen, G.K.H.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef] [Green Version]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Jeong, K.; Park, S.; Park, D.; Ahn, M.; Han, J.; Yang, W.; Jeong, H.S.; Cho, M.H. Evolution of crystal structures in GeTe during phase transition. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Nonaka, T.; Ohbayashi, G.; Toriumi, Y.; Mori, Y.; Hashimoto, H. Crystal structure of GeTe and Ge2Sb2Te5 meta-stable phase. Thin Solid Film. 2000, 370, 258–261. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, Z.; Wang, H.; Yang, Z.; Liu, C. Tunable Electric Properties of Bilayer α-GeTe with Different Interlayer Distances and External Electric Fields. Nanoscale Res. Lett. 2018, 13, 400. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, K.H.; Mao, J.; Zhao, M.; Liu, Z.; Liu, F. Prediction of intrinsic topological superconductivity in Mn-doped GeTe monolayer from first-principles. Npj Comput. Mater. 2021, 7, 44. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef] [Green Version]
- Schlipf, M.; Gygi, F. Optimization algorithm for the generation of ONCV pseudopotentials. Comput. Phys. Commun. 2015, 196, 36–44. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- Giustino, F. Materials Modelling Using Density Functional Theory: Properties and Predictions; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Dresselhaus, M.; Dresselhaus, G.; Cronin, S.B.; Souza Filho, A.G. Solid State Properties; Springer: Berlin, Germany, 2018. [Google Scholar]
- Aryasetiawan, F.; Gunnarsson, O. The GW method. Rep. Prog. Phys. 1998, 61, 237. [Google Scholar] [CrossRef] [Green Version]
- Tung, Y.W.; Cohen, M.L. Relativistic band structure and electronic properties of SnTe, GeTe, and PbTe. Phys. Rev. 1969, 180, 823. [Google Scholar] [CrossRef]
- Korzhuev, M.A. On the fundamental energy gap in GeTe. Phys. Status Solidi B 1982, 112, K39–K41. [Google Scholar] [CrossRef]
- Okoye, C.M.I. Electronic and optical properties of SnTe and GeTe. J. Phys. Condens. Matter 2002, 14, 8625. [Google Scholar] [CrossRef]
- Kim, M.R.; Ma, D. Quantum-dot-based solar cells: Recent advances, strategies, and challenges. J. Phys. Chem. Lett. 2015, 6, 85–99. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, M.; Palummo, M.; Grossman, J.C. Extraordinary sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials. Nano Lett. 2013, 13, 3664–3670. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Tan, X.; Yin, K.; Liu, H.; Tang, X.; Shi, J.; Zhang, Q.; Uher, C. Convergence of Conduction Bands as a Means of Enhancing Thermoelectric Performance of n-Type Mg2Si1−xSnx Solid Solutions. Phys. Rev. Lett. 2012, 108, 166601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, Y.; Gibbs, Z.M.; Agapito, L.A.; Li, G.; Kim, H.S.; Nardelli, M.B.; Curtarolo, S.; Snyder, G.J. Convergence of multi-valley bands as the electronic origin of high thermoelectric performance in CoSb3 skutterudites. Nat. Mater. 2015, 14, 1223–1228. [Google Scholar] [CrossRef] [PubMed]
- Hicks, L.D.; Dresselhaus, M.S. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 1993, 47, 12727. [Google Scholar] [CrossRef]
- Hung, N.T.; Hasdeo, E.H.; Nugraha, A.R.T.; Dresselhaus, M.S.; Saito, R. Quantum Effects in the Thermoelectric Power Factor of Low-Dimensional Semiconductors. Phys. Rev. Lett. 2016, 117, 036602. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).