Abstract
In this paper we investigate the temperature dependent behavior of a liquid crystal (LC) loaded tunable dielectric image guide (DIG) phase shifter at millimeter-wave frequencies from 80 to 110 for future high data rate communications. The adhesive, necessary for precise fabrication, is analyzed before temperature dependent behavior of the component is shown, using the nematic LC-mixture GT7-29001. The temperature characterization is conducted by changing the temperature of the LC DIG’s ground plane between and 80 . The orientation of the LC molecules, and therefore the effective macroscopic relative permittivity of the DIG, is changed by inserting the temperature setup in a fixture with rotatable magnets. Temperature independent matching can be observed, while the insertion loss gradually increases with temperature for both highest and lowest permittivity of the LC. At 80 the insertion loss is up to higher and at it is lower than the insertion loss present at 20 . In addition, the achievable differential phase is reduced with increasing temperature. The impact of molecule alignment to this reduction is shown for the phase shifter and an estimated 85% of the anisotropy is still usable with an LC DIG phase shifter when increasing the temperature from 20 to 80 . Higher reduction of differential phase is present at higher frequencies as the electrical length of the phase shifter increases. A maximum difference in differential phase of 72 is present at 110 , when increasing the temperature from 20 to 80 . Nevertheless, a well predictable, quasi-linear behavior can be observed at the covered temperature range, highlighting the potential of LC-based dielectric components at millimeter wave frequencies.
1. Introduction
In addition to their well known application in displays, liquid crystals (LCs) are of special interest in the millimeter-wave (mmW) regime between 30 GHz and 300 GHz. Due to the dielectric anisotropy , different relative permittivities of an LC volume can be achieved when changing the orientation of the nematic rod-like LC molecules with respect to the RF-polarization . If the long molecule axis is parallel to a high permittivity can be achieved, while the long molecule axis perpendicular to results in a lower permittivity . The overall direction the LC molecules point towards is described by the LC director. Its orientation can be controlled by external electric or magnetic bias fields which force the molecules to align parallel to the field lines. This concept is visualized in Figure 1. The LC-mixtures usually are different than the conventional LC-mixtures used for display applications, such as K15 or E7 mixtures, in order to achieve higher in the mmW regime. In [1], a detailed summary of different LC-mixtures for micro- and millimeter-wave frequencies is provided. Further development of new mixtures for mmW applications is an ongoing process and promising stable material properties from microwave frequencies up to several THz have been confirmed [2,3,4]. New physical mechanisms, such as the recently reported splay polar nematic phase [5,6], underline the necessity to gather data on LC such that reliable and predictable LC-based mmW components can be employed in the future. In addition, temperature dependent degradation of the achievable order, which is commonly represented by the order parameter S, is expected to effect the reconfigurable LC loaded devices. As higher temperature leads to less order in the LC volume, the extend of this effect needs to be quantified in the individual components.
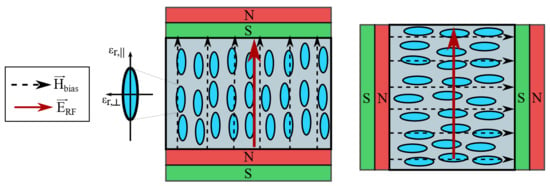
Figure 1.
Bias of a volume of liquid crystal (LC) with magnets. The LC molecules are represented as rod-like forms, showing a long and a short axis. Depending on the molecules’ orientation with respect to the LC volume shows different macroscopic permittivity, (left) or (right), to an electromagnetic wave.
The LC mixture used in this work is GT7-29001 from Merck KGaA, Darmstadt, Germany. A broad spectrum of LC-based components, such as filters [7,8], phase shifters and antennas [9,10,11] in different topologies and at various frequencies has been presented. Especially phase shifters are key components for phase correction or phase manipulation in phased-array applications. As the demand for higher data rate is an ongoing trend [12], mmW frequencies will be increasingly used in future communication standards. Usable spectra for communication bands have been investigated in V-band (50 GHz to 75 GHz) [13] and W-band (75 GHz to 110 GHz) [14]. At frequencies towards 100 GHz, conventional waveguide topologies, such as microstrip lines, show high loss. Therefore, different dielectric waveguide-based approaches have been proposed in recent years [11]. As many of the proposed topologies are hard to integrate to common printed circuit board (PCB)-based circuitry, the dielectric image guide (DIG) poses an attractive link between the low-loss dielectric topology and the planar environment of PCBs. First insights to electrically tunable LC loaded DIG phase shifters are presented in [15,16]. However, precise fabrication proved to be a problem, as an air gap between the DIG and its ground plane degraded the achievable maximum differential phase shift [15]. For proper operation and the temperature characterization in this manuscript, a defined contact between DIG and its ground plane is crucial. The air gap can be eliminated by using a thin layer of glue between metallic ground and DIG. Data of the glue have to be acquired first before conducting the temperature characterization. With the DIG properly connected to its ground plane, a reliable temperature analysis of the LC loaded DIG can be conducted and hence more insight on the potential of LC-based DIG components can be gained.
In this paper, we introduce the waveguide topology of the DIG in Section 2 before providing data of the possible adhesives that can be used for avoiding an air gap in the temperature measurement setup. Section 3 introduces the setup for the temperature dependent characterization of the LC phase shifter. The measurement results are presented in Section 3.2, followed by a discussion and final remarks in Section 4.
2. Waveguide Topology and Microwave Characterization of Adhesives
In this section, the basic waveguide topology is shortly revised before the setup for glue characterization is introduced. The most suitable glue is chosen to be used in the temperature characterization setup based on the obtained results.
2.1. Dielectric Image Guide Topology for LC-Based Components
Dielectric image guides (DIGs) have been proposed for mmW circuits starting in the 1950s, and continued to be of interest during the following decades [17,18,19]. However, since the need for high data rate communications was not as demanding at that time as it is today, DIGs were not further investigated. In recent years, however, DIGs have been in renewed focus of research [20,21,22]. Figure 2 depicts the cross section of an LC-based DIG compared to an LC-based fully dielectric waveguide. The effective permittivity of the waveguides changes if the LC molecule orientation with respect to the RF-polarization () changes. Hence, by controlling the permittivity, a phase shift of the propagating RF wave can be achieved in a continuous manner by changing the orientation between LC molecules and accordingly. Dielectric structures can show low loss even at higher frequencies, as parts of the propagating wave are present as evanescent field components outside the dielectric waveguide. The height of the fully dielectric guide can be effectively reduced by a factor of two by introducing a metallic image plane, which results in mechanical stability and faster response time of the DIG phase shifter when compared to its fully dielectric counterpart [15]. In its fundamental mode of operation, the -mode, is perpendicular to the ground plane. Therefore, when considering practical applications, the contact between image guide and ground has to be ensured for predictable operation of the image guide. In [15], the disturbing effect of this air gap in a first demonstrator of an LC-based DIG phase shifter is stated. It has to be eliminated when aiming for a proper temperature characterization of the component. Since the DIG used in this paper is mechanically fabricated from Rexolite, which has a relative permittivity of and a loss tangent of at 95 [23], a glue with similar permittivity and low loss should be used to adhere the DIG to the ground plane.
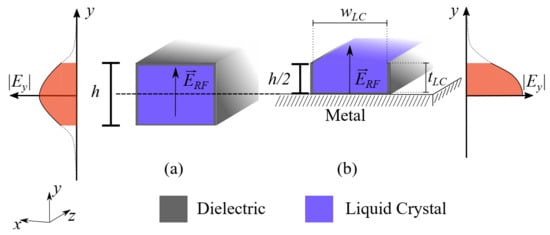
Figure 2.
Waveguide topology and qualitative representation of the E-field distribution of a fully dielectric guide with an LC cavity (a) and its corresponding dielectric image guide (DIG) with an LC trench (b). Field components inside the waveguide are highlighted in red, and evanescent field components are indicated by dashed lines.
2.2. Adhesive Selection
Characterization of adhesive is challenging since the adhesive has to cure before a solid form can be used for common characterization setups. Especially at frequencies towards 100 , the small dimensions can pose a non-negligible problem. We meet this problem by filling a WR10 waveguide shim of known thickness d with adhesive and let it cure inside the shim. The shim can then be inserted between two standard WR10 hollow waveguides. Therefore, as d is known, permittivity and loss can be extracted by measuring the insertion and return loss. In particular, we use the Nicholson–Ross–Weir (NRW) method [24,25], which has been successfully used for materials which have to cure [26]. Figure 3 depicts a schematic of the measurement principle as well as a photograph of the measurement setup. The shims are cut by a laser from Tombak and have a thickness of .
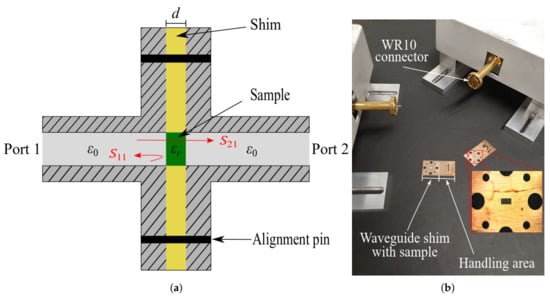
Figure 3.
Measurement principle of the transmit/reflect characterization by placing a sample of known thickness d inside the rectangular WR10 waveguide (a). The rectangular sample holders have a handling area and a sample area containing the necessary holes for alignment pins and the actual sample (b).
After filling and curing of the glue the shim is carefully cleaned using acetone and polished, such that a flat surface of the material is ensured. In total, five adhesives—Pattex Plastix superglue, UHU PLUS Sofortfest epoxy glue, Rexolilte Adhesive 12,517, Norland Optical Adhesive 81 and QuickStick 135 Temporary Mounting Wax—together with one reference material, Teflon, have been characterized. The obtained results regarding permittivity are depicted in Figure 4. In general, all characterized adhesives are in the range of the relative permittivity of Rexolite (), with epoxy glue being the most different in permittivity with a maximum difference of 0.7. Figure 5 shows a clear difference in loss tangent of the adhesives. It has to be stated that the NRW approach can only provide well reliable results for lossy materials due to its broadband nature. For precise measurement of loss, resonance methods should be used. Using the NRW approach, noise or small deviations in the measured can cause an increase or decrease in the extracted loss tangent and limits resolution [27,28]. Especially for low-loss materials (Teflon reference and Rexolite adhesive) higher loss than given in literature for Teflon and solid Rexolite is obtained [29]. The results shown in Figure 5 are therefore not a highly precise determination of the loss tangent of the adhesives, but an evaluation of the loss of the adhesives compared to each other and are included for the sake of completeness. With the obtained results of permittivity and loss tangent, the clear difference in adhesives indicates that Rexolite glue is most suitable for adhering the DIG to the metallic ground plane. However, it was found during measurements that Rexolite glue has low adhesion on metal. While in the following temperature measurement setup the glue is mostly necessary to eliminate a possible air gap, and additional mechanical support is applied by the setup itself, we advise to use the optical adhesive if strong mechanical stability is desired.
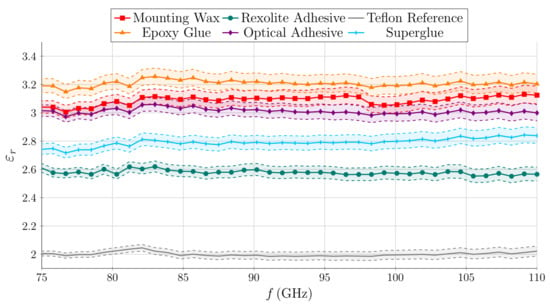
Figure 4.
Extracted relative permittivity of different adhesives using the Nicholson–Ross–Weir (NRW) method. The results include a margin of dashed lines around the extracted values, which represent a confidence interval when the samples show deviation from the desired sample thickness.
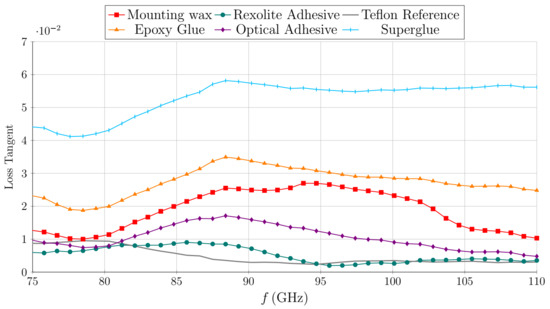
Figure 5.
Extracted and smoothed loss tangent of different adhesives using the NRW method.
3. Temperature Characterization
3.1. Measurement Setup
Figure 6 depicts a schematic of the LC-based DIG phase shifter. The DIG phase shifter consists of a DIG with width and height . A trench of length , width and depth for LC hosting is milled in the Rexolite DIG. The trench is tapered over a length of 3 at its beginning and end for matching the LC section to the Rexolite DIG. In order to measure the propagating and reflected wave components with lab equipment, a WR10 waveguide transition from WR10 waveguide to DIG and vice versa is necessary. The same transition as used in previous work [15] is utilized for the present setup.
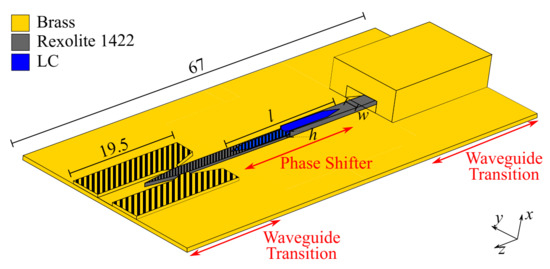
Figure 6.
Partially cut model of the phase shifter with waveguide transitions. All dimensions are given in mm.
Figure 7 shows the temperature characterization setup. A brass block forms the ground plane on which the DIG is placed. A Pt100 temperature sensor is inserted in the brass ground plane in order to monitor the temperature in the ground plane. Since the DIG phase shifter is directly placed on the ground plane, this is the best position for temperature reading without disturbing the propagating RF-wave. In order to heat or cool the ground plane, it is mounted on a copper block with fluidic channels connected to a Julabo FP50 temperature controller. With corresponding feedback from the temperature sensor a stable temperature in the ground plane is maintained by the Julabo FP50. The nematic LC used for the measurements is GT-7 29001, which shows a parallel permittivity of with an accompanied loss tangent of and a perpendicular permittivity of with an accompanied loss tangent of (data provided by Merck KGaA at 19 ). Hence, the anisotropy of the LC-mixture is . After filling the DIG structure and connecting the measurement equipment to the waveguide transitions, the temperature control setup (Figure 7a) is inserted into a fixture with rotatable magnets. The magnets provide a magnetic flux density of , such that both parallel and perpendicular permittivity of the LC-mixture can be stimulated (Figure 7b). The rotatable magnets are enclosed by a transparent plastic box. A steady flow of nitrogen in box prevents moist or frost on the structure. The overall temperature range from −10 to 80 is limited by the capabilities the Rexolite material, which starts to degrade at higher temperatures than 80 , and the warming of the fluid along its way from Julabo FP50 to the structure when cooling the device.

Figure 7.
The assembled temperature controlled measurement setup. The temperature control unit in (a) can be inserted into the fixture with rotatable magnets, as shown in (b).
3.2. Measurement Results
Figure 8, Figure 9 and Figure 10 show the obtained measurement results at different temperatures . Figure 8 illustrates the matching of the phase shifter. Matching with is achieved at all investigated frequencies. Only slight deviations in can be observed with temperature and no significant difference in behavior for parallel or perpendicular LC alignment with respect to the RF-polarization can be made.
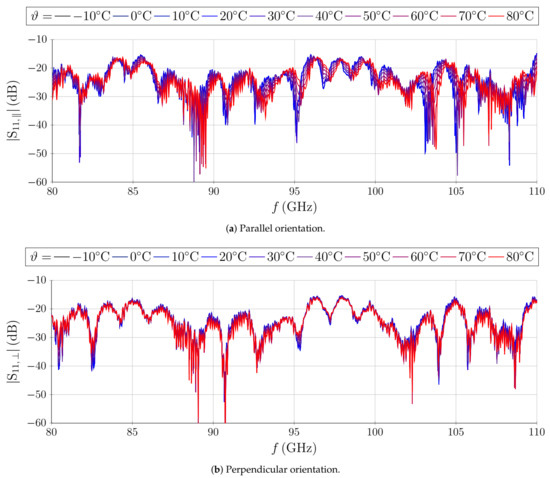
Figure 8.
of the phase shifter at different ground plane temperatures in (a) parallel and (b) perpendicular LC director orientation. No significant influence of change in temperature can be observed.
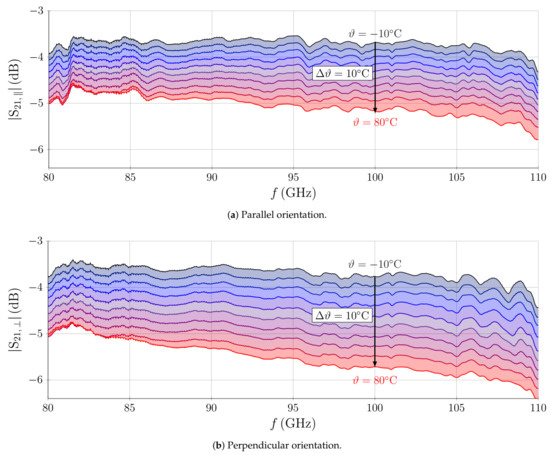
Figure 9.
of the phase shifter at different ground plane temperatures in (a) parallel and (b) perpendicular LC director orientation.
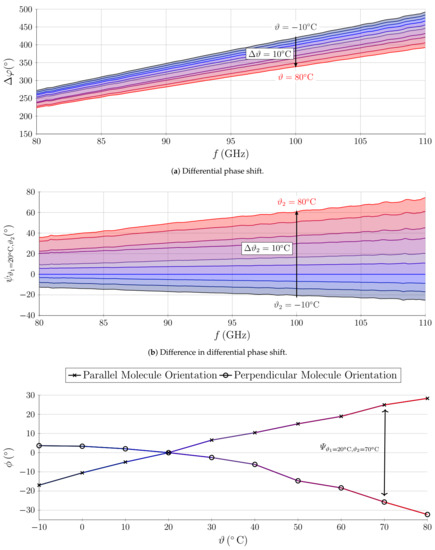
Figure 10.
Differential phase shift of the phase shifter in dependence of temperature (a), the difference in differential phase shift between operation at and (b) and the deviation in phase from the phase incident at depending on the LC molecule orientation at 100 (c).
In contrast, a clear trend in transmission behavior can be observed, as Figure 9 shows. A magnitude offset in the frequency characteristic of with temperature both in parallel and perpendicular LC orientation is noticed. This offset is almost constant across all frequencies. In the investigated temperature range, the maximum offset is ca. in parallel orientation and ca. in perpendicular orientation. A solid Rexolite DIG has been measured in the same setup in order to assess the influence on on the conductor loss of the ground plane. It was found that a temperature change from to influences the loss of the line itself by maximally . Hence an uncertainty of about is present per 10 temperature change in the graphs depicted in Figure 9. In total, the maximum increase in insertion loss by is defined by the perpendicular alignment at 100 when comparing the measurement at to the one at .
In general, the dielectric anisotropy of LC decreases with increasing temperature due to decreasing order of the LC molecules. Therefore, the differential phase shift
which arises when comparing the phase of the RF signal in low permittivity alignment to the phase in high permittivity alignment, is of special interest. The measured results are provided in Figure 10a. The differential phase increases with frequency, since the phase shifter is electrically longer for higher frequencies, and overall decreases with temperature. In particular, we observe that the frequency where shifts from to in the investigated temperature range. At the phase shift is achieved at . However, stable and predictable behavior of the GT7-29001 mixture in terms of achievable phase can be observed.
In general, a phase shifter is not intended to be used in the whole frequency range which our measurements cover, but in a more narrow frequency band. The margin in achievable differential phase depending on temperature at a certain frequency of operation is therefore a valuable information. We define
as the difference in differential phase shift between reference temperature and second temperature . Figure 10b depicts with respect to room temperature, hence . We observe that increases both with frequency and temperature . However, the frequency dependence changes strongly with . The slope of reveals how much the frequency dependent differential phase shift differs from the reference temperature .
While at the slope is , at the slope increases to . A total phase margin of 80 is present at 100 when covering temperatures from to 80 .
It is of particular interest to analyze to which extent the change of permittivity is dependent on molecule alignment. In order to do so we compare the raw measurement phase of at different temperatures to the phase of at for both alignment states of the LC molecules. We note the deviation from the reference phase at by
The corresponding behavior at 100 is depicted in Figure 10c. We observe a clear difference in change of phase between both molecule alignments. The parallel orientation, responsible for high permittivity, shows a clear quasi-linear temperature dependence. The phase change is close to / at all temperatures. The overall phase decreases with temperature, since decreases with increasing temperature. The perpendicular orientation, responsible for low permittivity, is less affected by temperature change below and starts to get more temperature dependent at . While small slopes can be observed for , the slope increases to up to at . Here, increases with temperature. The change to lower permittivity in parallel alignment and to higher permittivity in perpendicular alignment causes the total difference in phase shift , as indicated in Figure 10c. From the acquired data displayed in Figure 10, the achievable anisotropy at 100 can be evaluated by a CST Microwave Studio simulation model of the phase shifter. The model is created according to Figure 7a and the permittivity of the LC section is changed such that the measured phase change is reached.
When adapting the simulation model to the measurement data at 100 , is first reduced at before the is reduced as well, in order to take the behavior given in Figure 10c into account. At , the fitted values match to and (provided values at 19 by Merck KGaA at room temperature). When increasing the temperature to , the high permittivity has to be reduced to (deviation of 2%) while the low permittivity remains at . Hence, we observe at room temperature and 100 that the full anisotropy of the LC () cannot be utilized and we are facing utilizable anisotropy of . This corresponds to a deviation of 6.5% between theoretically present anisotropy and realizable anisotropy. At , both high permittivity is further reduced to and low permittivity is increased to in order to match to the measured phase shift at 100 . This corresponds to a 2% change in and a 5% change in . The utilizable anisotropy, , reduces further to 79.4% of the value provided at 19 at room temperature. The corresponding deviation to the utilizable anisotropy at room temperature at 100 is 85%. Hence, a high realizable anisotropy is still present when utilized in a temperature varying scenario.
In order to evaluate the phase shifter in its performance, the figure-of-merit (FoM) is provided with respect to the temperature of the ground plane. The FoM is defined by the relation of maximum achievable phase shift and maximum insertion loss:
The FoM with respect to temperature is depicted in Figure 11a. Since both and degrade with temperature, the overall FoM degrades as well according to Equation (4). The maximum FoM of / at 109 and is reduced to / at . The difference in FoM is depicted in Figure 11b. We can observe that the FoM degrades by / to 8/ per 10 temperature increase.
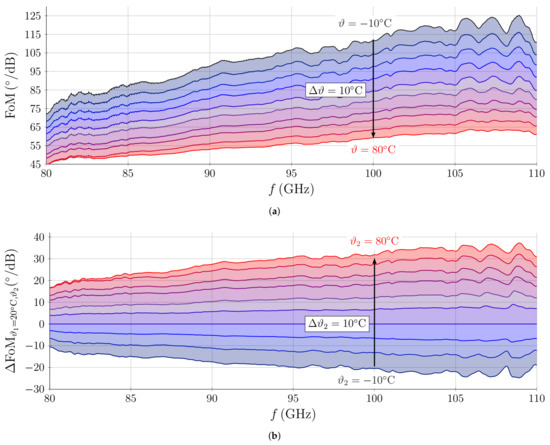
Figure 11.
Figure-of-merit (FoM) (a) and difference in FoM (b) of the magnetically biased LC DIG phase shifter in dependence of temperature.
4. Conclusions
This paper provides temperature dependent data of an LC-based dielectric image guide (DIG) phase shifter. By selecting a suitable adhesive using the broadband Nicholson–Ross–Weir method, an air gap is prevented and a defined measurement environment is created. The elimination of the air gap results in higher differential phase shift when compared to previous work [15]. The temperature dependent data are generated by changing the temperature of the DIG’s ground plane from to . Using a setup with rotatable magnets, LC-molecule alignment with respect to the incident RF-polarization can be changed and characterized at different temperatures. The S-parameters show little frequency dependent behavior at all temperatures with an increase of insertion loss by maximally . However, as the temperature increases the anisotropy of the used LC-mixture GT7-29001 is reduced. Therefore, a degradation of differential phase can be observed with increasing temperature. As the electrical length of the LC section increases with frequency, this degradation of increases with frequency, too. The difference in differential phase at compared to is 72 at 110 . The raw measurement data of the phase of in both parallel and perpendicular alignment reveal the impact of changing temperature in these alignment states and the individual contribution to reduction in achievable . By remodeling the phase behavior, more insight on the reduction of the anisotropy of the used LC-mixture with increasing temperature, and overall impact on LC-based DIG components is provided. The obtained results are essential for evaluating challenges and opportunities of integrated LC-based devices in image line topology at mmW-frequencies. With the image line topology, quasi planar circuitry can be realized, which allows implementation in applications where low profiles are required. At mmW-frequencies, phase shifters are essential for phased-arrays used to enable wireless communications or imaging applications. Together with image line rod antennas [22], LC-based quasi-planar dielectric phased arrays can be realized. While assembly in this manuscript is reliant on glue and single milled components, more sophisticated manufacturing technologies such as injection molding or 3D printing can be used for industrial, large scale production with the possibility of substrate integration [30]. As the development of nematic microwave LC is still an ongoing process [2], the provided data can prove to be beneficial for further development of LC-mixtures tailored to the needs of dielectric applications.
Author Contributions
Conceptualization, H.T.; investigation, H.T., R.R.; validation, H.M., E.P. and D.W.; resources, R.J.; data curation, H.T.; writing—original draft preparation, H.T.; writing—review and editing, R.R., E.P., D.W., H.M. and R.J.; supervision, H.M., R.J.; project administration, H.M., R.J.; funding acquisition, H.M., R.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deutsche Forschungsgemeindschaft (DFG), grant number JA921/68-1.
Acknowledgments
The authors gratefully acknowledge Merck KGaA, Darmstadt, Germany, for supplying Liquid Crystal mixtures. We acknowledge support by the German Research Foundation and the Open Access Publishing Fund of Technische Universität Darmstadt.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DIG | Dielectric image guide |
| FoM | Figure-of-merit |
| IL | Insertion loss (IL = ) |
| LC | Liquid crystal |
| mmW | Millimeter wave |
| NRW | Nicholson–Ross–Weir |
| PCB | Printed circuit board |
References
- Zografopoulos, D.C.; Ferraro, A.; Beccherelli, R. Liquid-Crystal High-Frequency Microwave Technology: Materials and Characterization. Adv. Mater. Technol. 2018, 4, 1800447. [Google Scholar] [CrossRef]
- Fritzsch, C.; Wittek, M. Recent developments in liquid crystals for microwave applications. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 1217–1218. [Google Scholar] [CrossRef]
- Weickhmann, C.; Jakoby, R.; Constable, E.; Lewis, R.A. Time-domain spectroscopy of novel nematic liquid crystals in the terahertz range. In Proceedings of the 2013 38th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Mainz, Germany, 1–6 September 2013; pp. 1–2. [Google Scholar] [CrossRef]
- Polat, E.; Reese, R.; Tesmer, H.; Schmidt, S.; Spaeth, M.; Nickel, M.; Schuster, C.; Jakoby, R.; Maune, H. Characterization of Liquid Crystals Using a Temperature-Controlled 60 GHz Resonator. In Proceedings of the IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Bochum, Germany, 16–18 July 2019; pp. 19–21. [Google Scholar] [CrossRef]
- Mertelj, A.; Cmok, L.; Sebastián, N.; Mandle, R.J.; Parker, R.R.; Whitwood, A.C.; Goodby, J.W.; Čopič, M. Splay Nematic Phase. Phys. Rev. X 2018, 8, 041025. [Google Scholar] [CrossRef]
- Sebastián, N.; Cmok, L.; Mandle, R.J.; De la Fuente, M.R.; Olenik, I.D.; Čopič, M.; Mertelj, A. Ferroelectric-Ferroelastic Phase Transition in a Nematic Liquid Crystal. Phys. Rev. Lett. 2020, 124, 037801. [Google Scholar] [CrossRef] [PubMed]
- Polat, E.; Reese, R.; Jost, M.; Schuster, C.; Nickel, M.; Jakoby, R.; Maune, H. Tunable Liquid Crystal Filter in Nonradiative Dielectric Waveguide Technology at 60 GHz. IEEE Microw. Wirel. Components Lett. 2019, 29, 44–46. [Google Scholar] [CrossRef]
- Franke, T.; Gaebler, A.; Prasetiadi, A.E.; Jakoby, R. Tunable Ka-band waveguide resonators and a small band band-pass filter based on liquid crystals. In Proceedings of the European Microwave Conference (EuMC), Rome, Italy, 6–9 October 2014; pp. 339–342. [Google Scholar] [CrossRef]
- Maune, H.; Jost, M.; Reese, R.; Polat, E.; Nickel, M.; Jakoby, R. Microwave Liquid Crystal Technology. Crystals 2018, 8, 355. [Google Scholar] [CrossRef]
- Nose, T.; Ito, R.; Honma, M. Potential of Liquid-Crystal Materials for Millimeter-Wave Application. Appl. Sci. 2018, 8, 2544. [Google Scholar] [CrossRef]
- Polat, E.; Tesmer, H.; Reese, R.; Nickel, M.; Wang, D.; Schumacher, P.; Jakoby, R.; Maune, H. Reconfigurable Millimeter-Wave Components Based on Liquid Crystal Technology for Smart Applications. Crystals 2020, 10, 346. [Google Scholar] [CrossRef]
- Cudak, M.; Ghosh, A.; Kovarik, T.; Ratasuk, R.; Thomas, T.A.; Vook, F.; Moorut, P. Moving Towards Mmwave-Based Beyond-4G (B-4G) Technology. In Proceedings of the IEEE Vehicular Technology Conference (VTC), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Rappaport, T.S.; Qiao, Y.; Lauffenburger, S.J. Millimeter-Wave 60 GHz Outdoor and Vehicle AOA Propagation Measurements Using a Broadband Channel Sounder. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), Houston, TX, USA, 5–9 December 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Kyro, M.; Ranvier, S.; Kolmonen, V.; Haneda, K.; Vainikainen, P. Long range wideband channel measurements at 81–86 GHz frequency range. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Barcelona, Spain, 12–16 April 2010; pp. 1–5. [Google Scholar]
- Tesmer, H.; Reese, R.; Polat, E.; Jakoby, R.; Maune, H. Dielectric Image Line Liquid Crystal Phase Shifter at W-Band. In Proceedings of the 2020 German Microwave Conference (GeMiC), Cottbus, Germany, 9–11 March 2020; pp. 156–159. [Google Scholar]
- Tesmer, H.; Reese, R.; Polat, E.; Jakoby, R.; Maune, H. Liquid Crystal Based Parallel-Polarized Dielectric Image Guide Phase Shifter at W-Band. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 305–308. [Google Scholar] [CrossRef]
- King, D.; Schlesinger, S. Dielectric Image Lines. IEEE Trans. Microw. Theory Tech. 1958, 6, 291–299. [Google Scholar] [CrossRef]
- Shindo, S.; Itanami, T. Low-Loss Rectangular Dielectric Image Line for Millimeter-Wave Integrated Circuits. IEEE Trans. Microw. Theory Tech. 1978, 26, 747–751. [Google Scholar] [CrossRef]
- Knox, R. Dielectric Waveguide Microwave Integrated Circuits—An Overview. IEEE Trans. Microw. Theory Tech. 1976, 24, 806–814. [Google Scholar] [CrossRef]
- Dolatsha, N.; Hesselbarth, J. Millimeter-Wave Antenna Array Fed by an Insulated Image Guide Operating in Higher-Order Mode. IEEE Trans. Antennas Propag. 2013, 61, 3369–3373. [Google Scholar] [CrossRef]
- Wu, K.; Cheng, Y.J.; Djerafi, T.; Hong, W. Substrate-Integrated Millimeter-Wave and Terahertz Antenna Technology. Proc. IEEE 2012, 100, 2219–2232. [Google Scholar] [CrossRef]
- Patrovsky, A.; Wu, K. 94-GHz Planar Dielectric Rod Antenna With Substrate Integrated Image Guide (SIIG) Feeding. IEEE Antennas Wirel. Propag. Lett. 2006, 5, 435–437. [Google Scholar] [CrossRef]
- Friedsam, G.; Biebl, E. Precision free-space measurements of complex permittivity of polymers in the W-band. In Proceedings of the 1997 IEEE MTT-S International Microwave Symposium Digest, Denver, CO, USA, 8–13 June 1997; Volume 3, pp. 1351–1354. [Google Scholar] [CrossRef]
- Nicolson, A.M.; Ross, G.F. Measurement of the Intrinsic Properties of Materials by Time-Domain Techniques. IEEE Trans. Instrum. Meas. 1970, 19, 377–382. [Google Scholar] [CrossRef]
- Weir, W. Automatic measurement of complex dielectric constant and permeability at microwave frequencies. Proc. IEEE 1974, 62, 33–36. [Google Scholar] [CrossRef]
- Sahin, S.; Nahar, N.K.; Sertel, K. Permittivity and Loss Characterization of SUEX Epoxy Films for mmW and THz Applications. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 397–402. [Google Scholar] [CrossRef]
- Khanal, S.; Kiuru, T.; Mallat, J.; Luukkonen, O.; Räisänen, A.V. Measurement of Dielectric Properties at 75–325 GHz using a Vector Network Analyzer and Full Wave Simulator. Radioengineering 2012, 21, 551–556. [Google Scholar]
- Costa, F.; Borgese, M.; Degiorgi, M.; Monorchio, A. Electromagnetic Characterisation of Materials by Using Transmission/Reflection (T/R) Devices. Electronics 2017, 6, 95. [Google Scholar] [CrossRef]
- Jablonski, D. Attenuation Characteristics of Circular Dielectric Waveguide at Millimeter Wavelengths. IEEE Trans. Microw. Theory Tech. 1978, 26, 667–671. [Google Scholar] [CrossRef]
- Jimenez-Saez, A.; Schubler, M.; Krause, C.; Pandel, D.; Rezer, K.; Bogel, G.V.; Benson, N.; Jakoby, R. 3D Printed Alumina for Low-Loss Millimeter Wave Components. IEEE Access 2019, 7, 40719–40724. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).