Abstract
The simplest possible structural transition that an electronic system can undergo is Wigner crystallization. The aim of this short review is to discuss the main aspects of three recent experimets on the one-dimensional Wigner molecule, starting from scratch. To achieve this task, the Luttinger liquid theory of weakly and strongly interacting fermions is briefly addressed, together with the basic properties of carbon nanotubes that are required. Then, the most relevant properties of Wigner molecules are addressed, and finally the experiments are described. The main physical points that are addressed are the suppression of the energy scales related to the spin and isospin sectors of the Hamiltonian, and the peculiar structure that the electron density acquires in the Wigner molecule regime.
1. Introduction
The story of Wigner crystals is a very old one: indeed its roots are almost a century old. In 1934, while studying the effects of electron interactions on the band structure of metals, E. Wigner suggested that the electron liquid at very low densities should actually crystallize [1], with electrons sharply localized around equilibrium positions. The model considered by E. Wigner for electrons is the jellium, one of the most general and fundamental ones in condensed matter [2], in which the effects of the interacting electron liquid and the neutralizing background provided by the lattice ion charges are taken into account [3]. As it turns out, the jellium model is governed by a single parameter: the Wigner-Seitz radius which is defined in d spatial dimensions as the adimentionalized radius of the d-sphere that contains on average just one electron, in units of the Bohr radius. Clearly, for small the electron density is large and the opposite is true for large . Dimensional analysis on the jellium model shows that the kinetic energy of electrons scales as while the electron repulsion scales as : in the low density limit, when exceeds some critical value, Coulomb interactions become dominant over the kinetic term and electrons manage to minimize their energy by arranging themselves in a crystal. At a theoretical level, several different analytical and numerical methods have been employed to the problem of determining at which electrons actually crystallize and what lattice structure they eventually form: a very informative survey of these approaches can be found in Ref. [2]. The overall picture is that for electrons arrange in a BCC lattice (the FCC phase is almost degenerate in some calculations) when . Attaining such low densities in a three-dimensional (3D) material has proven to be exceedingly difficult, especially because of the unavoidable impurities and defects that would disrupt the electron crystalline phase. Thus, so far there have not been direct evidences of a true 3D Wigner crystal.
The situation in is more favourable: recent numerical estimates [4] place the threshold for the formation of a Wigner crystal at with a hexagonal lattice structure. Confining electrons in a two-dimensional (2D) system [5] has the additional advantage to potentially produce much cleaner systems. Finally, 45 years after the initial prediction by E. Wigner, in 1979 C. Grimes and G. Adams provided the first experimental evidence [6] of a Wigner crystal formed in a low-density 2D sheet of electrons floating atop the flat surface of liquid He. For a detailed review of this key topic, see e.g., Refs. [7,8]. Another paradigmatic system which has provided an excellent template to study the physics of Wigner crystals is the 2D electron liquid formed in metal-oxide silicon field effect transistors (MOSFETs in short). Here, the most notable discovery of the quantized hall effect [9] has triggered subsequent observations of the formation of Wigner crystals in the bulk of quantum Hall bars both at integer [10] and fractional [11,12,13,14] filling factors.
The high level of control achieved in modern nanofabrication techniques of semiconductors has further enriched the playground of Wigner physics [15]. The further confinement of a 2D electron system in the plane achieved in quantum dots [16,17] allows the formation of Wigner molecules—the finite size counterpart of Wigner crystals—with a number of electrons N that can be controlled with extreme precision [17,18,19]. The theoretical study of Wigner molecules is even more complicated than that of crystals: the lack of translational invariance effectively turns the parameter introduced above a local quantity, as the average spacing between electrons can strongly depends on their position in the system.
As far as one dimension (the subject of this review) is concerned, the effects of electron-electron interactions are extremely interesting. Indeed, even the metallic phases violate the Fermi liquid paradigm usually accepted to describe the effects of interactions in the high density limit in . On the contrary, the low-energy sector is described by the so called Luttinger liquid [20]. Interestingly, the Luttinger liquid also applies to bosonic [21], and spin one-dimensional systems [22,23], thus providing a very powerful tool. The experimental consequences of the Luttinger liquid behavior of fermionic systems can be found in very different contexts, ranging from Bechgaard salts [24,25], to quantum wires [26,27,28,29], quantum Hall edges [30,31,32], quantum spin Hall edges [33,34], and carbon nanotubes [35], even in the presence of mechanical vibrations [36,37]. Interestingly, strongly out of equilibrium scenarios can also be inspected within this framework [38,39,40,41,42,43,44,45,46,47,48,49]. While genuine long range order cannot be established at non-zero temperature, typical correlation lengths exceeding the size of the sample have been conjectured in very diverse contexts [50,51,52,53,54] and are responsible for the so called one-dimensional Wigner molecule. Intuitively, such structure is the one-dimensional counterpart of the Wigner molecule in higher dimensions. In order to analyze the Wigner molecule, both analytical and numerical tools have been widely employed, and a rather clear scenario has been developed. As we shall see, when equipped with the bosonization technique, the Luttinger liquid model can become an extremely powerful model to analytically tackle the study of Wigner molecules in 1D. Also this aspect, in a certain sense, sets the case apart from higher dimensionality where computationally demanding numerical methods are unavoidable. However, it was only very recently that the one-dimensional Wigner molecule could be experimentally realized in three beautiful and diverse experiments.
The aim of this short review is to make the main aspects of those three experiments transparent to readers who are not familiar with the peculiarities of one-dimensional systems. In particular, Section 2 gives an incomplete and intuitive introduction to the topic. Section 3 and Section 4 deal with the Luttinger liquid tools, while Section 5 and Section 6 are focused on the aspects that are more relevant for the experiments: the indicators of the Wigner molecule and the properties carbon nanotubes. In Section 7, the three experiments are discussed. Finally, Section 8 is devoted to the perspectives.
2. The Ground State Density
In order to understand the physics of the one-dimensional Wigner molecule, one can start by inspecting a simple, abstract, yet far reaching model: interacting spinful electrons, confined on a segment of length L by an infinite potential. The Hamiltonian H of the system is
with ()
and
Here, is the fermionic annihilation operator for an electron with spin projection s, m is its (effective) mass, and is a generic repulsive inter-particle potential, invariant under spin rotations. Not that in the solid state context is not the bare Coulomb potential [2], due to both the ionic background and the unavoidable presence of gates. Moreover, the spread of the wavefunctions in directions other than the one considered and the higher confinement sub-bands also contribute to the actual shape of [55]. The strength of the interacting term is parametrized by . The precise form of is here not specified further. While the properties of the observables do depend on the range of v, for a preliminary discussion no further details are required.
Due to the infinite confining potential, the many-body wave function is forced to be zero at the boundaries of the system. The hard wall boundary conditions then impose
An important observable is the ground state local electron density given by
with the many body ground state of H, with particles. For , the calculation of is very simple. One finds
The ground-state density is characterized by N peaks, with a typical wavevector which coincides with the Fermi momentum. Such wave vector is reminiscent of the Friedel oscillations [56,57] that develop around an impurity in a Fermi liquid. Crucially, the number of peaks is half of the number of electrons in the system for this regime. Qualitatively speaking, although the electron wavefunctions are not localized—a fact confirmed also by the relatively small amplitude of the oscillations—each maximum can be thought to accomodate two electrons with opposite spins. The situation is schematically shown in Figure 1a.
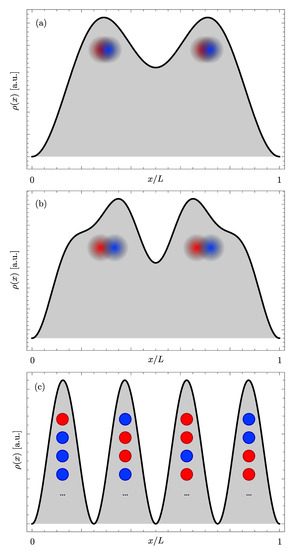
Figure 1.
The transition from the Friedel to the Wigner regime for the ground state density profile , for the case of particle—see text for details. (a) For non-interacting electrons, Friedel oscillations occur, characterized by density peaks; (b) for moderate electrons, additional peaks appear but with a small peak-valley ratio; (c) for strong interactions peaks in the density develop. Here, red (blue) dots represent electrons with spin up (down), a blurred dot denoting delocalized electron wave functions, while a sharp dot implying strongly localized electrons. In panel (c), some of the 16 possible degenerate spin configurations are shown as an example.
As electron-electron interactions are turned on and increased in strength, electrons begin to repel each other and the number of peaks tend to double. The situation is illustrated in Figure 1b. Finally, for strong interactions, electrons localize sharply around given equilibrium positions: peaks occur in the density and the oscillation wavevector doubles to . As a consequence of this sharp localization, the minima of become negligible and the peak-valley ratio is maximized: we have entered the Wigner molecule regime—represented schematically in Figure 1c. The crossover between the dominance of the Friedel and the Wigner regimes [58] can be viewed as a structural transition which takes up the role of the true phase transition which is prohibited in one spatial dimension due to fluctuations. Another crucial aspect to observe here is that, in the Wigner regime, electrons essentially do not overlap anymore. As a consequence, interactions between their spins become negligible which implies that the distinct spin configurations for the Wigner molecule become essentially degenerate [59].
To substantiate the qualitative scenario described above we report in Figure 2 the results of Ref. [57] for the exact diagonalization of a system of four interacting electrons bound in a box of length L with a slightly smoother confinement than hard walls. Several density profiles are shown for different values of the parameter modeling the strength of the interactions. For , with the effective Bohr radius, the electrons are only weakly interacting and the profile of a Friedel oscillations with two maxima is found. As interactions increase, for four maxima appear, with a small peak-valley ratio: electrons become to repel but are not yet quite localized. As is further increased, the peak-valley ratio increases as the minima of the density tend to zero. This signals the arrangement of electrons into a Wigner molecules. Interestingly, one can notice that peaks at the edges of the molecule are higher than those in the center. This effect can be attributed to the actual shape of the confinement. Indeed, as will be discussed in the last part of this review, the actual shape of the confinement plays a crucial role in shaping the properties of a Wigner molecule and produces effects that can be actually measured in experiments.
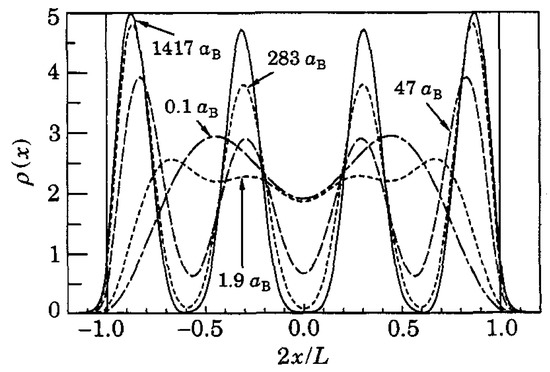
Figure 2.
Electron density, n units , corresponding to four electrons on a segment, as a function of position (x axis) and interaction strength (increasing corresponds to stronger interactions). The transition between two and four peaks can be clearly seen. Figure adapted from [57].
The qualitative behavior of the ground state electron density of the model is somehow intuitive and certainly useful for understanding the mechanisms leading to the Wigner molecule. However, since one has to deal with many interacting fermions, transparent effective models describing the formation of the Wigner molecule are not straightforward. To better understand the electron density, its finite temperature counterpart, the transport properties, and the energetics of the Wigner molecule, the bosonization technique, as applied to Wigner molecules, should be briefly presented.
3. Standard Bosonization
Interacting gapless one-dimensional systems are described, at low energy, by a free bosonic Hamiltonian, or, in the majority of the relevant fermionic cases, by a collection of free bosons [20]. This statement is at the heart of the Luttinger liquid conjecture. The peculiarity of one-dimensional systems emerges from the fact that most low energy excitations of interacting one-dimensional systems are collective in nature [60]. Interacting spinful electrons on a segment are not an exception to this paradigm.
In order to understand how the Luttinger liquid conjecture works, a good starting point is represented by the exact mapping between interacting fermions with linear dispersion (Dirac-like fermions—relevant for the rest of this review) and free bosons. The treatment given here is based on Ref. [61]. Here, we refer to Dirac-like fermions instead of Dirac fermions to stress the fact that we are not dealing with a fundamental theory with linear dispersion. Natural cut offs, related to the presence of other confinement sub-bands and to the existence of a lattice spacing, should always be considered.
We call the whole Hamiltonian . Considering again a system of lenght L, the free part of the fermionic Hamiltonian is
with a Fermi spinor composed by a right (R) and a left (L) mover, the Fermi velocity, and the third Pauli matrix in the usual representation, acting on the space. The physical Fermi operator is, in conventional quantum wires , where , as in the previous section, represents the Fermi momentum. Moreover, open boundary conditions imply that . More general twisted boundary conditions are relevant in the case of topological insulators [62,63,64,65].
To write the interaction term that we now consider, it is useful to introduce charge () spin () density operators, defined as
with
the spin and chirality resolved density operators.
By reserving the possibility of having spin dependent interactions, that can emerge for example due to spin-orbit coupling [60] we write the short range interaction term as
with
Note that the interaction terms are here written in a density-density form rather than in the usual form emerging from second quantization. This choice enables to effectively take into account finite range interactions by means of an apparently local term [66]. The effect of finite range interactions is irrelevant in the renormalization group sense [60].
Astonishingly, the Hamiltonian can be diagonalized exactly [66] and cast into the form
The left moving field is readily calculated from this. Here, are bosonic operators, , with the number operator of electrons with spin ±, as counted from the Fermi level. Moreover, (n is a positive integer), , with .
Here, the key result is the spin-charge separation phenomenon: a Hamiltonian of interacting spinful fermions is mapped onto that of two species () of non-interacting bosons that do not talk to each other. The parameters that control all correlation functions are the so called Luttinger parameters . Rather generally, , for repulsive interactions, with the equal sign valid in the case of non-interacting fermions. On the other hand, in the absence of spin-orbit coupling that implies [60,67] , one can usually set . Another important parameter is the velocity at which the bosons propagate. It will indeed turn out that in the Wigner molecule regime the velocity of the spin excitations is strongly suppressed with respect to the one of the charge ones [59]. This crucial aspect will be discussed in the next section. It is now useful to give the bosonic form of the Fermi operator and of the density operator. One finds
Here, is a cutoff length, the operator satisfies and satisfies implementing the correct anticommutation relations of the fermionic field . The boson fields , are ()
Now the total particle density operator , with can be bosonized. One has (identifying ) [68]
Here, the second term of Equation (15) corresponds to the long-wave part and is proportional to the derivative of the antisymmetric field
while is the contribution due to Friedel oscillations given (neglecting the zero modes in comparison to ) by
where
We are now in the position to compute the ground state average electron density in this linearized model, , with the interacting ground state. Assuming the system filled up to the Fermi momentum one has [61]
Two aspects are here particularly important. Firstly, only Friedel oscillations are present: no Wigner oscillations are visible. Moreover, the peak to valley ratio of the Friedel oscillations is governed by an enveloping function with a power law dependence on the interaction parameter with the non-universal exponent . The Dirac-like model for interacting electrons is hence not appropriate for the description of strongly interacting quantum wires. Indeed, while the second point is observed in strongly interacting quantum wires, the absence of Wigner oscillations implies the need of moving to more involved models.
Several extensions can be made in order to assess a general form of Luttinger liquid beyond the solution of the linear Dirac-like model. At the level of the Hamiltonian, umklapp-like terms, reading as
can be introduced [60]. While such a modification indeed allows for a positive result in terms of the incipience of the Wigner molecule [69,70], at a closer inspection, the mechanism involves hole states [71]. Indeed, since is translationally invariant, it mixes right and left movers with the same momentum and hence, necessarily, electron and hole states. While this road is definitely meaningful in the case of carbon nanotubes [72] and topological insulators [73,74,75,76], it can hardly apply to standard quantum wires.
Another possibility to explore is to express the Fermionic operator as a series of different powers of the bosonic operators [77,78]. Qualitatively speaking, one has
As a consequence, the density operator becomes a series as well [78]. The most relevant in the context of our discussion is
and we note that this term displays the correct wavelength to produce Wigner oscillations [78]. It is important to note that we have repeatedly use the ∼ sign instead of the equal sign since the proposed extensions to the interacting Dirac model are not universal and the precise forms are hence model dependent. The therm alone, however, cannot produce oscillation dominating over the Friedel contribution, even for strong repulsive interactions. Another possible route is to observe the Dirac-like model presented above neglects many interaction terms, most notably
The perturbative effect of on the density contribution is to introduce averages that do not involve the spin field and that can become dominant for strong interactions [60]. A more faithful expression for the density operator, that implicitly takes into account is
where is a model dependent phenomenological parameter ensuring that the density is zero at the boundaries [79,80], with (no Wigner term). The Wigner contribution to the density is given by
While containing a free parameter (), the density operator is extremely powerful in the description of quantum wires in view of its very good agreement with numerical results [69]. Indeed, one can compute the ground state average of the contribution and hence assess the total ground state density. The result is
To summarize, the total average density is hence
The most important aspect is here that Wigner oscillations dominate over Friedel oscillations for [78] , that is for strong repulsive interactions. Here, strong interaction means that the interaction must be not only parametrically strong, but also of non-zero range. Indeed, in the bosonization of the Hubbard model with on site repulsion the smallest value that can reach is [81] . For unscreened Coulomb interactions, on the other hand, one has [81] . A closer inspection of the latter situation reveals that the Wigner contribution to the density-density correlation function decays as , slower than any power law [58].
While the picture now appears convincing thanks to the introduction of the Wigner contribution in the density, a conceptual point remains open: the introduction of such a term is based on a perturbative argument, but in the Wigner molecule regime its effect is far from perturbative! In other words, how is it justified that one can start from a bosonization scheme that is valid in the weak interaction regime and push its validity all the way to a crystalline system? Moreover, a major point remains unclear: Why are the spin excitations way slower than the charge excitations? In order to answer these questions, in the next section we will describe a bosonization scheme that has a strongly interacting starting point. In this short review, more formal nonperturbative approaches [82,83,84] will not be discussed, since effective models suffice for correctly interpreting the experimental results.
4. Bosonization in the Strong Interaction Limit
Let us now take a step back and consider a more intuitive perspective. The simplest model one can adopt for describing the 1D Wigner molecule consists in a chain of electrons [85,86,87], free to oscillate around their equilibrium positions, and interacting via a small antiferromagnetic coupling due to the Lieb-Mattis theorem, stating that the ground state of one-dimensional electrons cannot be spin polarized [88]. The model is schematically shown in Figure 3.
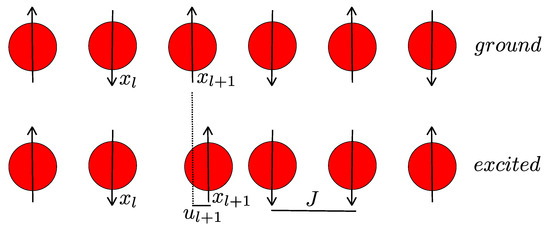
Figure 3.
Schematic representation of the chain of electrons suitable as a starting point to describe a one-dimensional Wigner molecule in the regime of strong interactions.
The equilibrium position of the l-th electron in the chain is given by , where a is the average inter-particle distance. The displacement (operator) of the l-th particle from its equilibrium position is , such that its position is .
The Hamiltonian H consists in two contributions: . describes the ‘phonons’ of the chain of electrons and describes the spin contribution. Considering a chain of N electrons which perform small oscillations about the equilibrium positions (elastic limit)
where is the momentum of the l-th electron, m, as before, is the effective mass in the material, and is an effective frequency. Concerning the spin sector, one can rather generically write the Heisenberg Hamiltonian
where is the spin operator attached to the l-th electron of the chain and is a positive parameter. The residual spin coupling is governed by the exchange parameter , which is small in comparison to the typical energies of the charge sector . For a more accurate analysis of , see for example Ref. [86].
When temperature and external voltages are low compared to the bandwidths of the spin and charge Hamiltonians one can consider the low energy limit of the theory. As long as is concerned, the quantities are replaced by the field , defined as a slowly varying field, with the condition . A new rescaled field is now introduced
and one gets
with a bosonic field, its conjugate and
with and . Furthermore, is the Fermi velocity of a Fermi gas containing N electrons, confined in a segment of length L. Overall, the procedure is the same one performed for obtaining the dispersion relation of the phonons of a one-dimensional chain of identical equivalent particles [89].
A crucial point to observe here is that has the same form of the Hamiltonian of the charge sector introduced in the previous section, but in this model the interaction parameter can become as small as wanted as the parameter is increased.
Also the low energy theory for can be expressed in terms of a free bosonic theory. The most accurate way to do so is to extract it from the exact Bethe-ansatz solution of the 1D Heisenberg Hamiltonian [90]. However a good physical insight into the problem can be obtained by mapping the Heisenberg Hamiltonian onto interacting spinless fermions, and hence using standard bosonization techniques to map the interacting fermion onto a free bosonic Hamiltonian. The mapping onto the interacting spinless fermions is carried out using the Wigner–Jordan transformation [90], that first simply translates the spin operators onto linear combinations of the the Pauli matrices (Equation (34)), and then expresses the algebra in terms of fermionic operators. Explicitly
where are spinless fermions.
At the end of this procedure one obtains a bosonized low energy Hamiltonian given by [90,91]
with a bosonic field, its conjugate, and .
The total Hamiltonian is hence given, in the low energy sector, by the Hamiltonian of a two channel Luttinger liquid with one Luttinger parameter, , satisfying , one Luttinger parameter satisfying and . The last condition is due to the fact that is, for small , bigger than the Fermi velocity, while tends to zero as J tends to zero, that is in the relevant strongly interacting case.
It can also be shown that the the electron operator , which destroys an electron with spin s at the position x along the one-dimensional system, admits a representation in terms of bosonic operators. Such a mapping gives the usual expression characterizing the Luttinger liquid fermionic operator [92,93].
To recapitulate in one sentence what we have learned so far: the Luttinger liquid picture, which is well known to be valid for weak interactions, is also valid for strong electron-electron interaction. The most important difference between the weak interaction and the strong interaction regimes is that latter the velocities of the spin mode is very small with respect to the velocity of the charge mode.
There are now interesting aspects that should be mentioned.
First of all, depending on , is might be meaningful to bosonize the spin Hamiltonian, or not. Indeed, when the temperature scale becomes comparable to the bandwidth of the spin Hamiltonian, its high energy structure matters and the full spin properties must be addressed. When interactions become even stronger, the bandwidth can become negligible with respect to temperature. In this case, the spin Hamiltonian is just approximated by the identity operator. This regime is called spin incoherent regime [59,85]. Within this approximation, the Wigner molecule becomes strongly degenerate.
A second aspect to address is the particle density in the model presented in this section. While in the standard bosonization scheme it is difficult to justify the presence of oscillations, in the current model Friedel oscillations appear to be absent. It can be shown that they emerge thanks to the following mechanism: When the oscillations of the electrons around their equilibrium positions become significant, the coupling J acquires a dependence on the operators . A spin-Peierls’ mechanism can hence drive an effective dimerization of the chain and let oscillations to emerge.
In this context, it is worth to notice that, since Friedel oscillations are sensitive to the spin sector, differently from Wigner oscillations, their signatures are more likely to be ‘melted’ by temperature [80,94,95,96].
5. Indicators of the Wigner Molecule
We can now summarize, on the basis of the discussion carried out in the former sections, the signatures of the Wigner molecule that are most likely to be observed in an experiment.
- (i)
- The electron density shows, in the Wigner molecule regime, a number of (well separated) peaks that equals the number of electrons in the system.
- (ii)
- The low-energy excitations, that are in the spin sector, have typical energies that are strongly suppressed with respect to the non-interacting case (the Wigner molecule, as mentioned, tends to be degenerate).
- (iii)
- More surprisingly, the following effect can be predicted [86]: when the temperature is low as compared to the bandwidth of the spin Hamiltonian, the conductance is characterized by the typical Luttinger liquid value. On the other hand, in the spin incoherent regime, the system behaves more like a spinless Luttinger liquid and the conductance tends to .
On a more theoretical perspective, features of the localization tensor, the particle-hole entropy, and the current noise can also be linked to the formation of a Wigner molecule [97,98].
6. Carbon Nanotubes
Before addressing the experimental evidences of the Wigner molecule, an important clarification is in order. The theories just summarized do not completely apply to the one-dimensional system that is most often employed to study the Wigner molecule: carbon nanotubes [35,99,100,101,102,103,104,105,106]. While all the basic arguments addressed in the preceding sections are qualitatively correct even in the case of carbon nanotubes, a careful analysis would be required in order to make quantitative predictions.
Carbon nanotubes, in their single wall versions, are, qualitatively speaking, cylinders made of rolled up graphene sheets. Depending on the direction of the axis of the cylinder with respect to the lattice, they can be either metallic or semiconducting, with the semiconducting ones being the most interesting for Wigner crystallization. The typical length is up to the micrometer scale, while the diameter can be below the nanometer. From the point of view of quantum confinement, they can hence be brought into the one-dimensional regime, similarly to semiconducting quantum wires. From the point of view of Wigner crystallization they have several advantages with respect to quantum wires: they can be grown with a negligible amount of defects, they are intrinsically strongly interacting, and they can be suspended between contacts, so as to minimize the screening effects. However, it is worth noticing that, due to the underlying honeycomb lattice, electrons at low energy necessitate an extra index: the valley degree of freedom. This property, that is shared by carbon nanotubes and graphene, is due to the fact that there are two inequivalent points in the Brillouin zone that need to be considered in a low energy expansion. From the perspective of the density oscillations, this means that the number of peaks is not doubled, but becomes four times bigger in the transition between Friedel and Wigner oscillations. From the point of view of the spin physics, the presence of the valley degree of freedom implies that, even in the simplest case, the Heisenberg Hamiltonian must be replaced by more involved models such as [107]
Here represents the isospin term associated to the valley degree of freedom. This Hamiltonian is more complicated than the Heisenberg Hamiltonian In Equation (29), nevertheless it is integrable, and it can be shown that its low energy sector can be described in terms of a three channel Luttinger liquid [108,109,110]. Thus, when the phonons of the chain are included in the Hamiltonian, the picture drawn for weakly interacting CNTs is recovered even for the Wigner molecule in CNTs.
Spin-orbit coupling, that can be significant in carbon nanotubes, couples the spin and the valley degree of freedom and can further enrich the physics, mainly lifting degeneracies and altering the transport properties in the Kondo regime [111,112,113,114]. Another relevant topic is the behavior of the electrons hosted by carbon nanotubes in the presence of an external magnetic field. Being associated to the chirality, the valley degree of freedom is related to an orbital magnetic field, so that a suitable gyromagnetic factor should be taken into account. The scale of strongly depends on the radius R of the nanotube according to the qualitative rule [115], although it can be dependent on the confinement. On the other hand, the coupling between the magnetic field and the spin degree of freedom is parametrized by [115] . In the prototypical cases, hence, the coupling to the valley degree of freedom is stronger than the one to the spin degree of freedom.
7. Experiments
In this section, we describe three prominent experiments that revealed, with different techniques, a one-dimensional Wigner molecule. All experiments are performed on suspended, high quality, semiconducting carbon nanotubes.
In Ref. [116], by Deshphande and Bockrath, the nanotube is contacted with a source-drain voltage and brought in the Coulomb blockade regime—see Figure 4a. A gate, biased at the voltage , allows to control the number of holes in the system in the range between 0 and around 30. The focus of the experiment is measuring the linear differential conductance as a function of the gate voltage and of a magnetic field applied parallel to the axis of the nanotube. From such a measure, the energy levels of the systems can be resolved. The experimental results are shown in Figure 5a. Three distinct regions can be distinguished. For a low density of holes (the region I) a Wigner crystal develops. In this regime, the coupling constant J is very small, so that at any finite magnetic field the electrons tunneling into the nanotube are polarized both in the spin and in the valley degree of freedom. Indeed, a single slope is visible. As the filling is increased (with the Boltzmann constant) increases up to several tens of Kelvin and two regions appear: one where the valley degree of freedom is polarized, while the spin is antiferromagnetically ordered. In the picture this is highlighted as region II, between the red and the yellow lines, where consecutive lines have different positive slopes. Moreover, below the yellow line the spin degree of freedom is not polarized. For even higher numbers of holes, a regime where both the spin and the valley degrees of freedom are antiferromagnetic (region III) appears. A quantitative analysis of the phase boundaries is rather involved: while in the original article the results are interpreted in terms of solitons in a homogeneous, multi-flavour Luttinger liquid [117], it was later recognized that it is crucial to take into account the effects of confinement [118]. Indeed, the holes are confined in the nanotube by means of two Schottky barriers, that can be modelled as inducing a parabolic confinement. The holes will hence be denser close to the center of the nanotube and more diluted at the edges. In the spin-isospin Hamiltonian, it is then important to keep a position dependent J. Consequently, it can happen that in the nanotube a phase separation can be present. By taking this effect into account, in Ref. [118] it was possible to obtain a precise agreement between the experimental results and the theoretical calculations.
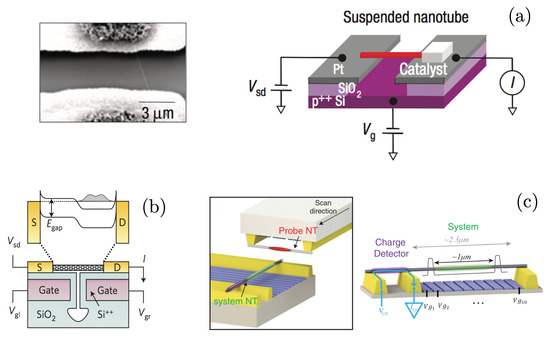
Figure 4.
The experimental setup for the three key experiments assessing the properties of Wigner molecules in one-dimensional system discussed in this review: (a) a suspended semiconducting nanotube in the hole regime [116]; (b) a suspended tunable carbon nanotube [119]; (c) a complex setup, with a nanotube split into two parts which respectively act as the region where the Wigner molecule is formed and as a charge detector with an additional transverse suspended nanotube capacitively coupled to the Wigner molecule [120].
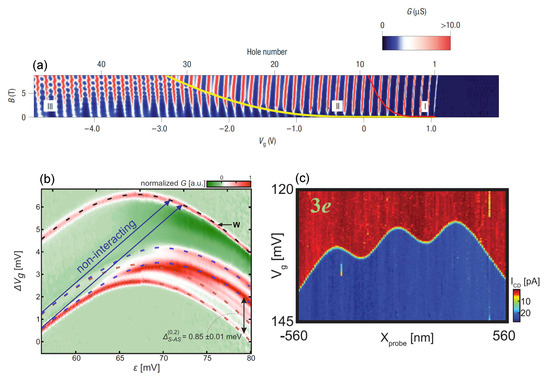
Figure 5.
(a) Differential conductance as a function of gate voltage and magnetic field as measured in Ref. [116]. The three regions are highlighted with the red and the yellow curves. (b) Differential conductance as a function of gate voltage and a detuning parameter in Ref. [119]. The key aspect is here the energy scale highlighted by the black arrow, that demonstrates the suppression of the energy of the spin excitations. (c) Current in the control nanotube as a function of gate voltage position of the scanning nanotube for three electrons in the system as measured in [120]. The characteristic three peak structure is clearly visible.
A complementary signature of the Wigner molecule was obtained by S. Pecker et al. [119]. In this case, the system is again a nanotube which however hosts only two electrons. The experimental setup is shown in Figure 4b. The quantity measured to assess the presence of a Wigner molecule is the the energy gap between the ground state and the first excited state. This quantity is interesting since the two states correspond to a spin 1 singlet and triplet respectively, which should eventually become degenerate in the deep Wigner regime. In details, the idea is the following: If interactions were absent, said gap would simply correspond to the single particle level spacing, a quantity easily obtained measuring the properties of the nanotube when only one electron occupies it. On the other hand, in the Wigner molecule regime, the strongly suppressed energy difference is controlled by the effective exchange parameter J. Measurements are shown in Figure 5b where the energy gap is reported as a function of a detuning parameter . Here, the high detuning regime corresponds to the physical situation discussed in the present review, with the two electrons confined onto a portion of the nanotube. In this regime, The Authors report a gap suppression of a factor 10 between the single particle levels and the two particle levels and are able to link this behavior to the formation of a Wigner molecule comparing their results with an exact diagonalization of the system. The physical mechanism is hence the collapse of the spin and isospin sectors of the Hamiltonian.
Both the above experiments provide significant and convincing evidence of the formation of a Wigner molecule, basically focusing on one of the hallmarks discussed previously: the tendency to develop a marked degeneracy of spin multiplets in the molecular regime. Neither of the two however has been able to pinpoint the most direct evidence of a Wigner molecule, namely the spatial localization and separation of electrons. This gap has been filled by the experiment by Shapir et al. [120].
The setup of this experiment, shown in Figure 4c, is way more complex and consists of two nanotubes with different purposes. The first nanotube is split into two segments: one hosts the Wigner molecule to be probed while the other—electrically insulated and independently contacted, serves as a detector of the number of electrons forming the Wigner molecule. The detection is performed locating linear conductance peaks as a function of the bias applied to the back gates below the molecule. The second nanotube is suspended above the first one perpendicularly to it and is free to move along the region where the molecule sits. Independently biased and capacitively coupled to the molecule, it acts as a scanning gate probe for the system, allowing to locally shift the electron density of the molecule. The equilibrium number of electrons in the Wigner molecule as a function of the gate voltage then depends on the position of the scanning nanotube. The experimental result is shown in Figure 5c: the conductance map essentially allows to visualize the electron density [121,122] providing a direct probe of the Wigner molecule in one dimension. What is indeed observed is a number of peaks that equals the number of electrons in the system. The minima are not expected to be close to zero even in the strongly interacting regime [120].
8. Perspectives
The three representative experiments discussed reveal an interesting issue: the typical inspected are either smaller than 5, or around 20. In the first case, the spin excitations are well visible. On the other hand, in the second case, the system is in the spin incoherent regime. A full analysis of how the spin incoherent regime develops is hence still missing. Connected to this point, a fundamental question is also emerging: the dimerization of the Wigner molecule happens via a spin-Peierls’ mechanism. From the point of view of the spectrum, a gap should correspondingly open in the spectrum. A quantum phase transition could hence mark the appearance of the Wigner molecule in one dimension. While the gap is supposed to be undetectably small, clarifying this point would be conceptually extraordinarily important.
Finally, the peculiar temperature dependence of the conductance characterizing the Wigner molecule has also not been observed yet.
Author Contributions
Conceptualization, F.C. and M.S.; methodology, K.G.B.; software, N.T.Z.; validation, F.C. and M.S.; formal analysis, F.C.; writing original draft preparation, N.T.Z.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
N.T.Z. acknowledges enlightening discussions with G. Zarand.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wigner, E. On the Interaction of Electrons in Metals. Phys. Rev. 1934, 46, 1002. [Google Scholar] [CrossRef]
- Giuliani, G.; Vignale, G. Quantum Theory of the Electron Liquid; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Usually, in the jellium model the background of positive ions is treated as a continuum positive charge density, rather than considering in details the underlying lattice structure—Hence the name “jellium”.
- Drummond, N.D.; Needs, R.D. Hybrid Phase at the Quantum Melting of the Wigner Crystal. Phys. Rev. Lett. 2005, 94, 046801. [Google Scholar]
- At a practical level, a 2D electron system is obtained when the motion in one spatial dimension (the transverse direction) is constrained so that the discrete energy level separation corresponding to the motion in the transverse directions exceeds the other typical energy scales.
- Grimes, C.C.; Adams, G. Evidence for a Liquid-to-Crystal Phase Transition in a Classical, Two-Dimensional Sheet of Electrons. Phys. Rev. Lett. 1979, 42, 795. [Google Scholar] [CrossRef]
- Monarkha, Y.P.; Syvokon, V.E. A two-dimensional Wigner crystal. Low Temp. Phys. 2012, 38, 1067. [Google Scholar] [CrossRef]
- Solyom, J. Wigner crystals: New realizations of an old idea. Epj Conf. 2014, 78, 01009. [Google Scholar] [CrossRef]
- Klitzing, K.V.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494. [Google Scholar] [CrossRef]
- Andrei, E.Y.; Deville, G.; Glattli, D.C.; Williams, F.I.B.; Paris, E.; Etienne, B. Observation of a Magnetically Induced Wigner Solid. Phys. Rev. Lett. 1989, 60, 2765. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, Y.P.; Jiang, P.; Engel, L.W.; Tsui, D.C.; Pfeiffer, L.N.; West, K.W. Observation of a Pinning Mode in a Wigner Solid with ν=1/3 Fractional Quantum Hall Excitations. Phys. Rev. Lett. 2010, 105, 126803. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Kamburov, D.; Hasdemir, S.; Shayegan, M.; Pfeiffer, L.N.; West, K.W.; Baldwin, K.W. Fractional Quantum Hall Effect and Wigner Crystal of Interacting Composite Fermions. Phys. Rev. Lett. 2014, 113, 246803. [Google Scholar] [CrossRef]
- Liu, Y.; Hasdemir, S.; Pfeiffer, L.N.; West, K.W.; Baldwin, K.W.; Shayegan, M. Observation of an Anisotropic Wigner Crystal. Phys. Rev. Lett. 2016, 117, 106802. [Google Scholar] [CrossRef]
- Knighton, T.; Wu, Z.; Huang, J.; Serafin, A.; Xia, J.S.; Pfeiffer, L.N.; West, K.W. Evidence of two-stage melting of Wigner solids. Phys. Rev. B 2018, 97, 085135. [Google Scholar] [CrossRef]
- Corrigan, J.; Dodson, J.P.; Ekmel Ercan, H.; Abadillo-Uriel, J.C.; Thorgrimsson, B.; Knapp, T.J.; Holman, N.; McJunkin, T.; Neyens, S.F.; MacQuarrie, E.R.; et al. Coherent control and spectroscopy of a semiconductor quantum dot Wigner molecule. arXiv arXiv:2009.13572.
- Hawrylak, P.; Jacak, L.; Wojs, A. Quantum Dots; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Kouwenhoven, L.P.; Austing, D.G.; Tarucha, S. Few-electron quantum dots. Rep. Prog. Phys. 2001, 64, 6. [Google Scholar] [CrossRef]
- Reimann, S.; Manninen, M. Electronic structure of quantum dots. Rev. Mod. Phys. 2002, 74, 1283. [Google Scholar] [CrossRef]
- Yannouleas, C.; Landman, U. Symmetry breaking and quantum correlations. Rep. Prog. Phys. 2007, 70, 2067. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Effective Harmonic-Fluid Approach to Low-Energy Properties of One-Dimensional Quantum Fluids. Phys. Rev. Lett. 1981, 47, 1840. [Google Scholar] [CrossRef]
- Cazalilla, M.A.; Citro, R.; Giamarchi, T.; Orignac, E.; Rigol, M. One dimensional bosons: From condensed matter systems to ultracold gases. Rev. Mod. Phys. 2011, 83, 1405. [Google Scholar] [CrossRef]
- Haldane, F.D.M. General Relation of Correlation Exponents and Spectral Properties of One-Dimensional Fermi Systems: Application to the Anisotropic S=1/2 Heisenberg Chain. Phys. Rev. Lett. 1980, 45, 1358. [Google Scholar] [CrossRef]
- Konik, R.M.; Fendley, P. Haldane-gapped spin chains as Luttinger liquids: Correlation functions at finite field. Phys. Rev. B 2002, 66, 144416. [Google Scholar] [CrossRef]
- Vescoli, V.; Degiorgi, L.; Henderson, W.; Grüner, G.; Starkey, K.P.; Montgomery, L.K. Dimensionality-driven insulator-to-metal transition in the bechgaard salts. Science 1998, 281, 1181. [Google Scholar] [CrossRef]
- Schwartz, A.; Dressel, M.; Grüner, G.; Vescoli, V.; Degiorgi, L.; Giamarchi, T. On-chain electrodynamics of metallic (TMTSF)2X salts: Observation of Tomonaga-Luttinger liquid response. Phys. Rev. B 1998, 58, 1261. [Google Scholar] [CrossRef]
- Blumenstein, C.; Schäfer, J.; Mietke, S.; Meyer, S.; Dollinger, A.; Lochner, M.; Cui, X.Y.; Patthey, L.; Matzdorf, R.; Claessen, R. Atomically controlled quantum chains hosting a Tomonaga—Luttinger liquid. Nat. Phys. 2010, 7, 776. [Google Scholar] [CrossRef]
- Heedt, S.; Traverso Ziani, N.; Crépin, F.; Prost, W.; Schubert, J.; Grützmacher, D.; Trauzettel, B.; Schäpers, T. Signatures of interaction-induced helical gaps in nanowire quantum point contacts. Nat. Phys. 2017, 13, 563. [Google Scholar] [CrossRef]
- Guinea, F.; Santos, G.G.; Sassetti, M.; Ueda, M. Asymptotic Tunnelling Conductance in Luttinger Liquids. Europhys. Lett. 1995, 30, 561. [Google Scholar] [CrossRef]
- Braggio, A.; Grifoni, M.; Sassetti, M.; Napoli, F. Plasmon and charge quantization effects in a double-barrier quantum wire. Europhys. Lett 2000, 50, 236. [Google Scholar] [CrossRef]
- Kamata, H.; Kumada, N.; Hashisaka, M.; Muraki, K.; Fujisawa, T. Fractionalized wave packets from an artificial Tomonaga–Luttinger liquid. Nat. Nanotech. 2014, 9, 177. [Google Scholar] [CrossRef]
- Chang, A.M. Chiral Luttinger liquids at the fractional quantum Hall edge. Rev. Mod. Phys. 2003, 75, 1449. [Google Scholar] [CrossRef]
- Rech, J.; Ferraro, D.; Jonckheere, T.; Vannucci, L.; Sassetti, M.; Martin, T. Minimal Excitations in the Fractional Quantum Hall Regime. Phys. Rev. Lett. 2017, 118, 076801. [Google Scholar] [CrossRef]
- Stühler, R.; Reis, F.; Müller, T.; Helbig, T.; Schwemmer, T.; Thomale, R.; Schäfer, J.; Claessen, R. Tomonaga–Luttinger liquid in the edge channels of a quantum spin Hall insulator. Nat. Phys. 2020, 16, 47. [Google Scholar] [CrossRef]
- Strunz, J.; Wiedenmann, J.; Fleckenstein, C.; Lunczer, L.; Beugeling, W.; Müller, V.L.; Shekhar, P.; Traverso Ziani, N.; Shamim, S.; Kleinlein, J.; et al. Interacting topological edge channels. Nat. Phys. 2020, 16, 83. [Google Scholar] [CrossRef]
- Postma, H.W.C.; Teepen, T.; Yao, Z.; Grifoni, M.; Dekker, C. Carbon nanotube single-electron transistors at room temperature. Science 2001, 293, 76. [Google Scholar] [CrossRef] [PubMed]
- Traverso Ziani, N.; Piovano, G.; Cavaliere, F.; Sassetti, M. Electrical probe for mechanical vibrations in suspended carbon nanotubes. Phys. Rev. B 2011, 84, 155423. [Google Scholar] [CrossRef]
- Donarini, A.; Yar, A.; Grifoni, M. Spectrum and Franck–Condon factors of interacting suspended single-wall carbon nanotubes. New J. Phys. 2012, 14, 023045. [Google Scholar] [CrossRef]
- Cazalilla, M.A. Effect of Suddenly Turning on Interactions in the Luttinger Model. Phys. Rev. Lett. 2006, 97, 156403. [Google Scholar] [CrossRef]
- Cazalilla, M.A.; Chung, M.-C. Quantum Quenches in the Luttinger model and its close relatives. J. Stat. Mech. 2016, 2016, 064004. [Google Scholar] [CrossRef]
- Perfetto, E.; Stefanucci, G. On the thermalization of a Luttinger liquid after a sequence of sudden interaction quenches. Europhys. Lett. 2011, 95, 10006. [Google Scholar] [CrossRef][Green Version]
- Kennes, D.M.; Meden, V. Luttinger liquid properties of the steady state after a quantum quench. Phys. Rev. B 2013, 88, 165131. [Google Scholar] [CrossRef]
- Kennes, D.M.; Klockner, C.; Meden, V. Spectral Properties of One-Dimensional Fermi Systems after an Interaction Quench. Phys. Rev. Lett. 2014, 113, 116401. [Google Scholar] [CrossRef]
- Schiro, M.; Mitra, A. Transient Orthogonality Catastrophe in a Time-Dependent Nonequilibrium Environment. Phys. Rev. Lett. 2014, 112, 246401. [Google Scholar] [CrossRef]
- Schiro, M.; Mitra, A. Transport across an impurity in one-dimensional quantum liquids far from equilibrium. Phys. Rev. B 2015, 91, 235126. [Google Scholar] [CrossRef]
- Porta, S.; Gambetta, F.M.; Cavaliere, F.; Traverso Ziani, N.; Sassetti, M. Out-of-equilibrium density dynamics of a quenched fermionic system. Phys. Rev. B 2016, 94, 085122. [Google Scholar] [CrossRef]
- Calzona, A.; Acciai, M.; Carrega, M.; Cavaliere, F.; Sassetti, M. Time-resolved energy dynamics after single electron injection into an interacting helical liquid. Phys. Rev. B 2016, 94, 035404. [Google Scholar] [CrossRef]
- Dora, B.; Haque, M.; Zarand, G. Crossover from Adiabatic to Sudden Interaction Quench in a Luttinger Liquid. Phys. Rev. Lett. 2011, 106, 156406. [Google Scholar] [CrossRef] [PubMed]
- Bacsi, A.; Dora, B. Quantum quench in the Luttinger model with finite temperature initial state. Phys. Rev. B 2013, 88, 155115. [Google Scholar] [CrossRef]
- Porta, S.; Gambetta, F.M.; Traverso Ziani, N.; Kennes, D.M.; Sassetti, M.; Cavaliere, F. Nonmonotonic response and light-cone freezing in fermionic systems under quantum quenches from gapless to gapped or partially gapped states. Phys. Rev. B 2018, 97, 035433. [Google Scholar] [CrossRef]
- Meyer, J.S.; Matveev, K.A.J. Wigner crystal physics in quantum wires. Phys. Condens. Matter 2009, 21, 023203. [Google Scholar] [CrossRef]
- Ronetti, F.; Vannucci, L.; Ferraro, D.; Jonckheere, T.; Rech, J.; Martin, T.; Sassetti, M. Crystallization of levitons in the fractional quantum Hall regime. Phys. Rev. B 2018, 98, 075401. [Google Scholar] [CrossRef]
- Loosa, P.-F.; Gill, P.M.W. Uniform electron gases. I. Electrons on a ring. J. Chem. Phys. 2013, 138, 164124. [Google Scholar] [CrossRef]
- Porta, S.; Privitera, L.; Traverso Ziani, N.; Sassetti, M.; Cavaliere, F.; Trauzettel, B. Feasible model for photoinduced interband pairing. Phys. Rev. B 2019, 100, 024513. [Google Scholar] [CrossRef]
- Vu, D.; Das Sarma, S. One-dimensional few-electron effective Wigner crystal in quantum and classical regimes. Phys. Rev. B 2020, 101, 125113. [Google Scholar] [CrossRef]
- Mayrhofer, L.; Grifoni, M. Linear and nonlinear transport across carbon nanotube quantum dots. Eur. Phys. J. B 2007, 56, 107. [Google Scholar] [CrossRef]
- Friedel, J. Effect of impurities on the electronic density in metals. Nuovo Cimento 1958, 7, 287. [Google Scholar] [CrossRef]
- Jauregui, K.; Häusler, W.; Kramer, B. Wigner Molecules in Nanostructures. Europhys. Lett. 1993, 24, 581. [Google Scholar] [CrossRef]
- Schulz, H.J. Wigner crystal in one dimension. Phys. Rev. Lett. 1993, 71, 1864. [Google Scholar] [CrossRef] [PubMed]
- Fiete, G.A. Colloquium: The spin-incoherent Luttinger liquid. Rev. Mod. Phys. 2007, 79, 801. [Google Scholar] [CrossRef]
- Giamarchi, T. Quantum Physics in One Dimension; Science: Oxford, UK, 2004. [Google Scholar]
- Fabrizio, M.; Gogolin, A.O. Interacting one-dimensional electron gas with open boundaries. Phys. Rev. B 1995, 51, 17827. [Google Scholar] [CrossRef]
- Dolcetto, G.; Traverso Ziani, N.; Biggio, M.; Cavaliere, F.; Sassetti, M. Coulomb blockade microscopy of spin-density oscillations and fractional charge in quantum spin Hall dots. Phys. Rev. B 2013, 87, 235423. [Google Scholar] [CrossRef]
- Fleckenstein, C.; Traverso Ziani, N.; Trauzettel, B. Chiral anomaly in real space from stable fractional charges at the edge of a quantum spin Hall insulator. Phys. Rev. B 2016, 94, 241406. [Google Scholar] [CrossRef]
- Traverso Ziani, N.; Fleckenstein, C.; Vigliotti, L.; Trauzettel, B.; Sassetti, M. From fractional solitons to Majorana fermions in a paradigmatic model of topological superconductivity. Phys. Rev. B 2020, 101, 195303. [Google Scholar] [CrossRef]
- Fleckenstein, C.; Traverso Ziani, N.; Privitera, L.; Sassetti, M.; Trauzettel, B. Transport signatures of a Floquet topological transition at the helical edge. Phys. Rev. B 2020, 101, 201401. [Google Scholar] [CrossRef]
- Voit, J. One-dimensional Fermi liquids. Rep. Prog. Phys. 1995, 58, 977. [Google Scholar] [CrossRef]
- Fleckenstein, C.; Traverso Ziani, N.; Trauzettel, B. Z4 parafermions in Weakly Interacting Superconducting Constrictions at the Helical Edge of Quantum Spin Hall Insulators. Phys. Rev. Lett. 2020, 122, 066801. [Google Scholar] [CrossRef]
- Gindikin, Y.; Sablikov, V.A. Deformed Wigner crystal in a one-dimensional quantum dot. Phys. Rev. B 2007, 76, 045122. [Google Scholar] [CrossRef]
- Söffing, S.A.; Bortz, M.; Schneider, I.; Struck, A.; Eggert, S.F. Wigner crystal versus Friedel oscillations in the one-dimensional Hubbard model. Phys. Rev. B 2009, 79, 195114. [Google Scholar] [CrossRef]
- Kane, C.; Balents, L.; Fisher, M.P.A. Coulomb Interactions and Mesoscopic Effects in Carbon Nanotubes. Phys. Rev. Lett. 1997, 79, 5086. [Google Scholar] [CrossRef]
- Traverso Ziani, N.; Fleckenstein, C.; Dolcetto, G.; Trauzettel, B. Fractional charge oscillations in quantum dots with quantum spin Hall effect. Phys. Rev. B 2017, 95, 205418. [Google Scholar] [CrossRef]
- Egger, R.; Gogolin, A.O. Effective Low-Energy Theory for Correlated Carbon Nanotubes. Phys. Rev. Lett. 1997, 79, 5082. [Google Scholar] [CrossRef]
- Zhang, F.; Kane, C.L. Time-Reversal-Invariant Z4 Fractional Josephson Effect. Phys. Rev. Lett. 2014, 113, 036401. [Google Scholar] [CrossRef]
- Orth, C.P.; Tiwari, R.P.; Meng, T.; Schmidt, T.L. Non-Abelian parafermions in time-reversal-invariant interacting helical systems. Phys. Rev. B 2015, 91, 081406. [Google Scholar] [CrossRef]
- Dolcetto, G.; Traverso Ziani, N.; Biggio, M.; Cavaliere, F.; Sassetti, M. Spin textures of strongly correlated spin Hall quantum dots. Phys. Stat. Sol. (RRL) 2013, 7, 1059. [Google Scholar] [CrossRef]
- Traverso Ziani, N.; Crepin, F.; Trauzettel, B. Fractional Wigner crystal in the Helical Luttinger Liquid. Phys. Rev. Lett. 2015, 115, 206402. [Google Scholar] [CrossRef] [PubMed]
- Kane, C.L.; Fisher, M.P.A. Transport in a one-channel Luttinger liquid. Phys. Rev. Lett. 1992, 68, 1220. [Google Scholar] [CrossRef] [PubMed]
- Safi, I.; Schulz, H.J. Interacting electrons with spin in a one-dimensional dirty wire connected to leads. Phys. Rev. B 1999, 59, 3040. [Google Scholar] [CrossRef]
- Traverso Ziani, N.; Cavaliere, F.; Sassetti, M. Signatures of Wigner correlations in the conductance of a one-dimensional quantum dot coupled to an AFM tip. Phys. Rev. B 2012, 86, 125451. [Google Scholar] [CrossRef]
- Traverso Ziani, N.; Cavaliere, F.; Sassetti, M. Temperature-induced emergence of Wigner correlations in a STM-probed one-dimensional quantum dot. New J. Phys. 2013, 15, 063002. [Google Scholar] [CrossRef]
- Schulz, H.J. Correlation exponents and the metal-insulator transition in the one-dimensional Hubbard model. Phys. Rev. Lett. 1990, 64, 2831. [Google Scholar] [CrossRef]
- Aizenman, M.; Jansen, S.; Jung, P. Symmetry Breaking in Quasi-1D Coulomb Systems. Ann. Henri Poincaré 2010, 11, 1453. [Google Scholar] [CrossRef][Green Version]
- Jansen, S.; Jung, P. Wigner Crystallization in the Quantum 1D Jellium at All Densities. Comm. Math. Phys. 2014, 331, 1133. [Google Scholar] [CrossRef]
- Hirsch, C.; Jansen, S.; Jung, P. Large deviations in the quantum quasi-1D jellium. arXiv 2009, arXiv:2009.14144. [Google Scholar]
- Fiete, G.A.; Le Hur, K.; Balents, L. Coulomb drag between two spin-incoherent Luttinger liquids. Phys. Rev. B 2006, 73, 165104. [Google Scholar] [CrossRef]
- Matveev, K.A. Conductance of a Quantum Wire in the Wigner-Crystal Regime. Phys. Rev. Lett. 2004, 92, 106801. [Google Scholar] [CrossRef] [PubMed]
- Häusler, W. Correlations in quantum dots. Z. Phys. B 1996, 99, 551. [Google Scholar] [CrossRef]
- Lieb, E.; Mattis, D. Theory of Ferromagnetism and the Ordering of Electronic Energy Levels. Phys. Rev. 1962, 125, 164. [Google Scholar] [CrossRef]
- Mahan, G.D. Electron–optical phonon interaction in carbon nanotubes. Phys. Rev. B 2003, 68, 125409. [Google Scholar] [CrossRef]
- Franchini, F. An Introduction to Integrable Techniques for One-Dimensional Quantum Systems; Springer: Berlin/Heidelberg, Germany, 2017; Volume 940. [Google Scholar]
- Porta, S.; Cavaliere, F.; Sassetti, M.; Traverso Ziani, N. Topological classification of dynamical quantum phase transitions in the xy chain. Sci. Rep. 2020, 10, 1. [Google Scholar] [CrossRef]
- Matveev, K.A.; Furusaki, A.; Glazman, L.I. Asymmetric Zero-Bias Anomaly for Strongly Interacting Electrons in One Dimension. Phys. Rev. Lett. 2007, 98, 096403. [Google Scholar] [CrossRef]
- Matveev, K.A.; Furusaki, A.; Glazman, L.I. Bosonization of strongly interacting one-dimensional electrons. Phys. Rev. B 2007, 76, 155440. [Google Scholar] [CrossRef]
- Secchi, A.; Rontani, M. Spectral function of few electrons in quantum wires and carbon nanotubes as a signature of Wigner localization. Phys. Rev. B 2012, 85, 121410. [Google Scholar] [CrossRef]
- Cavaliere, F.; Traverso Ziani, N.; Negro, F.; Sassetti, M. Thermally enhanced Wigner oscillations in two-electron 1D quantum dots. J. Phys. Condens. Matter 2014, 26, 505301. [Google Scholar] [CrossRef]
- Kylänpää, I.; Cavaliere, F.; Traverso Ziani, N.; Sassetti, M.; Räsänen, E. Thermal effects on the Wigner localization and Friedel oscillations in many-electron nanowires. Phys. Rev. B 2016, 94, 115417. [Google Scholar] [CrossRef]
- Diaz-Marquez, A.; Battaglia, S.; Bendazzoli, G.L.; Evangelisti, S.; Leininger, T.; Berger, J.A. Signatures of Wigner localization in one-dimensional systems. J. Chem. Phys. 2018, 148, 124103. [Google Scholar] [CrossRef] [PubMed]
- Azor, M.E.; Brooke, L.; Evangelisti, S.; Leininger, T.; Loos, P.F.; Suaud, N.; Berger, J.A. A Wigner molecule at extremely low densities: A numerically exact study. SciPost Phys. Core 2019, 1, 001. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56. [Google Scholar] [CrossRef]
- Bockrath, M.; Cobden, D.H.; McEuen, D.L.; Chopra, N.G.; Zettl, A.; Thess, A.; Smalley, R.E. Single-Electron Transport in Ropes of Carbon Nanotubes. Science 1997, 725, 1922. [Google Scholar] [CrossRef] [PubMed]
- Tans, S.J.; Devoret, M.H.; Dai, H.; Thess, A.; Smalley, R.E.; Geerligs, L.J.; Dekker, C. Individual single-wall carbon nanotubes as quantum wires. Nature 1997, 386, 474. [Google Scholar] [CrossRef]
- Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Physical Properties of Carbon Nanotubes; Imperial College Press: London, UK, 1998. [Google Scholar]
- Cobden, D.H.; Nygard, J. Shell Filling in Closed Single-Wall Carbon Nanotube Quantum Dots. Phys. Rev. Lett. 2002, 89, 046803. [Google Scholar] [CrossRef]
- Charlier, J.-C.; Blase, X.; Roche, S. Electronic and transport properties of nanotubes. Rev. Mod. Phys. 2007, 79, 677. [Google Scholar] [CrossRef]
- Hüttel, A.K.; Steele, G.A.; Witkamp, B.; Poot, M.; Kouwenhoven, L.P.; van der Zant, H.S.J. Bending-Mode Vibration of a Suspended Nanotube Resonatorpubs. Nano Lett. 2009, 9, 2547. [Google Scholar]
- Laird, A.E.; Kuemmeth, F.; Steele, G.A.; Grove-Rasmussen, K.; Nygard, J.; Flensberg, K.; Kouwenhoven, L.P. Quantum transport in carbon nanotubes. Rev. Mod. Phys. 2015, 87, 703. [Google Scholar] [CrossRef]
- Rohling, N.; Burkard, G. Universal quantum computing with spin and valley states. New J. Phys. 2012, 14, 083008. [Google Scholar] [CrossRef]
- Wang, Y. Exact solution of a spin-ladder model. Phys. Rev. B 1999, 60, 9236. [Google Scholar] [CrossRef]
- Batchelor, M.T.; Guan, X.W.; Oelkers, N.; Ying, Z.J. Quantum Phase Diagram of an Exactly Solved Mixed Spin Ladder. J. Stat. Phys. 2004, 116, 571. [Google Scholar] [CrossRef]
- Traverso Ziani, N.; Cavaliere, F.; Sassetti, M. Theory of the STM detection of Wigner molecules in spin-incoherent CNTs. Europhys. Lett. 2013, 102, 47006. [Google Scholar] [CrossRef]
- Secchi, A.; Rontani, M. Wigner molecules in carbon-nanotube quantum dots. Phys. Rev. B 2010, 82, 035417. [Google Scholar] [CrossRef]
- Secchi, A.; Rontani, M. Intervalley scattering induced by Coulomb interaction and disorder in carbon-nanotube quantum dots. Phys. Rev. B 2013, 88, 125403. [Google Scholar] [CrossRef]
- Gambetta, F.M.; Traverso Ziani, N.; Barbarino, S.; Cavaliere, F.; Sassetti, M. Anomalous Friedel oscillations in a quasihelical quantum dot. Phys. Rev. B 2015, 91, 235421. [Google Scholar] [CrossRef]
- Kornich, V.; Pedder, C.J.; Schmidt, T.L. Spin-orbit coupling in quasi-one-dimensional Wigner crystals. Phys. Rev. B 2017, 95, 045413. [Google Scholar] [CrossRef]
- Jespersen, T.; Grove, F.; Paaske, J.; Muraki, K.; Fujisawa, T.; Nygard, J.; Flensberg, K. Gate-dependent spin–orbit coupling in multielectron carbon nanotubes. Nat. Phys. 2011, 7, 348. [Google Scholar] [CrossRef]
- Deshpande, V.V.; Bockrath, M. The one-dimensional Wigner crystal in carbon nanotubes. Nat. Phys. 2008, 4, 314. [Google Scholar] [CrossRef]
- Levitov, S.L.; Tsvelik, A.M. Narrow-Gap Luttinger Liquid in Carbon Nanotubes. Phys. Rev. Lett. 2003, 90, 016401. [Google Scholar] [CrossRef]
- Sarkány, L.; Szirmai, E.; Moca, C.P.; Glazman, L.I.; Zarand, G. Wigner crystal phases in confined carbon nanotubes. Phys. Rev. B 2017, 95, 115433. [Google Scholar] [CrossRef]
- Pecker, S.; Kuemmeth, F.; Secchi, A.; Rontani, M.; Ralph, D.C.; McEuen, P.L.; Ilani, S. Observation and spectroscopy of a two-electron Wigner molecule in an ultraclean carbon nanotube. Nat. Phys. 2013, 9, 576. [Google Scholar] [CrossRef]
- Shapir, I.; Hamo, A.; Pecker, S.; Moca, C.P.; Legeza, O.; Zarand, G.; Ilani, S. Imaging the electronic Wigner crystal in one dimension. Science 2019, 364, 870. [Google Scholar] [CrossRef] [PubMed]
- Qian, J.; Halperin, B.I.; Heller, E.J. Imaging and manipulating electrons in a one-dimensional quantum dot with Coulomb blockade microscopy. Phys. Rev. B 2010, 81, 125323. [Google Scholar] [CrossRef]
- Boyd, E.E.; Westervelt, R.M. Extracting the density profile of an electronic wave function in a quantum dot. Phys. Rev. B 2011, 84, 205308. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).