Convective Transport of Fluid–Solid Interaction: A Study between Non-Newtonian Casson Model with Dust Particles
Abstract
1. Introduction
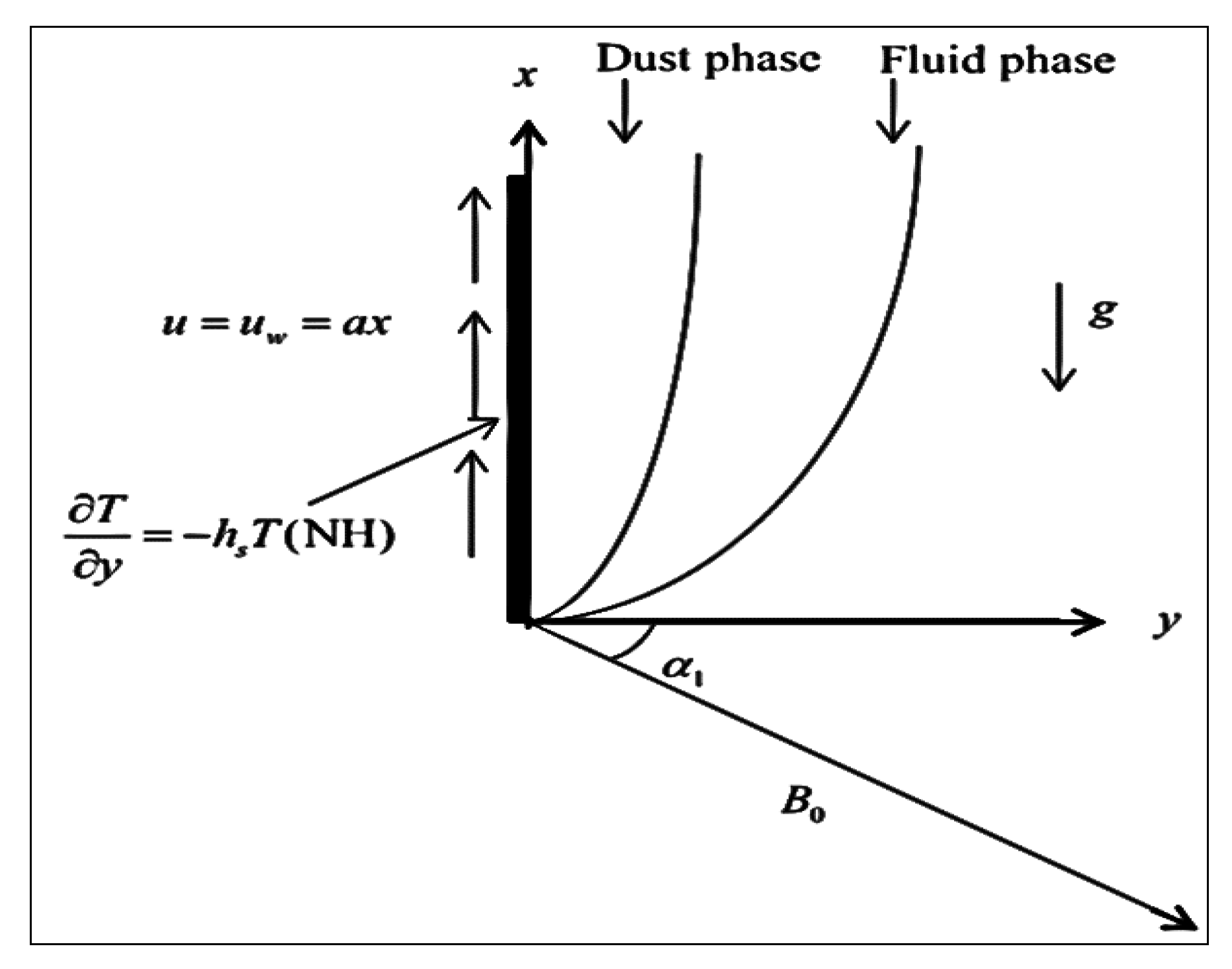
2. Problem Formulation
3. Numerical Procedure
4. Results and Discussion
5. Conclusions
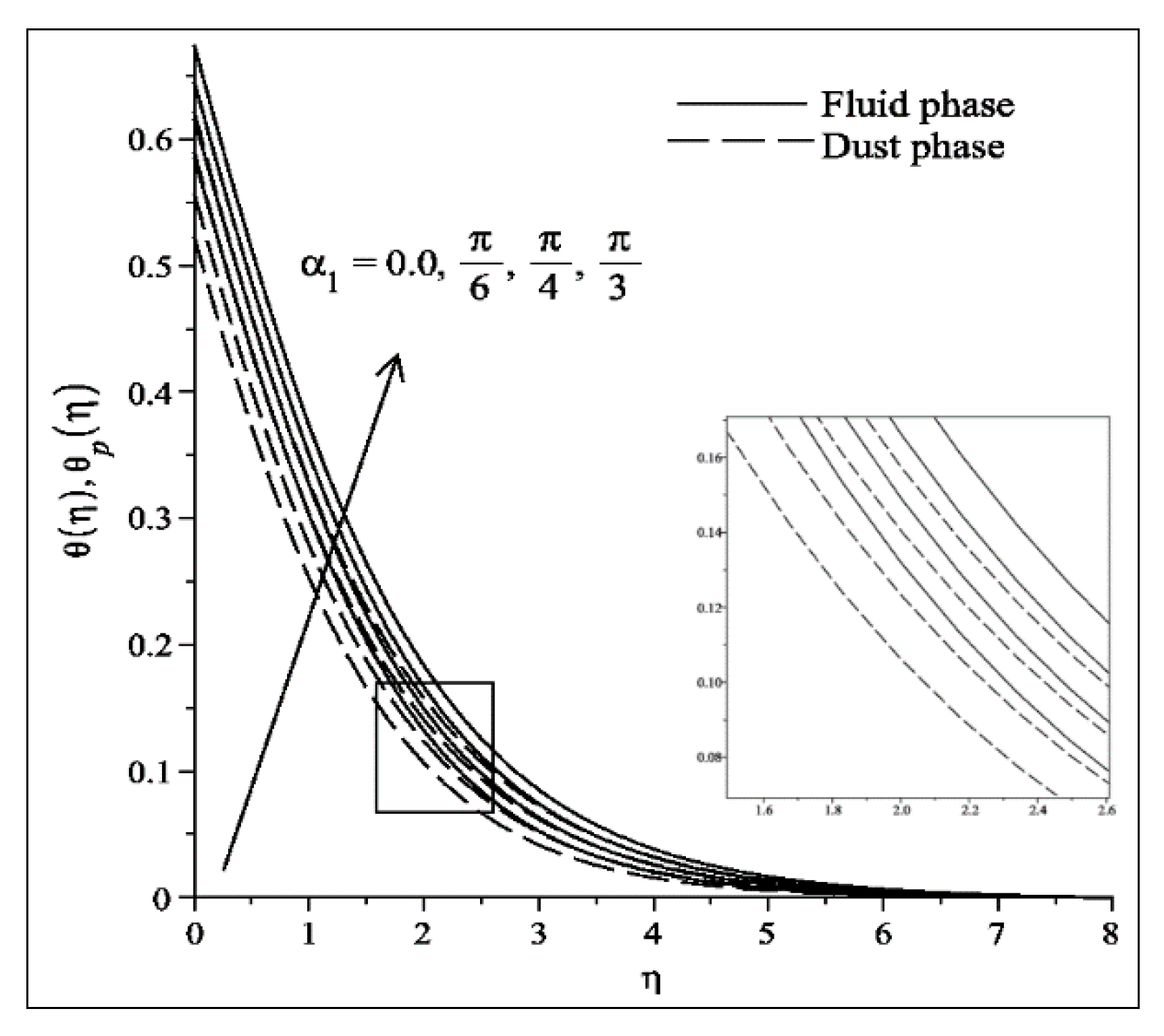
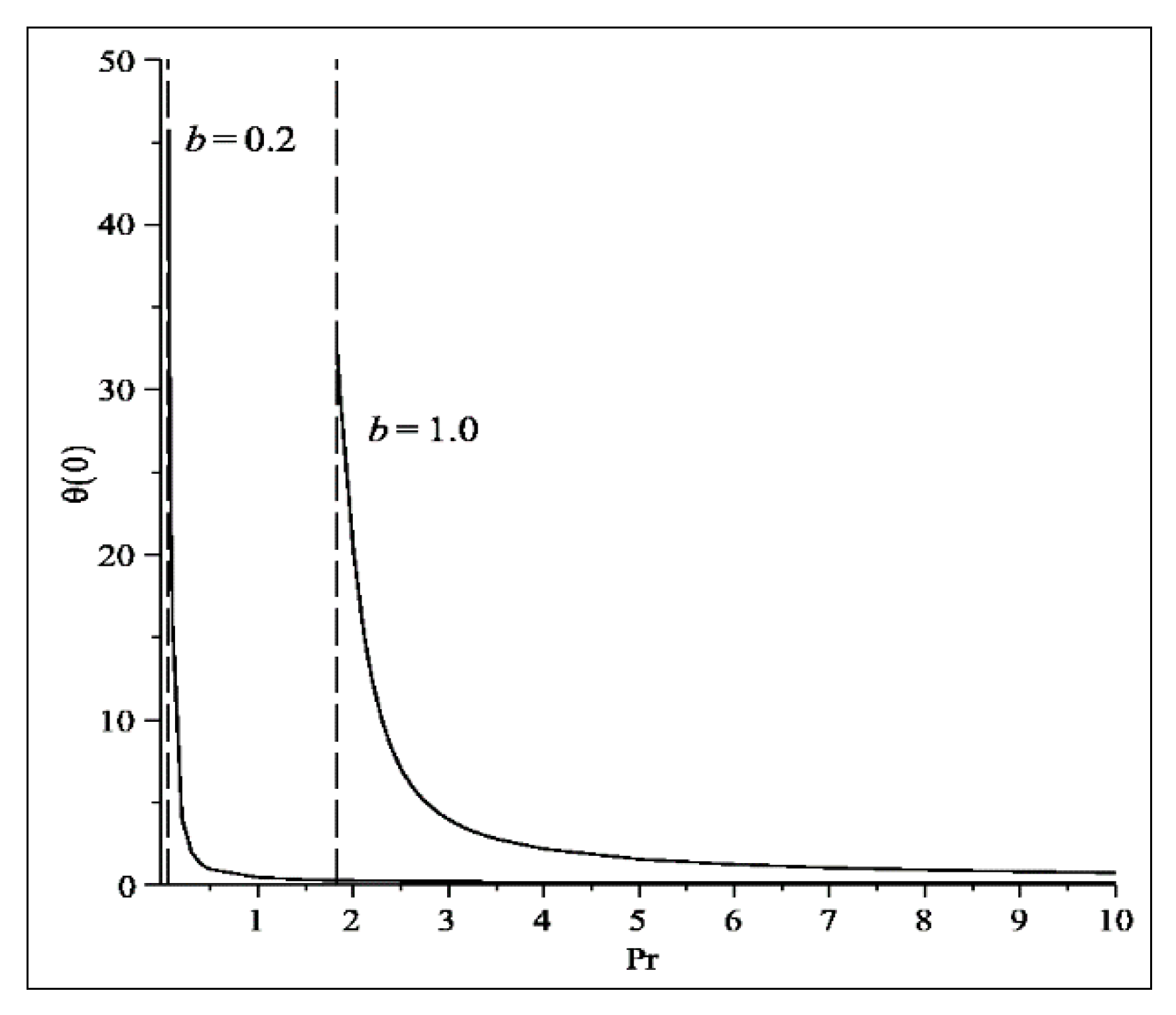
- The distributions of and provide an important insight into the circumstances that happen on the surface of the sheet.
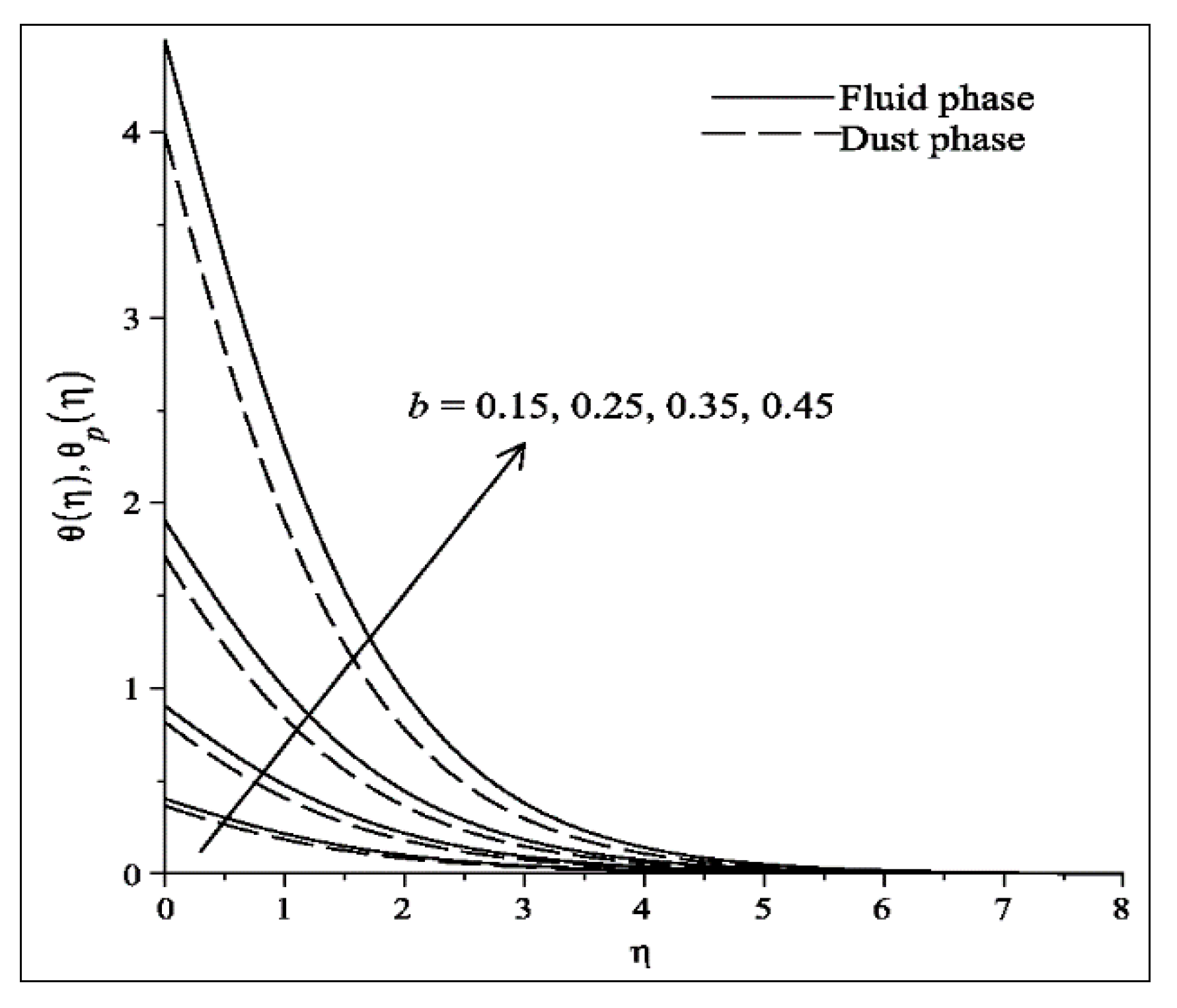
- The dust particle is found to be the reasoning factor, which decreases fluid transport and increases the fluid heating process, when is increased.
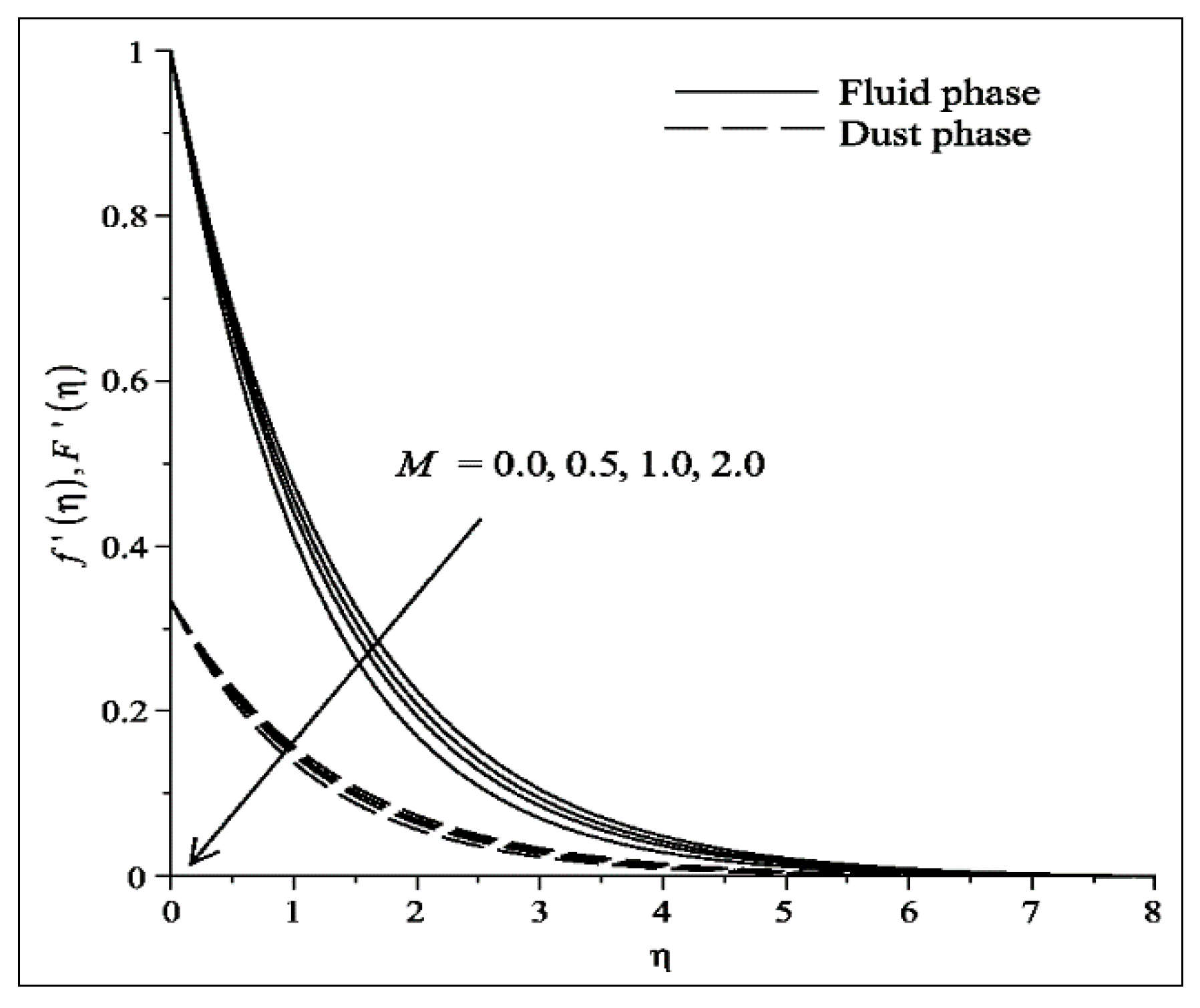
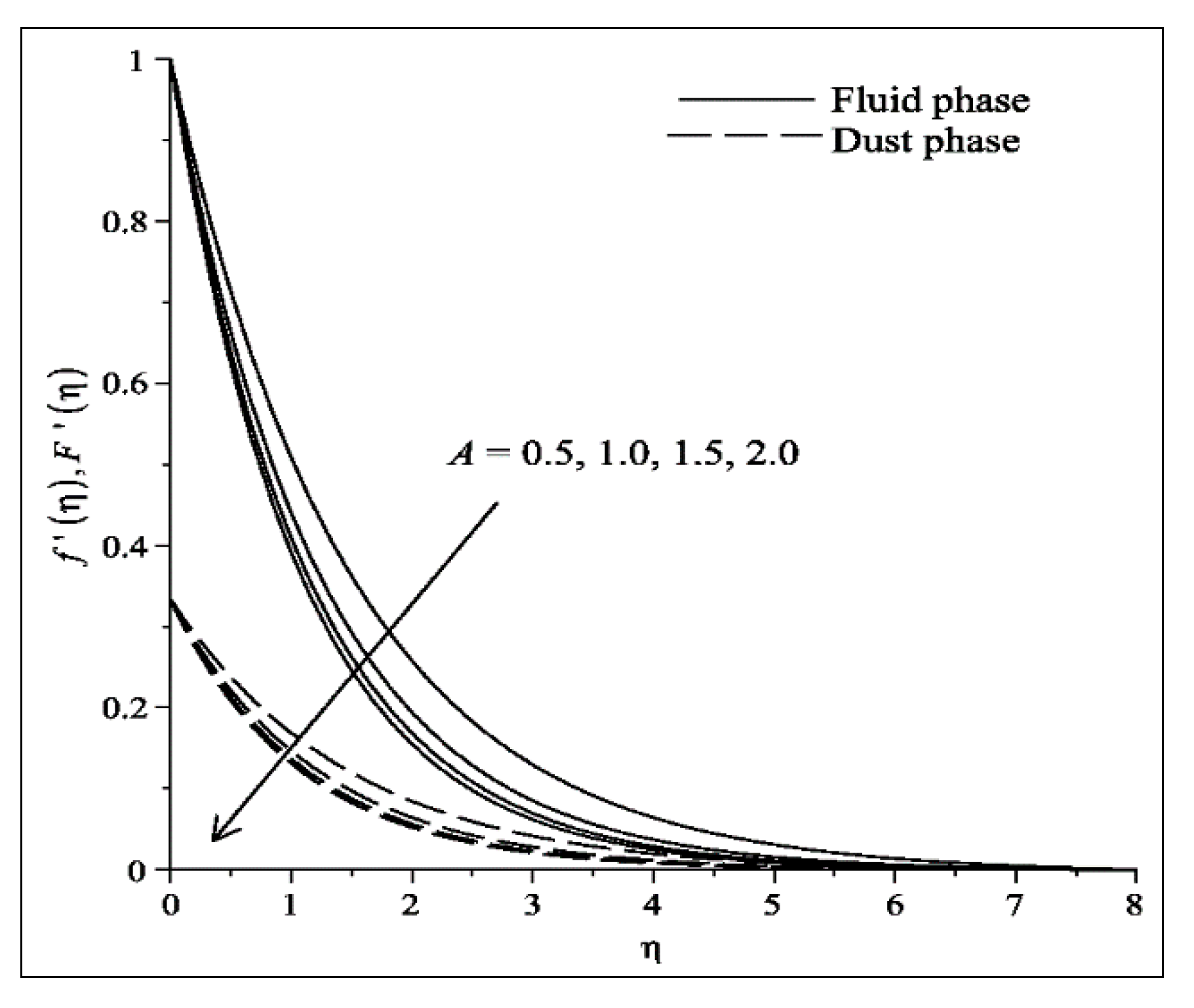
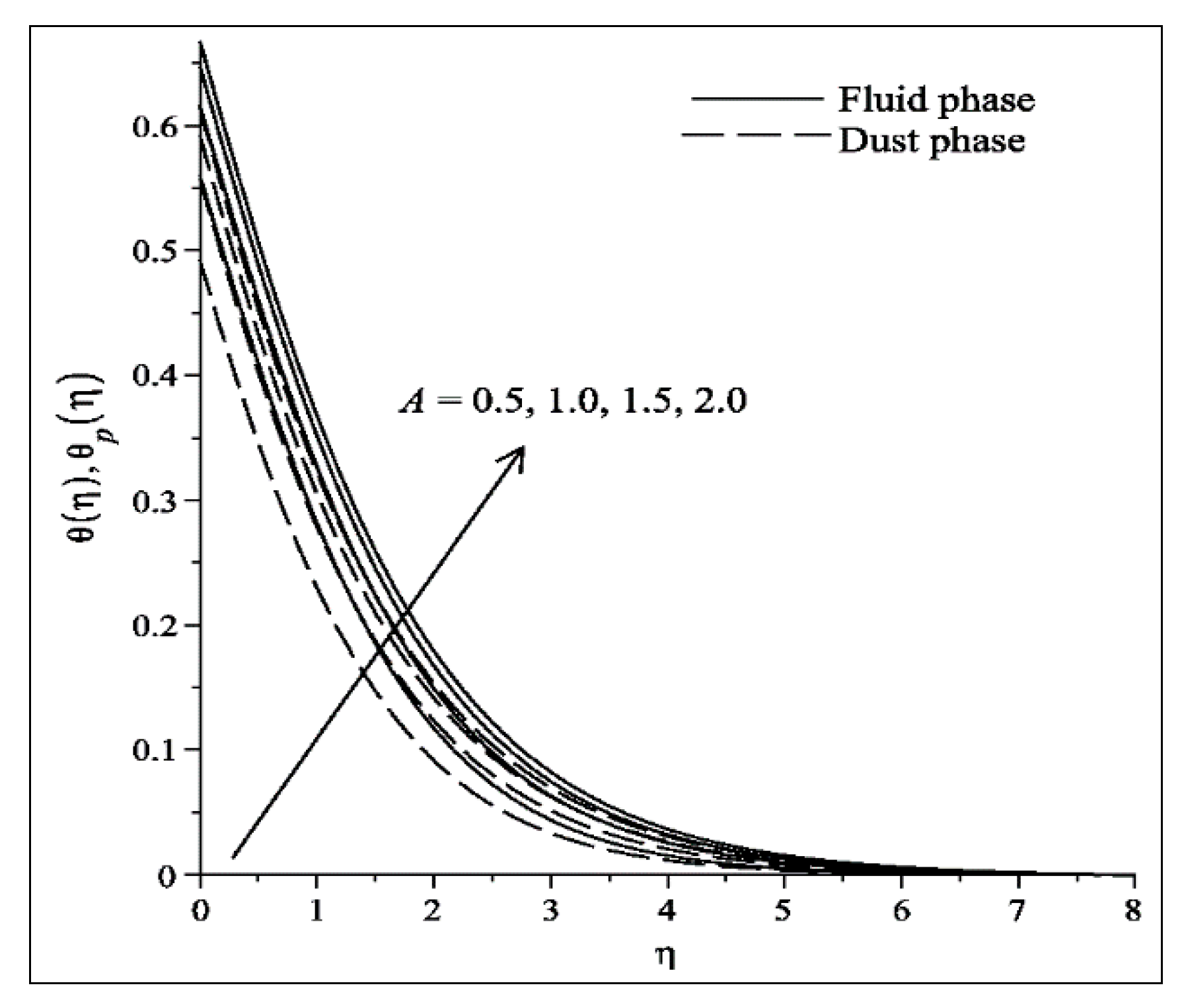
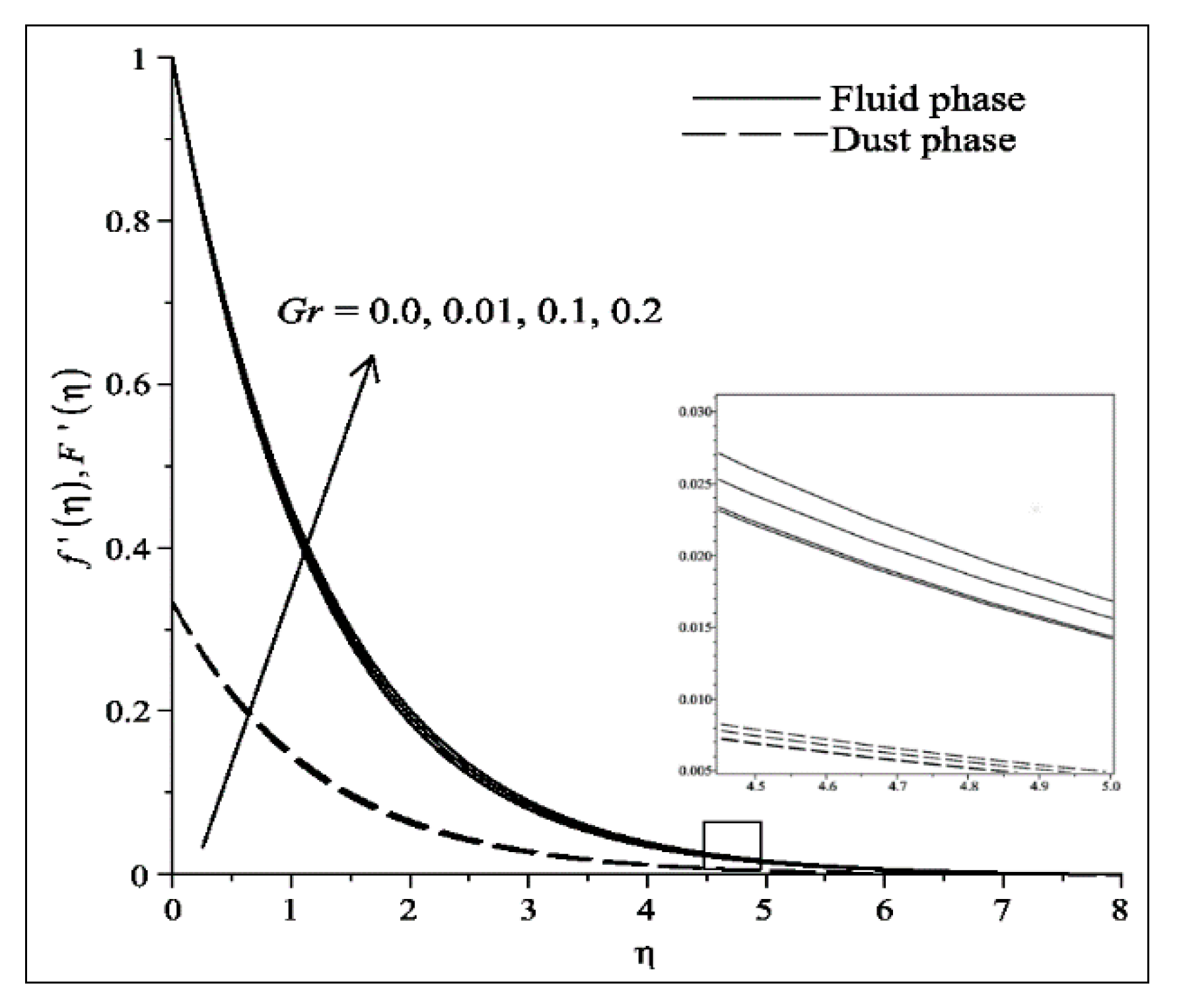
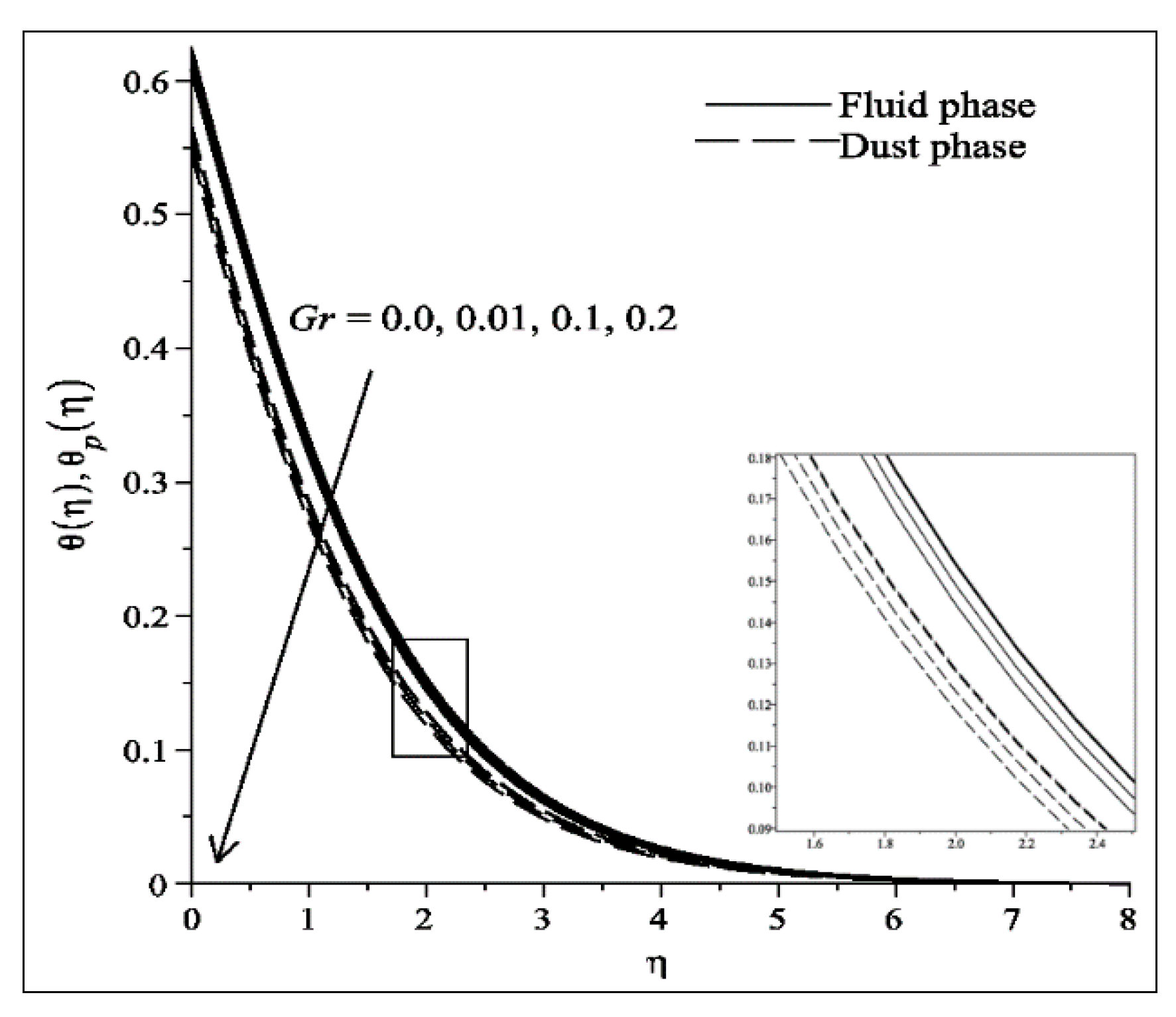
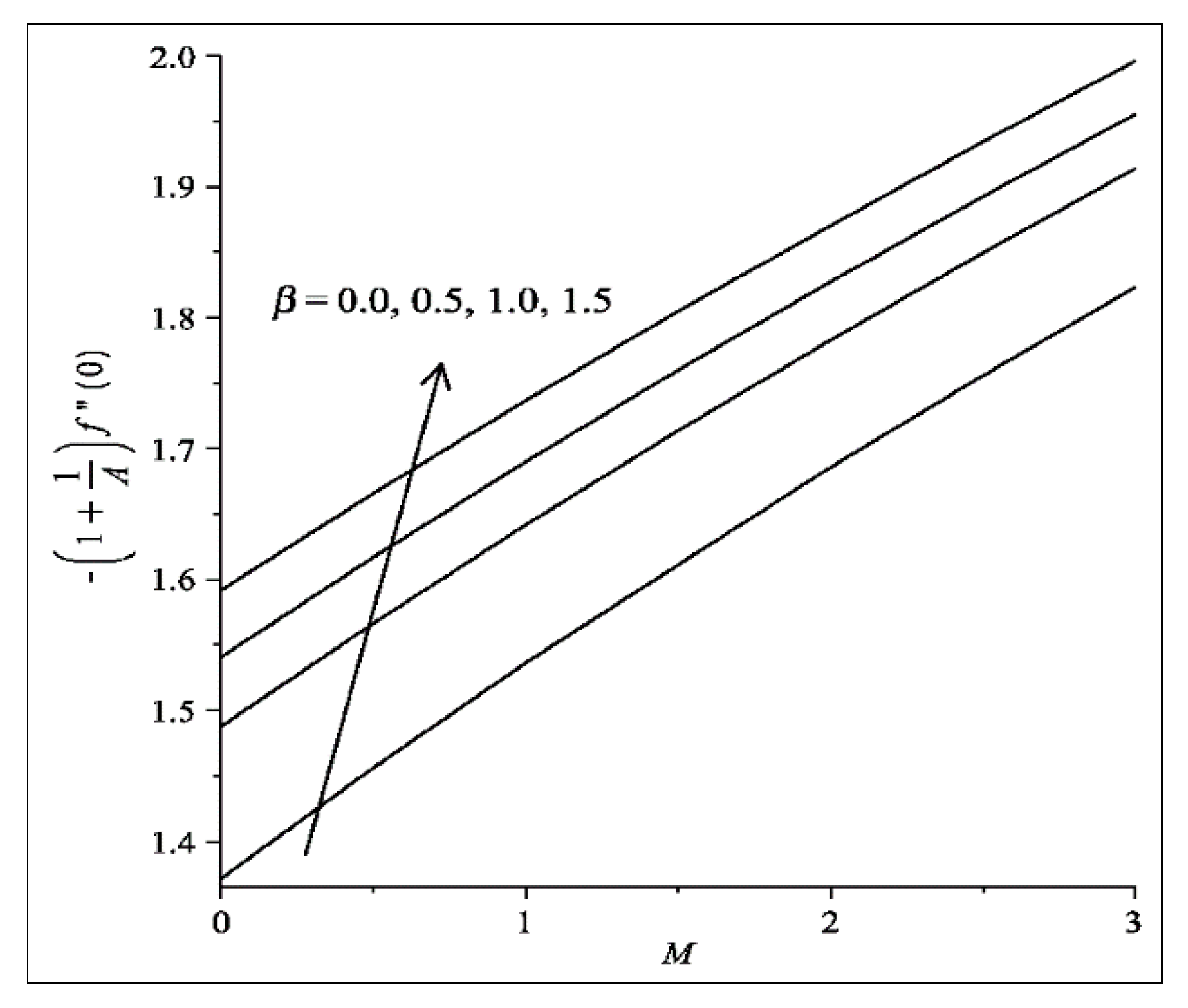
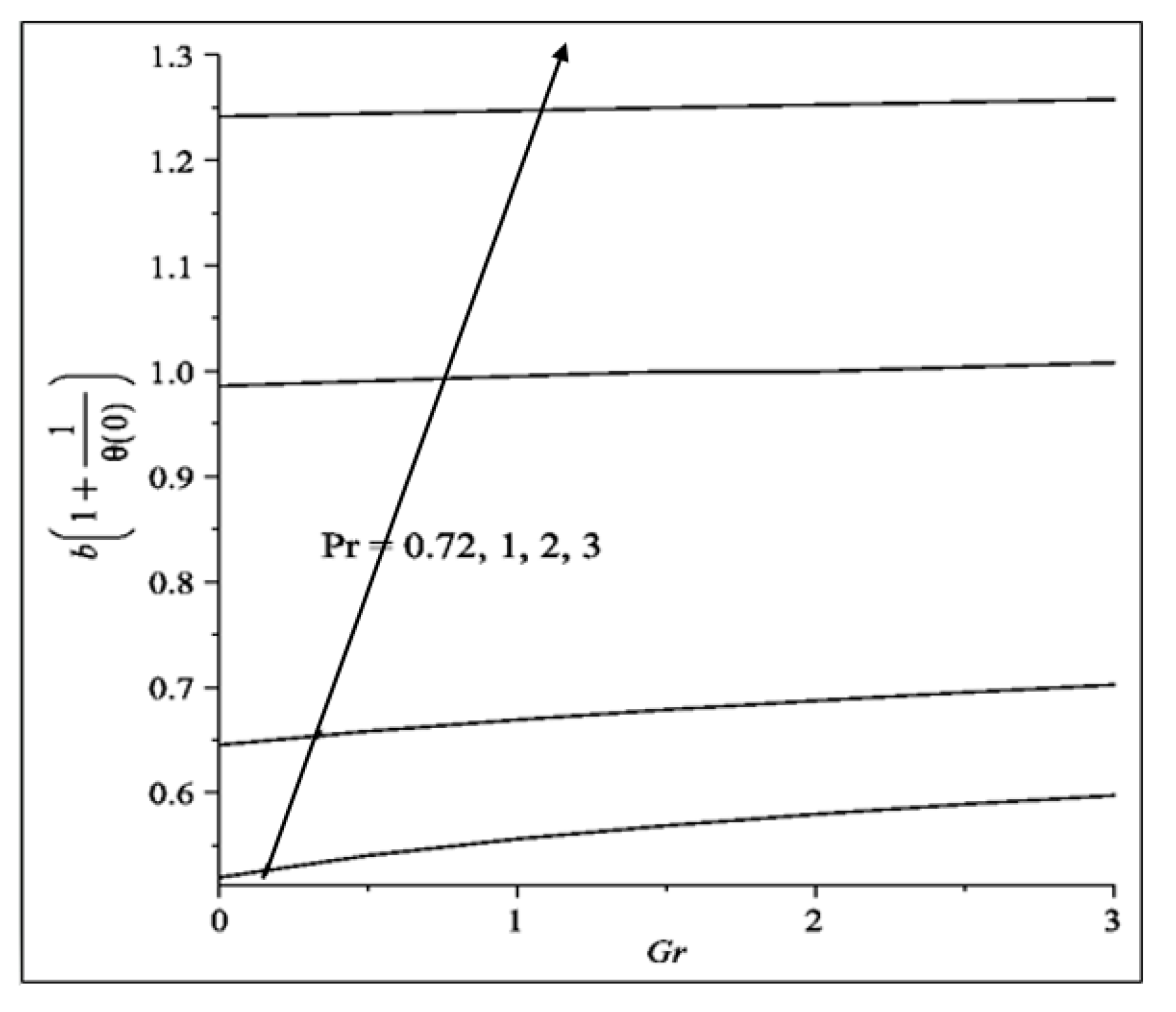
- The velocities of fluid and dust particles (temperature) decreases (increases) with the increase in and .
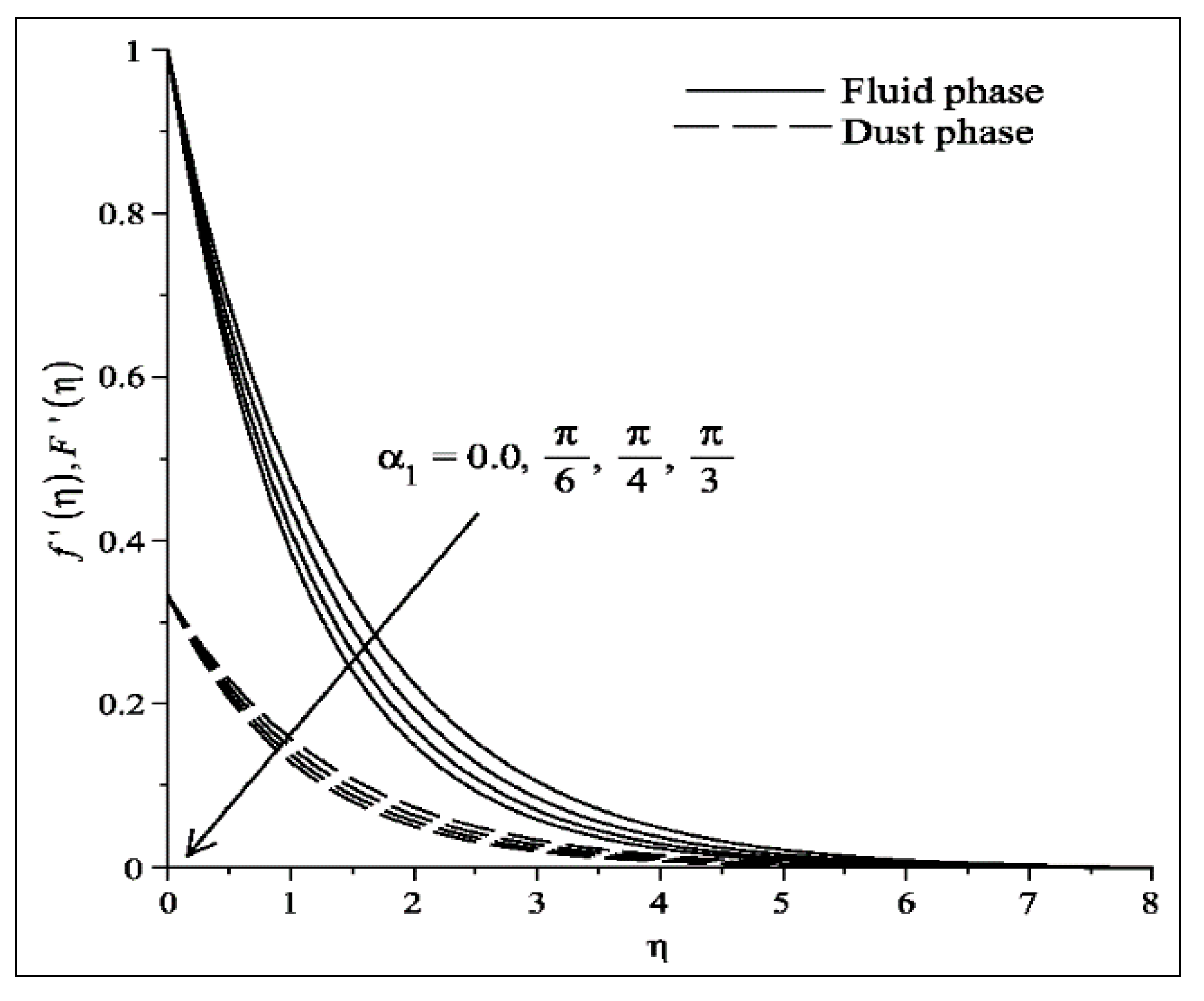
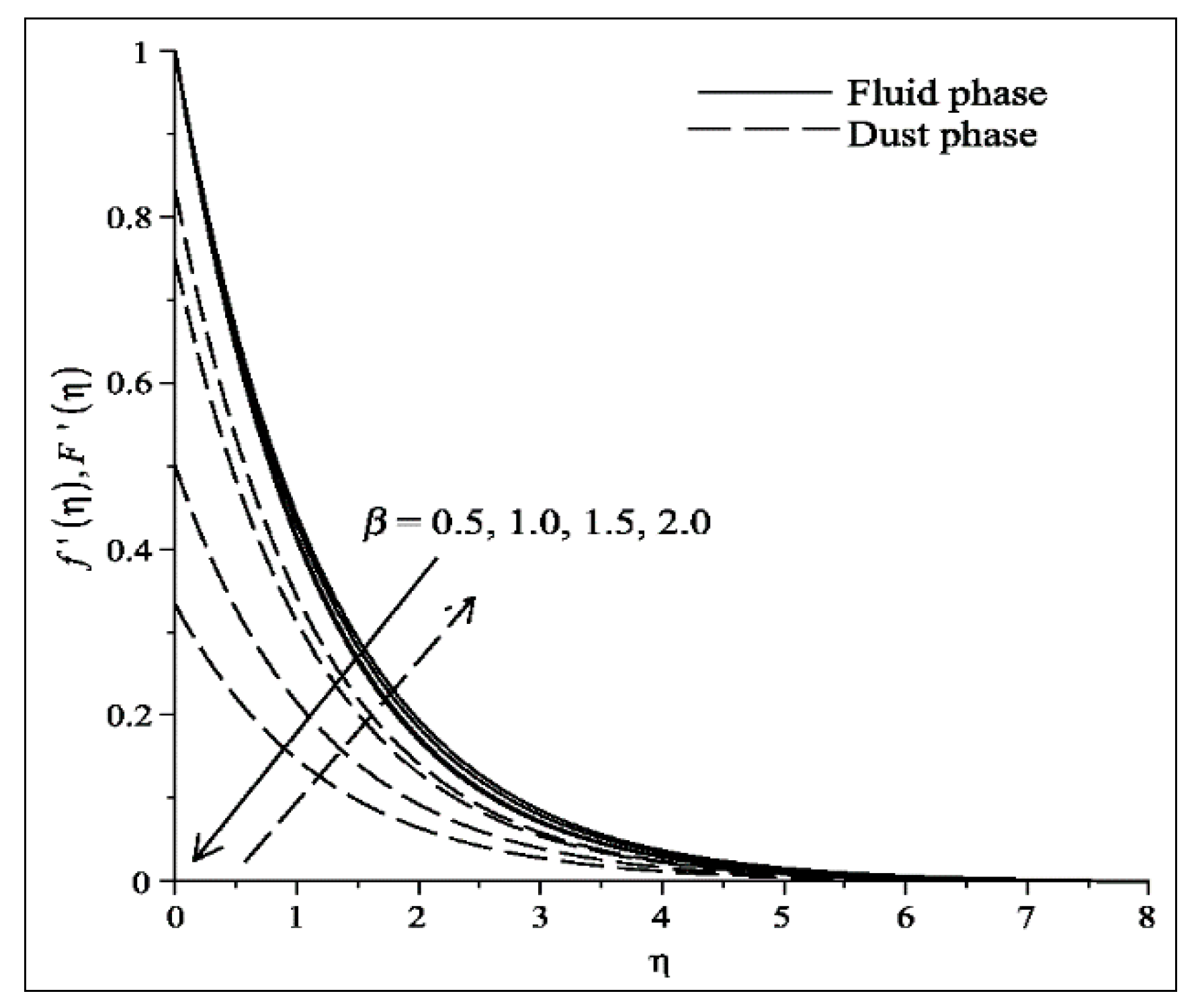
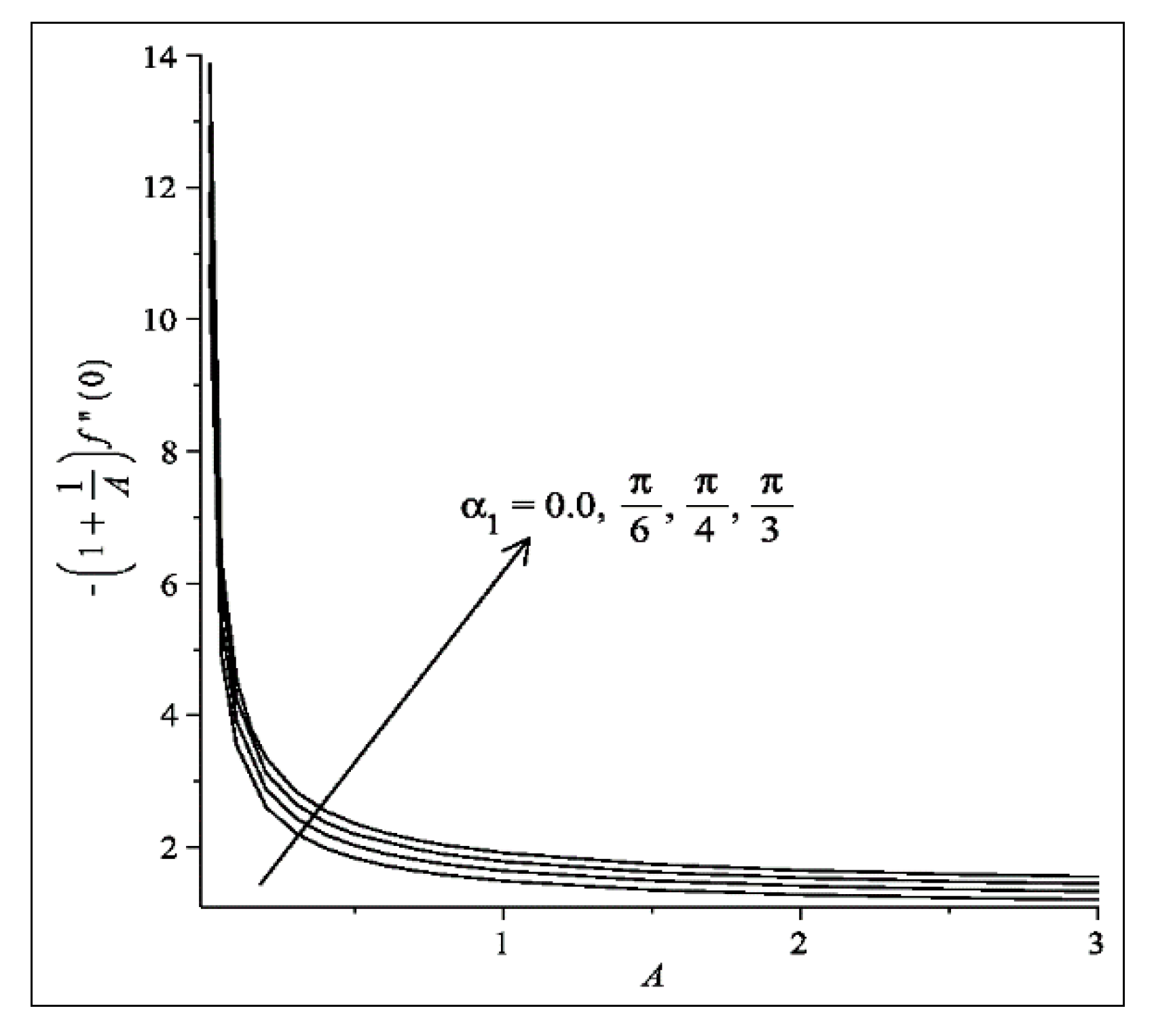
- The velocity (temperature) profile of fluid and dust phases increases (decreases) as is increased.
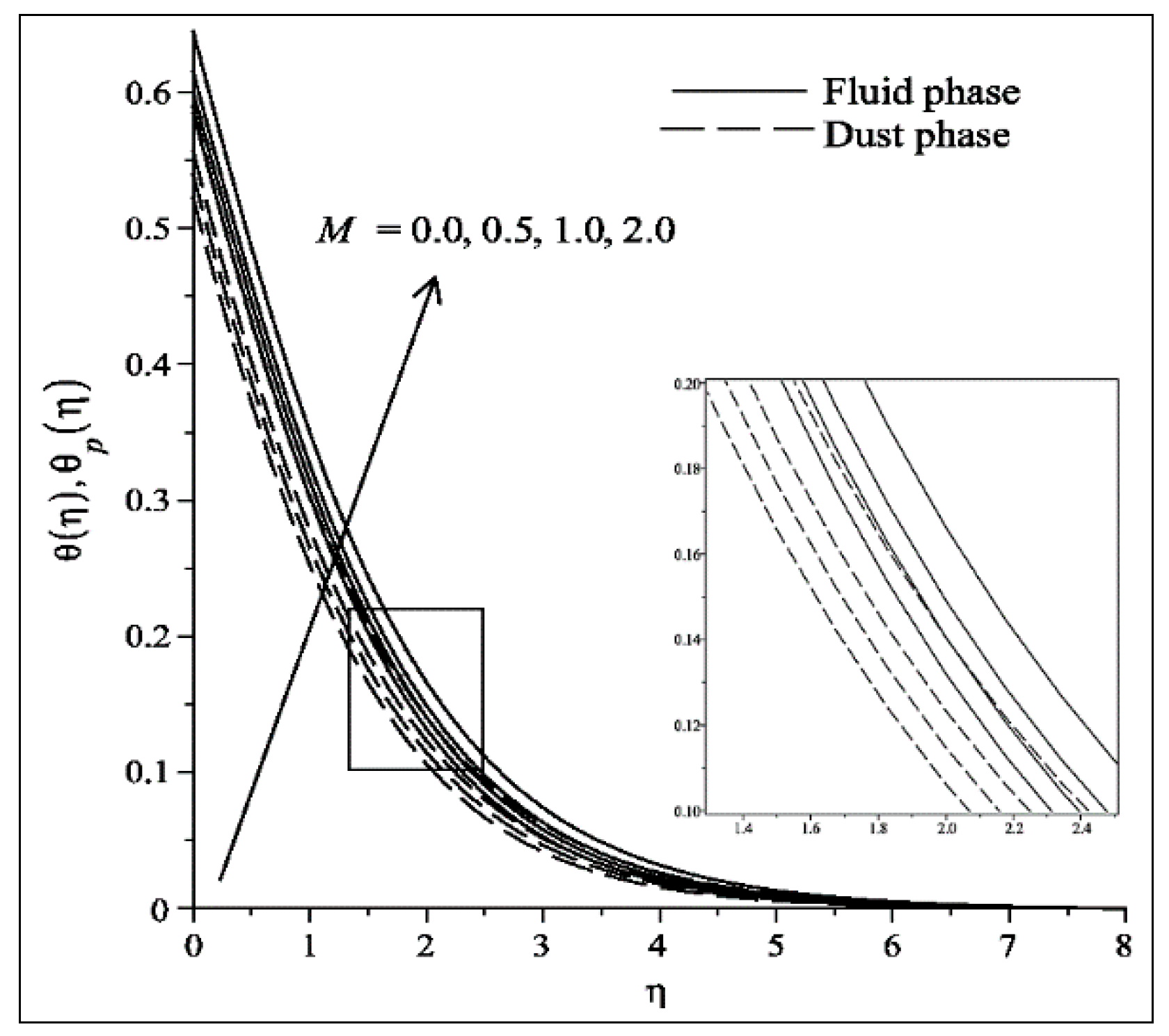
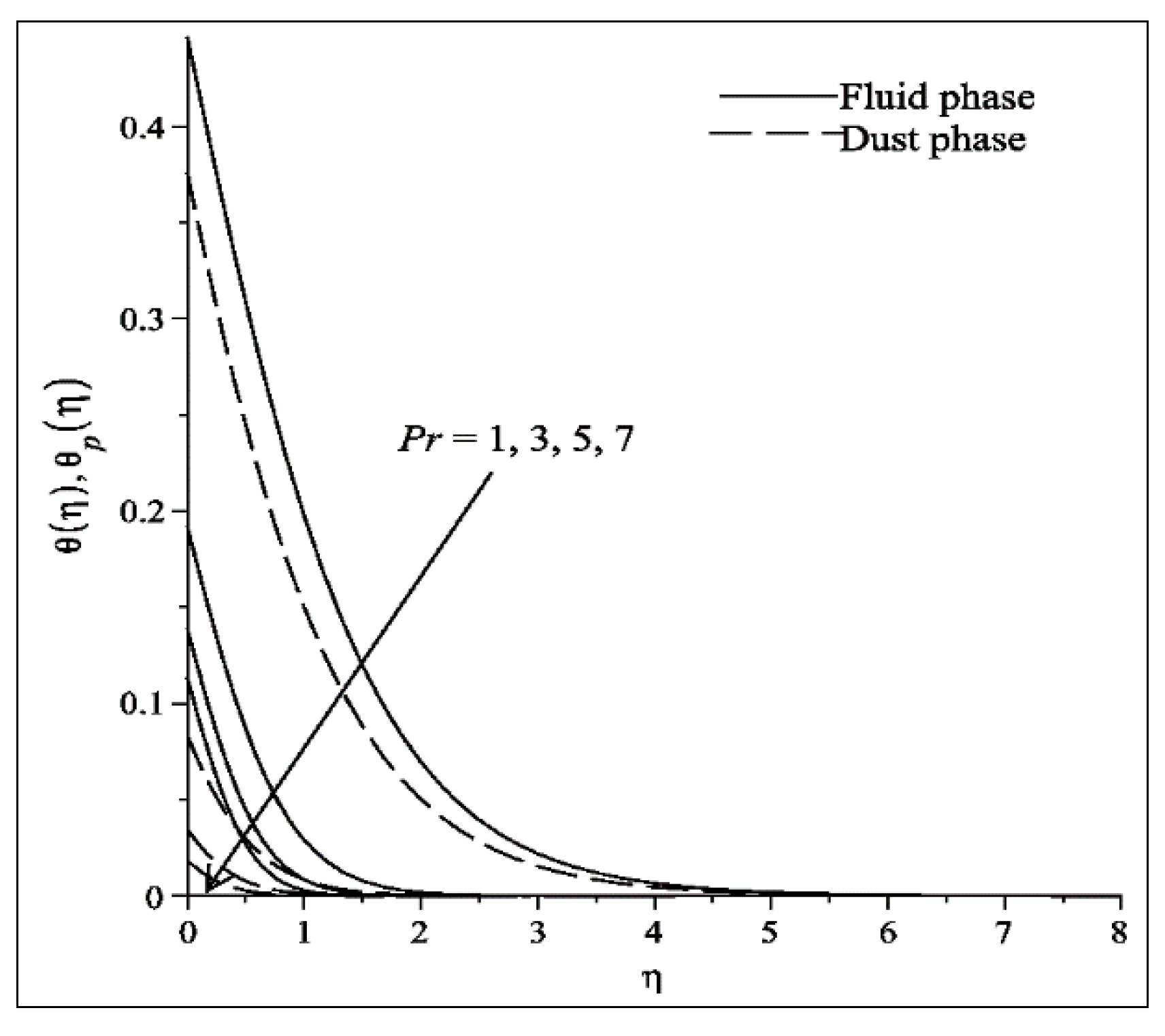
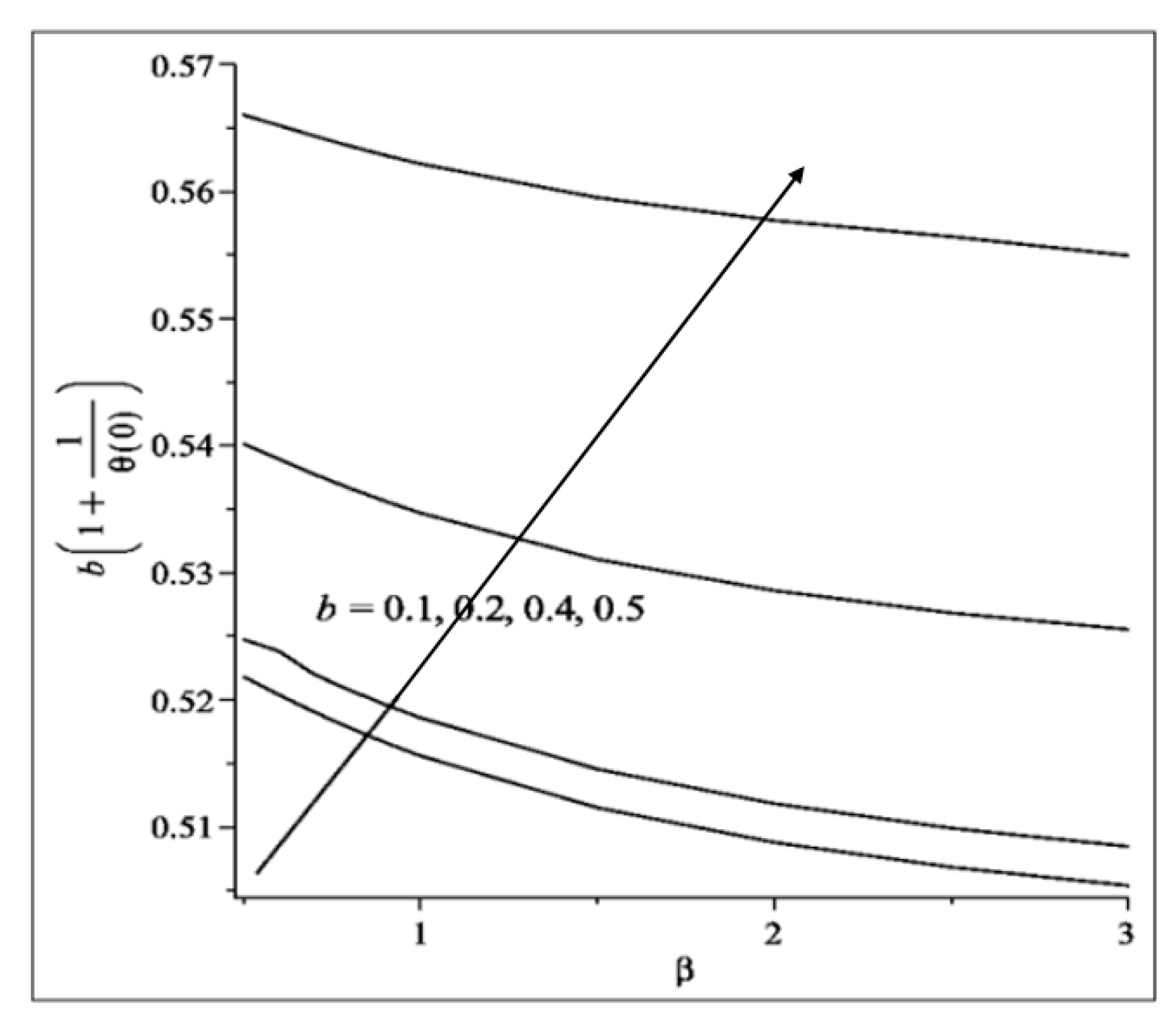
- The temperature profile of both fluid and dust phases increases as increases. Conversely, a reverse trend is clearly depicted when grows.
- The skin friction coefficient and Nusselt number possess the similar behavior under the effects of and . Meanwhile, an opposite trend in Nusselt number is noticed with the presence of and .
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| components of fluid velocity along and direction | |
| fluid’s temperature | |
| particle’s temperature | |
| plastic dynamic viscosity | |
| fluid density | |
| dust particle density | |
| aligned angle | |
| electric conductivity of fluid | |
| Particles’s relaxation time | |
| drag forces | |
| specific fluid’s heat | |
| specific dust’s heat | |
| thermal relaxation time | |
| magnetic-field strength | |
| Casson parameter | |
| gravity acceleration | |
| thermal expansion | |
| kinematic viscosity | |
| heat transfer coefficient |
References
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng. Sci. Technol. Int. J. 2015, 18, 309–317. [Google Scholar] [CrossRef]
- Vajravelu, K. Convection heat transfer at a stretching sheet with suction or blowing. J. Math. Anal. Appl. 1994, 188, 1002–1011. [Google Scholar] [CrossRef]
- Vajravelu, K.; Hadjinicolaou, A. Convective heat transfer in an electrically conducting fluid at a stretching surface with uniform free stream. Int. J. Eng. Sci. 1997, 35, 1237–1244. [Google Scholar] [CrossRef]
- Merkin, J. Natural-convection boundary-layer flow on a vertical surface with Newtonian heating. Int. J. Heat Fluid Flow 1994, 15, 392–398. [Google Scholar] [CrossRef]
- Lesnic, D.; Ingham, D.B.; Pop, I. Free convection boundary-layer flow along a vertical surface in a porous medium with Newtonian heating. Int. J. Heat Mass Transf. 1999, 42, 2621–2627. [Google Scholar] [CrossRef]
- Chaudhary, R.; Jain, P. An exact solution to the unsteady free-convection boundary-layer flow past an impulsively started vertical surface with Newtonian heating. J. E. Phys. Thermophys. 2007, 80, 954–960. [Google Scholar] [CrossRef]
- Kasim, A.; Mohammad, N.; Aurangzaib, S.S. Natural convection boundary layer flow of a viscoelastic fluid on solid sphere with Newtonian heating. World Acad. Sci. Eng. 2012, 64, 628–633. [Google Scholar] [CrossRef]
- Salleh, M.; Nazar, R.; Pop, I. Numerical solutions of free convection boundary layer flow on a solid sphere with Newtonian heating in a micropolar fluid. Meccanica 2012, 47, 1261–1269. [Google Scholar] [CrossRef]
- Kasim, A.; Mohammad, N.; Anwar, I.; Shafie, S. MHD effect on convective boundary layer flow of a viscoelastic fluid embedded in porous medium with Newtonian heating. Recent Adv. Math. 2013, 4, 182–189. [Google Scholar]
- Mohamed, M.K.A.; Salleh, M.Z.; Nazar, R.; Ishak, A. Stagnation point flow over a stretching sheet with Newtonian heating. Sains Malays 2012, 41, 1467–1473. [Google Scholar]
- Kasim, A.; Shafie, S. Mixed Convection Boundary Layer of a Viscoelastic Fluid past a Circular Cylinder with Constant Heat Flux. In Proceedings of the 1st Regional Conference on Applied and Engineering Mathematics 1, Eastern & Oriental Hotel, Penang, Malaysia, 2–3 June 2010; pp. 124–129. [Google Scholar]
- Kasim, A.; Mohammad, N.; Shafie, S. Unsteady MHD mixed convection flow of a micropolar fluid along an inclined stretching plate. Heat Transf. Asian Res. 2013, 42, 89–99. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Shehzad, N.; Alamri, S.Z. Structural impact of kerosene-Al2O3 nanoliquid on MHD Poiseuille flow with variable thermal conductivity: Application of cooling process. J. Mol. Liq. 2018, 264, 607–615. [Google Scholar] [CrossRef]
- Ellahi, R.; Fetecau, C.; Sheikholeslami, M. Recent Advances in the Application of Differential Equations in Mechanical Engineering Problems. Math. Probl. Eng. 2018, 2018, 1584920. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Study of Shiny Film Coating on Multi-Fluid Flows of a Rotating Disk Suspended with Nano-Sized Silver and Gold Particles: A Comparative Analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef]
- Ellahi, R.; Alamri, S.Z.; Basit, A.; Majeed, A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. J. Taibah Univ. Sci. 2018, 12, 476–482. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of spherical and nonspherical nanoparticles in mixed convection flow over a vertical stretching permeable sheet. Mech. Adv. Mater. Struct. 2017, 1231–1238. [Google Scholar] [CrossRef]
- Ellahi, R.; Tariq, M.H.; Hassan, M.; Vafai, K. On boundary layer nano-ferroliquid flow under the influence of low oscillating stretchable rotating disk. J. Mol. Liq. 2017, 229, 339–345. [Google Scholar] [CrossRef]
- Ellahi, R.; Raza, M.; Akbar, N.S. Study of peristaltic flow of nanofluid with entropy generation in a porous medium. J. Porous Media 2017, 20, 461–478. [Google Scholar] [CrossRef]
- Kasim, A.M.; Zarith, S.O.; Shafie, S.; Pop, I. Generalized Blasius problem for a viscoelastic fluid with viscous dissipation and suction/injection effects. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 1242–1255. [Google Scholar] [CrossRef]
- Kasim, A.R.M.; Jiann, L.Y.; Shafie, S.; Ali, A. The effects of heat generation or absorption on MHD stagnation point of Jeffrey fluid. AIP Conf. Proc. 2014, 1605, 404–409. [Google Scholar] [CrossRef]
- Khan, Z.; Rasheed, H.U.; Abbas, T.; Khan, W.; Khan, I.; Baleanu, D.; Sooppy Nisar, K. Analysis of Eyring–Powell Fluid Flow Used as a Coating Material for Wire with Variable Viscosity Effect along with Thermal Radiation and Joule Heating. Crystals 2020, 10, 168. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Khan, I.; Baleanu, D.; Nisar, K.S. Enhanced heat transfer in moderately ionized liquid due to hybrid MoS2/SiO2 nanofluids exposed by nonlinear radiation: Stability analysis. Crystals 2020, 10, 142. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Baleanu, D.; Sooppy Nisar, K. Triple Solutions and Stability Analysis of Micropolar Fluid Flow on an Exponentially Shrinking Surface. Crystals 2020, 10, 283. [Google Scholar] [CrossRef]
- Zokri, S.M.; Arifin, N.S.; Mohamed, M.K.A.; Salleh, M.Z.; Kasim, A.R.M.; Mohammad, N.F. Influence of radiation and viscous dissipation on magnetohydrodynamic Jeffrey fluid over a stretching sheet with convective boundary conditions. Mal. J. Fund. Appl. Sci. 2017, 13, 279–284. [Google Scholar] [CrossRef]
- Abdelsalam, S.; Bhatti, M. Anomalous reactivity of thermo-bioconvective nanofluid towards oxytactic microorganisms. Appl. Math. Mech.-Engl. Ed. 2020, 41, 711–724. [Google Scholar] [CrossRef]
- Abumandour, R.M.; Eldesoky, I.M.; Kamel, M.H.; Ahmed, M.M.; Abdelsalam, S.I. Peristaltic thrusting of a thermal-viscosity nanofluid through a resilient vertical pipe. Z. Naturforsch. A 2020, 75, 727–738. [Google Scholar] [CrossRef]
- Sadaf, H.; Abdelsalam, S.I. Adverse effects of a hybrid nanofluid in a wavy non-uniform annulus with convective boundary conditions. RSC Adv. 2020, 10, 15035–15043. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Bhatti, M. The study of non-Newtonian nanofluid with hall and ion slip effects on peristaltically induced motion in a non-uniform channel. RSC Adv. 2018, 8, 7904–7915. [Google Scholar] [CrossRef]
- Saffman, P. On the stability of laminar flow of a dusty gas. J. Fluid Mech. 1962, 13, 120–128. [Google Scholar] [CrossRef]
- Datta, N.; Mishra, S. Boundary layer flow of a dusty fluid over a semi-infinite flat plate. Acta. Mech. 1982, 42, 71–83. [Google Scholar] [CrossRef]
- Ramesh, G.; Gireesha, B.; Bagewadi, C. MHD flow of a dusty fluid near the stagnation point over a permeable stretching sheet with non-uniform source/sink. Int. J. Heat Mass Transfer 2012, 55, 4900–4907. [Google Scholar] [CrossRef]
- Manjunatha, P.; Gireesha, B.; Prasannakumara, B. Effect of radiation on flow and heat transfer of MHD dusty fluid over a stretching cylinder embedded in a porous medium in presence of heat source. Int. J. Appl. Comput. Math. 2017, 3, 293–310. [Google Scholar] [CrossRef]
- Prakash, O.; Kumar, D.; Dwivedi, Y. Heat transfer in MHD flow of dusty viscoelastic (Walters’ liquid model-B) stratified fluid in porous medium under variable viscosity. Pramana J. Phys. 2012, 79, 1457–1470. [Google Scholar] [CrossRef]
- Gireesha, B.; Mahanthesh, B.; Gorla, R.S.R.; Krupalakshmi, K. Mixed convection two-phase flow of Maxwell fluid under the influence of non-linear thermal radiation, non-uniform heat source/sink and fluid-particle suspension. Ain Shams Eng. J. 2018, 9, 735–746. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B. Thermal Marangoni convection in two-phase flow of dusty Casson fluid. Results Phys. 2018, 8, 537–544. [Google Scholar] [CrossRef]
- Arifin, N.S.; Zokri, S.M.; Kasim, A.R.M.; Salleh, M.Z.; Arifin, N.A.N. Jeffrey fluid embedded with dust particles over a shrinking sheet: A numerical investigation. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 74, 196–209. [Google Scholar] [CrossRef]
- Kasim, A.R.M.; Arifin, N.S.; Ariffin, N.A.N.; Salleh, M.Z.; Anwar, M.I. Mathematical model of simultaneous flow between Casson fluid and dust particle over a vertical stretching sheet. Int. J. Integr. Eng. 2020, 12, 253–260. [Google Scholar] [CrossRef]
- Kasim, A.R.M.; Arifin, N.S.; Zokri, S.M.; Salleh, M.Z. The investigation of a fluid-solid interaction mathematical model under combined convective Jeffrey flow and radiation effect embedded Newtonian Heating as the thermal boundary condition over a vertical stretching sheet. Defect Diffus. Forum 2020, 399, 65–75. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Hayat, T.; Alsaedi, A. Exact solution for boundary layer flow of Casson fluid over a permeable stretching/shrinking sheet. Z. Angew. Math. Mech. 2013, 10, 522–528. [Google Scholar] [CrossRef]
- Siddiqa, S.; Hossain, M.A.; Saha, S.C. Two-phase natural convection flow of a dusty fluid. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1542–1556. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I.; Shafie, S. Analytical solution for suction and injection flow of a viscoplastic Casson fluid past a stretching surface in the presence of viscous dissipation. Neural Comput. Appl. 2018, 29, 1507–1515. [Google Scholar] [CrossRef]
- Makinde, O. Similarity solution of hydromagnetic heat and mass transfer over a vertical plate with a convective surface boundary condition. Int. J. Phys. Sci. 2010, 5, 700–710. [Google Scholar] [CrossRef]
- Gangadhar, K.; Reddy, N.B.; Kameswaran, P. Similarity solution of hydromagnetic heat and mass transfer over a vertical plate with convective surface boundary condition and chemical reaction. Int. J. Nonlin. Sci. 2012, 13, 298–307. [Google Scholar]
- Seshadri, R.; Munjam, S.R. Mixed convection flow due to a vertical plate in the presence of heat source and chemical reaction. Ain Shams Eng. J. 2016, 7, 671–682. [Google Scholar] [CrossRef][Green Version]
- Mukhopadhyay, S. Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin. Phys. B 2013, 22, 074701. [Google Scholar] [CrossRef]
- Isa, S.M.; Ali, A.; Shafie, S. Stagnation point flow of MHD dusty fluid toward stretching sheet with convective surface. J. Teknologi 2016, 78, 95–100. [Google Scholar] [CrossRef]
- Ramesh, G.; Gireesha, B.; Gorla, R.S.R. Boundary layer flow past a stretching sheet with fluid-particle suspension and convective boundary condition. Heat Mass Transfer 2015, 51, 1061–1066. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.; Vaidya, H.; Basha, N.Z.; Ng, C.-O. Mixed convective flow of a Casson fluid over a vertical stretching sheet. Int. J. Appl. Comput. Math. 2017, 3, 1619–1638. [Google Scholar] [CrossRef]


| A | Exact Equation (21) | Vajravelu et al. [49] | Present |
|---|---|---|---|
| 1.0000 | 1.0000 | 1.0000 | |
| 1 | 0.707107 | 0.707107 | 0.707107 |
| 2 | 0.816497 | 0.816497 | 0.816497 |
| 3 | 0.866025 | 0.866025 | 0.866025 |
| 4 | 0.894427 | 0.866025 | 0.894427 |
| 0.5 | π/6 | 1 | 0.5 | 0.1 | 0.2 | 0.72 | 0.67448 | 0.55931 |
| 1 | 0.82101 | 0.61584 | ||||||
| 1.5 | 0.89639 | 0.64724 | ||||||
| 2 | 0.94288 | 0.66730 | ||||||
| 1 | 0 | 1 | 0.5 | 0.1 | 0.2 | 0.72 | 0.74410 | 0.58564 |
| π/6 | 0.82101 | 0.61584 | ||||||
| π/4 | 0.89159 | 0.64544 | ||||||
| π/3 | 0.95714 | 0.67457 | ||||||
| 1 | π/6 | 0 | 0.5 | 0.1 | 0.2 | 0.72 | 0.74409 | 0.58564 |
| 1 | 0.78344 | 0.60082 | ||||||
| 1.5 | 0.82101 | 0.61584 | ||||||
| 2 | 0.85700 | 0.63071 | ||||||
| 1 | π/6 | 1 | 0.5 | 0.1 | 0.2 | 0.72 | 0.82101 | 0.61584 |
| 1 | 0.84512 | 0.62775 | ||||||
| 1.5 | 0.85922 | 0.63581 | ||||||
| 2 | 0.86848 | 0.64135 | ||||||
| 1 | π/6 | 1 | 0.5 | 0 | 0.2 | 0.72 | 0.84172 | 0.62508 |
| 0.01 | 0.83961 | 0.62411 | ||||||
| 0.1 | 0.82101 | 0.61584 | ||||||
| 0.2 | 0.80118 | 0.60758 | ||||||
| 1 | π/6 | 1 | 0.5 | 0.1 | 0.15 | 0.72 | 0.82816 | 0.40201 |
| 0.25 | 0.81147 | 0.90284 | ||||||
| 0.35 | 0.77880 | 1.90256 | ||||||
| 0.45 | 0.69712 | 4.49964 | ||||||
| 1 | π/6 | 1 | 0.5 | 0.1 | 0.2 | 1 | 0.82852 | 0.44655 |
| 3 | 0.83811 | 0.19196 | ||||||
| 5 | 0.83962 | 0.13876 | ||||||
| 7 | 0.84024 | 0.11334 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohd Kasim, A.R.; Arifin, N.S.; Mohd Zokri, S.; Salleh, M.Z.; Mohammad, N.F.; Chuan Ching, D.L.; Shafie, S.; Ariffin, N.A.N. Convective Transport of Fluid–Solid Interaction: A Study between Non-Newtonian Casson Model with Dust Particles. Crystals 2020, 10, 814. https://doi.org/10.3390/cryst10090814
Mohd Kasim AR, Arifin NS, Mohd Zokri S, Salleh MZ, Mohammad NF, Chuan Ching DL, Shafie S, Ariffin NAN. Convective Transport of Fluid–Solid Interaction: A Study between Non-Newtonian Casson Model with Dust Particles. Crystals. 2020; 10(9):814. https://doi.org/10.3390/cryst10090814
Chicago/Turabian StyleMohd Kasim, Abdul Rahman, Nur Syamilah Arifin, Syazwani Mohd Zokri, Mohd Zuki Salleh, Nurul Farahain Mohammad, Dennis Ling Chuan Ching, Sharidan Shafie, and Noor Amalina Nisa Ariffin. 2020. "Convective Transport of Fluid–Solid Interaction: A Study between Non-Newtonian Casson Model with Dust Particles" Crystals 10, no. 9: 814. https://doi.org/10.3390/cryst10090814
APA StyleMohd Kasim, A. R., Arifin, N. S., Mohd Zokri, S., Salleh, M. Z., Mohammad, N. F., Chuan Ching, D. L., Shafie, S., & Ariffin, N. A. N. (2020). Convective Transport of Fluid–Solid Interaction: A Study between Non-Newtonian Casson Model with Dust Particles. Crystals, 10(9), 814. https://doi.org/10.3390/cryst10090814






