Omindirectional Non-Reciprocity via 2D Modulated Radial Sonic Crystals
Abstract
:1. Introduction
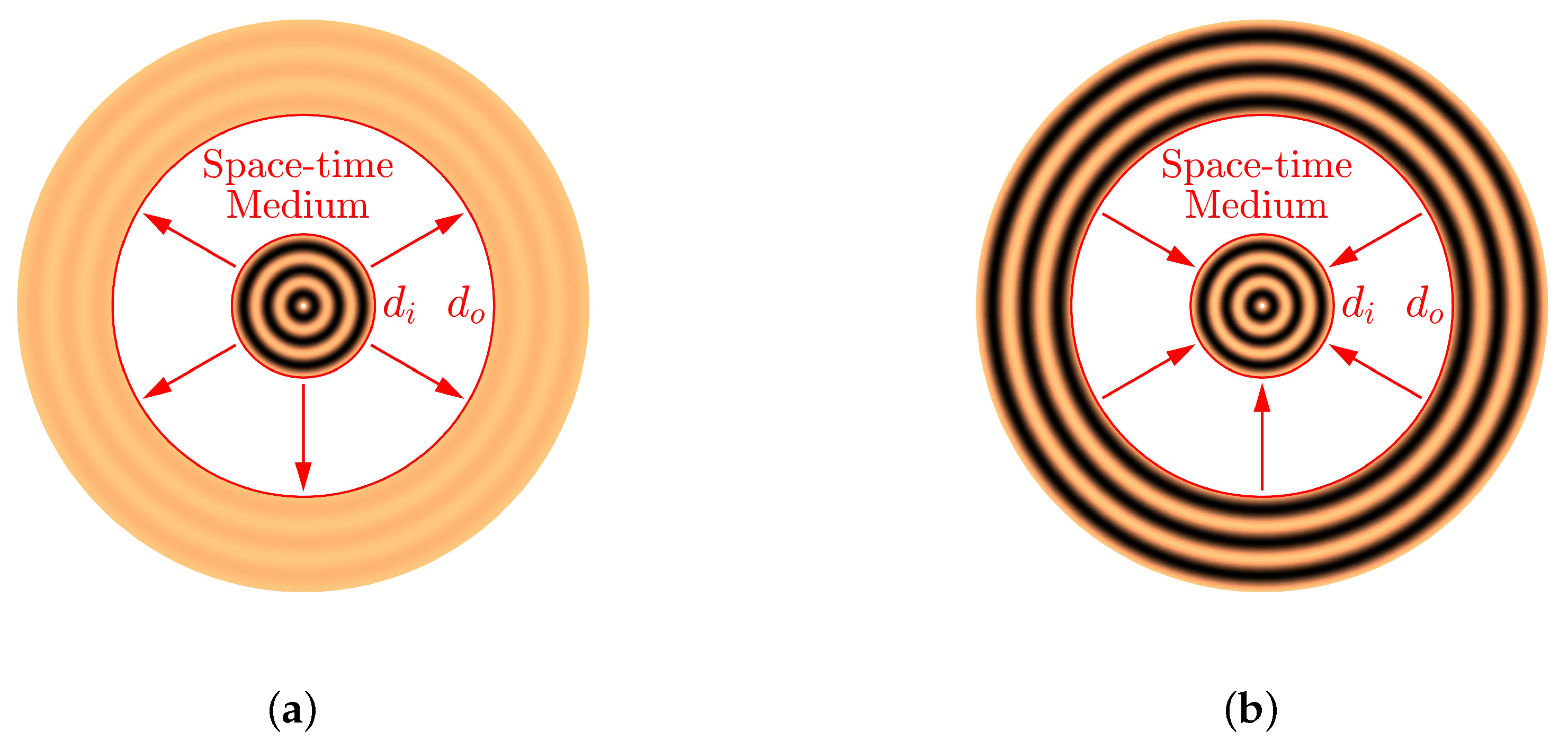
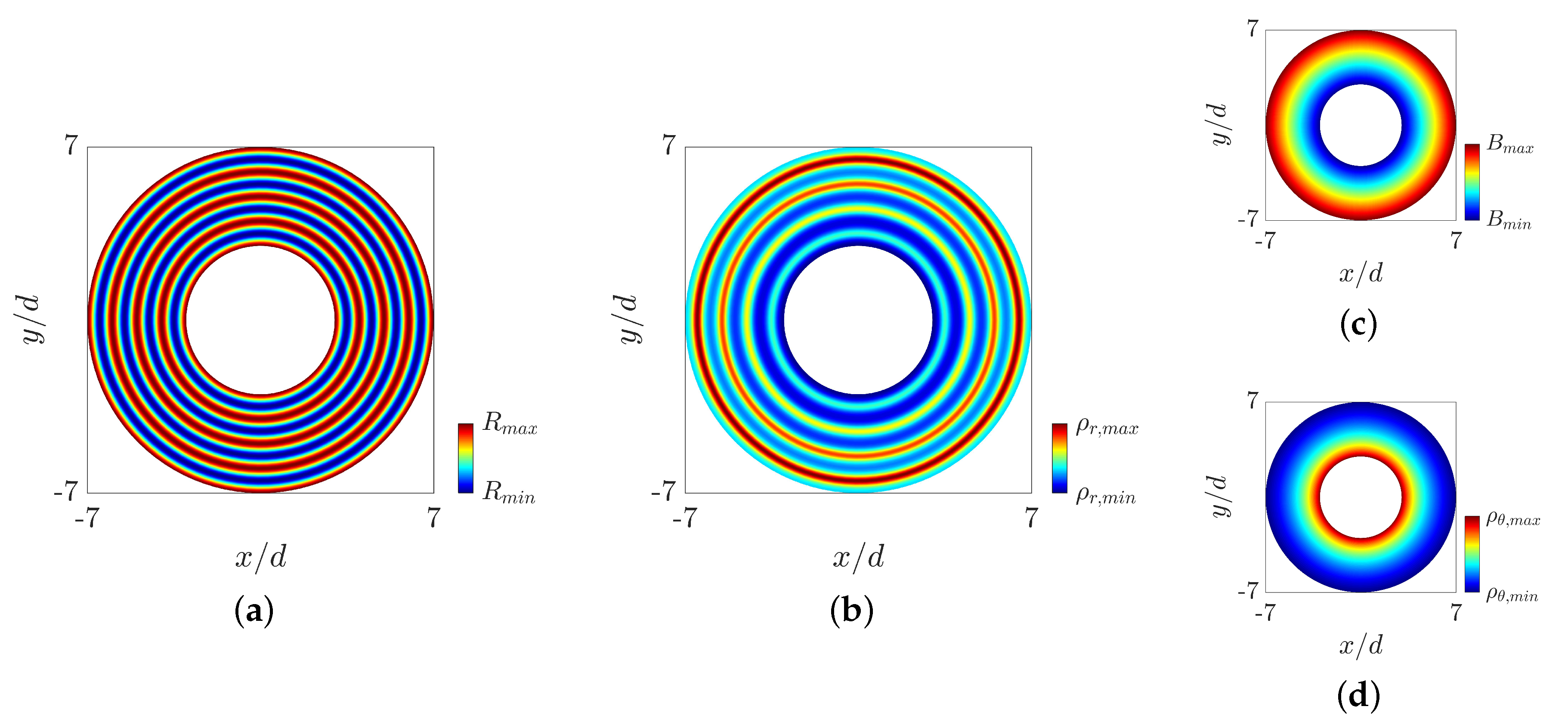
2. Materials and Methods
3. Results
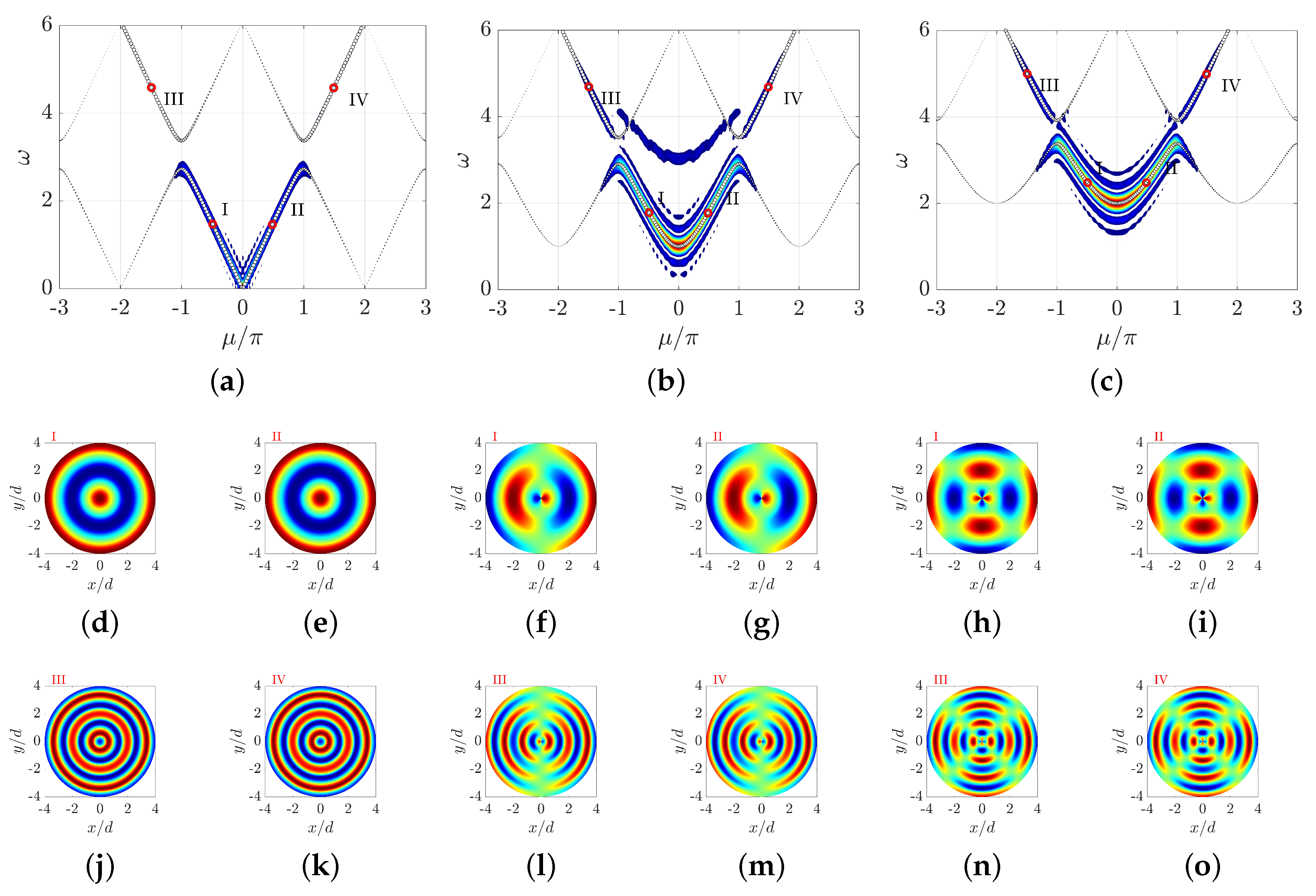
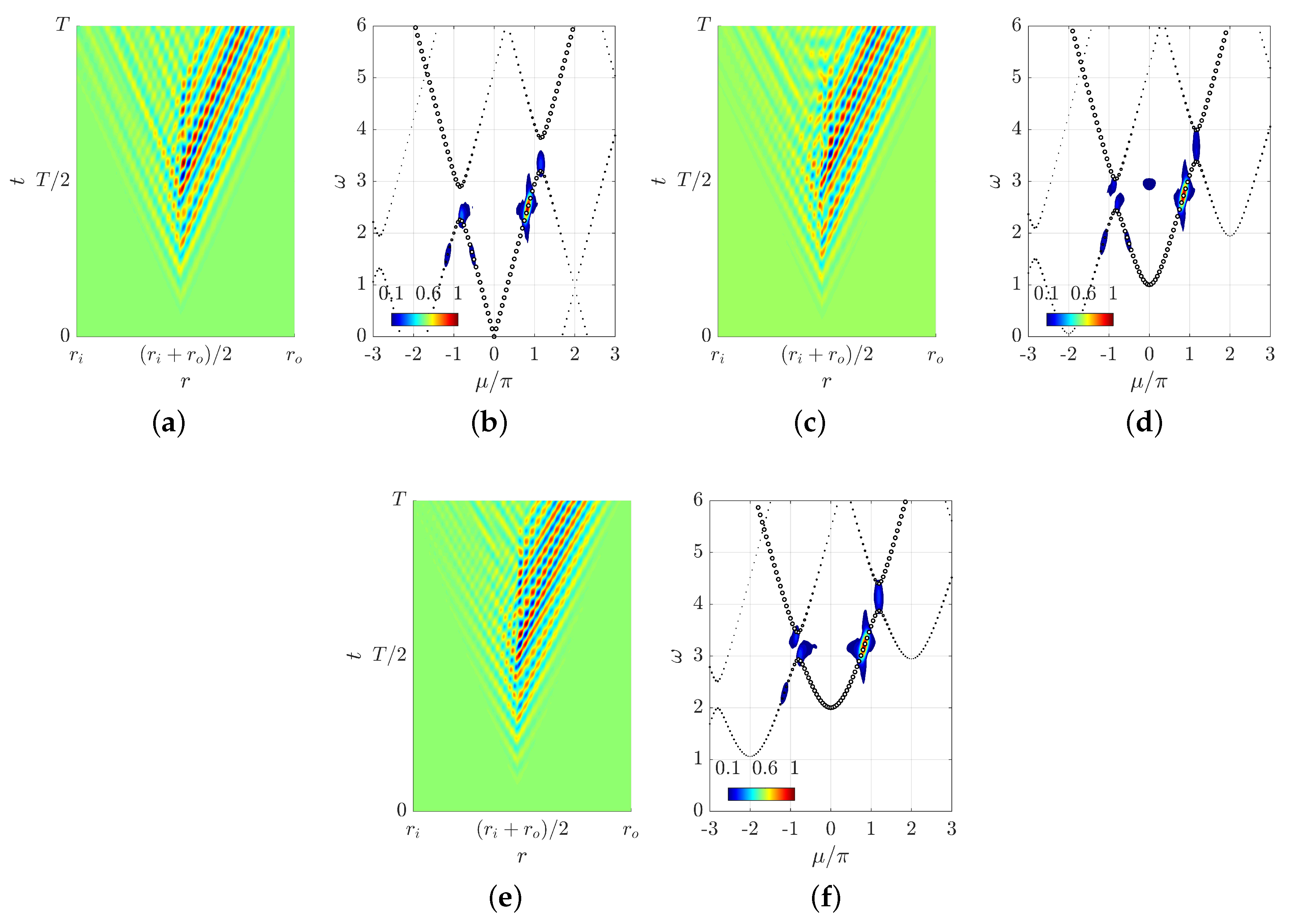
3.1. Space-Varying Radial Crystals
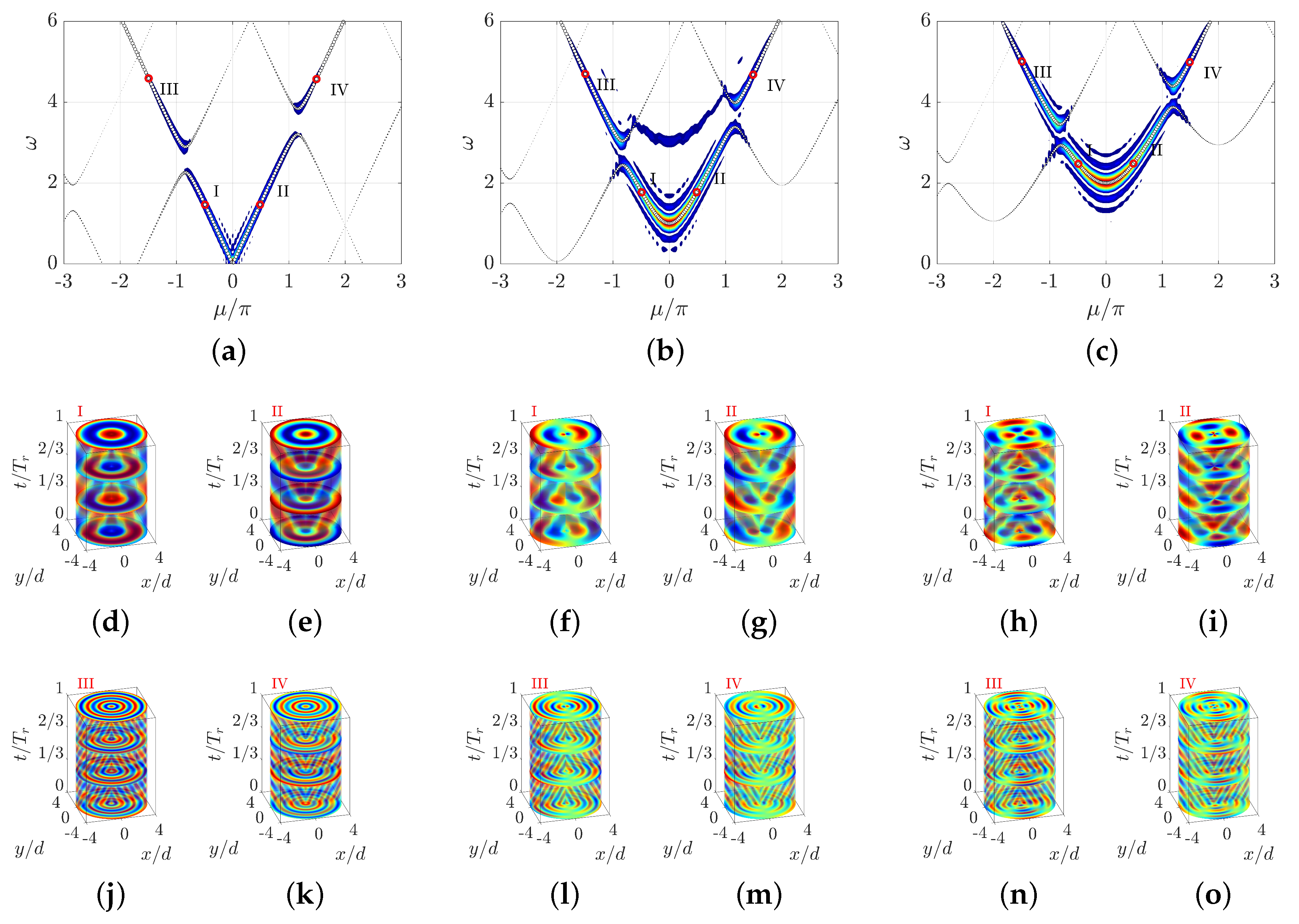
3.2. Space–Time-Varying Radial Crystals
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PWEM | Plane Wave Expansion Method |
| RSC | Radial Sonic Crystal |
Appendix A. PWEM for a Spatially Modulated RSC
Appendix B. PWEM for a Spatiotemporally Modulated RSC
References
- Trainiti, G.; Ruzzene, M. Non-reciprocal elastic wave propagation in spatiotemporal periodic structures. New J. Phys. 2016, 18, 083047. [Google Scholar] [CrossRef]
- Vila, J.; Pal, R.K.; Ruzzene, M.; Trainiti, G. A bloch-based procedure for dispersion analysis of lattices with periodic time-varying properties. J. Sound Vib. 2017, 406, 363–377. [Google Scholar] [CrossRef] [Green Version]
- Riva, E.; Marconi, J.; Cazzulani, G.; Braghin, F. Generalized plane wave expansion method for non-reciprocal discretely modulated waveguides. J. Sound Vib. 2019, 449, 172–181. [Google Scholar] [CrossRef]
- Nassar, H.; Chen, H.; Norris, A.; Haberman, M.; Huang, G. Non-reciprocal wave propagation in modulated elastic metamaterials. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170188. [Google Scholar] [CrossRef] [Green Version]
- Marconi, J.; Cazzulani, G.; Riva, E.; Braghin, F. Observations on the behavior of discretely modulated spatiotemporal periodic structures. In Active and Passive Smart Structures and Integrated Systems XII; International Society for Optics and Photonics: Bellingham, WA USA, 2018; Volume 10595, p. 105952N. [Google Scholar]
- Riva, E.; Quadrelli, D.E.; Marconi, J.; Cazzulani, G.; Braghin, F. Design and experimental analysis of nonreciprocal wave propagation in a space-time modulated beam. In Active and Passive Smart Structures and Integrated Systems IX; International Society for Optics and Photonics: Bellingham, WA USA, 2020; Volume 11376, p. 1137613. [Google Scholar]
- Li, J.; Shen, C.; Zhu, X.; Xie, Y.; Cummer, S.A. Nonreciprocal sound propagation in space-time modulated media. Phys. Rev. B 2019, 99, 144311. [Google Scholar] [CrossRef] [Green Version]
- Karkar, S.; De Bono, E.; Collet, M.; Matten, G.; Ouisse, M.; Rivet, E. Broadband Nonreciprocal Acoustic Propagation Using Programmable Boundary Conditions: From Analytical Modeling to Experimental Implementation. Phys. Rev. Appl. 2019, 12, 054033. [Google Scholar] [CrossRef] [Green Version]
- Fleury, R.; Sounas, D.L.; Alù, A. Subwavelength ultrasonic circulator based on spatiotemporal modulation. Phys. Rev. B 2015, 91, 174306. [Google Scholar] [CrossRef] [Green Version]
- Chamanara, N.; Taravati, S.; Deck-Léger, Z.L.; Caloz, C. Optical isolation based on space-time engineered asymmetric photonic band gaps. Phys. Rev. B 2017, 96, 155409. [Google Scholar] [CrossRef] [Green Version]
- Marconi, J.; Riva, E.; Di Ronco, M.; Cazzulani, G.; Braghin, F.; Ruzzene, M. Experimental Observation of Nonreciprocal Band Gaps in a Space-Time-Modulated Beam Using a Shunted Piezoelectric Array. Phys. Rev. Appl. 2020, 13, 031001. [Google Scholar] [CrossRef] [Green Version]
- Riva, E.; Casieri, V.; Resta, F.; Braghin, F. Adiabatic pumping via avoided crossings in stiffness modulated quasiperiodic beams. arXiv 2020, arXiv:2003.11525. [Google Scholar] [CrossRef]
- Attarzadeh, M.; Callanan, J.; Nouh, M. Experimental observation of nonreciprocal waves in a resonant metamaterial beam. Phys. Rev. Appl. 2020, 13, 021001. [Google Scholar] [CrossRef] [Green Version]
- Attarzadeh, M.; Maleki, S.; Crassidis, J.; Nouh, M. Non-reciprocal wave phenomena in energy self-reliant gyric metamaterials. J. Acoust. Soc. Am. 2019, 146, 789–801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Li, X.; Nassar, H.; Norris, A.N.; Daraio, C.; Huang, G. Nonreciprocal wave propagation in a continuum-based metamaterial with space-time modulated resonators. Phys. Rev. Appl. 2019, 11, 064052. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.; Li, J.; Jia, Z.; Xie, Y.; Cummer, S.A. Nonreciprocal acoustic transmission in cascaded resonators via spatiotemporal modulation. Phys. Rev. B 2019, 99, 134306. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhu, X.; Shen, C.; Peng, X.; Cummer, S.A. Transfer matrix method for the analysis of space-time-modulated media and systems. Phys. Rev. B 2019, 100, 144311. [Google Scholar] [CrossRef] [Green Version]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef] [Green Version]
- Zangeneh-Nejad, F.; Fleury, R. Active times for acoustic metamaterials. Rev. Phys. 2019, 4, 100031. [Google Scholar] [CrossRef]
- Deck-Léger, Z.L.; Chamanara, N.; Skorobogatiy, M.; Silveirinha, M.G.; Caloz, C. Uniform-velocity spacetime crystals. Adv. Photonics 2019, 1, 056002. [Google Scholar] [CrossRef] [Green Version]
- Taravati, S.; Chamanara, N.; Caloz, C. Nonreciprocal electromagnetic scattering from a periodically space-time modulated slab and application to a quasisonic isolator. Phys. Rev. B 2017, 96, 165144. [Google Scholar] [CrossRef] [Green Version]
- Cassedy, E.; Oliner, A. Dispersion relations in time-space periodic media: Part I—Stable interactions. Proc. IEEE 1963, 51, 1342–1359. [Google Scholar] [CrossRef]
- Cassedy, E. Dispersion relations in time-space periodic media part II—Unstable interactions. Proc. IEEE 1967, 55, 1154–1168. [Google Scholar] [CrossRef]
- Attarzadeh, M.; Nouh, M. Non-reciprocal elastic wave propagation in 2D phononic membranes with spatiotemporally varying material properties. J. Sound Vib. 2018, 422, 264–277. [Google Scholar] [CrossRef]
- Riva, E.; Di Ronco, M.; Elabd, A.; Cazzulani, G.; Braghin, F. Non-reciprocal wave propagation in discretely modulated spatiotemporal plates. J. Sound Vib. 2020, 471, 115186. [Google Scholar] [CrossRef] [Green Version]
- Torrent, D.; Sánchez-Dehesa, J. Radial Wave Crystals: Radially Periodic Structures from Anisotropic Metamaterials for Engineering Acoustic or Electromagnetic Waves. Phys. Rev. Lett. 2009, 103, 064301. [Google Scholar] [CrossRef] [Green Version]
- Zigoneanu, L.; Popa, B.I.; Starr, A.F.; Cummer, S.A. Design and measurements of a broadband two-dimensional acoustic metamaterial with anisotropic effective mass density. J. Appl. Phys. 2011, 109, 054906. [Google Scholar] [CrossRef]
- Zigoneanu, L.; Popa, B.I.; Cummer, S.A. Three-dimensional broadband omnidirectional acoustic ground cloak. Nat. Mater. 2014, 13, 352–355. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pendry, J.; Li, J. An acoustic metafluid: Realizing a broadband acoustic cloak. New J. Phys. 2008, 10, 115032. [Google Scholar] [CrossRef] [Green Version]
- Torrent, D.; Sánchez-Dehesa, J. Anisotropic mass density by two-dimensional acoustic metamaterials. New J. Phys. 2008, 10, 023004. [Google Scholar] [CrossRef]
- Chen, S.; Fan, Y.; Fu, Q.; Wu, H.; Jin, Y.; Zheng, J.; Zhang, F. A review of tunable acoustic metamaterials. Appl. Sci. 2018, 8, 1480. [Google Scholar] [CrossRef] [Green Version]
- Baz, A.M. An active acoustic metamaterial with tunable effective density. J. Vib. Acoust. 2010, 132. [Google Scholar] [CrossRef]
- Akl, W.; Baz, A. Experimental characterization of active acoustic metamaterial cell with controllable dynamic density. J. Appl. Phys. 2012, 112, 084912. [Google Scholar] [CrossRef]
- Allam, A.; Elsabbagh, A.; Akl, W. Experimental demonstration of one-dimensional active plate-type acoustic metamaterial with adaptive programmable density. J. Appl. Phys. 2017, 121, 125106. [Google Scholar] [CrossRef]
- Popa, B.I.; Zigoneanu, L.; Cummer, S.A. Tunable active acoustic metamaterials. Phys. Rev. B 2013, 88, 024303. [Google Scholar] [CrossRef] [Green Version]
- Allam, A.; Elsabbagh, A.; Akl, W. Modeling and design of two-dimensional membrane-type active acoustic metamaterials with tunable anisotropic density. J. Acoust. Soc. Am. 2016, 140, 3607–3618. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enrico Quadrelli, D.; Riva, E.; Cazzulani, G.; Braghin, F. Omindirectional Non-Reciprocity via 2D Modulated Radial Sonic Crystals. Crystals 2020, 10, 624. https://doi.org/10.3390/cryst10070624
Enrico Quadrelli D, Riva E, Cazzulani G, Braghin F. Omindirectional Non-Reciprocity via 2D Modulated Radial Sonic Crystals. Crystals. 2020; 10(7):624. https://doi.org/10.3390/cryst10070624
Chicago/Turabian StyleEnrico Quadrelli, Davide, Emanuele Riva, Gabriele Cazzulani, and Francesco Braghin. 2020. "Omindirectional Non-Reciprocity via 2D Modulated Radial Sonic Crystals" Crystals 10, no. 7: 624. https://doi.org/10.3390/cryst10070624
APA StyleEnrico Quadrelli, D., Riva, E., Cazzulani, G., & Braghin, F. (2020). Omindirectional Non-Reciprocity via 2D Modulated Radial Sonic Crystals. Crystals, 10(7), 624. https://doi.org/10.3390/cryst10070624





