Ideal Photonic Weyl Nodes Stabilized by Screw Rotation Symmetry in Space Group 19
Abstract
1. Introduction
2. Results
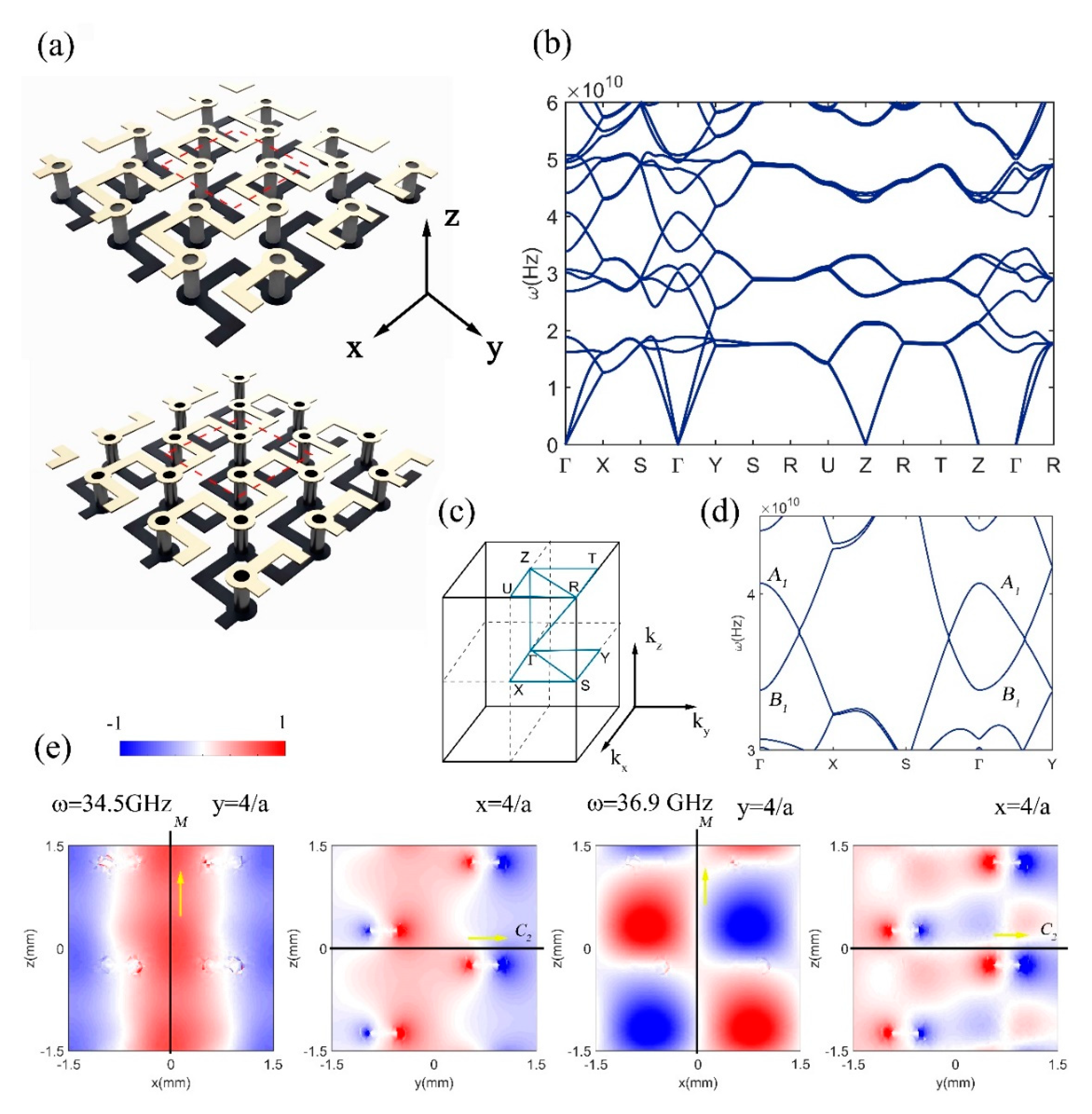
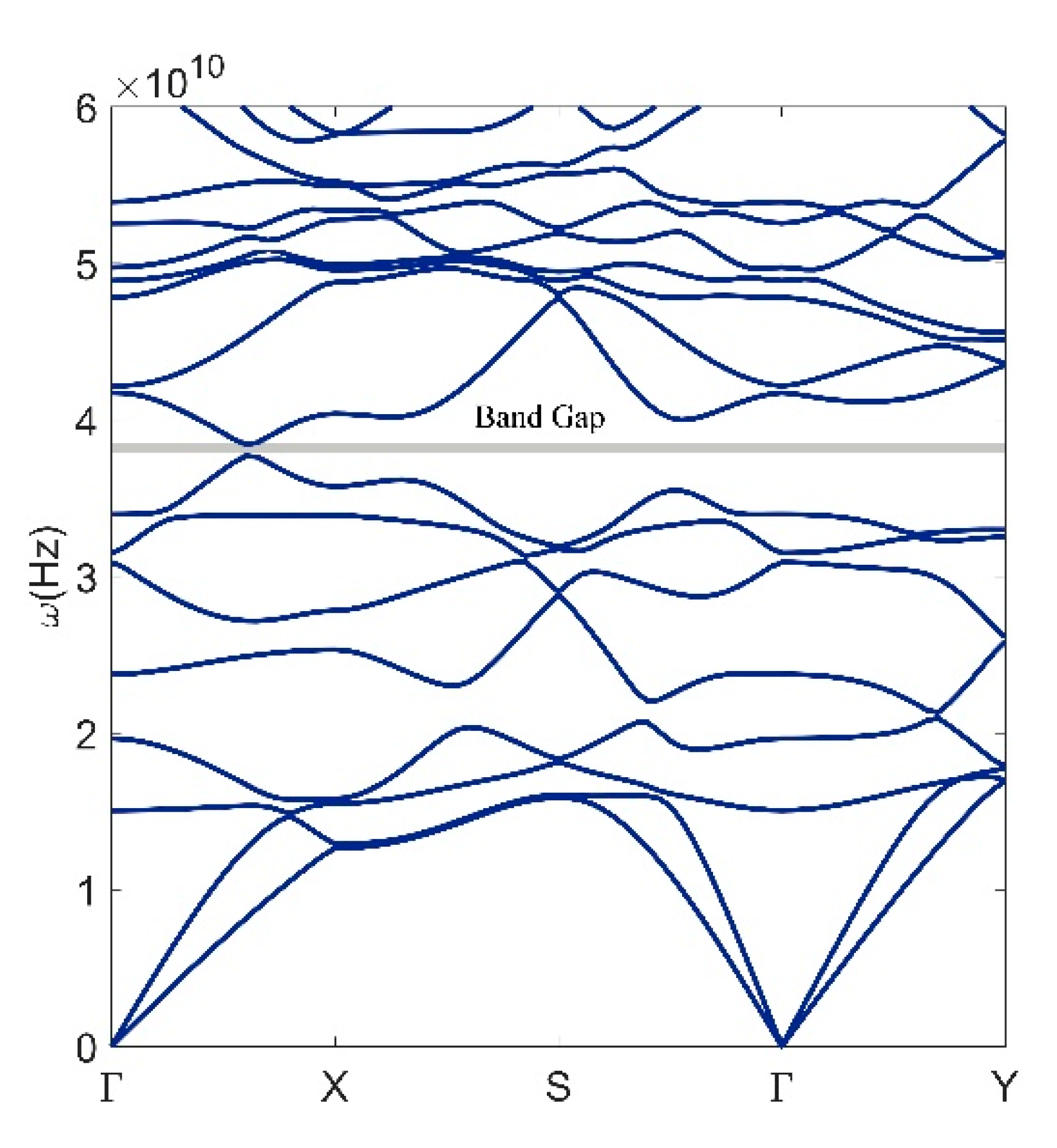
2.1. Line Node from SG 61
2.2. Group Theory Analysis
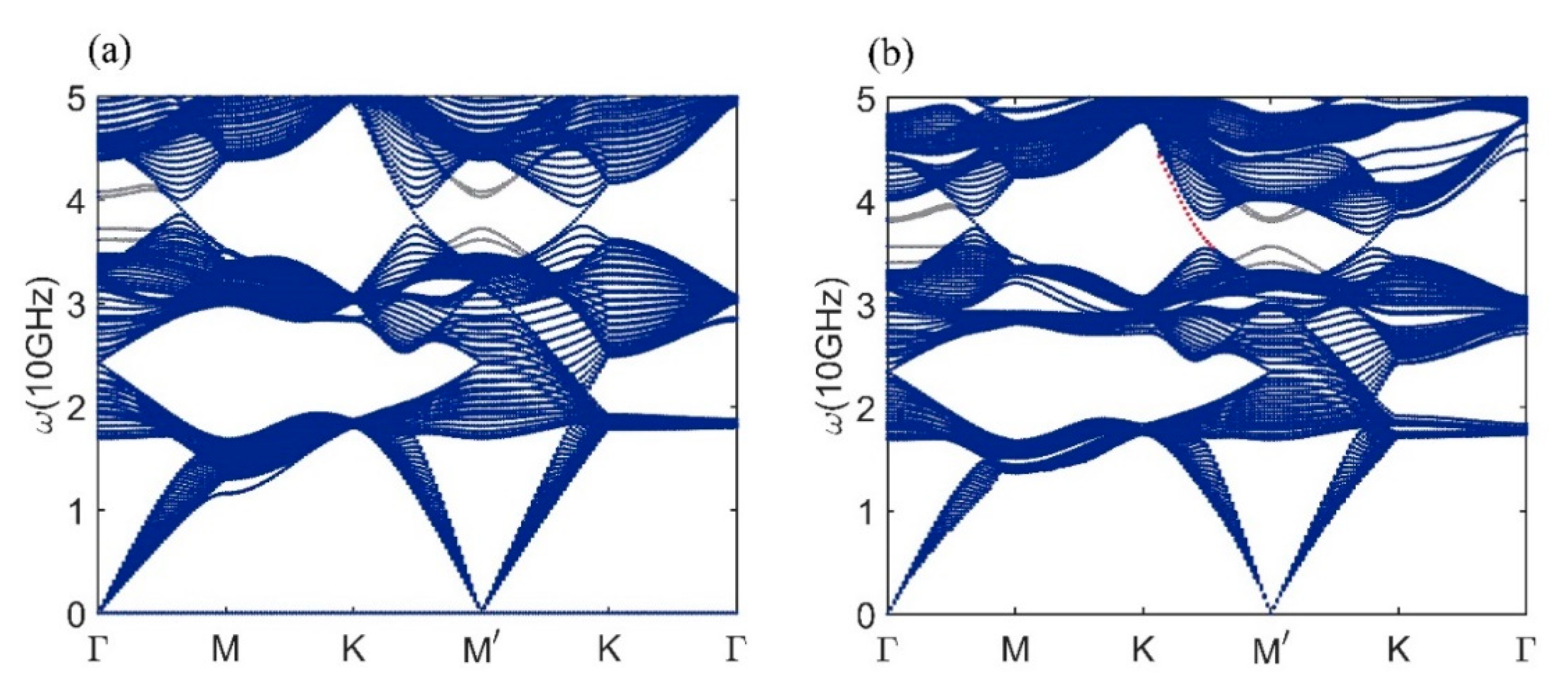
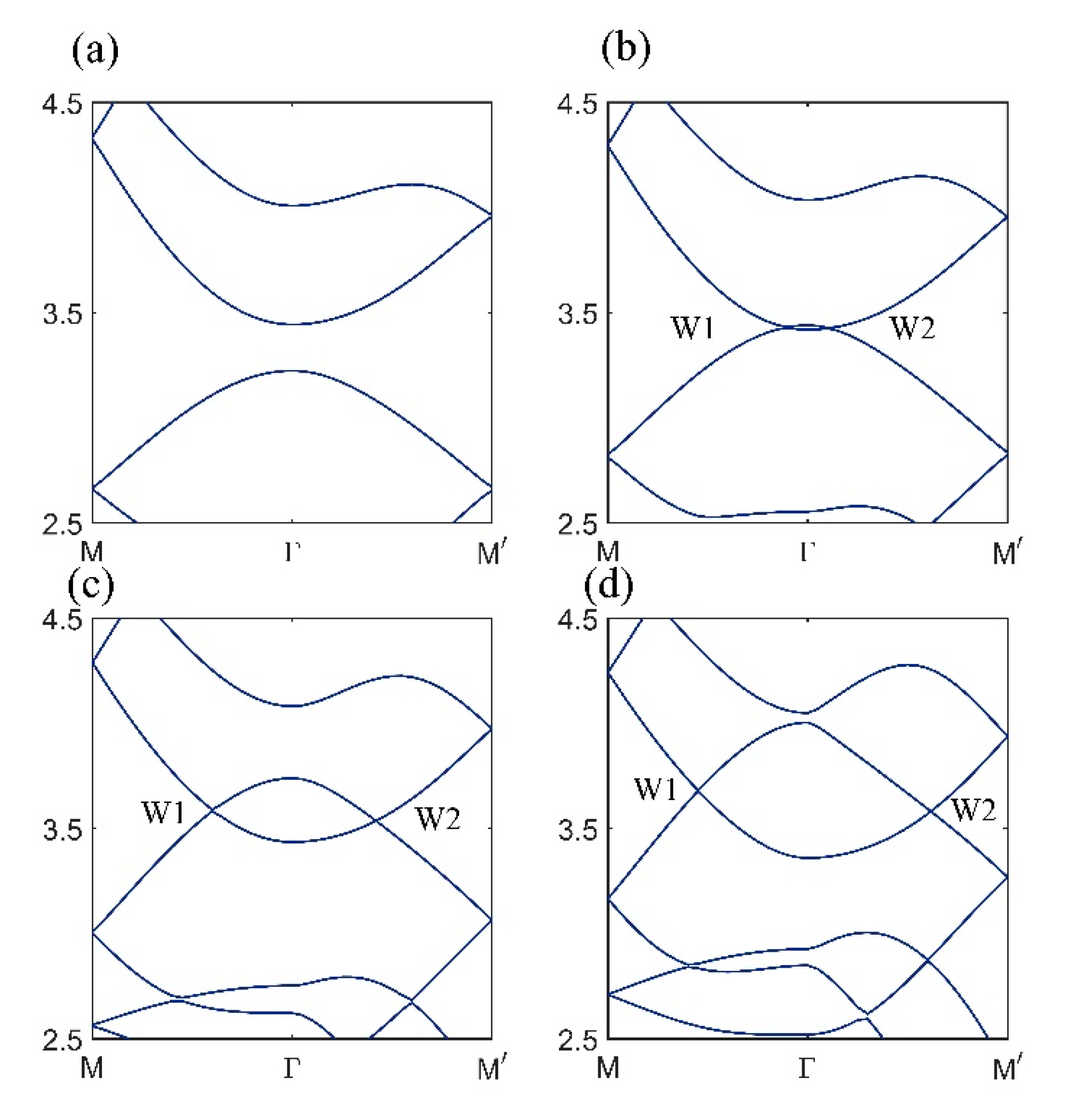
2.3. Weyl Point from SG 19
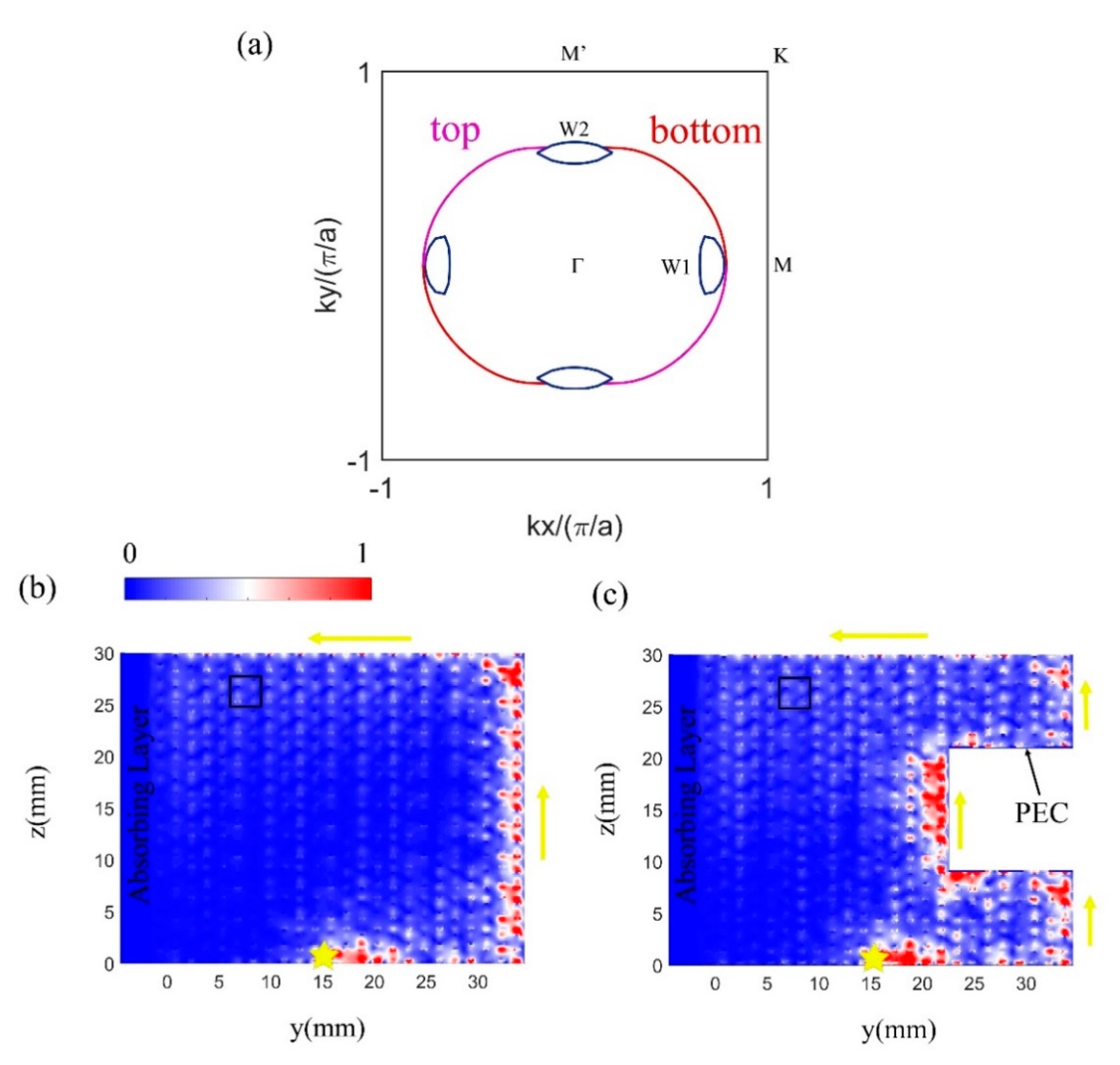
2.4. Surface States of the LN and the WN
3. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Burkov, A.A.; Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 2011, 107, 127205. [Google Scholar] [CrossRef] [PubMed]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, L.; Long, Y.; Wang, P.; Chen, D.; Yang, Z.; Liang, H.; Xue, M.; Weng, H.; Fang, Z.; et al. Observation of the chiral-anomaly-induced negative magnetoresistance: In 3D Weyl semimetal TaAs. Phys. Rev. X 2015, 5, 031023. [Google Scholar] [CrossRef]
- Li, Q.; Kharzeev, D.E.; Zhang, C.; Huang, Y.; Pletikosić, I.; Fedorov, A.V.; Zhong, R.D.; Schneeloch, J.A.; Gu, G.D.; Valla, T. Chiral magnetic effect in ZrTe5. Nat. Phys. 2016, 12, 550–554. [Google Scholar] [CrossRef]
- Xiong, J.; Kushwaha, S.K.; Liang, T.; Krizan, J.W.; Hirschberger, M.; Wang, W.; Cava, R.J.; Ong, N.P. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 2015, 350, 413–416. [Google Scholar] [CrossRef]
- Fang, C.; Lu, L.; Liu, J.; Fu, L. Topological semimetals with helicoid surface states. Nat. Phys. 2016, 12, 936–941. [Google Scholar] [CrossRef]
- Xu, S.-Y.; Belopolski, I.; Sanchez, D.S.; Guo, C.; Chang, G.; Zhang, C.; Bian, G.; Yuan, Z.; Lu, H.; Feng, Y.; et al. Experimental discovery of a topological Weyl semimetal state in TaP. Sci. Adv. 2015, 1, e1501092. [Google Scholar] [CrossRef]
- Lv, B.Q.; Xu, N.; Weng, H.M.; Ma, J.Z.; Richard, P.; Huang, X.C.; Zhao, L.X.; Chen, G.F.; Matt, C.E.; Bisti, F.; et al. Observation of Weyl nodes in TaAs. Nat. Phys. 2015, 11, 724–727. [Google Scholar] [CrossRef]
- Weng, H.; Fang, C.; Fang, Z.; Andrei Bernevig, B.; Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 2015, 5, 011029. [Google Scholar] [CrossRef]
- Yang, L.X.; Liu, Z.K.; Sun, Y.; Peng, H.; Yang, H.F.; Zhang, T.; Zhou, B.; Zhang, Y.; Guo, Y.F.; Rahn, M.; et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 2015, 11, 728–732. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Xu, S.-Y.; Belopolski, I.; Huang, S.-M. Discovery of Weyl fermion semimetals and topological Fermi arc states. Annu. Rev. Condens. Matter Phys. 2017, 8, 289–309. [Google Scholar]
- Sanchez, D.S.; Belopolski, I.; Cochran, T.A.; Xu, X.; Yin, J.X.; Chang, G.; Xie, W.; Manna, K.; Süß, V.; Huang, C.Y.; et al. Topological chiral crystals with helicoid-arc quantum states. Nature 2019, 567, 500–505. [Google Scholar] [CrossRef]
- Wang, C.M.; Sun, H.P.; Lu, H.Z.; Xie, X.C. 3D Quantum Hall Effect of Fermi Arc in Topological Semimetals. Phys. Rev. Lett. 2017, 119, 136806. [Google Scholar] [CrossRef] [PubMed]
- Deng, K.; Wan, G.; Deng, P.; Zhang, K.; Ding, S.; Wang, E.; Yan, M.; Huang, H.; Zhang, H.; Xu, Z.; et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2. Nat. Phys. 2016, 12, 1105–1110. [Google Scholar] [CrossRef]
- Burkov, A.A. Anomalous hall effect in weyl metals. Phys. Rev. Lett. 2014, 113, 187202. [Google Scholar] [CrossRef]
- Sodemann, I.; Fu, L. Quantum Nonlinear Hall Effect Induced by Berry Curvature Dipole in Time-Reversal Invariant Materials. Phys. Rev. Lett. 2015, 115, 216806. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, S.Y.; Shen, H.; MacNeill, D.; Fatemi, V.; Chang, T.R.; Mier Valdivia, A.M.; Wu, S.; Du, Z.; Hsu, C.H.; et al. Observation of the nonlinear Hall effect under time-reversal-symmetric conditions. Nature 2019, 565, 337–342. [Google Scholar] [CrossRef]
- Bradlyn, B.; Cano, J.; Wang, Z.; Vergniory, M.G.; Felser, C.; Cava, R.J.; Bernevig, B.A. Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals. Science 2016, 353, aaf5037. [Google Scholar] [CrossRef]
- Yang, B.J.; Nagaosa, N. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nat. Commun. 2014, 5, 1–10. [Google Scholar] [CrossRef]
- Hu, J.; Tang, Z.; Liu, J.; Liu, X.; Zhu, Y.; Graf, D.; Myhro, K.; Tran, S.; Lau, C.N.; Wei, J.; et al. Evidence of Topological Nodal-Line Fermions in ZrSiSe and ZrSiTe. Phys. Rev. Lett. 2016, 117, 016602. [Google Scholar] [CrossRef]
- Gibson, Q.D.; Schoop, L.M.; Muechler, L.; Xie, L.S.; Hirschberger, M.; Ong, N.P.; Car, R.; Cava, R.J. Three-dimensional Dirac semimetals: Design principles and predictions of new materials. Phys. Rev. B 2015, 91, 205128. [Google Scholar] [CrossRef]
- Young, S.M.; Zaheer, S.; Teo JC, Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac semimetal in three dimensions. Phys. Rev. Lett. 2012, 108, 140405. [Google Scholar] [CrossRef] [PubMed]
- Neupane, M.; Xu, S.Y.; Sankar, R.; Alidoust, N.; Bian, G.; Liu, C.; Belopolski, I.; Chang, T.R.; Jeng, H.T.; Lin, H.; et al. Observation of a three-dimensional topological dirac semimetal phase in high-mobility cd3 as2. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Weng, H.; Wu, Q.; Dai, X.; Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd 3As2. Phys. Rev. B 2013, 88, 125427. [Google Scholar] [CrossRef]
- Borisenko, S.; Gibson, Q.; Evtushinsky, D.; Zabolotnyy, V.; Büchner, B.; Cava, R.J. Experimental realization of a three-dimensional dirac semimetal. Phys. Rev. Lett. 2014, 113, 027603. [Google Scholar] [CrossRef]
- Chang, G.; Xu, S.Y.; Wieder, B.J.; Sanchez, D.S.; Huang, S.M.; Belopolski, I.; Chang, T.R.; Zhang, S.; Bansil, A.; Lin, H.; et al. Unconventional Chiral Fermions and Large Topological Fermi Arcs in RhSi. Phys. Rev. Lett. 2017, 119, 206401. [Google Scholar] [CrossRef]
- Wang, R.; Xia, B.W.; Chen, Z.J.; Zheng, B.B.; Zhao, Y.J.; Xu, H. Symmetry-Protected Topological Triangular Weyl Complex. Phys. Rev. Lett. 2020, 124, 105303. [Google Scholar] [CrossRef]
- Tang, P.; Zhou, Q.; Zhang, S.C. Multiple Types of Topological Fermions in Transition Metal Silicides. Phys. Rev. Lett. 2017, 119, 206402. [Google Scholar] [CrossRef]
- Zhang, T.; Song, Z.; Alexandradinata, A.; Weng, H.; Fang, C.; Lu, L.; Fang, Z. Double-Weyl Phonons in Transition-Metal Monosilicides. Phys. Rev. Lett. 2018, 120, 016401. [Google Scholar] [CrossRef]
- Lu, L.; Wang, Z.; Ye, D.; Ran, L.; Fu, L.; Joannopoulos, J.D.; Soljačić, M. Experimental observation of Weyl points. Science 2015, 349, 622–624. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Fu, L.; Joannopoulos, J.D.; Soljacic, M. Weyl points and line nodes in gyroid photonic crystals. Nat. Photonics 2013, 7, 294. [Google Scholar] [CrossRef]
- Chang, M.L.; Xiao, M.; Chen, W.J.; Chan, C.T. Multiple Weyl points and the sign change of their topological charges in woodpile photonic crystals. Phys. Rev. B. 2017, 95, 125136. [Google Scholar] [CrossRef]
- Chen, W.J.; Xiao, M.; Chan, C.T. Photonic crystals possessing multiple Weyl points and the experimental observation of robust surface states. Nat. Commun. 2016, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Guo, Q.; Tremain, B.; Liu, R.; Barr, L.E.; Yan, Q.; Gao, W.; Liu, H.; Xiang, Y.; Chen, J.; et al. Ideal Weyl points and helicoid surface states in artificial photonic crystal structures. Science 2018, 359, 1013–1016. [Google Scholar] [CrossRef]
- Yang, B.; Guo, Q.; Tremain, B.; Barr, L.E.; Gao, W.; Liu, H.; Béri, B.; Xiang, Y.; Fan Di Hibbins, A.P.; Zhang, S. Direct observation of topological surface-state arcs in photonic metamaterials. Nat. Commun. 2017, 8, 1–7. [Google Scholar] [CrossRef]
- Xiao, M.; Lin, Q.; Fan, S. Hyperbolic Weyl Point in Reciprocal Chiral Metamaterials. Phys. Rev. Lett. 2016, 117, 057401. [Google Scholar] [CrossRef]
- Gao, W.; Yang, B.; Lawrence, M.; Fang, F.; Béri, B.; Zhang, S. Photonic Weyl degeneracies in magnetized plasma. Nat. Commun. 2016, 7, 1–8. [Google Scholar] [CrossRef]
- Wang, D.; Yang, B.; Gao, W.; Jia, H.; Yang, Q.; Chen, X.; Wei, M.; Liu, C.; Navarro-Cía, M.; Han, J.; et al. Photonic Weyl points due to broken time-reversal symmetry in magnetized semiconductor. Nat. Phys. 2019, 15, 1150–1155. [Google Scholar] [CrossRef]
- Lin, Q.; Xiao, M.; Yuan, L.; Fan, S. Photonic Weyl point in a two-dimensional resonator lattice with a synthetic frequency dimension. Nat. Commun. 2016, 7, 1–7. [Google Scholar] [CrossRef]
- Wang, Q.; Xiao, M.; Liu, H.; Zhu, S.; Chan, C.T. Optical interface states protected by synthetic weyl points. Phys. Rev. X 2017, 7, 031032. [Google Scholar] [CrossRef]
- Ruan, J.; Jian, S.K.; Yao, H.; Zhang, H.; Zhang, S.C.; Xing, D. Symmetry-protected ideal Weyl semimetal in HgTe-class materials. Nat. Commun. 2016, 7, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.S.; Liu, Y.; Yu, Z.M.; Sheng, X.L.; Yang, S.A. Hourglass Dirac chain metal in rhenium dioxide. Nat. Commun. 2017, 8, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Young, S.M.; Kane, C.L. Dirac Semimetals in Two Dimensions. Phys. Rev. Lett. 2015, 115, 126803. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Wang, S.S.; Yu, Z.M.; Guan, S.; Sheng, X.L.; Yao, Y.; Yang, S.A. Nonsymmorphic-symmetry-protected hourglass Dirac loop, nodal line, and Dirac point in bulk and monolayer X3SiTe6 (X = Ta, Nb). Phys. Rev. B 2018, 97, 045131. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photonics. 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Jia, H.; Zhang, R.; Gao, W.; Guo, Q.; Yang, B.; Hu, J.; Bi, Y.; Xiang, Y.; Liu, C.; Zhang, S. Observation of chiral zero mode in inhomogeneous three-dimensional Weyl metamaterials. Science 2019, 363, 148–151. [Google Scholar] [CrossRef]

| E | ||||
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | |
| 1 | 1 | −1 | −1 | |
| 1 | −1 | 1 | −1 | |
| 1 | −1 | −1 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Wang, Y.-T. Ideal Photonic Weyl Nodes Stabilized by Screw Rotation Symmetry in Space Group 19. Crystals 2020, 10, 605. https://doi.org/10.3390/cryst10070605
Gao W, Wang Y-T. Ideal Photonic Weyl Nodes Stabilized by Screw Rotation Symmetry in Space Group 19. Crystals. 2020; 10(7):605. https://doi.org/10.3390/cryst10070605
Chicago/Turabian StyleGao, Wenlong, and Yao-Ting Wang. 2020. "Ideal Photonic Weyl Nodes Stabilized by Screw Rotation Symmetry in Space Group 19" Crystals 10, no. 7: 605. https://doi.org/10.3390/cryst10070605
APA StyleGao, W., & Wang, Y.-T. (2020). Ideal Photonic Weyl Nodes Stabilized by Screw Rotation Symmetry in Space Group 19. Crystals, 10(7), 605. https://doi.org/10.3390/cryst10070605




