Synthesis, Structure and Bonding Analysis of the Zwitterionic PPP-Pincer Complex (6-Ph2P-Ace-5-)2P(O)AuCl2
Abstract
1. Introduction
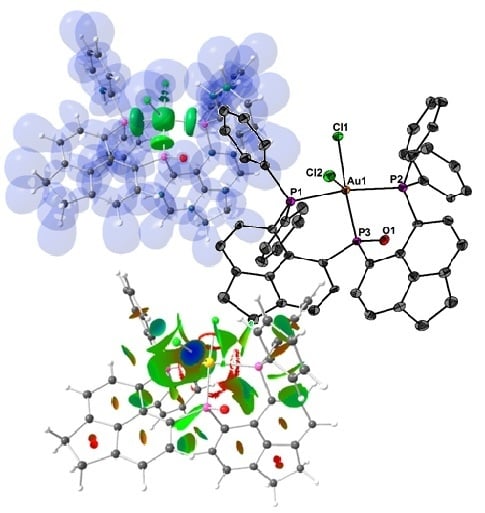
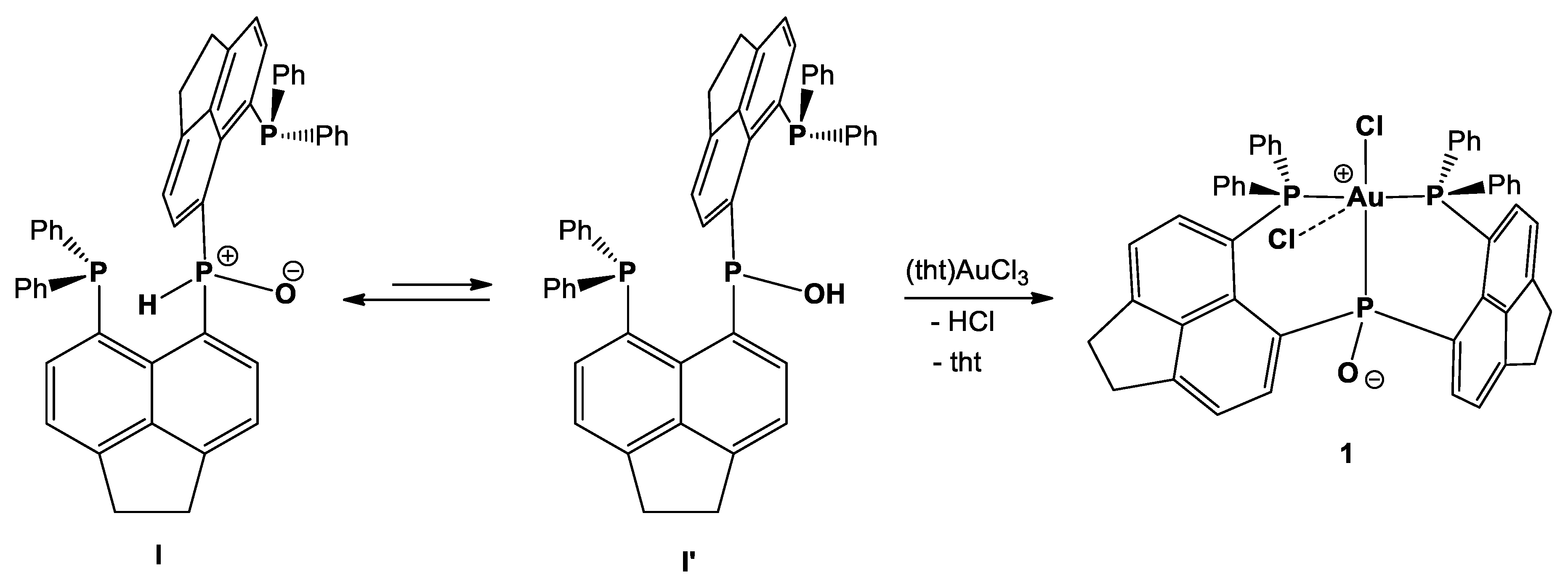
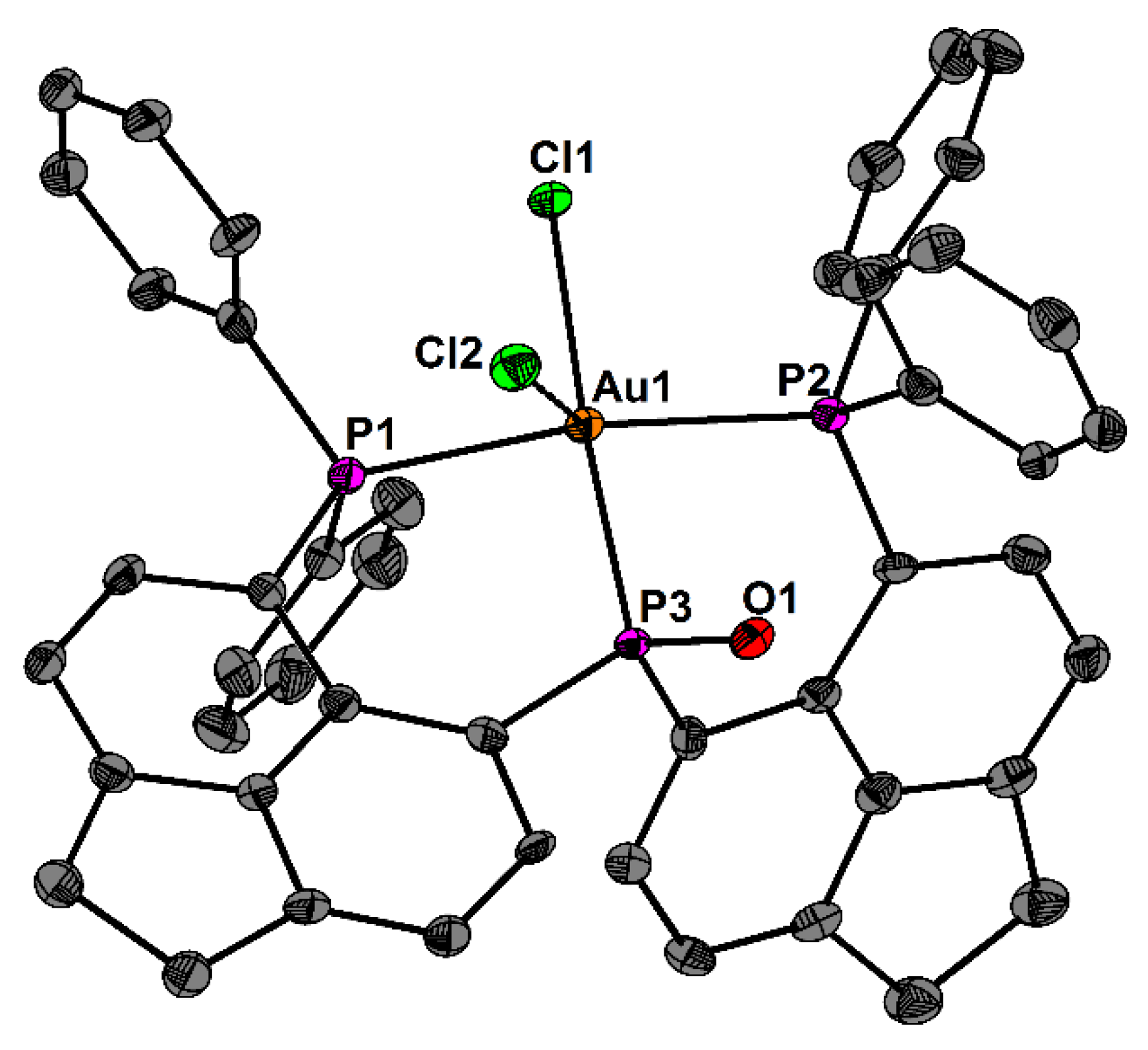
2. Results and Discussion
3. Experimental Section
3.1. X-ray Crystallography
3.2. Computational Methodology
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Duvinage, D.; Puylaert, P.; Wieduwilt, E.; Malaspina, L.A.; Piltz, R.O.; Edwards, A.J.; Lork, E.; Hupf, E.; Mebs, S.; Grabowsky, S.; et al. Bis(6-diphenylphosphinoacenaphth-5-yl) phosphine oxide: A New PPP-Pincer Ligand Based upon a Secondary Phosphine Oxide (SPO). 2020 to be submitted.
- Bader, R.W.F. Atoms in Molecules; A Quantum Theory; Cambridge University Press: Oxford, UK, 1991. [Google Scholar]
- Johnson, E.R.; Keinan, S.; Mori-Sanchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Kohout, M. A Measure of Electron Localizability. Int. J. Quantum Chem. 2004, 97, 651–658. [Google Scholar] [CrossRef]
- Stalke, D. Meaningful Structural Descriptors from Charge Density. Chem. Eur. J. 2011, 17, 9264–9278. [Google Scholar] [CrossRef] [PubMed]
- Mebs, S.; Kalinowski, R.; Grabowsky, S.; Förster, D.; Kickbusch, R.; Justus, E.; Morgenroth, W.; Paulmann, C.; Luger, P.; Gabel, D.; et al. Real-Space Indicators for Chemical bonding. Experimental and Theoretical Electron Density Studies of Four Deltahedral Boranes. Inorg. Chem. 2011, 50, 90–103. [Google Scholar] [CrossRef] [PubMed]
- Mebs, S.; Chilleck, M.A.; Grabowsky, S.; Braun, T. Hapticity Uncovered: Real-Space Bonding Indicators for Zincocene Chemistry. Chem. Eur. J. 2012, 18, 11647–11661. [Google Scholar] [CrossRef]
- Lane, J.R.; Contreras-Garcia, J.; Piquemal, J.-P.; Miller, B.J.; Kjaergaard, H.G. Are Bond Critical Points Really Critical for Hydrogen Bonding? J. Chem. Theory Comp. 2013, 9, 3263–3266. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Gillet, N.; Chaudret, R.; Contreras-Garcia, J.; Yang, W.; Silvi, B.; Piquemal, J.P. Coupling Quantum Interpretative Techniques: Another look at Chemical Mechanisms in Organic Reactions. J. Chem. Theory Comp. 2012, 8, 3993–3997. [Google Scholar] [CrossRef]
- Mebs, S. Complex modes of bonding: NCI/ELI-D vs. DORI surface analyses of hapticities and hydrogen-hydrogen contacts in zincocene related compounds. Chem. Phys. Lett. 2016, 651, 172–177. [Google Scholar] [CrossRef]
- Raub, S.; Jansen, G.A. Quantitative Measure of Bond Polarity from the Electron Localization Function and the Theory of Atoms in Molecules. Theor. Chem. Acc. 2001, 106, 223–232. [Google Scholar] [CrossRef]
- Addison, A.W.; Rao, N.T.; Reedijk, J.; van Rijn, J.; Verschoor, G.C. Synthesis, structure, and spectroscopic properties of copper(II) compounds containing nitrogen–sulphur donor ligands; the crystal and molecular structure of aqua[1,7-bis(N-methylbenzimidazol-2′-yl)-2,6-dithiaheptane]copper(II) perchlorate. J. Chem. Soc. Dalton Trans. 1984, 1349–1356. [Google Scholar] [CrossRef]
- Fugel, M.; Beckmann, J.; Jayatilaka, D.; Gibbs, G.V.; Grabowsky, S. A Variety of Bond Analysis Methods, One Answer? An Investigation of the Element−Oxygen Bond of Hydroxides Hn XOH. Chem. Eur. J. 2018, 24, 6248–6261. [Google Scholar] [CrossRef] [PubMed]
- Upmann, D.; Näther, C.; Jess, I.; Jones, P.G. Four Crystalline Forms of (Tetrahydrothiophene)trichloridogold(III): Polymorphism and Reversible Low-temperature Phase Transitions. Z. Anorg. Allg. Chem. 2017, 643, 311–316. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Brandenburg, K. Diamond, Version 4.0.4; Crystal Impact GbR: Bonn, Germany, 2012. [Google Scholar]
- CCDC. Available online: http://www.ccdc.cam.ac.uk (accessed on 1 July 2020).
- Becke, A.D. A New Mixing of Hartree-Fock and Local-Density-Functional Theories. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Figgen, D.; Rauhut, G.; Dolg, M.; Stoll, H. Energy-consistent pseudopotentials for group 11 and 12 atoms: Adjustment to multi-configuration Dirac–Hartree–Fock data. Chem. Phys. 2005, 311, 227–244. [Google Scholar] [CrossRef]
- Peterson, K.A.; Puzzarini, C. Systematically convergent basis sets for transition metals. II. Pseudopotential-based correlation consistent basis sets for the group 11 (Cu, Ag, Au) and 12 (Zn, Cd, Hg) elements. Theor. Chem. Acc. 2005, 114, 283–296. [Google Scholar]
- Biegler-König, F.; Schönbohm, J.; Bayles, D. A Program to Analyze and Visualize Atoms in Molecules. J. Comput. Chem. 2001, 22, 545–559. [Google Scholar]
- Kohout, M. DGRID-4.6; Springer: Radebeul, Germany, 2015. [Google Scholar]
- Contreras-García, J.; Johnson, E.; Keinan, S.; Chaudret, R.; Piquemal, J.-P.; Beratan, D.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theor. Comp. 2011, 7, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Hübschle, C.B.; Luger, P. MolIso—A Program for Colour-Mapped Iso-Surfaces. J. Appl. Crystallogr. 2006, 39, 901–904. [Google Scholar] [CrossRef]

| Contact or Basin | d [Å] | ρ(r)bcp [eÅ−3] | ∇2ρ(r)bcp [eÅ−5] | ε | G/ρ(r)bcp [a.u.] | H/(r)bcp [a.u.] | NELI [e] | VELI [Å3] | γELI | RJI % |
|---|---|---|---|---|---|---|---|---|---|---|
| P–O | 1.483 | 1.64 | 29.3 | 0.04 | 2.18 | −0.93 | 1.64 | 2.0 | 1.56 | 77.8 |
| Au–P3 | 2.297 | 0.80 | −1.3 | 0.03 | 0.40 | −0.51 | 1.67 | 5.1 | 1.68 | 59.4 |
| Au–P1 | 2.345 | 0.72 | 1.4 | 0.01 | 0.57 | −0.43 | 1.91 | 6.9 | 1.77 | 73.8 |
| Au–P2 | 2.365 | 0.70 | 1.3 | 0.03 | 0.55 | −0.42 | 1.89 | 6.9 | 1.78 | 73.9 |
| Au–P | 2.336 | 0.74 | 0.5 | 0.03 | 0.51 | −0.45 | 1.83 | 6.3 | 1.74 | 69.0 |
| Au–Cl1 | 2.392 | 0.58 | 4.2 | 0.02 | 0.82 | –0.31 | 0.30 | 0.4 | 1.54 | 82.1 |
| Au–Cl2 | 2.830 | 0.25 | 2.3 | 0.01 | 0.74 | −0.09 |
| Contact | d [Å] | d1+d2 [Å] | dt-d [Å] | d1/d | ρ(r)bcp [eÅ-3] | ∇2ρ(r)bcp [eÅ-5] | ε | G/ρ(r)bcp [a.u.] | H/(r)bcp [a.u.] |
|---|---|---|---|---|---|---|---|---|---|
| Cl2···H73 | 2.476 | 2.478 | 0.002 | 0.65 | 0.11 | 1.1 | 0.02 | 0.62 | 0.12 |
| Cl1···H88 | 2.901 | 2.928 | 0.027 | 0.63 | 0.05 | 0.5 | 1.53 | 0.60 | 0.14 |
| Cl2···H34 | 2.905 | 2.921 | 0.017 | 0.61 | 0.05 | 0.6 | 0.10 | 0.62 | 0.15 |
| Cl1···Cπ | 3.271 | 3.289 | 0.019 | 0.53 | 0.07 | 0.8 | 3.43 | 0.69 | 0.17 |
| fragm. | Q001 (e) | fragm. | Q001 (e) |
|---|---|---|---|
| ace1 | −0.94 | ace2 | −0.99 |
| (ace1)Ph1 | −0.38 | (ace2)Ph1 | −0.39 |
| (ace1)Ph2 | −0.46 | (ace2)Ph2 | −0.42 |
| P1 | 1.80 | P2 | 1.84 |
| sum | 0.02 | sum | 0.04 |
| P3 | 2.55 | Au | 0.11 |
| O | −1.45 | Cl1 | −0.54 |
| Cl2 | −0.73 | ||
| sum | 1.10 | sum | −1.16 |
| 1·3 CH2Cl2 | |
|---|---|
| Formula | C51H42AuCl8OP3 |
| Formula weight, g mol−1 | 1244.32 |
| Crystal system | Triclinic |
| Crystal size, mm | 0.08 × 0.07 × 0.06 |
| Space group | P |
| a, Å | 11.540(5) |
| b, Å | 11.606(5) |
| c, Å | 21.251(5) |
| α, ° | 86.058(5) |
| β, ° | 79.833(5) |
| γ, ° | 60.908(5) |
| V, Å3 | 2447.6(16) |
| Z | 2 |
| ρcalcd, Mg m−3 | 1.688 |
| T, K | 100 |
| μ (Mo Kα), mm−1 | 3.579 |
| F(000) | 1232 |
| θ range, deg | 2.21 to 28.59 |
| Index ranges | −15 ≤ h ≤ 15 |
| −15 ≤ k ≤ 15 | |
| −28≤ l ≤ 28 | |
| No. of reflns collected | 116915 |
| Completeness to θ max | 99.3% |
| No. indep. reflns | 12425 |
| No. obsd reflns with (I>2σ(I)) | 10491 |
| No. refined params | 577 |
| GooF (F2) | 1.164 |
| R1 (F) (I > 2σ(I)) | 0.0505 |
| wR2 (F2) (all data) | 0.1079 |
| (Δ/σ)max | <0.001 |
| Largest diff peak/hole, e Å−3 | 2.574/−2.984 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duvinage, D.; Lork, E.; Grabowsky, S.; Mebs, S.; Beckmann, J. Synthesis, Structure and Bonding Analysis of the Zwitterionic PPP-Pincer Complex (6-Ph2P-Ace-5-)2P(O)AuCl2. Crystals 2020, 10, 564. https://doi.org/10.3390/cryst10070564
Duvinage D, Lork E, Grabowsky S, Mebs S, Beckmann J. Synthesis, Structure and Bonding Analysis of the Zwitterionic PPP-Pincer Complex (6-Ph2P-Ace-5-)2P(O)AuCl2. Crystals. 2020; 10(7):564. https://doi.org/10.3390/cryst10070564
Chicago/Turabian StyleDuvinage, Daniel, Enno Lork, Simon Grabowsky, Stefan Mebs, and Jens Beckmann. 2020. "Synthesis, Structure and Bonding Analysis of the Zwitterionic PPP-Pincer Complex (6-Ph2P-Ace-5-)2P(O)AuCl2" Crystals 10, no. 7: 564. https://doi.org/10.3390/cryst10070564
APA StyleDuvinage, D., Lork, E., Grabowsky, S., Mebs, S., & Beckmann, J. (2020). Synthesis, Structure and Bonding Analysis of the Zwitterionic PPP-Pincer Complex (6-Ph2P-Ace-5-)2P(O)AuCl2. Crystals, 10(7), 564. https://doi.org/10.3390/cryst10070564