1. Introduction
Thermoelectric technology shows a great potential in power generation, cooling and applications of related mechanisms [
1,
2,
3]. According to the theoretical mode [
4], the performance of thermoelectric material used in such devices is evaluated by a dimensionless factor, the figure of merit (
ZT). The
ZT here is defined as
α2σT/κ, where
α is the Seebeck coefficient,
σ is the electrical conductivity,
κ is the total thermal conductivity, and
T is the temperature. The larger the figure is, the higher a thermoelectric conversion efficiency is likely to be achieved. Furthermore, another important parameter is the power factor, which is defined as
PF =
α2σ. It evaluates the material’s ability of generating electrical energy from a constrained space.
Many thermoelectric materials are being explored for power generation applications, such as silicides [
5], PbTe [
6], half-Heusler [
7] and skutterudites [
8], and different thermoelectric material should be taken advantage of under different temperature conditions. In situations from room temperature to around 500 K, bismuth telluride, a V–VI semiconductor with a narrow band gap, and bismuth-telluride-based materials are a promising choice. The
ZT of bulk bismuth telluride is around 1, which is considered to be the critical value to be utilized in a practical thermoelectric device. Besides, different methods are applied in improving
ZT to achieve a larger energy conversion efficiency. Doping is one of the methods used, and a
ZT of 1.4 at 373 K was achieved in bulk BiSbTe
3 [
9]. Besides, modification on nanostructures also helps improve
ZT. For instance, an outstanding factor of 2.4 is observed in a superlattice structure of p-type Bi
2Te
3/Sb
2Te
3 [
10].
Recent years, different methods have been studied and utilized to synthesize bismuth telluride, including but not limited to chemical synthesis [
11], electrodeposition [
12,
13,
14], ion beam sputtering deposition [
15], magnetron sputtering deposition [
16,
17,
18,
19,
20] and molecular beam epitaxy [
21]. Among these methods, magnetron sputtering is frequently used for the merit of being cost-effective and time-saving, and having the potential to be used in industrial manufacturing. Former studies have also shown that the polycrystalline structure created by magnetron sputtering has a positive effect on
ZT, for the lattice boundaries help reflect phonons to greatly reduce the thermal conductivity but have a minor influence on electronics [
16,
17,
22,
23]. While most studies of magnetron sputtered bismuth telluride film concentrated on the effect of deposition temperature [
20] or post-treatment of deposited films [
18,
19], the effect of other parameters in the sputtering process seems to be less looked into.
In this work, the effect of deposition power on the as-prepared bismuth telluride films deposited by RF sputtering is studied. The thin film samples prepared at different powers are afterwards investigated with SEM, XRD, Hall and thermoelectric measurements. Both crystalline characteristics and thermoelectric properties are compared to study how the power will affect the deposition of bismuth telluride thin films to find a simple approach to synthesize bismuth telluride with higher thermoelectric performance.
2. Materials and Methods
The films were deposited on polished glass substrates by radio frequency (RF) sputtering with an electron beam assisted sputtering system (INFOVION, Seoul, Korea) at room temperature with a background pressure of 4.5 × 10−6Torr. A sputter target of Bi2Te3 (diameter: 76.2 mm, thickness: 4 mm, 99.999% purity, Jiangxi Ketai Advanced Material Co., Ltd., Gao’an City, Jiangxi Province, China) was used in the sputtering. The distance between the target and the substrate is 145 mm, and the angle between the axis of the target and that of the substrate is 30°. The growth pressure was set to 5 mTorr by a throttle valve with the Argon gas flow rate at 40 sccm. The sputtering power was set to be 20 W, 30 W, 50 W, and 70 W. The corresponding power density was 0.44 W/cm2, 0.66 W/cm2, 1.10 W/cm2 and 1.54 W/cm2. In order to control the thickness of the films, the growth rates corresponding to the powers were determined first. A step-profiler was used to measure the thickness of sample films prepared under different powers, and the growth rates were calculated. After the preparatory work was done, 300 nm-thick films were deposited under each fixed power condition.
The surface morphology and composition of the films were determined by field emission scanning electron microscopy (FE-SEM) and energy dispersive spectrometer (EDS) (Hitachi S-4800 FE-SEM, Tokyo, Japan). Furthermore, the crystal structure was analyzed with X-ray diffraction (XRD) (BRUKER D8 ADVANCE, Berlin, German). The samples were scanned from 10° to 80° in the θ–2 θ mode.
A Hall Effect measurement system (SWIN Hall 8800, Xinzhu City, Taiwan, China) was used to determine the electrical properties of the samples at room temperature. The sheet resistance was measured with a four-probe method, and the carrier concentration and mobility were tested with the Hall measurement.
The conductivity and Seebeck coefficients were measured over a temperature range from room temperature to 473 K with ZEM-3 (Ulvac Riko Inc., Kanagawa, Japan) system and a self-made zirconium dioxide holder for films. The conductivity was also compared with the result from Hall 8800 test.
3. Results and Discussion
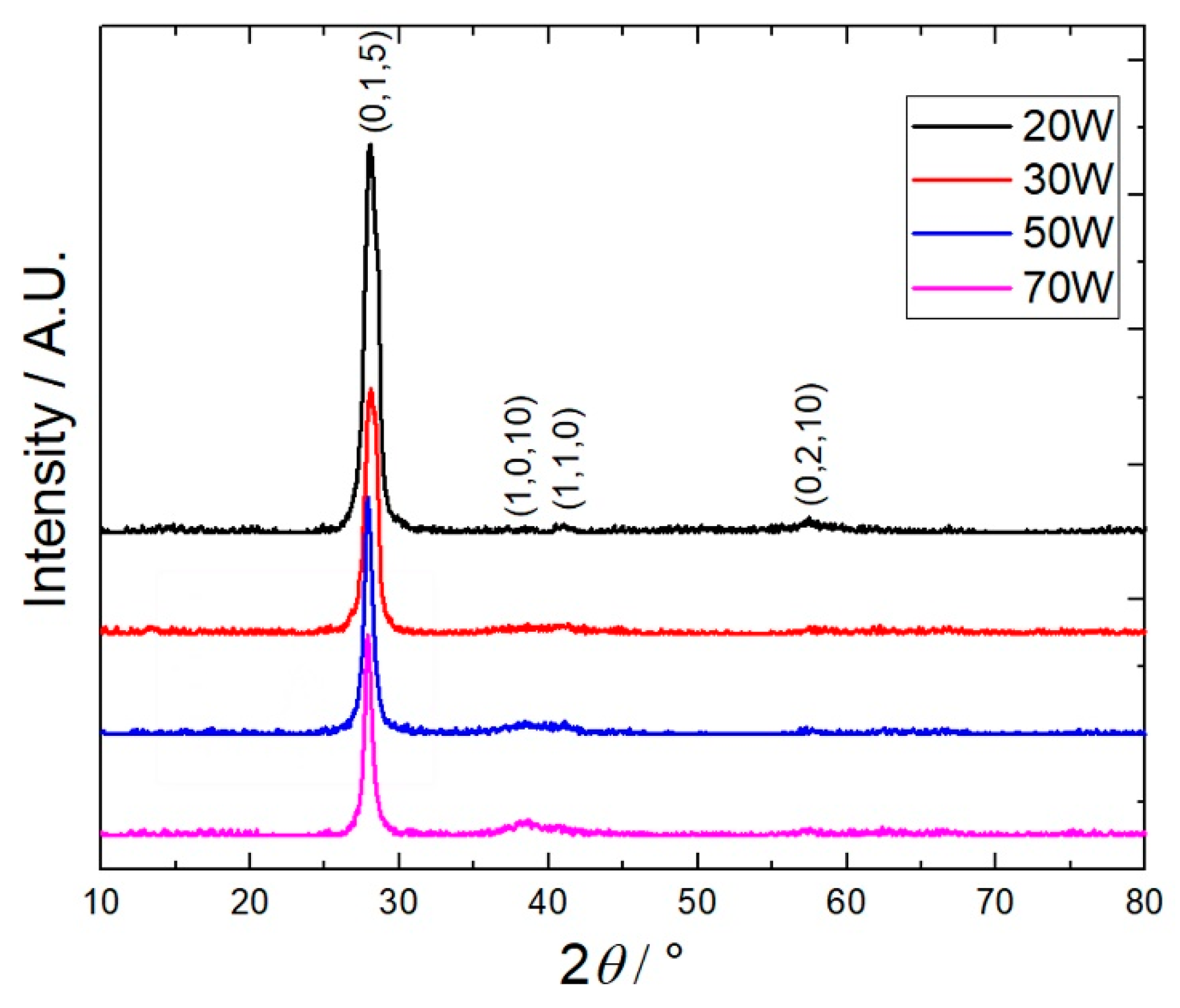
Samples prepared under different power were first looked into with SEM, EDS and XRD, and research concentrated on the crystalline properties. SEM results show that all the samples were densely deposited into polycrystalline structure as shown in
Figure 1. Furthermore, the bismuth telluride grains were irregularly shaped with different sizes. By conducting random sampling over the crystalline grains in the SEM images, the average grain sizes are estimated. It turns out that the average grain size grows with the deposition power. It is calculated to be around 40 nm for the films deposited under 20 W and 30 W, and close to 50nm for the films deposited under 50 W and 70 W.
EDS results shows that all samples are a bit of Bi-rich and the atomic ratio between Bi and Te is about 42.7:57.3, slightly deviated from the stoichiometric ratio of 40:60, corresponding to the condition to produce assumedly the best thermoelectric performance. The atomic ratio is mainly determined by the activity of the atoms in the sputtering process with working parameters such as the growth pressure that will affect the activity to be varying little with the deposition power [
24]. Furthermore, according to the subsequent XRD tests, the formation of other compounds was not observed, but the lattice parameters were affected.
XRD test is applied to determine the crystallization properties. The recorded data was processed to remove the background, and the peaks were marked as shown in
Figure 2. In the diagram, it is found that only the peaks of Bi
2Te
3 (R
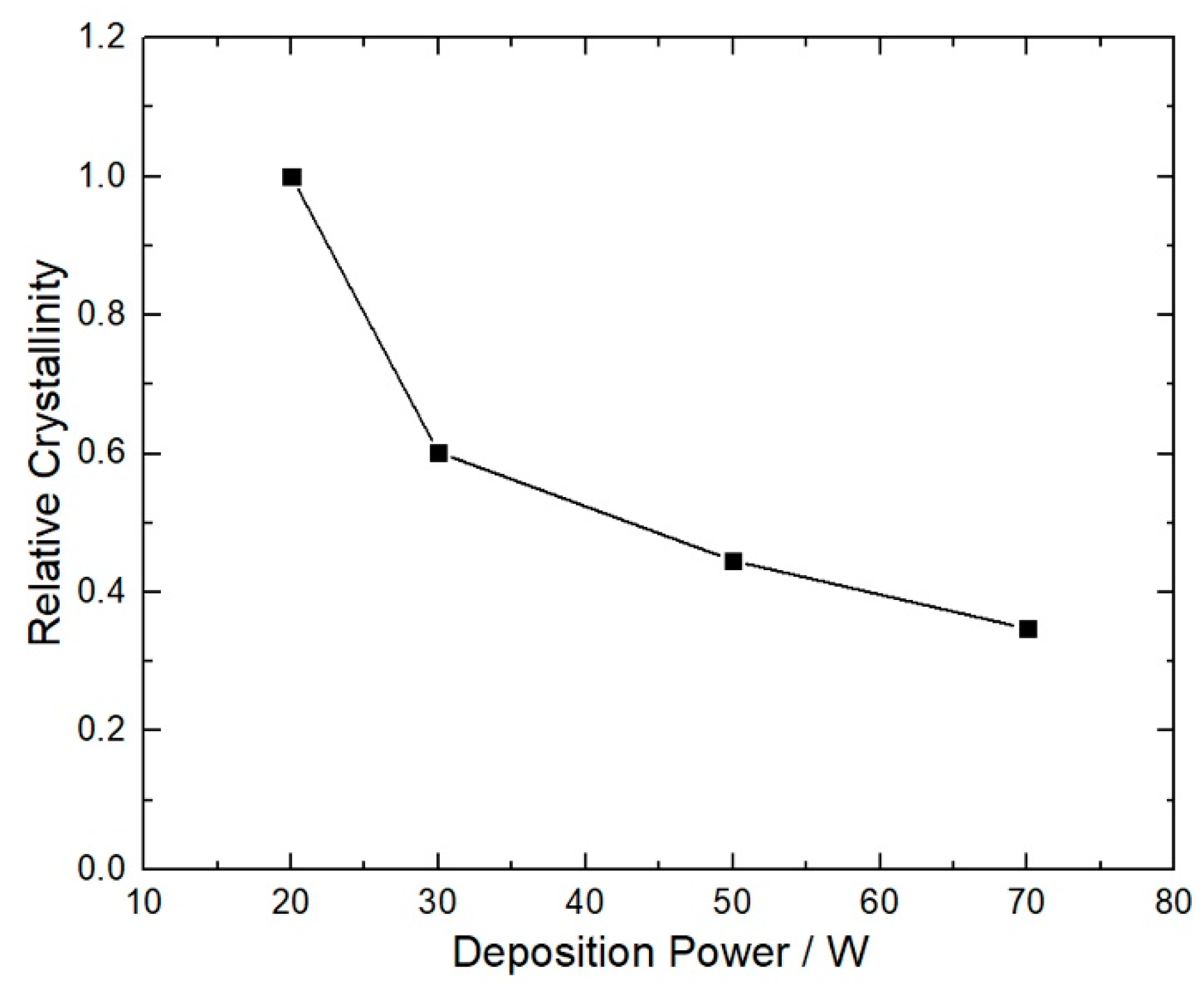
m) exist and the (0 1 5) peak is especially prominent, indicating a preferred growth orientation. In other words, there were no other compounds of bismuth and tellurium induced by the extra bismuth. Besides, the position of the (0 1 5) peak shifted to a slightly larger angle, indicating a smaller lattice size than the standard samples used in the PDF card (The Powder Diffraction File, International Centre for Diffraction Data), which might result from the vacancies formed due to the lack of tellurium in the non-stoichiometric bismuth-telluride film. Moreover, the variation of the lattice sizes makes the Scherrer equation less precise in predicting the crystalline properties from the XRD results. The grain sizes were estimated to be between 10 nm and 20 nm according to the Scherrer equation, which were much smaller than the SEM results to make them unreliable. The data were confirmed on another set of XRD apparatus, and the errors may be attributed to the extra broadening of the peaks resulted from the variation of grain sizes and lattice parameters mentioned above. However, since the intensity of the XRD peaks is proportional to the crystalline quality of the samples, the relative crystallinity, which is calculated by comparing the areas of the peaks, can still be applied here to measure the crystalline quality of the films deposited under different powers. The calculated results are shown in
Figure 3. It is clear that the crystallinity becomes worse with the power rising, and it may be the main effect of the deposition power on the structural characteristics of the films, along with a small growth of crystalline grain size.
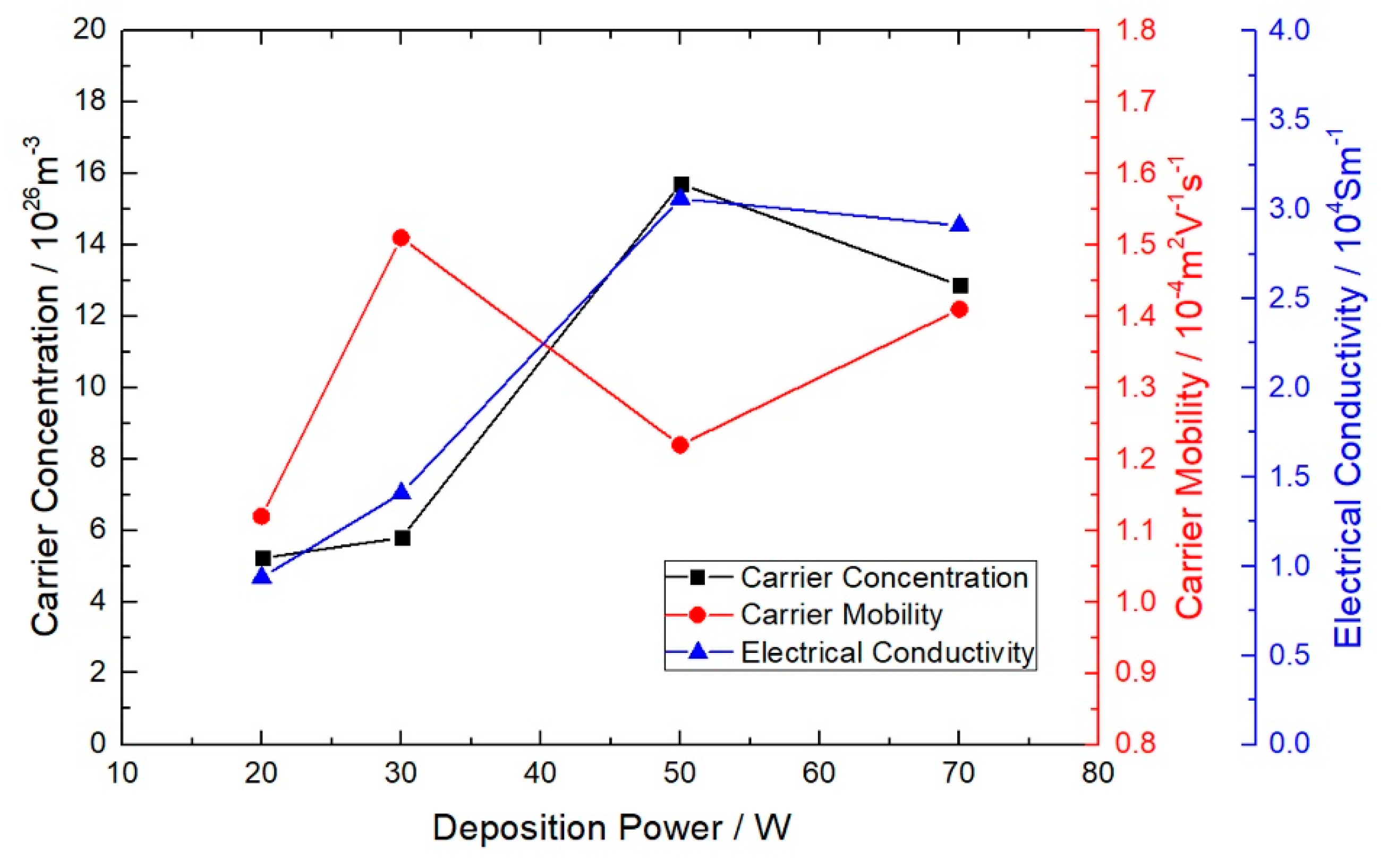
Hall test was performed to study the average semiconductor performance of the films under the room temperature. All the majority carriers of the samples are found to be electrons, and the films are thus n-type semiconductors, with the results shown in
Figure 4. According to the results, the samples can be divided into two groups, the group of films deposited under lower powers, which are 20 W and 30 W, respectively, and the group of films deposited under relatively higher powers, 50 W and 70 W. The semiconductor properties of the two groups differ distinctly in carrier concentration and electrical conductivity. The lower-power group of films appear to have lower carrier concentration than the other group. Since that both groups have similar carrier mobility, the group which possesses larger carrier concentration turns out to have higher conductivity. Combined with the former experiments, it can be inferred that larger deposition power will result in a higher deposition speed and there will be less relaxation time for deposited atoms to fit into the lattice. As a result, it will also result in a lower crystallinity in the preparation of the Bi
2Te
3 films, which induces the production of more carriers and thus an increase in the conductivity. However, compared with the results from the ZEM-3 system in the next part, the conductivity here is relatively lower due to the difference in ambient temperature.
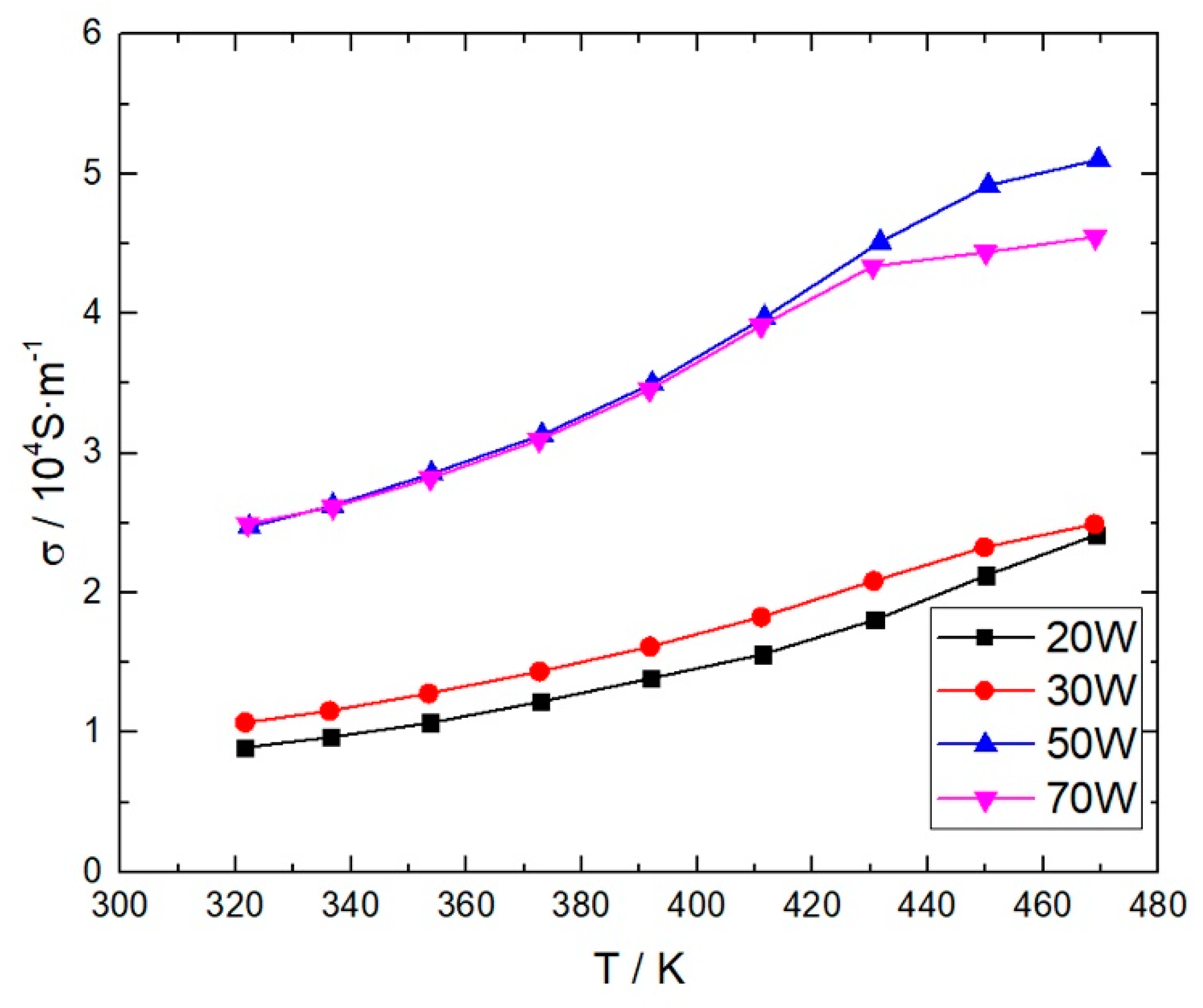
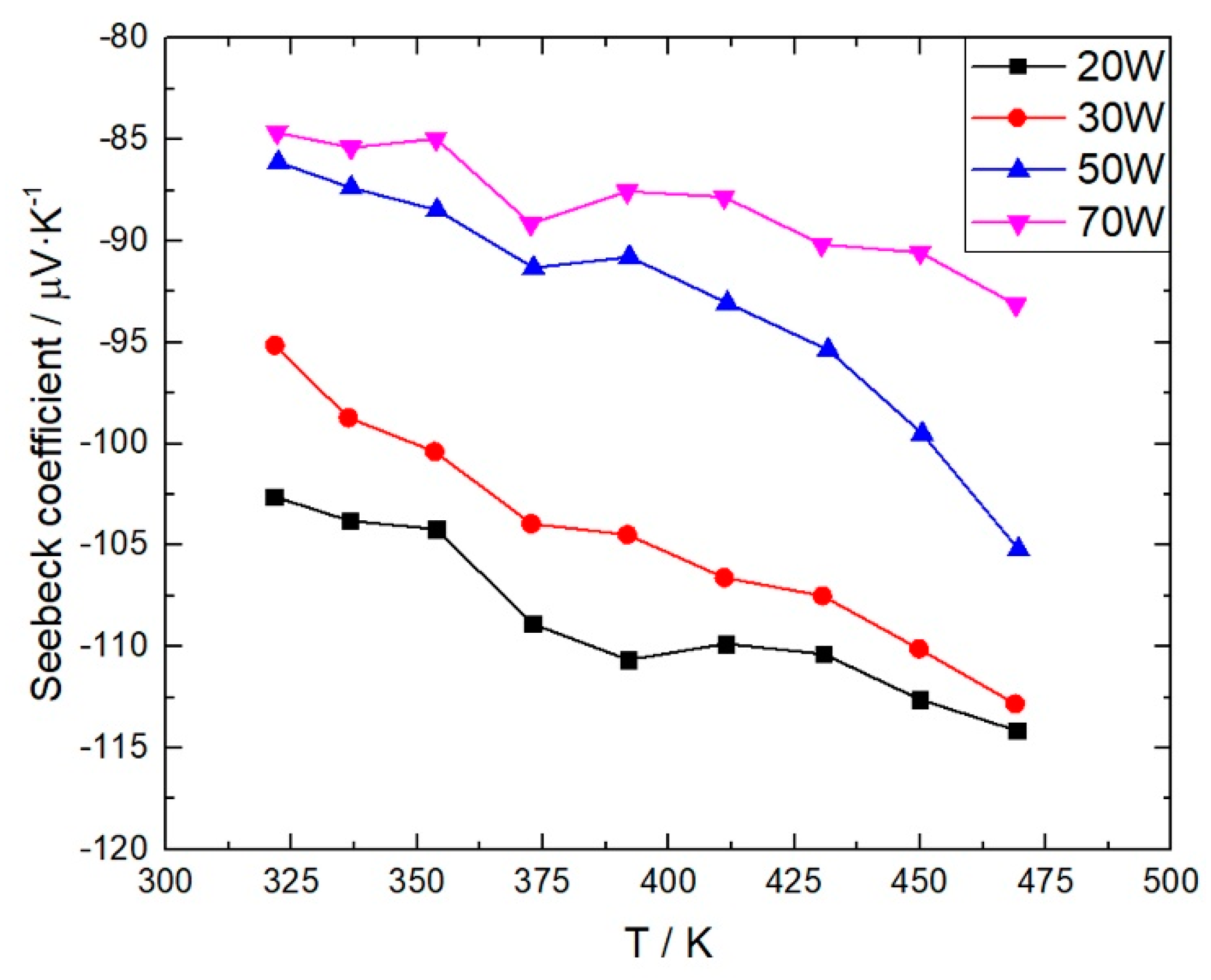
The conductivity and Seebeck coefficients of the films and their change trend with the temperature were studied afterwards by the ZEM-3 system with the results shown in
Figure 5 and
Figure 6. Like the results shown in the Hall test, the samples can also be classified into two groups according to their thermoelectric behavior and conductivity. Both the conductivity and absolute value of the Seebeck coefficients of the films prepared in our work increase with the temperature, but the curves differ clearly between the groups. In general, the conductivity of the films prepared under larger powers are higher, and the other group has an advantage in the absolute value of the Seebeck coefficients. All of the Seebeck coefficients are negative, indicating that the samples are n-type semiconductors.
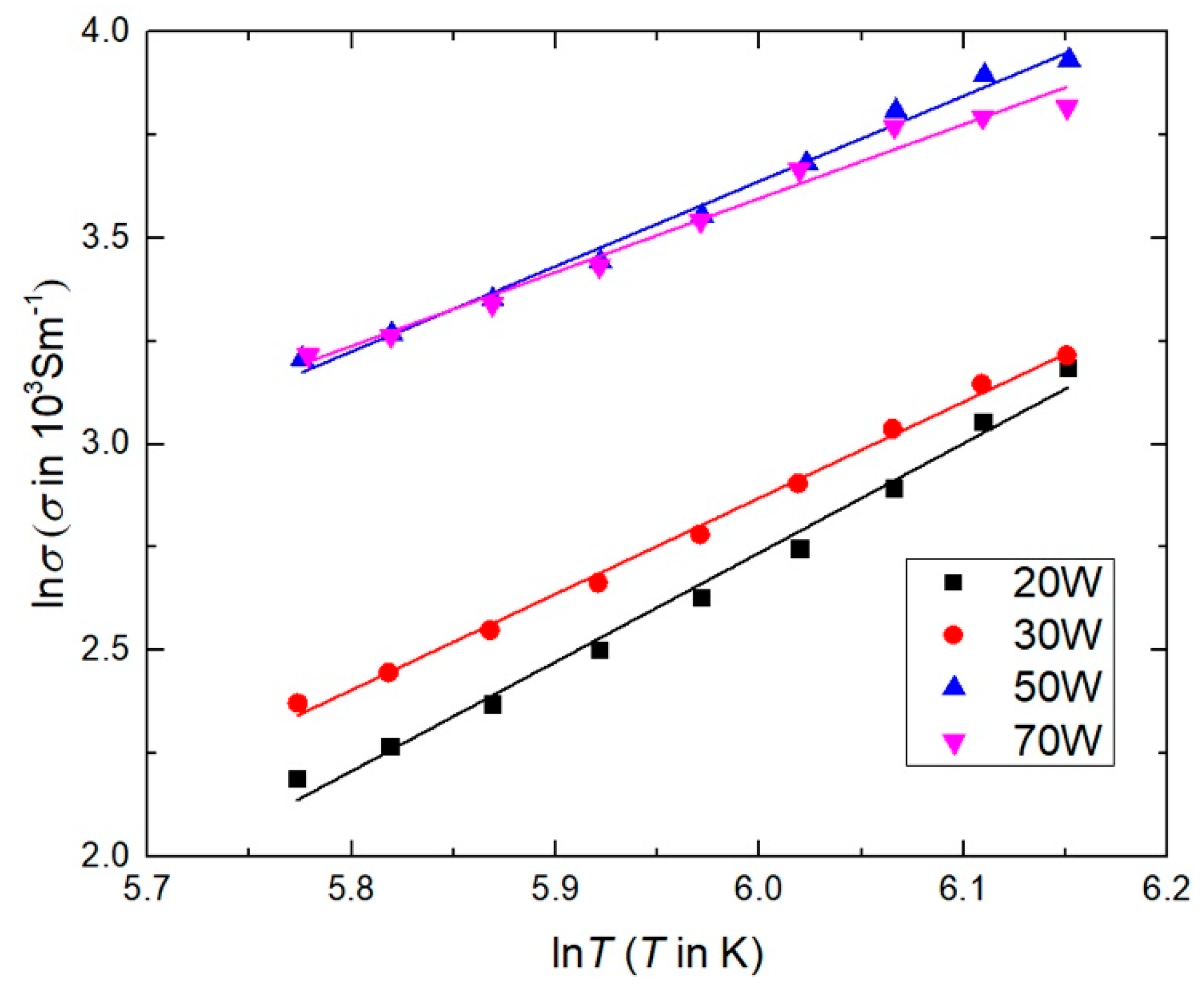
Additionally, different curve fittings were done and compared on the temperature-based behavior of the electrical conductivity and the Seebeck coefficients. The electrical conductivity
σ of the films increases monotonously with the temperature
T, showing a semiconductor behavior. The results can be fitted into an exponential relationship as shown in
Figure 7, in which ln
σ and ln
T are used to show it more clearly. The slopes of the curves are the fitted exponents being 2.65, 2.33, 2.07 and 1.80. Thus, in the research range, the larger the deposition power is, the higher the electrical conductivity could be, but the conductivity would increase more slowly with the temperature. Considering that the conductivity
σ is the product of the electron concentration
n, the electronic charge
e, and the electron mobility
μ, as
σ =
neμ, the temperature-related behavior could be the result of change in
n or
μ. However, because of the inherent relationship between the thermoelectric phenomenon and the temperature-dependent change of carrier concentration, subsequent research on the Seebeck coefficients will show that the electron concentration of different samples might change with the temperature with a similar magnitude. So, it is believed that the difference of the exponents here is mainly due to the influence of different scattering mechanisms. For the samples deposited under relatively higher powers with lower crystallinity, there are more carriers to achieve a better electrical conductivity, but meanwhile the electrons are also scattered more frequently by other electrons and grain boundaries, which results in a slightly different curve of
σ ~
T.
Considering the Seebeck coefficients, the literature [
25,
26] has proved that the Seebeck coefficient α of a degenerate semiconductor can be expressed approximately as:
where
k is the Boltzmann constant,
e is the electronic charge,
T is the temperature,
EF is the Fermi energy of electrons defined with respect to the conduction band edge, and
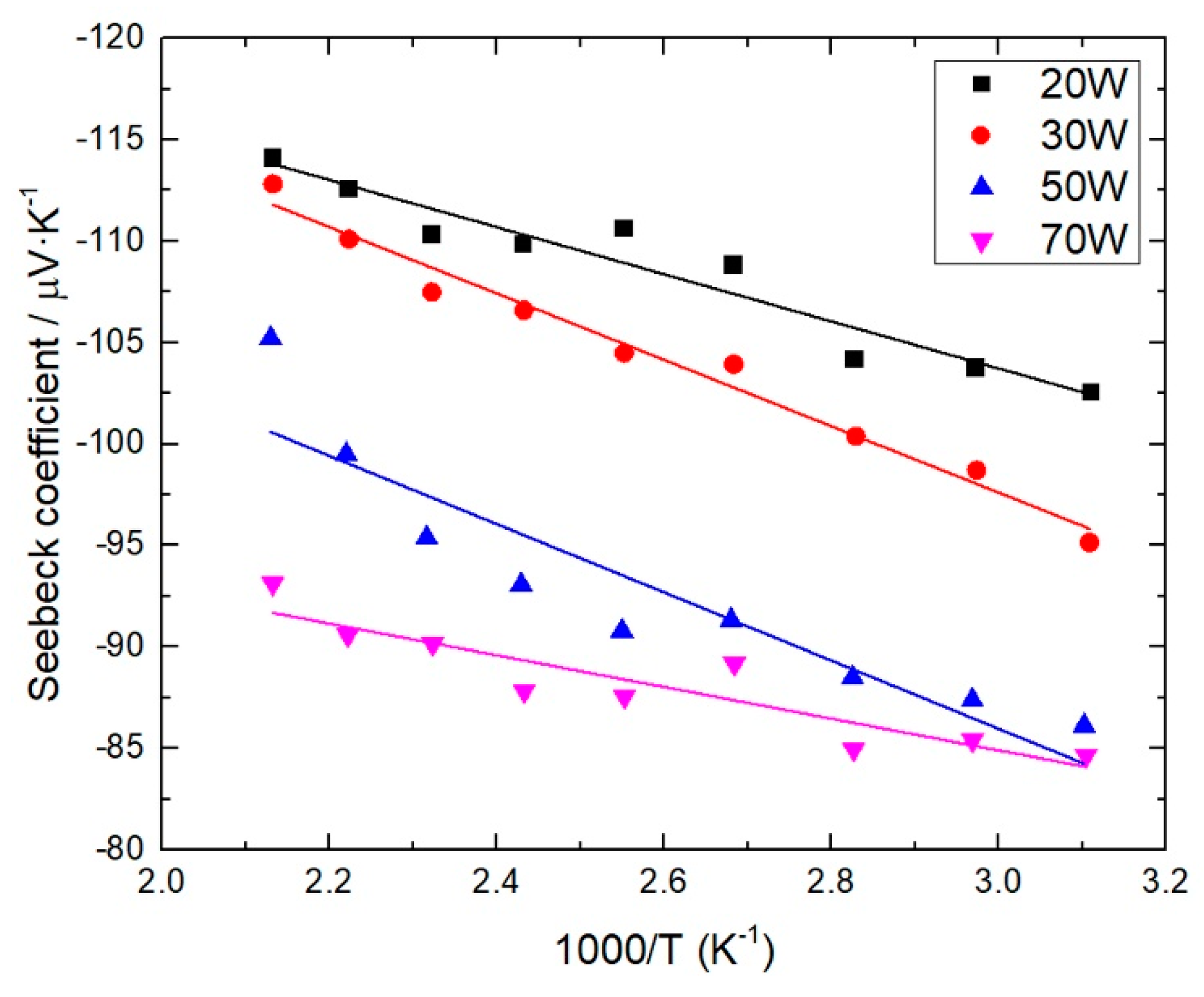
A is a function of the effective mass of the electron, the electron energy and the relaxation time of the electrons. So, the Seebeck coefficient and the reciprocal of the temperature could be fitted into a linear curve, where the magnitude is related to the band structure and the scattering mechanisms of the electrons, and the slope is related to the Fermi energy
EF. In other words, the difference of the Seebeck coefficients between the higher power group and lower one is also a reflection of the structural distinction resulted from the different crystallinity. The linear curve fittings were done on
α and the reciprocal of
T as shown in
Figure 8, where 1000/
T was used. The values of
EF were fitted to be −0.012 eV, −0.016 eV, −0.017 eV, and −0.008 eV, which are all above −2
kT and very close to zero, confirming that the samples are degenerate semiconductors. However, the slopes are small and sensitive to the fluctuation of the data which possibly resulted from the random noise in measurement. As a result, the reference that
EF is close to zero is true.
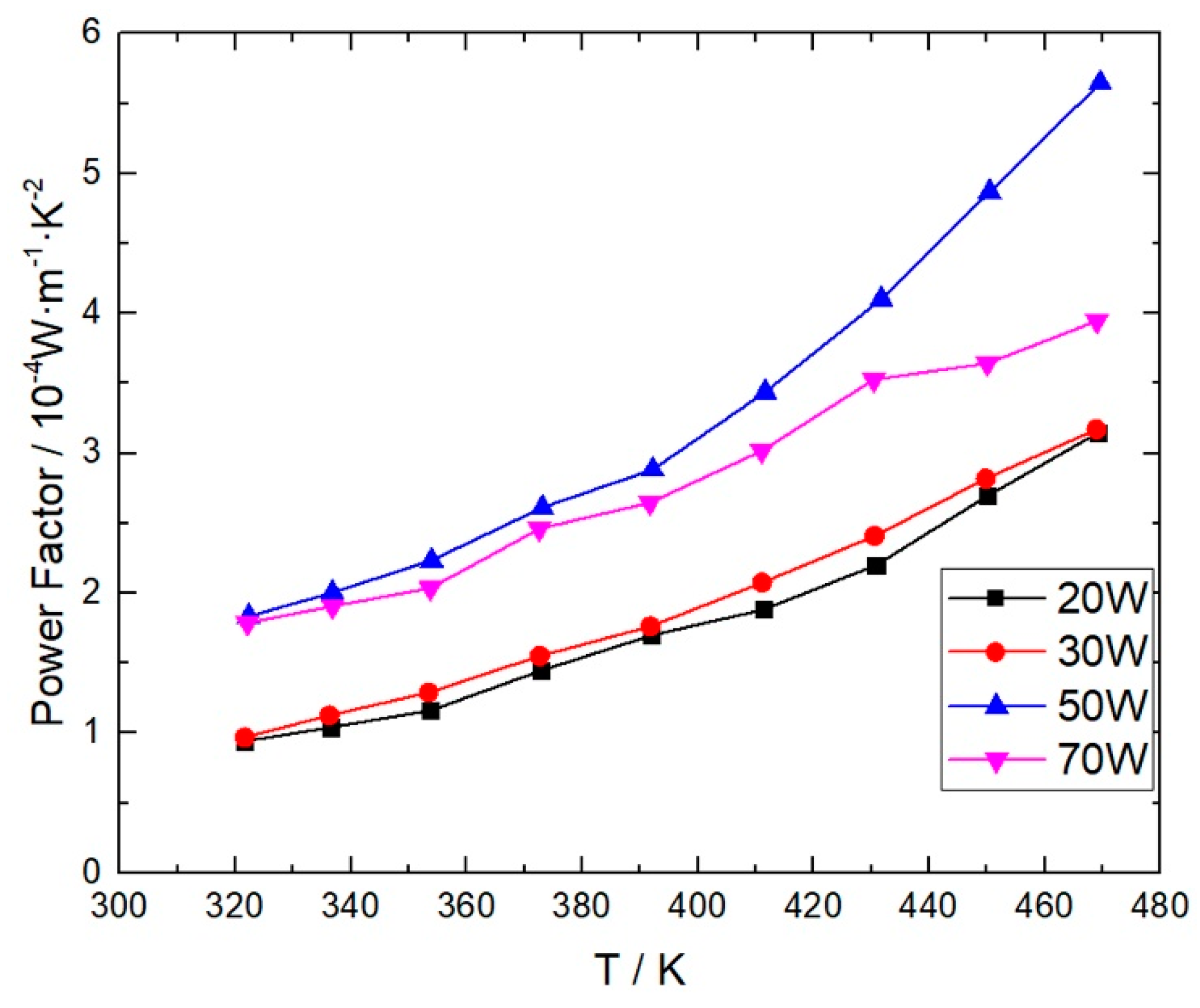
The power factors are calculated from the Seebeck coefficients and the electrical conductivity as
PF =
α2σ. The results are shown in
Figure 9. All the calculated power factors rise with the temperature at different speeds. Although the Seebeck coefficients of the lower-power group are slightly larger, the higher-power group has a greater advantage on the conductivity to achieve a larger
PF. The samples deposited under 50 W possess a maximum power factor in all over the temperature range. Furthermore, it is expected for the power factor to rise a bit more with the temperature increasing towards 500 K, which was not yet measured in this work. The power factor of samples deposited under 70 W, which is very close to the one of 50 W under 440 K, falls behind evidently above 440 K, mainly due to a slowdown of growth in conductivity. However, it is still much larger than that of the samples in the other group.
The higher the power factor is, the larger power of electricity the films are able to generate from a restricted volume. So, by raising the deposition power, the bismuth telluride films could be deposited into a desired polycrystalline structure, and thus a better thermoelectric performance could be achieved. Besides, compared with other method to modify the thermoelectric performance of materials, the method in this work has the advantage of being simple and cost-saving, and is expected to achieve a competitive thermoelectric conversion efficiency by decreasing the thermal conductivity resulted from a reduced crystallinity. Moreover, the method is in-situ and compatible with other materials or fabrication methods. As a result, a combination of raising deposition power and other reported methods could lead to a more promising thermoelectric performance.
In this work, a maximum power factor of 5.65 × 10
−4 W·m
−1·K
−2 is observed at 470 K with the sample deposited under 50 W. Considering the figure of merit, it is expected to grow monotonously with the temperature like the power factor, and a thermal conductivity lower than 0.5 W·m
−1·K
−1 is required to achieve a practical
ZT at 470 K. Report [
23] shows that the value is possible to be achieved in bismuth telluride samples with a minor grain size. Furthermore, we are still working on the precise measurement of the thermal conductivity, especially by getting rid of the side effect from the substrate.