Microwave Liquid Crystal Enabling Technology for Electronically Steerable Antennas in SATCOM and 5G Millimeter-Wave Systems
Abstract
1. Introduction
- ▪
- ▪
- ▪
- by using functional materials such as ferrites [26,27,28], ferroelectrics, mainly Barium Strontium Titanate (BST) capacitors, filters, and phase shifters in thin or thick-film technology [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44] and the Microwave Liquid Crystal (MLC) technology beyond optics.
2. Microwave Liquid Crystal Technology
2.1. Performance Metric of Microwave Liquid Crystals
2.2. Orientation Mechanisms and Biasing Schemes
- ➢
- Var1 with w = 1000 µm, ℓ = 450 µm, hLC ≈ 5 µm, C = 0.95 pF, fR = 7 GHz, = 22 ms, = 92 ms and
- ➢
- Var2 with w = 300 µm, ℓ = 225 µm, hLC ≈ 1 µm, C = 0.8 pF, fR = 7.5 GHz, = 1 ms, = 4 ms,
2.3. Software Design Tool for MLC Devices
- the finite difference method for static fields to simulate the director dynamics and
- the finite difference frequency domain method for a full RF wave simulation.
2.4. Next Generation of Microwave Liquid Crystals for Electronically Steerable Antennas
- (1.)
- Important improvements have been made to the low-temperature stability of the third generation of mixture classes by lowering the crystallization temperature Tc down to below −20 °C and −30 °C, respectively.
- (2.)
- The dielectric anisotropy at low frequencies Δε1 kHz could be increased significantly to values of 10 to 20 and above, leading to much lower threshold voltages, and hence, lower tuning voltages.
- (3.)
- Response times are proportional to the rotational viscosity. This parameter has been decreased to around 0.3 Pa·s for the third-generation LCs compared to 2100 Pa·s for second-generation LC TUD-566, thus enabling considerable improvements in response time, as can be seen from Figure 8.
3. Passive Phased Arrays with Integrated Metallic and Dielectric Waveguide Phase Shifters
3.1. High-Performance Metallic Waveguide Phase Shifter
3.2. Electronic Steerable Horn Antenna Array
3.3. Fully Dielectric Beam-Steering Rod-Antenna Array
4. Flat-Panel Beam-Steering Antennas with Low-Profile Phase Shifters with Fast Response
4.1. Low-Profile Planar Inverted Microstrip Line and Grounded Coplanar Waveguide Phase Shifter
4.2. Fast Tuning Low-Profile Planar Delay Line Phase Shifter
4.3. Flat-Panel Beam-Steering Antenna Arrays
5. Conclusions
- Next-generation microwave LCs are aiming for higher low-temperature stability in the range of −30 °C, higher anisotropy in relative permittivity up to 1.2, and a larger ratio of rotational viscosity over the elastic constant for even faster switch-off response times of less than 25 ms for an LC layer height of 4 µm.
- Progress in the processing and manufacturing of the phase shifter stack (1) with a lower LC layer height hLC < 2.5 µm, which reduces the response time significantly, down to below 10 ms, without affecting the other performance parameters, (2) using thinner glass with low dielectric constant and low dielectric losses, and (3) with compacter loaded lines for 360° phase shift.
- Progress in the assembly technology of the whole electronically steerable antenna, including the electronics for the antenna control unit, the feeding network, and the radiator stack.
6. Patents
- Jakoby, R.; Karabey, O.H.; Goelden, F.; Manabe, A. Electronically steerable planar phased array antenna. US20190260139A1, 2011.
- Jakoby, R.; Karabey, O.H.; Hu, W. Phase shift device. US20190103644A1, 2013.
- Gölden, F.; Gäbler, A.; Karabey, O.H. Radio frequency phase shifting device. US20200044300A1, 2018.
- Gölden, F.; Gäbler, A.; Karabey, O.H. Funkfrequenz phasen ver schieb ungs vor richt ung. EP3609017A1, 2018.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- ▪
- Mobile Internet (MI) focused on people-oriented communications with use cases such as Ultra-High Density (UHD) and 3D video, augmented reality, virtual reality, online gaming, mobile cloud, remote computing, tactile internet, 3D connectivity to aircrafts and drones, collaborative robots, smart office and
- ▪
- Internet of Things (IoT), including Machine-to-Machine (M2M) and Device-to-Device (D2D) communications, which provides communications between things AND between things and people with use cases such as smart grid and critical infrastructure monitoring, mobile surveillance, environmental monitoring, industrial automation, eHealth services, smart wearables and smart body area networks, sensor networks, smart homes/buildings, smart cities, smart transportation, self-driving and connected cars (Internet of Vehicles).
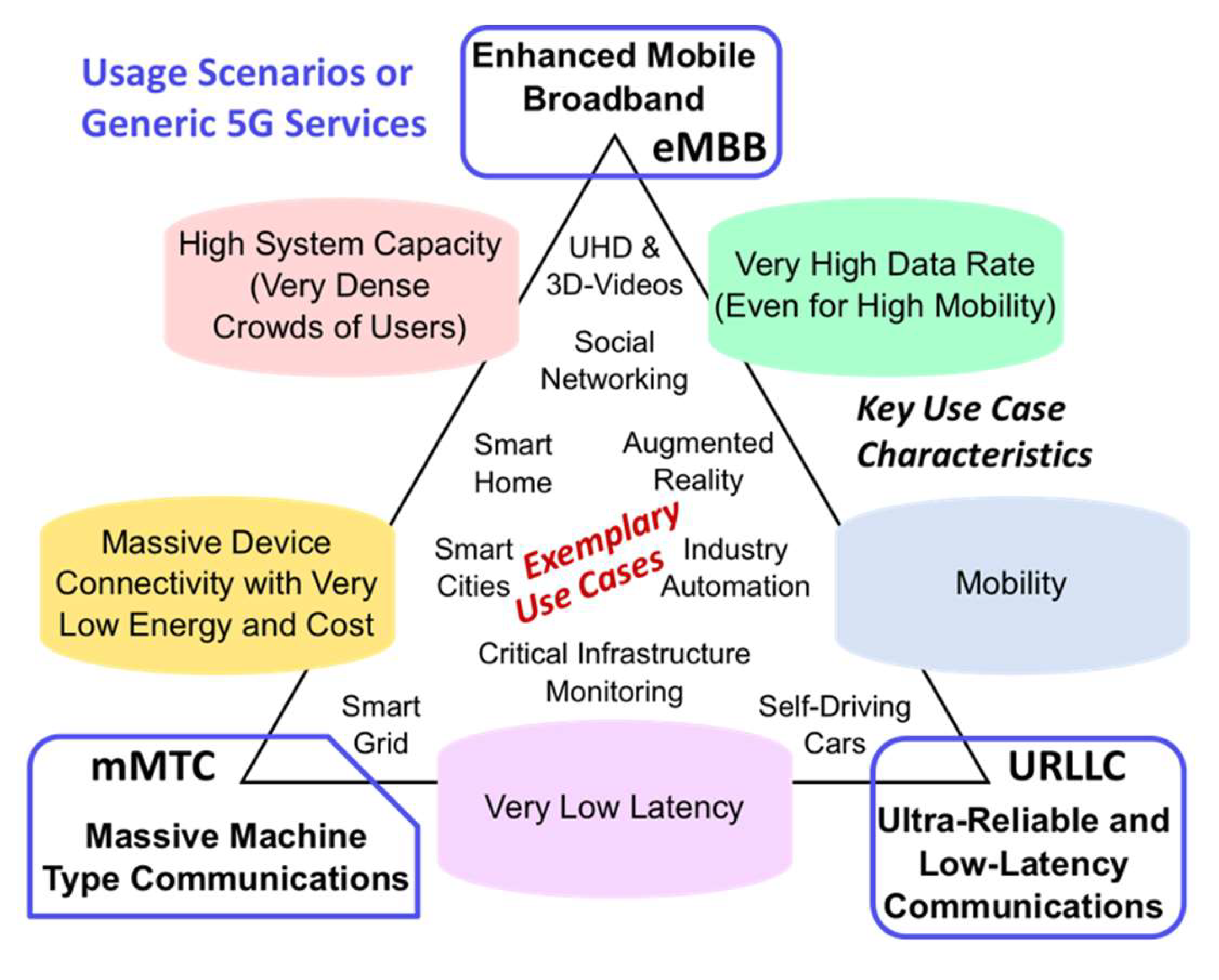
- ▪
- enhanced mobile broadband, in particular by video usage with 75% of all global mobile traffic,
- ▪
- application uptake, i.e., the rate at which applications are being adopted, e.g., annual global downloading of applications was about 270 billion apps in 2017 and
- ▪
- device proliferation, accompanied with an evolution toward ever smarter mobile devices in different form factors and with continuously enhanced capabilities and intelligence, which require increasing bit rates and bandwidth.
- ▪
- Wireless communication platforms and infrastructure such as 5G (IMT-2020) systems and beyond, High-Throughput Satellites (HTS) in geostationary (GEO) or Medium Earth Orbits (MEOs), Low Earth Orbit (LEO) satellite mega-constellations, High Altitude Platforms (HAPS) and future hybrid terrestrial–satellite networks will enable new forms of connectivity for the delivery of broadband services and the possibility of being always connected. Their evolution, key technology drivers, the markets, and perspectives are summarized in [2].
- ▪
- Spectrum resources: in order to cope with the higher traffic capacity and higher typical user data rate in 5G and in mobile satellite networks, considerably more spectrum is required than currently available. Spectrum has been in the past and will be also in the future one of the most valuable resources for mobile communications. Therefore, agencies and standardization organizations worldwide aim for international harmonized spectrum and full-spectrum access, especially above 6 GHz. Hence, beyond the sub-6 GHz bands for 5G in Europe 3.4–3.8 GHz, USA 3.1–3.55 GHz and 3.7–4.2 GHz, Japan 3.6–4.2 GHz and 4.4–4.9 GHz and China 3.3–3.6 GHz, 4.4–4.5 GHz and 4.8–4.99 GHz for 5G Phase I, frequency bands in the mm-wave range are already foreseen for 5G Phase II: in Europe 24.25–27.5 GHz and 31.8–33.4 GHz, USA 27.5–28.35 GHz and 37–40 GHz, Japan 27.5–29.5 GHz, 4.4–4.9 GHz, China 24.75–27.5 GHz, South Korea 26.5–29.5 GHz [275]. The technical feasibility of radio interface technology and systems operating in these frequency bands, taking into account propagation characteristics, antenna technology, active and passive components, physical layers, and medium access control design as well as deployment architectures, are carried out by simulations and performance tests and trials. Some are published in [271,276,277,278,279]. In Europe, the European Telecommunications Standards Institute (ETSI) is working to facilitate the use of the E-Band from 71–76 GHz and 81–86 GHz, and in the future, on the channelization of the W-band from 92 to 114.5 GHz and the D-band from 130 to 174.8 GHz for large-volume (high capacity) backhaul and front-haul systems as well as for innovative solutions for fixed broadband access [279]. Most of the HTS in GEO and MEO make efficient use of both, Ku-band and Ka-band (e.g., O3b downlink 17.7–20.2 GHz, uplink 27.5–30 GHz). Low Earth Orbit (LEO) high-throughput satellite constellations also aiming to operate in the Ku-band and Ka-band.
- ▪
- Network architectures: while previous generations of wireless networks are characterized by fixed radio parameters and spectrum blocks, software advances, and other complementary technologies will increase the flexibility, configurability, and efficiency of services such as cloud-radio access network (RAN), heterogeneous networks, network slicing, and network function virtualization (NFV) [270,271,280,281].
- ▪
- Integrated access node and backhaul design will enable the ultra-dense networking of radio nodes, where such nodes will need to access and self-organize available spectrum blocks for both access and backhauling. This capability will be a key for enabling high-frequency spectrum radio access. It will allow for the best delivery of services and to speed up the creation of massive-scale services and applications with flexibility, including ubiquitous ultra-broadband network infrastructure, mass-scale cloud architectures, ultra-dense radio networking with self-backhauling, M2M and D2D communications, and dynamic radio access infrastructure sharing [280].
- ▪
- Programmable/flexible air interfaces will be enabled by various advanced waveform technologies combined with advances in modulation and coding as well as advances in multiple access schemes such as filtered OFDM (Orthogonal Frequency Division Multiplexing), filter bank multi carrier, pattern division multiple access, sparse code multiple access, interleave division multiple access and beam division multiple access (BDMA) [270,271,274,282]. These schemes are essential to achieve continuing improvements in spectral efficiency, which correspondingly increases the capacity of the system. Moreover, flexible uplink/downlink resource allocation such as TDD–FDD joint operation and dynamic TDD (FDD/TDD = Frequency/Time Division Duplex) will address the growing traffic demand and allow more efficient and flexible use of radio resources. This could also be attained by advanced RF-domain processing, e.g., using single-frequency full-duplex radio technologies, where simultaneous transmission and reception on the same frequency with self-interference cancellation could increase spectrum efficiency significantly. Improvements in all these areas will drive overall network costs down while achieving improved energy efficiency [270,274,280,281]. Moreover, smart antenna and new reconfigurable hardware concepts, in particular at higher frequencies are required for programmable/flexible air interfaces.
References
- Maune, H.; Jost, M.; Wiens, A.; Weickhmann, C.; Reese, R.; Nikfalazar, M.; Schuster, C.; Franke, T.; Hu, W.; Nickel, M.; et al. Tunable Microwave Component Technologies for SatCom-Platforms. Frequenz 2017, 71, 129–142. [Google Scholar] [CrossRef]
- Jakoby, R.; Rehder, G.; Ferrari, P.; Karabey, O.H.; Maune, H. Reconfigurable Circuits and Technologies for Smart Millimeter-Wave Systems; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Osseiran, A.; Monserrat, J.F.; Marsch, P. 5G Mobile and Wireless Communications Technology; Cambridge University Press: Cambridge, UK, 2016; ISBN 978-1-107-13009-8. [Google Scholar]
- Xiang, W.; Zheng, K.; Shen, X. 5G Mobile Communications; Springer International Publisher: Cham, Switzerland, 2017; ISBN 9783319342061. [Google Scholar]
- Vorhaus, J.L.; Pucel, R.A.; Tajima, Y. Monolithic Dual-Gate GaAs FET Digital Phase Shifter. IEEE Trans. Microw. Theory Tech. 1982, 30, 982–992. [Google Scholar] [CrossRef]
- Shih, S.E.; Duan, D.; Fordham, O.; Törnquist, K.; Zeng, X.; Chang, P.C.; Tsai, R.S. A W-Band 4-Bit Phase Shifter in Multilayer Scalable Array Systems. In Proceedings of the 2007 IEEE Compound Semiconductor Integrated Circuits Symposium, Portland, OR, USA, 14–17 October 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Kang, D.-W.; Kim, J.-G.; Min, B.-W.; Rebeiz, G.M. Single and Four-Element Ka-Band Transmit/Receive Phased-Array Silicon RFICs With 5-bit Amplitude and Phase Control. IEEE Trans. Microw. Theory Tech. 2009, 57, 3534–3543. [Google Scholar] [CrossRef]
- Yang, J.G.; Yang, K. Ka-Band 5-Bit MMIC Phase Shifter Using InGaAs PIN Switching Diodes. IEEE Microw. Wirel. Compon. Lett. 2011, 21, 151–153. [Google Scholar] [CrossRef]
- Deng, X.; He, Z.; Yuan, S.; Shao, Z.; Liu, L. W-band high bit passive phase shifter for automotive radar applications in BiCMOS. In Proceedings of the International Conference on Computational Problem-Solving (ICCP), Chengdu, China, 21–23 October 2011; pp. 115–119. [Google Scholar] [CrossRef]
- Chen, N.; Zhen, J.; Pang, Q. A millimeter-wave GaAs 5-bit MMIC digital phase shifter. In Proceedings of the 2013 International Workshop on Microwave and Millimeter Wave Circuits and System Technology, Chengdu, China, 24–25 October 2013; pp. 444–447. [Google Scholar] [CrossRef]
- Barker, S.; Rebeiz, G.M. Distributed MEMS true-time delay phase shifters and wide-band switches. IEEE Trans. Microw. Theory Tech. 1998, 46, 1881–1890. [Google Scholar] [CrossRef]
- Barker, N.S.; Rebeiz, G.M. Optimization of distributed MEMS phase shifters. In Proceedings of the 1999 IEEE MTT-S International Microwave Symposium Digest (Cat. No.99CH36282), Anaheim, CA, USA, 13–19 June 1999; Volume 1, pp. 299–302. [Google Scholar] [CrossRef]
- Kim, H.-T.; Park, J.-H.; Lee, S.; Kim, S.; Kim, J.-M.; Kim, Y.-K.; Kwon, Y. V-band 2-b and 4-b low-loss and low-voltage distributed MEMS digital phase shifter using metal-air-metal capacitors. IEEE Trans. Microw. Theory Tech. 2002, 50, 2918–2923. [Google Scholar] [CrossRef]
- Scardelletti, M.C.; Ponchak, G.E.; Varaljay, N.C. MEMS, Ka-band single-pole double-throw (SPDT) switch for switched line phase shifters. In Proceedings of the IEEE Antennas and Propagation Society International Symposium (IEEE Cat. No.02CH37313), San Antonio, TX, USA, 16–21 June 2002; Volume 2, pp. 2–5. [Google Scholar] [CrossRef][Green Version]
- Stehle, A.; Georgiev, G.; Ziegler, V.; Schoenlinner, B.; Prechtel, U.; Seidel, H.; Schmid, U. RF-MEMS Switch and Phase Shifter Optimized for W-Band. In Proceedings of the European Microwave Conference, Amsterdam, The Netherlands, 27–31 October 2008; pp. 104–107. [CrossRef]
- Pillans, B.; Coryell, L.; Malczewski, A.; Moody, C.; Morris, F.; Brown, A. Advances in RF MEMS phase shifters from 15 GHz to 35 GHz. In Proceedings of the IEEE MTT-S International Microwave Symposium, Montreal, QC, Canada, 17–22 June 2012; pp. 1–3. [Google Scholar] [CrossRef]
- Reyaz, S.; Samuelsson, C.; Malmqvist, R.; Kaynak, M.; Rydberg, A. Millimeter-wave RF-MEMS SPDT switch networks in a SiGe BiCMOS process technology. In Proceedings of the 2012 7th European Microwave Integrated Circuit Conference, Amsterdam, The Netherlands, 29–30 October 2012; pp. 691–694. [Google Scholar]
- Somjit, N.; Stemme, G.; Oberhammer, J. Performance optimization of multi-stage MEMS W-band dielectric-block phase-shifters. In Proceedings of the 2012 7th European Microwave Integrated Circuit Conference, Amsterdam, The Netherlands, 29–30 October 2012; pp. 433–436. [Google Scholar]
- Chang, C.; Chen, Y.; Hsieh, S. A V-Band Three-State Phase Shifter in CMOS-MEMS Technology. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 264–266. [Google Scholar] [CrossRef]
- Psychogiou, D.; Peroulis, D.; Li, Y.; Hafner, C. V-band bandpass filter with continuously variable centre frequency. IET Microw. Antennas Propag. 2013, 7, 701–707. [Google Scholar] [CrossRef]
- Ozturk, E.; Nemati, M.H.; Kaynak, M.; Tillack, B.; Tekin, I. SiGe process integrated full-360° microelectromechanical systems-based active phase shifter for W-band automotive radar. IET Microw. Antennas Propag. 2014, 8, 835–841. [Google Scholar] [CrossRef]
- Zahr, A.H.; Blondy, P.; Zhang, L.; Dorion, C.; Stefanini, R.; Courtade, F.; Pressecq, F. A DC-30 GHz high performance packaged RF MEMS SPDT switch. In Proceedings of the 2015 European Microwave Conference (EuMC), Paris, France, 7–10 September 2015; pp. 1015–1017. [Google Scholar] [CrossRef]
- Shah, U.; Decrossas, E.; Jung-Kubiak, C.; Reck, T.; Chattopadhyay, G.; Mehdi, I.; Oberhammer, J. Submillimeter-Wave 3.3-bit RF MEMS Phase Shifter Integrated in Micromachined Waveguide. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 706–715. [Google Scholar] [CrossRef]
- Chakraborty, A.; Gupta, B. Paradigm Phase Shift: RF MEMS Phase Shifters: An Overview. IEEE Microw. Mag. 2017, 18, 22–41. [Google Scholar] [CrossRef]
- Koul, S.K.; Bhat, B. Microwave and Millimeter Wave Phase Shifters; Artech House: Norwood, MA, USA, 1991. [Google Scholar]
- Patton, C.E. Hexagonal ferrite materials for phase shifter applications at millimeter wave frequencies. IEEE Trans. Magn. 1988, 24, 2024–2028. [Google Scholar] [CrossRef]
- Nafe, A.; Shamim, A. An Integrable SIW Phase Shifter in a Partially Magnetized Ferrite LTCC Package. IEEE Trans. Microw. Theory Tech. 2015, 63, 2264–2274. [Google Scholar] [CrossRef]
- Wang, Z.; Song, Y.-Y.; Sun, Y.; Bevivino, J.; Wu, M.; Veerakumar, V.; Fal, T.J.; Camley, R.E. Millimeter wave phase shifter based on ferromagnetic resonance in a hexagonal barium ferrite thin film. Appl. Phys. Lett. 2010, 97, 072509. [Google Scholar] [CrossRef]
- Kozyrev, A.B.; Ivanov, A.V.; Soldatenkov, O.I.; Tumarkin, A.V.; Razumov, S.V.; Aigunova, S.Y. Ferroelectric (Ba,Sr)TiO3 thin-film 60-GHz phase shifter. Tech. Phys. Lett. 2001, 27, 1032–1034. [Google Scholar] [CrossRef]
- Shi, S.; Purden, J.; Lin, J.; York, R.A. A 24 GHz wafer scale electronically scanned antenna using BST phase shifters for collision avoidance systems. In Proceedings of the 2005 IEEE Antennas and Propagation Society International Symposium, Washington, DC, USA, 3–8 July 2005; Volume 1B, pp. 84–87. [Google Scholar] [CrossRef]
- Velu, G.; Blary, K.; Burgnies, L.; Marteau, A.; Houzet, G.; Lippens, D.; Carru, J.-C. A 360° BST Phase Shifter with Moderate Bias Voltage at 30 GHz. IEEE Trans. Microw. Theory Tech. 2007, 55, 438–444. [Google Scholar] [CrossRef]
- Sigman, J.; Nordquist, C.D.; Clem, P.G.; Kraus, G.M.; Finnegan, P.S. Voltage-Controlled Ku-Band and X-Band Tunable Combline Filters Using Barium-Strontium-Titanate. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 593–595. [Google Scholar] [CrossRef]
- Gevorgian, S. Ferroelectrics in Microwave Devices, Circuits and Systems: Physics, Modeling, Fabrication and Measurements; Springer Science & Business Media: London, UK, 2009. [Google Scholar]
- Choi, K.; Courreges, S.; Zhao, Z.; Papapolymerou, J.; Hunt, A. X-band and Ka-band tunable devices using low-loss BST ferroelectric capacitors. In Proceedings of the 18th IEEE International Symposium on the Applications of Ferroelectrics, Xi’an, China, 23–27 August 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Courreges, S.; Li, Y.; Zhao, Z.; Choi, K.; Hunt, A.; Horst, S.; Cressler, J.; Papapolymerou, J. A Ka-Band Electronically Tunable Ferroelectric Filter. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 356–358. [Google Scholar] [CrossRef]
- Jiang, H.; Lacroix, B.; Choi, K.; Wang, Y.; Hunt, A.T.; Papapolymerou, J. Ka- and Ku-Band Tunable Bandpass Filters Using Ferroelectric Capacitors. IEEE Trans. Microw. Theory Tech. 2011, 59, 3068–3075. [Google Scholar] [CrossRef]
- Sazegar, M.; Zheng, Y.; Maune, H.; Damm, C.; Zhou, X.; Jakoby, R. Compact Tunable Phase Shifters on Screen-Printed BST for Balanced Phased Arrays. IEEE Trans. Microw. Theory Tech. 2011, 59, 3331–3337. [Google Scholar] [CrossRef]
- Sazegar, M.; Zheng, Y.; Maune, H.; Damm, C.; Zhou, X.; Binder, J.; Jakoby, R. Low-Cost Phased-Array Antenna Using Compact Tunable Phase Shifters Based on Ferroelectric Ceramics. IEEE Trans. Microw. Theory Tech. 2011, 59, 1265–1273. [Google Scholar] [CrossRef]
- Nikfalazar, M.; Kohler, C.; Friederich, A.; Sazegar, M.; Zheng, Y.; Wiens, A.; Binder, J.R.; Jakoby, R. Fully printed tunable phase shifter for L/S-band phased array application. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Paolis, R.D.; Coccetti, F.; Payan, S.; Maglione, M.; Guegan, G. Characterization of ferroelectric BST MIM capacitors up to 65 GHz for a compact phase shifter at 60 GHz. In Proceedings of the 2014 44th European Microwave Conference, Rome, Italy, 6–9 October 2014; pp. 492–495. [Google Scholar] [CrossRef]
- Paolis, R.D.; Payan, S.; Maglione, M.; Guegan, G.; Coccetti, F. High-Tunability and High-$Q$-Factor Integrated Ferroelectric Circuits up to Millimeter Waves. IEEE Trans. Microw. Theory Tech. 2015, 63, 2570–2578. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, M.; Ling, S.; Chen, P.; Zhu, X.; Yu, X. K-band tunable phase shifter with microstrip line structure using BST technology. In Proceedings of the Asia-Pacific Microwave Conference (APMC), Nanjing, China, 6–9 December 2015; Volume 2, pp. 1–3. [Google Scholar] [CrossRef]
- Walk, D.; Kienemund, D.; Zeinar, L.; Salg, P.; Radetinac, A.; Komissinskiy, P.; Alff, L.; Jakoby, R.; Maune, H. Characterization and Deembedding of Negative Series Inductance in On-Wafer Measurements of Thin-Film All-Oxide Varactors. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 213–215. [Google Scholar] [CrossRef]
- Salg, P.; Zeinar, L.; Radetinac, A.; Walk, D.; Maune, H.; Jakoby, R.; Alff, L.; Komissinskiy, P. Oxygen diffusion barriers for epitaxial thin-film heterostructures with highly conducting SrMoO3 electrode. J. Appl. Phys. 2020, 127, 065302. [Google Scholar] [CrossRef]
- Weil, C.; Luessem, G.; Jakoby, R. Tunable inverted-microstrip phase shifter device using nematic liquid crystals. In Proceedings of the IEEE MTT-S International Microwave Symposium, Seattle, WA, USA, 2–7 June 2002; Volume 1, pp. 367–371. [Google Scholar] [CrossRef]
- Weil, C.; Muller, S.; Scheele, P.; Best, P.; Lussem, G.; Jakoby, R. Highly-anisotropic liquid-crystal mixtures for tunable microwave devices. Electron. Lett. 2003, 39, 1732–1734. [Google Scholar] [CrossRef]
- Mueller, S.; Scheele, P.; Weil, C.; Wittek, M.; Hock, C.; Jakoby, R. Tunable passive phase shifter for microwave applications using highly anisotropic liquid crystals. In Proceedings of the IEEE MTT-S International Microwave Symposium, Fort Worth, TX, USA, 6–11 June 2004; Volume 2, pp. 1153–1156. [Google Scholar]
- Czub, J.; Urban, S.; Dąbrowski, R.; Gestblom, B. Dielectric Properties of Liquid Crystalline Isothiocyanato-tolane Derivatives with Fluorine Atom at Various Lateral Positions. Acta Phys. Pol. A 2005, 107, 947–958. [Google Scholar] [CrossRef]
- Dubois, F.; Krasinski, F.; Splingart, B.; Tentillier, N.; Legrand, C.; Spadlo, A.; Dabrowski, R. Large Microwave Birefringence Liquid-Crystal Characterization for Phase-Shifter Applications. Jpn. J. Appl. Phys. 2008, 47, 3564–3567. [Google Scholar] [CrossRef]
- Goelden, F.; Lapanik, A.; Gaebler, A.; Mueller, S.; Lapanik, V.; Bezborodov, V.; Haase, W.; Jakoby, R. Tunable Microwave Phase Shifter using thin Layer Ferroelectric Liquid Crystals. In Proceedings of the 11th International Conference on Ferroelectric Liquid Crystals, Hokkaido University, Sapporo, Japan, 3–8 September 2007; Available online: http://tubiblio.ulb.tu-darmstadt.de/29060/ (accessed on 5 June 2020).
- Lapanik, A. Liquid Crystal Systems for Microwave Applications: Single Compounds and Mixtures for Microwave Applications; Dielectric, Microwave Studies on Selected Systems. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2009. Available online: https://tuprints.ulb.tu-darmstadt.de/id/eprint/1922 (accessed on 5 June 2020).
- James, R.; Fernández, F.A.; Day, S.E.; Bulja, S.; Mirshekar-Syahkal, D. Characterisation and Applications of Nematic Liquid Crystals in Microwave Devices. Mol. Cryst. Liquid Cryst. 2011, 542, 196–718. [Google Scholar] [CrossRef]
- Lapanik, A.; Goelden, F.; Lapanik, V.; Mueller, S.; Penirschke, A.; Jakoby, R.; Haase, W. Nematic LCs mixtures with high birefringence in the microwave region. Frequenz 2011, 65, 15–19. [Google Scholar] [CrossRef]
- Lapanik, A.; Haase, W.; Golden, F.; Muller, S.; Jakoby, R. Highly birefringent nematic mixtures at room temperature for microwave applications. Opt. Eng. 2011, 50, 081208. [Google Scholar]
- Dąbrowski, R.; Kula, P.; Herman, J. High Birefringence Liquid Crystals. Crystals 2013, 3, 443–482. [Google Scholar] [CrossRef]
- Manabe, A. Liquid crystals for microwave applications. In Proceedings of the SPIE—The International Society for Optical Engineering, San Francisco, CA, USA, 19 March 2013. [Google Scholar] [CrossRef]
- Jost, M.; Gaebler, A.; Weickhmann, C.; Strunck, S.; Hu, W.; Karabey, O.H.; Jakoby, R. Evolution of Microwave Nematic Liquid Crystal Mixtures and Development of Continuously Tuneable Micro- and Millimetre Wave Components. Mol. Cryst. Liq. Cryst. 2015, 610, 173–186. [Google Scholar] [CrossRef]
- Fritzsch, C.; Wittek, M. Recent developments in liquid crystals for microwave applications. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 1431–1432. [Google Scholar]
- Fritzsch, C.; Snow, B.; Sargent, J.; Klass, D.; Kaur, S.; Parri, O. Liquid Crystals beyond Displays: Smart Antennas and Digital Optics. Sid Symp. Dig. Tech. Pap. 2019. [Google Scholar] [CrossRef]
- Lapanik, V.; Sasnouski, G.; Timofeev, S.; Shepeleva, E.; Evtyushkin, G.; Haase, W. New highly anisotropic liquid crystal materials for high-frequency applications. Liq. Cryst. 2018, 45, 1242–1249. [Google Scholar] [CrossRef]
- Mueller, S.; Felber, C.; Scheele, P.; Wittek, M.; Hock, C.; Jakoby, R. Passive tunable liquid crystal finline phase shifter for millimeter waves. In Proceedings of the 2005 European Microwave Conference, Paris, France, 4–6 October 2005; Volume 1, p. 4. [Google Scholar]
- Mueller, S.; Goelden, F.; Scheele, P.; Wittek, M.; Hock, C.; Jakoby, R. Passive Phase Shifter for W-Band Applications using Liquid Crystals. In Proceedings of the 2006 European Microwave Conference, Manchester, UK, 10–15 September 2006; pp. 306–309. [Google Scholar]
- Utsumi, Y.; Bach, N.T.; Kamei, T.; Ozaki, R.; Moritake, H. Measurements and Theoretical Calculations of Dielectric Birefringence for a Liquid Crystal Loaded CPW-FE Phase Shifter. Mol. Cryst. Liq. Cryst. 2009, 510, 197–1331. [Google Scholar] [CrossRef]
- Gaebler, A.; Goelden, F.; Manabe, A.; Goebel, M.; Mueller, S.; Jakoby, R. Investigation of high performance transmission line phase shifters based on liquid crystal. In Proceedings of the European Microwave Conference (EuMC), Rome, Italy, 29 September–1 October 2009; pp. 594–597. [Google Scholar]
- Bulja, S.; Mirshekar-Syahkal, D. Meander line millimetre-wave liquid crystal based phase shifter. Electron. Lett. 2010, 46, 769–771. [Google Scholar] [CrossRef]
- Garbovskiy, Y.; Agorodnii, V.; Krivosik, P.; Lovejoy, J.; Camley, R.E.; Celinski, Z.; Glushchenko, A.; Dziaduszek, J.; Dąbrowski, R. Liquid crystal phase shifters at millimeter wave frequencies. J. Appl. Phys. 2012, 111, 054504. [Google Scholar] [CrossRef]
- Jost, M.; Fritzsch, C.; Karabey, O.; Weickhmann, C.; Jakoby, R.; Gäbler, A.; Strunck, S. Liquid crystal based low-loss phase shifter for W-band frequencies. Electron. Lett. 2013, 49, 1460–1462. [Google Scholar] [CrossRef]
- Weickhmann, C.; Nathrath, N.; Gehring, R.; Gaebler, A.; Jost, M.; Jakoby, R. A light-weight tunable liquid crystal phase shifter for an efficient phased array antenna. In Proceedings of the European Microwave Conference (EuMC), Nuremberg, Germany, 6–10 October 2013; pp. 428–431. [Google Scholar]
- Weickhmann, C.; Nathrath, N.; Genning, R.; Gaebler, A.; Jost, M.; Jakoby, R. Recent measurements of compact electronically tunable liquid crystal phase shifter in rectangular waveguide topology. Electron. Lett. 2013, 49, 1345–1347. [Google Scholar] [CrossRef]
- Strunck, S.; Karabey, O.H.; Weickhmann, C.; Gaebler, A.; Jakoby, R. Continuously tunable phase shifters for phased arrays based on liquid crystal technology. In Proceedings of the 2013 IEEE International Symposium on Phased Array Systems and Technology, Waltham, MA, USA, 15–18 October 2013; pp. 82–88. [Google Scholar] [CrossRef]
- Franc, A.; Karabey, O.H.; Rehder, G.; Pistono, E.; Jakoby, R.; Ferrari, P. Compact and Broadband Millimeter-Wave Electrically Tunable Phase Shifter Combining Slow-Wave Effect with Liquid Crystal Technology. IEEE Trans. Microw. Theory Tech. 2013, 61, 3905–3915. [Google Scholar] [CrossRef]
- Nguyen, T.; Umeno, S.; Higuchi, H.; Kikuchi, H.; Moritake, H. Improvement of decay time in nematic-liquid-crystal-loaded coplanar-waveguide-type microwave phase shifter by polymer stabilizing method. Jpn. J. Appl. Phys. 2013, 53, 01AE08. [Google Scholar] [CrossRef]
- Jost, M.; Strunck, S.; Heunisch, A.; Wiens, A.; Prasetiadi, A.E.; Weickhmann, C.; Schulz, B.; Quibeldey, M.; Karabey, O.H.; Rabe, T.; et al. Continuously tunable liquid crystal based stripline phase shifter realized in LTCC technology. In Proceedings of the IEEE European Microwave Conference (EuMC), Lisabon, Portugual, 7–10 September 2015; pp. 264–267. [Google Scholar] [CrossRef]
- Gaebler, A. Synthese steuerbarer Hochfrequenzschaltungen und Analyse Flüssigkristall-basierter Leitungsphasenschieber in Gruppenantennen für Satellitenanwendungen im Ka-Band. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2015. Available online: http://tuprints.ulb.tu-darmstadt.de/4691/ (accessed on 5 June 2020).
- Weickhmann, C. Liquid Crystals towards Terahertz: Characterisation and Tunable Waveguide Phase Shifters for Millimetre-Wave and Terahertz Beamsteering Antennas. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2017. Available online: https://tuprints.ulb.tu-darmstadt.de/id/eprint/6216 (accessed on 5 June 2020).
- Tebbe, M.; Hoehn, A.; Nathrath, N.; Weickhmann, C. Manufacturing and testing of liquid crystal phase shifters for an electronically steerable array. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–12. [Google Scholar]
- Cai, L.; Xu, H.; Li, J.; Chu, D. High figure-of-merit compact phase shifters based on liquid crystal material for 1–10 GHz applications. Jpn. J. Appl. Phys. 2017, 56, 011701. [Google Scholar] [CrossRef]
- Reese, R.; Jost, M.; Maune, H.; Jakoby, R. Design of a continuously tunable W-band phase shifter in dielectric waveguide topology. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017; pp. 180–183. [Google Scholar] [CrossRef]
- Reese, R.; Polat, E.; Jost, M.; Nickel, M.; Jakoby, R.; Maune, H. Liquid crystal based phase shifter in a parallel-plate dielectric waveguide topology at V-band. In Proceedings of the European Microwave Integrated Circuit Conference (EuMIC), Nuremburg, Germany, 8–10 October 2017; pp. 353–356. [Google Scholar]
- Jost, M.; Reese, R.; Nickel, M.; Maune, H.; Jakoby, R. Fully dielectric interference-based SPDT with liquid crystal phase shifters. IET Microw. Antennas Propag. 2018, 12, 850–857. [Google Scholar] [CrossRef]
- Jost, M.; Gautam, J.S.K.; Gomes, L.G.; Reese, R.; Polat, E.; Nickel, M.; Pinheiro, J.M.; Serrano, A.L.C.; Maune, H.; Rehder, G.P.; et al. Miniaturized Liquid Crystal Slow Wave Phase Shifter Based on Nanowire Filled Membranes. IEEE Microw. Wirel. Comp. Lett. 2018, 28, 681–683. [Google Scholar] [CrossRef]
- Bui, V.B.; Inoue, Y.; Moritake, H. NRD waveguide-type terahertz phase shifter using nematic liquid crystal. Jpn. J. Appl. Phys. 2019, 58, 022001. [Google Scholar] [CrossRef]
- Reese, R.; Polat, E.; Tesmer, H.; Strobl, J.; Schuster, C.; Nickel, M.; Granja, A.B.; Jakoby, R.; Maune, H. Liquid crystal based dielectric waveguide phase shifters for phased arrays at W-band. IEEE Access 2019, 7, 127032–127041. [Google Scholar] [CrossRef]
- Wang, D.; Nickel, M.; Tesmer, H.; Polat, E.; Schumacher, P. Performance Analysis of Highly Miniaturized Continuously Tunable Phase Shifters based on Liquid Crystal and Metallic Nanowire-Filled Membrane Technologies. IEEE Trans. Microw. Theory Tech. 2020, submitted. [Google Scholar]
- Gobel, T.; Meissner, P.; Gaebler, A.; Koeberle, M.; Mueller, S.; Jakoby, R. Dual-frequency switching Liquid Crystal based tunable THz Filter. In Proceedings of the Conference on Lasers and Electro-Optics and 2009 Conference on Quantum electronics and Laser Science Conference, Baltimore, ML, USA, 2–4 June 2009; pp. 1–2. [Google Scholar] [CrossRef]
- Goelden, F.; Gaebler, A.; Karabey, O.; Goebel, M.; Manabe, A.; Jakoby, R. Tunable band-pass filter based on Liquid Crystal. In Proceedings of the German Microwave Conference Digest of Papers, Berlin, Germany, 15–17 March 2010; pp. 98–101. [Google Scholar]
- Yazdanpanahi, M.; Mirshekar-Syahkal, D. Millimeter-wave liquid-crystal-based tunable bandpass filter. In Proceedings of the 2012 IEEE Radio and Wireless Symposium, Santa Clara, CA, USA, 15–18 January 2012. [Google Scholar]
- Yaghmaee, P.; Fumeaux, C.; Bates, B.; Manabe, A.; Karabey, O.H.; Jakoby, R. Frequency tunable S-band resonator using nematic liquid crystal. Electron. Lett. 2012, 48, 798–800. [Google Scholar] [CrossRef]
- Yaghmaee, P.; Withayachumnankul, W.; Horestani, A.K.; Ebrahimi, A.; Bates, B.; Fumeaux, C. Tunable electric-LC resonators using liquid crystal. In Proceedings of the IEEE Antennas and Propagation Society International Symposium (APSURSI), Orlando, FL, USA, 7–13 July 2013; pp. 382–383. [Google Scholar]
- Torrecilla, J.; Marcos, C.; Urruchi, V.; Sánchez-Pena, J.M. Tunable dual-mode bandpass filter based on liquid crystal technology. In Proceedings of the European Microwave Conference (EuMC), Nuremberg, Germany, 6–10 October 2013; pp. 806–809. [Google Scholar]
- Urruchi, V.; Marcos, C.; Torrecilla, J.; Sánchez-Pena, J.M.; Garbat, K. Note: Tunable notch filter based on liquid crystal technology for microwave applications. Rev. Sci. Instrum. 2013, 84, 026102. [Google Scholar] [CrossRef]
- Follmann, R.; Kother, D.; Campo, M.A.; Franke, T.; Gabler, A.; Jakoby, R.; Manabe, A.; Rabe, T.; Heunisch, A.; Rauch, A.; et al. Liquida-Sky—A tunable liquid crystal filter for space applications. In Proceedings of the 2013 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), Torino, Italy, 9–13 September 2013. [Google Scholar] [CrossRef]
- Franke, T.; Gaebler, A.; Prasetiadi, A.E.; Jakoby, R. Tunable Ka-band waveguide resonators and a small band band-pass filter based on liquid crystals. In Proceedings of the 2014 44th European Microwave Conference (EuMC), Rome, Italy, 6–9 October 2014; pp. 339–342. [Google Scholar]
- Prasetiadi, A.E.; Franke, T.; Jakoby, R.; Nickel, M.; Karabey, O.; Hu, W.; Weickhmann, C.; Jost, M. Continuously tunable substrate integrated waveguide bandpass filter in liquid crystal technology with magnetic biasing. Electron. Lett. 2015, 51, 1584–1585. [Google Scholar] [CrossRef]
- Novin, S.N.; Jarchi, S.; Yaghmaee, P. Tunable frequency selective surface based on IDC-loaded electric-LC resonator incorporated with liquid crystal. In Proceedings of the 2017 Conference on Microwave Techniques (COMITE), Brno, Czech Republic, 20–21 April 2017; pp. 1–4. [Google Scholar]
- Economou, E.E.; Lovejoy, J.; Harward, I.; Nobles, J.; Kula, P.; Herman, J.; Glushchenko, A.; Celinski, Z. Electrically Tunable Open-Stub Bandpass Filters Based on Nematic Liquid Crystals. Phys. Rev. Appl. 2017, 8. [Google Scholar] [CrossRef]
- Prasetiadi, A.E. Tunable Substrate Integrated Waveguide Bandpass Filter and Amplitude Tuner Based on Microwave Liquid Crystal Technology. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2017. [Google Scholar]
- Polat, E.; Reese, R.; Jost, M.; Schuster, C.; Nickel, M.; Jakoby, R.; Maune, H. Tunable Liquid Crystal Filter in Nonradiative Dielectric Waveguide Technology at 60 GHz. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 44–46. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Jiang, D.; Cao, W.; Chen, H.; Xia, L.; Xu, R. Tunable microwave bandpass filter integrated power divider based on the high anisotropy electro-optic nematic liquid crystal. Rev. Sci. Instrum. 2016, 87, 074709. [Google Scholar] [CrossRef] [PubMed]
- Jost, M.; Reese, R.; Weickhmann, C.; Schuster, C.; Karabey, O.H.; Maune, H.; Jakoby, R. Tunable dielectric delay line phase shifter based on liquid crystal technology for a SPDT in a radiometer calibration scheme at 100 GHz. In Proceedings of the IEEE MTT-S International Microwave Symposium, San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Reese, R.; Tesmer, H.; Jost, M.; Polat, E.; Nickel, M.; Jakoby, R.; Maune, H. A Compact Two-dimensional Power Divider for a Dielectric Rod Antenna Array Based on Multimode Interference. J. Infrared Millim. Terahertz Waves 2018, 39, 1185–1202. [Google Scholar] [CrossRef]
- Jost, M.; Reese, R.; Nickel, M.; Schmidt, S.; Maune, H.; Jakoby, R. Interference based W-band single-pole double-throw with tunable liquid crystal based waveguide phase shifters. In Proceedings of the IEEE MTT-S International Microwave Symposium, Honolulu, HI, USA, 4–9 June 2017. [Google Scholar]
- Jost, M.; Heunisch, A.; Prasetiadi, A.E.; Schulz, B.; Reese, R.; Nickel, M.; Polat, E.; Quibeldey, M.; Maune, H.; Rabe, T.; et al. Liquid Crystal Based SPDT with Adjustable Power Splitting Ratio in LTCC Technology. In Proceedings of the IEEE European Microwave Conference (EuMC), Madrid, Spain, 23–27 September 2017. [Google Scholar] [CrossRef]
- Nickel, M.; Müh, M.; Reese, R.; Polat, E.; Jost, M.; Damm, C.; Jakoby, R.; Maune, H. Liquid Crystal Based Tunable Reflection-Type Power Divider. In Proceedings of the European Microwave Conference (EuMC), Madrid, Spain, 23–28 September 2018; pp. 45–48. [Google Scholar] [CrossRef]
- Khoo, I.C.; Werner, D.H.; Liang, X.; Diaz, A.; Weiner, B. Nanosphere dispersed liquid crystals for tunable negative-zero-positive index of refraction in the optical and terahertz regimes. Opt. Lett. 2006, 31, 2592. [Google Scholar] [CrossRef] [PubMed]
- Werner, D.H.; Kwon, D.-H.; Khoo, I.-C.; Kildishev, A.V.; Shalaev, V.M. Liquid crystal clad near-infrared metamaterials with tunable negative-zero-positive refractive indices. Opt. Express 2007, 15, 3342–3347. [Google Scholar] [CrossRef]
- Kwon, D.-H.; Werner, D.H.; Khoo, I.-C.; Kildishev, A.V.; Shalaev, V.M. Liquid crystal clad metamaterial with a tunable negative-zero-positive index of refraction. In Proceedings of the 2007 IEEE Antennas and Propagation Society International Symposium, Piscataway, NJ, USA, 9–15 June 2007; pp. 2881–2884. [Google Scholar]
- Hu, W.; Dickie, R.; Cahill, R.; Gamble, H.; Ismail, Y.; Fusco, V.; Linton, D.; Grant, N.; Rea, S. Liquid Crystal Tunable mm Wave Frequency Selective Surface. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 667–669. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, Q.; Kang, L.; Gaillot, D.P.; Zhao, X.; Zhou, J.; Lippens, D. Magnetic Control of Negative Permeability Metamaterials based on Liquid Crystals. In Proceedings of the European Microwave Conference (EuMC), Amsterdam, The Netherlands, 28–30 October 2008; pp. 801–804. [Google Scholar] [CrossRef]
- Xiande, W.; Do-Hoon, K.; Werner, D.H.; Iam-Choon, K. Anisotropic liquid crystals for tunable optical negative-index metamaterials. In Proceedings of the 2008 IEEE Antennas and Propagation Society International Symposium, San Diego, CA, USA, 5–11 July 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Bossard, J.A.; Liang, X.; Li, L.; Yun, S.; Werner, D.H.; Weiner, B.; Mayer, T.S.; Cristman, P.F.; Diaz, A.; Khoo, I.C. Tunable Frequency Selective Surfaces and Negative-Zero-Positive Index Metamaterials Based on Liquid Crystals. IEEE Trans. Antennas Propag. 2008, 56, 1308–1320. [Google Scholar] [CrossRef]
- Fusco, V.F.; Cahill, R.; Hu, W.; Simms, S. Ultra-thin tunable microwave absorber using liquid crystals. Electron. Lett. 2008, 44, 37. [Google Scholar] [CrossRef]
- Seman, F.C.; Cahill, R.; Fusco, V.F. Electronically tunable liquid crystal based Salisbury screen microwave absorber. In Proceedings of the 2009 Loughborough Antennas & Propagation Conference, Loughborough, UK, 16–17 November 2009; pp. 93–96. [Google Scholar]
- Minovich, A.; Farnell, J.; Neshev, D.N.; McKerracher, I.; Karouta, F.; Tian, J.; Powell, D.A.; Shadrivov, I.V.; Tan, H.H.; Jagadish, C.; et al. Liquid crystal based nonlinear fishnet metamaterials. Appl. Phys. Lett. 2012, 100, 121113. [Google Scholar] [CrossRef]
- Maasch, M.; Groudas, A.; Karabey, O.; Damm, C.; Jakoby, R. Electrically Tunable Open Split-Ring Resonators based on Liquid Crystal Material. In Proceedings of the Metamaterials 2012: The Sixth International Congress on Advanced Electromagnetic Materials in Microwaves and Optics, St. Petersburg, Russia, 17–22 September 2012; ISBN 978-952-67611-2-1. [Google Scholar]
- Chang, C.-L.; Wang, W.-C.; Lin, H.-R.; Hsieh, F.J.; Pun, Y.-B.; Chan, C.-H. Tunable terahertz fishnet metamaterial. Appl. Phys. Lett. 2013, 102. [Google Scholar] [CrossRef]
- Maasch, M.; Roig, M.; Damm, C.; Jakoby, R. Voltage-Tunable Artificial Gradient-Index Lens Based on a Liquid Crystal Loaded Fishnet Metamaterial. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1581–1584. [Google Scholar] [CrossRef]
- Maasch, M.; Roig, M.; Damm, C.; Jakoby, R. Realization of a voltage tunable gradient-index fishnet loaded with liquid crystal. In Proceedings of the 8th International Congress Advanced Electromagnetic Materials in Microwaves and Optics, Copenhagen, Denmark, 25–28 August 2014; pp. 196–198. [Google Scholar]
- Zografopoulos, D.C.; Beccherelli, R. Tunable terahertz fishnet metamaterials based on thin nematic liquid crystal layers for fast switching. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Maasch, M. Tunable Microwave Metamaterial Structures; Springer International Publishing: Cham, Switzerland, 2016; ISBN 2190-5053. [Google Scholar]
- Mohamad, S.; Cahill, R. Spiral antenna with reconfigurable HIS using liquid crystals for monopulse radar application. In Proceedings of the IEEE Conference Antenna Measurements Applications (CAMA), Tsukuba, Japan, 4–6 December 2017; pp. 55–58. [Google Scholar]
- Martin, N.; Laurent, P.; Person, C.; Gelin, P.; Huret, F. Patch Antenna Adjustable in Frequency Using Liquid Crystal. In Proceedings of the European Microwave Conference (EuMC), Munich, Germany, 7 October 2003; pp. 699–702. [Google Scholar]
- Martin, N.; Laurent, P.; Person, C.; Gelin, P.; Huret, F. Size reduction of a liquid crystal-based, frequency-adjustable patch antenna. In Proceedings of the European Microwave Conference (EuMC), Amsterdam, The Netherlands, 12–14 October 2004; Volume 2, pp. 825–828. [Google Scholar]
- Liu, L.; Langley, R.J. Liquid crystal tunable microstrip patch antenna. Electron. Lett. 2008, 44, 1179–1180. [Google Scholar] [CrossRef]
- Fritzsch, C.; Bildik, S.; Jakoby, R. Ka-band frequency tunable patch antenna. In Proceedings of the 2012 IEEE International Symposium on Antennas and Propagation, Prague, Czech Republic, 26–30 July 2012. [Google Scholar]
- Christou, M.A.; Papanicolaou, N.C.; Polycarpou, A.C. A nematic liquid crystal tunable patch antenna. In Proceedings of the IEEE European Conference on Antennas and Propagation (EUCAP), The Hague, The Netherlands, 6–11 April 2014. [Google Scholar]
- Papanicolaou, N.C.; Christou, M.A.; Polycarpou, A.C. Polycarpou, Frequency-agile microstrip patch antenna on a biased liquid crystal substrate. Electron. Lett. 2015, 51, 202–204. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, C.; Qing, A.; Luo, X. A Frequency and Pattern Reconfigurable Antenna Array Based on Liquid Crystal Technology. IEEE Photonics J. 2017, 9, 1–7. [Google Scholar] [CrossRef]
- Strunck, S.; Karabey, O.H.; Gaebler, A.; Jakoby, R. Reconfigurable waveguide polariser based on liquid crystal for continuous tuning of linear polarization. Electron. Lett. 2012, 48, 441–443. [Google Scholar] [CrossRef]
- Karabey, O.H.; Bausch, S.; Bildik, S.; Strunck, S.; Gaebler, A.; Jakoby, R. Design and application of a liquid crystal varactor based tunable coupled line for polarization agile antennas. In Proceedings of the European Microwave Conference (EuMC), Amsterdam, The Netherlands, 31 October–2 November 2012; pp. 739–742. [Google Scholar]
- Karabey, O.H.; Bildik, S.; Bausch, S.; Strunck, S.; Gaebler, A.; Jakoby, R. Continuously Polarization Agile Antenna by Using Liquid Crystal-Based Tunable Variable Delay Lines. IEEE Trans. Antennas Propag. 2013, 61, 70–76. [Google Scholar] [CrossRef]
- Doumanis, E.; Goussetis, G.; Dickie, R.; Cahill, R.; Baine, P.; Bain, M.; Fusco, V.; Encinar, J.A.; Toso, G. Electronically Reconfigurable Liquid Crystal Based Mm-Wave Polarization Converter. IEEE Trans. Antennas Propag. 2014, 62, 2302–2307. [Google Scholar] [CrossRef]
- Nickel, M.; Schuster, C.; Maune, H.; Jakoby, R.; Dill, S.; Peichl, M. A liquid crystal based tunable polarization selector in a microwave imaging radiometer. In Proceedings of the 11th German Microwave Conference (GeMiC), Freiburg, Germany, 12–14 March 2018; pp. 91–94. [Google Scholar] [CrossRef]
- Tanaka, M.; Nose, T.; Sato, S. Millimeter-Wave Transmission Properties of Nematic Liquid-Crystal Cells with a Grating-Patterned Electrode Structure. Jpn. J. Appl. Phys. 2000, 9, 6393–6396. [Google Scholar] [CrossRef]
- Tanaka, M.; Sato, S. Millimeter-Wave Deflection Properties of Liquid Crystal Prism Cells with Stack-Layered Structure. Jpn. J. Appl. Phys. 2001, 40, L1123–L1125. [Google Scholar] [CrossRef]
- Tanaka, M.; Sato, S. Electrically Controlled Millimeter-Wave Focusing Properties of Liquid Crystal Lens. Jpn. J. Appl. Phys. 2002, 41, 5332–5333. [Google Scholar] [CrossRef]
- Yang, F.; Sambles, J.R. Microwave liquid-crystal variable phase grating. Appl. Phys. Lett. 2004, 85, 2041–2043. [Google Scholar] [CrossRef]
- Kamoda, H.; Kuki, T.; Fujikake, H.; Nomoto, T. Millimeter-wave beam former using liquid crystal. Electron. Commun. Jpn. (Part. II Electron.) 2005, 88, 10–18. [Google Scholar] [CrossRef]
- Pan, C.-L.; Lin, C.-J.; Yang, C.-S.; Wu, W.-T.; Pan, R.-P. Liquid-Crystal-Based Phase Gratings and Beam Steerers for Terahertz Waves. In Liquid Crystals - Recent Advancements in Fundamental and Device Technologies; IntechOpen: London, UK, 2018. [Google Scholar]
- Reese, R.; Jost, M.; Polat, E.; Tesmer, H.; Strobl, J.; Schuster, C.; Nickel, M.; Jakoby, R.; Maune, H. A Millimeter Wave Beam Steering Lens Antenna with Reconfigurable Aperture using Liquid Crystal. IEEE Trans. Antennas Propag. 2019, 1. [Google Scholar] [CrossRef]
- Shi, H.; Li, J.; Zhu, S.; Zhang, A.; Xu, Z. Radiation Pattern Reconfigurable Waveguide Slot Array Antenna Using Liquid Crystal. Int. J. Antennas Propag. 2018, 1–9. [Google Scholar] [CrossRef]
- Christie, S.; Cahill, R.; Mitchell, N.; Manabe, A.; Munro, Y. Electronically scanned Rotman lens antenna with liquid crystal phase shifters. Electron. Lett. 2013, 49, 445–447. [Google Scholar] [CrossRef]
- Jost, M. Liquid Crystal Mixed Beam-Switching and Beam-Steering Network in Hybrid Metallic and Dielectric Waveguide Technology. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2018. [Google Scholar]
- Marin, R.; Mossinger, A.; Freese, J.; Muller, S.; Jakoby, R. Basic Investigations of 35 GHz Reflectarrays and Tunable Unit-Cells for Beamsteering Applications. In Proceedings of the IEEE European Radar Conference (EURAD), Paris, France, 3–4 October 2005. [Google Scholar]
- Marin, R.; Mossinger, A.; Freese, J.; Manabe, A.; Jakoby, R. Realization of 35 GHz Steerable Reflectarray using Highly Anisotropic Liquid Crystal. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM, USA, 9–14 July 2006. [Google Scholar]
- Moessinger, A.; Marin, R.; Mueller, S.; Freese, J.; Jakoby, R. Electronically reconfigurable reflectarrays with nematic liquid crystals. Electron. Lett. 2006, 42, 899–900. [Google Scholar] [CrossRef]
- Mössinger, A.; Eicher, D.; Gaebler, A.; Marin, R.; Mueller, S.; Jakoby, R.; Schlaak, H.F. Electronically Reconfigurable LC-Reflectarray with 2D Scanning Capability and SU-8 structured Cavity. Frequenz 2008, 62. [Google Scholar] [CrossRef]
- Hu, W.; Ismail, M.; Cahill, R.; Gamble, H.; Dickie, R.; Fusco, V.; Linton, D.; Rea, S.; Grant, N. Tunable liquid crystal reflectarray patch element. Electron. Lett. 2006, 42, 509. [Google Scholar] [CrossRef]
- Hu, W.; Ismail, M.; Cahill, R.; Encinar, J.; Fusco, V.; Gamble, H.; Linton, D.; Dickie, R.; Grant, N.; Rea, S. Liquid-crystal-based reflectarray antenna with electronically switchable monopulse patterns. Electron. Lett. 2007, 43, 744. [Google Scholar] [CrossRef]
- Hu, W.; Cahill, R.; Encinar, J.A.; Dickie, R.; Gamble, H.; Fusco, V.; Grant, N. Design and Measurement of Reconfigurable Millimeter Wave Reflectarray Cells with Nematic Liquid Crystal. IEEE Trans. Antennas Propag. 2008, 56, 3112–3117. [Google Scholar] [CrossRef]
- Hu, W.; Arrebola, M.; Cahill, R.; Encinar, J.; Fusco, V.; Gamble, H.; Alvarez, Y.; Las-Heras, F. 94 GHz Dual-Reflector Antenna with Reflectarray Subreflector. IEEE Trans. Antennas Propag. 2009, 57, 3043–3050. [Google Scholar] [CrossRef]
- Dieter, S.; Moessinger, A.; Mueller, S.; Jakoby, R.; Menzel, W. Characterization of Reconfigurable LC-Reflectarrays Using Near-Field Measurements. In Proceedings of the 2009 German Microwave Conference, Berlin, Germany, 16–18 March 2009. [Google Scholar]
- Perez-Palomino, G.; Encinar, J.A.; Barba, M.; Carrasco, E. Design and evaluation of multi-resonant unit cells based on liquid crystals for reconfigurable reflectarrays. Antennas Propag. Iet Microw. 2012, 6, 348–354. [Google Scholar] [CrossRef]
- Perez-Palomino, G.; Encinar, J.A.; Barba, M.; Dickie, R.; Baine, P.; Cahill, R.; Florencio, R.; Boix, R.R. Wideband unit-cell based on liquid crystals for reconfigurable reflectarray antennas in f-band. In Proceedings of the IEEE International Symposium Antennas and Propagation, Chicago, IL, USA, 8–14 July 2012; pp. 1–2. [Google Scholar] [CrossRef]
- Perez-Palomino, G.; Baine, P.; Dickie, R.; Bain, M.; Encinar, J.A.; Cahill, R.; Barba, M.; Toso, G. Design and Experimental Validation of Liquid Crystal-Based Reconfigurable Reflectarray Elements with Improved Bandwidth in F-Band. IEEE Trans. Antennas Propag. 2013, 61, 1704–1713. [Google Scholar] [CrossRef]
- Bildik, S.; Dieter, S.; Fritzsch, C.; Menzel, W.; Jakoby, R. Reconfigurable Folded Reflectarray Antenna Based Upon Liquid Crystal Technology. IEEE Trans. Antennas Propag. 2015, 63, 122–132. [Google Scholar] [CrossRef]
- Gao, S.; Yang, J.; Wang, P.; Zheng, A.; Lu, H.; Deng, G.; Lai, W.; Yin, Z. Tunable Liquid Crystal Based Phase Shifter with a Slot Unit Cell for Reconfigurable Reflectarrays in F-Band. Appl. Sci. 2018, 8, 2528. [Google Scholar] [CrossRef]
- Damm, C.; Maasch, M.; Gonzalo, R.; Jakoby, R. Tunable composite right/left-handed leaky wave antenna based on a rectangular waveguide using liquid crystals. In Proceedings of the IEEE MTT-S International Microwave Symposium, Anaheim, CA, USA, 23–28 May 2010. [Google Scholar]
- Damm, C. Artificial Transmission Line Structures for Tunable Microwave Components and Microwave Sensors; Shaker Verlag: Düren, Germany, 2011. [Google Scholar]
- Roig, M.; Maasch, M.; Damm, C.; Karabey, O.H.; Jakoby, R. Liquid crystal based tunable composite right/left-handed leaky-wave antenna for Ka-Band applications. In Proceedings of the European Microwave Conference (EuMC), Nuremberg, Germany, 6–10 October 2013; pp. 759–762. [Google Scholar]
- Roig, M.; Maasch, M.; Damm, C.; Jakoby, R. Dynamic beam steering properties of an electrically tuned liquid crystal based CRLH leaky wave antenna. In Proceedings of the 2014 8th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics, Copenhagen, Denmark, 25–28 August 2014; pp. 253–255. [Google Scholar] [CrossRef]
- Roig, M.; Maasch, M.; Damm, C.; Jakoby, R. Investigation and application of a liquid crystal loaded varactor in a voltage tunable CRLH leaky-wave antenna at Ka-band. Int. J. Microw. Wirel. Technol. 2015, 7, 361–367. [Google Scholar] [CrossRef]
- Roig, M. Tunable Metamaterial Leaky Wave Antenna Based on Microwave Liquid Crystal Technology. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2015. Available online: http://tuprints.ulb.tu-darmstadt.de/5136/ (accessed on 5 June 2020).
- Che, B.-J.; Meng, F.-Y.; Lyu, Y.-L.; Wu, Q. A Novel liquid crystal based leaky wave antenna. In Proceedings of the 2016 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Chengdu, China, 20–22 July 2016. [Google Scholar]
- Gaebler, A.; Moessinger, A.; Goelden, F.; Manabe, A.; Goebel, M.; Follmann, R.; Koether, D.; Modes, C.; Kipka, A.; Deckelmann, M.; et al. Liquid Crystal-Reconfigurable Antenna Concepts for Space Applications at Microwave and Millimeter Waves. Int. J. Antennas Propag. 2009, 1–7. [Google Scholar] [CrossRef]
- Sanadgol, B.; Holzwarth, S.; Kassner, J. 30 GHz liquid crystal phased array. In Proceedings of the IEEE 2009 Loughborough Antennas & Propagation Conference, Loughborough, UK, 16–17 November 2009. [Google Scholar] [CrossRef]
- Wolff, I. Integrated beam steerable antennas in LTCC-technology. In Proceedings of the Int. Workshop Antenna Technology (iWAT), Lisbon, Portugal, 1–3 March 2010; pp. 1–4. [Google Scholar]
- Karabey, O.H.; Bildik, S.; Fritzsch, C.; Strunck, S.; Gaebler, A.; Jakoby, R.; Manabe, A. Liquid Crystal Based Reconfigurable Antenna Arrays. October 2010. Available online: http://tubiblio.ulb.tu-darmstadt.de/56398/, (accessed on 5 June 2020).
- Hoefle, M.; Koeberle, M.; Chen, M.; Penirschke, A.; Jakoby, R. Reconfigurable Vivaldi antenna array with integrated antipodal finline phase shifter with liquid crystal for W-Band applications. In Proceedings of the 35 International Conference on Infrared, Millimeter, and Terahertz Waves, Rome, Italy, 5–10 September 2010; pp. 1–2. [Google Scholar]
- Karabey, O.H.; Gaebler, A.; Strunck, S.; Jakoby, R. A 2-D Electronically Steered Phased-Array Antenna With 2 x 2 Elements in LC Display Technology. IEEE Trans. Microw. Theory Tech. 2012, 60, 1297–1306. [Google Scholar] [CrossRef]
- Hoefle, M.; Koeberle, M.; Penirschke, A.; Jakoby, R. Improved millimeter wave Vivaldi antenna array element with high performance liquid crystals. In Proceedings of the IEEE 2011 International Conference on Infrared, Millimeter, and Terahertz Waves, Houston, TX, USA, 2–7 October 2011. [Google Scholar]
- Hoefle, M.; Koeberle, M.; Penirschke, A.; Jakoby, R. Millimeterwave Vivaldi Antenna with Liquid Crystal Phase Shifter for Electronic Beam Steering. Presented at the 6th ESA Workshop on Millimetre-Wave Technology and Applications, Espoo, Finland, 23–25 May 2011; Available online: http://tubiblio.ulb.tu-darmstadt.de/56414/ (accessed on 5 June 2020).
- Deo, P.; Mirshekar-Syahkal, D.; Seddon, L.; Day, S.E.; Fernández, F.A.B. 60 GHz liquid crystal phased array using reflection-type phase shifter. In Proceedings of the European Conference on Antennas and Propagation (EUCAP), Gothenburg, Sweden, 8–12 April 2013; pp. 927–929. [Google Scholar]
- Deo, P.; Mirshekar-Syahkal, D.; Seddon, L.; Day, S.E.; Fernandez, F.A. Liquid crystal based patch antenna array for 60 GHz applications. In Proceedings of the 2013 IEEE Radio and Wireless Symposium, Austin, TX, USA, 20–23 January 2013; pp. 127–129. [Google Scholar]
- Karabey, O.H. Electronic Beam Steering and Polarization Agile Planar Antennas in Liquid Crystal Technology; Springer Science and Business Media LLC: Berlin, Germany, 2014. [Google Scholar] [CrossRef]
- Tebbe, M.; Hoehn, A.; Nathrath, N.; Weickhmann, C. Simulation of an electronically steerable horn antenna array with liquid crystal phase shifters. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016; pp. 1–15. [Google Scholar] [CrossRef]
- Reese, R.; Jost, M.; Nickel, M.; Polat, E.; Jakoby, R.; Maune, H. A Fully Dielectric Lightweight Antenna Array Using a Multimode Interference Power Divider at W-Band. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3236–3239. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, S.-Q.; Ma, L.-Q.; Meng, F.-Y.; Erni, D.; Zhu, L.; Fu, J.-H.; Wu, Q. Compact planar array antenna with electrically beam steering from backfire to endfire based on liquid crystal. IET Microw. Antennas Propag. 2018, 12, 1140–1146. [Google Scholar] [CrossRef]
- Weickhmann, C.; Mehmood, A.; Olcen, A.B.; Sun, Y.; Jakoby, R. A Low-cost, Flat, Electronically Steerable Array Antenna for New Massive NGEO Constellations Ground Terminals and Future 5G. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019. [Google Scholar]
- Yaghmaee, P.; Karabey, O.H.; Bates, B.; Fumeaux, C.; Jakoby, R. Electrically Tuned Microwave Devices Using Liquid Crystal Technology. Int. J. Antennas Propag. 2013, 1–9. [Google Scholar] [CrossRef]
- Maune, H.; Jost, M.; Reese, R.; Polat, E.; Nickel, M.; Jakoby, R. Microwave Liquid Crystal Technology. Crystals 2018, 8, 355. [Google Scholar] [CrossRef]
- Zografopoulos, D.C.; Ferraro, A.; Beccherelli, R. Liquid-Crystal High-Frequency Microwave Technology: Materials and Characterization. Adv. Mater. Technol. 2018, 1800447. [Google Scholar] [CrossRef]
- Heunisch, A.; Schulz, B.; Rabe, T.; Strunck, S.; Follmann, R.; Manabe, A. LTCC Antenna Array with Integrated Liquid Crystal Phase Shifter for Satellite Communication. In Proceedings of the Additional Conferences (Device Packaging, HiTEC, HiTEN, & CICMT), September 2012; No. CICMT. pp. 97–102. [Google Scholar] [CrossRef]
- Goelden, F.; Mueller, S.; Scheele, P.; Wittek, M.; Jakoby, R. IP3 Measurements of Liquid Crystals at Microwave Frequencies. In Proceedings of the IEEE European Microwave Conference (EuMC), Manchester, UK, 10–15 September 2006. [Google Scholar] [CrossRef]
- Goelden, F. Liquid Crystal Based Microwave Components with Fast Response Times: Material, Technology, Power Handling Capability. 2010. Available online: http://tuprints.ulb.tu-darmstadt.de/2203/ (accessed on 5 June 2020).
- Mueller, S. Grundlegende Untersuchungen steuerbarer passiver Flüssigkristall Komponenten für die Mikrowellentechnik; Shaker Verlag: Düren, Germany, 2007; ISBN 10: 3832260765. [Google Scholar]
- Imanaka, Y. Multilayered Low Temperature Cofired Ceramics (LTCC) Technology; Springer US: New York, NY, USA, 2005; ISBN 978-0-387-23130-3. [Google Scholar] [CrossRef]
- Kawamoto, H. The history of liquid-crystal displays. Proc. IEEE 2002, 90, 460–500. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystal; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Goodby, J.W.; Collings, P.J.; Kato, T.; Tschierske, C.; Gleeson, H.; Raynes, P. Handbook of Liquid Crystals; Wiley-VCH: Weinheim, Germany, 1998. [Google Scholar]
- Yang, D.-K.; Wu, S.-T. Fundamentals of Liquid Crystal Devices; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Collings, P.J.; Hird, M. Introduction to Liquid Crystals: Chemistry and Physics; CRC Press: London, UK, 2017. [Google Scholar]
- Oseen, C.W. The theory of liquid crystals. Trans. Faraday Soc. 1933, 29, 883–899. [Google Scholar] [CrossRef]
- Frank, F.C.I. Liquid crystals. On the theory of liquid crystals. Discuss. Faraday Soc. 1958, 25, 19–28. [Google Scholar] [CrossRef]
- Ong, H.L. Measurement of nematic liquid crystal splay and bend elastic constants with obliquely incident light. J. Appl. Phys. 1991, 70, 2023–2030. [Google Scholar] [CrossRef]
- Tarumi, K.; Finkenzeller, U.; Schuler, B. Dynamic Behaviour of Twisted Nematic Liquid Crystals. Jpn. J. Appl. Phys. 1992, 31, 2829–2836. [Google Scholar] [CrossRef]
- Blinov, L.M.; Chigrinov, V.G. Electrooptic Effects in Liquid Crystal Materials; Springer Science and Business Media LLC: Berlin, Germany, 1994. [Google Scholar]
- Stewart, I.W. The Static and Dynamic Continuum Theory of Liquid Crystals: A Mathematical Introduction; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Kleman, M.; Laverntovich, O.D. Soft Matter Physics. An Introduction; Springer: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Penirschke, A.; Muller, S.; Scheele, P.; Weil, C.; Wittek, M.; Hock, C.; Jakoby, R. Cavity perturbation method for characterization of liquid crystals up to 35 GHz. In Proceedings of the European Microwave Conference (EuMC), Amsterdam, The Netherlands, 12–14 October 2004; Volume 2, pp. 545–548. [Google Scholar]
- Mueller, S.; Moessinger, A.; Marin, R.; Goelden, F.; Lapanik, A.; Haase, W.; Jakoby, R. Liquid Crystals—Microwave Characterization and Tunable Devices. Frequenz 2007, 61. [Google Scholar] [CrossRef]
- Krupka, J.; Derzakowski, K.; Riddle, B.; Baker-Jarvis, J. A dielectric resonator for measurements of complex permittivity of low loss dielectric materials as a function of temperature. Meas. Sci. Technol. 1998, 9, 1751–1756. [Google Scholar] [CrossRef]
- Parka, J.; Krupka, J.; Dąbrowski, R.; Wosik, J. Measurements of anisotropic complex permittivity of liquid crystals at microwave frequencies. J. Eur. Ceram. Soc. 2007, 27, 2903–2905. [Google Scholar] [CrossRef]
- Gaebler, A.; Goelden, F.; Mueller, S.; Jakoby, R. Triple-Mode Cavity Perturbation Method for the Characterization of Anisotropic Media. In Proceedings of the European Microwave Conference (EuMC), Amsterdam, The Netherlands, 27–31 October 2008; pp. 909–912. [Google Scholar]
- Yazdanpanahi, M.; Bulja, S.; Mirshekar-Syahkal, D.; James, R.; Day, S.E.; Fernandez, F.A. Measurement of Dielectric Constants of Nematic Liquid Crystals at mm-Wave Frequencies Using Patch Resonator. IEEE Trans. Instrum. Meas. 2010, 59, 3079–3085. [Google Scholar] [CrossRef]
- Schaub, D.E.; Oliver, D.R. A Circular Patch Resonator for the Measurement of Microwave Permittivity of Nematic Liquid Crystal. IEEE Trans. Microw. Theory Tech. 2011, 59, 1855–1862. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Parka, J.; Krupka, J.; Olifierczuk, M.; Nowinowski-Kruszelnicki, E.; Jaroszewicz, L.; Chojnowska, O. Dielectric properties of highly anisotropic nematic liquid crystals for tunable microwave components. Appl. Phys. Lett. 2013, 103, 172902. [Google Scholar] [CrossRef]
- Weickhmann, C.; Schmidt, S.; Jost, M.; Hu, W.; Jakoby, R.; Manabe, A.; Fritzsch, C.; Wittek, M. Measuring Liquid Crystal Permittivity with High Accuracy. In Proceedings of the Annual Condensed Matter and Materials Meeting, Wagga, Australia, 3–6 February 2015; Available online: http://aip.org.au/wp-content/uploads/cmm/2015/Wagga2015_8_FM5_Weickhmann.pdf (accessed on 5 June 2020).
- Mueller, S.; Penirschke, A.; Damm, C.; Scheele, P.; Wittek, M.; Weil, C.; Jakoby, R. Broadband microwave characterization of liquid crystals using a temperature-controlled coaxial transmission line. IEEE Trans. Microw. Theory Tech. 2005, 53, 1937–1945. [Google Scholar] [CrossRef]
- Karabey, O.H.; Goelden, F.; Gaebler, A.; Jakoby, R. Precise broadband microwave material characterization of liquids. In Proceedings of the European Microwave Conference (EuMC), Paris, France, 28–30 September 2010; pp. 1591–1594. [Google Scholar]
- Hu, W.; Karabey, O.H.; Prasetiadi, A.E.; Jost, M.; Jakoby, R. Temperature Controlled Artificial Coaxial Line for Microwave Characterization of Liquid Crystal. In Proceedings of the GeMiC 2014 German Microwave Conference, Aachen, Germany, 10–12 March 2014; pp. 1–4. [Google Scholar]
- Yang, F.; Sambles, J.R. Determination of the microwave permittivities of nematic liquid crystals using a single-metallic slit technique. Appl. Phys. Lett. 2002, 81, 2047–2049. [Google Scholar] [CrossRef]
- Mueller, S.; Koeberle, M.; Goelden, F.; Penirschke, A.; Gaebler, A.; Lapanik, A.; Haase, W.; Jakoby, R. W-Band Characterization of Anisotropic Liquid Crystals at Room Temperature. In Proceedings of the 2008 38th European Microwave Conference, Amsterdam, The Netherlands, 27–31 October 2008; pp. 119–122. [Google Scholar] [CrossRef]
- James, R.; Fernandez, F.A.; Day, S.E.; Bulja, S.; Mirshekar-Syahkal, D. Accurate Modeling for Wideband Characterization of Nematic Liquid Crystals for Microwave Applications. IEEE Trans. Microw. Theory Tech. 2009, 57, 3293–3297. [Google Scholar] [CrossRef]
- Bulja, S.; Mirshekar-Syahkal, D.; James, R.; Day, S.E.; Fernandez, F.A.B. Measurement of Dielectric Properties of Nematic Liquid Crystals at Millimeter Wavelength. IEEE Trans. Microw. Theory Tech. 2010. [Google Scholar] [CrossRef]
- Deo, P.; Mirshekar-Syahkal, D.; Seddon, L.; Day, S.E.; Fernandez, F.A. Microstrip Device for Broadband (15–65 GHz) Measurement of Dielectric Properties of Nematic Liquid Crystals. IEEE Trans. Microw. Theory Tech. 2015, 63, 1388–1398. [Google Scholar] [CrossRef]
- Koeberle, M.; Goebel, T.; Schoenherr, D.; Mueller, S.; Jakoby, R.; Meissner, P.; Hartnagel, H.-L. Material Characterization of Liquid Crystals at THz-Frequencies using a Free Space Measurement Setup. In Proceedings of the German Microwave Conference, Hamburg, Germany, 10–12 March 2008; pp. 1–4. [Google Scholar]
- Pogson, E.M.; Lewis, R.A.; Koeberle, M.; Jakoby, R. Terahertz time-domain spectroscopy of nematic liquid crystals. SPIE Photonics Eur. 2010, 7728, 77281Y. [Google Scholar] [CrossRef]
- Reuter, M.; Vieweg, N.; Fischer, B.M.; Mikulicz, M.; Koch, M.; Garbat, K.; Dąbrowski, R. Highly birefringent, low-loss liquid crystals for terahertz applications. APL Mater. 2013, 1, 012107. [Google Scholar] [CrossRef]
- Weickhmann, C.; Jakoby, R.; Constable, E.; Lewis, R.A. Time-domain spectroscopy of novel nematic liquid crystals in the terahertz range. In Proceedings of the 2013 38th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Mainz, Germany, 1–6 September 2013; pp. 1–2. [Google Scholar] [CrossRef]
- Gaebler, A.; Goelden, F.; Mueller, S.; Penirschke, A.; Jakoby, R. Direct simulation of material permittivities by using an eigen-susceptibility formulation of the vector variational approach. In Proceedings of the 2009 IEEE Intrumentation and Measurement Technology Conference, Singapore, 5–7 May 2009. [Google Scholar]
- Gaebler, A.; Goelden, F.; Karabey, O.H.; Jakoby, R. A FDFD based eigen-dielectric formulation of the Maxwell equations for material characterization in arbitrary waveguide structures. In Proceedings of the IEEE MTT-S International Microwave Symposium, Anaheim, CA, USA, 23–28 May 2010. [Google Scholar]
- Polat, E.; Reese, R.; Tesmer, H.; Schmidt, S.; Spaeth, M.; Nickel, M.; Schuster, C.; Jakoby, R.; Maune, H. Characterization of Liquid Crystals Using a Temperature-Controlled 60 GHz Resonato. In Proceedings of the 2019 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Bochum, Germany, 16–18 July 2019. [Google Scholar] [CrossRef]
- Yaghmaee, P.; Kaufmann, T.; Bates, B.; Fumeaux, C. Effect of polyimide layers on the permittivity tuning range of liquid crystals. In Proceedings of the European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; pp. 3579–3582. [Google Scholar]
- Goelden, F.; Gaebler, A.; Mueller, S.; Lapanik, A.; Haase, W.; Jakoby, R. Liquid-crystal varactors with fast switching times for microwave applications. Electron. Lett. 2008, 44, 480. [Google Scholar] [CrossRef]
- Goelden, F.; Lapanik, A.; Gaebler, A.; Mueller, S.; Haase, W.; Jakoby, R. Characterization and Application of Liquid Crystals at Microwave Frequencies. Frequenz 2008, 62, 57–61. [Google Scholar] [CrossRef]
- Goelden, F.; Gaebler, A.; Goebel, M.; Manabe, A.; Mueller, S.; Jakoby, R. Tunable liquid crystal phase shifter for microwave frequencies. Electron. Lett. 2009, 45, 686–687. [Google Scholar] [CrossRef]
- Karabey, O.H.; Goelden, F.; Gaebler, A.; Strunck, S.; Jakoby, R. Tunable loaded line phase shifters for microwave applications. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar]
- Gaebler, A.; Goelden, F.; Mueller, S.; Jakoby, R. Modeling of electrically tunable transmission line phase shifter based on liquid crystal. In Proceedings of the 2008 IEEE Antennas and Propagation Society International Symposium, San Diego, CA, USA, 5–11 July 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Gaebler, A.; Goelden, F.; Mueller, S.; Jakoby, R. Multiphysics Simulations for Tunability Efficiency Evaluation of Liquid Crystal Based RF. Frequenz 2008, 62, 240–245. [Google Scholar] [CrossRef]
- Gaebler, A.; Goelden, F.; Mueller, S.; Jakoby, R. Efficiency considerations of tuneable liquid crystal microwave devices. In Proceedings of the German Microwave Conference, Hamburg-Harburg, Germany, 10–12 March 2008; pp. 1–4. [Google Scholar]
- Karabey, O.H.; Saavedra, B.G.; Fritzsch, C.; Strunck, S.; Gaebler, A.; Jakoby, R. Methods for improving the tuning efficiency of liquid crystal based tunable phase shifters. In Proceedings of the European Microwave Integrated Circuit Conference (EuMIC), Piscataway, NJ, USA, 10–11 October 2011; pp. 494–497. [Google Scholar]
- Fujikake, H.; Kuki, T.; Nomoto, T.; Tsuchiya, Y.; Utsumi, Y. Thick polymer-stabilized liquid crystal films for microwave phase control. J. Appl. Phys. 2001, 89, 5295–5298. [Google Scholar] [CrossRef]
- Utsumi, Y.; Kamei, T.; Saito, K.; Moritake, H. Increasing the speed of microstrip line-type PDLC devices. In Proceedings of the IEEE MTT-S International Microwave Symposium, Long Beach, CA, USA, 17 June 2005. [Google Scholar]
- Kuki, T.; Fujikake, H.; Kamoda, H.; Nomoto, T. Microwave variable delay line using a membrane impregnated with liquid crystal. In Proceedings of the IEEE MTT-S International Microwave Symposium, Seattle, WA, USA, 2–7 June 2002. [Google Scholar]
- Ito, R.; Kumagai, T.; Yoshida, H.; Takeya, K.; Ozaki, M.; Tonouch, M.; Nose, T. THz Nematic Liquid Crystal Devices Using Stacked Membrane Film Layers. Mol. Cryst. Liq. Cryst. 2011, 543, 77–843. [Google Scholar] [CrossRef]
- Paul, S.N.; Dhar, R.; Verma, R.; Sharma, S.; Dabrowski, R. Change in Dielectric and Electro-Optical Properties of a Nematic Material (6CHBT) Due to the Dispersion of BaTiO3Nanoparticles. Mol. Cryst. Liq. Cryst. 2011, 545, 1051329–1111335. [Google Scholar] [CrossRef]
- Ryzhkova, A.V.; Podgornov, F.V.; Gaebler, A.; Jakoby, R.; Haase, W. Measurements of the electrokinetic forces on dielectric microparticles in nematic liquid crystals using optical trapping. J. Appl. Phys. 2013, 113, 244902. [Google Scholar] [CrossRef]
- Karabey, O.H. Microwave Material Properties of Nanoparticle-Doped Nematic Liquid Crystals. Frequenz 2015, 69. [Google Scholar] [CrossRef]
- Garbovskiy, Y.; Glushchenko, A. Ferroelectric Nanoparticles in Liquid Crystals: Recent Progress and Current Challenges. Nanomaterials 2017, 7, 361. [Google Scholar] [CrossRef]
- Moritake, H.; Kim, J.; Toda, K.; Yoshino, K. Dynamic viscosity change measurement of liquid and liquid crystal using propagation velocity change of shear horizontal wave. In Proceedings of the IEEE International Conference on Dielectric Liquids, ICDL, Coimbra, Portugal, 26 June–1 July 2005; pp. 257–260. [Google Scholar] [CrossRef]
- Goelden, F.; Lapanik, A.; Mueller, S.; Gaebler, A.; Haase, W.; Jakoby, R. Investigations on the behavior of ferroelectric liquid crystals at microwave frequencies. In Proceedings of the 2007 European Microwave Conference (EuMC), Munich, Germany, 9–12 October 2007; pp. 106–109. [Google Scholar]
- Arora, P.; Mikulko, A.; Podgornov, F.; Haase, W. Dielectric and Electro-Optic Properties of New Ferroelectric Liquid Crystalline Mixture Doped with Carbon Nanotubes. Mol. Cryst. Liq. Cryst. 2009, 502, 1–8. [Google Scholar] [CrossRef]
- Mikułko, A.; Arora, P.; Glushchenko, A.; Lapanik, A.; Haase, W. Complementary studies of BaTiO3nanoparticles suspended in a ferroelectric liquid-crystalline mixture. EPL (Europhys. Lett.) 2009, 87, 27009. [Google Scholar] [CrossRef]
- Kuki, T.; Fujikake, H.; Nomoto, T. Microwave variable delay line using dual-frequency switching-mode liquid crystal. IEEE Trans. Microw. Theory Tech. 2002, 50, 2604–2609. [Google Scholar] [CrossRef]
- Hindle, P. Comprehensive Survey of Commercial mmWave Phased Array Companies Focused on SATCOM and 5G Applications. Microw. J. 2020. Available online: https://www.microwavejournal.com/articles/33357-comprehensive-survey-of-commercial-mmwave-phased-array-companies (accessed on 5 June 2020).
- Anokiwaves Inc. Introduction to All Silicon Millimeter-Wave 5G Arrays. Microw. J. 2019. Available online: https://www.microwavejournal.com/articles/31937-introduction-to-all-silicon-millimeter-wave-5g-arrays.com (accessed on 5 June 2020).
- Kundtz, N. Next Generation Communications for Next Generation Satellites. Microw. J. 2014, 57, 56. [Google Scholar]
- Kymeta; Posthuma, B. A Hybrid Network Solution for Reliable, Wide-Coverage First Responder Communications. Available online: https://www.kymetacorp.com/wp-content/uploads/2019/02/Kymeta-Hybrid-Nework-Whitepaper-2019.pdf (accessed on 5 June 2020).
- Kymeta. Metamaterial-Surface Flat-Panel Antenna Technology. 2019. Available online: https://www.kymetacorp.com/wp-content/uploads/2019/06/Metamaterial-Surface-Antenna-Technology.pdf (accessed on 5 June 2020).
- Kymeta. A Hybrid Satellite-Cellular Communications Terminal for Connected and Autonomous Vehicles. Available online: https://www.kymetacorp.com/wp-content/uploads/2019/06/Hybrid-Network-for-CC.pdf (accessed on 5 June 2020).
- ALCAN Systems, SES and ALCAN, a German Smart Antenna Company, Are Working Together to Develop a New Flat Panel Antenna for SESs O3b mPOWER system. 2018. Available online: https://www.alcansystems.com/ (accessed on 5 June 2020).
- ALCAN Systems, ALCAN Successfully Completes World’s First Liquid Crystal Based Phased Array Antenna Field Test for Satellite Communication. 2018. Available online: https://www.alcansystems.com/press-release-alcan-successfully-completes-worlds-first-liquid-crystal-based-phased-array-antenna-field-test-for-satellite-communication/ (accessed on 5 June 2020).
- ALCAN Systems, M.R. Dehghani, ALCAN’s Smart Antenna’s 5G Opportunities and Solutions. 2019. Available online: https://www.alcansystems.com/alcans-smart-antennas-5g-opportunities-and-solutions/ (accessed on 5 June 2020).
- Doll, A.; Dehghani, M.R.; ALCAN Systems. 5G and Beyond: The Power Consumption Challenge. 2020. Available online: https://www.alcansystems.com/5g-and-beyond-the-power-consumption-challenge/ (accessed on 5 June 2020).
- ALCAN Systems, Public Link. Multi-Beam ESA Demonstration. Available online: https://www.youtube.com/watch?v=ArLNgMnYVMY&feature=youtu.be (accessed on 5 June 2020).
- Lim, K.C.; Margerum, J.D.; Lackner, A.M. Liquid crystal millimeter wave electronic phase shifter. Appl. Phys. Lett. 1993, 62, 1065–1067. [Google Scholar] [CrossRef]
- Polat, E.; Tesmer, H.; Reese, R.; Nickel, M.; Wang, D.; Schumacher, P.; Jakoby, R.; Maune, H. Reconfigurable Millimeter-Wave Components Based on Liquid Crystal Technology for Smart Applications. Crystals 2020, 10, 346. [Google Scholar] [CrossRef]
- Dolfi, D.; Labeyrie, M.; Joffre, P.; Huignard, J.P. Liquid crystal microwave phase shifter. Electron. Lett. 1993, 29, 926–928. [Google Scholar] [CrossRef]
- Kuki, T.; Fujikake, H.; Nomoto, T.; Utsumi, Y. Design of a microwave variable delay line using liquid crystal, and a study of its insertion loss. Electron. Commun. Jpn. (Part. II Electron.) 2002, 85, 36–42. [Google Scholar] [CrossRef]
- Martin, N.; Laurent, P.; Prigent, G.; Gelin, P.; Huret, F. Technological evolution and performances improvements of a tunable phase-shifter using liquid crystal. Microw. Opt. Technol. Lett. 2004, 43, 338–341. [Google Scholar] [CrossRef]
- Sahbani, F.; Tentillier, N.; Gharsallah, A.; Gharbi, A.; Legrand, C. New tunable coplanar microwave phase shifter with nematic crystal liquid. In Proceedings of the 3rd International Design and Test Workshop, Monastir, Tunisia, 20–22 December 2008; pp. 78–81. [Google Scholar] [CrossRef]
- Bulja, S.; Mirshekar, D.; James, R.; Day, S.E.; Fernández, F.A. Effective dielectric constant of top grounded coplanar waveguide on liquid crystal superstrate. Microw. Opt. Technol. Lett. 2013, 55, 1416–1418. [Google Scholar] [CrossRef][Green Version]
- Prasetiadi, A.E.; Jost, M.; Schulz, B.; Quibeldey, M.; Rabe, T.; Follmann, R.; Jakoby, R. Liquid-crystal-based amplitude tuner and tunable SIW filter fabricated in LTCC technology. Int. J. Microw. Wirel. Technol. 2018, 10, 674–681. [Google Scholar] [CrossRef]
- Strunck, S.; Gaebler, A.; Karabey, O.H.; Heunisch, A.; Schulz, B.; Rabe, T.; Follmann, R.; Kassner, J.; Koether, D.; Manabe, A.; et al. Reliability study of a tunable Ka-band SIW-phase shifter based on liquid crystal in LTCC-technology. Int. J. Microw. Wirel. Technol. 2014, 7, 521–527. [Google Scholar] [CrossRef]
- Strunck, S. Flüssigkristall-basierte und LTCC-Integrierte Elektrisch Steuerbare Mikrowellenphasenschieber und –Polarisatoren; Shaker Verlag: Düren, Germany, 2015. [Google Scholar]
- Fritzsch, C.; Giacomozzi, F.; Karabey, O.H.; Bildik, S.; Colpo, S.; Jakoby, R. Advanced characterization of a W-band phase shifter based on liquid crystals and MEMS technology. Int. J. Microw. Wirel. Technol. 2012, 4, 379–386. [Google Scholar] [CrossRef]
- Fritzsch, C. Flüssigkristallbasierte Elektronisch Steuerbare Gruppenantennen Technologie, Konzepte und Komponenten. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2015. [Google Scholar]
- Serrano, A.L.; Franc, A.-L.; Assis, D.P.; Podevin, F.; Rehder, G.P.; Corrao, N.; Ferrari, P. Modeling and Characterization of Slow-Wave Microstrip Lines on Metallic-Nanowire- Filled-Membrane Substrate. IEEE Trans. Microw. Theory Tech. 2014, 62, 3249–3254. [Google Scholar] [CrossRef]
- International Telecommunication Union (ITU). MT Vision—Framework and Overall Objectives of the Future Development of IMT for 2020 and beyond; Recommendation ITU-R M.2083-0; International Telecommunication Union (ITU): Geneva, Switzerland, 2015. [Google Scholar]
- FP7 METIS (ICT 317669). Available online: https://www.metis2020.com/documents/deliverables/ (accessed on 5 June 2020).
- International Telecommunication Union (ITU). IMT Traffic Estimates for the Years 2020 to 2030; Report ITU-R M.2370-0; Electronic Publication of ITU: Geneva, Switzerland, 2015. [Google Scholar]
- Martin, K.; O’Keefe, K.; Finucan, L. Emerging Technologies and the Global Regulatory Agenda. May 2016. Available online: https://www.itu.int/en/ITU-D/Conferences/GSR/Documents/ITU_EmergingTech_GSR16.pdf (accessed on 5 June 2020).
- International Telecommunication Union (ITU). Future Technology Trends of Terrestrial IMT Systems; Recommendation ITU-R M.2320-0; Electronic Publication of ITU: Geneva, Switzerland, 2014. [Google Scholar]
- 5G Frequenzen. Available online: https://www.5g-anbieter.info/technik/5g-frequenzen.html (accessed on 5 June 2020).
- International Telecommunication Union (ITU). Technical Feasibility of IMT in Bands above 6 GHz; Recommendation ITU-R M.2376-0; Electronic Publication of ITU: Geneva, Switzerland, 2015. [Google Scholar]
- Rappaport, T.S.; Heath, R.W., Jr.; Daniels, R.C.; Murdock, J.N. Millimeter Wave Wireless Communications; Prentice Hall: Upper Saddle River, NJ, USA, 2015; ISBN 10-0132172283. [Google Scholar]
- Spectrum Frontiers: The New World of Millimeter-Wave Mobile Communication. 2016. Available online: https://transition.fcc.gov/oet/5G/Workshop/Keynote%20Rappaport%20NYU.pdf (accessed on 5 June 2020).
- ETSI Work Programme 2016–2017. Available online: http://www.etsi.org/images/files/WorkProgramme/etsi-work-programme-2016-2017.pdf (accessed on 5 June 2020).
- 5G: A Technology Vision—Huawei. Available online: www.huawei.com/ilink/en/download/HW_314849 (accessed on 5 June 2020).
- Tripathi, S.R.; Khaparde, S. Analysis and Survey on Past, Present and Future Generation in Mobile communication. J. Comput. Eng. (IOSR-JCE) 2016, 30–36. Available online: www.iosrjournals.org (accessed on 5 June 2020).
- Rafay, A. Evolution of Wireless Technologies. Available online: https://www.linkedin.com/pulse/evolution-wireless-technologies-arqam-rafay?articleId=7418986240225826962 (accessed on 5 June 2020).
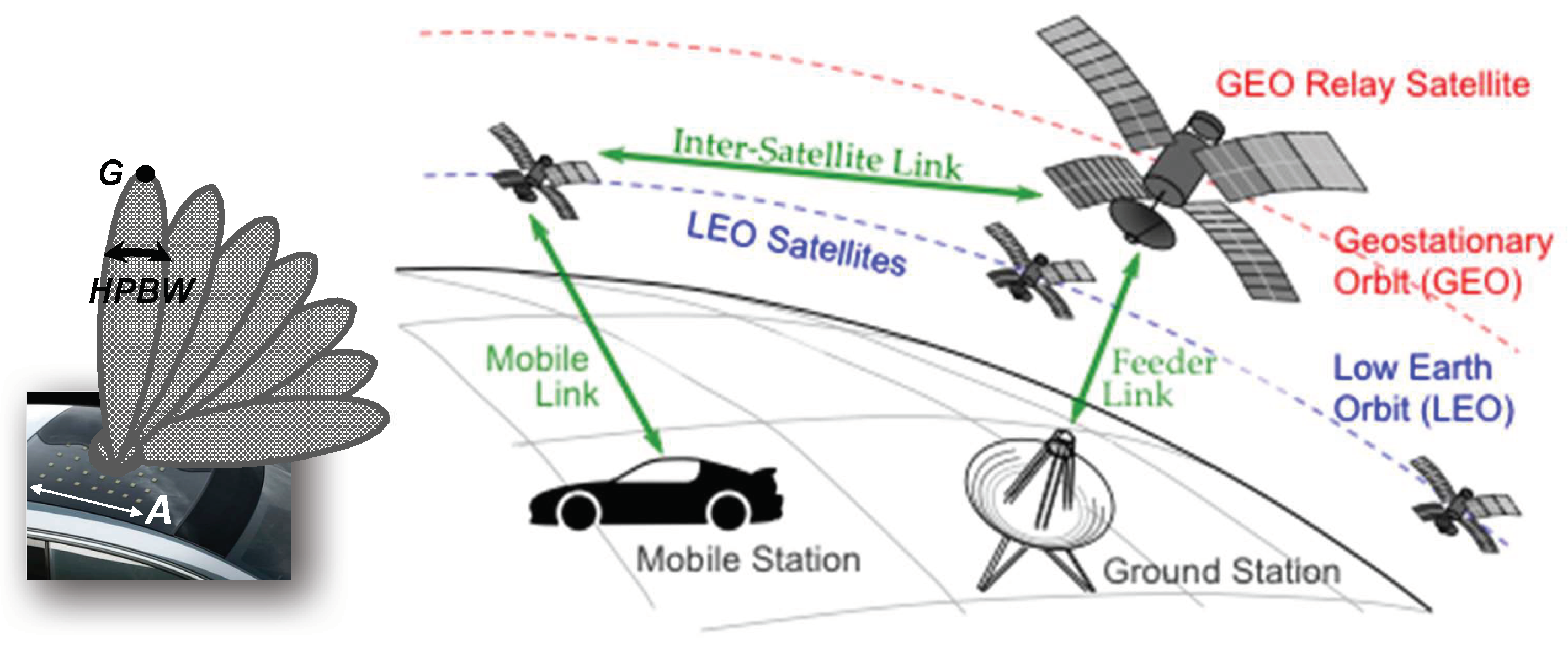
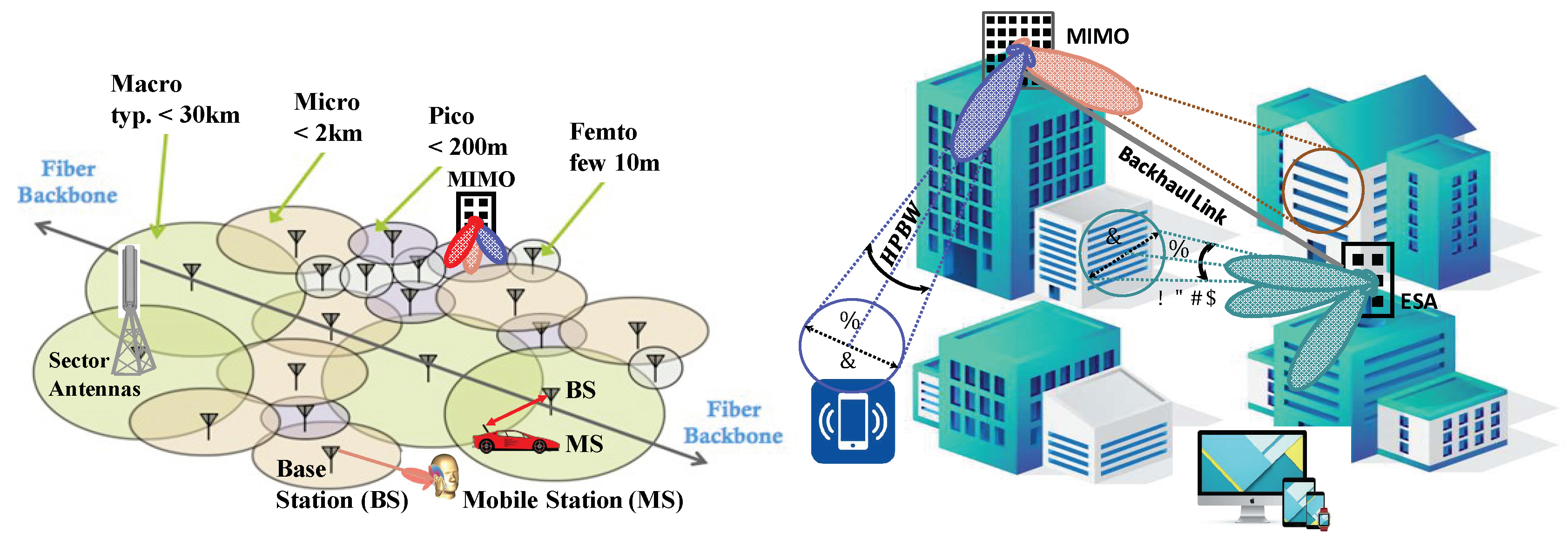
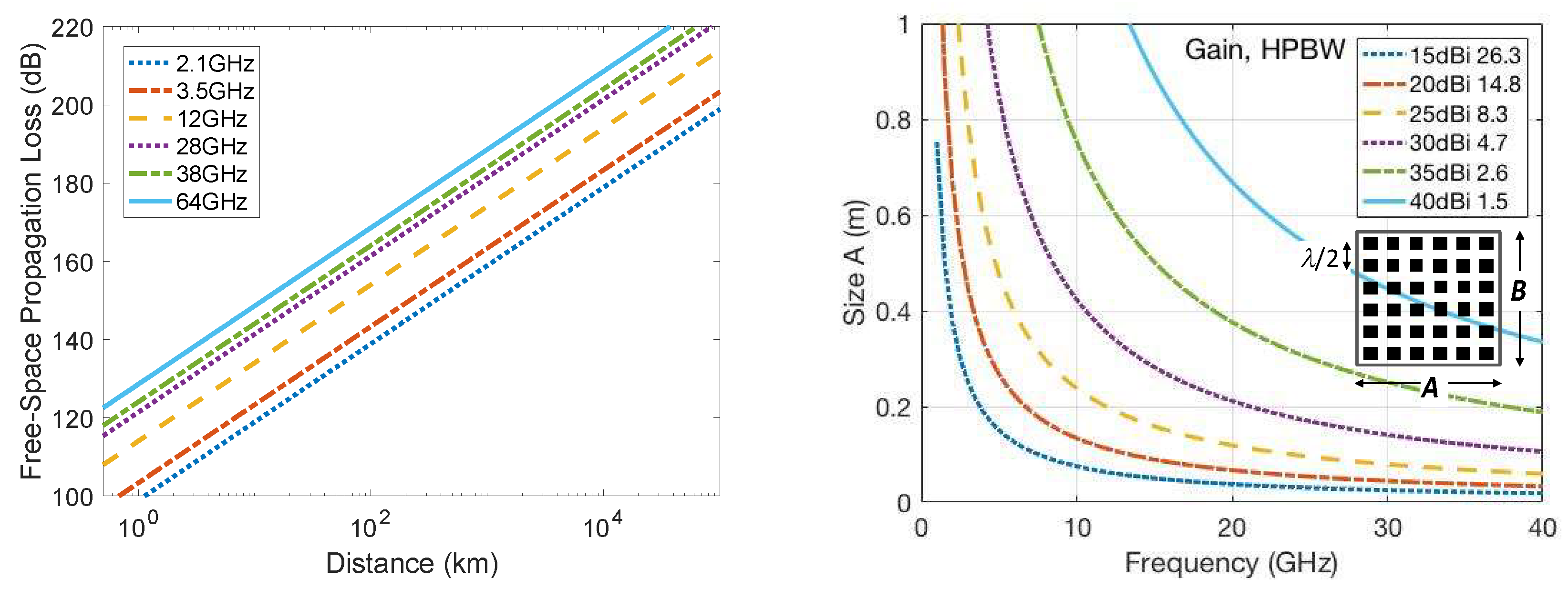
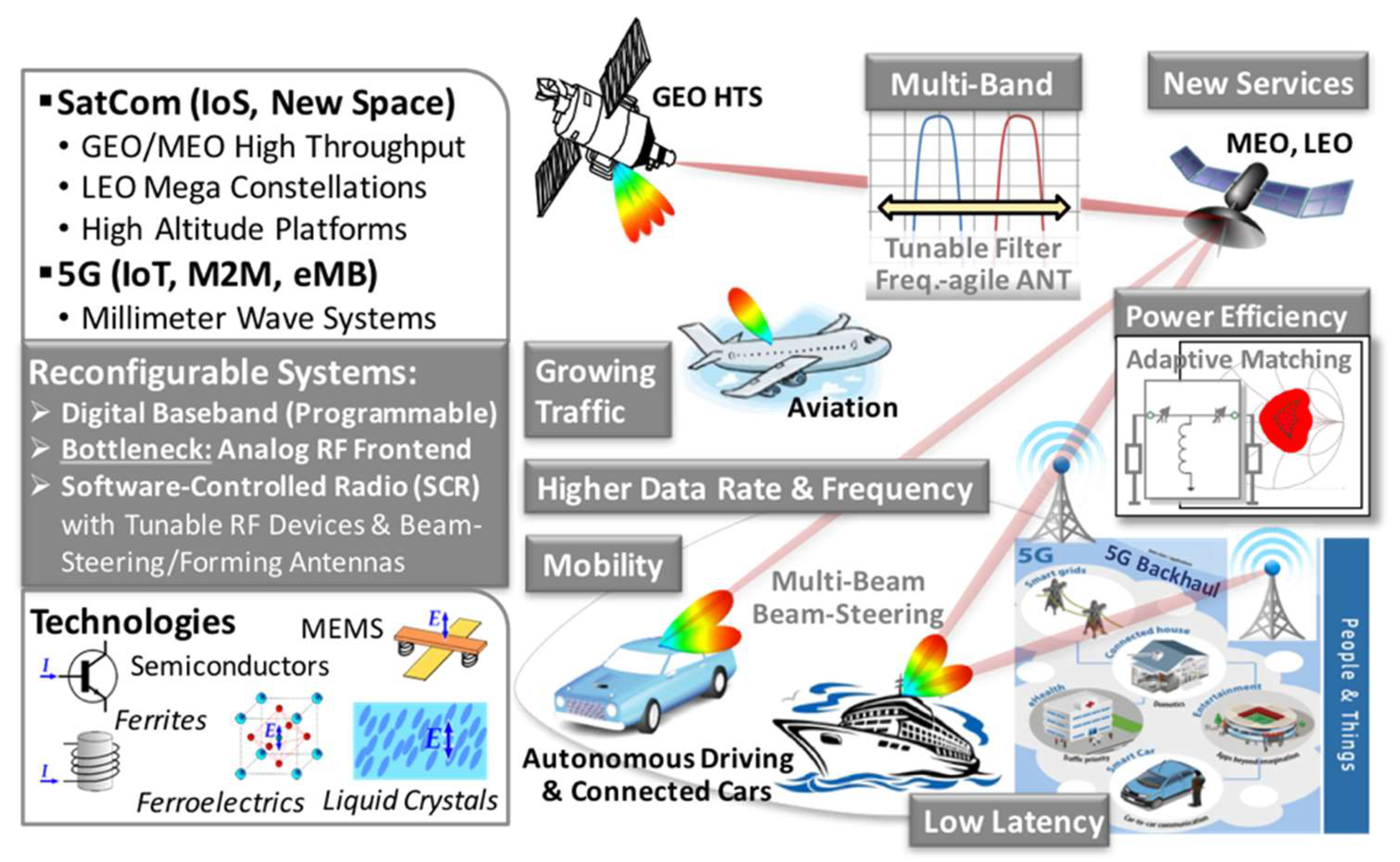
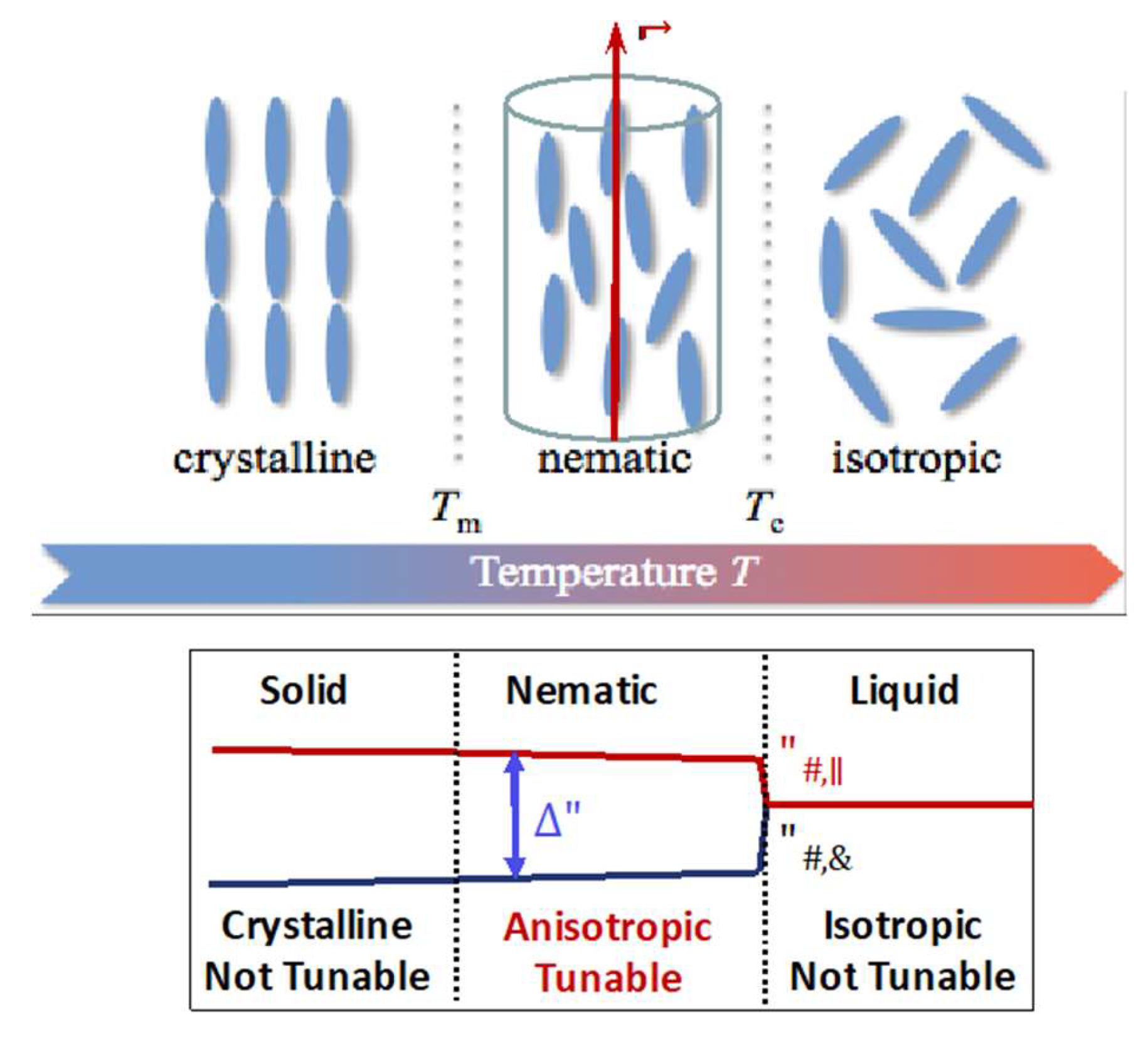
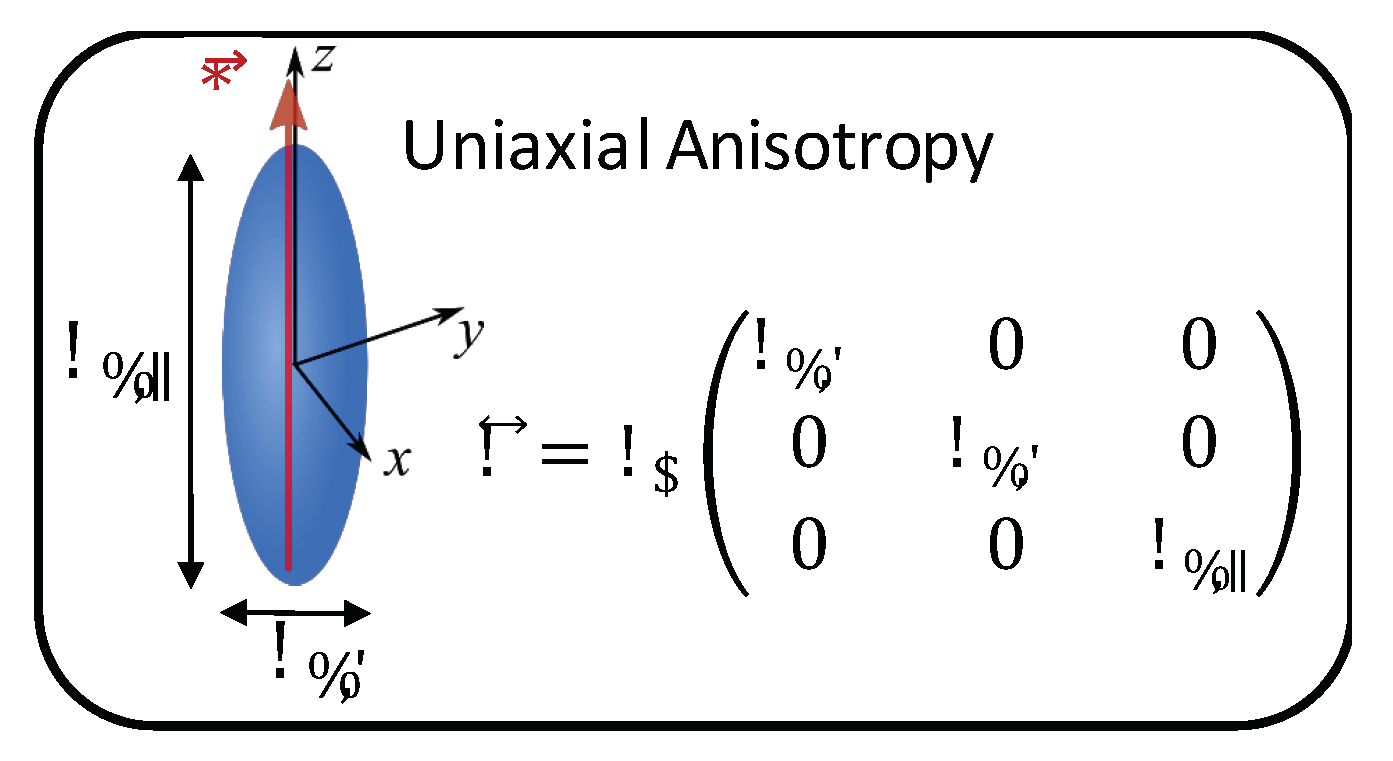
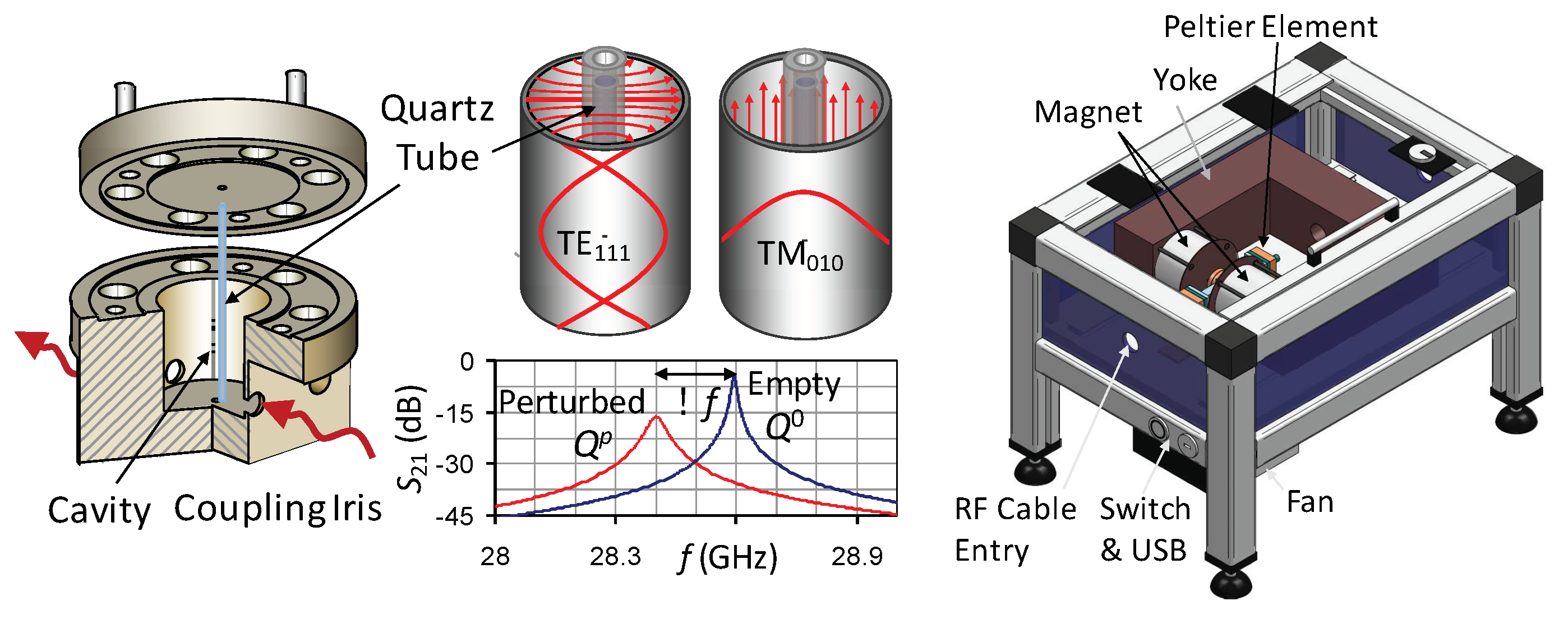
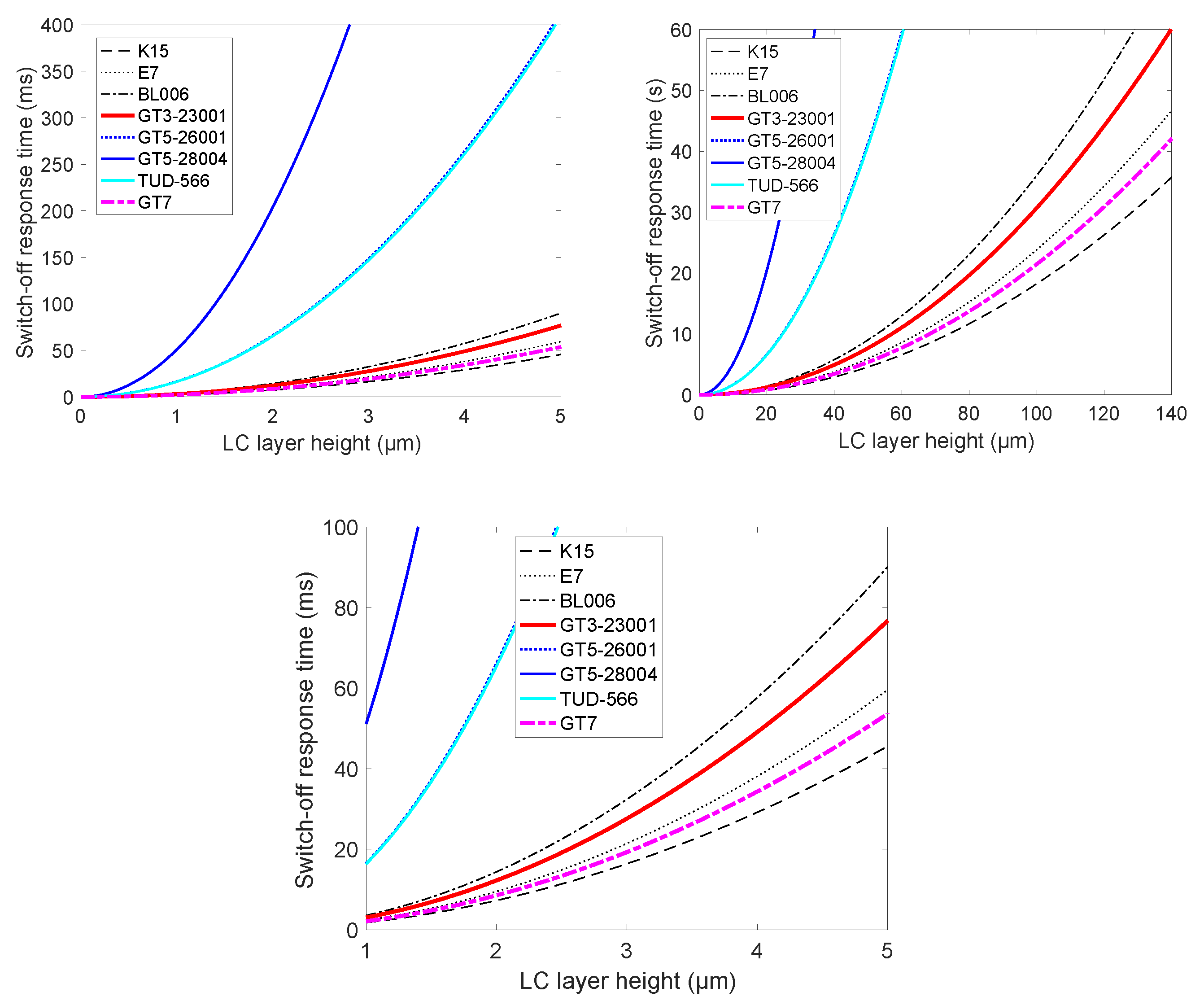
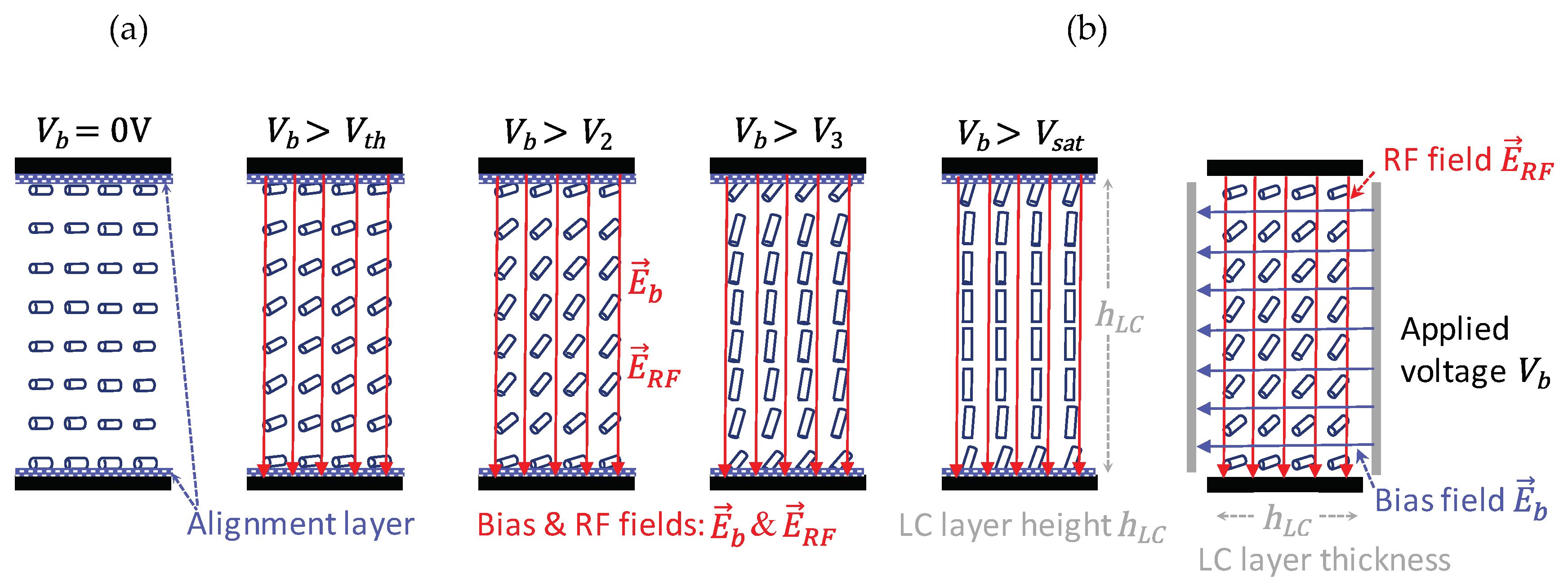
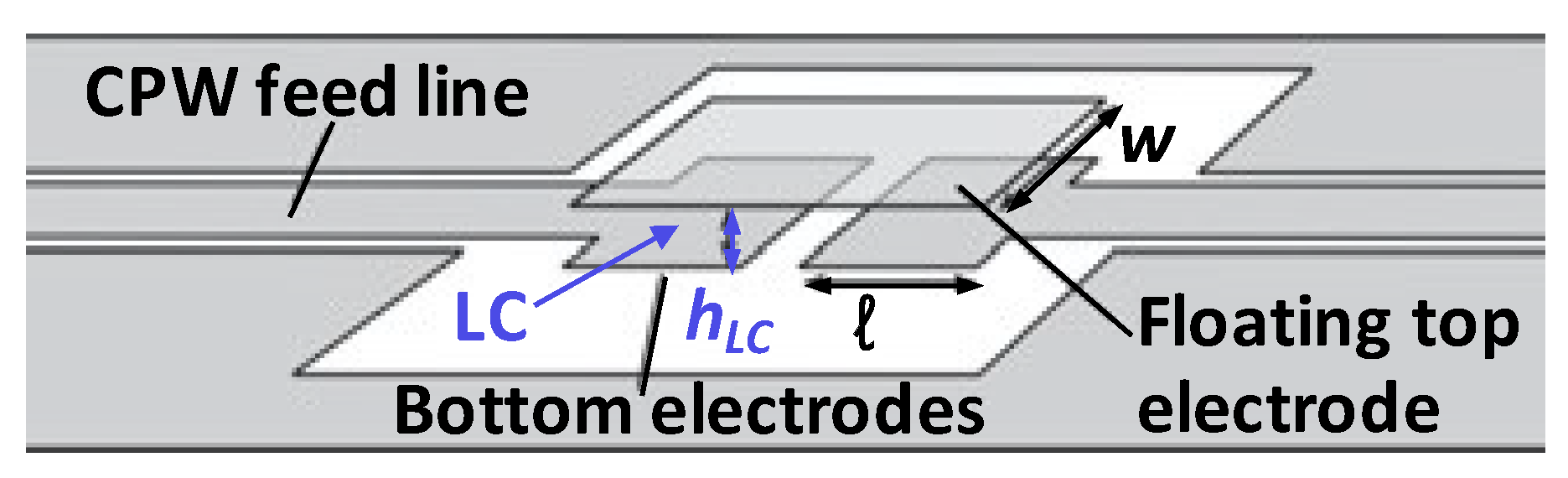
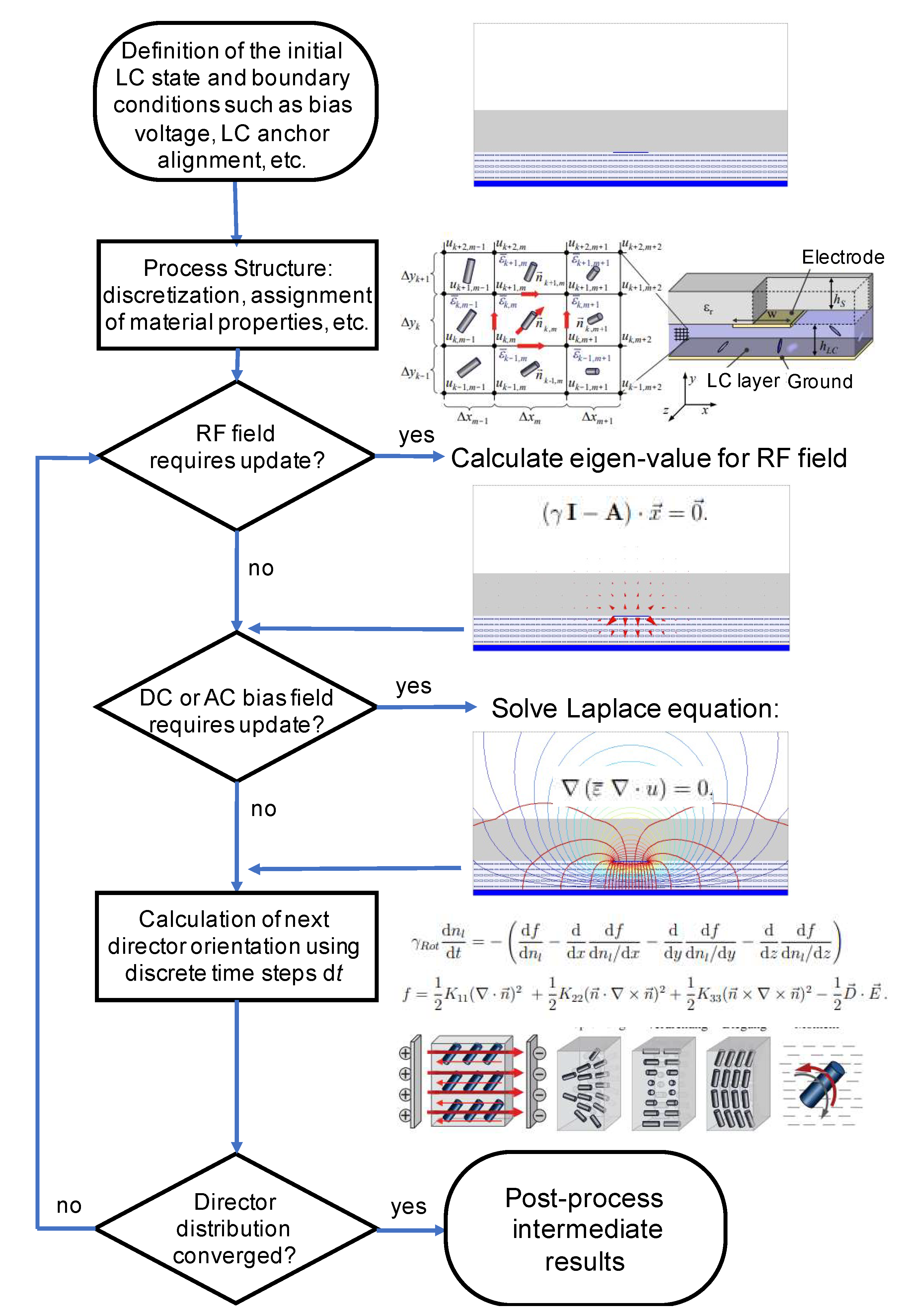
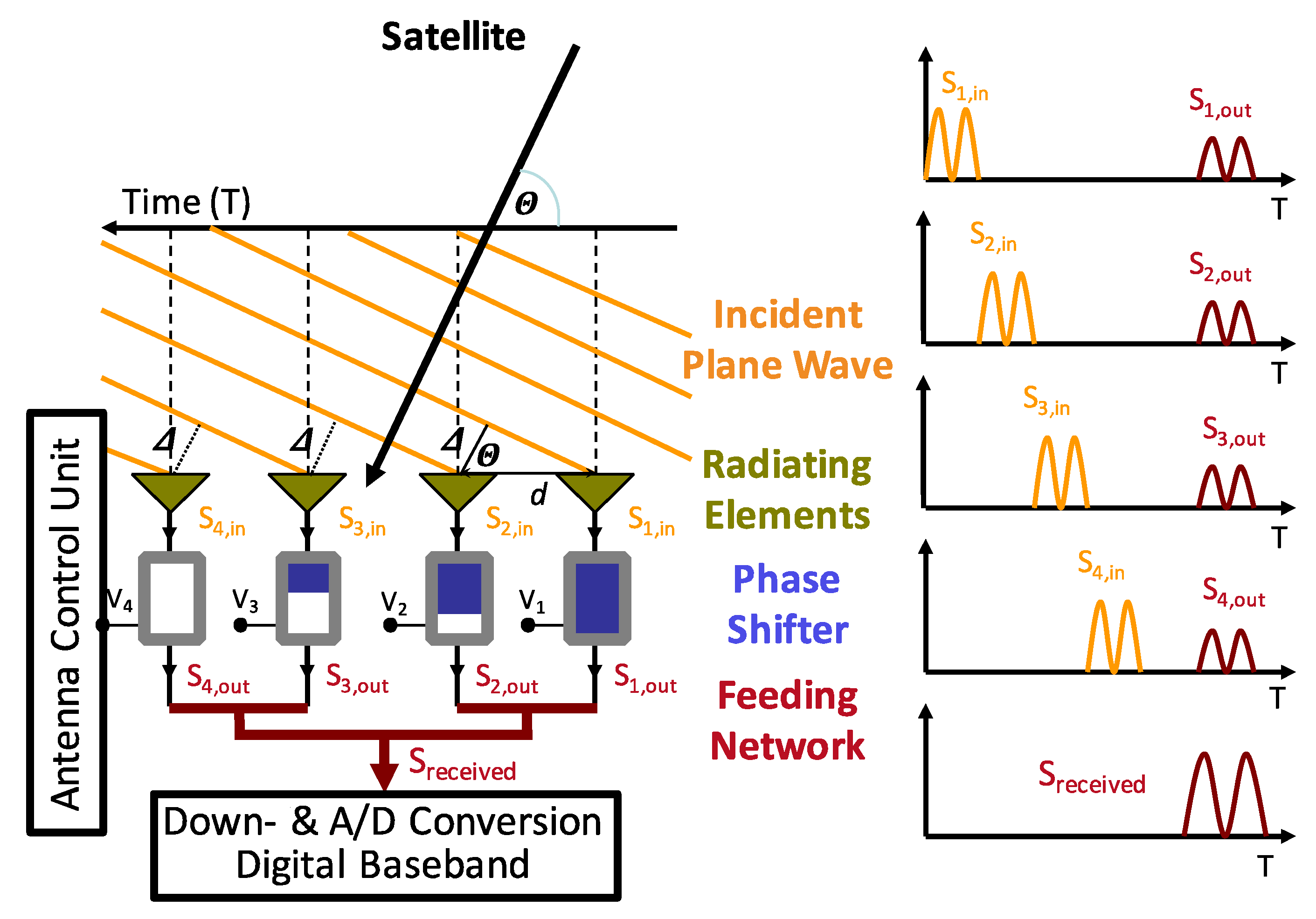
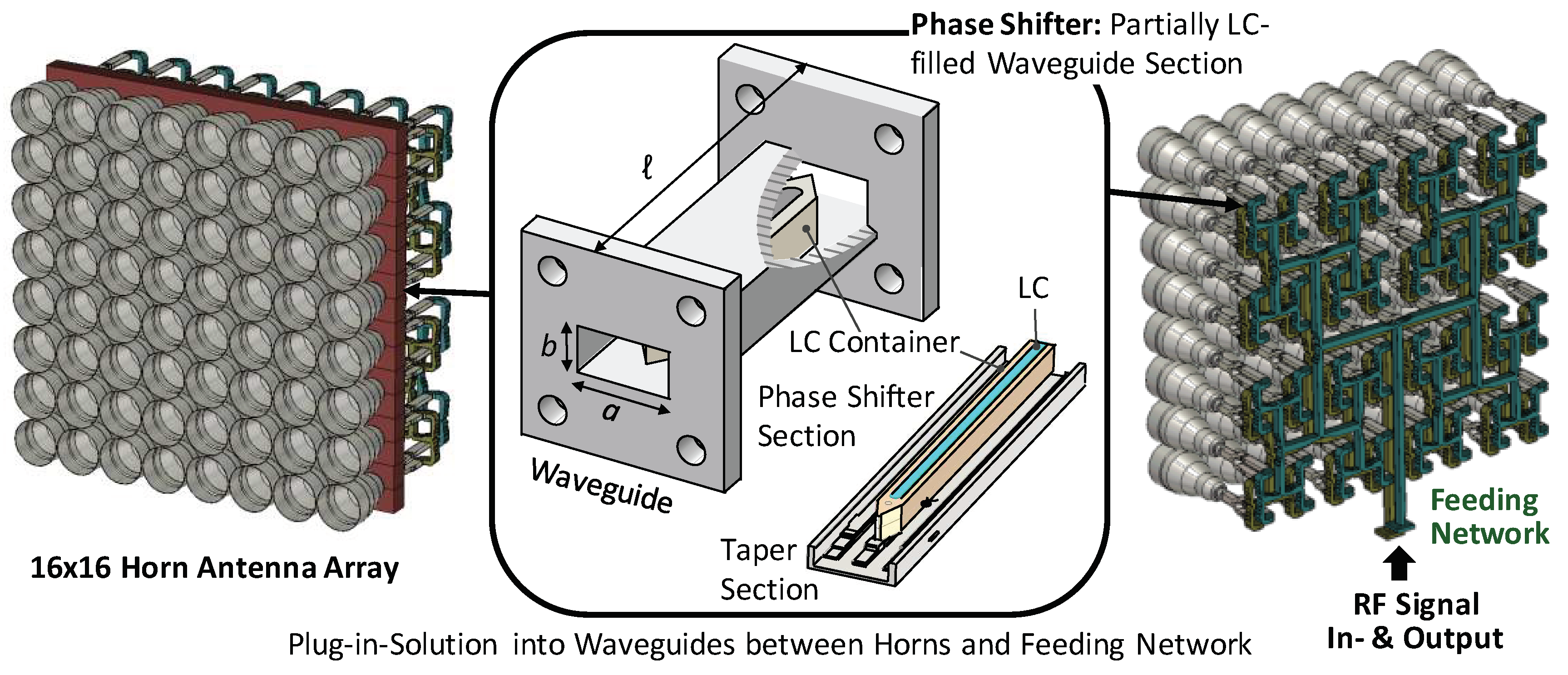
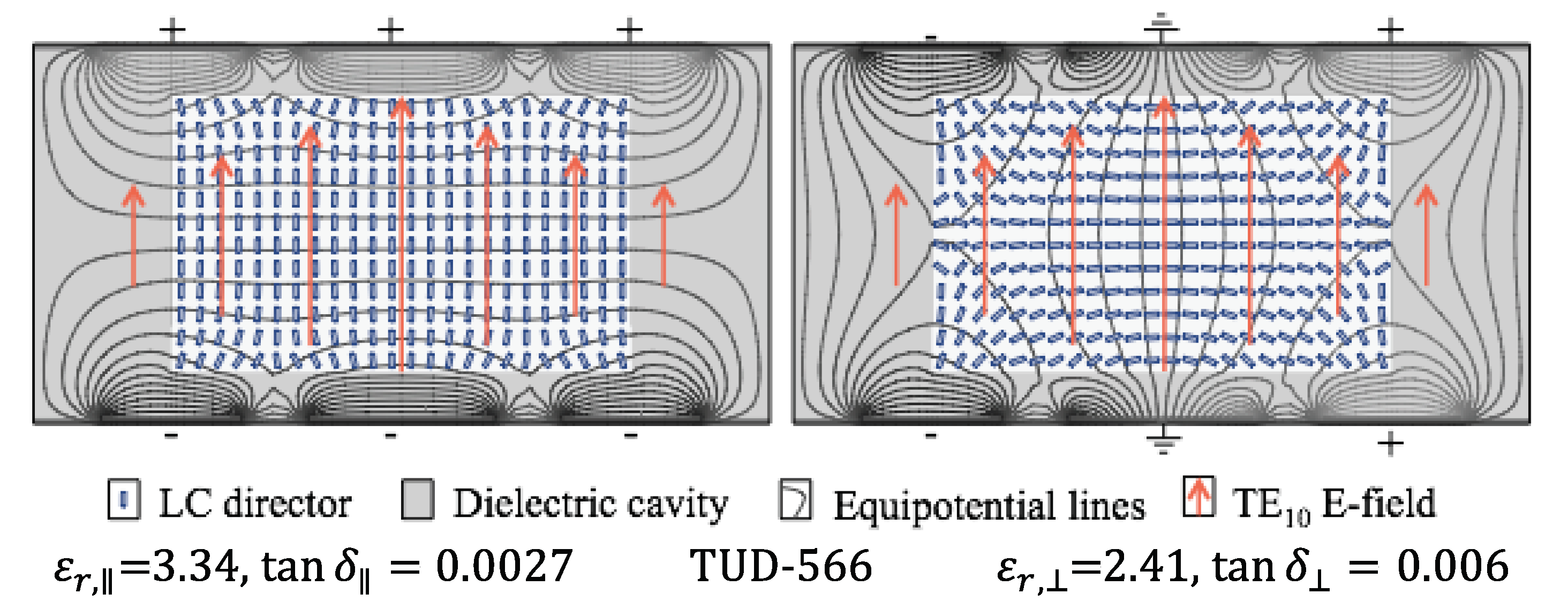
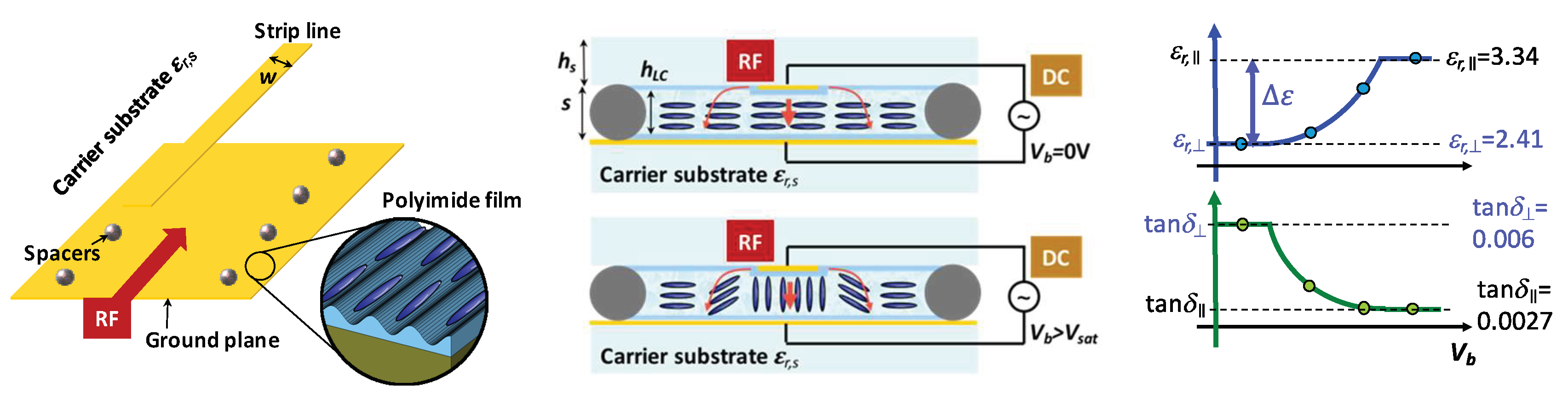
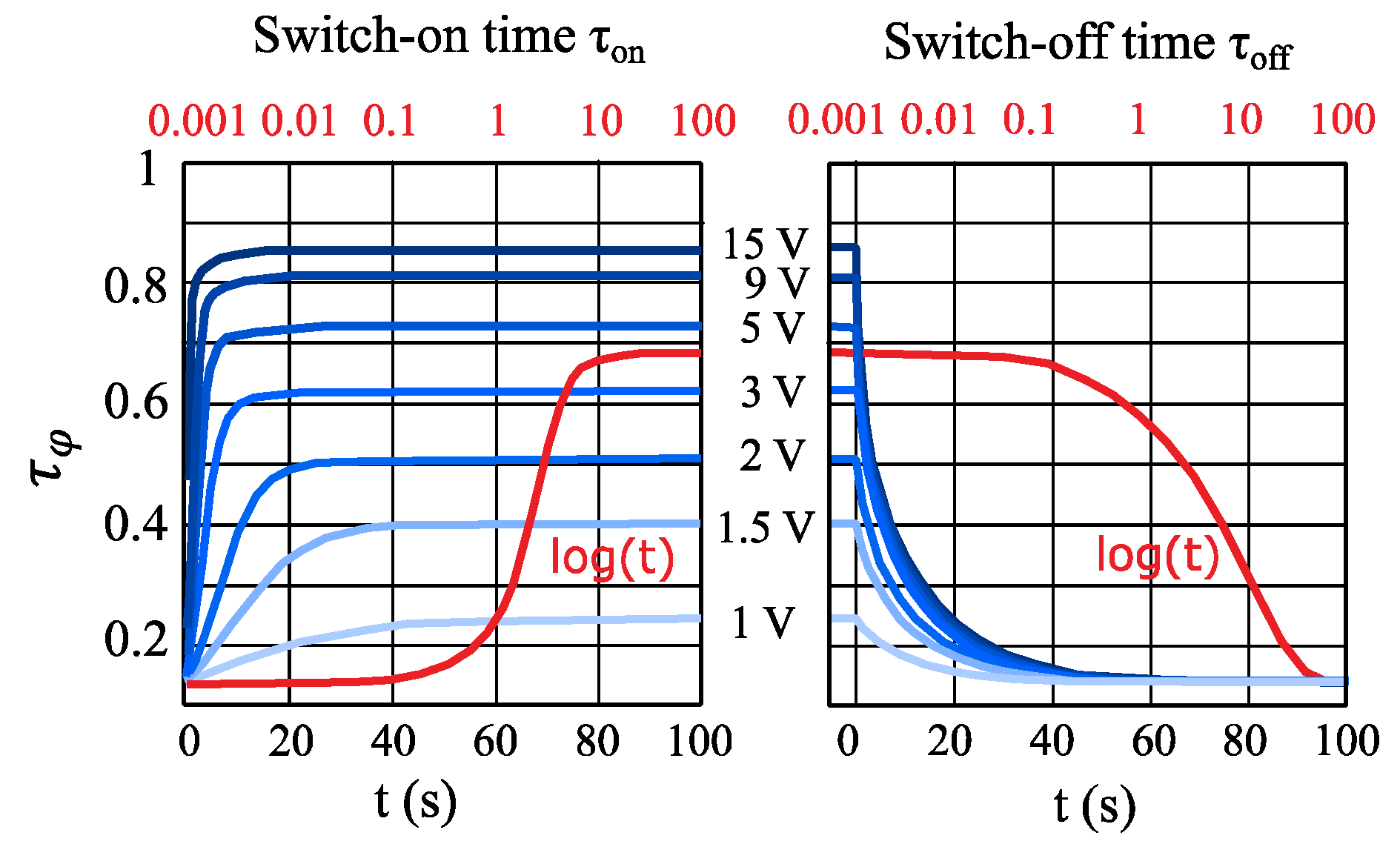
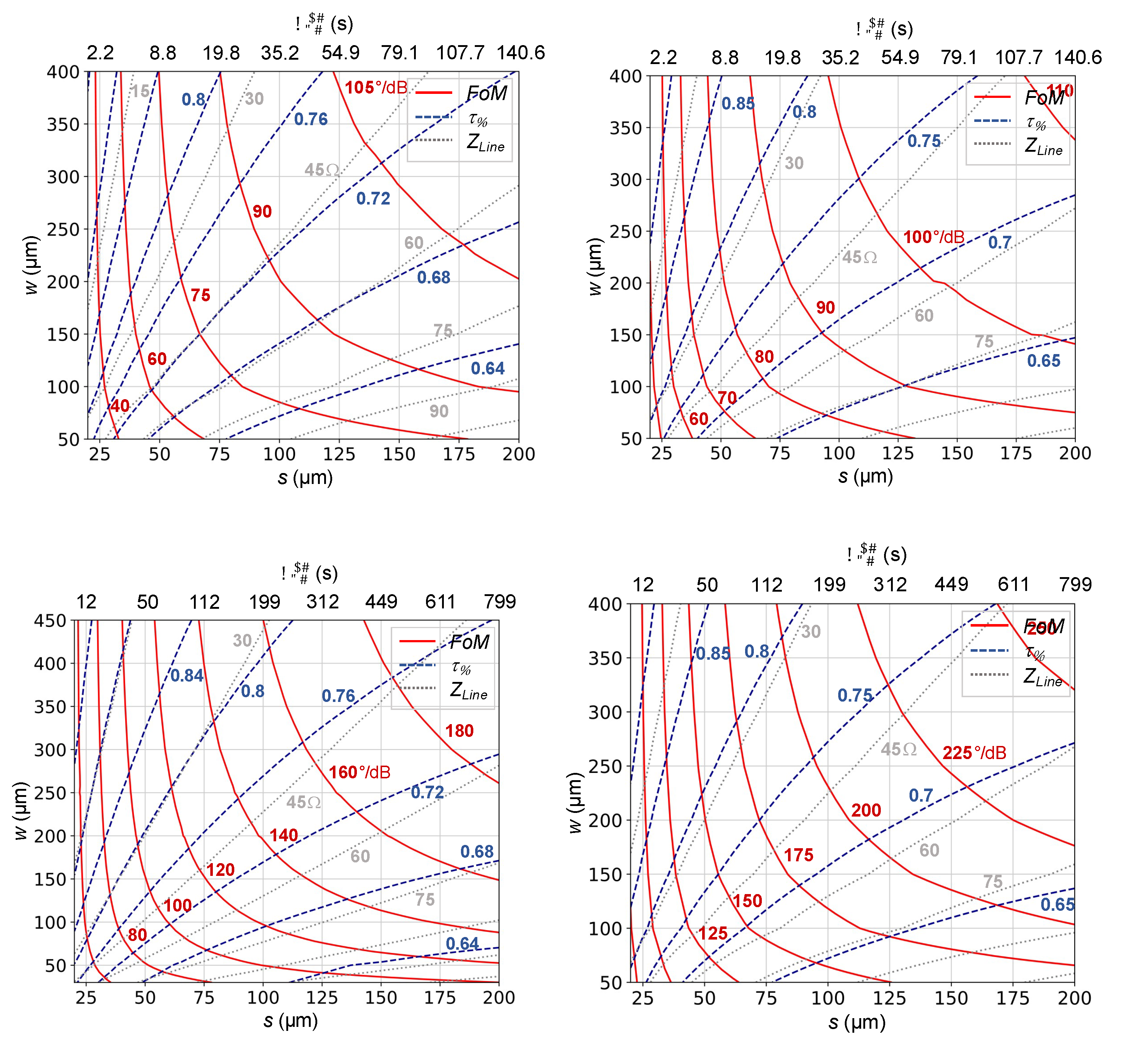
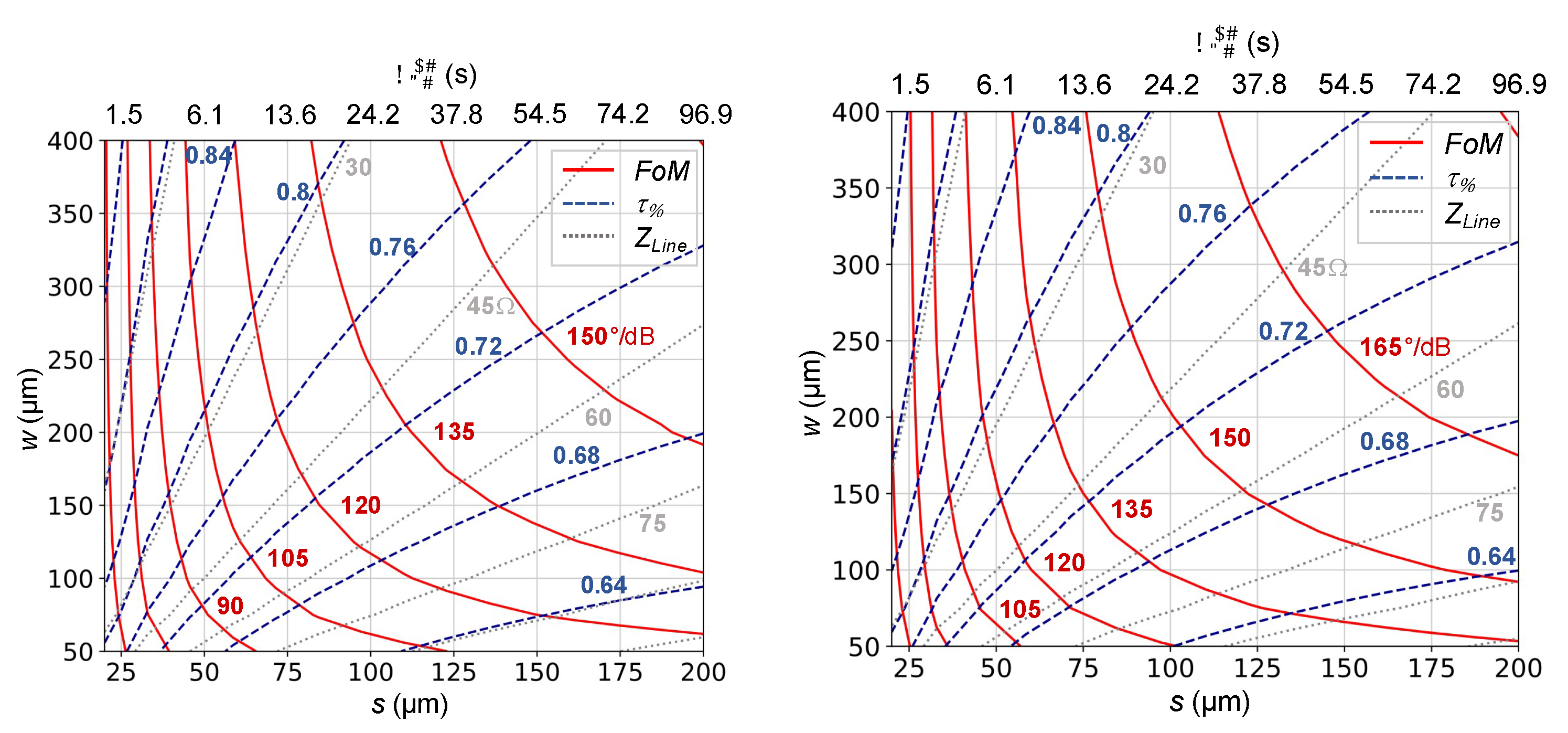
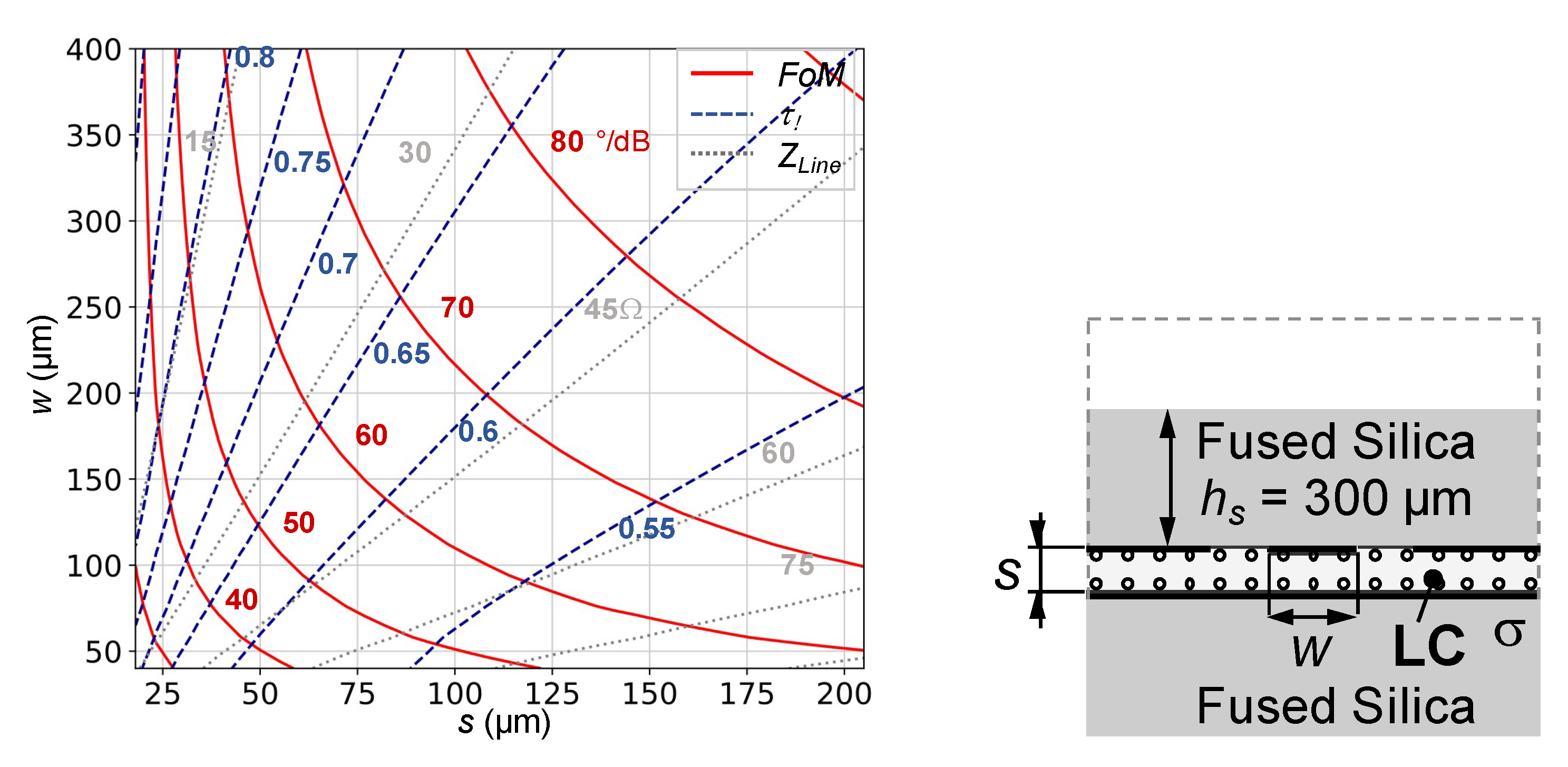

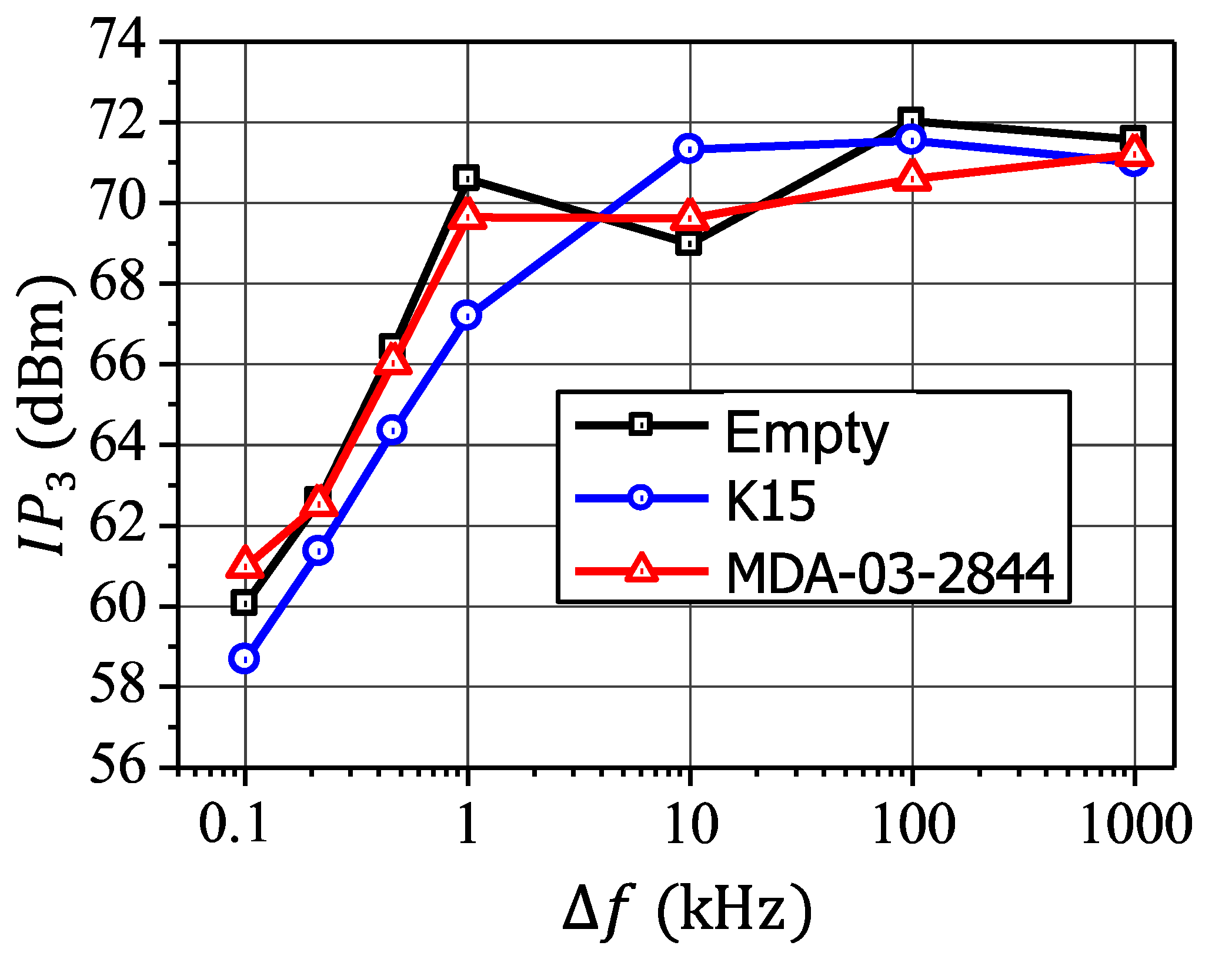
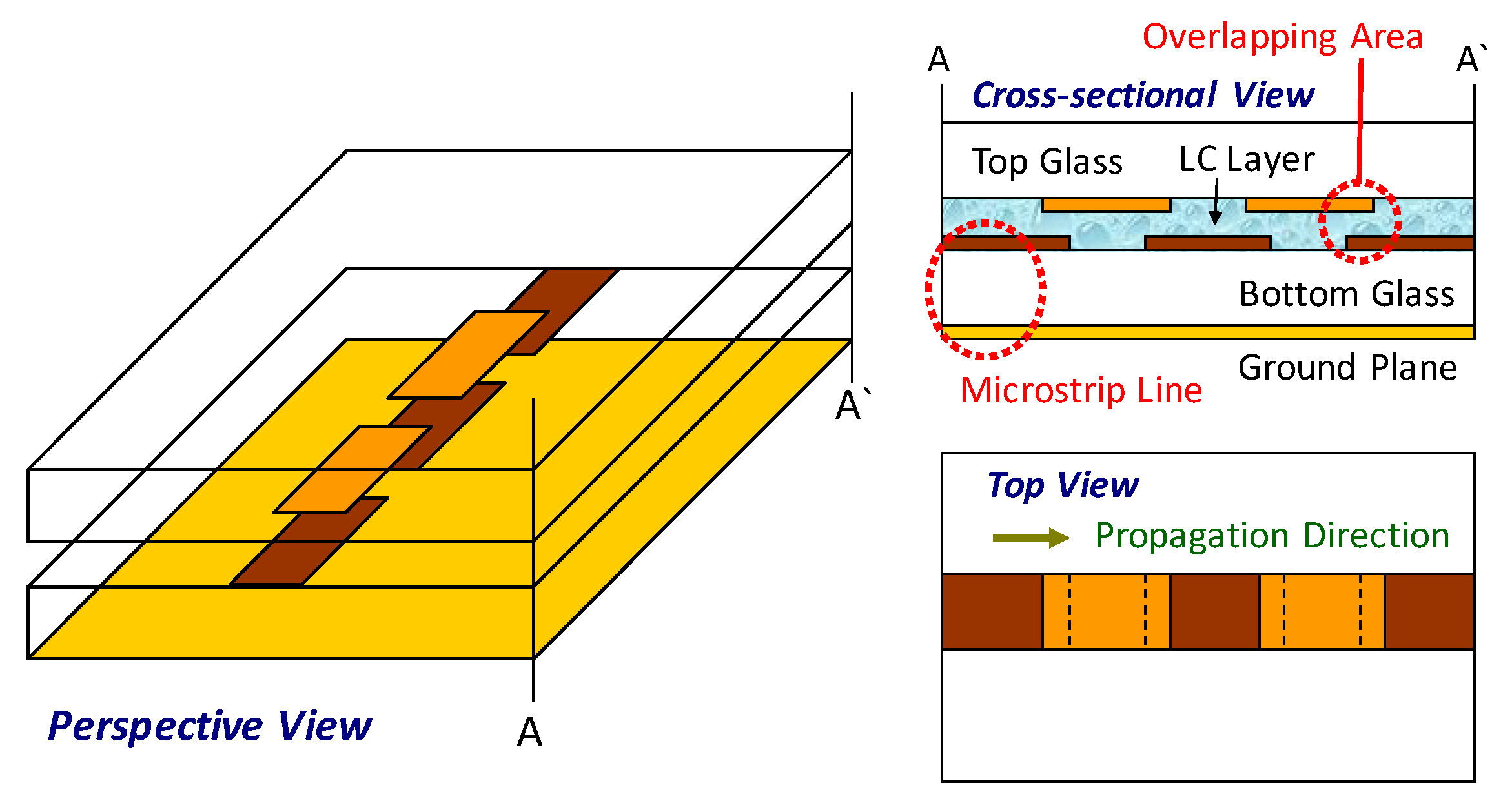
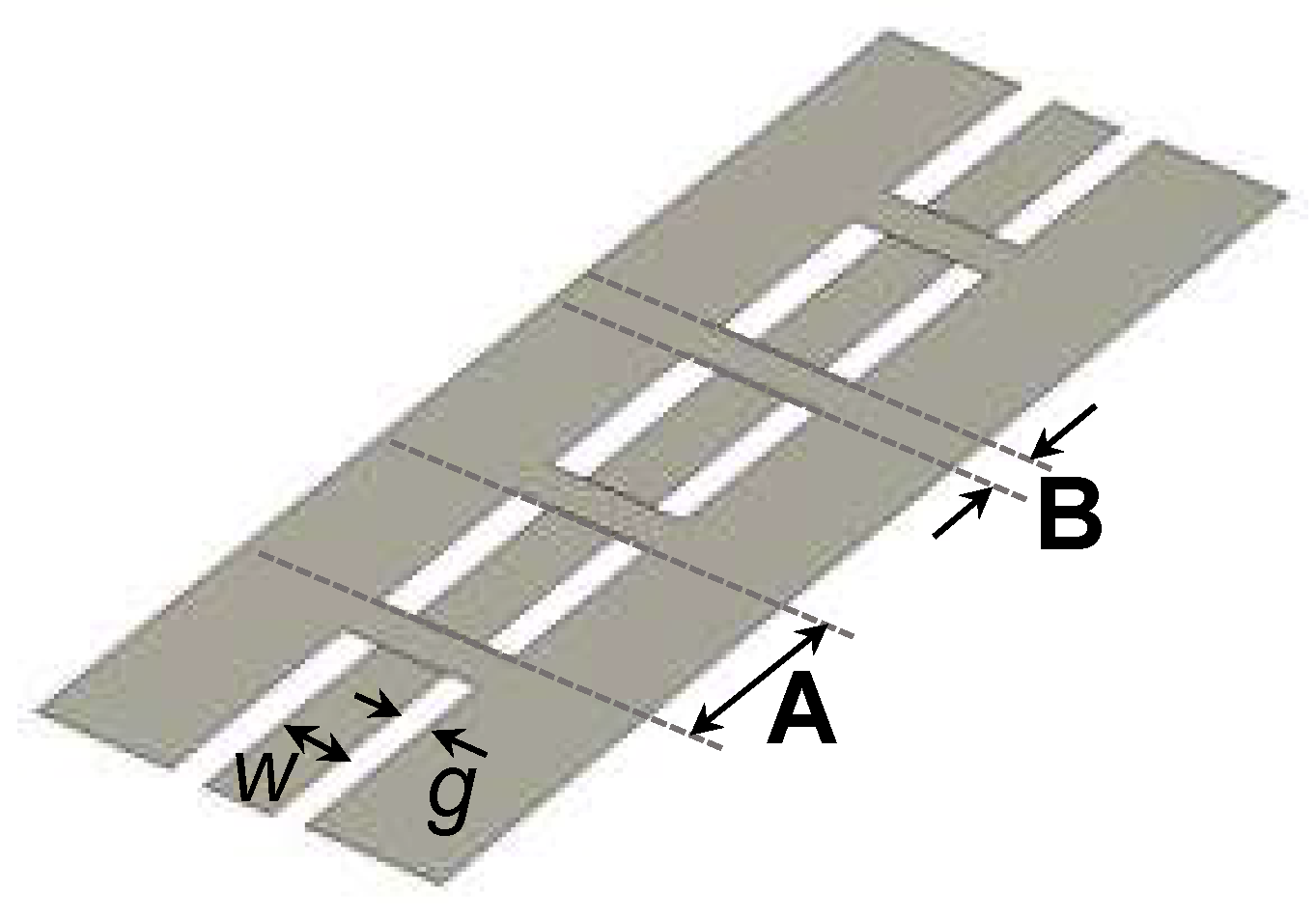
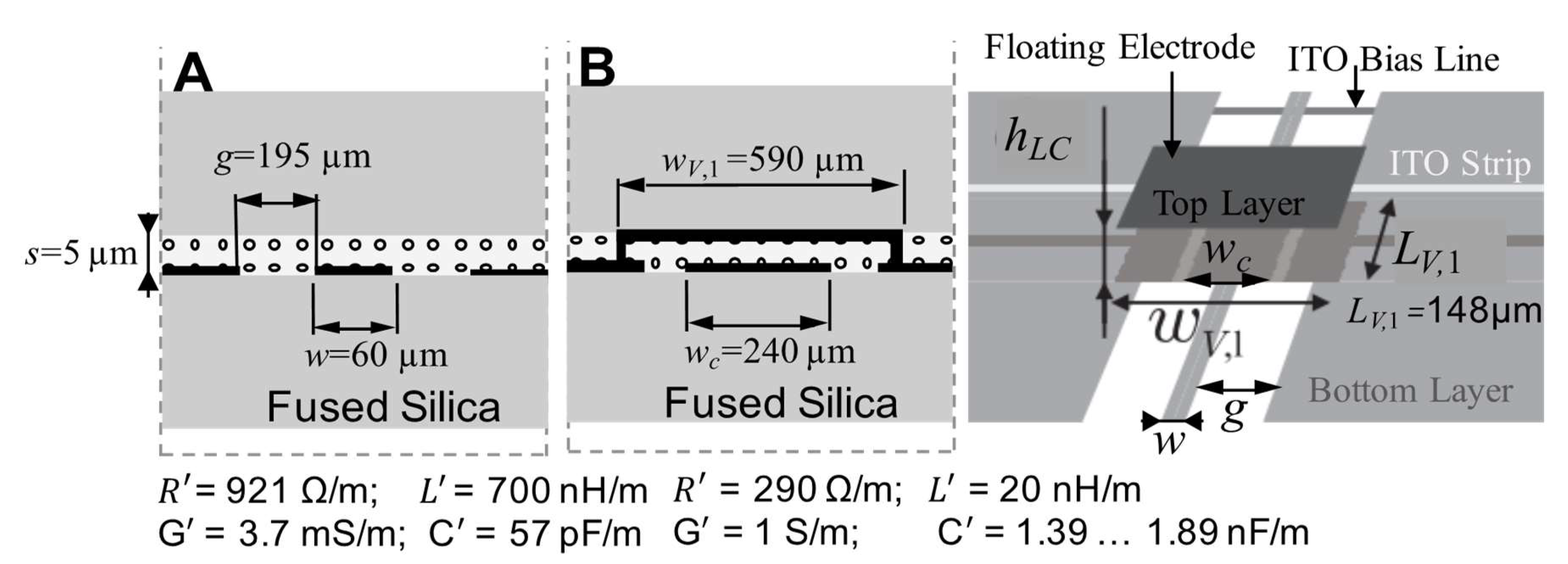
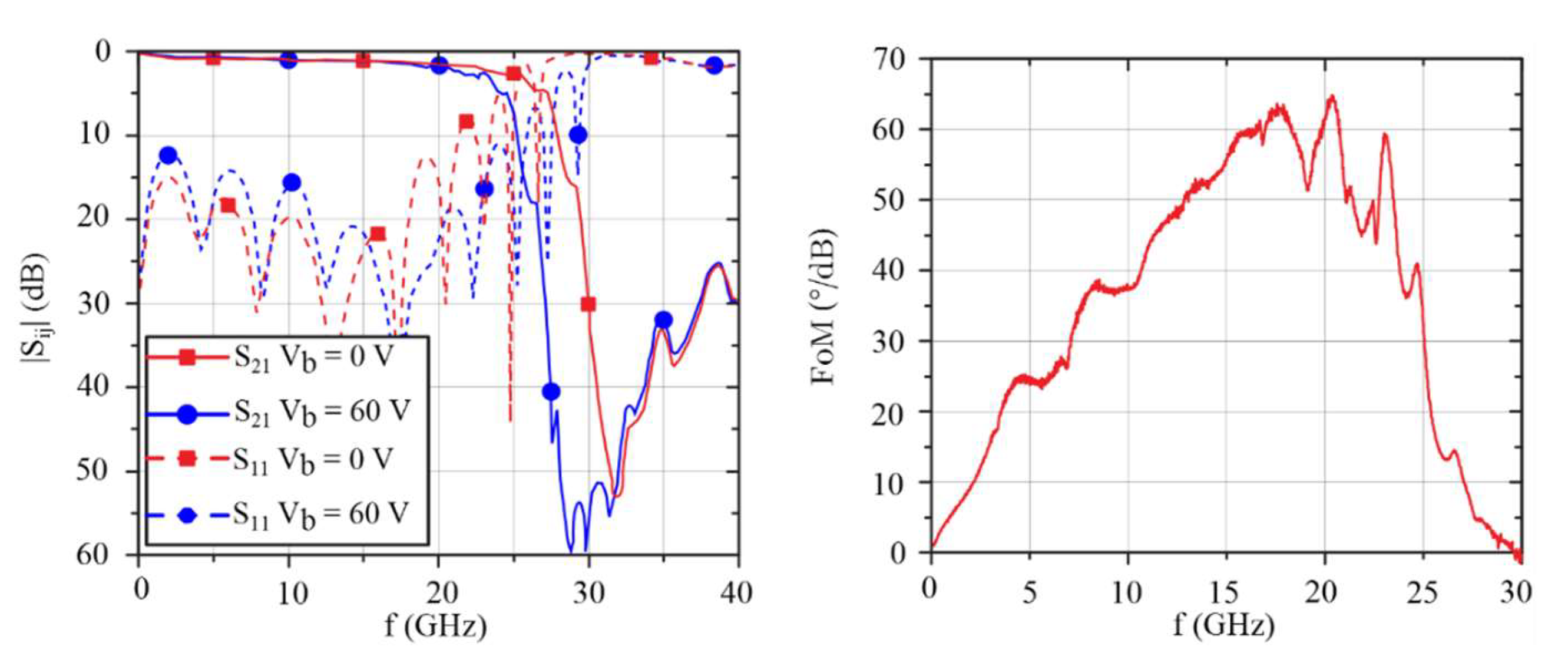
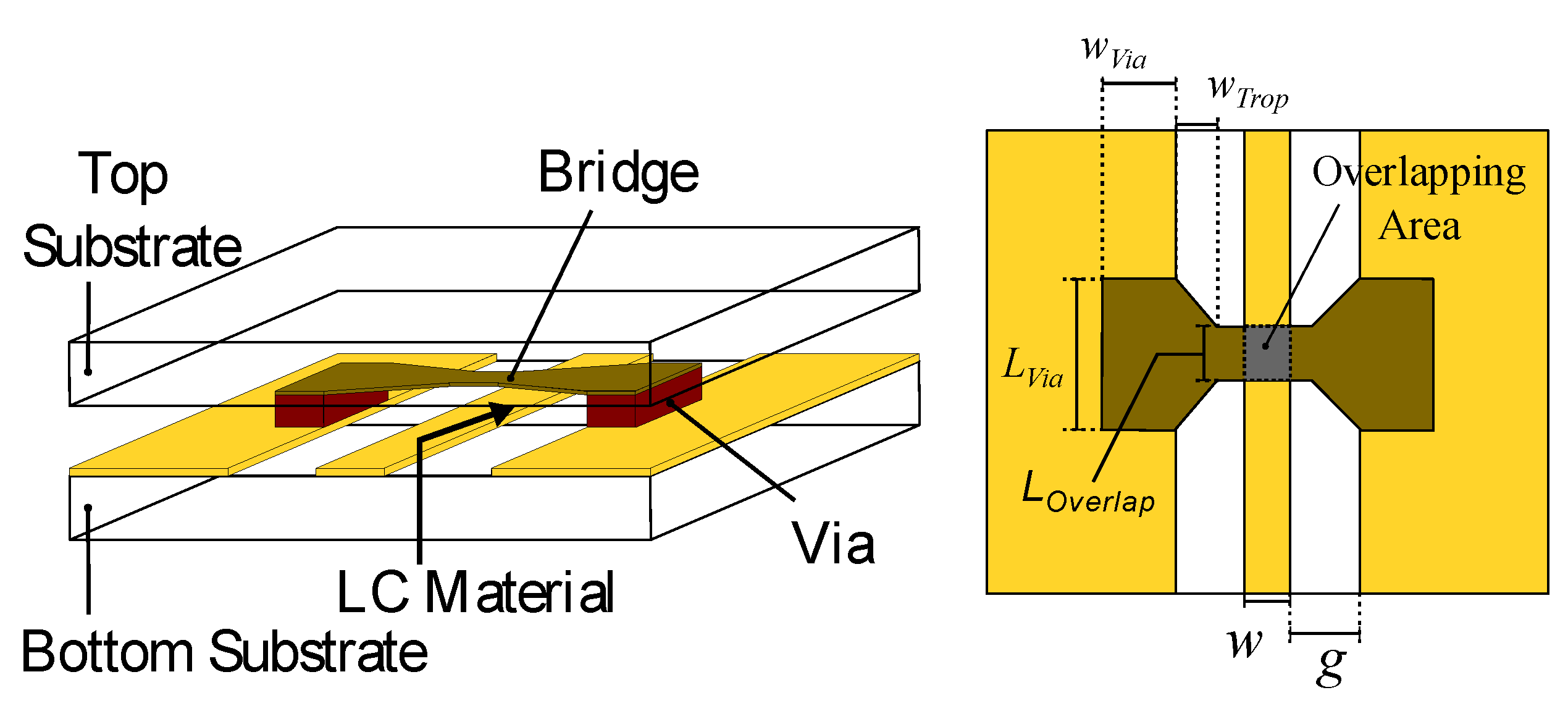
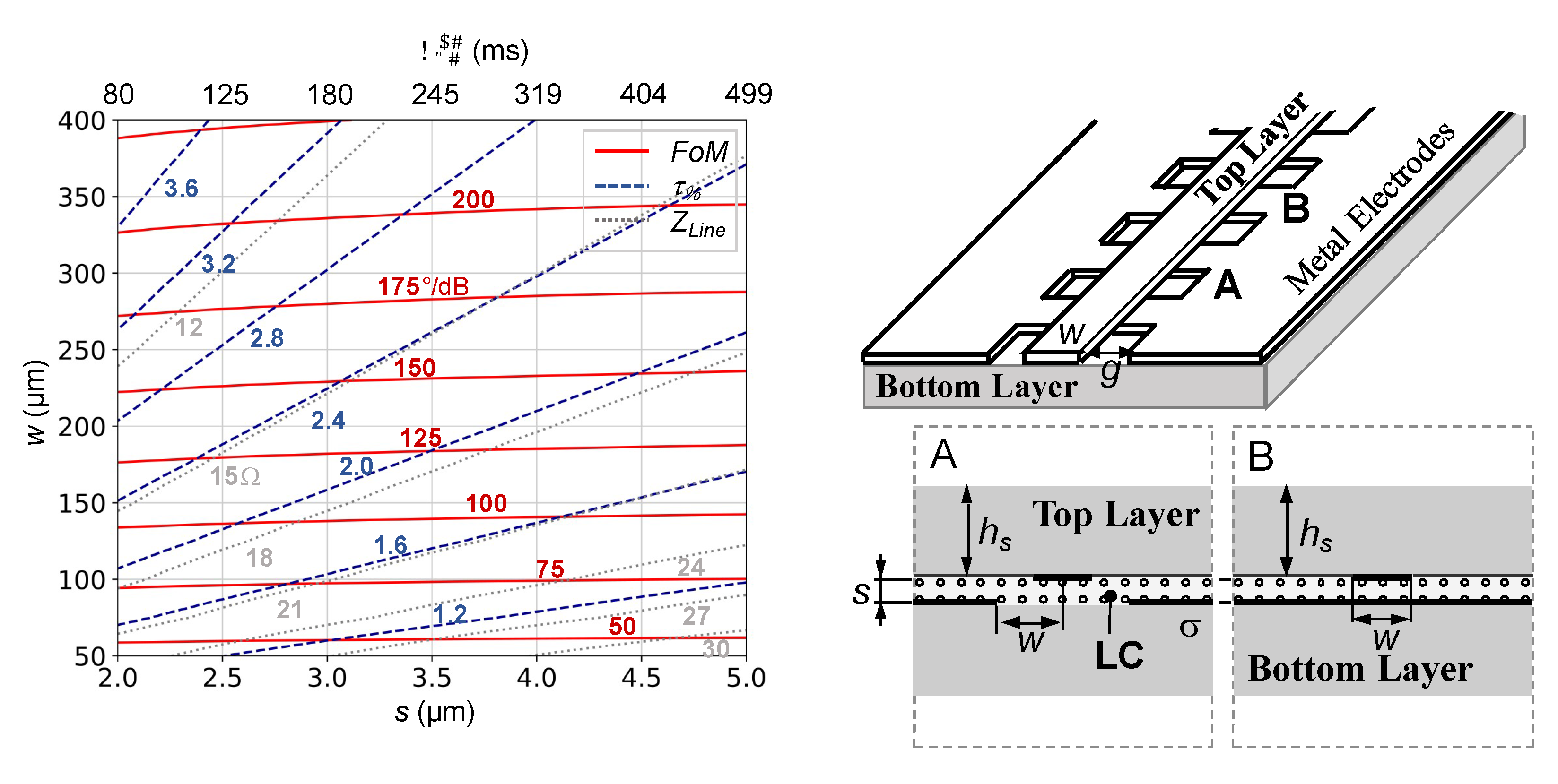
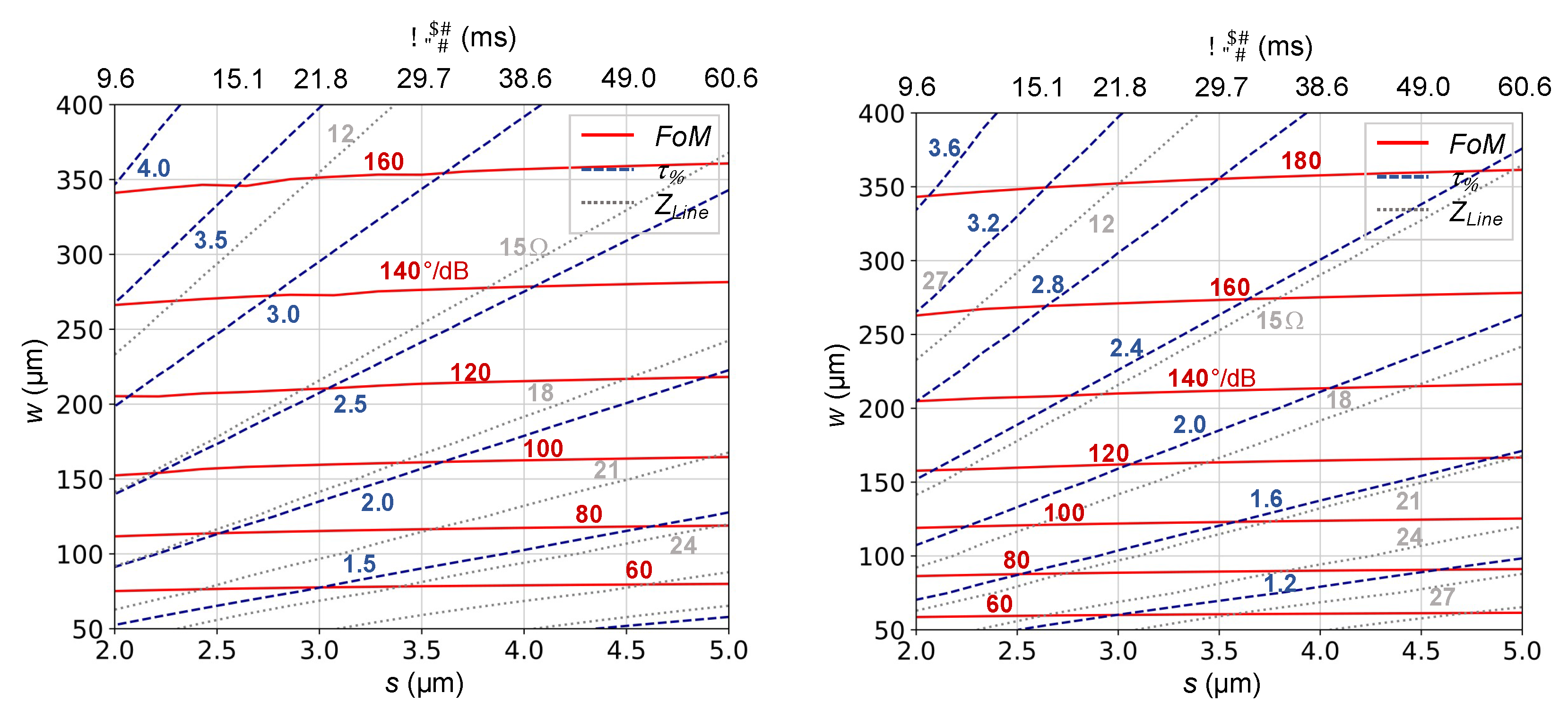
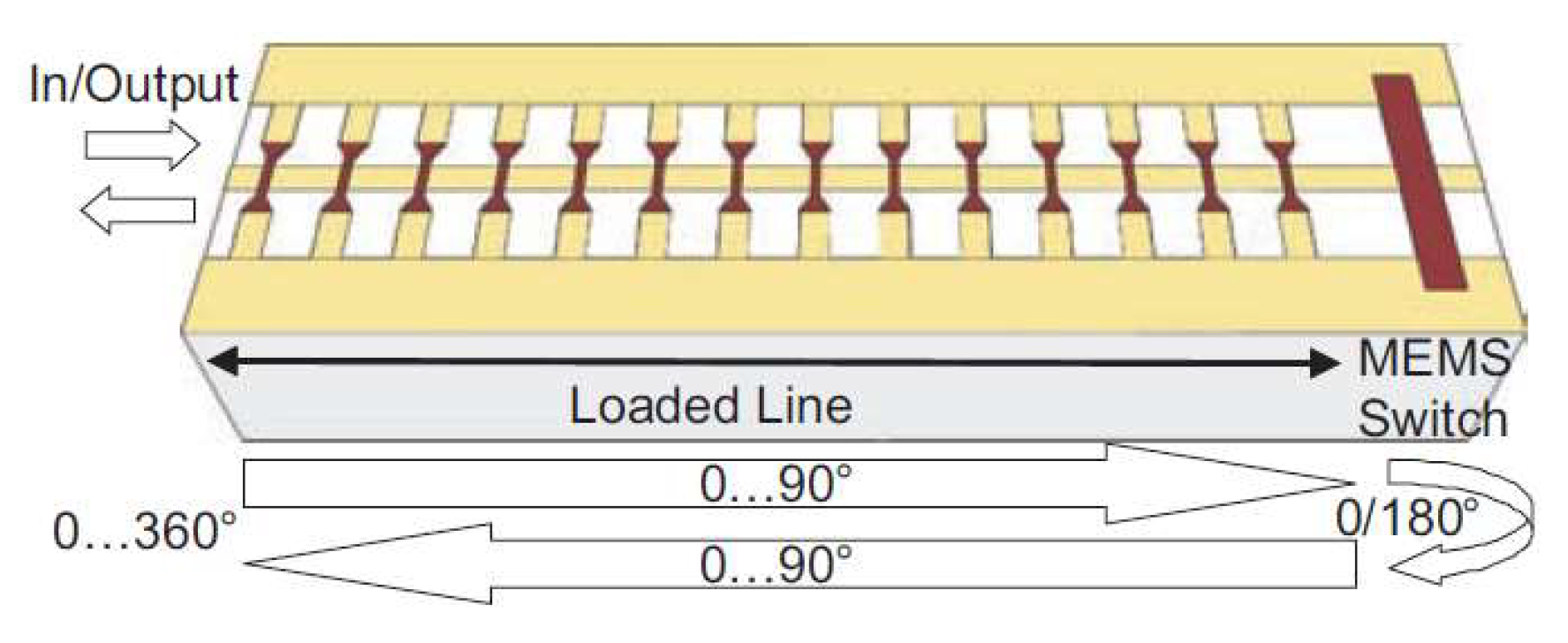
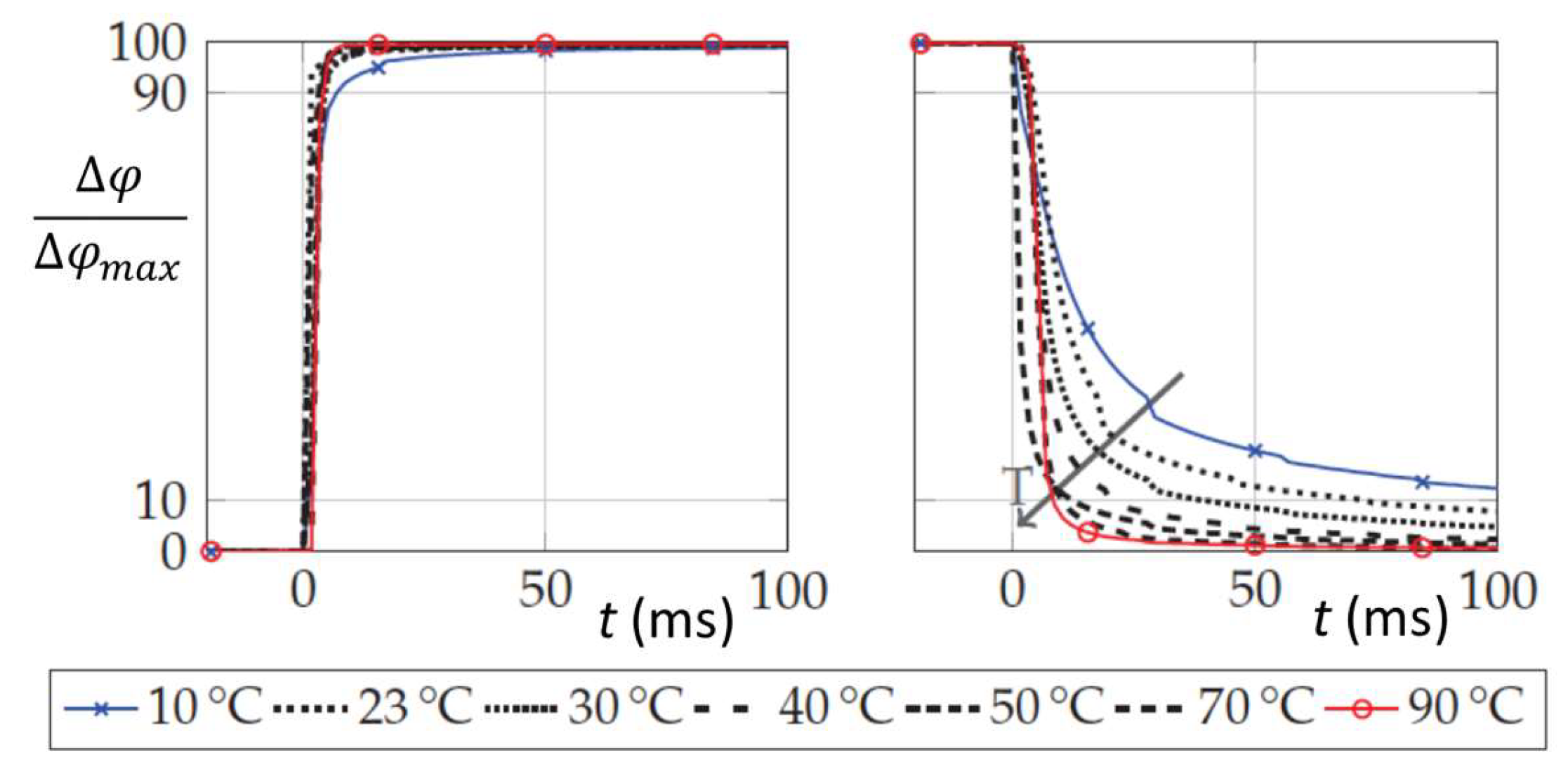
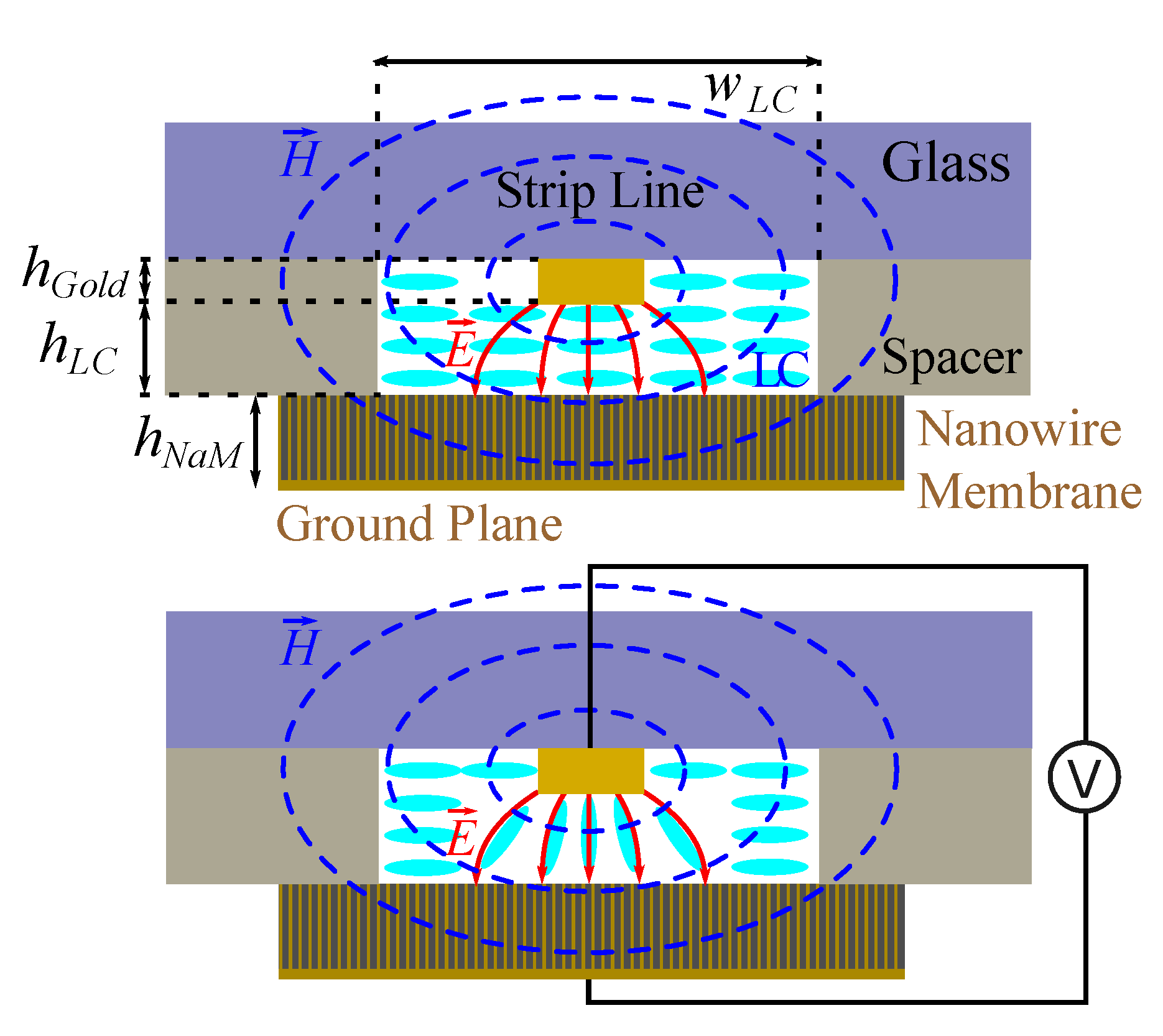

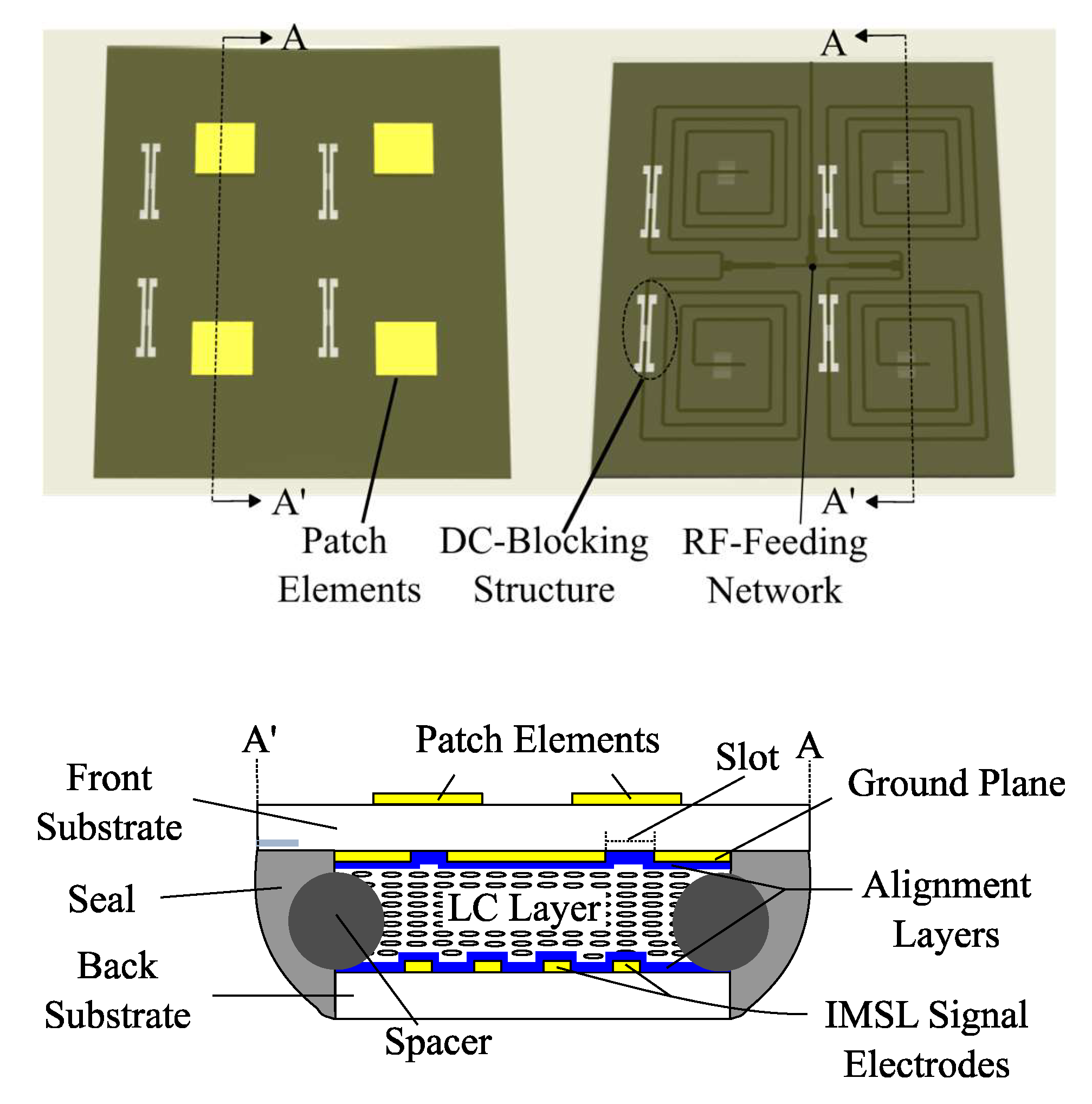
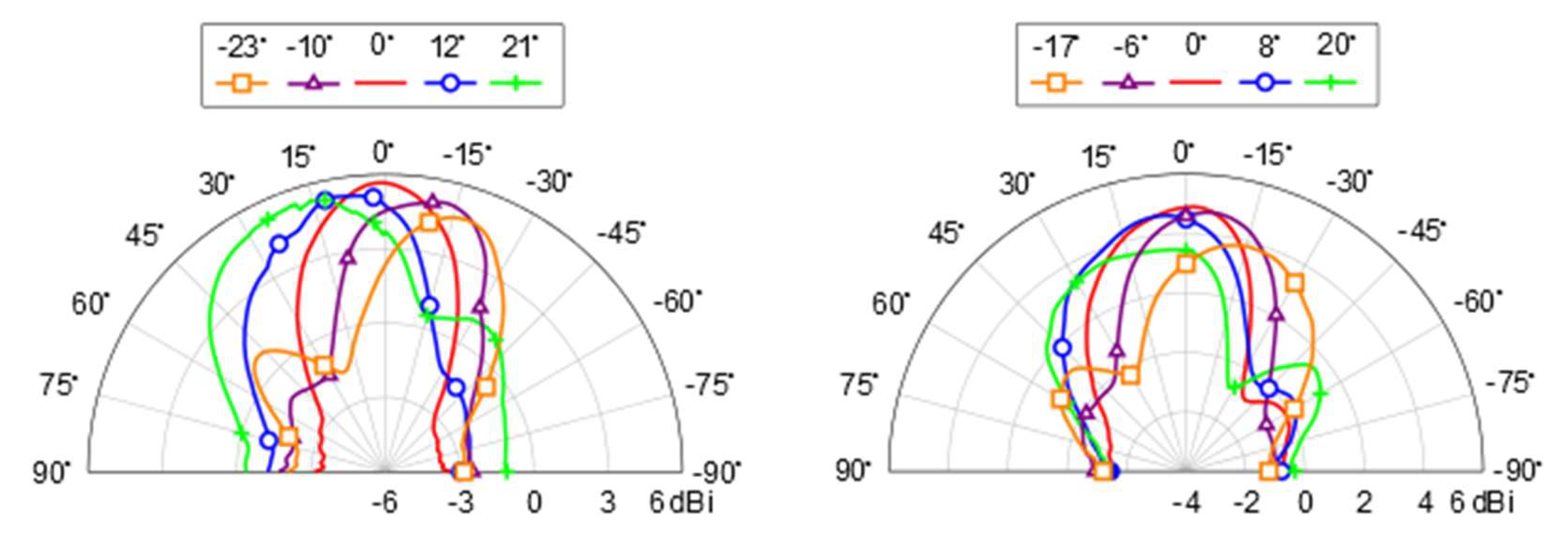
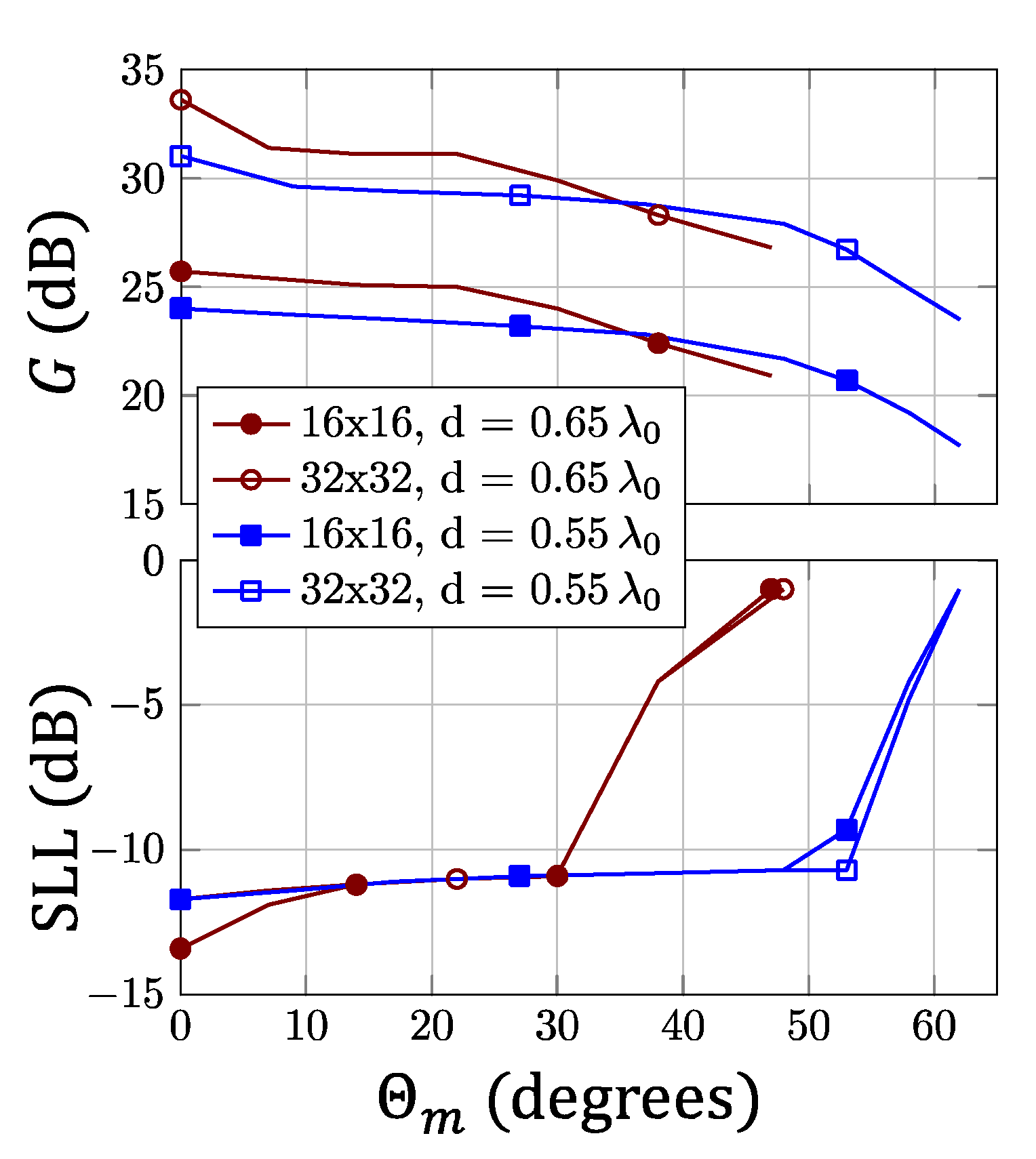
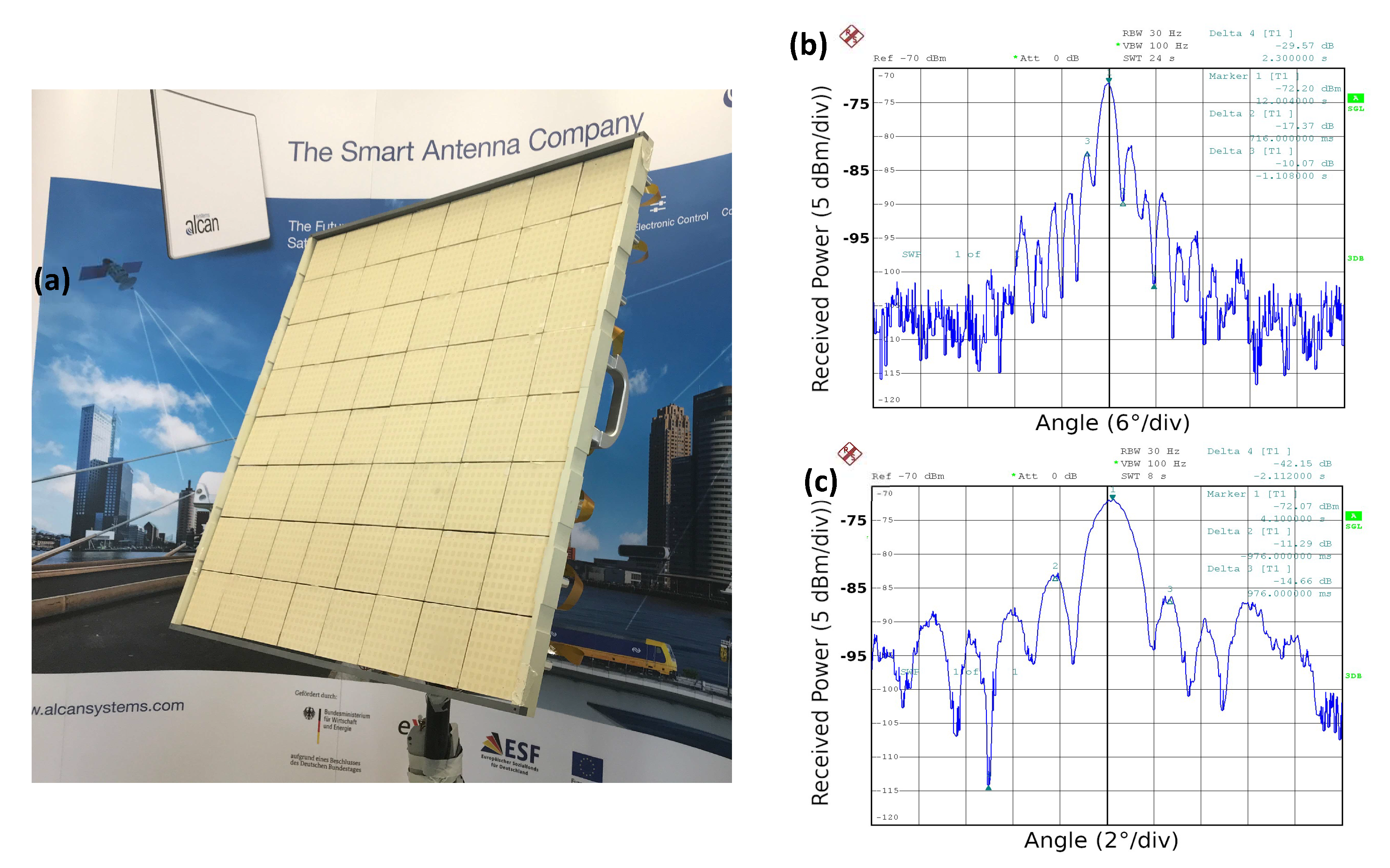
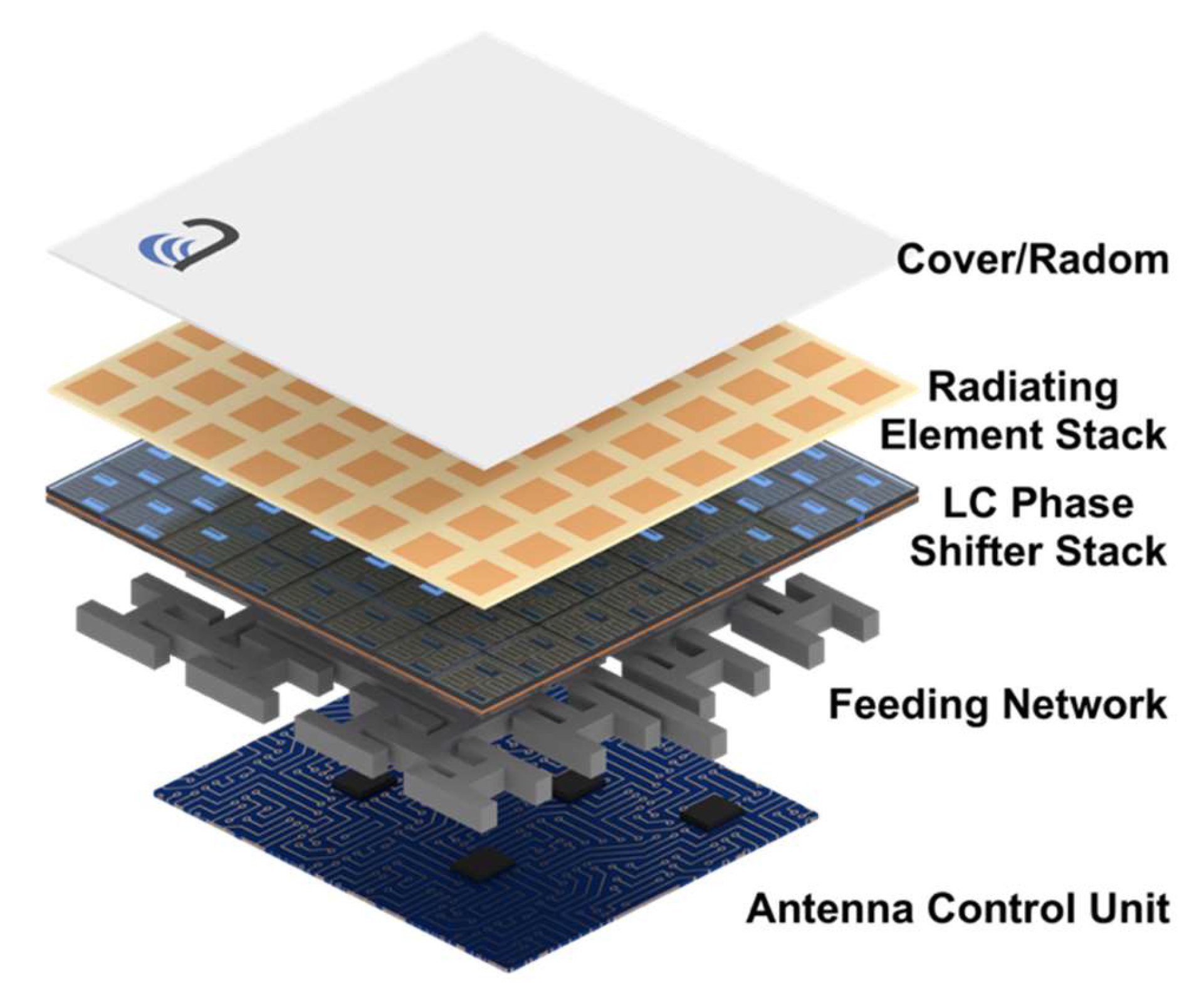

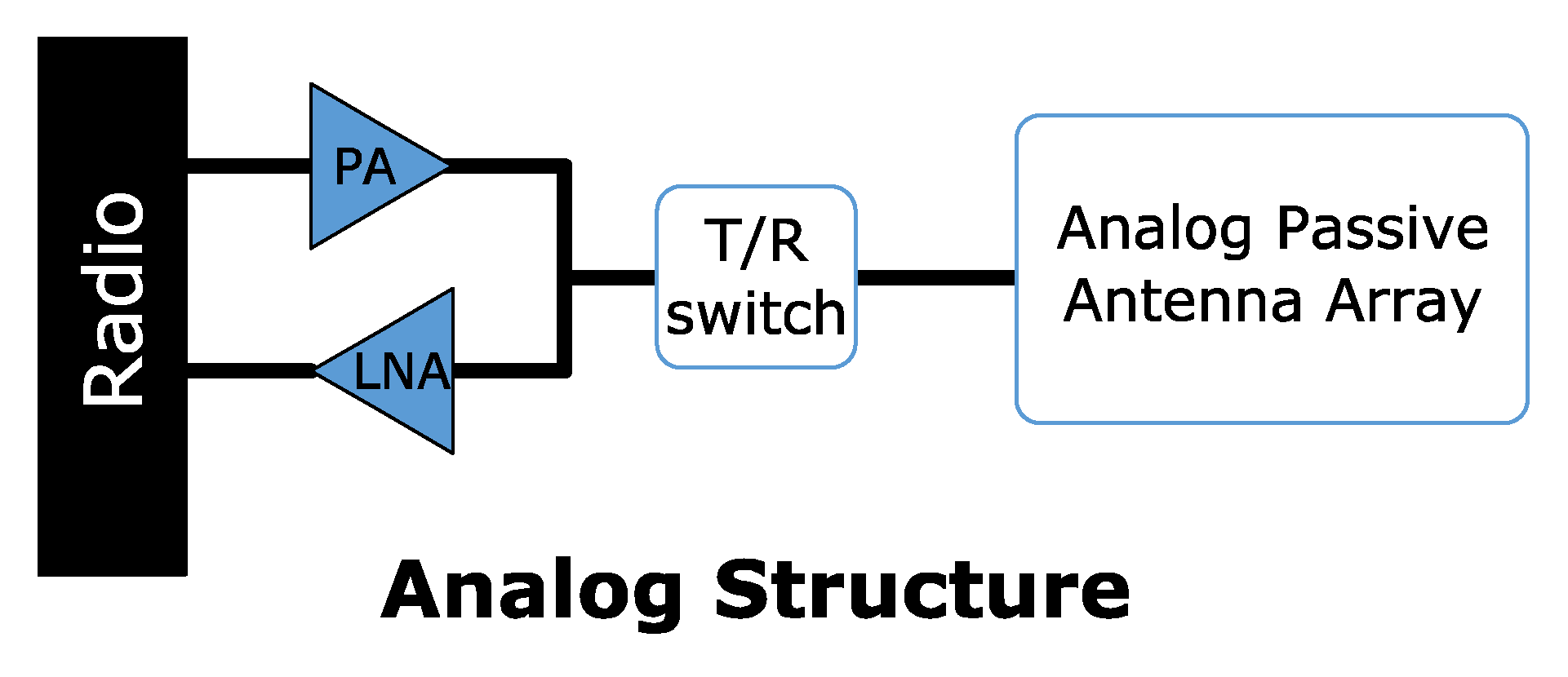
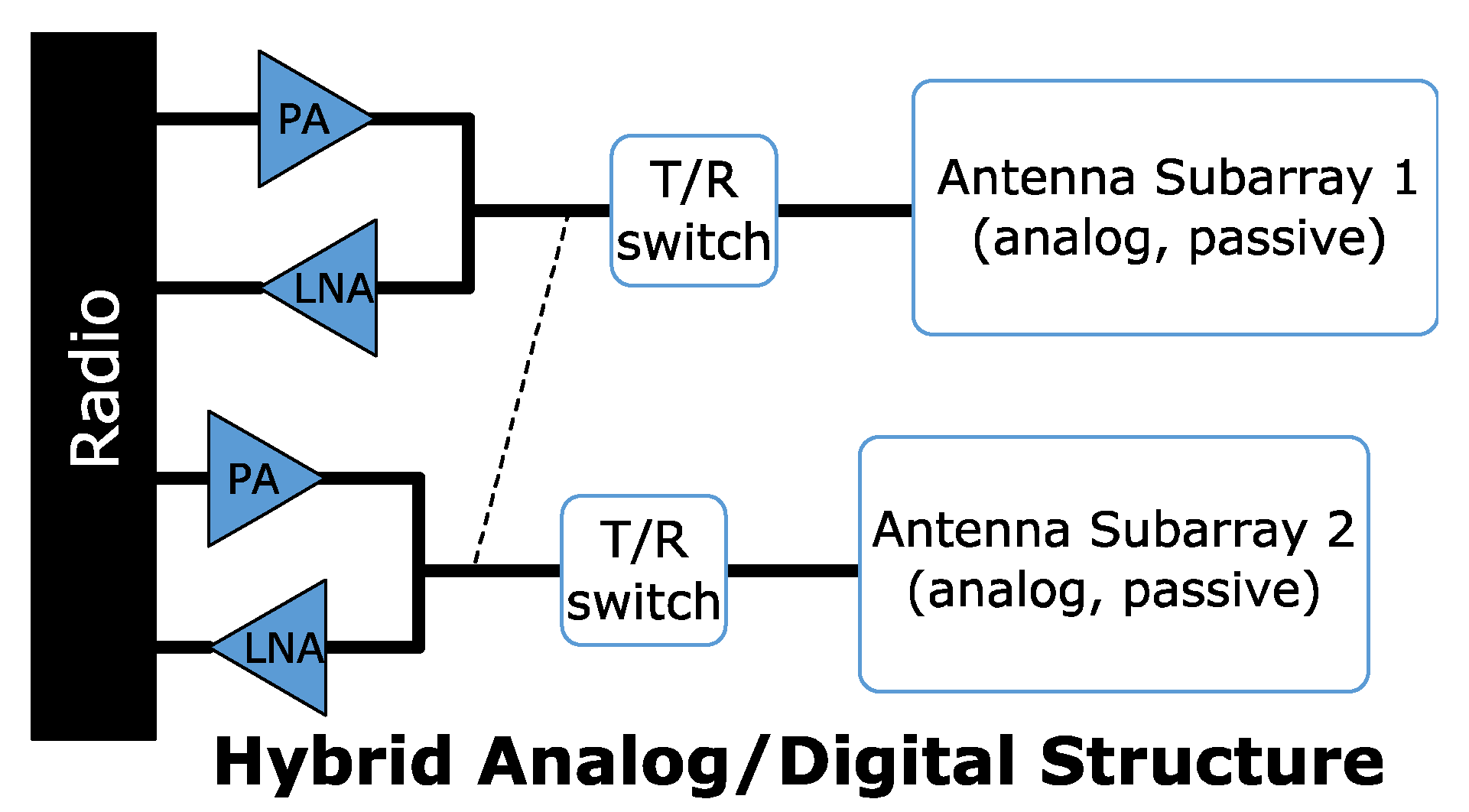
| LC | Δε | τLC (%) | ηLC | Δε1 kHz | Tc (°C) | Ref. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K15 (5CB) | 2.7 | 0.0273 | 3.1 | 0.0132 | 0.4 | 12.9 | 4.7 | 7.0 | 4.2 | 13.5 | 0.126 | 14.4 | 38.0 | [56] |
| E7 | 2.53 | 0.022 | 2.98 | 0.009 | 0.45 | 15.1 | 6.86 | 10.8 | 0.254 | 14.3 | 58.0 | [59] | ||
| BL006 | 2.58 | 0.0191 | 3.16 | 0.0069 | 0.58 | 18.4 | 9.6 | 16.0 | 0.569 | 17.1 | 118.5 | [59] | ||
| MDA-03-2838 | 2.55 | 0.026 | 3.68 | 0.008 | 1.13 | 30.7 | 11.8 | [186] | ||||||
| MDA-03-2844 | 2.4 | 0.021 | 3.4 | 0.007 | 1.0 | 29.4 | 14.0 | [186] | ||||||
| GT3-23001 | 2.41 | 0.0141 | 3.18 | 0.0037 | 0.77 | 24.2 | 17.2 | 24.0 | 14.0 | 34.5 | 0.727 | 4.0 | 173.5 | [59] |
| GT5-26001 | 2.39 | 0.007 | 3.27 | 0.0022 | 0.88 | 26.9 | 38.4 | 12.0 | 41.9 | 1.958 | 1.0 | 146.0 | [75] | |
| GT5-28004 | 2.40 | 0.0043 | 3.32 | 0.0014 | 0.92 | 27.7 | 64.4 | 11.8 | 52.9 | 5.953 | 0.8 | 151.0 | [75] | |
| TUD-566 | 2.41 | 0.006 | 3.34 | 0.0027 | 0.93 | 27.8 | 46.4 | 13.0 | 8.0 | 48.0 | 2.100 | 1.0 | 105.5 | [75] |
| GT7-29001 | 2.46 | 0.0116 | 3.53 | 0.0064 | 1.07 | 30.3 | 26.1 | 14.5 | 18.0 | 0.307 | 22.1 | 124.0 | [59] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jakoby, R.; Gaebler, A.; Weickhmann, C. Microwave Liquid Crystal Enabling Technology for Electronically Steerable Antennas in SATCOM and 5G Millimeter-Wave Systems. Crystals 2020, 10, 514. https://doi.org/10.3390/cryst10060514
Jakoby R, Gaebler A, Weickhmann C. Microwave Liquid Crystal Enabling Technology for Electronically Steerable Antennas in SATCOM and 5G Millimeter-Wave Systems. Crystals. 2020; 10(6):514. https://doi.org/10.3390/cryst10060514
Chicago/Turabian StyleJakoby, Rolf, Alexander Gaebler, and Christian Weickhmann. 2020. "Microwave Liquid Crystal Enabling Technology for Electronically Steerable Antennas in SATCOM and 5G Millimeter-Wave Systems" Crystals 10, no. 6: 514. https://doi.org/10.3390/cryst10060514
APA StyleJakoby, R., Gaebler, A., & Weickhmann, C. (2020). Microwave Liquid Crystal Enabling Technology for Electronically Steerable Antennas in SATCOM and 5G Millimeter-Wave Systems. Crystals, 10(6), 514. https://doi.org/10.3390/cryst10060514





