Tris(ethylenediamine) Cobalt(II) and Manganese(II) Nitrates
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
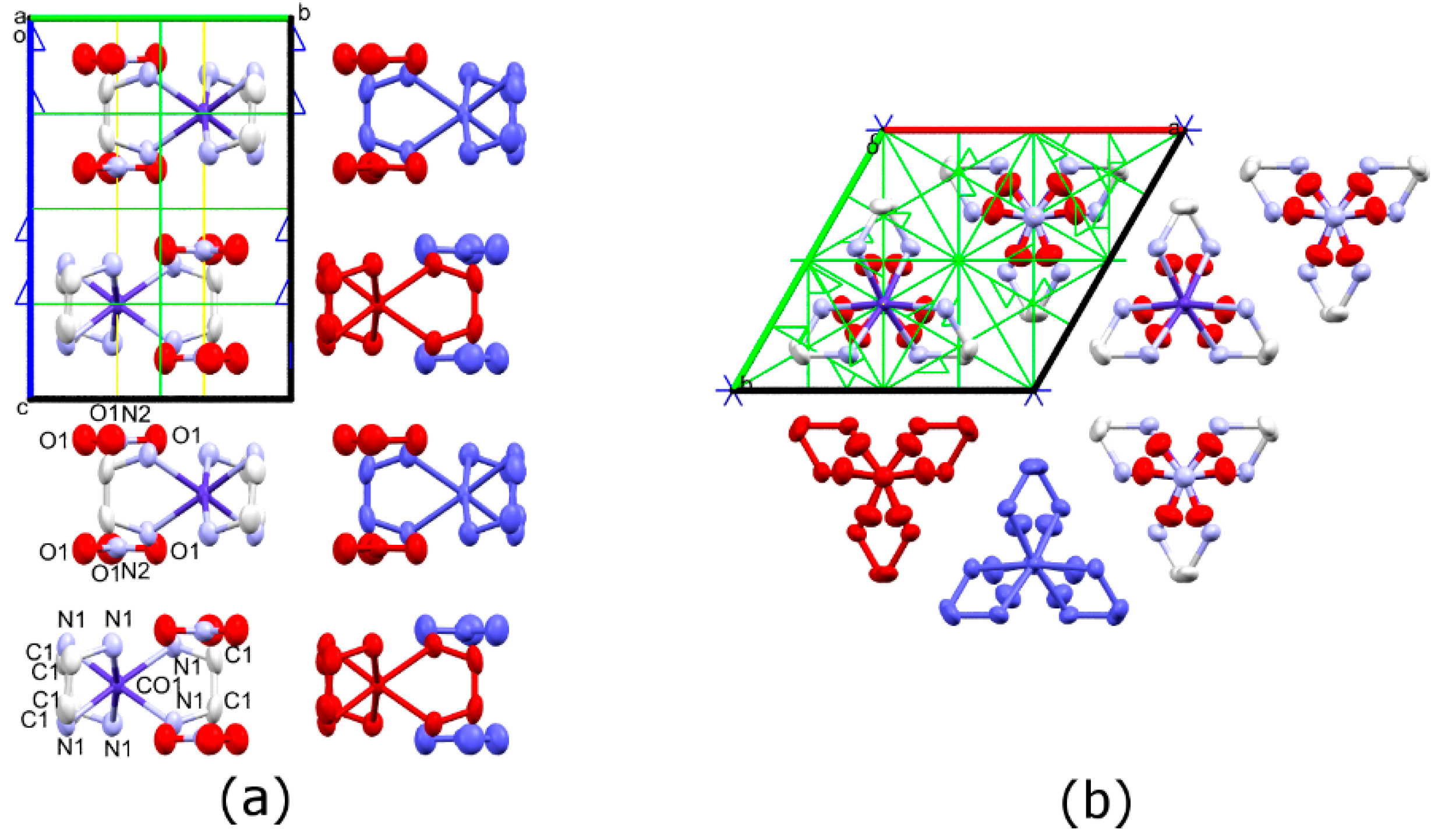
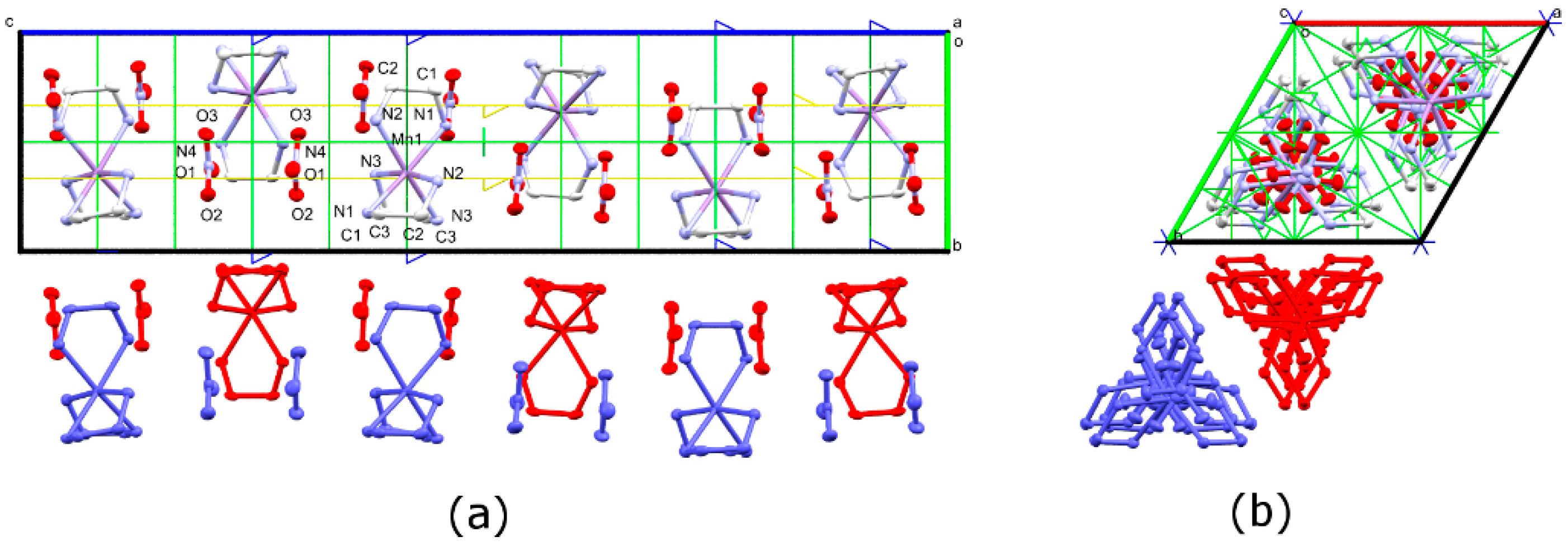
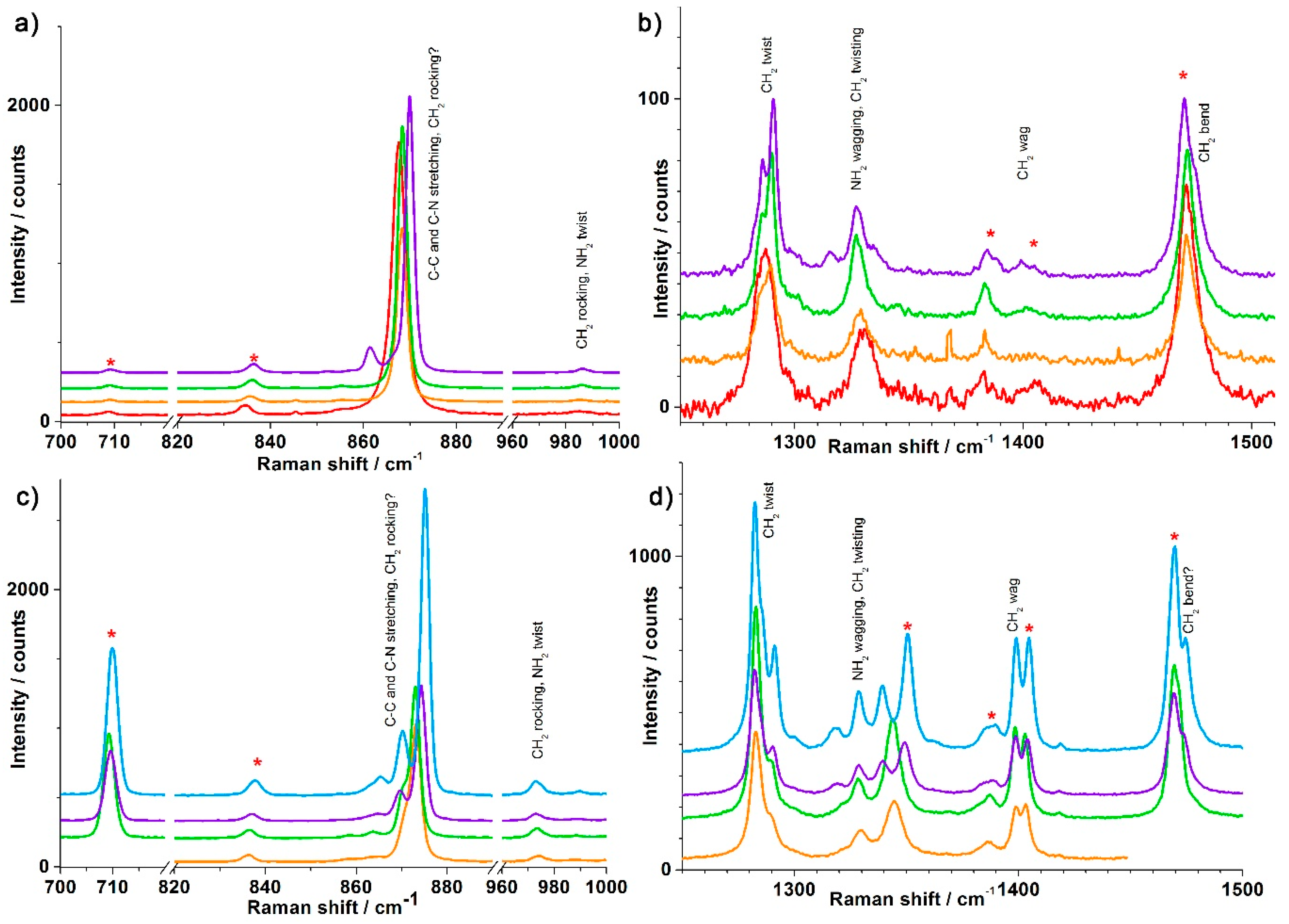
3.1. Synthesis and Crystal Structures
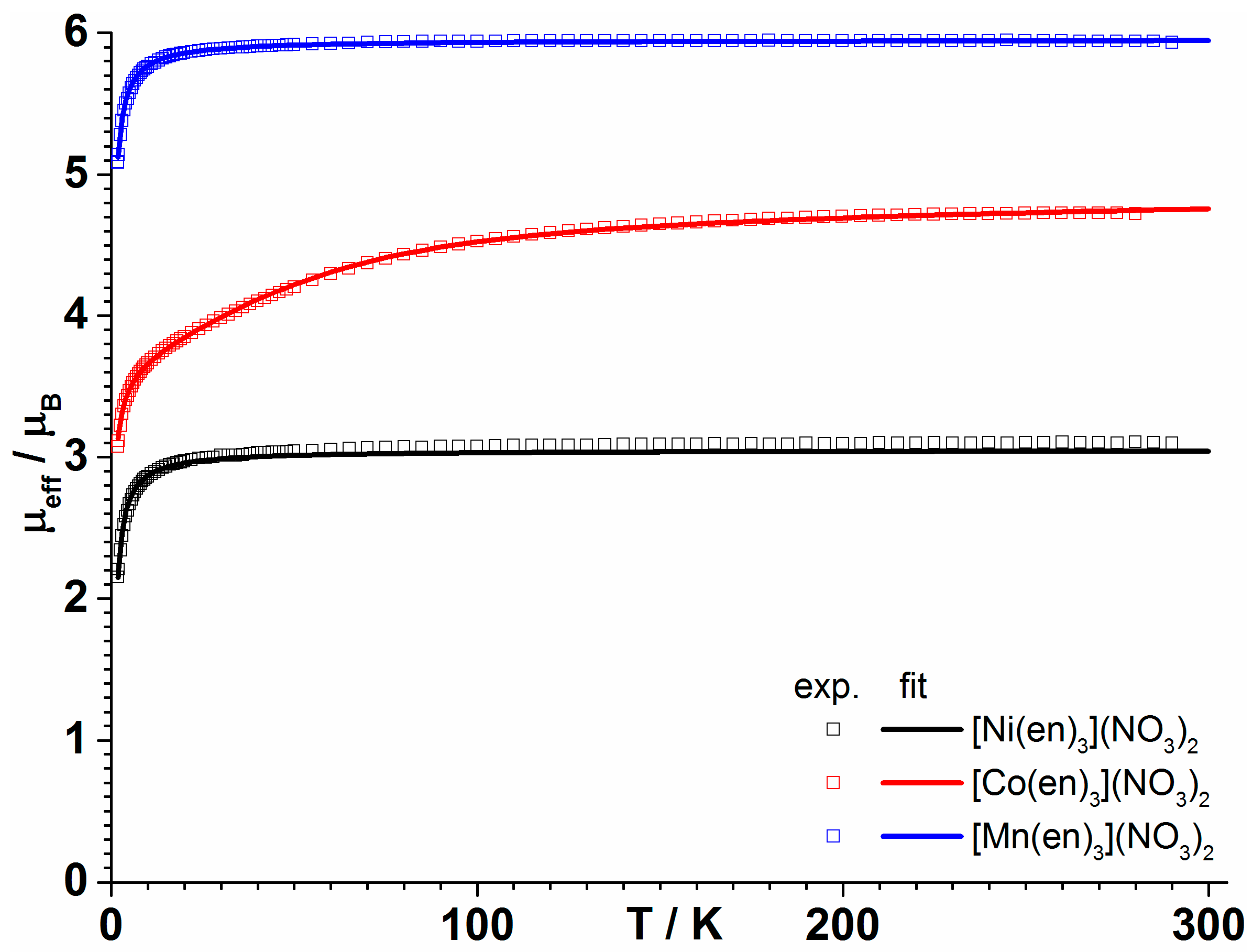
3.2. Magnetic Properties
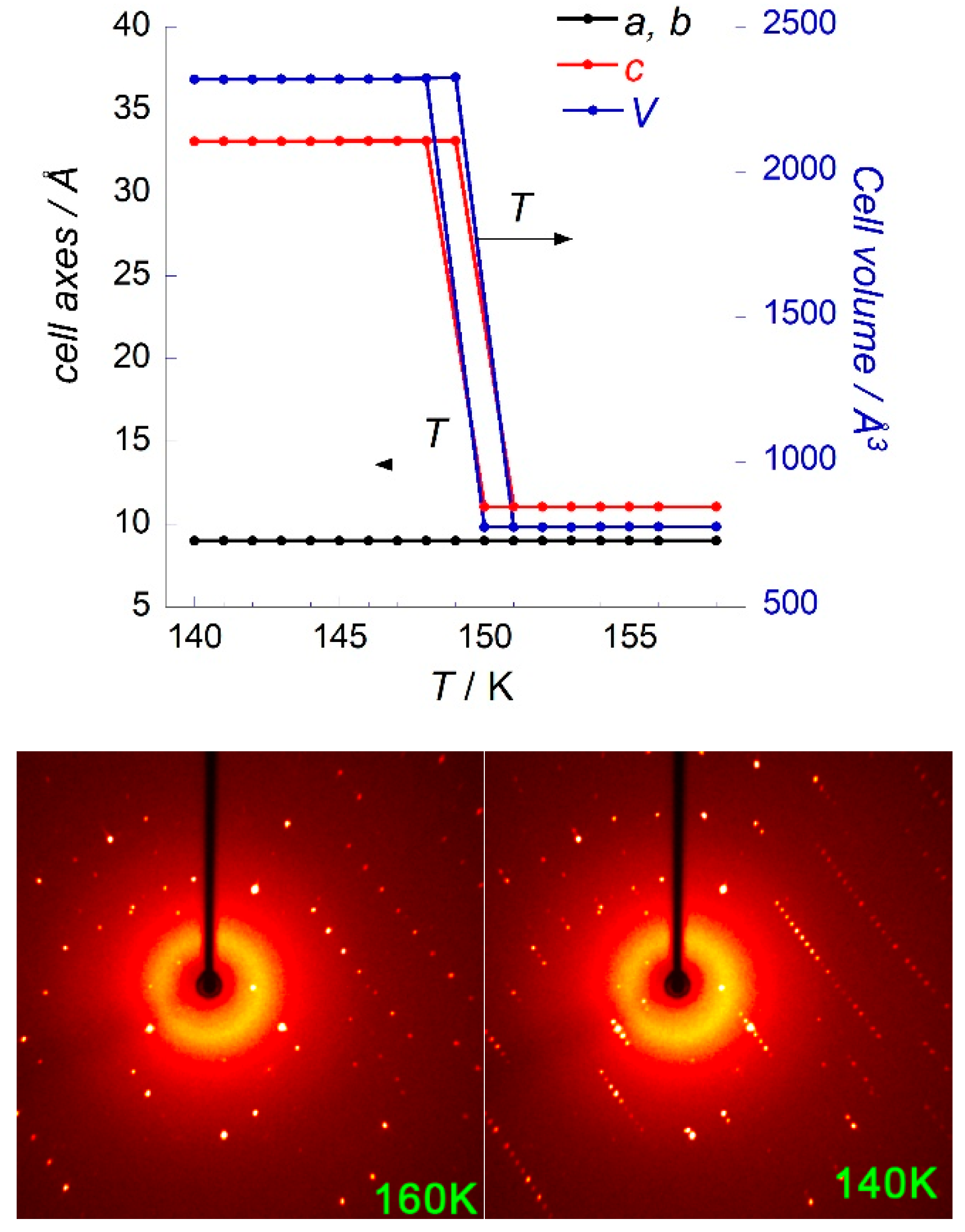
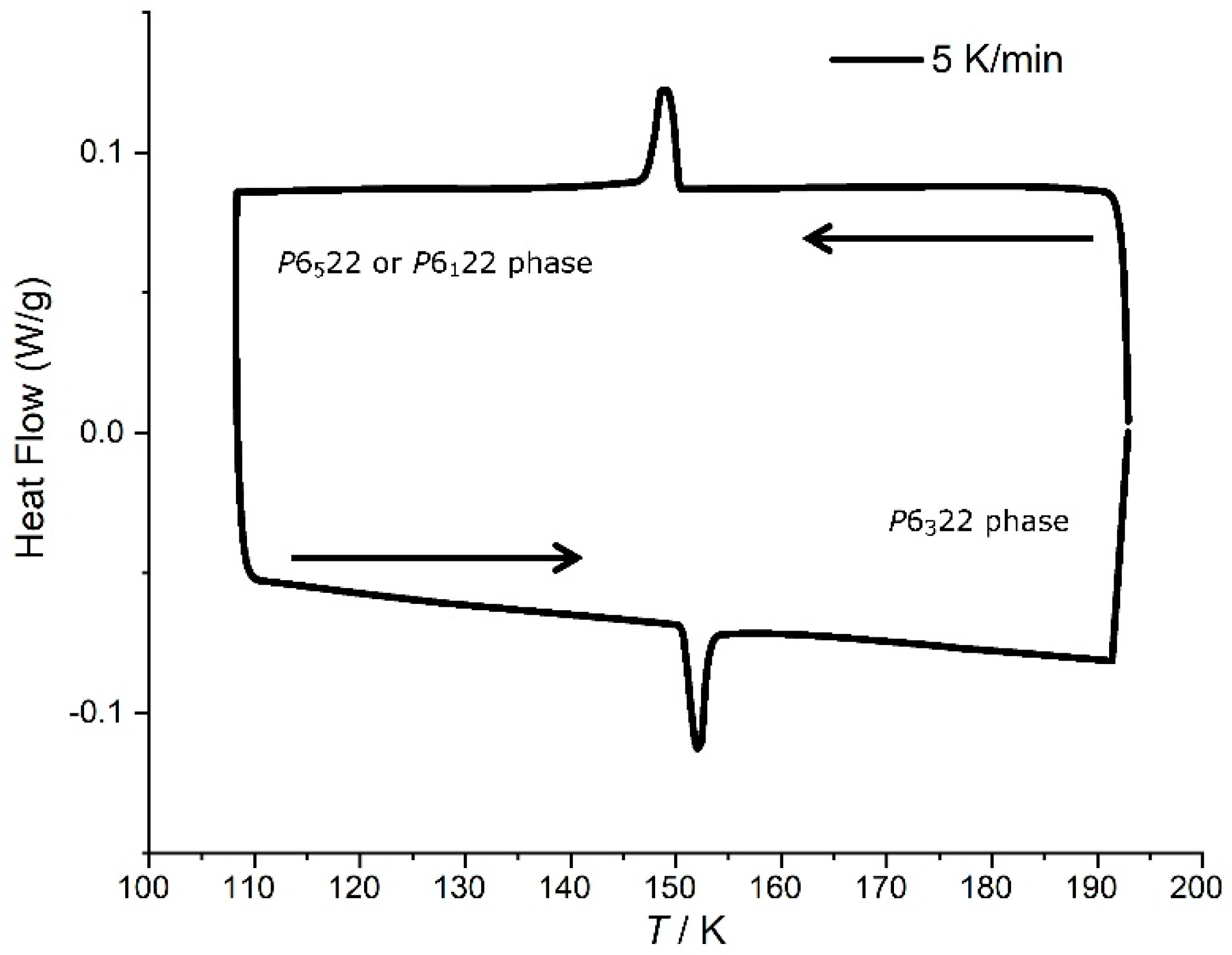
3.3. Phase Transition in [Mn(en)3](NO3)2
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Werner, A. Zur Kenntnis des asymmetrischen Kobaltatoms X. Eur. J. Inorg. Chem. 1914, 47, 1961–1979. [Google Scholar] [CrossRef]
- Jacques, J.; Collet, A.; Wilen, S.H. Enantiomers, Racemates and Resolution; John Wiley and Sons, Inc.: New York, NY, USA, 1981. [Google Scholar]
- Groom, C.; Bruno, I.J.; Lightfoot, M.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Bernal, I.; Kauffman, G.B. The spontaneous resolution of cis-bis(ethylenediamine)dinitrocobalt(III) salts: Alfred Werner’s overlooked opportunity. J. Chem. Educ. 1987, 64, 604. [Google Scholar] [CrossRef]
- Swink, L.N.; Atoji, M. The Crystal Structure of Triethylenediaminenickel(II) Nitrate, Ni(NH2CH2CH2NH2)3(NO3)2. Acta. Cryst. 1960, 13, 639–643. [Google Scholar] [CrossRef]
- Neill, D.; Riley, M.J.; Kennard, C.H.L. Tris(ethylenediamine-N,N’)zinc(II) Dinitrate. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1997, 53, 701–703. [Google Scholar] [CrossRef]
- Farrugia, L.J.; Macchi, P.; Sironi, A. Reversible displacive phase transition in [Ni(en)3]2+(NO3−)2: A potential temperature calibrant for area-detector diffractometers. J. Appl. Cryst. 2003, 36, 141–145. [Google Scholar] [CrossRef]
- Bernhardt, P.V.; Riley, M.J. Structural Definition of the Low-Temperature Phase Transition of Tris(ethane-1,2-diamine)zinc(II) Dinitrate. Aust. J. Chem. 2003, 56, 287. [Google Scholar] [CrossRef]
- Cameron, C.A.; Allan, D.R.; Kamenev, K.V.; Moggach, S.A.; Murrie, M.; Parsons, S. A pressure-induced displacive phase transition in Tris(ethylenediamine) Nickel(II) nitrate. Z. Krist. Cryst. Mater. 2014, 229, 200–209. [Google Scholar] [CrossRef]
- Train, C.; Nuida, T.; Gheorghe, R.; Gruselle, M.; Ohkoshi, S.-I. Large Magnetization-Induced Second Harmonic Generation in an Enantiopure Chiral Magnet. J. Am. Chem. Soc. 2009, 131, 16838–16843. [Google Scholar] [CrossRef]
- Ohkoshi, S.-I.; Takano, S.; Imoto, K.; Yoshikiyo, M.; Namai, A.; Tokoro, H. 90-degree optical switching of output second-harmonic light in chiral photomagnet. Nat. Photonics 2013, 8, 65–71. [Google Scholar] [CrossRef]
- Reisinger, S.A.; De Sousa, A.S.; Fernandes, M.A.; Perry, C.B.; Varadwaj, P.R.; Marques, H.M. Crystallographic and computational investigation of nitrate salts of nickel(II) ethylenediamine complexes. Inorg. Chem. Commun. 2010, 13, 584–588. [Google Scholar] [CrossRef]
- Bennett, A.M.; Foulds, G.A.; Thornton, D.A. The i.r. spectra of ethylenediamine complexes—I. The tris(ethylenediamine) complexes of first transition series metal(II) sulphates. Spectrochim. Acta Part A Mol. Spectrosc. 1989, 45, 219–223. [Google Scholar] [CrossRef]
- ASTM E1840-96(2014) Standard Guide for Raman Shift Standards for Spectrometer Calibration ASTM International; ASTM: West Conshohocken, PA, USA, 2014.
- Bruker-AXS APEX2, SADABS, and SAINT; Software Reference Manuals: Madison, WI, USA, 2009.
- Sheldrick, G.M. SHELXS-97 and SHELXL-97, Program for Crystal Structure Solution and Refinement; University of Gottingen: Gottingen, Germany, 1997. [Google Scholar]
- Sheldrick, G.M. SHELXT-integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A Found. Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Dolomanov, O.; Bourhis, L.J.; Gildea, R.; Howard, J.A.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Otwinowski, Z.; Minor, W. Methods in Enzymology, Volume 276: Macromolecular Crystallography, Part A; Carter, C.W., Sweet, R.M., Jr., Eds.; Academic Press: Cambridge, MA, USA, 1997; pp. 307–326. [Google Scholar]
- SHAPE. Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous Shape Measures and Associated Tools, User’s Manual, Version 2.1; SHAPE: Barcelona, Spain, 2013. [Google Scholar]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef]
- Lloret, F.; Julve, M.; Cano, J.; Ruiz-García, R.; Pardo, E. Magnetic properties of six-coordinated high-spin cobalt(II) complexes: Theoretical background and its application. Inorg. Chim. Acta 2008, 361, 3432–3445. [Google Scholar] [CrossRef]
- Walsh, J.P.S.; Bowling, G.; Ariciu, A.-M.; Jailani, N.F.M.; Chilton, N.F.; Waddell, P.; Collison, D.; Tuna, F.; Higham, L.J. Evidence of Slow Magnetic Relaxation in Co(AcO)2(py)2(H2O)2. Magnetochemistry 2016, 2, 23. [Google Scholar] [CrossRef]
- Gransbury, G.K.; Boulon, M.-E.; Mole, R.A.; Gable, R.W.; Moubaraki, B.; Murray, K.S.; Sorace, L.; Soncini, A.; Boskovic, C. Single-ion anisotropy and exchange coupling in cobalt(ii)-radical complexes: Insights from magnetic and ab initio studies. Chem. Sci. 2019, 10, 8855–8871. [Google Scholar] [CrossRef]
- Sakiyama, H.; Ito, R.; Kumagai, H.; Inoue, K.; Sakamoto, M.; Nishida, Y.; Yamasaki, M. Dinuclear Cobalt(II) Complexes of an Acyclic Phenol-Based Dinucleating Ligand with Four Methoxyethyl Chelating Arms − First Magnetic Analyses in an Axially Distorted Octahedral Field. Eur. J. Inorg. Chem. 2001, 2027–2032, 2705. [Google Scholar] [CrossRef]
- Krishnan, K.; Plane, R.A. Raman and Infrared Spectra of Complexes of Ethylenediamine with Zinc(II), Cadmium(II), and Mercury(II). Inorg. Chem. 1966, 5, 852–857. [Google Scholar] [CrossRef]
- Brooker, M.H. Ionic Interactions in Crystals: Infrared and Raman Spectra of Powdered Ca(NO3)2, Sr(NO3)2, Ba(NO3)2, and Pb(NO3)2. J. Chem. Phys. 1970, 53, 1083–1087. [Google Scholar] [CrossRef]
- Palmer, R.A.; Yang, M.C.-L. Single crystal circular and linear dichroism spectra and absolute configuration of M(en)3(NO3)2 (M = Zn(II), Cu(II), Ni(II), Co(II), Mn(II) and Ru(II). Chem. Phys. Lett. 1975, 31, 492–497. [Google Scholar] [CrossRef]
| Para- Meters | Δ-Mn | Λ-Mn | Δ-Co | Λ-Co |
|---|---|---|---|---|
| Formula | C6H24MnN8O6 | C6H24MnN8O6 | C6H24CoN8O6 | C6H24CoN8O6 |
| Formula weight | 359.25 | 359.25 | 363.26 | 363.26 |
| Crystal system | hexagonal | |||
| Space group | P6322 (no. 182) | |||
| a, b | 9.057(3) Å | 9.0572(7) Å | 8.9285(8) Å | 8.9158(8) Å |
| c | 11.301(3) Å | 11.3115(10) Å | 11.3126(11) Å | 11.2970(10) Å |
| α, β | 90° | |||
| γ | 120° | |||
| Volume | 802.8(4) Å3 | 803.60(11) Å3 | 781.00(16) Å3 | 777.70(16) Å3 |
| Z | 2 | |||
| ρcalc | 1.4861 g/cm3 | 1.4846 g/cm3 | 1.545 g/cm3 | 1.551 g/cm3 |
| μ (Mo Kα) | 0.861 mm-1 | 0.860 mm−1 | 1.138 mm−1 | 1.143 mm−1 |
| Reflections collected | 21940 (5.2° ≤ 2θ ≤ 56.6°) | 9221 (5.2° ≤ 2θ ≤ 52.8°) | 6378 (5.3° ≤ 2θ ≤ 52.7°) | 20782 (6.4° ≤ 2θ ≤ 52.9°) |
| Unique | 675 [Rint = 0.0356] | 560 [Rint = 0.0301] | 545 [Rint = 0.0216] | 542 [Rint = 0.0213] |
| Final R indexes [all data] | R1 = 0.0279 wR2 = 0.0742 | R1 = 0.0343 wR2 = 0.0894 | R1 = 0.0232 wR2 = 0.0766 | R1 = 0.0176 wR2 = 0.0462 |
| Flack para. | 0.07(5) | 0.04(7) | −0.007(8) | 0.02(5) |
| Atoms | Δ-Mn | Λ-Mn | Δ-Co | Λ-Co |
|---|---|---|---|---|
| M1-N1 | 2.2832(17) | 2.280(2) | 2.180(3) | 2.1773(12) |
| C1-N1 | 1.476(3) | 1.473(4) | 1.474(4) | 1.472(2) |
| N2-O1 | 1.234(2) | 1.228(3) | 1.232(3) | 1.2322(14) |
| N1-M1-N1chelate | 78.23(7) | 78.05(11) | 80.61(15) | 80.68(7) |
| N1-M1-N1 | 93.08(8) | 93.22(11) | 91.56(16) | 91.44(7) |
| N1-M1-N1 | 94.75(5) | 94.79(7) | 94.14(10) | 94.16(5) |
| Para- meters | Δ-Mn | Λ-Mn | Δ-Co | Λ-Co |
|---|---|---|---|---|
| Formula | C6H24MnN8O6 | C6H24MnN8O6 | C6H24CoN8O6 | C6H24CoN8O6 |
| Formula weight | 359.25 | 359.25 | 363.24 | 363.26 |
| Crystal system | hexagonal | |||
| Space group | P6522 (no. 179) | P6122 (no. 178) | P6322 (no. 182) | P6322 (no. 182) |
| a, b | 8.9999(3) Å | 8.9970(3) Å | 8.901(2) Å | 8.8970(4) Å |
| c | 33.0883(14) Å | 33.0623(11) Å | 11.065(3) Å | 11.0675(4) Å |
| α, β | 90° | |||
| γ | 120° | |||
| Volume | 2321.03(15) Å3 | 2317.71(13) Å3 | 759.2(3) Å3 | 758.70(7) Å3 |
| Z | 6 | 6 | 2 | 2 |
| ρcalc | 1.542 g/cm3 | 1.5442 g/cm3 | 1.5889 g/cm3 | 1.590 g/cm3 |
| μ (Mo Kα) | 0.893 mm−1 | 0.894 mm−1 | 1.171 mm−1 | 1.172 mm−1 |
| Reflections collected | 19332 (5.2° ≤ 2θ ≤ 56.6°) | 33347 (5.2° ≤ 2θ ≤ 50.7°) | 5187 (5.3° ≤ 2θ ≤ 50.6°) | 2055 (5.3° ≤ 2θ ≤ 52.7°) |
| Unique | 1920 [Rint = 0.0300] | 1419 [Rint = 0.0350] | 475 [Rint = 0.0285] | 522 [Rint = 0.0199] |
| Final R indexes [all data] | R1 = 0.0255 wR2 = 0.0656 | R1 = 0.0203 wR2 = 0.0474 | R1 = 0.0163 wR2 = 0.0444 | R1 = 0.0186 wR2 = 0.0488 |
| Flack para. | 0.04(3) | 0.01(3) | 0.01(5) | 0.006(8) |
| Atoms | Δ-Mn | Λ-Mn2 | Δ-Co | Λ-Co |
|---|---|---|---|---|
| M1-N1 | 2.2787(14) | 2.2803(18) | 2.1820(15) | 2.1802(14) |
| M1-N2 | 2.2802(15) | 2.2828(19) | - | - |
| M1-N3 | 2.2825(14) | 2.2837(18) | - | - |
| C1-N1 | 1.475(2) | 1.473(3) | 1.480(2) | 1.479(2) |
| C2-N2 | 1.477(2) | 1.481(3) | - | - |
| C3-N3 | 1.476(2) | 1.478(3) | - | - |
| N4-O1 | 1.257(2) | 1.260(2) | 1.2535(14) | 1.2508(15) |
| N4-O2 | 1.248(2) | 1.249(2) | - | - |
| N4-O3 | 1.251(2) | 1.251(2) | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortijo, M.; Valentín-Pérez, Á.; Rouzières, M.; Clérac, R.; Rosa, P.; Hillard, E.A. Tris(ethylenediamine) Cobalt(II) and Manganese(II) Nitrates. Crystals 2020, 10, 472. https://doi.org/10.3390/cryst10060472
Cortijo M, Valentín-Pérez Á, Rouzières M, Clérac R, Rosa P, Hillard EA. Tris(ethylenediamine) Cobalt(II) and Manganese(II) Nitrates. Crystals. 2020; 10(6):472. https://doi.org/10.3390/cryst10060472
Chicago/Turabian StyleCortijo, Miguel, Ángela Valentín-Pérez, Mathieu Rouzières, Rodolphe Clérac, Patrick Rosa, and Elizabeth A. Hillard. 2020. "Tris(ethylenediamine) Cobalt(II) and Manganese(II) Nitrates" Crystals 10, no. 6: 472. https://doi.org/10.3390/cryst10060472
APA StyleCortijo, M., Valentín-Pérez, Á., Rouzières, M., Clérac, R., Rosa, P., & Hillard, E. A. (2020). Tris(ethylenediamine) Cobalt(II) and Manganese(II) Nitrates. Crystals, 10(6), 472. https://doi.org/10.3390/cryst10060472