Abstract
(Sc,Ti)Fe2 Laves phases present a relatively unique case of first-order ferro-ferromagnetic transition originating from an instability of the Fe moment. In addition to large magnetoelastic effects making them potential negative thermal expansion materials, here, we show that Sc0.28Ti0.72Fe2 and related alloys also present sizable magnetocaloric and magnetoresistance effects. Both effects are found substantially larger at the ferro-ferromagnetic transition (Tt1) than near the Curie temperature TC, yet they remain limited in comparison to other classes of giant magnetocaloric materials. We suggest a strategy to improve these properties by bringing the transition at Tt1 close to TC, and test its possible realization by Co or Mn for Fe substitutions. The structural and magnetic phase diagrams of Sc0.28Ti0.72Fe2−xTx alloys with T = Mn or Co are explored. Substitutions for Fe by adjacent Mn or Co elements give rise to a breakdown of the long-range ferromagnetic order, as well as a swift disappearance of finite moment magnetism.
1. Introduction
Laves phases, AB2, form a particularly large materials family exhibiting a vast array of intriguing properties, including those related to magnetism [1,2]. Transition-metal-based Laves phases AT2 (with A an early 3, 4, or 5d transition metal and T a late 3d transition metal) are a typical example of this richness in properties since the crystal, electronic, and magnetic structures of binary and ternary alloys are highly sensitive to chemical composition. Hexagonal C14 transition-metal-based Laves phases such as Hf1−xTaxFe2 or Hf1−xNbxFe2 show a first-order ferromagnetic (FM) to antiferromagnetic (AFM) transition when increasing the temperature and have attracted particular interest in recent years for the specific mechanisms of this transition [3,4,5,6,7,8,9,10,11] and the associated magnetocaloric [4,12], giant negative expansion [9], or magnetoresistance effects [5]. On the other hand, Sc1−xTixFe2 Laves phases were intensively studied from the 1970s to 1990s for their complex magnetic phase diagram, in particular the compositions with 0.6 ≤ x ≤ 0.75 showing a ferromagnetic–paramagnetic transition around 300–400 K, and an additional, and quite unique, discontinuous ferromagnetic–ferromagnetic transition (Tt1) around 50–120 K with a change in amplitude of the magnetic moment [13,14,15,16]. This FM–FM transition is associated with a large magnetoelastic effect and corresponds to an increase upon cooling of the Fe magnetic moments from ~0.9 µB/Fe to ~1.3 µB/Fe, breaking down a local moment description. Local probes such as Mössbauer spectroscopy have shown that the Fe moment in the 2a position is highly dependent on the composition [14], and neutron diffraction experiments revealed that an instability of the Fe moment in the 2a position occurs as a function of temperature [17]. Interestingly, similar Fe moment instabilities are believed to be at the very heart of the exceptionally strong magnetoelastic first-order transitions and giant magnetocaloric effects observed in MnFe(P,Si) and La(Fe,Si)13 materials systems [18,19].
In Sc0.35Ti0.65Fe1.95, the low-temperature FM–FM first-order transition (Tt1) is accompanied by a large cell-volume contraction upon heating (ΔV/V ~ −1.1%) [15] and sizable transition entropy ΔStr estimated between 8 and 16 Jkg−1K−1 [20], which makes these materials interesting candidates for negative thermal expansion or magnetocaloric applications. It is, however, needed to find control parameters to adjust Tt1 and TC transition temperatures. Ideally, one should aim to make both transitions coincide in order to create a synergy between the magnetic moment fluctuation at Tt1 and the change in magnetic order at TC, which could potentially lead to a first-order magnetic transition with a large discontinuity in magnetization. Due to the large cell-volume contraction upon heating at Tt1, it could have been anticipated that negative chemical pressure such as that induced by Mn for Fe substitution would increase the Tt1 transition temperature. However, while the evolution of Tt1 and TC due to alloying in Sc1−zTizFe2 ternaries [17,20], high pressure [21], or high magnetic fields [22] have been established, the effect of 3d electron count on the Fe sites remains unclear. In particular, AT2 Laves phases are known to present complex structural or magnetic phase diagrams with competitions between different structural phases (C14/C15), different magnetic orders (FM, AFM, paramagnetic, or short-range magnetism, etc.), and different degrees of localization of the magnetic moment. Accurate predictions of the outcome of substitutions are thus virtually impossible at present. In this work, we explore the influence of Mn or Co for Fe substitutions in Sc0.28Ti0.72Fe2−xTx and establish structural and magnetic phase diagrams of these quaternary alloys.
2. Materials and Methods
Sc0.28Ti0.72Fe2−xTx with T = Mn and Co were prepared by arc-melting in a purified Ar atmosphere of commercial staring materials with purity greater than 99.9% (from the Baotou Research Institute of Rare Earths (Baotou, China) for Sc, and from Alfa Aesar (Haverhill, MA, USA) for the other transition metals). Each button is melted and stirred 5 times. For the parent composition Sc0.28Ti0.72Fe2, the structural and magnetic properties were compared for samples: (i) as-cast, (ii) annealed at 1000 °C for 4 days and furnace cooled, and (iii) annealed at 1000 °C for 4 days and quenched. The three heat treatments led to comparable cell parameters, magnetic saturation, and transition temperatures. The first-order FM–FM transition Tt1 is, however, broader for (ii) furnace cooling than for (i) and (iii) as-cast and quenched samples, the latter two being on par with each other. Accordingly, for most compositions, only as-cast samples are reported, with a few exceptions indicated in the manuscript.
Powder X-ray diffraction experiments were carried out in reflection on an Empyrean diffractometer (Panalytical, Almelo, The Netherlands) using Cu Kα radiation. A TTK600 (Anton Paar, Graz, Austria) low-temperature chamber was used for temperature-dependent measurements. The powders used for XRD experiments were sieved below 36 μm in diameter. The diffraction patterns were analyzed using Fullprof software (version 7.20) [23], and VESTA software (version 3.4.6) was used for crystal structure representation [24]. Physical properties measurements were carried out using a Verslab system (Quantum Design, San Diego, CA, USA) equipped with a vibrating sample magnetometer or AC resistance options (with 4 points contacted with Cerasolzer® (Kuroda Techno Co. Ltd., Yokohama, Japan) and ultrasonic iron), for magnetization and resistivity measurements, respectively.
3. Results and Discussion
3.1. Magnetocaloric and Magnetoresitance of Sc0.28Ti0.72Fe2 Ternary Alloy
Sc0.28Ti0.72Fe2 was chosen as the starting composition for this study as, according to former reports [17,20], it offers a compromise between relatively high Tt1-transition temperature and sharpness of the transition. As illustrated in the next subsections, the cell parameters and basic magnetic properties of our Sc0.28Ti0.72Fe2 sample are in line with former reports [17,20]. Figure 1 shows detailed magnetic data for Sc0.28Ti0.72Fe2 around Tt1 and TC. Though not particularly sharp, the Tt1 transition is a first-order magnetic transition (FOMT), as demonstrated by the relatively large thermal hysteresis of ~10 K. The shift of the transition due to the field dTt1/dB is about +7.1(1) K/T, which is larger than the +4 K/T reported for Sc0.25Ti0.75Fe2 [22] or +3.8 K/T Sc0.35Ti0.65Fe1.95 [15]. Within Clausius–Clapeyron formalism, this results in a limited transition entropy ΔStr = −ΔM/(dTt1/dB) ~2.8 Jkg−1K−1. Given that larger transition entropies were reported [22], this suggests that the strength of the FM–FM transition at Tt1 is highly sensitive to chemical composition, both the Sc/Ti ratio and Fe sub-stoichiometry. Limited transition entropy also results in a limited magnetocaloric effect as calculated from MB(T) curves using the Maxwell relation [25], with ΔS = −1.4 and −2.2 Jkg−1K−1 at Tt1 for 1 and 2 T, respectively. The magnetocaloric effect is conventional, with a negative isothermal entropy change for a positive field change, both at Tt1 and TC. Around TC ≈ 325 K, the shape of the MT(B) curves is typical of a second-order transition, and it corresponds to a magnetocaloric effect of ΔS = −0.4 and −0.8 Jkg−1K−1 for 1 and 2 T, respectively, spreading over a large temperature range. In comparison to other giant magnetocaloric materials [25], the magnetocaloric effect occurring at Tt1 and TC is sizable, yet not among the best candidates known in each temperature range. For instance, in 1 T, a giant magnetocaloric effect of −10 up to −20 Jkg−1K−1 can be observed in MnFe(P,Si) and related materials [19,26,27], −18 Jkg−1K−1 in LaFe11.44Si1.56 [28], −13 Jkg−1K−1 in (Mn,Fe)(Fe,Ni)(Si,Ge,Al) alloys [29,30,31,32], or an inverse effect of +12 Jkg−1K−1 in FeRh [33] or +15 Jkg−1K−1 in Ni-Co-Mn-Ti alloys [34,35,36,37]. Part of the reason is that the magnetocaloric ΔS scales as dM/dT. At Tt1, the transition remains relatively sharp, about 15 K in width, but the change in magnetization is limited, approximately 0.3 μB/Fe. At TC, the decrease in magnetization upon heating is larger (~0.8 μB/Fe) but spread over a much broader temperature range (nearly 150 K), leading to limited dM/dT. We thus believe that better magnetocaloric properties could be achieved in derivatives from (Sc,Ti)Fe2 by bringing Tt1 and TC close to each other, ideally by achieving a coupling between both transitions.
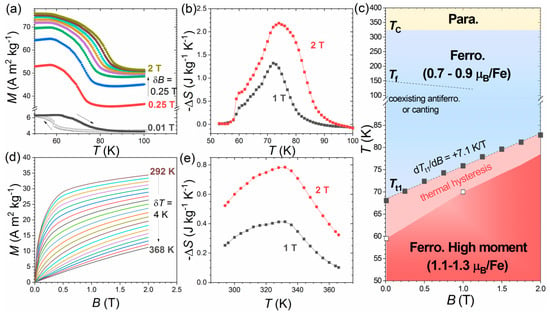
Figure 1.
Temperature/field dependence of the magnetization and magnetocaloric effect of Sc0.28Ti0.72Fe2. (a) MB(T) curves measured upon heating (full symbols) and cooling (open symbol) around the first-order ferro-ferromagnetic transition Tt1; (b) opposite of the isothermal entropy change near Tt1; (c) magnetic phase diagram; (d) magnetization MT(B) curves at different temperatures near TC; (e) opposite of the isothermal entropy change near TC.
To illustrate the very different nature of the magnetic transitions at Tt1 and TC, electrical resistivity (ρ) and magnetoresistance (MR) were measured and are presented in Figure 2. The temperature dependence of the resistivity is metallic, but a linear-like regime is not yet reached on the present data, suggesting a Debye temperature higher than 300 K. TC does not correspond to any significant ρ anomaly; by contrast, a relatively discontinuous ρ increase of ~30% is observed at Tt1 with a thermal hysteresis in line with the first-order character of this transition. Due to the magnetic field sensitivity of Tt1, it results in a significant magnetoresistance whose maximum of −17% for ΔB = 3 T is reached near Tt1. In this low temperature range, the MR field dependence is also typical of that of a FOMT with a clear field-induced character and a finite magnetic hysteresis. By contrast, the magnetoresistance near TC is limited, reaching a maximum of only −0.9%, as is usually found in metallic ferromagnets. The reduction in net magnetization at Tt1 is smaller than that at TC, yet the MR is very significantly larger. This suggests that not only an evolution of magnon–electron interactions takes place at Tt1, but also that other contributions are involved, such as a change in magnon–phonon terms due to the large magnetoelastic effect occurring at Tt1.
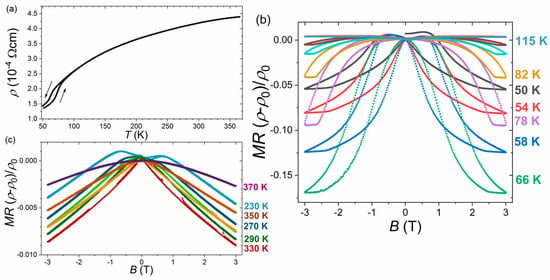
Figure 2.
(a) Temperature dependence of the resistivity for Sc0.28Ti0.72Fe2 in B = 2 T. Magnetoresistance at selected temperatures around Tt1 (b) and TC (c).
3.2. Co for Fe Substitution in Sc0.28Ti0.72Fe2
Figure 3 presents the powder diffraction patterns of Sc0.28Ti0.72Fe2−xCox alloys and the corresponding cell volume and parameters. From x = 0 until x = 1, all XRD peaks can be indexed in the C14 hexagonal structure. The change from hexagonal to cubic C15 structure occurs around x = 1.5. This latter composition shows a coexistence of both phases (~35% hexagonal phase). After 3 days annealing at 1000 °C and quenching to avoid contamination from unreacted CoTi secondary phase, the fully substituted Sc0.28Ti0.72Co2 sample is found to fully crystallize into the cubic C15 structure. Co substitution in Sc0.28Ti0.72Fe2−xCox corresponds to a significant cell-volume contraction, in line with the smaller atomic radius of Co than that of Fe. The boundary between hexagonal and cubic structures marks out a large difference in volume (~1.2%). Within the hexagonal phase, the unit cell contraction appears relatively isotropic, as from x = 0 to 1 both a and c axes decrease, so that the lattice parameters ratio c/a experiences only a limited increase of about +0.07%.
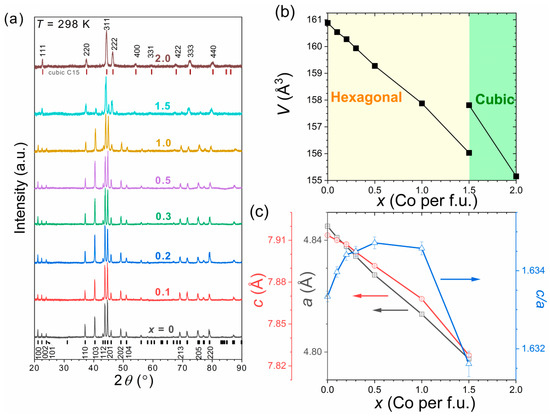
Figure 3.
Crystal structure of Sc0.28Ti0.72Fe2−xCox alloys at room temperature as a function of Co content (x): (a) powder diffraction patterns measured at room temperature—the ticks for the bottom and upper patterns mark out the reflections for hexagonal C14 and cubic C15 structures, respectively; (b) cell volume (half-cell volume for the cubic phase); (c) lattice parameters of the hexagonal phase.
Figure 4 presents the magnetic properties of Sc0.28Ti0.72Fe2−xCox alloys. The unsubstituted sample x = 0 shows a Curie temperature near 325 K and the ferro-ferromagnetic transition Tt1 at 75 K in B = 1 T, in line with former reports on stoichiometric (Sc,Ti)Fe2 or Fe-deficient (Sc,Ti)Fe1.95 [13,14,15,16,20]. In addition, below ~150 K, one can notice a weak decrease in magnetization upon cooling before reaching Tt1. This leads to the appearance of a broad bump centered at Tf~150 K, also present in former studies, and which was ascribed to the development of a coexisting antiferromagnetic phase or of a canting [17,22]. In the range 0 < x ≤ 0.5, Co substitution leads to a rapid decrease in Curie temperature and a strong reduction in magnetization. Alloys with x > 0.5 no longer show signs of long-range ferromagnetic order on M(B) or M(T) curves, and no spontaneous magnetization could be observed on Arrott plots at 50 K (not shown). The change in crystal structure does not appear directly responsible for the loss of long-range magnetic order, as finite magnetic moments and ferromagnetism disappear within the compositional range of the C14 crystal structure. The fully substituted alloy Sc0.28Ti0.72Co2 presents a very small magnetization (magnetization at room temperature is four orders of magnitude smaller than paramagnetic x = 0.5) and has only limited temperature dependence, recalling the Pauli paramagnetism of its TiCo2 or ScCo2 C15 parents [38,39]. The intermediate compositions with Co partially substituting Fe cannot be compared with closely related C14 ternaries such as TiFe2−xCox, as Sc plays a critical role in stabilizing ferromagnetism in Sc0.28Ti0.72Fe2−xCox with x ≤ 0.5. In addition, in contrast to TiFe2−xCox with x ≤ 0.6 [40], no clear signature of long-range antiferromagnetic order is observed. The saturation magnetization at T = 50 K and B = 3 T is about 1.1 µB/Fe, 0.55, 0.43, and 0.32 µB per Fe or Co atom for x = 0, 0.1, 0.2, and 0.3, respectively, and the induced magnetization ~3 × 10−3 µB/Co for x = 2. The decrease in magnetization is faster than what could have been anticipated due to magnetic dilution of Fe by non-magnetic Co. In addition, the FM–FM transition at Tt1 is no longer observed in Co-substituted samples.
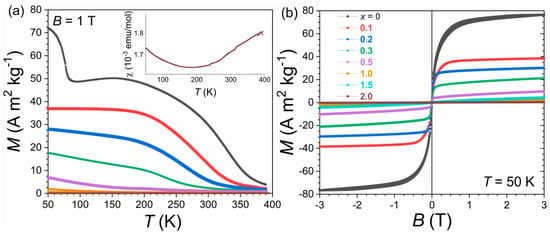
Figure 4.
Magnetic properties of Sc0.28Ti0.72Fe2−xCox alloys as a function of Co content (x): (a) magnetization versus temperature upon heating in B = 1 T, in inset magnetic susceptibility for x = 2; (b) hysteresis loop at T = 50 K.
In (Sc,Ti)Fe2 and (Sc,Ti)Fe1.95, a typical signature of the Fe moment fluctuation at Tt1 was a large cell-volume contraction ΔV/V ~ −1.1% upon heating [15,16,17]. Powder X-ray diffraction experiments were carried out in Sc0.28Fe0.72Fe1.9Co0.1 between 100 and 480 K; see Figure 5. The absence of noticeable cell-volume anomaly further confirms the absence of the Tt1 transition in Co-substituted samples (in the investigated temperature range). The volume coefficient of thermal expansion ~ +15 ppm/K is nearly constant from 100 to 330 K, then increases in the paramagnetic phase +25 ppm/K, which is close to former reports on ternary alloys [15,16].
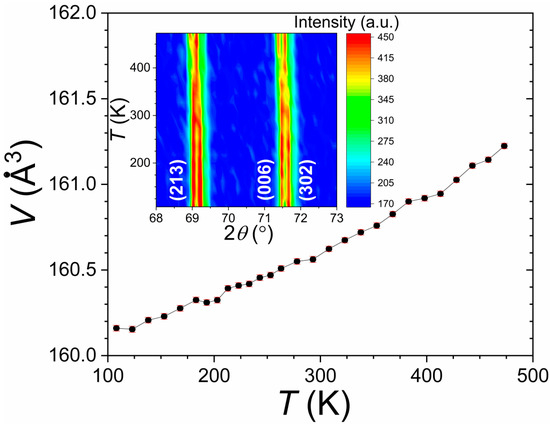
Figure 5.
Temperature dependence of X-ray diffraction for Sc0.28Fe0.72Fe1.9Co0.1.
3.3. Mn for Fe Substitution in Sc0.28Ti0.72Fe2
Figure 6 presents the crystal structure of Sc0.28Ti0.72Fe2−yMny alloys determined from powder X-ray diffraction experiments. All alloys crystallize in the C14 crystal structure, so that Mn for Fe substitutions form a continuous solid solution. Some scatter on the cell-volume vs. composition curve is noticeable, most likely originating from two challenges met during the synthesis: (i) Mn evaporation occurs during the arc-melting process, which is only imperfectly compensated for by the addition of extra-manganese; (ii) Mn substitutions lead to the formation of a minor cubic impurity phase resembling FeTi alloys (up to ~4 w% in y = 1), on which annealing at 1000 °C has only minor effect. Nevertheless, Mn for Fe substitutions clearly show a cell-volume increase (+2.2%) due to an expansion of both a and c axes, but slightly anisotropic with an increase in the c/a ratio (+0.5%).
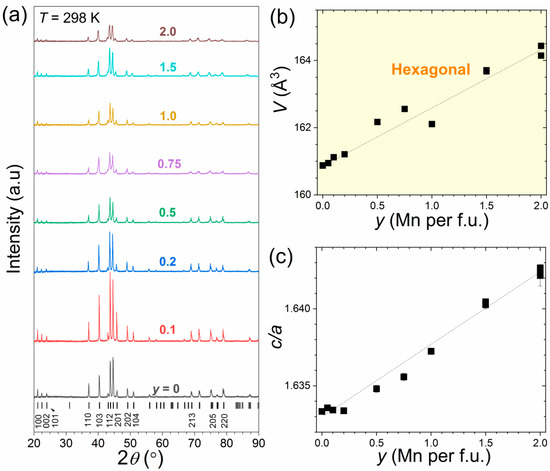
Figure 6.
XRD patterns and structural parameters at room temperature of Sc0.28Ti0.72Fe2−yMny alloys as a function of Mn content (y): (a) XRD patterns measured at room temperature, with, at the bottom, ticks marking the reflections of the C14 hexagonal structure; (b) unit cell volume; and (c) ratio of the cell parameters.
Figure 7 shows the magnetic properties of Sc0.28Ti0.72Fe2−yMny alloys. Mn substitutions lead to a decrease in Curie temperature, in magnetization, and a disappearance of the Tt1 transition. Mn substitutions also drives the development of the coexisting antiferromagnetic-like phase at Tf toward lower temperatures, so that the magnetization in the finite magnetic field is found to increase around 100 K from y = 0 to y = 0.2. From y = 0.5 and above, the magnetization swiftly decreases; for Mn content larger than y ≥ 1, a long-range ferromagnetic order is no longer observed. In contrast to Ti(Fe,Mn)2 alloys [40], no clear signature of bulk long-range antiferromagnetic order is found in the present Sc0.28Ti0.72Fe2−yMny samples. The fully substituted sample Sc0.28Ti0.72Mn2 does not exhibit a linear 1/χ Curie–Weiss behavior and is closer to a nearly temperature-independent paramagnet with χ0 = 10−3 emu·mol−1. This is in line with the “non-magnetic” Pauli paramagnetism reported for its TiMn2 and ScMn2 parents [41,42].
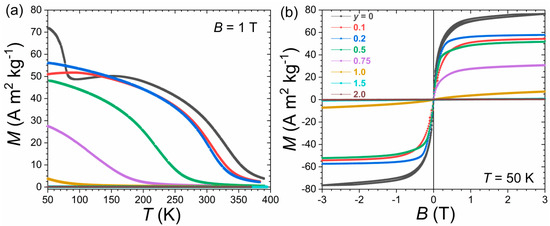
Figure 7.
Magnetic properties of Sc0.28Ti0.72Fe2−yMny alloys as a function of Mn content (y): (a) M(T) in B = 1 T upon heating, and (b) M(B) curves at T = 50 K.
Figure 8 summarizes the magnetic data for Sc0.28Ti0.72Fe2−xCox and Sc0.28Ti0.72Fe2−yMny alloys. Both Co or Mn substitutions lead to a decrease in Curie temperature and a disappearance of the Tt1 transition. The magnetization at 50 K and 3 T as a function of Mn or Co substitutions is presented in Figure 8b in terms of average valence electrons per 2a and 6h sites. Substitutions for Fe lead to a swift reduction in magnetization. The negative chemical pressure due to Mn substitution on Fe does not lead to an increase in Tt1. Structural parameters such as cell volume are unlikely to be the primary driving force for the control of transition temperature or for the magnetization reduction, as Mn for Fe or Co for Fe substitutions should have resulted in opposite evolutions. An influence of the electron count on moment formation and ordering temperature is anticipated in such an itinerant system. The curve in Figure 8b vaguely resembles the Slater–Pauling curve for binary alloys of 3d elements; however, the slopes are much sharper than 1 or −1, preventing the description of the present alloys in a rigid band model. In other respects, the present results differ from that obtained in Sc1−zTizFe2 ternaries. In these, high Fe moments are observed with a titanium content varying from z = 0.75 to 0, with a salient Tt1 transition in the range 0.75 ≤ z ≤ 0.5 [17,20,22]. The d-electron count of the A atom in AFe2 has a clear influence on the existence of Tt1 transition and on the transition temperature, with a finite range of possible compositions. By contrast, only 0.1 Mn or Co substitutions for Fe immediately led to the disappearance of the high moment state. The nonsimilar effect of Sc/Ti ratio or substitutions for Fe highlights that other mechanisms are involved in the occurrence of Tt1 than only the total electron count per f.u.
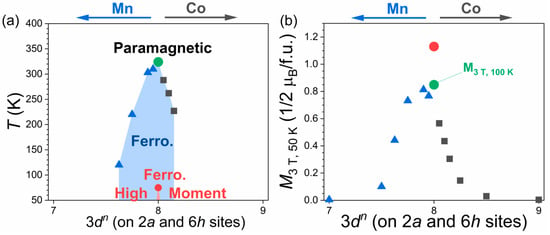
Figure 8.
(a) Transition temperatures for Sc0.28Ti0.72Fe2−yMny and Sc0.28Ti0.72Fe2−xCox alloys; (b) magnetization at 3 T and 50 K for Sc0.28Ti0.72Fe2−yMny (triangles) and Sc0.28Ti0.72Fe2−xCox (squares). For Sc0.28Ti0.72Fe2, the Tt1 transition temperature and the magnetization above Tt1 are also indicated (circles).
4. Conclusions
The magnetocaloric and magnetoresistance effects of Sc0.28Ti0.72Fe2 Laves phase were investigated. Both effects were found to be substantially larger at the first-order ferro-ferromagnetic transition (Tt1) than near TC. Though sizable, the magnetocaloric effect remains limited in comparison to other classes of giant magnetocaloric materials. We suggest a strategy to improve these properties by bringing the Tt1 transition temperature close to TC and testing its possible realization by Co or Mn for Fe substitutions. Substitutions of Fe by adjacent elements Mn and Co, both of which do not carry a significant magnetic moment of their own in these Laves phases, give rise to a breakdown of the long-range ferromagnetic order, as well as a disappearance of the finite moment magnetism. Substitutions for Fe were found to be dissimilar to the effect of the Sc/Ti ratio, which indicates that other mechanisms than only the total electron count are involved in the occurrence of the ferro-ferromagnetic transition Tt1, keeping the door open for future independent control of the Tt1 and TC transition temperatures.
Author Contributions
Investigation, L.S., H.Y., O.T. and F.G.; supervision, F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China, grant nos. 51850410514, 51961033, and 11904188; the Inner Mongolia Normal University, grant nos. CXJJS19102, 2018YJRC002, and 2018YJRC003; and supported by the Program for Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region NJYT-20-A17.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ishida, S.; Asano, S.; Ishida, J. Electronic structures of the C14 laves phase compounds AFe2 (A = Mo, Hf, Ta, W). J. Phys. Soc. Jpn. 1985, 54, 4695–4703. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K. Binary rare earth Laves phases—An overview. Z. Kristallogr. Cryst. Mater. 2006, 221, 375–381. [Google Scholar] [CrossRef]
- Nishihara, Y.; Yamaguchi, Y. Magnetic phase transitions in itinerant electron magnets Hf1−xTaxFe2. J. Phys. Soc. Jpn. 1983, 52, 3630–3636. [Google Scholar] [CrossRef]
- Herbst, J.F.; Fuerst, C.D.; McMichael, R.D. Structural, magnetic, and magnetocaloric properties of (Hf0.83Ta0.17)Fe2+x materials. J. Appl. Phys. 1996, 79, 5998–6000. [Google Scholar] [CrossRef]
- Nagata, Y.; Hagii, T.; Yashiro, S.; Samata, H.; Abe, S. Magnetism and transport properties of Hf1−xTaxFe2 and Mn2−xCrxSb. J. Alloys Compd. 1999, 292, 11–20. [Google Scholar] [CrossRef]
- Rechenberg, H.R.; Morellon, L.; Algarabel, P.A.; Ibarra, M.R. Magnetic moment at highly frustrated sites of antiferromagnetic Laves phase structure. Phys. Rev. B 2005, 71, 104412. [Google Scholar] [CrossRef]
- Diop, L.V.B.; Kastil, J.; Isnard, O.; Arnold, Z.; Kamarad, J. Collapse of ferromagnetism in itinerant-electron system: A magnetic, transport properties, and high pressure study of (Hf,Ta)Fe2 compounds. J. Appl. Phys. 2014, 116, 163907. [Google Scholar] [CrossRef]
- Diop, L.V.B.; Benea, D.; Mankovsky, S.; Isnard, O. Crossover between ferro and antiferromagnetic order in Fe itinerant electron magnetism: An experimental and theoretical study of the model (Hf,Ta)Fe2 Laves phases. J. Alloys Compd. 2015, 643, 239–246. [Google Scholar] [CrossRef]
- Li, B.; Luo, X.H.; Wang, H.; Ren, W.J.; Yano, S.; Wang, C.W.; Gardner, J.S.; Liss, K.D.; Miao, P.; Lee, S.H.; et al. Colossal Negative Thermal Expansion Induced by Magnetic Phase Competition on Frustrated Lattices in Laves Phase Compound (Hf,Ta)Fe2. Phys. Rev. B 2016, 93, 224405. [Google Scholar] [CrossRef]
- Bag, P.; Rawat, R.; Chaddah, P.; Babu, P.D.; Siruguri, V. Unconventional thermal effects across first-order magnetic transition in the Ta-doped HfFe2 intermetallic. Phys. Rev. B 2016, 93, 014416. [Google Scholar] [CrossRef]
- Yibole, H.; Pathak, A.K.; Mudryk, Y.; Guillou, F.; Zarkevich, N.; Gupta, S.; Balema, V.; Pecharsky, V.K. Manipulating the stability of crystallographic and magnetic sublattices: A first-order magnetoelastic transformation in transition metal based Laves phase. Acta Mater. 2018, 154, 365–374. [Google Scholar] [CrossRef]
- Han, Z.D.; Wang, D.H.; Huang, S.L.; Su, Z.H.; Tang, S.L.; Du, Y.W. Low-field magnetic entropy changes in Hf1−xTaxFe2. J. Alloys Compd. 2004, 377, 75–77. [Google Scholar] [CrossRef]
- Nishihara, Y.; Yamaguchi, Y. Magnetic Structures in the Sc1−xTixFe2 System—Magnetic Phase Transitions in Itinerant Electron Systems. J. Phys. Soc. Jpn. 1985, 54, 1122–1130. [Google Scholar] [CrossRef]
- Nishihara, Y.; Yamaguchi, Y. Ferromagnetic Transition in the Itinerant Electron Magnet (Sc0.35Ti0.65Fe2). J. Phys. Soc. Jpn. 1985, 54, 1689–1692. [Google Scholar] [CrossRef]
- Nishihara, Y.; Yamaguchi, Y.; Negishi, A. Magneto-volume of the Ferro- to Antiferromagnetic Transition in (Sc0.35Ti0.65)Fe2. J. Magn. Magn. Mater. 1986, 54–57, 945–946. [Google Scholar] [CrossRef]
- Nishihara, Y.; Yamaguchi, Y. Magnetic Properties of the (Sc1−xTix)Fe2 System Having Two Magnetic States with Different Degrees of Localization. J. Phys. Soc. Jpn. 1986, 55, 920–935. [Google Scholar] [CrossRef]
- Saoudi, M.; Desportes, J.; Ouladdiaf, B. Magnetic Ground State of Ti1−xScxFe2 System. J. Magn. Magn. Mater. 2001, 231, 265–272. [Google Scholar] [CrossRef]
- Gruner, M.E.; Keune, W.; Roldan Cuenya, B.; Weis, C.; Landers, J.; Makarov, S.I.; Klar, D.; Hu, M.Y.; Alp, E.E.; Zhao, J.; et al. Element-Resolved Thermodynamics of Magnetocaloric LaFe13−xSix. Phys. Rev. Lett. 2015, 114, 057202. [Google Scholar] [CrossRef]
- Dung, N.H.; Ou, Z.; Caron, L.; Zhang, L.; Thanh, D.T.C.; de Wijs, G.A.; de Groot, R.A.; Buschow, K.H.J.; Brück, E. Mixed Magnetism for Refrigeration and Energy Conversion. Adv. Energy Mater. 2011, 1, 1215. [Google Scholar] [CrossRef]
- Wada, H.; Shimamura, N.; Shiga, M. Thermal and Transport Properties of Sc1−xTixFe2. J. Phys. Soc. Japn. 1994, 63, 283–288. [Google Scholar] [CrossRef]
- Kanomata, T.; Yoshida, H.; Kaneko, T.; Nishihara, Y. Pressure Effect on the Magnetic Transition Temperatures of Sc1−xTixFe1.95 (x = 0.60, 0.70 and 0.85). J. Magn. Magn. Mater. 1992, 104–107, 2063–2064. [Google Scholar] [CrossRef]
- Kido, G.; Nakagawa, Y.; Nishihara, Y.; Yamaguchi, Y. Ferromagnetic to Ferromagnetic Phase Transition in Sc0.25Ti0.75Fe2 Under Pulsed High Magnetic Field. J. Magn. Magn. Mater. 1987, 70, 181–183. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter. 1993, 192, 55. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479–1539. [Google Scholar] [CrossRef]
- Guillou, F.; Porcari, G.; Yibole, H.; van Dijk, N.; Brück, E. Taming the First-Order Transition in Giant Magnetocaloric Materials. Adv. Mater. 2014, 26, 2671–2675. [Google Scholar] [CrossRef]
- Guillou, F.; Yibole, H.; Porcari, G.; van Dijk, N.; Brück, E. Magnetocaloric effect, cyclability and coefficient of refrigerant performance in the MnFe(P, Si, B) system. J. Appl. Phys. 2014, 116, 063903. [Google Scholar] [CrossRef]
- Fujieda, S.; Fujita, A.; Fukamichi, K. Large magnetocaloric effect in La(FexSi1−x)13 itinerant-electron metamagnetic compounds. Appl. Phys. Lett. 2002, 81, 1276. [Google Scholar] [CrossRef]
- Liu, E.; Wang, W.; Feng, L.; Feng, L.; Zhu, W.; Chen, J.; Zhang, H.; Wu, G.; Jiang, C.; Xu, H.; et al. Stable magnetostructural coupling with tunable magnetoresponsive effects in hexagonal ferromagnets. Nat. Commun. 2012, 3, 873. [Google Scholar] [CrossRef]
- Taubel, A.; Gottschall, T.; Fries, M.; Faske, T.; Skokov, K.P.; Gutfleisch, O. nfluence of magnetic field, chemical pressure and hydrostatic pressure on the structural and magnetocaloric properties of the Mn–Ni–Ge system. J. Phys. D Appl. Phys. 2017, 50, 464005. [Google Scholar] [CrossRef]
- Biwas, A.; Pathak, A.K.; Zarkevich, N.A.; Liu, X.; Mudryk, Y.; Balema, V.; Johnson, D.D.; Pecharsky, V.K. Designed materials with the giant magnetocaloric effect near room temperature. Acta Mater. 2019, 180, 341–348. [Google Scholar] [CrossRef]
- Hanggai, W.; Tegus, O.; Yibole, H.; Guillou, F. Structural and magnetic phase diagrams of MnFe0.6Ni0.4(Si,Ge) alloys and their giant magnetocaloric effect probed by heat capacity measurements. J. Magn. Magn. Mater. 2020, 494, 165785. [Google Scholar] [CrossRef]
- Sánchez-Valdés, C.F.; Gimaev, R.R.; López-Cruz, M.; Sánchez Llamazares, J.L.; Zverev, V.I.; Tishin, A.M.; Carvalho, A.M.G.; Aguiar, D.J.M.; Mudryk, Y.; Pecharsky, V.K. The effect of cooling rate on magnetothermal properties of Fe49Rh51. J. Magn. Magn. Mater. 2020, 498, 166130. [Google Scholar] [CrossRef]
- Planes, A.; Maňosa, L.; Acet, M. Magnetocaloric effect and its relation to shape memory properties in ferromagnetic Heusler alloys. J. Phys. Condens. Matter. 2009, 21, 233201. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Liu, E.K.; Chen, J.H.; Li, Y.; Liu, G.D.; Luo, H.Z.; Xi, X.K.; Zhang, H.W.; Wang, W.H.; Wu, G.H. Realization of multifunctional shape-memory ferromagnets in all-d-metal Heusler phases. Appl. Phys. Lett. 2015, 107, 022406. [Google Scholar] [CrossRef]
- Liu, K.; Han, X.; Yu, K.; Ma, C.; Zhang, Z.; Song, Y.; Ma, S.; Zeng, H.; Chen, C.; Luo, X.; et al. Magnetic-field-induced metamagnetic reverse martensitic transformation and magnetocaloric effect in all-d-metal Ni36.0Co14.0Mn35.7Ti14.3 alloy ribbons. Intermetallics 2019, 110, 106472. [Google Scholar] [CrossRef]
- Neves Bez, H.; Pathak, A.K.; Biswas, A.; Zarkevich, N.; Balema, V.; Mudryk, Y.; Johnson, D.D.; Pecharsky, V.K. Giant enhancement of the magnetocaloric response in Ni-Co-Mn-Ti rapid solidification. Acta Mater. 2019, 173, 225–230. [Google Scholar] [CrossRef]
- Abel, A.W.; Craig, R.S. Magnetic and structural characteristics of TiCr2, ZrCr2, HfCr2 and the TiCo2-ZrCo2 and YFe2-YCo2 alloy systems. J. Less-common Met. 1968, 16, 77–83. [Google Scholar] [CrossRef]
- Ishiyama, K.; Shinogi, A.; Endo, K. Exchange Enhanced Pauli Paramagnetism of ScCo2. J. Phys. Soc. Jpn. 1984, 53, 2456. [Google Scholar] [CrossRef]
- Yamada, Y.; Nakamura, K.; Kitagawa, K.; Obara, G.; Nakamura, T. Magnetic Properties of C14 Laves Phase Ti(Fe1−xTx)2 with T = Mn, Co and Ni (x ≤ 0.6). J. Magn. Magn. Mater. 2005, 285, 28–38. [Google Scholar] [CrossRef]
- Hempelmann, R.; Hilscher, G. Ferromagnetism in Ti-Mn ternary hydrides. J. Less Common Met. 1980, 74, 103–109. [Google Scholar] [CrossRef]
- Kulpa, M.; Talik, E.; Winiarski, A.; Mydlarz, T.; Gilewski, A.; Kusz, J.; Böhm, H.; Suski, W. Electronic structure and magnetic examination of ScMn2 single crystal. J. Alloys Compd. 2005, 386, 82–86. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).