The design of experiment software with response surface method was used to statistically study the effect of fly ash (FA), sliding speed (S) and applied load (L) on the wear rate of AA6063-FA composites and to build an empirical model for Wear rate based on the effects of these factors. The sequential F-test was conducted for testing the significance of the regression model.
The step-wise regression method was utilized for the wear rate model with the entire potential combinations of the control factors with exception of the cubic terms since these terms were aliased for the data ranges obtained. The selected terms along with the step-wise regression method led to the elimination of the less significant model terms automatically.
Table 7 shows the analysis of variance generated for wear rate model. The model F-value of 213.395 confirms the significance of the model. A
p-value of 0.0001 was indicative that there was a low chance of F-value which could occur as result of noise. The predicted R
2 of 0.9658, which represent the measure of the amount of variation about the mean explained by the model agrees well with the adjusted R
2 of 0.9745. The adjusted R
2 and predicted R
2 should be within approximately 0.20 of each other so as to be in agreement, or else setbacks may arise with either the data or the model. High R
2 value suggest there is a statistically significant interaction between factors. Resulting wear rate within the investigated ranges of parameters can be modeled by the final equation produced, Equation (5).
The order of the factors influencing the wear rate can be established through analysis of the F-value magnitude as follows: it can be observed the F-value of FA (837.432) was the most significant parameter having the highest statistical influence on the wear rate of AA6063-FA composites followed by applied load (483.037) and sliding speed (286.805) and S, which implies that the FA content has greater effect on wear rate value than the L and S factor.
Adequate precision ratio, which represent the signal-to-noise ratio, with values higher than 4 indicate adequate model discrimination [
17]. It compares the range between the predicted values at the design points to the average prediction error. As shown in
Table 7, the adequate ratio was 59.006, which indicates that the model has capacity of navigating the design space. The R
2 value of about 0.9791 indicates the variability of the response was 97.91% about the mean which proved the model provide a good fit for the data. This fact alongside with the remarkable residual analysis led to the conclusion that the model given in Equation (5) can predict the wear rate of the compound within the investigated range of all three parameters.
Furthermore, in
Table 7, both the
SL (BC) and
S2 (
B2) terms are considered to be insignificant as their
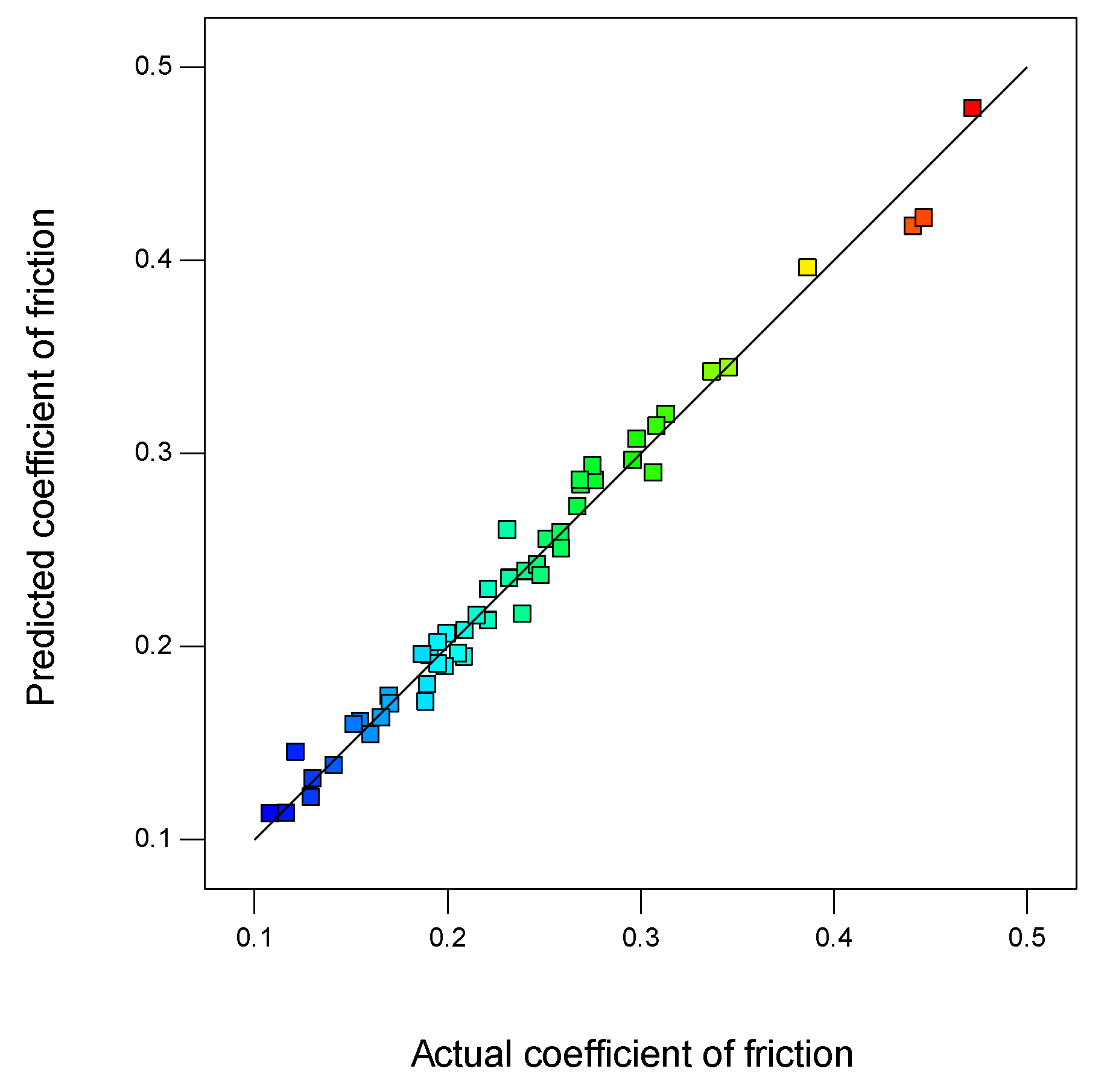
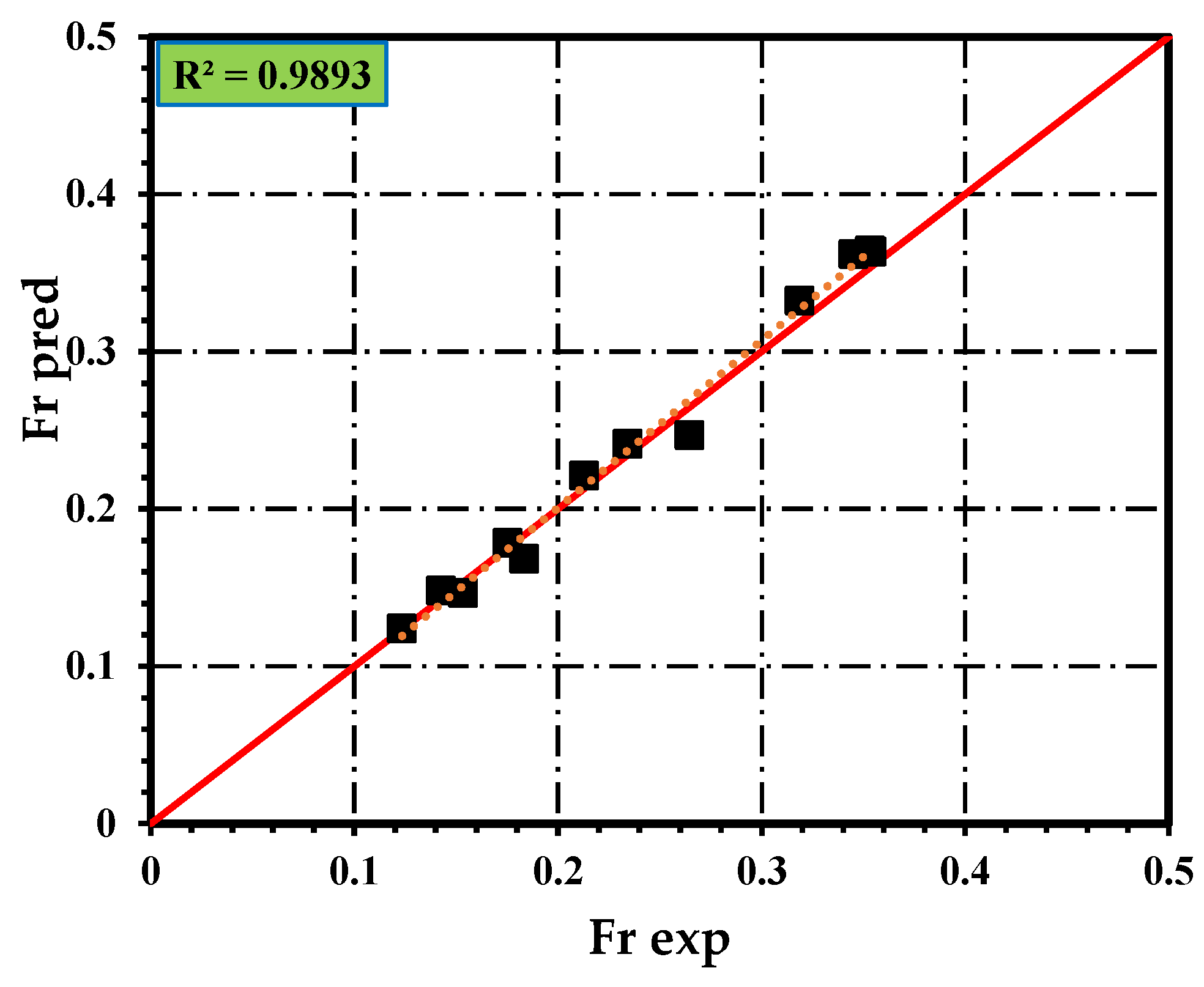
p-value was greater than 0.05. However, these terms were automatically added in order to support the model’s hierarchy. In contrast, it is evident that the combined interaction of FA×L has the strongest effect on the response. The essential effects of the parameters on the responses, i.e., wear rate and the coefficient of friction, are further illustrated using contour lines and 3D surface plots.
Graphical Results of Wear Rate Model
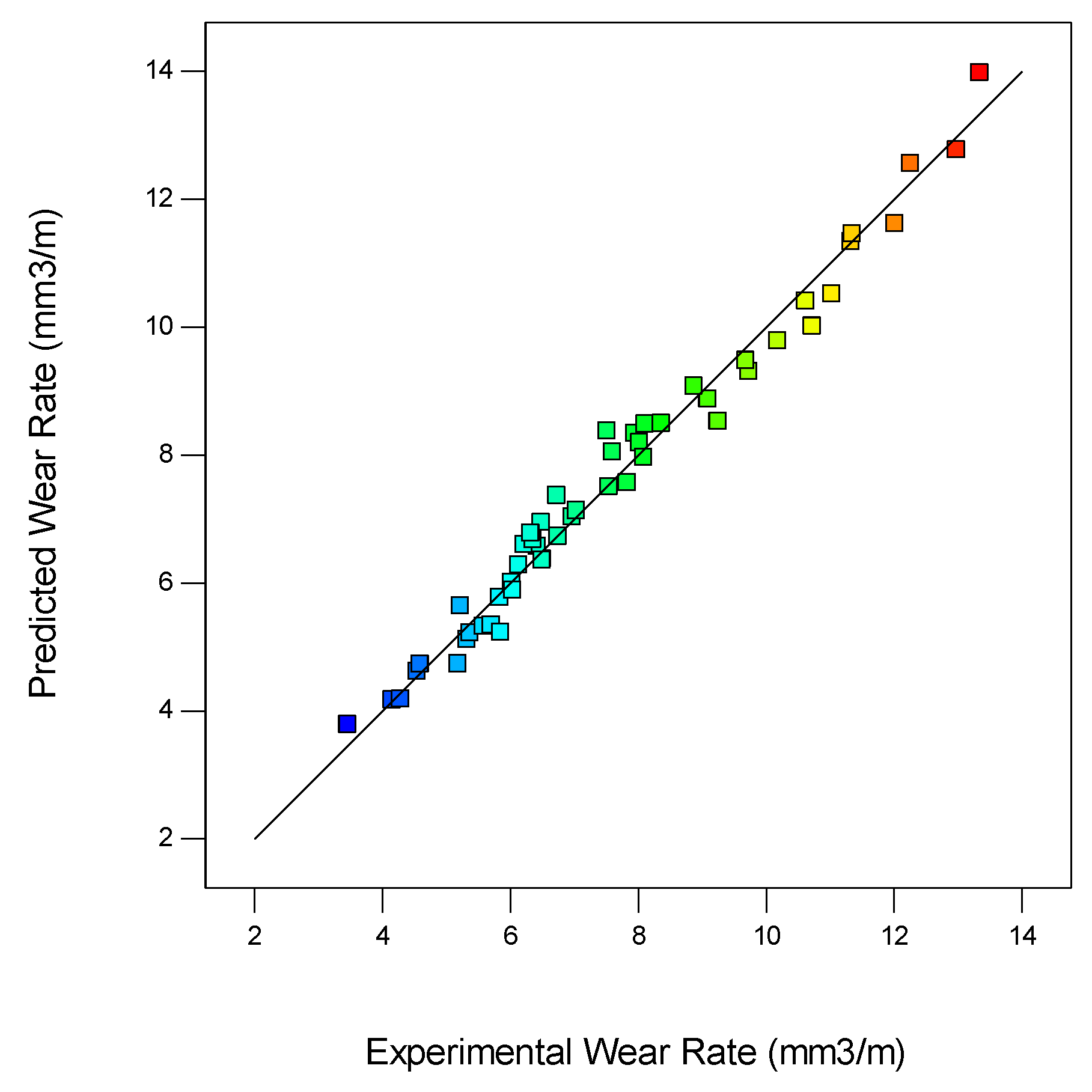
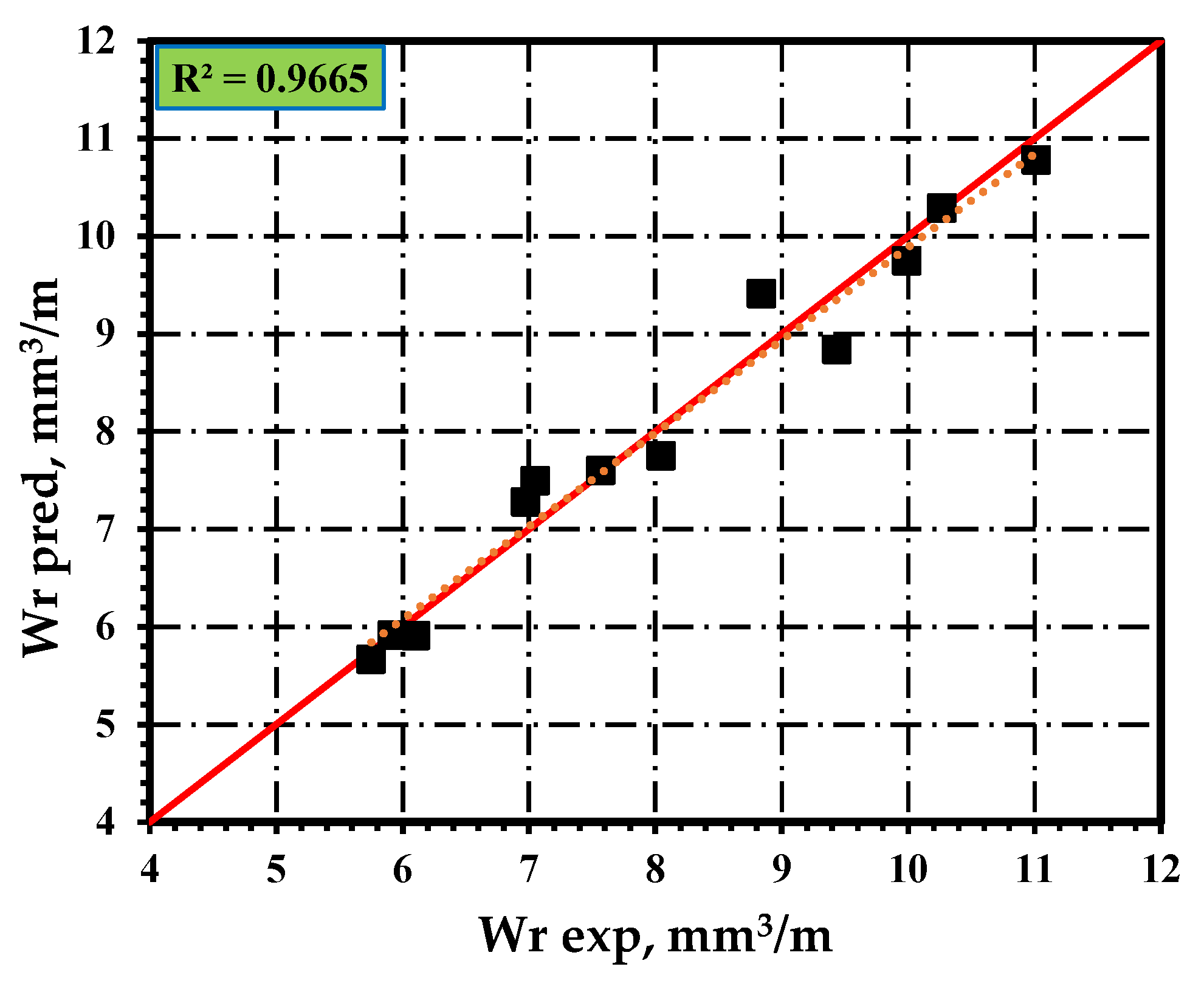
Figure 1 presents the variance of collected data points about the linearized line which relates the predicted values with the actual values. This observation clearly indicates the model provide a good fit for the wear rate response.
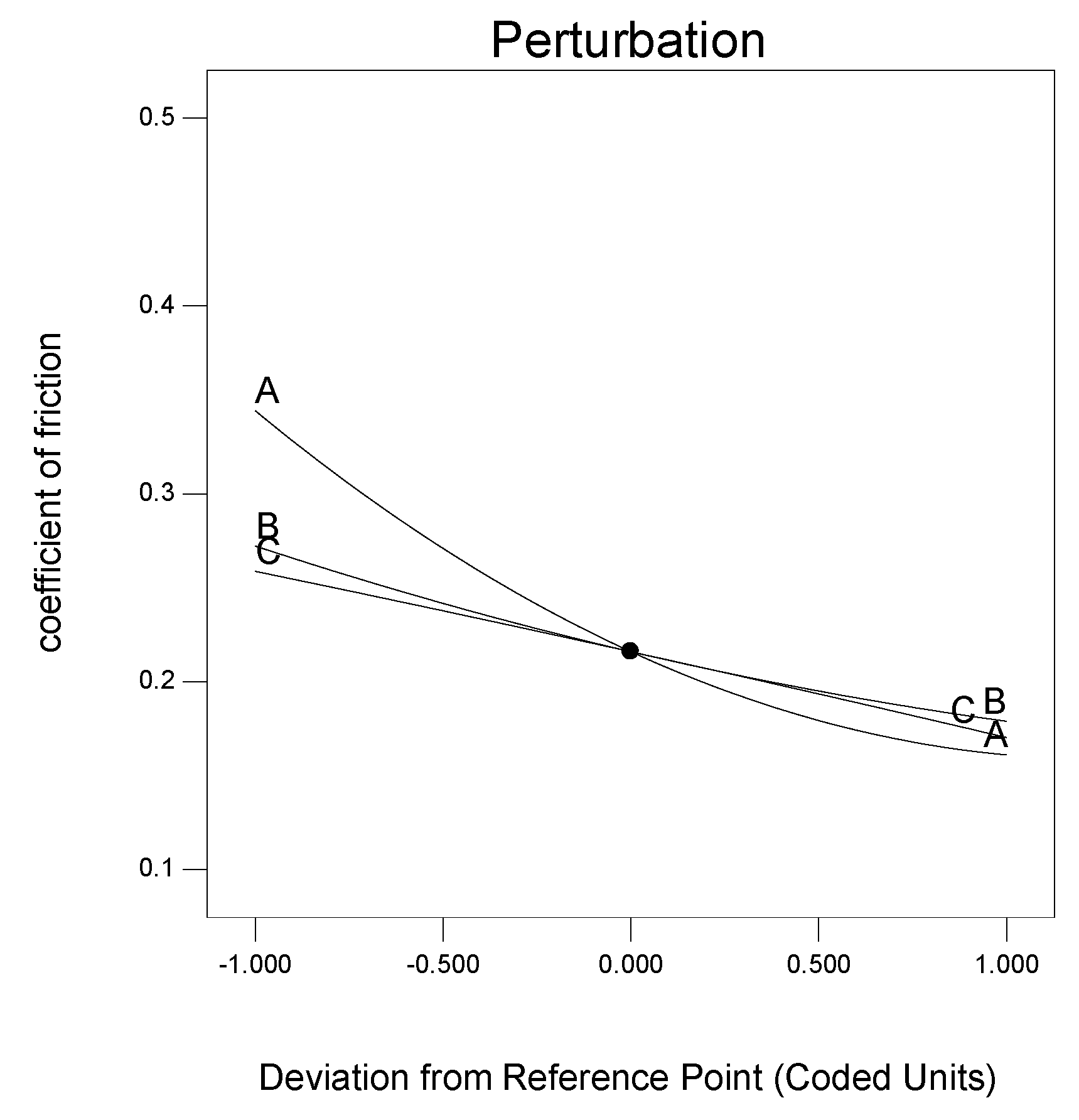
Figure 2 further presents the perturbation plot of the wear rate data at the experimented mid values of the process parameters. The comparison of the effects of all three parameters at a specific area in the design range can be enabled by the perturbation plot. The response (wear rate) was graphically plotted by changing a single parameter over its investigated limits while other parameters were maintained constant. Similar to the significance of the
p-value, this tool was also effective in identifying the interactive effects of parameters on the response [
17]. The X-axis of the plot showed the relative position of the chosen levels of the parameters to the coded scale. The slopes of the curves showed the rate at which the parameter influenced the response. In
Figure 2, the point selected in the design range was the central point (FA = 6 wt%, S 200 rpm and L 49 N).
The plot indicates that the fly ash content FA has the strongest inverse proportion (negative slope) on the wear rate while the load L has a smaller effect than FA, which was a direct proportional one (positive slope). The quadratic curves depicting the influence of the parameters on the wear rate were attributed to the quadratic terms in the model.
In summary, it is evident from
Figure 2 that the FA content has negative effect on wear rate while both the applied load and sliding speed exhibit a positive impact on the wear rate. By increasing the FA content, the wear rate can be decreased while the opposite can be obtained when the applied load and sliding speed were increased. This trend was similar to that obtained from the experimental results.
The combined effects of two process parameters on the wear rate, while the third was kept constant, were further evaluated and these are demonstrated in
Figure 3,
Figure 4 and
Figure 5. As described earlier for the perturbation plot, the third parameter could be changed, but again, it was kept at similar value selected for the perturbation figure. The red spheres on the graphs represent the experimental data points. Moreover, it is evident, especially on the 3D plots, that these spheres have close location to the surfaces, which indicate that the model fits properly with the data points. With respect to the effects of the combined parameters, they portrayed similar findings to those presented in the perturbation plot. However, by identifying their effects relative to the numerical values of the response, they offer a visual aid in selecting the desired ranges of the parameters. Furthermore, they were important in the optimization process of the ranges of the processing parameters so as to meet certain response criteria. Owing to these facts and to avoid redundancy, only brief discussions were given for each figure as provided in the following paragraph.
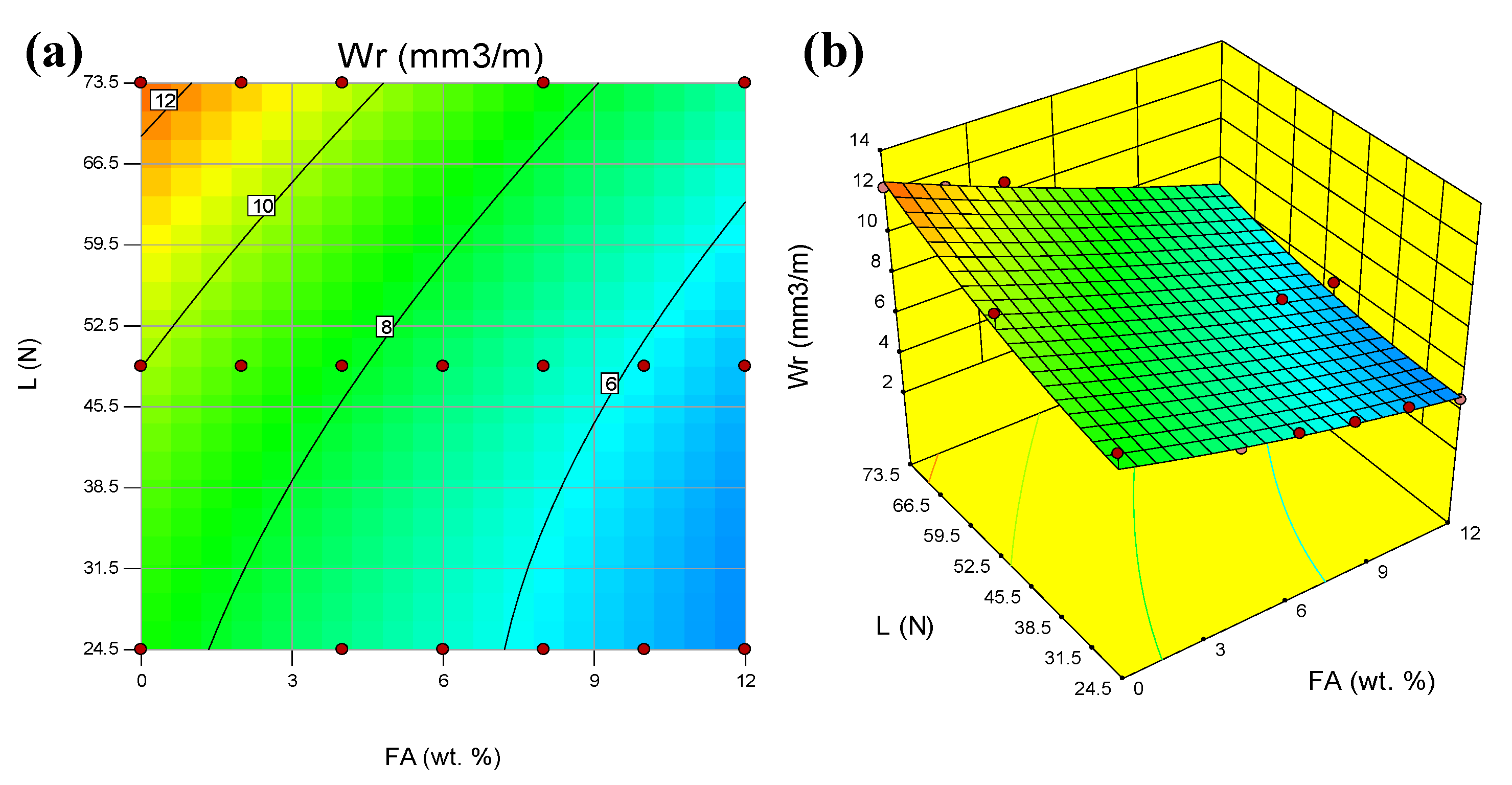
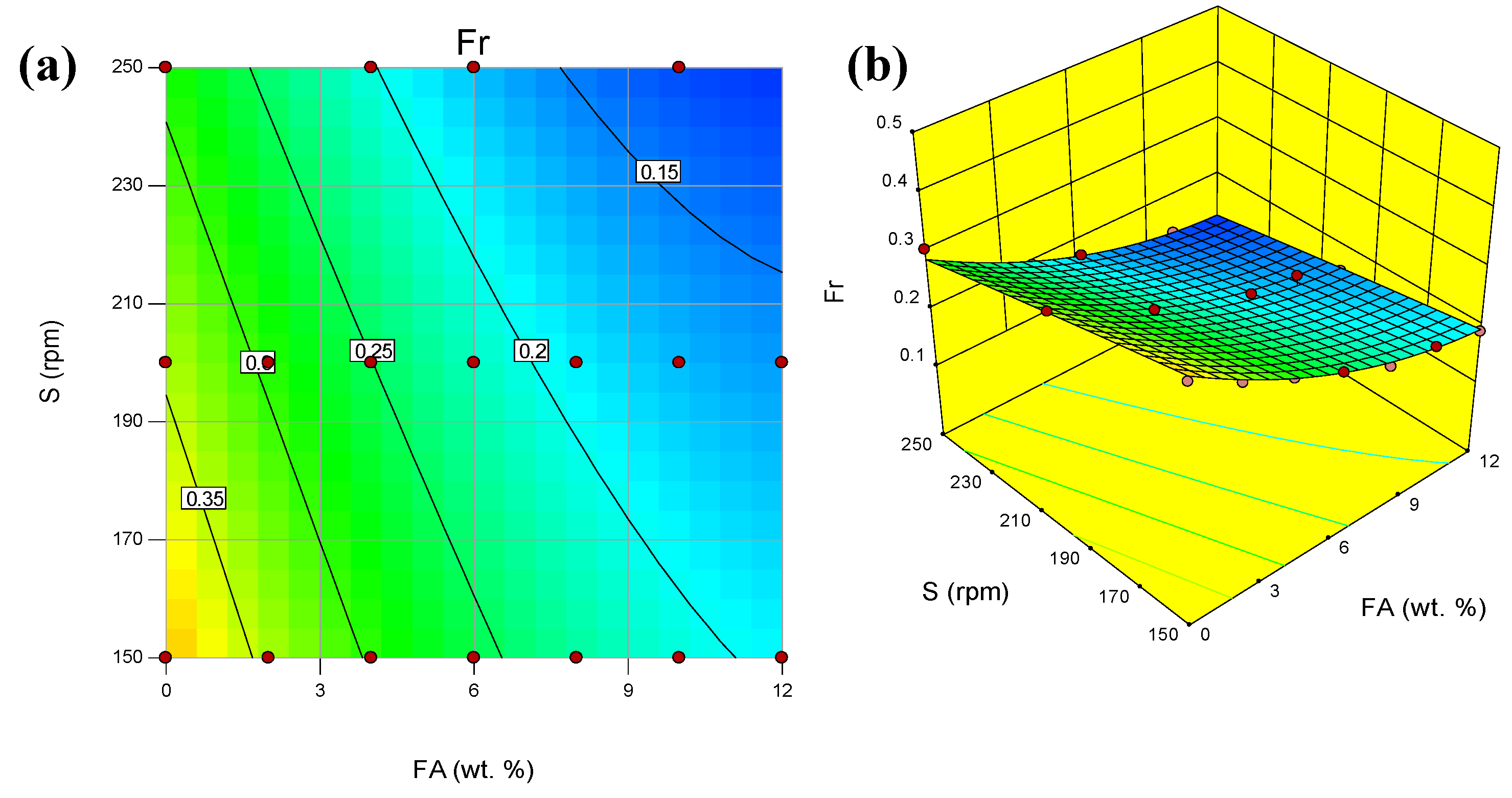
Figure 3a shows the contour plot of the effect of S and FA on the wear rate Wr. Each contour curve showed combinations of the two parameters that will predict a constant wear rate value. This wear rate value was observed inside the box situated at the middle of each contour curve. From the contour plot, S has a direct proportional effect on the predicted wear rate, while FA was inversely proportionate. The same data are further illustrated in 3D plot as shown in
Figure 3b. The 3D plot has the added advantage of visual display of the effect of one of the parameter changes when the value of the other parameter is modified. For instance, consider the effect of S at two different values of FA which were at 0- and 12-wt%, it can be observed that the FA effect was stronger in the first case.
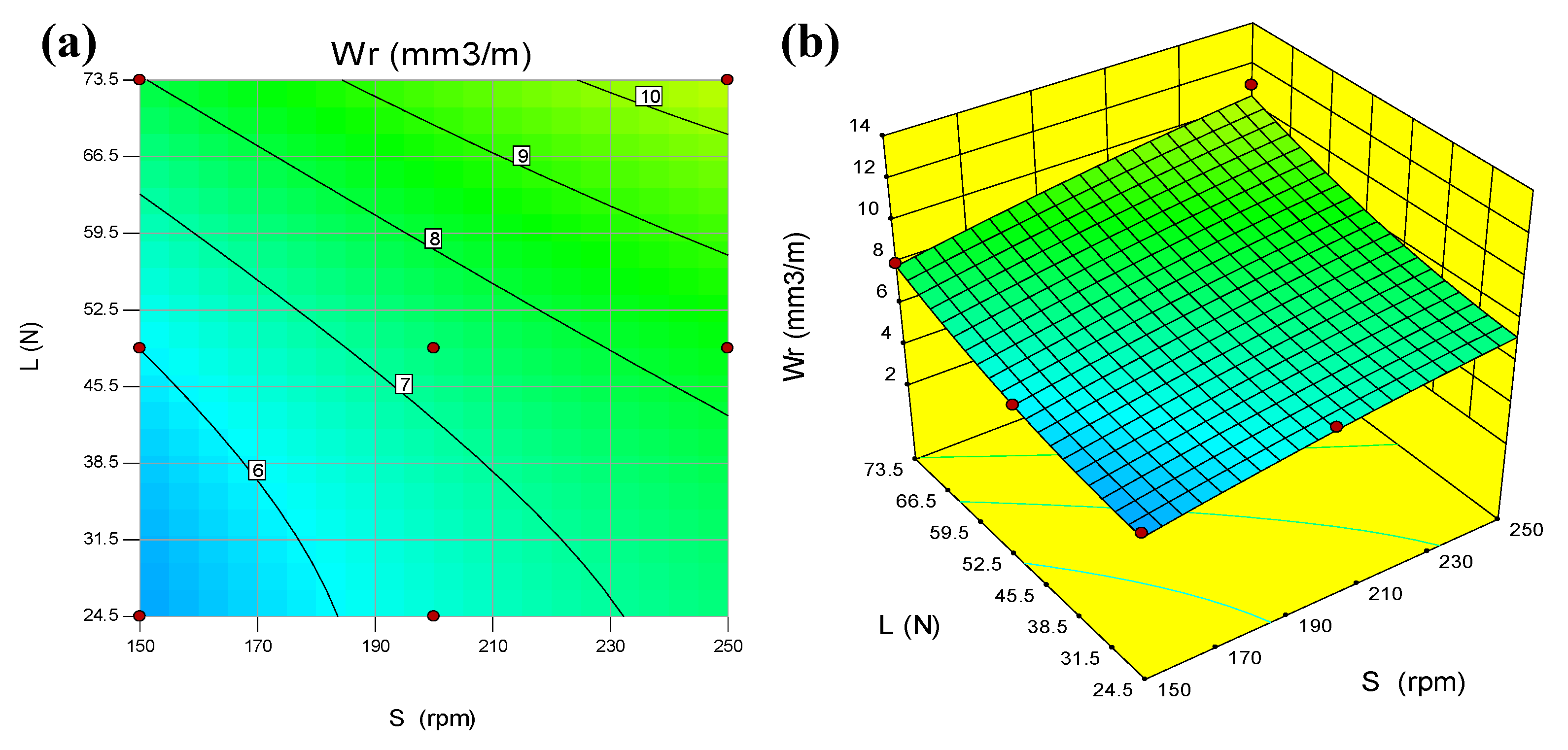
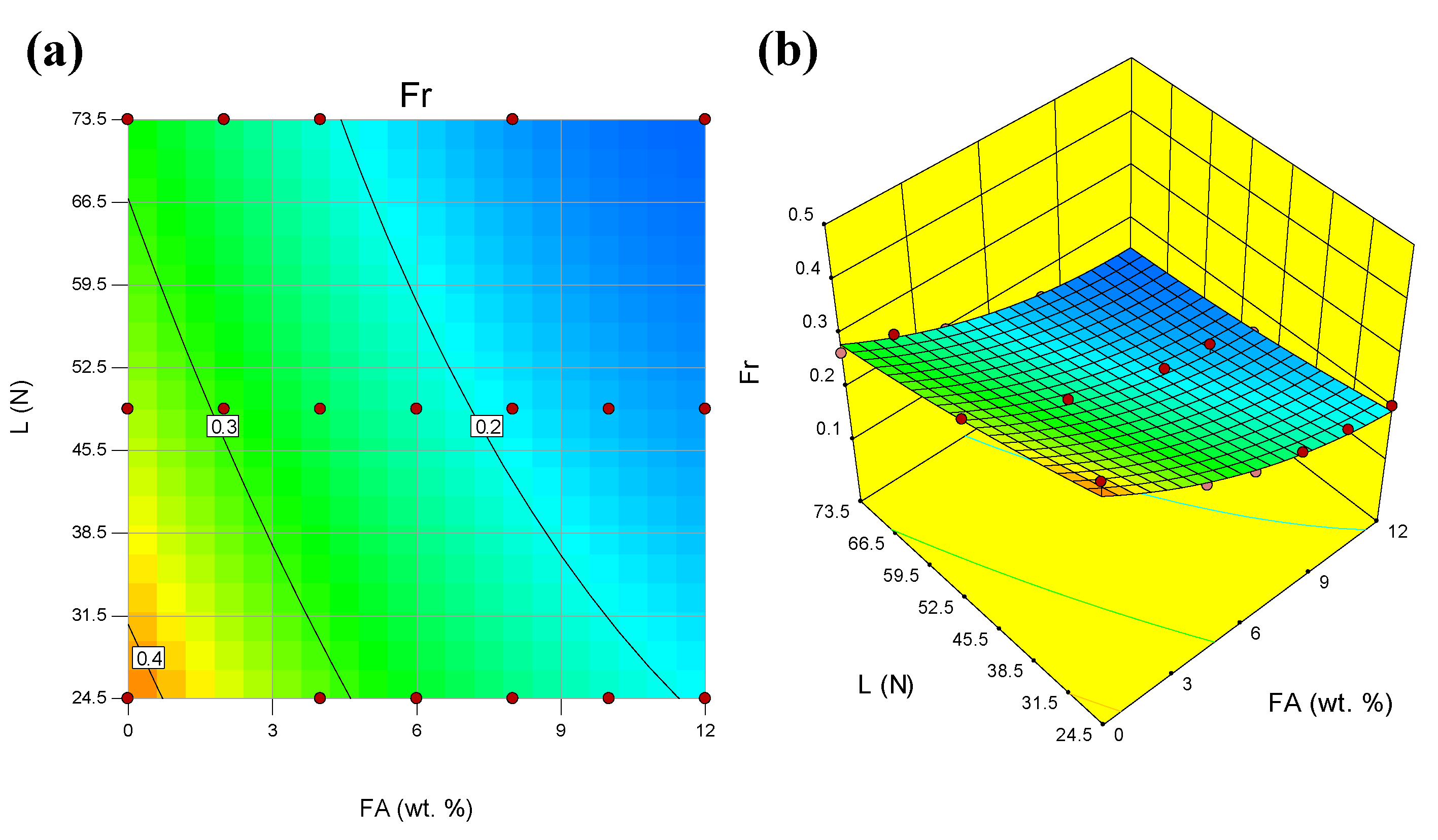
Figure 4a,b present that both S and L have directly proportional effects on the Wr. However, L has stronger effect than S. This indicated that variations in L led to larger variations in the Wr than those emanating from large variations in S.
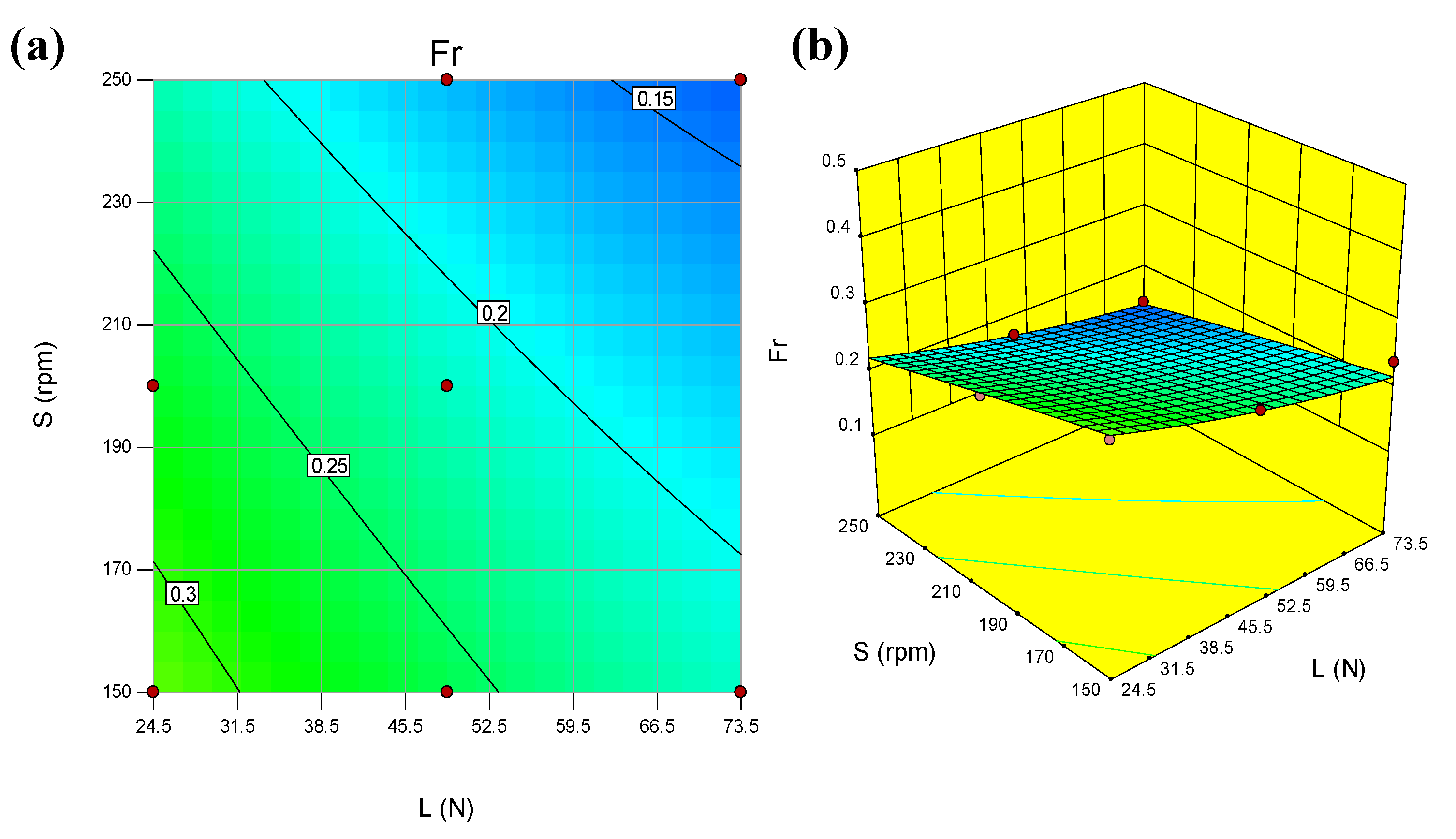
Figure 5a,b shows that FA has an inversely proportional effect on the Wr, while L has a directly proportional effect. Similarly, FA has stronger effect on the response than L exhibits.