Analysis of the Crack Initiation and Growth in Crystalline Materials Using Discrete Dislocations and the Modified Kitagawa–Takahashi Diagram
Abstract
1. Introduction
2. Crack Growth Analysis
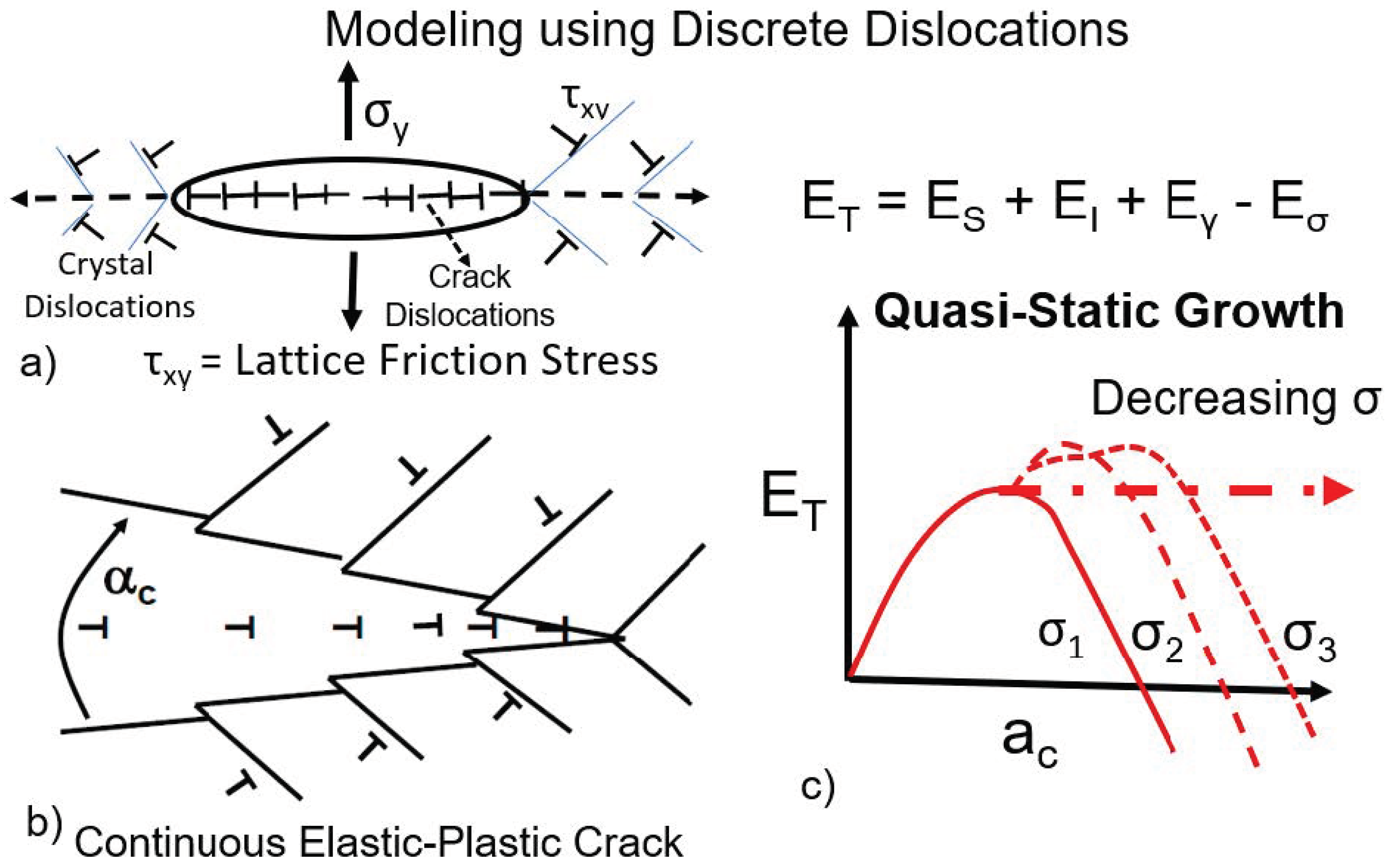
2.1. Discrete Dislocation Models
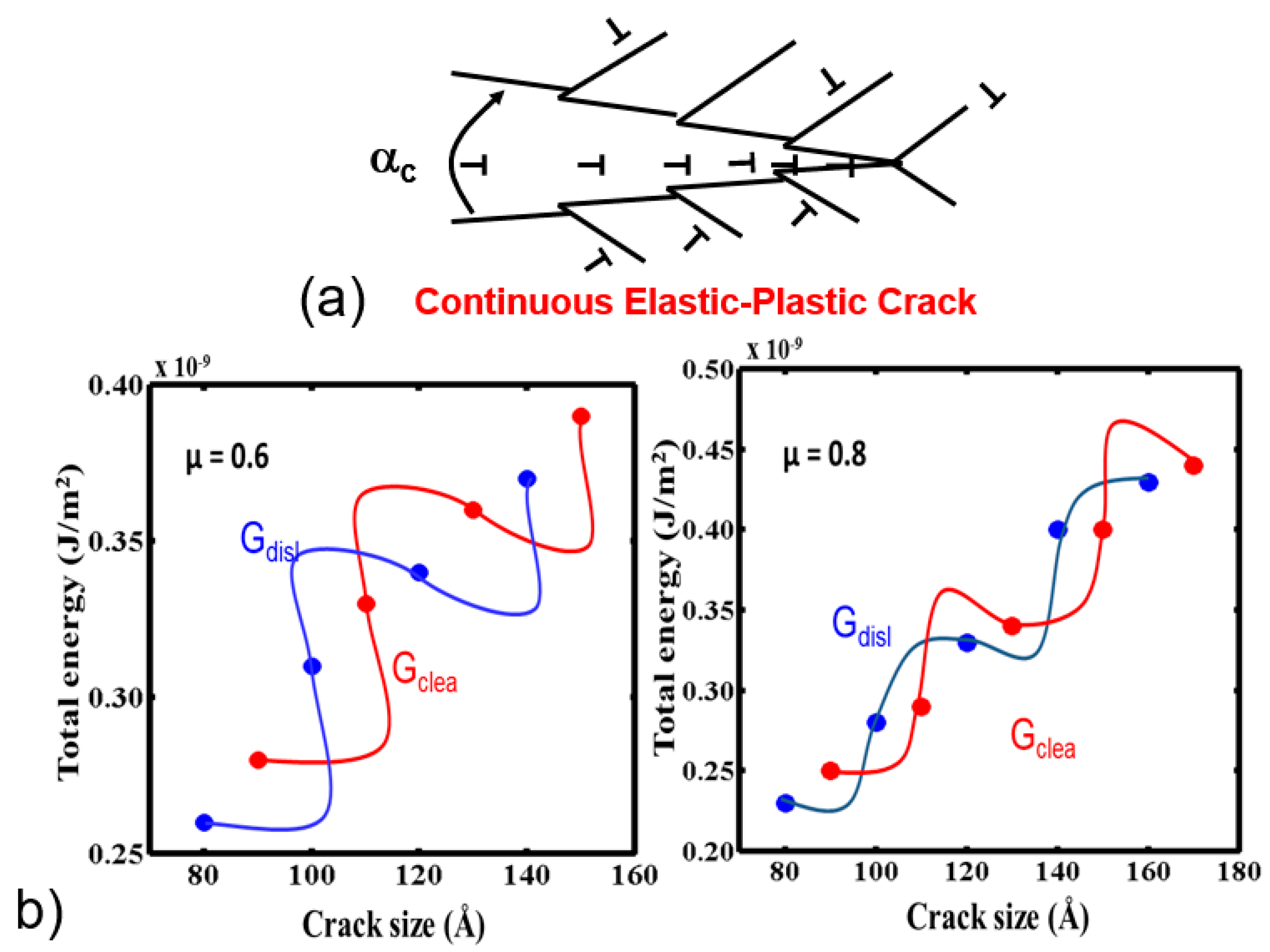
2.2. Continuous Elastic-Plastic Crack
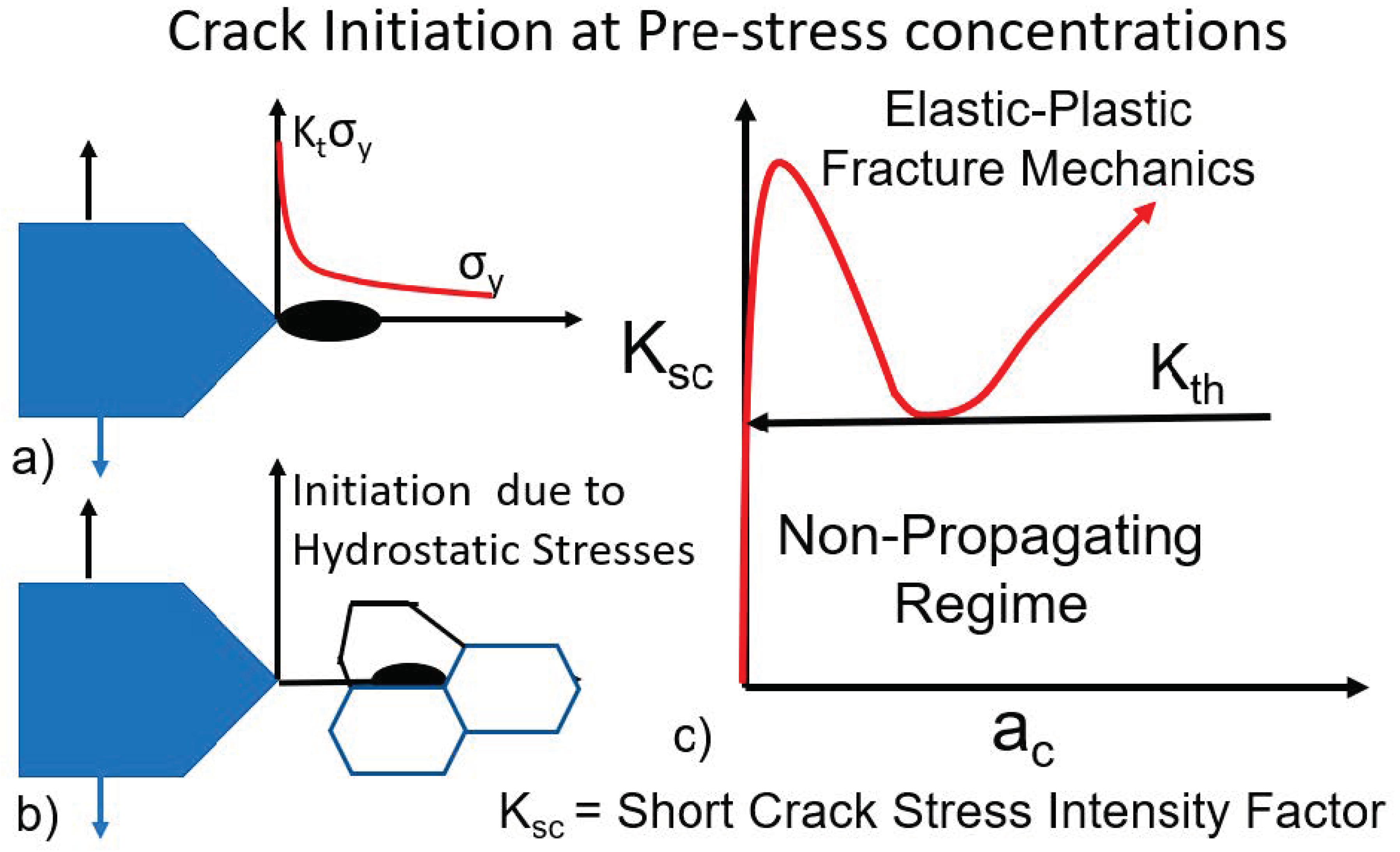
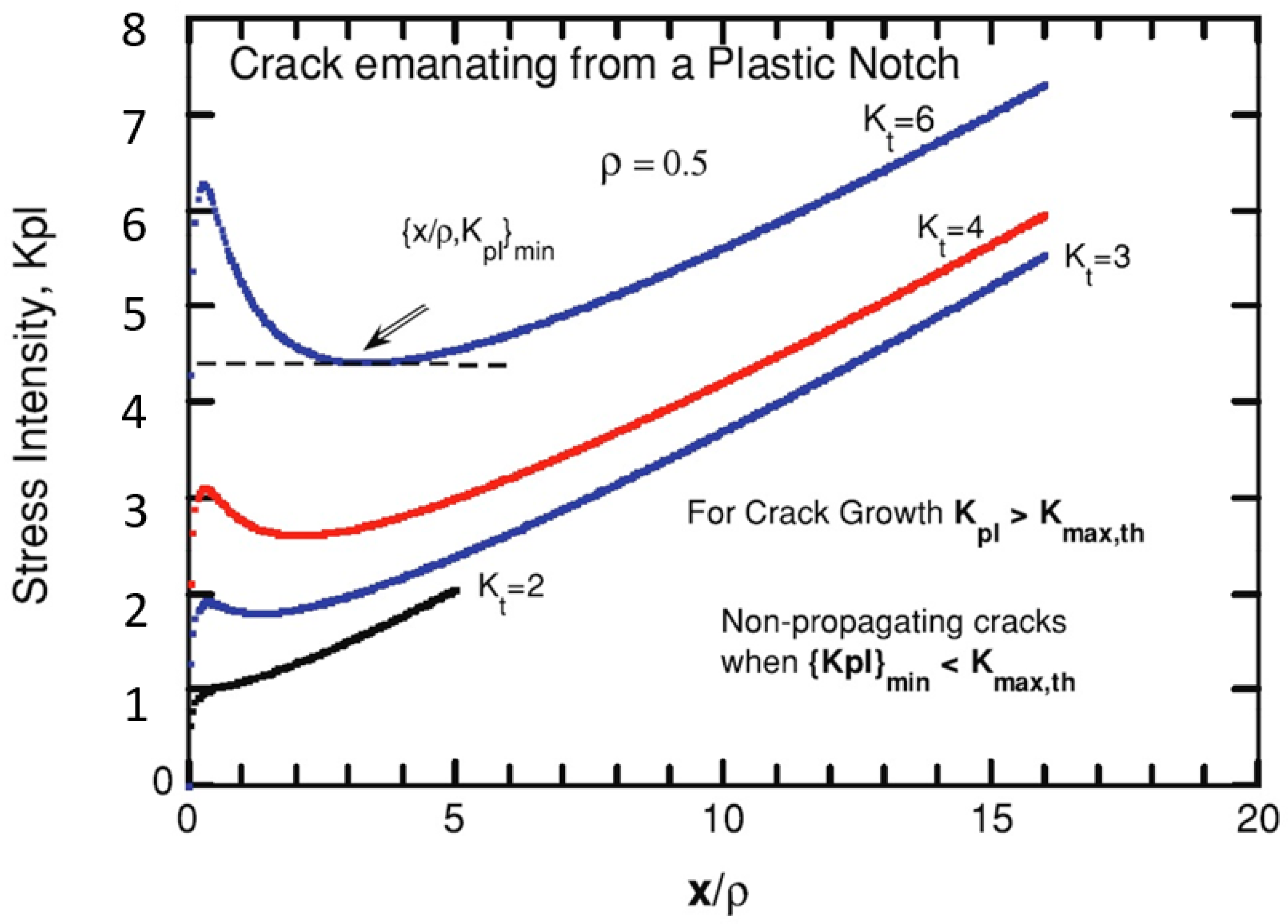
2.3. Crack Initiation at Pre-Existing Stress Concentrations
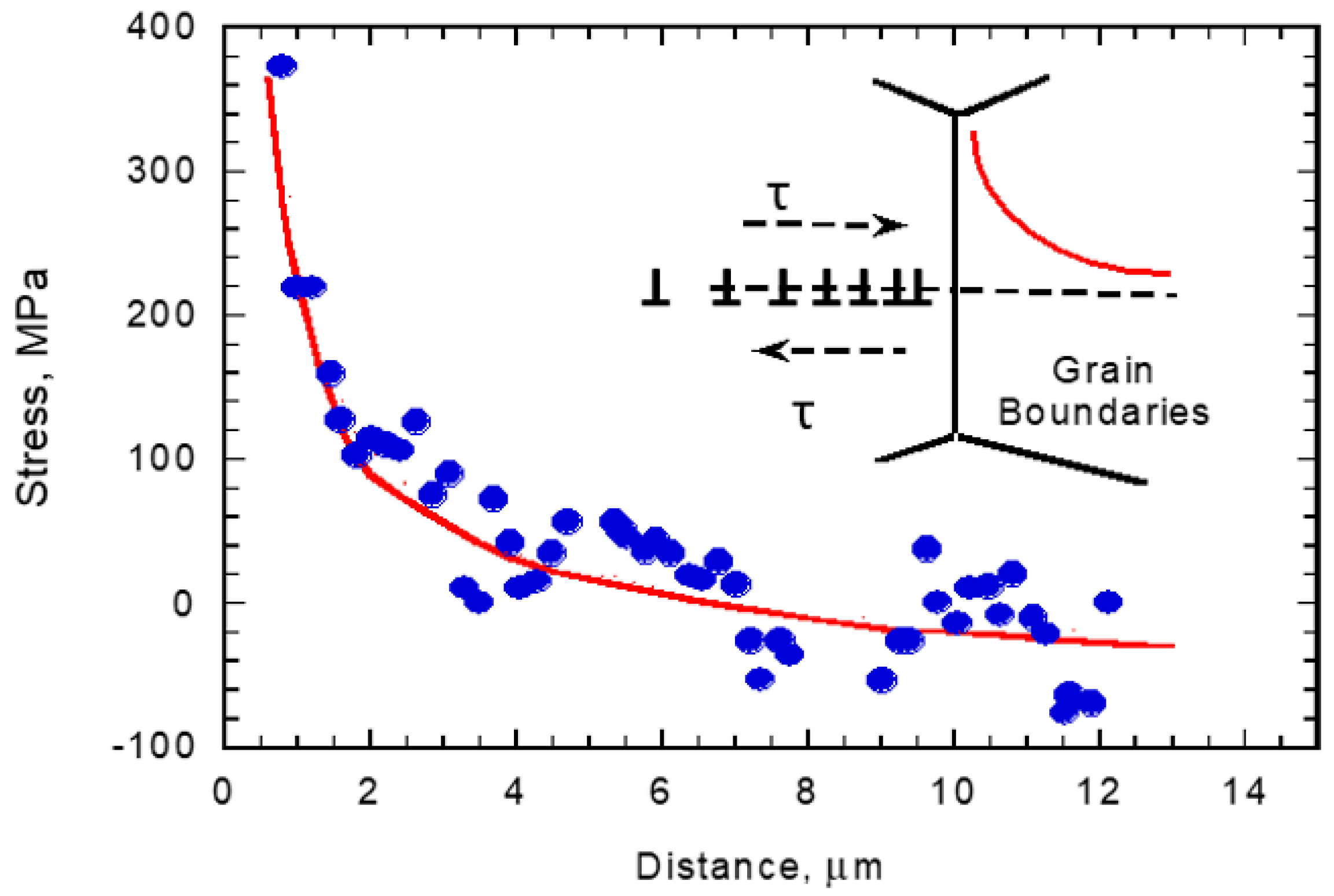
2.4. Crack Initiation at the In Situ Generated Stress-Concentrations
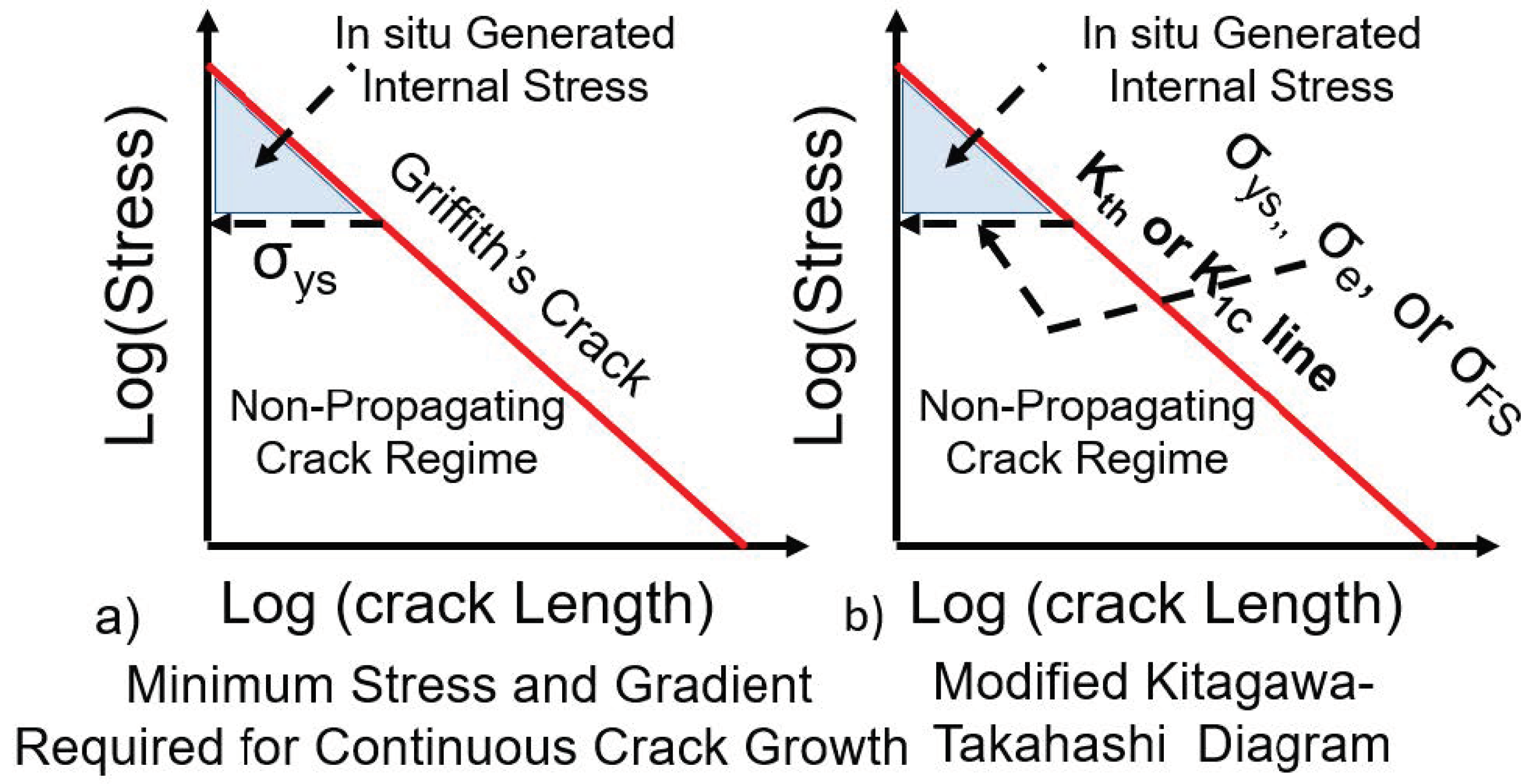
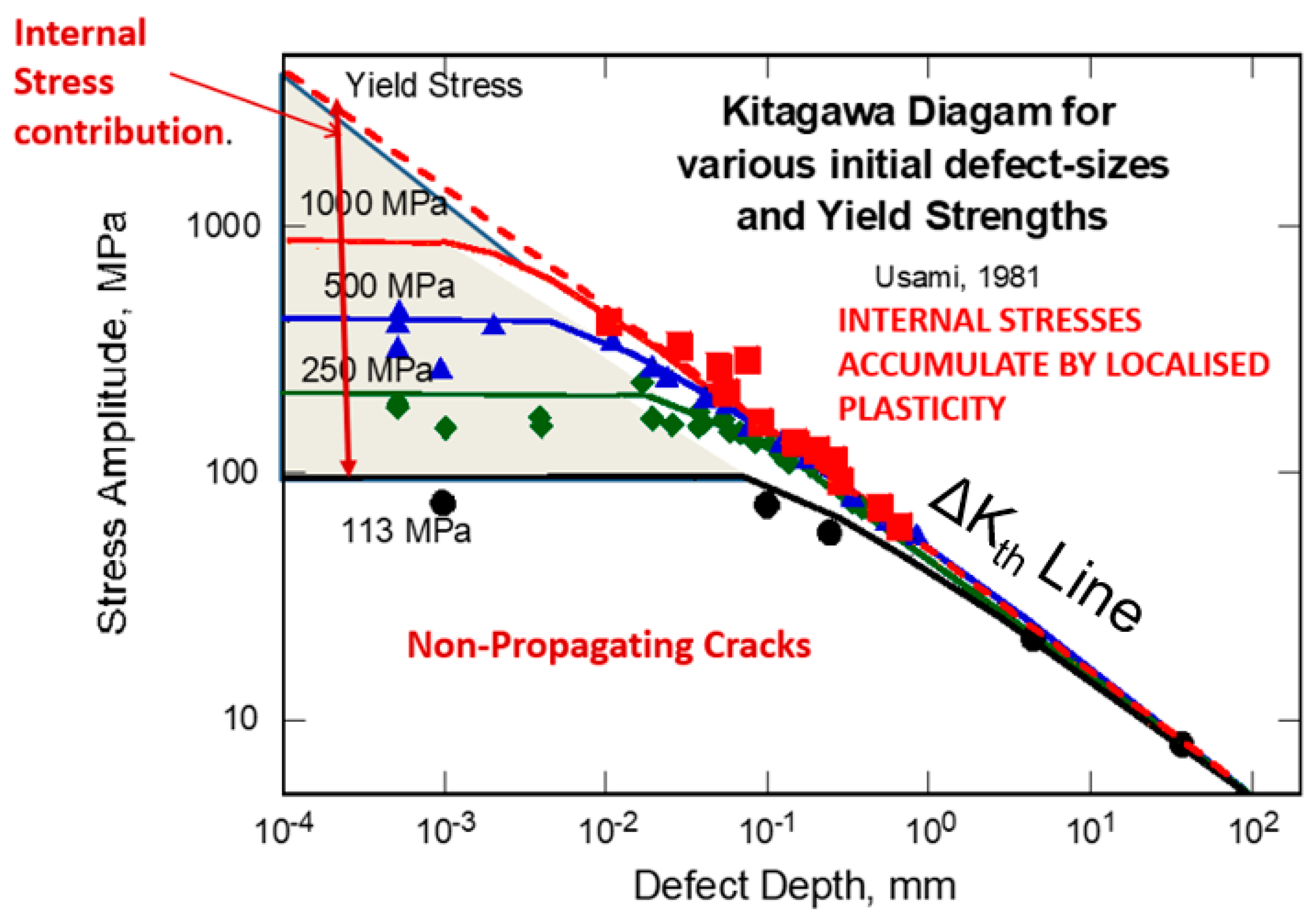
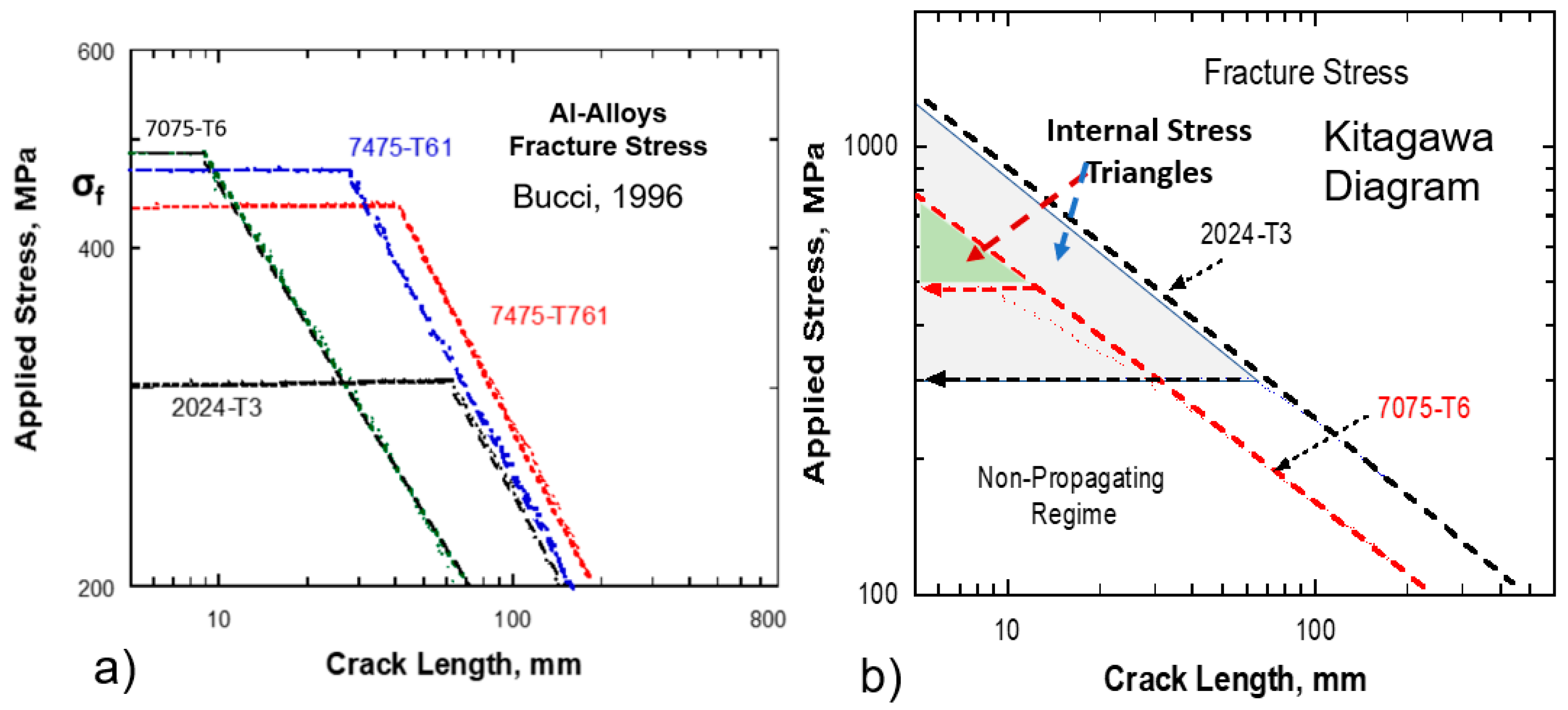
2.5. Role of Internal Stresses and the Modified Kitagawa-Takahashi Diagram
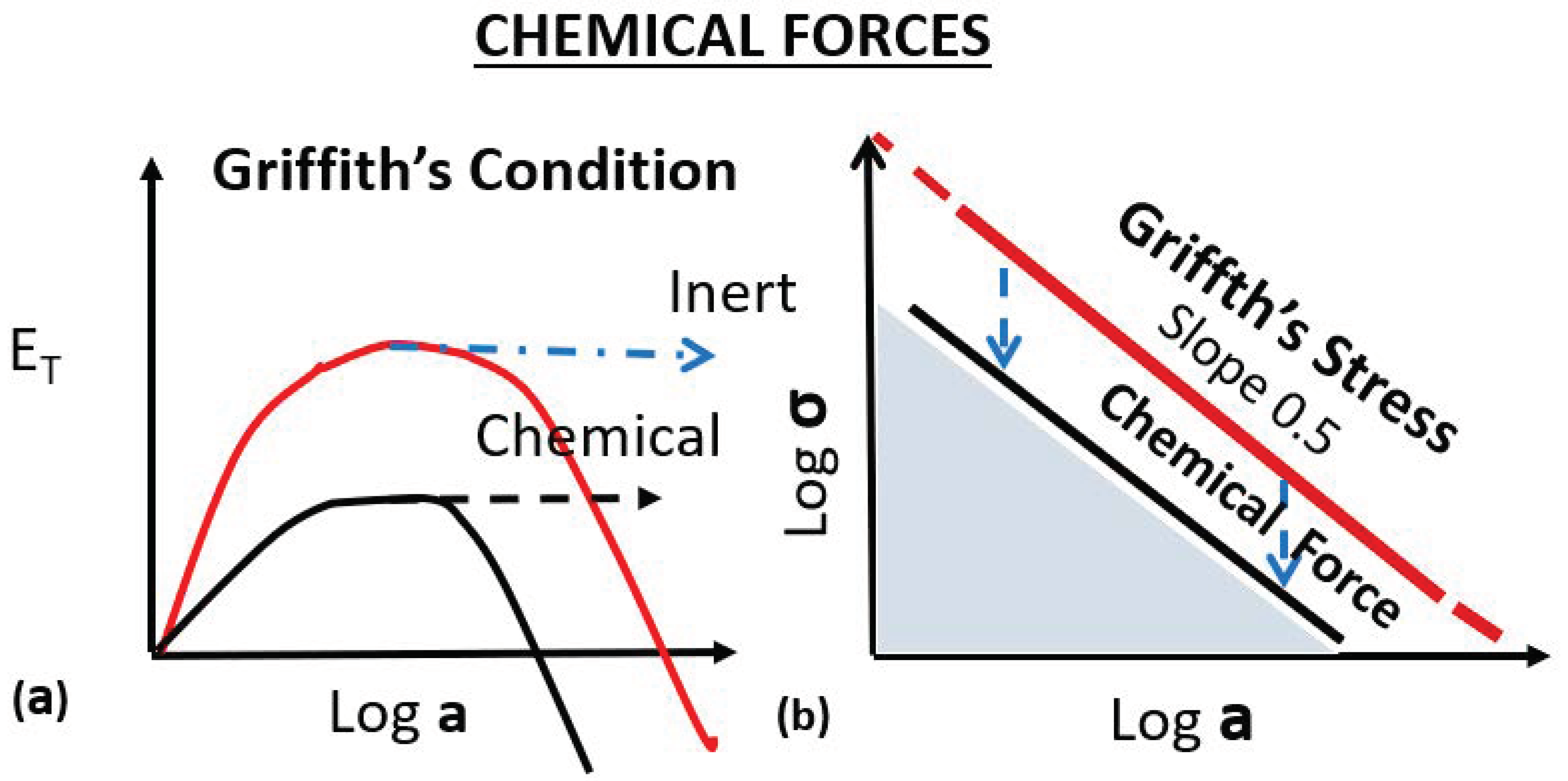
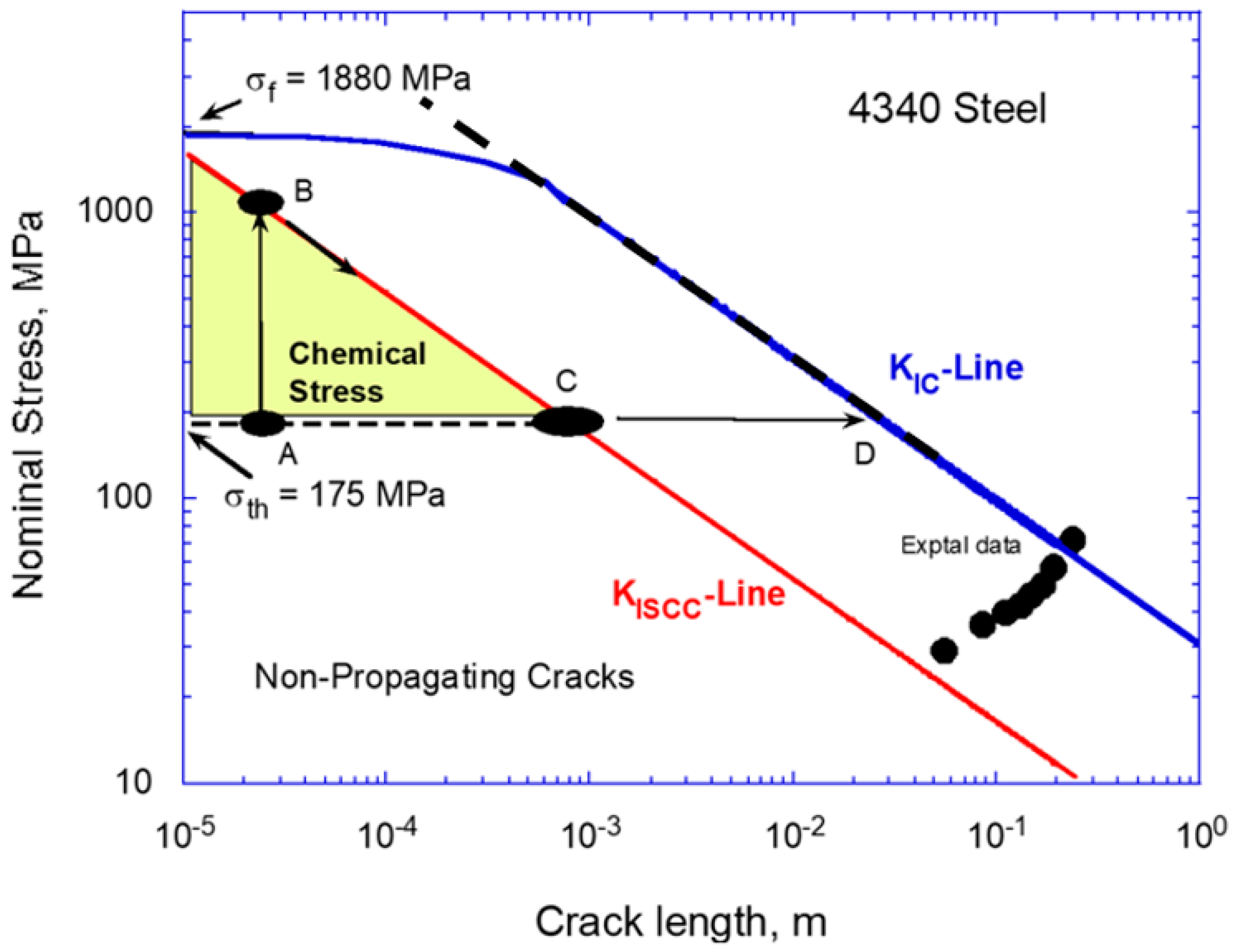
2.6. Role of Chemical Forces
3. Experimental Support for the Above Concepts
3.1. Application to Fracture Toughness
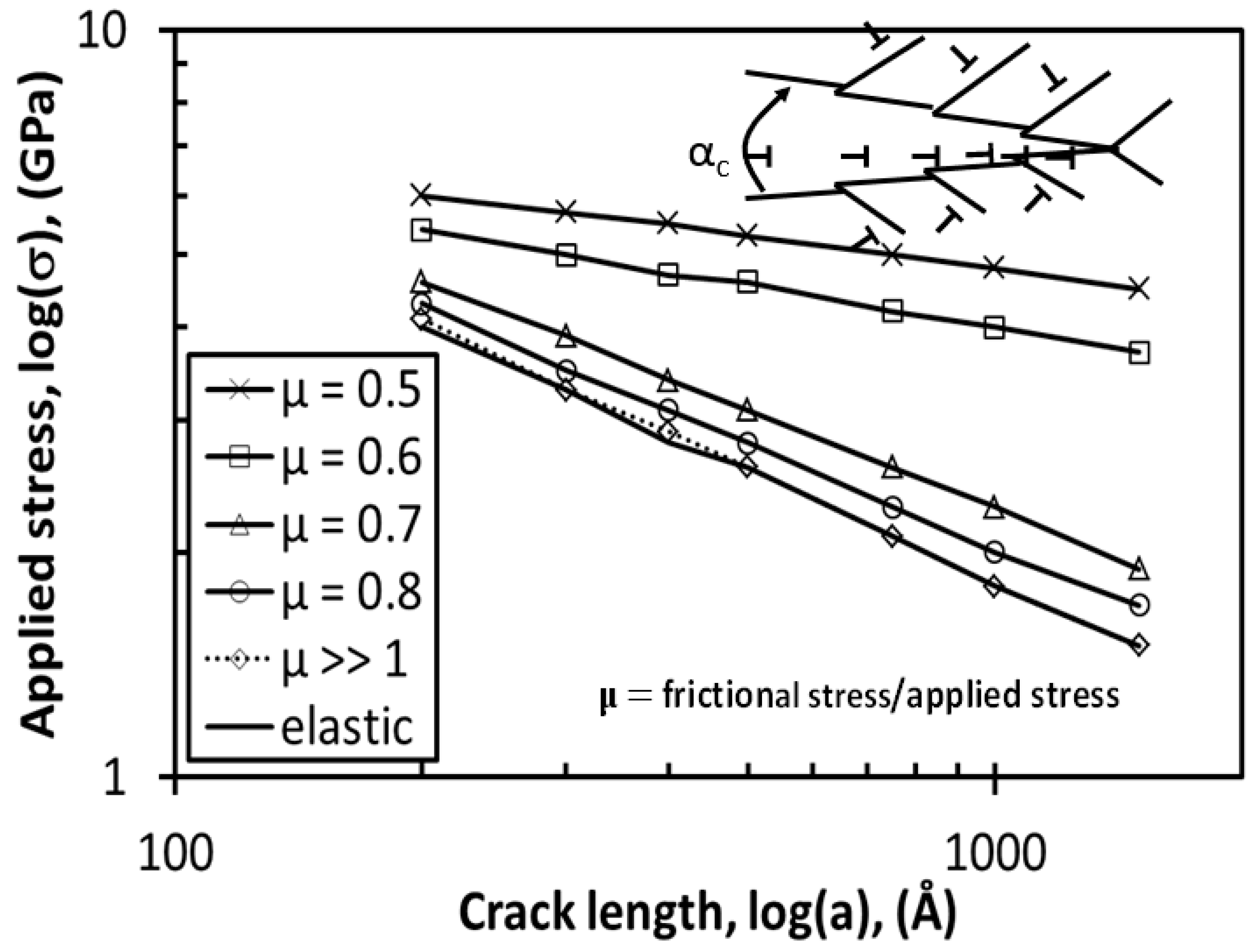
3.2. Discrete Dislocation Models
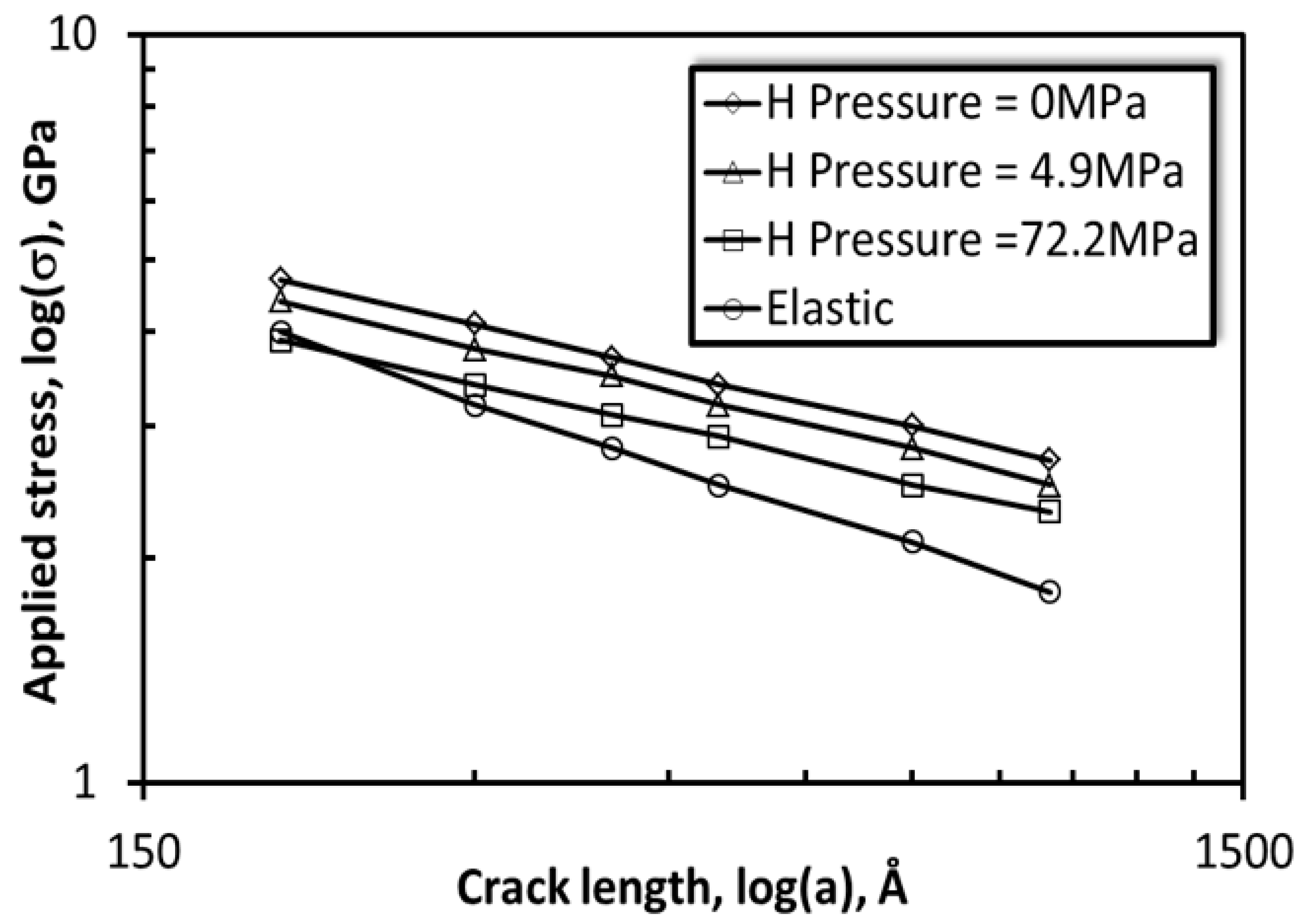
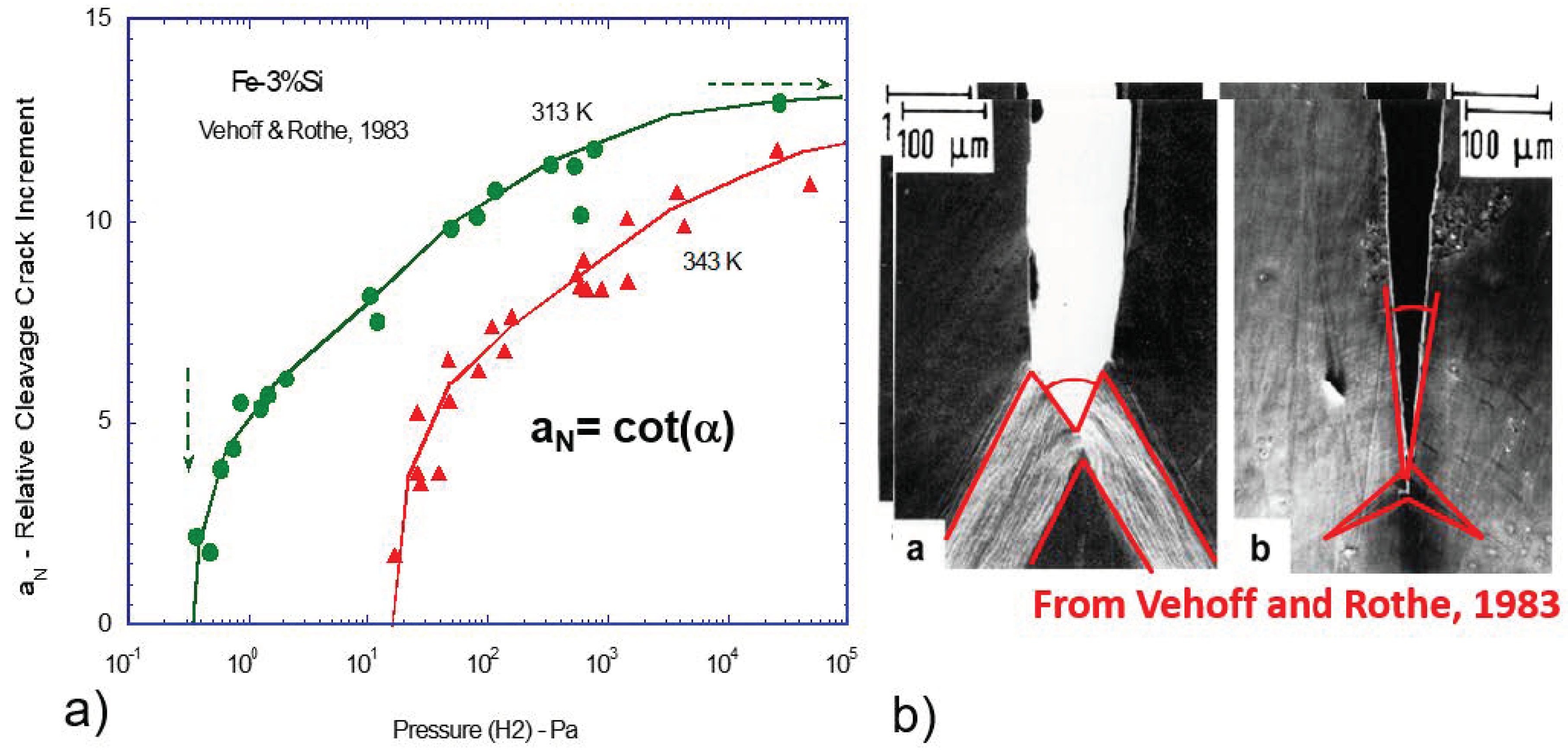
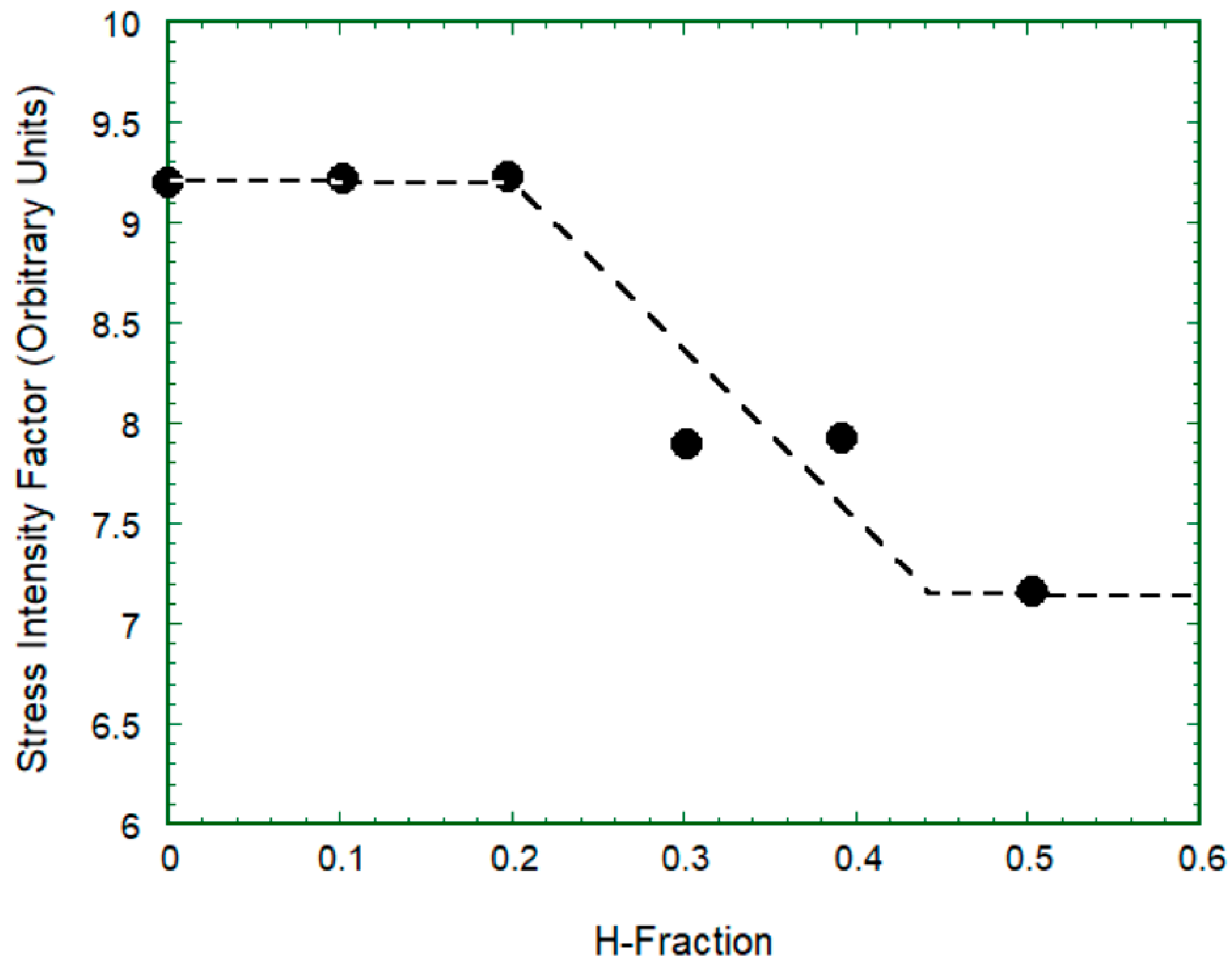
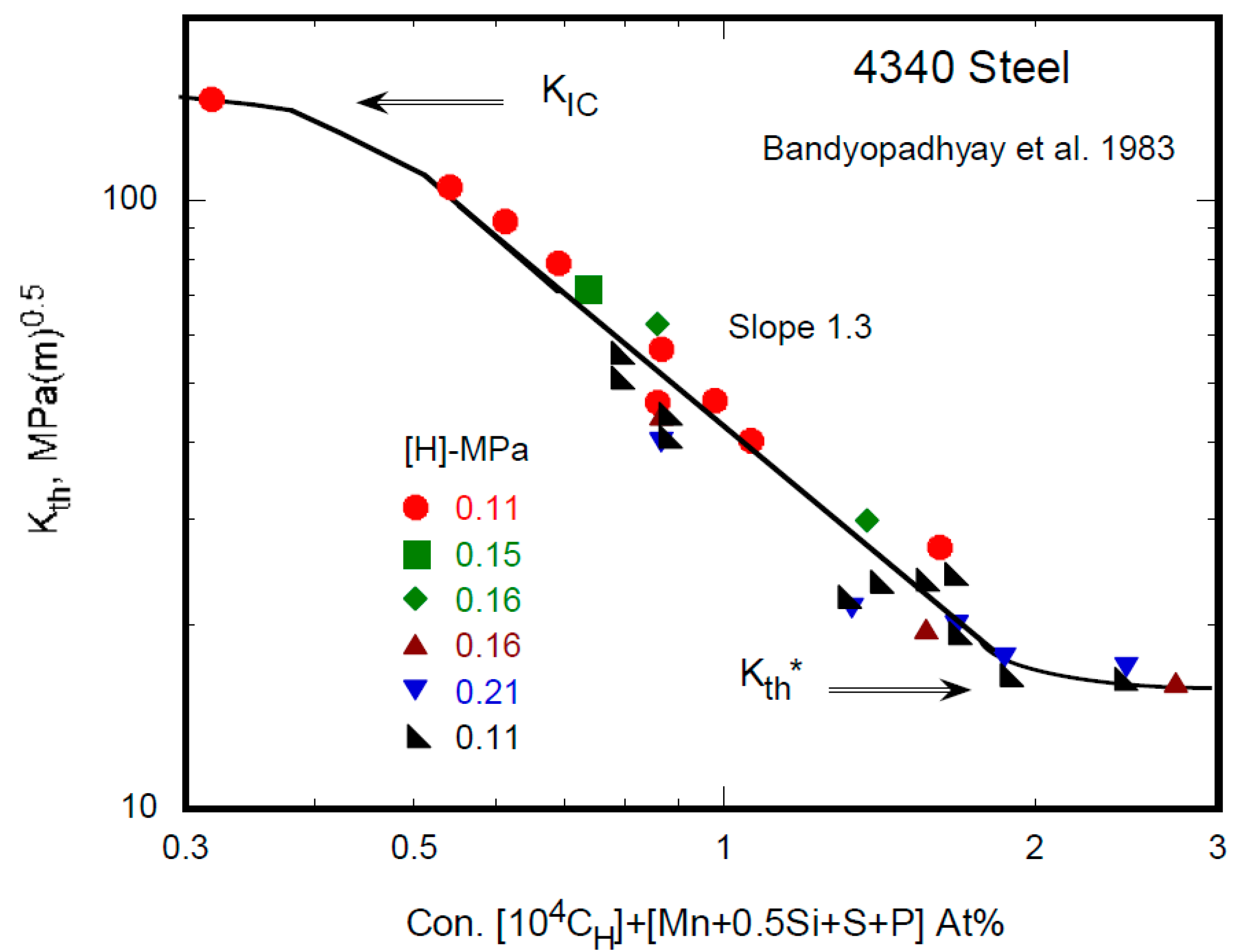
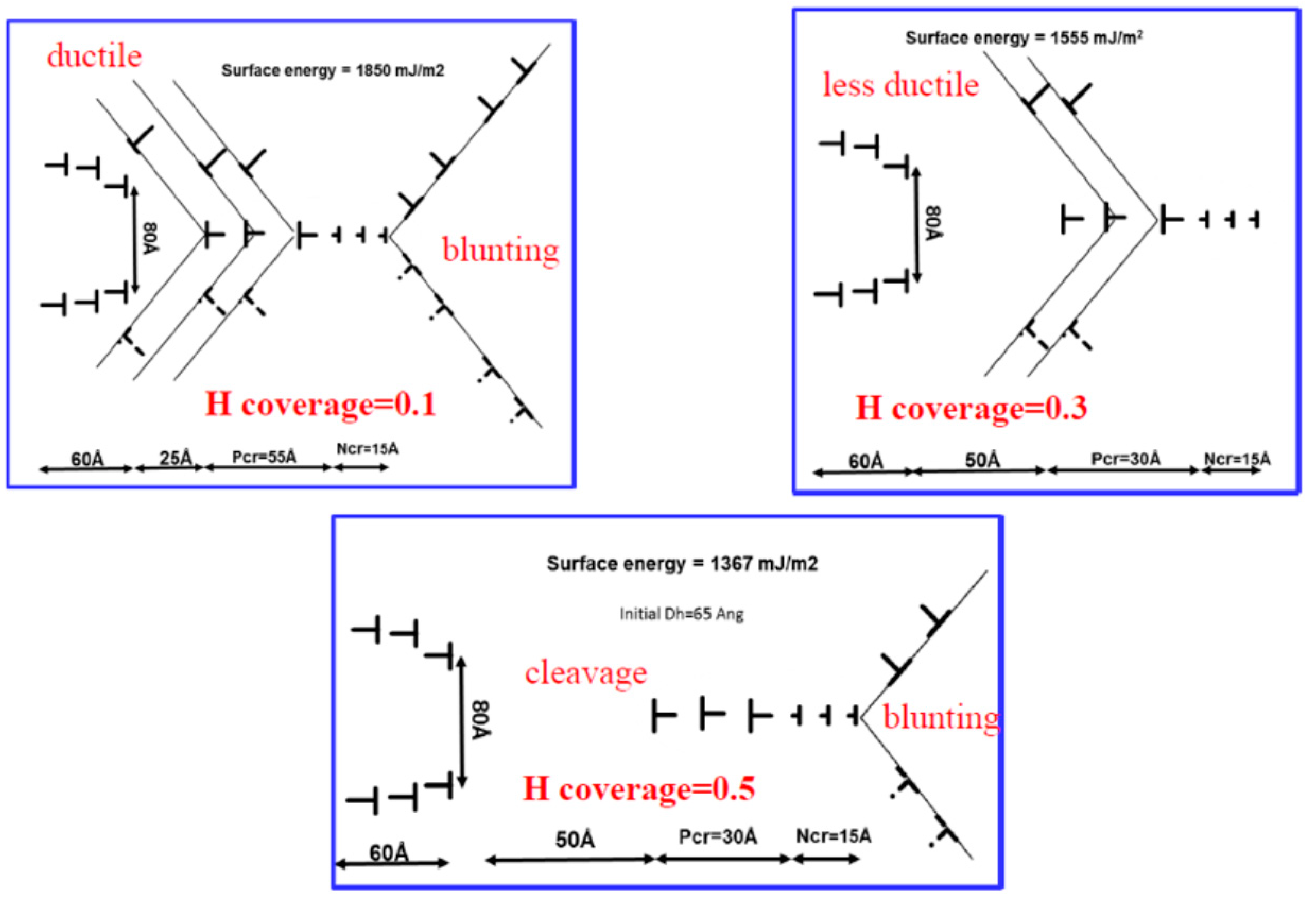
3.3. Effect of Hydrogen Pressure
3.4. Crack Initiation Ahead of the Main Crack
4. Summary
Author Contributions
Funding
Conflicts of Interest
Symbols Used
| ASTM—American Society of Testing and Materials |
| KT diagram—Kitagawa Takahashi |
| μ—Ratio of frictional stress to applied stress. |
| BCS model—Bilby, Cottrell, and Swindon model |
| a—Crack Length |
| ac—Critical Crack length |
| σy—Normal Stress |
| ET—Total Energy of the System |
| ES—Self Energy of all dislocations |
| EI—Interaction energy of all dislocation |
| Eγ—Surface energy |
| Eσ—Work done by applied stress |
| τxy—Lattice frictional stress |
| αc—Crack mouth angle |
| Kt—Elastic Stress Concentration Factor |
| ρ—Notch tip radius |
| KSC—Stress intensity factor for short crack |
| Kth—Threshold stress intensity factor for crack growth |
| KIC—Fracture Toughness |
| KISCC—Stress Corrosion Crack Growth Threshold |
| Kpl—Stress intensity factor for short crack in the elastic plastic notch tip field. |
| ΔKth—Fatigue crack growth threshold Stress intensity range. |
| σapl—Applied Stress |
| σys—Yield Stress |
| σe—Endurance Stress |
| σFS—Fracture Stress |
| E—Elastic Modulus |
| γ—Surface Energy |
| ν—Poisson ratio |
References and Note
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. 1921, 221, 163–198. [Google Scholar]
- Dieter, G.E. Mechanical Metallurgy, 3rd ed.; McGraw-Hill Inc.: New York, NY, USA, 1986; pp. 299–301, 452–453. ISBN 0-07-016893-8. [Google Scholar]
- Armstrong, R.W. Material grain size and crack size influences on cleavage fracturing. Philos. Trans. R. Soc. A 2015, 373, 20140124. [Google Scholar] [CrossRef] [PubMed]
- Jagannadham, K.; Marcinkowski, M.J. Unified Theory of Fracture; Trans Tech Publications Ltd.: Zurich, Switzerland, 1983. [Google Scholar]
- Rice, J.R. Elastic-plastic fracture mechanics. Eng. Fract. Mech. 1973, 5, 1019–1022. [Google Scholar] [CrossRef]
- Bilby, B.A.; Cottrell, A.H.; Swinden, K.H. The spread of plastic yield from a notch. Proc. R. Soc. Lond. A 1963, 272, 304–314. [Google Scholar]
- Orowan, E. Fracture and strength of solids. Rep. Prog. Phys. XII 1948, 12, 185–232. [Google Scholar] [CrossRef]
- Zhao, R.H.; Dai, S.-H.; Li, J.C.M. Dynamic emission of dislocations from a crack tip, a computer simulation. Int. J. Fract. 1985, 29, 3. [Google Scholar] [CrossRef][Green Version]
- Rice, J.R. Tensile crack tip fields in elastic-ideally plastic crystals. Mech. Mater. 1987, 6, 317–335. [Google Scholar] [CrossRef]
- Weertman, J. Mathematical Theory of Dislocations; Mura, T., Ed.; American Society of Mechanical Engineers: New York, NY, USA, 1969; p. 178. [Google Scholar]
- Marcinkowski, M.J. Dislocation model of a plastic tensile crack. J. Appl. Phys. 1975, 46, 496. [Google Scholar] [CrossRef]
- Marcinkowski, M.J.; Das, E.S.P. Relationship between crack dislocations and crystal lattice dislocations. Phys. Status Solidi A 1971, 8, 249. [Google Scholar] [CrossRef]
- Sadananda, K.; Jagannadham, K.; Marcinkowski, M.J. Discrete dislocation analysis of a plastic tensile crack. Phys. Status Solidi A 1977, 44, 633–642. [Google Scholar] [CrossRef]
- Adlakha, I.; Sadananda, K.; Solanki, K.N. Discrete dislocation modeling of stress corrosion cracking in an iron. Corros. Rev. 2015, 33, 467–475. [Google Scholar] [CrossRef]
- Sadananda, K.; Sakar, S. Modified Kitagawa Diagram and Transition from Crack Nucleation to Crack Propagation. Metall. Mater. Trans. 2012, 44, 1175–1189. [Google Scholar] [CrossRef]
- Sadananda, K.; Arcari, A.; Vasudevan, A.K. Does a nucleated crack propagate? Eng. Fract. Mech. 2017, 176, 144–160. [Google Scholar] [CrossRef]
- Rice, J.R.; Thomson, R.M. Ductile versus brittle behavior of crystals. Philos. Mag. 1974, 29, 73. [Google Scholar] [CrossRef]
- Rice, J.R. Dislocation nucleation from a crack tip: An analysis based on the Peierls concept. J. Mech. Phys. Solid. 1992, 40, 239–271. [Google Scholar] [CrossRef]
- Beltz, G.E.; Rice, J.R.; Shih, C.F.; Xia, L. A self-consistent model for cleavage in the presence of plastic flow. Acta Mater. 1996, 44, 3943–3954. [Google Scholar] [CrossRef][Green Version]
- Kitagawa, H.; Takahashi, S. Applicability of fracture mechanics to a very small crack or the cracks in the early stage. In Proceedings of the Second International Conference on Mechanical Behavior of Materials, Cleveland, OH, USA, 16–20 August 1976; pp. 627–631. [Google Scholar]
- Active Standard ASTM E399, Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness KIC of Metallic Materials.
- Raju, I.S.; Atluri, S.N.; Newman, J.C., Jr. Stress intensity factors for small surface and corner cracks in plates. In Fracture Mechanics: Perspectives and Directions (Twentieth Symposium); Wei, R.P., Gangloff, R.P., Eds.; American Society for Testing and Materials (ASTM): Philadelphia, PA, USA, 1989; pp. 297–316. [Google Scholar]
- Sadananda, K.; Vasudevan, A.K. Analysis of pit to crack transition under corrosion fatigue & the safe-life approach using the modified Kitagawa-Takahashi. Int. J. Fatigue 2020, 134, 105471. [Google Scholar]
- Rice, J.R.; Tracy, D.M. On the ductile enlargement of voids in the triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Ritchie, R.O.; Knott, J.F.; Rice, J.R. Relationship between critical tensile stress and fracture toughness in mild steel. J. Mech. Phys. Solids 1973, 21, 395–410. [Google Scholar] [CrossRef]
- McCoy, R.A.; Gerberich, W.W. Hydrogen Embrittlement Studies of a Trip Steel. Metall. Trans. 1973, 4, 539–547. [Google Scholar] [CrossRef]
- Eshelby, J.D.; Frank, F.C.; Nabarro, F.R.N. The equilibrium array of Dislocations. Philos. Mag. 1951, 42, 351–364. [Google Scholar] [CrossRef]
- Guo, Y.; Britton, T.B.; Wilkinson, A.J. Slip band grain boundary interactions in commercial pure Titanium. Acta Mater. 2014, 76, 1–12. [Google Scholar] [CrossRef]
- Glinka, G.; Newport, A. Universal function of elastic notch tip stress fields. Int. J. Fatigue 1987, 9, 144–150. [Google Scholar] [CrossRef]
- Sadananda, K.; Nani Babu, M.; Vasudevan, A.K. A Review of Fatigue crack growth resistance in the short crack growth regime. Mater. Sci. Eng. A 2019, 754, 674–701. [Google Scholar] [CrossRef]
- Usami, S. Applications of threshold cyclic-plastic-zone-size criterion to some limit problems. In Fatigue Thresholds; Blacklund, I., Bloom, A., Beevers, C.J., Eds.; EMAS: Stockholm, Sweden, 1981; pp. 205–238. [Google Scholar]
- Hirose, Y.; Mura, T. Nucleation mechanism of stress corrosion cracking from notches. Eng. Fract. Mech. 1984, 19, 317–329. [Google Scholar] [CrossRef]
- Bucci, R.J.; Nordmark, G.; Starke, E.A., Jr. Selecting Aluminum alloys to resist failure by fracture mechanisms. In ASM Handbook 19, Fatigue and Fracture; Materials Park, OH 44073-0002; ASM Handbook Committee: Oxfordshire, UK, 1996; pp. 771–812. [Google Scholar]
- Gangloff, R.P. Environmental Cracking-Corrosion Fatigue, Ch.26. In Corrosion Tests and Standard Manual, 2nd ed.; Baboian, R., Ed.; MIL-HDBK 729; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Adlakha, I.; Solanki, K.N. Critical assessment of hydrogen effects on the slip transmission across grain boundaries in α-Fe. Proc. R. Soc. A 2016, 472, 617. [Google Scholar] [CrossRef] [PubMed]
- Vehoff, H.; Rothe, W. Gaseous hydrogen embrittlement in FeSi and Ni single crystals. Acta Metall. 1983, 31, 1781–1793. [Google Scholar] [CrossRef]
- Bandyopadhyay, N.; Kameda, J.; McMahon, C.J., Jr. Hydrogen-induced cracking in 4340-type steel: Effects of composition, yield strength and hydrogen pressure. Metall. Trans. A 1983, 14, 881–888. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadananda, K.; Adlakha, I.; Solanki, K.N.; Vasudevan, A.K. Analysis of the Crack Initiation and Growth in Crystalline Materials Using Discrete Dislocations and the Modified Kitagawa–Takahashi Diagram. Crystals 2020, 10, 358. https://doi.org/10.3390/cryst10050358
Sadananda K, Adlakha I, Solanki KN, Vasudevan AK. Analysis of the Crack Initiation and Growth in Crystalline Materials Using Discrete Dislocations and the Modified Kitagawa–Takahashi Diagram. Crystals. 2020; 10(5):358. https://doi.org/10.3390/cryst10050358
Chicago/Turabian StyleSadananda, Kuntimaddi, Ilaksh Adlakha, Kiran N. Solanki, and A.K. Vasudevan. 2020. "Analysis of the Crack Initiation and Growth in Crystalline Materials Using Discrete Dislocations and the Modified Kitagawa–Takahashi Diagram" Crystals 10, no. 5: 358. https://doi.org/10.3390/cryst10050358
APA StyleSadananda, K., Adlakha, I., Solanki, K. N., & Vasudevan, A. K. (2020). Analysis of the Crack Initiation and Growth in Crystalline Materials Using Discrete Dislocations and the Modified Kitagawa–Takahashi Diagram. Crystals, 10(5), 358. https://doi.org/10.3390/cryst10050358




