Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study
Abstract
1. Introduction
2. Experimental
3. Results and Discussion
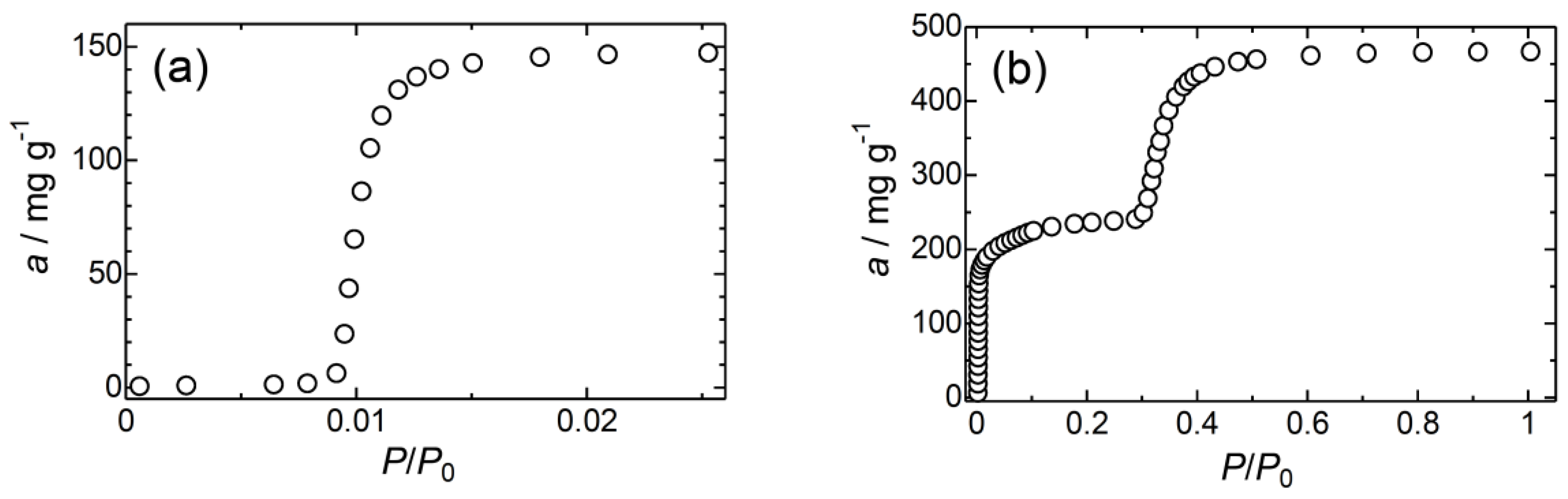
3.1. CO2 Sorption Isotherms
3.2. Calculating the Second Moment Plateau Values
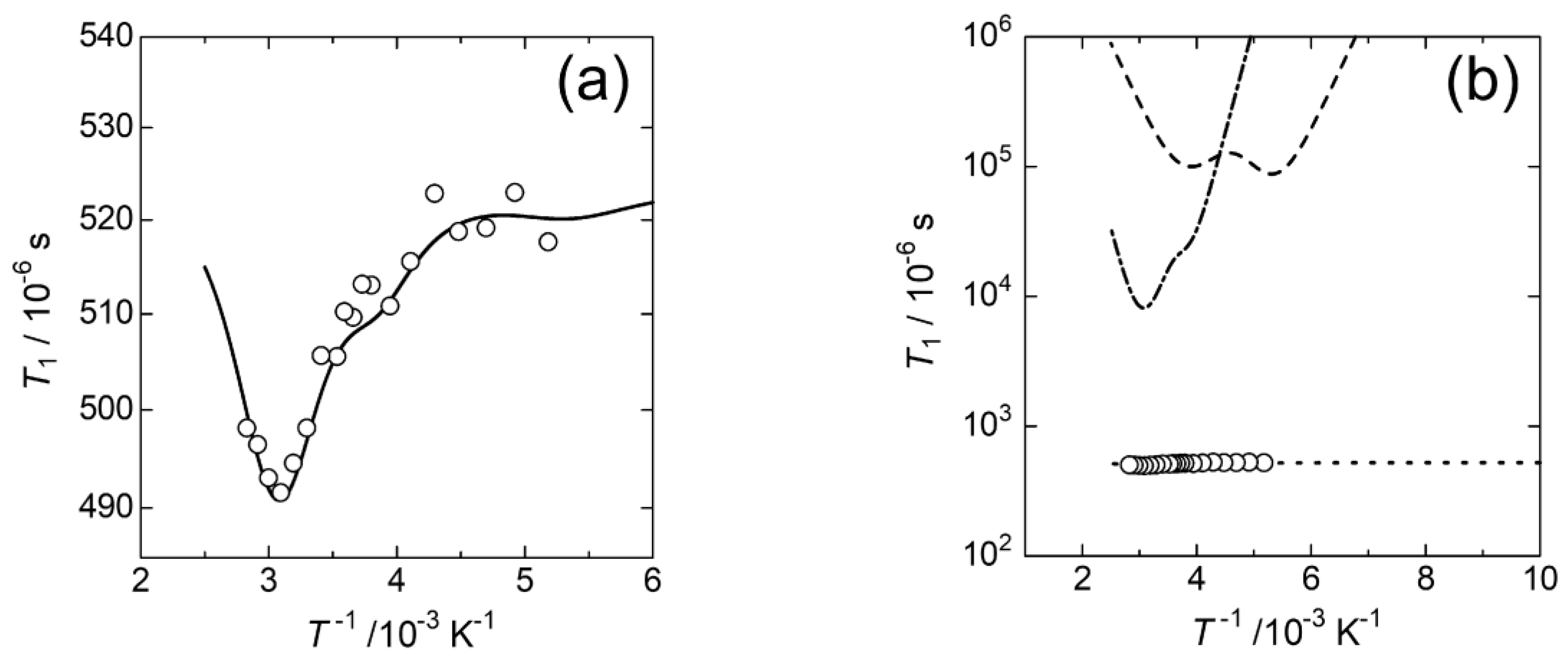
3.3. Temperature Dependence of T1 in the Closed form of ELM-11
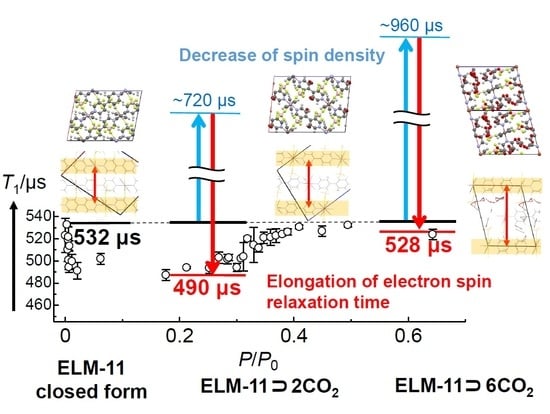
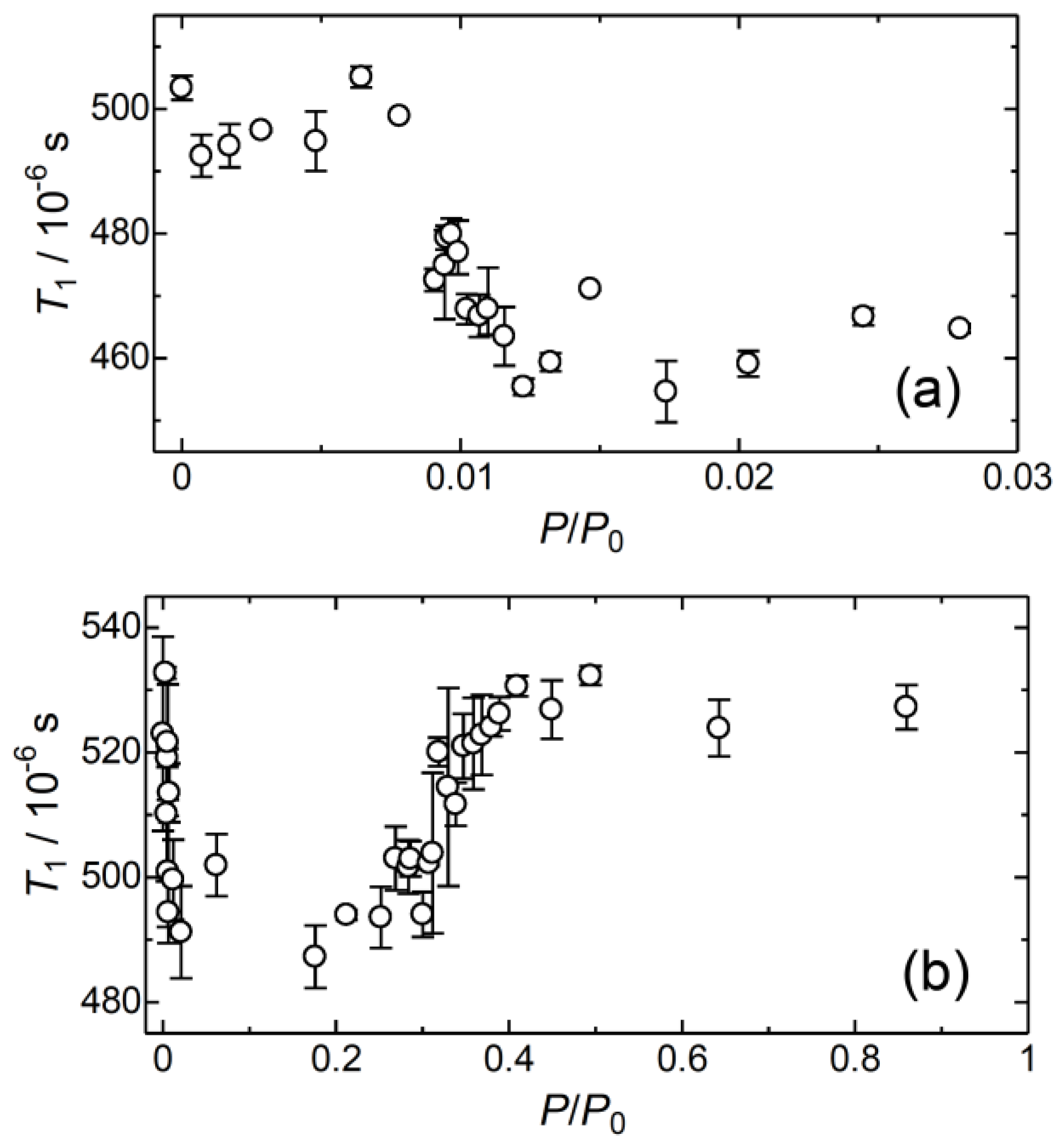
3.4. CO2-Uptake Dependence of T1 in ELM-11
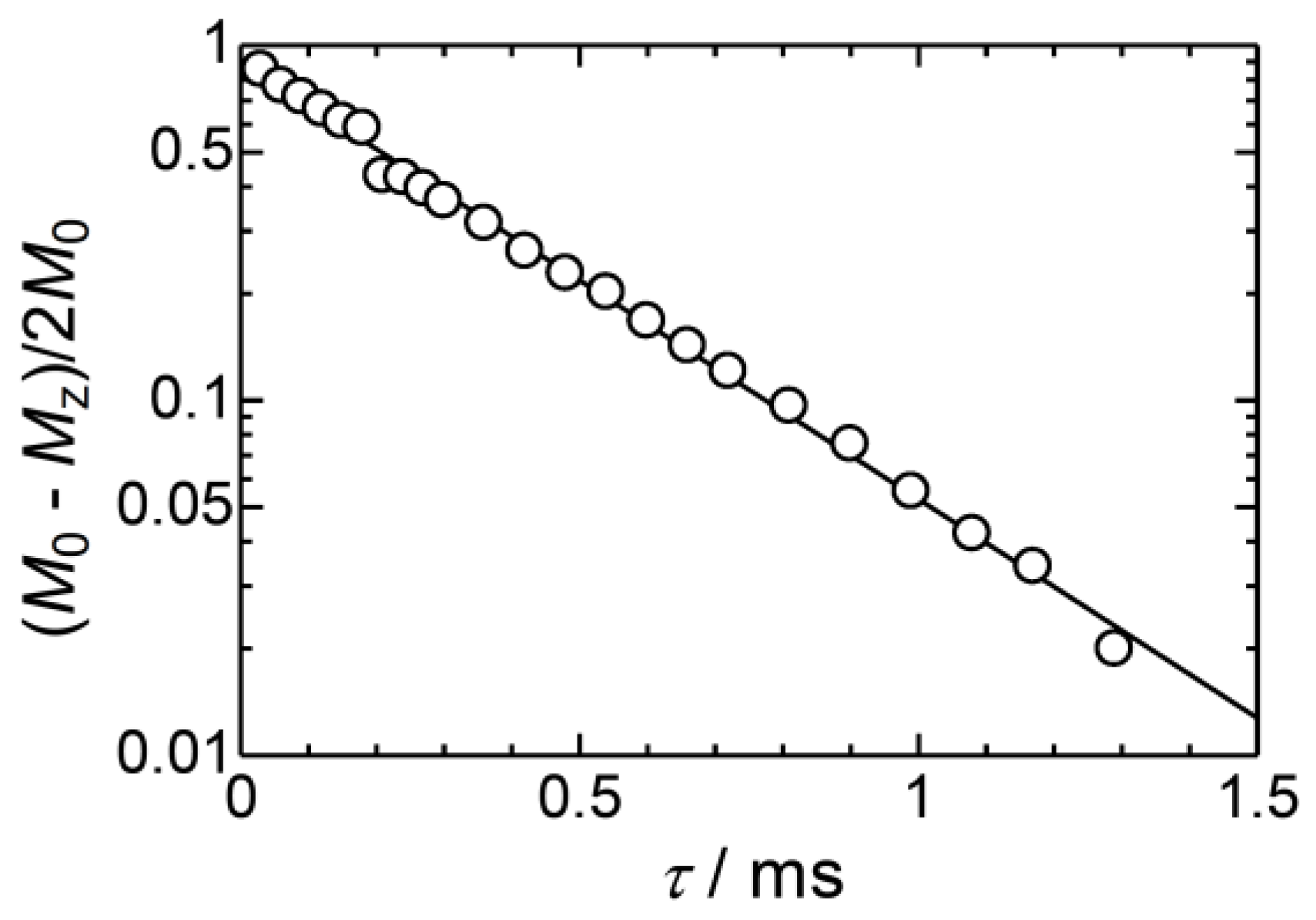
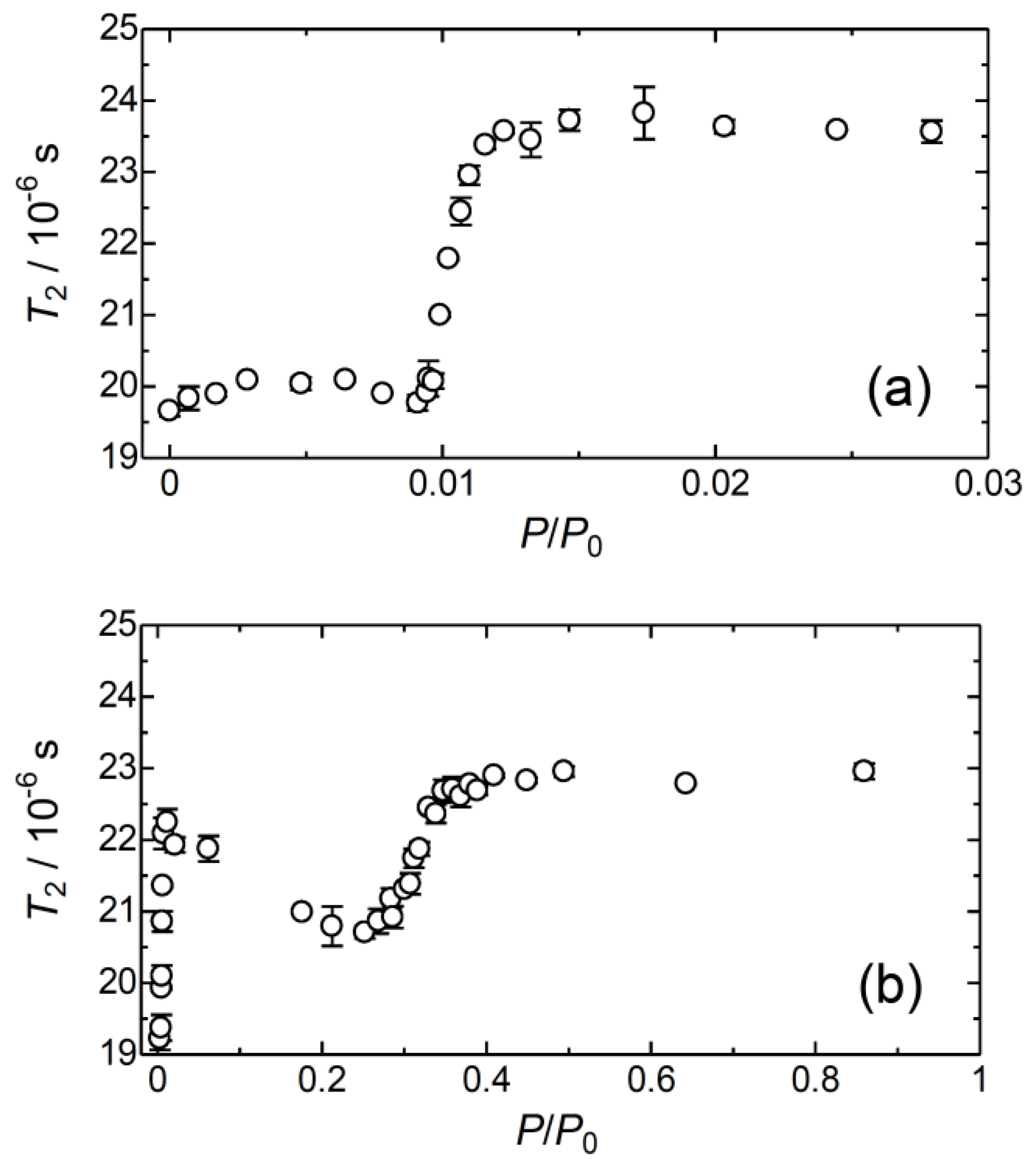
3.5. Spin–Spin Relaxation Time (T2) in ELM-11
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Calculating Second Moments for ELM-11
Appendix A.1. Theoretical Description of the NMR Second Moment
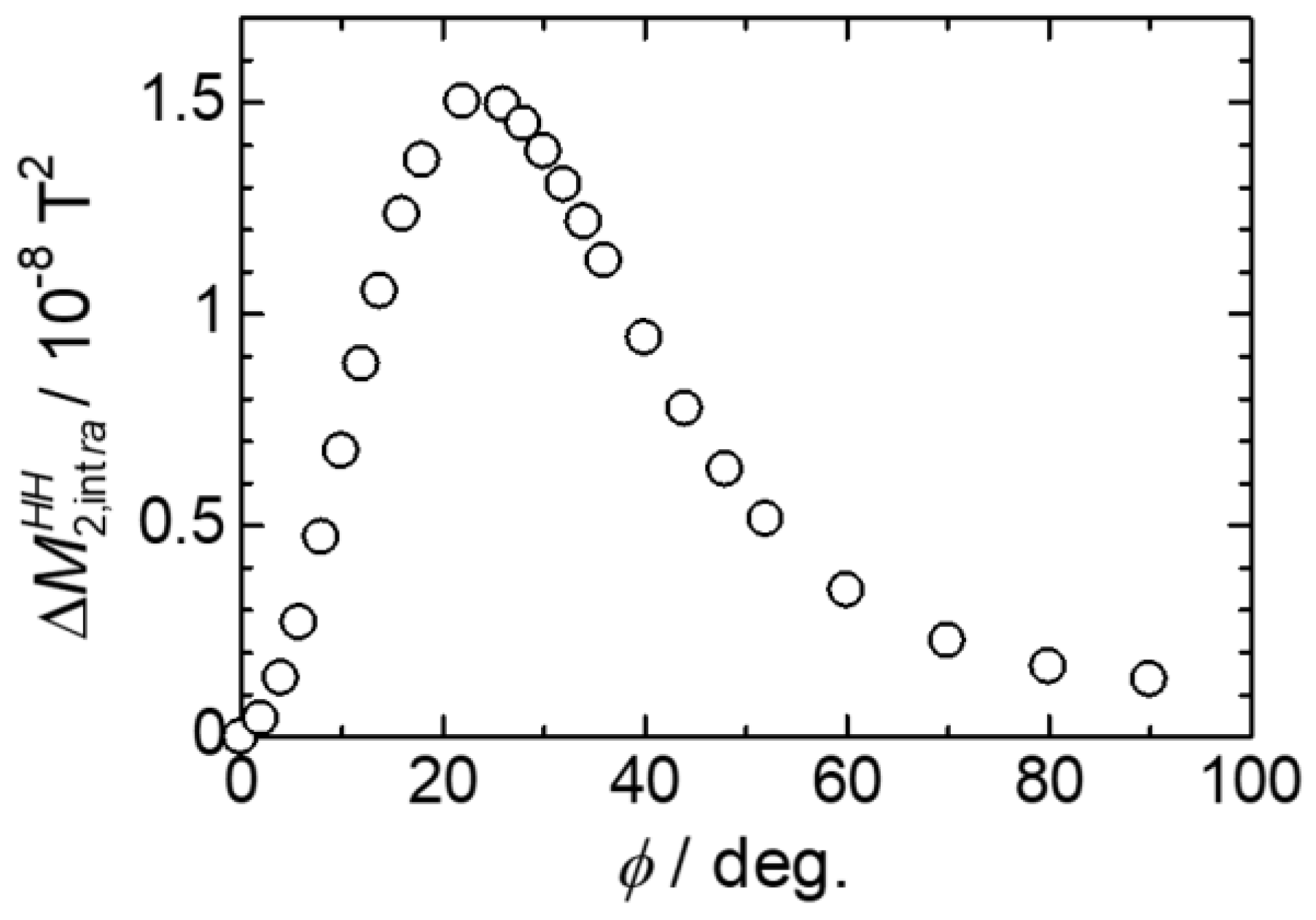
Appendix A.2. 1H Second Moments
| Interaction | Rigid Lattice | Averaged Value | ||
|---|---|---|---|---|
| bpy Flip | BF4− Rotation | bpy Flip + BF4− Rotation | ||
| 1 | ||||
| bpy 1 (0.09°)1 | ||||
| 7.348 | 7.348 | 7.348 | 7.348 | |
| 2.865 | 1.327 | 2.865 | 1.327 | |
| 1.217 | 1.217 | 0.692 | 0.692 | |
| total | 11.43 | 9.892 | 10.905 | 9.367 |
| bpy 2 (54.6°)1 | ||||
| 2.086 | 1.634 | 2.086 | 1.634 | |
| 2.829 | 2.264 | 2.829 | 2.264 | |
| 0.883 | 0.443 | 0.499 | 0.317 | |
| total | 5.798 | 4.341 | 5.414 | 4.215 |
| 2 | ||||
| bpy 1 (0.74°) 1 | ||||
| 5.683 | 5.683 | 5.683 | 5.683 | |
| 1.267 | 1.252 | 1.267 | 1.252 | |
| 1.301 | 1.301 | 0.637 | 0.637 | |
| total | 8.251 | 8.236 | 7.587 | 7.572 |
| bpy 2 (70.64°)1 | ||||
| 1.958 | 1.735 | 1.958 | 1.735 | |
| 1.278 | 1.152 | 1.278 | 1.152 | |
| 0.808 | 0.435 | 0.576 | 0.250 | |
| total | 4.044 | 3.322 | 3.812 | 3.137 |
| 3 | ||||
| bpy 1 (0.52°) 1 | ||||
| 8.454 | 8.454 | 8.454 | 8.454 | |
| 0.664 | 0.572 | 0.664 | 0.572 | |
| 0.712 | 0.712 | 0.370 | 0.370 | |
| total | 9.830 | 9.738 | 9.488 | 9.396 |
| bpy 2 (14.98°) 1 | ||||
| 6.202 | 5.045 | 6.202 | 5.045 | |
| 0.690 | 0.670 | 0.690 | 0.670 | |
| 0.612 | 0.612 | 0.368 | 0.368 | |
| total | 7.504 | 6.327 | 7.260 | 6.083 |
| bpy 1’ (17.52°) 1 | ||||
| 6.093 | 4.756 | 6.093 | 4.756 | |
| 0.725 | 0.540 | 0.725 | 0.540 | |
| 0.682 | 0.682 | 0.373 | 0.373 | |
| total | 7.500 | 5.978 | 7.191 | 5.669 |
| bpy 2’ (49.46°) 1 | ||||
| 2.357 | 1.770 | 2.357 | 1.770 | |
| 0.586 | 0.319 | 0.586 | 0.319 | |
| 0.507 | 0.146 | 0.299 | 0.079 | |
| total | 3.450 | 2.235 | 3.242 | 2.168 |
Appendix A.3. 19F Second Moment Values
| Interaction | Rigid Lattice | Averaged Value | ||
|---|---|---|---|---|
| bpy Flip | BF4− Rotation | bpy Flip + BF4− Rotation | ||
| 1 | ||||
| 6.507 | 6.507 | 0 | 0 | |
| 6.872 | 6.872 | 2.369 | 2.369 | |
| 5.337 | 4.220 | 3.028 | 2.563 | |
| 0.757 | 0.757 | 0 | 0 | |
| 8.660 | 8.660 | 0 | 0 | |
| total | 28.133 | 27.016 | 5.397 | 4.932 |
| 2 | ||||
| 6.337 | 6.337 | 0 | 0 | |
| 6.485 | 6.485 | 0.089 | 0.089 | |
| 5.358 | 5.088 | 3.080 | 2.622 | |
| 0.729 | 0.729 | 0 | 0 | |
| 8.343 | 8.343 | 0 | 0 | |
| total | 27.252 | 26.982 | 3.169 | 2.711 |
| 3 | ||||
| 5.478 | 5.478 | 0 | 0 | |
| 2.811 | 2.811 | 0.040 | 0.040 | |
| 6.302 | 2.486 | 3.537 | 1.308 | |
| 0.628 | 0.628 | 0 | 0 | |
| 7.189 | 7.189 | 0 | 0 | |
| total | 22.408 | 18.592 | 3.577 | 1.348 |
Appendix B. Theoretical Background for NMR Spin-Lattice Relaxation of Multi-Spins
References
- Kitagawa, S.; Kitaura, R.; Noro, S. Functional porous coordination polymers. Angew. Chem. Int. Ed. 2004, 43, 2334–2375. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, A.J.; Thomas, K.M.; Rosseinsky, M.J. Flexibility in metal-organic framework materials: Impact on sorption properties. J. Solid State Chem. 2005, 178, 2491–2510. [Google Scholar] [CrossRef]
- Férey, G. Hybrid porous solids: Past, present, future. Chem. Soc. Rev. 2008, 37, 191–214. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Kaneko, K. Hydrogen bond-regulated microporous nature of copper complex-assembled microcrystals. Chem. Phys. Lett. 2001, 335, 50–56. [Google Scholar] [CrossRef]
- Kitagawa, S.; Matsuda, R. Chemistry of coordination space of porous coordination polymers. Coord. Chem. Rev. 2007, 251, 2490–2509. [Google Scholar] [CrossRef]
- Tanaka, D.; Nakagawa, K.; Higuchi, M.; Horike, S.; Kubota, Y.; Kobayashi, T.C.; Takata, M.; Kitagawa, S. Kinetic gate-opening process in a flexible porous coordination polymer. Angew. Chem. Int. Ed. 2008, 47, 3914–3918. [Google Scholar] [CrossRef] [PubMed]
- Serre, C.; Millange, F.; Thouvenot, C.; Noguès, M.; Marsolier, G.; Louër, D.; Férey, G. Very large breathing effect in the first nanoporous chromium (III)-based solids: MIL-53 or CrIII(OH)·{O2C-C6H4-CO2}·{HO2C-C6H4-CO2H}x·H2Oy. J. Am. Chem. Soc. 2002, 124, 13519–13526. [Google Scholar] [CrossRef] [PubMed]
- Coudert, F.-X.; Jeffroy, M.; Fuchs, A.H.; Boutin, A.; Mellot-Draznieks, C. Thermodynamics of guest-induced structural transitions in hybrid organic-inorganic frameworks. J. Am. Chem. Soc. 2008, 130, 14294–14302. [Google Scholar] [CrossRef]
- Mason, J.A.; Oktawiec, J.; Taylor, M.K.; Hudson, M.R.; Rodriguez, J.; Bachman, J.E.; Gonzalez, M.I.; Cervellino, A.; Guagliardi, A.; Brown, C.M.; et al. Methane storage in flexible metal–organic frameworks with intrinsic thermal management. Nature 2015, 527, 357–361. [Google Scholar] [CrossRef]
- Krause, S.; Bon, V.; Senkovska, I.; Stoeck, U.; Wallacher, D.; Többens, D.M.; Zander, S.; Pillai, R.S.; Maurin, G.; Coudert, F.X.; et al. A pressure-amplifying framework material with negative gas adsorption transitions. Nature 2016, 532, 348–352. [Google Scholar] [CrossRef]
- Tanaka, H.; Hiraide, S.; Kondo, A.; Miyahara, M.T. Modeling and visualization of CO2 adsorption on elastic layer-structured metal−organic framework-11: Toward a better understanding of gate adsorption behavior. J. Phys. Chem. C 2015, 119, 11533–11543. [Google Scholar] [CrossRef]
- Hiraide, S.; Tanaka, H.; Miyahara, M.T. Understanding gate adsorption behaviour of CO2 on elastic layer-structured metal–organic framework-11. Dalton Trans. 2016, 45, 4193–4202. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yu, Q.; Zhao, Q.; Liang, J.; Dong, J.; Li, J. Adsorption CO2, CH4 and N2 on two different spacing flexible layer MOFs. Micropor. Mesopor. Mater. 2012, 161, 154–159. [Google Scholar] [CrossRef]
- Bon, V.; Senkovska, I.; Wallacher, D.; Heerwig, A.; Klein, N.; Zizak, I.; Feyerherm, R.; Dudzik, E.; Kaskel, S. In situ monitoring of structural changes during the adsorption on flexible porous coordination polymers by X-ray powder diffraction: Instrumentation and experimental results. Micropor. Mesopor. Mater. 2014, 188, 190–195. [Google Scholar] [CrossRef]
- Kondo, A.; Kojima, N.; Kajiro, H.; Noguchi, H.; Hattori, Y.; Okino, F.; Maeda, K.; Ohba, T.; Kaneko, K.; Kanoh, H. Gas adsorption mechanism and kinetics of an elastic layer-structured metal−organic framework. J. Phys. Chem. C 2012, 116, 4157–4162. [Google Scholar] [CrossRef]
- Bousquet, B.; Coudert, F.-X.; Fossati, A.G.J.; Neimark, A.V.; Fuchs, A.H.; Boutin, A. Adsorption induced transitions in soft porous crystals: An osmotic potential approach to multistability and intermediate structures. J. Chem. Phys. 2013, 138, 174706. [Google Scholar] [CrossRef]
- Watanabe, S.; Sugiyama, H.; Adachi, H.; Tanaka, H.; Miyahara, M.T. Free energy analysis for adsorption-induced lattice transition of flexible coordination framework. J. Chem. Phys. 2009, 130, 164707. [Google Scholar] [CrossRef]
- Numaguchi, R.; Tanaka, H.; Watanabe, S.; Miyahara, M.T. Simulation study for adsorption-induced structural transition in stacked-layer porous coordination polymers: Equilibrium and hysteretic adsorption behaviors. J. Chem. Phys. 2013, 138, 054708. [Google Scholar] [CrossRef] [PubMed]
- Kitaura, R.; Fujimoto, K.; Noro, S.; Kondo, M.; Kitagawa, S. A pillared-layer coordination polymer network displaying hysteretic sorption: [Cu2(pzdc)2(dpyg)]n (pzdc = pyrazine-2,3-dicarboxylate; dpyg = 1,2-di(4-pyridyl)-glycol). Angew. Chem. Int. Ed. 2002, 41, 133–135. [Google Scholar] [CrossRef]
- Kitaura, R.; Seki, K.; Akiyama, G.; Kitagawa, S. Porous coordination-polymer crystals with gated channels specific for supercritical gases. Angew. Chem. Int. Ed. 2003, 42, 428–431. [Google Scholar] [CrossRef]
- Seo, J.; Matsuda, R.; Sakamoto, H.; Bonneau, C.; Kitagawa, S. A Pillared-layer coordination polymer with a rotatable pillar acting as a molecular gate for guest molecules. J. Am. Chem. Soc. 2009, 131, 12792–12800. [Google Scholar] [CrossRef] [PubMed]
- Uemura, K.; Yamasaki, Y.; Komagawa, Y.; Tanaka, K.; Kita, H. Two-step adsorption/desorption on a jungle-gym-type porous coordination polymer. Angew. Chem. Int. Ed. 2007, 46, 6662–6665. [Google Scholar] [CrossRef] [PubMed]
- Hye, J.C.; Dinca, M.; Long, J.R. Broadly hysteretic H2 adsorption in the microporous metal-organic framework Co(1,4-benzenedipyrazolate). J. Am. Chem. Soc. 2008, 130, 7848–7850. [Google Scholar]
- Kondo, A.; Noguchi, H.; Ohnishi, S.; Kajiro, H.; Tohdoh, A.; Hattori, Y.; Xu, W.C.; Tanaka, H.; Kanoh, H.; Kaneko, K. Novel Expansion/shrinkage modulation of 2D layered MOF triggered by clathrate formation with CO2 molecules. Nano Lett. 2006, 6, 2581–2584. [Google Scholar] [CrossRef] [PubMed]
- Kondo, A.; Noguchi, H.; Carlucci, L.; Proserpio, D.M.; Ciani, G.; Kajiro, H.; Ohba, T.; Kanoh, H.; Kaneko, K. Double-step gas sorption of a two−dimensional metal−organic framework. J. Am. Chem. Soc. 2007, 129, 12362–12363. [Google Scholar] [CrossRef] [PubMed]
- Kanoh, H.; Kondo, A.; Noguchi, H.; Kajiro, H.; Tohdoh, A.; Hattori, Y.; Xu, W.C.; Inoue, M.; Sugiura, T.; Morita, K.; et al. Elastic layer-structured metal organic frameworks (ELMs). J. Colloid Interface Sci. 2009, 334, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Kajiro, H.; Noguchi, H.; Kondo, A.; Ohba, T.; Hattori, Y.; Kaneko, K.; Kanoh, H. Tuning of gate opening of an elastic layered structure MOF in CO2 sorption with a trace of alcohol molecules. Langmuir 2011, 27, 6905–6909. [Google Scholar] [CrossRef]
- Ichikawa, M.; Kondo, A.; Noguchi, H.; Kojima, N.; Ohba, T.; Kajiro, H.; Hattori, Y.; Kanoh, H. Double-step gate phenomenon in CO2 sorption of an elastic layer-structured MOF. Langmuir 2016, 32, 9722–9726. [Google Scholar] [CrossRef]
- Hiraide, S.; Tanaka, H.; Ishikawa, N.; Miyahara, M.T. Intrinsic thermal management capabilities of flexible metal−organic frameworks for carbon dioxide separation and capture. ACS Appl. Mater. Interfaces 2017, 9, 41066–41077. [Google Scholar] [CrossRef]
- Kultaeva, A.; Bon, V.; Weiss, M.S.; Pöppl, A.; Kaskel, S. Elucidating the formation and transformation mechanisms of the switchable metal−organic framework ELM-11 by powder and single-crystal EPR study. Inorg. Chem. 2018, 57, 11920–11929. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, J.; Kasumaj, B.; Jeschke, G.; Hunger, M.; Mallat, T.; Baiker, A. Adsorption-desorption induced structural changes of Cu-MOF evidenced by solid state NMR and EPR spectroscopy. J. Am. Chem. Soc. 2009, 131, 2058–2059. [Google Scholar] [CrossRef] [PubMed]
- Panich, A.M.; Sergeev, N.A. Towards determination of distances between nanoparticles and grafted paramagnetic ions by NMR relaxation. Appl. Magn. Reson. 2018, 49, 195–208. [Google Scholar] [CrossRef] [PubMed]
- Kristinaityte, K.; Zalewski, T.; Kempka, M.; Sakirzanovas, S.; Baziulyte-Paulaviciene, D.; Jurga, S.; Rotomskis, R.; Valeviciene, N.R. Spin–lattice relaxation and diffusion processes in aqueous solutions of gadolinium-based upconverting nanoparticles at different magnetic fields. Appl. Magn. Reson. 2019, 50, 553–561. [Google Scholar] [CrossRef]
- Yamabayashi, T.; Atzori, M.; Tesi, L.; Cosquer, G.; Santanni, F.; Boulon, M.-E.; Morra, E.; Benci, S.; Torre, R.; Chiesa, M.; et al. Scaling up electronic spin qubits into a three-dimensional metal−organic framework. J. Am. Chem. Soc. 2018, 140, 12090–12101. [Google Scholar] [CrossRef]
- Bokor, M.; Marek, T.; Tompa, K. Solid-state NMR of 1-propyltetrazole complexes of iron(II) and zinc(II). 1. 1H spin–lattice relaxation time. J. Magn. Reson. A 1996, 122, 157–164. [Google Scholar] [CrossRef]
- Lim, A.R. Tetragonal-orthorhombic-tetragonal phase transitions in organic-inorganic perovskite-type (CH3NH3)2MnCl4. Solid State Commun. 2017, 267, 18–22. [Google Scholar]
- Jang, S.E.; Kim, M.J.; Lim, A.R. Structural geometry of the layered perovskite-type (CH3CH2CH2NH3)2CuCl4 single crystal near phase transition temperatures. AIP Adv. 2018, 8, 105324. [Google Scholar] [CrossRef]
- Lim, A.R.; Kim, S.H. Study on paramagnetic interactions of (CH3NH3)2CoBr4 hybrid perovskites based on nuclear magnetic resonance (NMR) relaxation time. Molecules 2019, 24, 2895. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: New York, NY, USA, 1961. [Google Scholar]
- Mikuli, E.; Hetmańczyk, J.; Grad, B.; Kozak, A.; Wąsicki, J.W.; Bilski, P.; Hołderna-Natkaniec, K.; Medycki, W. The relationship between reorientational molecular motions and phase transitions in [Mg(H2O)6](BF4)2, studied with the use of 1H and 19F NMR and FT-MIR. J. Chem. Phys. 2015, 142, 064507. [Google Scholar] [CrossRef]
- Soda, G.; Chihara, H. Note on the theory of nuclear spin relaxation exact formulae in the weak collision limit. J. Phys. Soc. Jpn. 1974, 36, 954–958. [Google Scholar] [CrossRef]
- Wąsicki, J.; Pająk, Z.; Kozak, A. Cation and anion reorientation at phase transition in pyridinium tetrafluoroborate. Z. Naturforsch. 1990, 45a, 33–36. [Google Scholar] [CrossRef]
- Mikuli, E.; Hetmańczyk, Ł.; Medycki, W.; Kowalska, A. Phase transitions and molecular motions in [Zn(NH3)4](BF4)2 studied by nuclear magnetic resonance, infrared and Raman spectroscopy. J. Phys. Chem. Solids 2007, 68, 96–103. [Google Scholar] [CrossRef]
- Mikuli, E.; Grad, B.; Medycki, W.; Hołderna-Natkaniec, K. Phase transitions and molecular motions in [Cd(H2O)6](BF4)2 studied by DSC, 1H and 19F NMR and FT-MIR. J. Solid State Chem. 2004, 177, 3795–3804. [Google Scholar] [CrossRef]
- Pérez-Jiménez, Á.J.; Sancho-García, J.C.; Pérez-Jordá, J.M. Torsional potential of 4,4′-bipyridine: Ab initio analysis of dispersion and vibrational effects. J. Chem. Phys. 2005, 123, 134309. [Google Scholar] [CrossRef] [PubMed]
- Emsley, J.W.; Stephenson, D.S.; Lindon, J.C.; Lunazzi, L.; Pulga, S. Structure and conformation of 4,4′-bipyridyl by nuclear magnetic resonance spectroscopy of a nematic solution. J. Chem. Soc. Perkin Trans. 2 1975, 1541–1544. [Google Scholar] [CrossRef]
- Lowe, I.J.; Tse, D. Nuclear spin-lattice relaxation via paramagnetic centers. Phys. Rev. 1968, 166, 279–291. [Google Scholar] [CrossRef]
- Lee, C.E.; Choi, I.; Kim, J.E.; Lee, C.H. Nuclear magnetic relaxation in dense paramagnet CuF2·2H2O. J. Phys. Soc. Jpn. 1994, 63, 3509–3514. [Google Scholar] [CrossRef]
- Bloembergen, N. On the interaction of nuclear spins in a crystalline lattice. Physica 1949, 15, 386–426. [Google Scholar] [CrossRef]
- Albert, S.; Gutowsky, H.S. Nuclear relaxation and spin exchange in ammonium hexafluorophosphate (NH4PF6). J. Chem. Phys. 1973, 59, 3585–3594. [Google Scholar] [CrossRef]
- Blinc, R.; Lahajnar, G. Magnetic resonance study of molecular motion in cubic (NH4)2SiF6. J. Chem. Phys. 1967, 47, 4146–4152. [Google Scholar] [CrossRef]
- Zdanowska-Frączek, M.; Medycki, W. 1H NMR study of N(CH3)4H(ClF2CCOO)2. Solid State Nucl. Magn. Reson. 2000, 15, 189–193. [Google Scholar] [CrossRef]
- Satterlee, J.D. Fundamental concepts of NMR in paramagnetic systems. Part II: Relaxation effects. Concepts Magn. Reson. 1990, 2, 119–129. [Google Scholar] [CrossRef]
- Moreau, F.; Kolokolov, D.I.; Stepanov, A.G.; Easun, T.L.; Dailly, A.; Lewis, W.; Blake, A.J.; Nowell, H.; Lennox, M.J.; Besley, E.; et al. Tailoring porosity and rotational dynamics in a series of octacarboxylate metal-organic frameworks. Proc. Natl. Acad. Sci. USA 2017, 114, 3056–3061. [Google Scholar] [CrossRef] [PubMed]
- Inukai, M.; Fukushima, T.; Hijikata, Y.; Ogiwara, N.; Horike, S.; Kitagawa, S. Control of molecular rotor rotational frequencies in porous coordination polymers using a solid-solution approach. J. Am. Chem. Soc. 2015, 137, 12183–12186. [Google Scholar] [CrossRef]
- Takemura, H.; Nakashima, S.; Kon, N.; Yasutake, M.; Shinmyozu, T.; Inazu, T. A study of C-F···M+ interaction: Metal complexes of fluorine-containing cage compounds. J. Am. Chem. Soc. 2001, 123, 9293–9298. [Google Scholar] [CrossRef] [PubMed]
| Interaction | Motional Mode | ||
|---|---|---|---|
| bpy Flip | BF4− Rotation | bpy Flip + BF4− Rotation | |
| 1 | |||
| bpy 1 | |||
| 0 | 0 | 0 | |
| 1.538 | 0 | 1.538 | |
| 0 | 0.525 | 0.525 | |
| total | 1.538 | 0.525 | 2.063 |
| bpy 2 | |||
| 0.452 | 0 | 0.452 | |
| 0.565 | 0 | 0.565 | |
| 0.44 | 0.384 | 0.566 | |
| total | 1.457 | 0.384 | 1.583 |
| 2 | |||
| bpy 1 | |||
| 0 | 0 | 0 | |
| 0.015 | 0 | 0.015 | |
| 0 | 0.664 | 0.664 | |
| total | 0.015 | 0.664 | 0.679 |
| bpy 2 | |||
| 0.223 | 0 | 0.223 | |
| 0.126 | 0 | 0.126 | |
| 0.373 | 0.232 | 0.558 | |
| total | 0.722 | 0.232 | 0.907 |
| 3 | |||
| bpy 1 | |||
| 0 | 0 | 0 | |
| 0.092 | 0 | 0.092 | |
| 0 | 0.342 | 0.342 | |
| total | 0.092 | 0.342 | 0.434 |
| bpy 2 | |||
| 1.157 | 0 | 1.157 | |
| 0.02 | 0 | 0.02 | |
| 0 | 0.244 | 0.244 | |
| total | 1.177 | 0.244 | 1.421 |
| bpy 1’ | |||
| 1.337 | 0 | 1.337 | |
| 0.185 | 0 | 0.185 | |
| 0 | 0.309 | 0.309 | |
| total | 1.522 | 0.309 | 1.831 |
| bpy 2’ | |||
| 0.587 | 0 | 0.587 | |
| 0.267 | 0 | 0.267 | |
| 0.361 | 0.208 | 0.428 | |
| total | 1.215 | 0.208 | 1.282 |
| bpy 1 | |||
| 0 | 0 | 0 | |
| 0.092 | 0 | 0.092 | |
| 0 | 0.342 | 0.342 | |
| total | 0.092 | 0.342 | 0.434 |
| Interaction | Motional Mode | ||
|---|---|---|---|
| bpy Flip | BF4− Rotation | bpy Flip + BF4− Rotation | |
| 1 | |||
| 0 | 6.507 | 6.507 | |
| 0 | 4.503 | 4.503 | |
| 1.117 | 2.309 | 2.774 | |
| 0 | 0.757 | 0.757 | |
| 0 | 8.66 | 8.660 | |
| total | 1.117 | 22.736 | 23.201 |
| 2 | |||
| 0 | 6.337 | 6.337 | |
| 0 | 6.396 | 6.396 | |
| 0.270 | 2.278 | 2.736 | |
| 0 | 0.729 | 0.729 | |
| 0 | 8.343 | 8.343 | |
| total | 0.270 | 24.083 | 24.541 |
| 3 | |||
| 0 | 5.478 | 5.478 | |
| 0 | 2.771 | 2.771 | |
| 3.816 | 2.765 | 4.994 | |
| 0 | 0.628 | 0.628 | |
| 0 | 7.189 | 7.189 | |
| total | 3.816 | 18.831 | 21.06 |
| Parameter | Expt. | Calc. |
|---|---|---|
| 1H interaction | ||
| τH,0/s | 1.0 × 10−12 | ----- |
| Ea(H)/kJ mol−1 | 18 | ----- |
| ΔM2HH/10−8 T2 | 1.28 | 1.28 |
| ΔM2HF/10−8 T2 | 0.55 | 0.55 |
| 19F interaction | ||
| τF,0/s | 4.0 × 10−14 | ----- |
| Ea(F)/kJ mol−1 | 32 | ----- |
| ΔM2FF/10−8 T2 | 10 | 11.0 |
| ΔM2FH/10−8 T2 | 1.6 | 2.77 |
| ΔM2F11B/10−8 T2 | 7.0 | 8.66 |
| ΔM2F10B/10−8 T2 | 0.61 | 0.76 |
| Parameter | 1 | 2 | 3 | ||
|---|---|---|---|---|---|
| T/K | 273 | 195 | 273 | 195 | 195 |
| T1p, exp/μs | 500 | 532 | 455 | 490 | 529 |
| T1p, calc/μs | 523 | 449 | 490 | 528 | |
| τe/s | 1.22 × 10−11 | 3.08 × 10−11 | 2.59 × 10−11 | 4.05 × 10−11 | |
| D/m2s−1 | 2.87 × 10−16 | 2.87 × 10−16 | 2.87 × 10−16 | ||
| Np/m−3 | 1.91 × 1027 | 1.51 × 1027 | 1.21 × 1027 | ||
| rave.(Cu-Cu)/nm | 0.9105 | 0.9959 | 1.0692 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohazama, K.; Ueda, T.; Ukai, K.; Ichikawa, M.; Masu, H.; Kajiro, H.; Kanoh, H. Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study. Crystals 2020, 10, 328. https://doi.org/10.3390/cryst10040328
Ohazama K, Ueda T, Ukai K, Ichikawa M, Masu H, Kajiro H, Kanoh H. Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study. Crystals. 2020; 10(4):328. https://doi.org/10.3390/cryst10040328
Chicago/Turabian StyleOhazama, Kazuki, Takahiro Ueda, Kazuki Ukai, Manami Ichikawa, Hyuma Masu, Hiroshi Kajiro, and Hirofumi Kanoh. 2020. "Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study" Crystals 10, no. 4: 328. https://doi.org/10.3390/cryst10040328
APA StyleOhazama, K., Ueda, T., Ukai, K., Ichikawa, M., Masu, H., Kajiro, H., & Kanoh, H. (2020). Structural Dynamics of An ELM-11 Framework Transformation Accompanied with Double-Step CO2 Gate sorption: An NMR Spin Relaxation Study. Crystals, 10(4), 328. https://doi.org/10.3390/cryst10040328