Mechanical and Thermal Properties of Low-Density Al20+xCr20-xMo20-yTi20V20+y Alloys
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
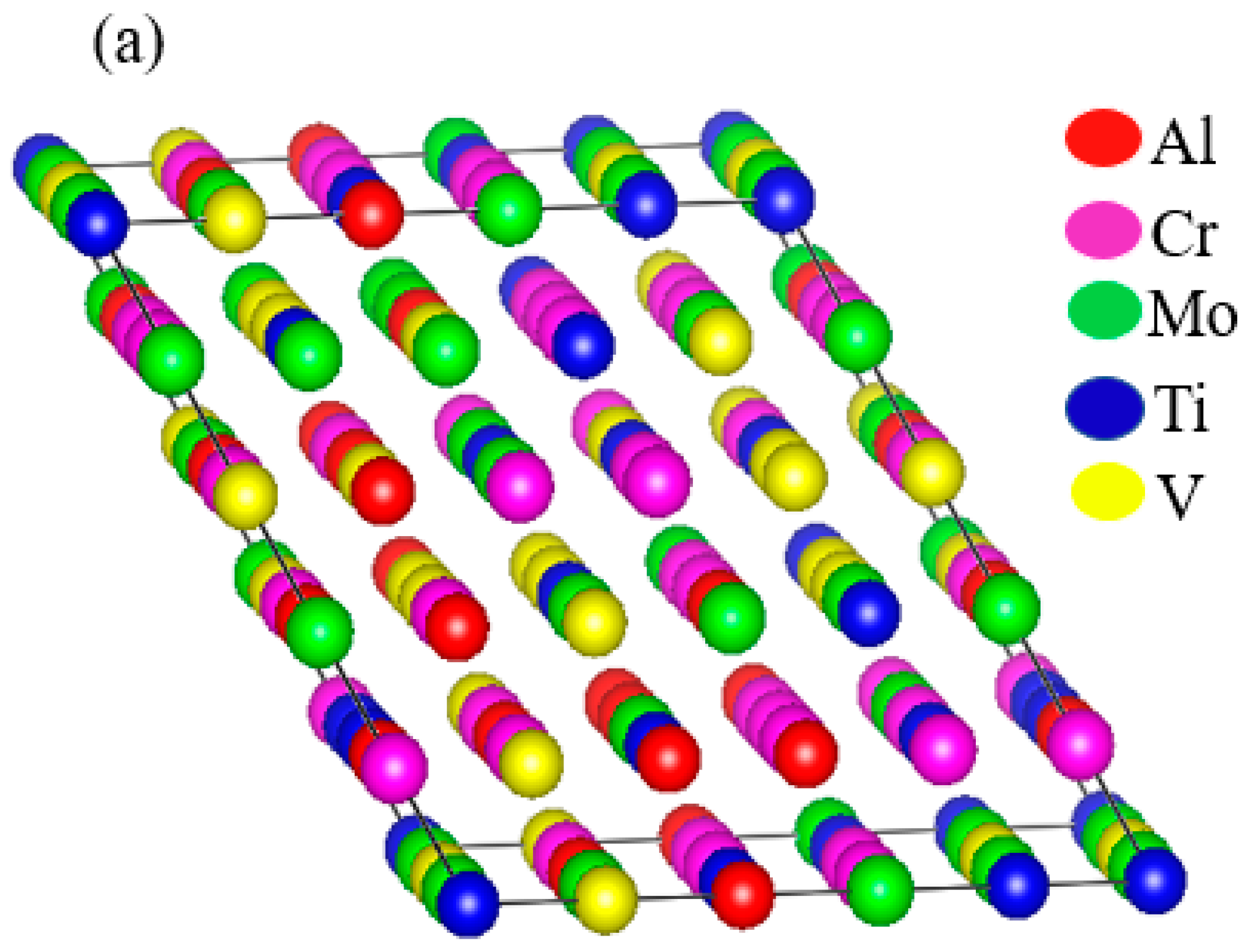
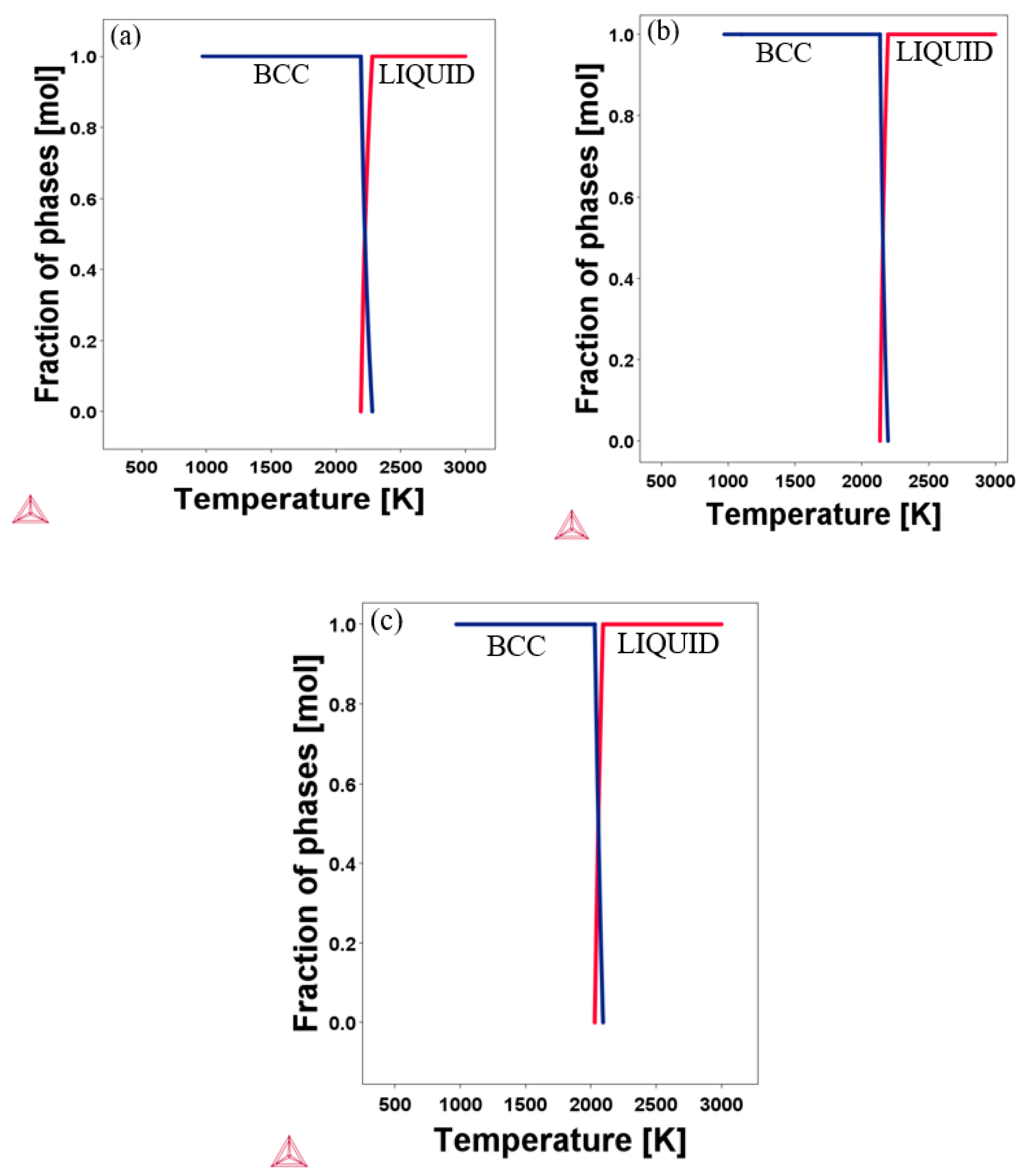
3.1. Structural Properties
3.2. Mechanical Properties
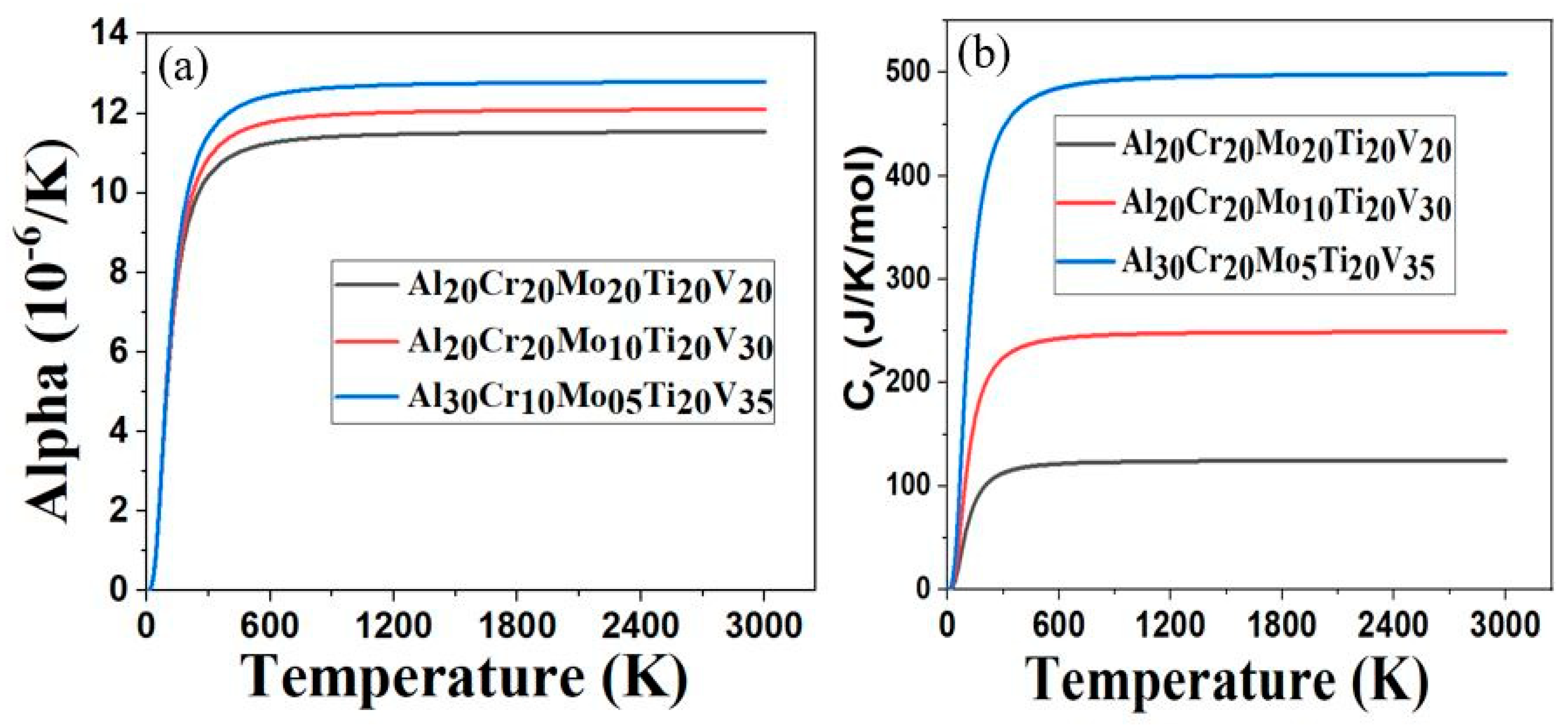
3.3. Thermal Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Perepezko, J.H. The Hotter the Engine, the Better. Science 2009, 326, 1068–1069. [Google Scholar] [CrossRef] [PubMed]
- Pollock, T.M. Alloy design for aircraft engines. Nat. Mater. 2016, 15, 809–815. [Google Scholar] [CrossRef] [PubMed]
- Albert, B.; Völkl, R.; Glatzel, U. High-temperature oxidation behavior of two nickel-based superalloys produced by metal injection molding for aero engine applications. Metall. Mater. Trans. A 2014, 45, 4561–4571. [Google Scholar] [CrossRef]
- Kuhn, H.A.; Biermann, H.; Ungár, T.; Mughrabi, H. An X-ray study of creep-deformation induced changes of the lattice mismatch in the γ′-hardened monocrystalline nickel-base superalloy SRR 99. Acta Metallurgica et Materialia 1991, 39, 2783–2794. [Google Scholar] [CrossRef]
- Zenk, C.H.; Povstugar, I.; Li, R.; Rinaldi, F.; Neumeier, S.; Raabe, D.; Göken, M. A novel type of Co–Ti–Cr-base γ/γ′ superalloys with low mass density. Acta Mater. 2017, 135, 244–251. [Google Scholar] [CrossRef]
- Xu, Z.Q.; Ma, Z.L.; Wang, M.; Chen, Y.W.; Tan, Y.D.; Cheng, X.W. Design of novel low-density refractory high entropy alloys for high-temperature applications. Mater. Sci. Eng. A 2019, 755, 318–322. [Google Scholar] [CrossRef]
- Youssef, K.M.; Zaddach, A.J.; Niu, C.; Irving, D.L.; Koch, C.C. A Novel Low-Density, High-Hardness, High-entropy Alloy with Close-packed Single-phase Nanocrystalline Structures. Mater. Res. Lett. 2015, 3, 95–99. [Google Scholar] [CrossRef]
- Kang, M.; Lim, K.R.; Won, J.W.; Lee, K.S.; Na, Y.S. Al-ti-containing lightweight high-entropy alloys for intermediate temperature applications. Entropy 2018, 20, 355. [Google Scholar] [CrossRef]
- Li, C.; Li, J.C.; Zhao, M.; Jiang, Q. Effect of alloying elements on microstructure and properties of multiprincipal elements high-entropy alloys. J. Alloy. Compd. 2009, 475, 752–757. [Google Scholar] [CrossRef]
- Zhang, Y. Mechanical properties and structures of high entropy alloys and bulk metallic glasses composites. Mater. Sci. Forum 2010, 654, 1058–1061. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Zhang, Y.; Wang, Y.L.; Chen, G.L. Solid solution alloys of AlCoCrFeNiTix with excellent room-temperature mechanical properties. Appl. Phys. Lett. 2007, 90, 181904. [Google Scholar] [CrossRef]
- Jung, C.; Kang, K.; Marshal, A.; Pradeep, K.G.; Seol, J.B.; Lee, H.M.; Choi, P.P. Effects of phase composition and elemental partitioning on soft magnetic properties of AlFeCoCrMn high entropy alloys. Acta Mater. 2009, 171, 31–39. [Google Scholar] [CrossRef]
- Senkov, O.N.; Senkova, S.; Woodward, C.; Miracle, D.B. Low-density, refractory multi-principal element alloys of the Cr-Nb-Ti-V-Zr system: Microstructure and phase analysis. Acta Mater. 2013, 61, 1545–1557. [Google Scholar] [CrossRef]
- Senkov, O.N.; Wilks, G.; Scott, J.; Miracle, D.B. Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 2011, 19, 698–706. [Google Scholar] [CrossRef]
- Senkov, O.; Wilks, G.; Miracle, D.; Chuang, C.; Liaw, P. Refractory high-entropy alloys. Intermetallics 2010, 18, 1758–1765. [Google Scholar] [CrossRef]
- Zou, Y.; Maiti, S.; Steurer, W.; Spolenak, R. Size-dependent plasticity in an Nb25Mo25Ta25W25 refractory high-entropy alloy. Acta Mater. 2014, 65, 85–97. [Google Scholar] [CrossRef]
- Thermo-Calc Software. Available online: https://www.thermocalc.com/ (accessed on 7 April 2020).
- Andersson, J.-O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar]
- Lederer, Y.; Toher, C.; Vecchio, K.S.; Curtarolo, S. The search for high entropy alloys: A high-throughput ab-initio approach. Acta Mater. 2018, 159, 364–383. [Google Scholar] [CrossRef]
- Chen, H.L.; Mao, H.; Chen, Q. Database development and Calphad calculations for high entropy alloys: Challenges, strategies, and tips. Mater. Chem. Phys. 2018, 210, 279–290. [Google Scholar] [CrossRef]
- Mao, H.; Chen, H.L.; Chen, Q. TCHEA1: A thermodynamic database not limited for “high entropy” alloys. J. Phase Equilibria Diffus. 2017, 38, 353–368. [Google Scholar] [CrossRef]
- Gao, M.C.; Zhang, B.; Yang, S.; Guo, S. Senary refractory high-entropy alloy HfNbTaTiVZr. Metall. Mater. Trans. A 2016, 47, 3333–3345. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- MedeA® Software. Available online: https://www.materialsdesign.com/medea-software (accessed on 7 April 2020).
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Knuth, E.D. The Art of Computer Programming, 3rd ed.; Addison-Wesley: Massachusetts, MA, USA, 1965. [Google Scholar]
- Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic coefficients from ab initio total energy calculations. Phys. Rev. B 2001, 63, 174103. [Google Scholar] [CrossRef]
- Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Andrews, K. Elastic moduli of polycrystalline cubic metals. J. Phys. D: Appl. Phys. 1978, 11, 2527. [Google Scholar] [CrossRef]
- Grüneisen, E. Zustand Thermische Eigenschaften der Stoffe; Springer: Berlin, Germany, 1926. [Google Scholar]
- Mayer, B.; Anton, H.; Bott, E.; Methfessel, M.; Sticht, J.; Harris, J.; Schmidt, P. Ab-initio calculation of the elastic constants and thermal expansion coefficients of Laves phases. Intermetallics 2003, 11, 23–32. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Holt-Saunders Int.: Philadelphia, PA, USA, 1976. [Google Scholar]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Takeuchi, A.; Inoue, A. Classification of bulk metallic glasses by atomic size difference, heat of mixing and period of constituent elements and its application to characterization of the main alloying element. Mater. Trans. 2005, 46, 2817–2829. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Guo, S.; Ng, C.; Lu, J.; Liu, C. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 2011, 109, 103505. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Y.; Yang, Y.; Wang, J.; Liu, C. Atomic-size effect and solid solubility of multicomponent alloys. Scripta Materialia 2015, 94, 28–31. [Google Scholar] [CrossRef]
- Sheng, G.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. Mater. Int. 2011, 21, 433–446. [Google Scholar]
- Yeh, J.W.; Chang, S.Y.; Hong, Y.D.; Chen, S.K.; Lin, S.J. Anomalous decrease in X-ray diffraction intensities of Cu-Ni-Al-Co-Cr-Fe-Si alloy systems with multi-principal elements. Mater. Chem. Phys. 2007, 103, 41–46. [Google Scholar] [CrossRef]
- Wallace, D.C. Thermodynamics of Crystals; Wiley: Hoboken, NJ, USA, 1972. [Google Scholar]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Gu, X.; McDermott, A.; Poon, S.J.; Shiflet, G.J. Critical Poisson’s ratio for plasticity in Fe-Mo-C-B-Ln bulk amorphous steel. Appl. Phys. Lett. 2006, 88, 211905. [Google Scholar] [CrossRef]
- Nguyen-Manh, D.; Mrovec, M.; Fitzgerald, S.P. Dislocation driven problems in atomistic modelling of materials. Mater. Trans. 2008, 49, 2497–2506. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y.; Hou, H.; Wen, Z.; Zhang, P.; Liang, J. Effect of anti-site point defects on the mechanical and thermodynamic properties of MgZn2, MgCu2 Laves phases: A first-principle study. J. Solid State Chem. 2018, 263, 18–23. [Google Scholar] [CrossRef]

| Name of Alloys | ΔSmix (J/K.mol) | ΔHmix (kJ/mol) | δ (%) | VEC |
|---|---|---|---|---|
| Al20Cr20Mo20Ti20V20 | 13.38 | −12.16 | 4.83 | 4.8 |
| Al20Cr20Mo10Ti20V30 | 12.94 | −13.04 | 4.92 | 4.7 |
| Al30Cr10Mo5Ti20V35 | 11.89 | −16.98 | 4.46 | 4.3 |
| Alloys | B | G | E | ν | B/G | ρ | a | Hv | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al20Cr20Mo20Ti20V20 | 255 | 119 | 69 | 186 | 165 | 61 | 163 | 0.33 | 2.72 | 6.28 | 3.07 | 5.48 |
| Al20Cr20Mo10Ti20V30 | 247 | 111 | 64 | 183 | 157 | 60 | 161 | 0.32 | 2.62 | 5.85 | 3.05 | 5.66 |
| Al30Cr10Mo5Ti20V35 | 246 | 90 | 63 | 183 | 143 | 56 | 149 | 0.32 | 2.71 | 5.16 | 3.08 | 5.56 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhandari, U.; Zhang, C.; Yang, S. Mechanical and Thermal Properties of Low-Density Al20+xCr20-xMo20-yTi20V20+y Alloys. Crystals 2020, 10, 278. https://doi.org/10.3390/cryst10040278
Bhandari U, Zhang C, Yang S. Mechanical and Thermal Properties of Low-Density Al20+xCr20-xMo20-yTi20V20+y Alloys. Crystals. 2020; 10(4):278. https://doi.org/10.3390/cryst10040278
Chicago/Turabian StyleBhandari, Uttam, Congyan Zhang, and Shizhong Yang. 2020. "Mechanical and Thermal Properties of Low-Density Al20+xCr20-xMo20-yTi20V20+y Alloys" Crystals 10, no. 4: 278. https://doi.org/10.3390/cryst10040278
APA StyleBhandari, U., Zhang, C., & Yang, S. (2020). Mechanical and Thermal Properties of Low-Density Al20+xCr20-xMo20-yTi20V20+y Alloys. Crystals, 10(4), 278. https://doi.org/10.3390/cryst10040278






