Abstract
This article focuses on the elucidation of a three-dimensional model of the structure of anhydrite crystal (CaSO4). The structure parameters of anhydrite crystal were obtained by means of first principles after structure optimization at 0~120 MPa. In comparison with previous experimental and theoretical calculation values, the results we obtained are strikingly similar to the previous data. The elastic constants and physical parameters of anhydrite crystal were also studied by the first-principles method. Based on this, we further studied the Young’s modulus and Poisson’s ratio of anhydrite crystal, the anisotropy factor, the speed of sound, the minimum thermal conductivity and the hardness of the material. It was shown that the bulk modulus and Poisson’s ratio of anhydrite crystal rose slowly with increasing pressure. The anisotropy characteristics of the Young’s modulus and shear modulus of anhydrite crystal were consistent under various pressure levels, while the difference in the anisotropy characteristics of the bulk modulus appeared. The acoustic velocities of anhydrite crystal tended to be stable with increasing pressure. The minimum thermal conductivity remained relatively unchanged with increasing pressure. However, the material hardness declined gradually with increasing pressure.
1. Introduction
The development and utilization of underground resources has always been an important aspect of human energy development. With the development of science and technology and the shortage of energy, the development depth of underground space has improved every year [1]. Therefore, the research and development of deep-underground technology has important strategic and military significance. The difference in the geological and environmental conditions between the deep underground and Earth’s surface is very large. The mechanical properties of deep rock mass are a critical factor of deep-underground projects, and anhydrite rock is one of the major components of rock mass, meaning that the mechanical properties of anhydrite make a great contribution to the mechanical properties of rock mass [2]. Therefore, the study of the mechanical properties of anhydrite rock is of great significance.
Mohamed Chikhaoui experimentally tested the hydraulic permeability, isotherm, shear properties and elastic parameters of gypsum soil [3]. Marius manufactured a new type of high-performance composite using gypsum material and tested its mechanical properties, such as tensile strength [4]. Austa studied the chemical mechanism for low-salinity enhanced oil-recovery effects in carbonates by using a preserved core material containing dissolvable anhydrite [5]. Scholars have also undertaken a large amount of research work that investigates the physical and mechanical properties of anhydrite crystals. Sytle M. Antao studied the spatial structure of anhydrite crystals and obtained the lattice constants of anhydrite crystals [6]. Ghazal Azimi et al. studied the mechanism and kinetics of transformation, rehydration and crystallization between gypsum and anhydrite [7,8,9]. Aquilano put forward the theoretical equilibrium and growth shape of anhydrite crystals by means of the theory of Hartman and Perdok and compared them with the morphology of natural samples [10].
With the development of quantum theory and quantum mechanics, many scholars have used first principles to theoretically study the physical and chemical properties of crystals. E. Narsimha Rao used first principles to study the mechanical and thermodynamic properties of fluorocarbon materials and obtained physical property parameters such as the crystal vibration mode, free energy and specific heat capacity [11]. Etienne Balan used first principles to add sulfate to different CaCO3 samples to study the stability of its crystal structure [12]. With the development of high-speed computing, some software companies have developed software to calculate first principles, which has accelerated the progress in material research. At present, the popular programs on the market for first-principles calculation are VASP and CASTEP. Weck studied the physical properties of anhydrite crystal using VASP software, such as the heat capacity, entropy and free energy [13]. Benmakhlouf and Walker used CASTEP software to study the energy band and thermodynamic properties of MgSO4 and carbonate [14,15]. In the early research, most scholars mainly used the first-principles method to study the physical and chemical properties of crystals, such as free energy, entropy and enthalpy. Later, Zhao et al. studied the elastic constant of CaCO3 using first principles and obtained the shear modulus, bulk modulus, Poisson’s ratio and other mechanical parameters of CaCO3 crystal [16]. DV Korabel’nikov also studied the physical properties of anhydrite rock using first principles, such as its structure parameter, elastic constants and vibrational energy states [17]. However, the specific research conditions—such as the pressure—were not specified in the research paper, nor is the specific elastic constant.
The static pressure of deep rock mass is about 120 MPa, and, in this paper, CASTEP software is mainly used to study mechanical properties such as the structural stability and elastic constants of anhydrite crystals at 0~120 MPa. Therefore, this work plays an important fundamental role in the study of the mechanical properties of deep rock mass.
2. Theoretical Methods
2.1. Research Methods
A three-dimensional model of anhydrite (CaSO4) crystal was first established. Because of the orthogonality of anhydrite crystals, there are nine independent elastic constants, which can be obtained through the following formula [18,19]:
where is the elastic constant, is the volume, is the Helmholtz free energy, and is the strain. The Helmholtz free energy of the crystal can be obtained by first principles when the crystals are under nine different strains. Therefore, the elastic tensor of the crystal can be obtained by solving Equation (1). The core of the first-principles method is defining the Hamiltonian in a Schrodinger equation. The Hamiltonian in the Schrodinger equation equals the sum of the atomic energy and electronic energy of the crystal. The electronic energy can be determined according to the Kohn–Sham equation. The exchange-correlation function is treated with PW91 of the generalized gradient approximation (GGA). The energy of the electron can be solved through repeated iterations of Equation (2) using a computer.
where is the reduced Planck constant, is the electronic mass, is the electronic potential, is the electron wave function, is the Lagrange constant, is the potential of the electron–nucleus attraction, is the potential of the electron–electron repulsion, represents the exchange-correlation energy, and is the charge density. Giving an initial value to , the electron wave function can be solved by Equation (2a). Therefore, the charge density can be solved by Equation (2c). Then, a new can be obtained by substituting Equation (2c) into Equation (2b). The same is done for the iterative calculation. The iterative calculation is finally stopped by the control of the self-consistent field function.
2.2. Specific Parameter Setting
All calculations were based on density functional theory, and the calculation processes were performed using the CASTEP software package. The electronic potential was treated with ultra-soft pseudopotential approximation. The exchange-correlation potential energy was treated with PW91 of the generalized gradient approximation. The cut-off energy of the plane-wave was set at 500 eV. A convergence criterion of 10−6 eV/atom was used for the electronic self-consistency loop. The sampling unit of k points in the Brillouin zone was 2 × 2 × 2. The optimization of the structure was calculated at six pressure points between 0~120 MPa. The values of the convergence thresholds in each set are given in Table 1.

Table 1.
Values of the convergence thresholds for each parameter.
3. Results and Discussion
3.1. Properties of Unit Cell Under 0 MPa Pressure
Figure 1 is a 3D drawing of unit cell of anhydrite (CaSO4) and shows the spatial distribution of anhydrite crystal atoms under a pressure of 0 MPa. Table 2 shows the fractional coordinates of each atom. There are 24 atoms in the unit cell.
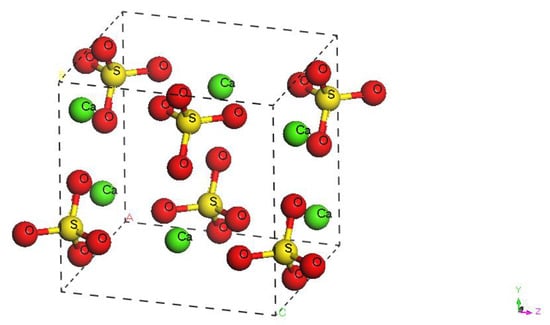
Figure 1.
Spatial distribution of atoms in anhydrite unit cell.

Table 2.
Fractional coordinates of the atoms in the anhydrite unit cell.
The lattice constants were measured by Antao using synchrotron high-resolution powder X-ray diffraction [20]. Hawthorne also reported the lattice parameters of anhydrite crystals through experiments [13]. In addition, Weck and Korabel’nikov analyzed the anhydrite crystal lattice constant theoretically [13,17]. Table 3 shows the comparison of the lattice parameters between the data used in this paper and previous data. It is concluded that the lattice parameters used in this paper are in good agreement with the former experimental and theoretical values. It also suggests that the structural model of anhydrite crystal that is established in this paper is reliable.

Table 3.
Comparison of lattice parameters of anhydrite (unit: Å).
Through calculation, we can obtain the elastic tensor of the crystal as follows (GPa):
According to the mechanical stability condition of the orthogonal crystal system [20]:
It is known that anhydrite rock is stable at 0 MPa.
3.2. Relationship of Crystal Structure Parameters with Pressure Variation
Lattice parameters and densities of anhydrite crystals measured under different pressures are presented in Table 4. It is clear from the table that the lattice parameters decline slowly with increasing pressure. It shows the compressible property of anhydrite rock. The parameters b/a and c/a tend to stabilize at about 1.126 and 1.13, respectively. It follows from the above information that the compressible property of anhydrite crystals is almost identical in all directions. The crystal density increases slowly with the increasing pressure. There is a minimum density of 2.855 g/cm3 at 0 MPa. In order to more clearly describe the changing relationship between the lattice constant and pressure, the lattice parameters and volume change ratio of the lattice under pressure are represented by a graph (as shown in Figure 2). The a0, b0 and c0 are the lattice parameters of anhydrite crystals under pressure of 0 MPa. It can be seen from the graph that the ratio of the lattice constant in each direction decreases with the increase of pressure.

Table 4.
Lattice parameters and densities of anhydrite crystals under different pressures.
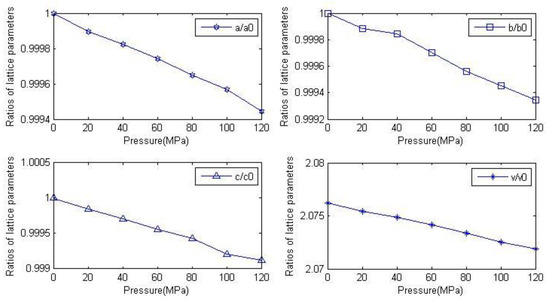
Figure 2.
Relationship between lattice constants and volume ratio of anhydrite crystals and pressure.
A polynomial was used to fit the lattice parameter curve, and the functional expressions of the lattice parameters in the region [0,120] MPa were obtained as follows:
The above equation was used to draw the curve of the fitting function, as shown in Figure 3. It can be seen from the figure that all the parameters have good fitting degrees. Therefore, the relationship between pressure and lattice parameters can be approximately described by this expression in the region 0~120 MPa.
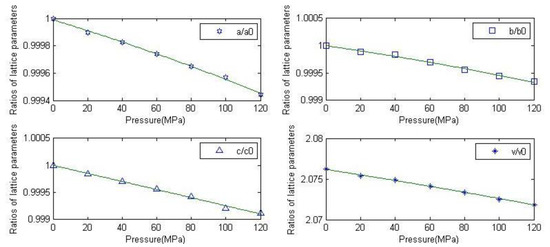
Figure 3.
Fitting function curves of the lattice constant of anhydrite.
3.3. Pressure-Dependent Elastic Constants and Mechanical Properties
Table 5 shows the elastic constants of anhydrite crystals under different pressures. The elastic constants fluctuate and tend to increase slightly with the increase of pressure.
where

Table 5.
Elastic constants of anhydrite crystals under different pressures (GPa).
- —GPa.
- —MPa.
As can be seen from Table 5, each elastic constant varies with the change of pressure. The constant is much greater than and . This means that the anhydrite crystals are harder to compress in the [010] direction than in the [100] and [001] directions. Additionally, the constant is much smaller than and . This indicates that, under the same pressure, the shear deformation of anhydrite crystals in the [100] direction is much larger than that in the [001] and [010] directions. It is evident that the elastic constants meet the demand of the Formula (3) under a pressure of 0~120 MPa.
The bulk modulus B reflects the volume change of the crystal under pressure, the shear modulus G reflects the degree of shear deformation of the crystal, and the Young’s modulus E reflects the deformation capacity of the crystal in the axial tensile load.
Once the elastic constant of the crystal is determined, the bulk modulus B and shear modulus G of the crystal can be obtained by Voigt–Reuss–Hill approximation. The bulk modulus B and shear modulus G of the crystal can be calculated by the following formula [21]:
where B is the bulk modulus, G is the shear modulus, BR and GR are, respectively, the bulk modulus and shear modulus of Reuss, and BV and GV are the bulk modulus and shear modulus of Voigt, respectively. In addition, Young’s modulus and Poisson’s ratio can also be obtained by the following formula:
Figure 4 shows the variation of modulus under different pressures. The figure shows that the bulk modulus rises slowly with the increase of pressure. The shear modulus and Young’s modulus of anhydrite crystals oscillate with the increase of pressure. In summary, the value of the three parameters is stable under the pressure of 0~120 MPa.
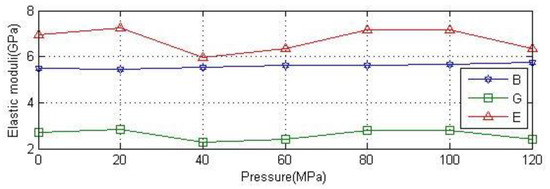
Figure 4.
Variation of modulus of anhydrite crystal with pressure.
In 1954, Pugh proposed the use of the ratio of the bulk modulus to shear modulus to evaluate the toughness/brittleness of materials [22]. If the B/G value is large, the toughness of the material is good (i.e., the value is greater than 1.75 B/G, meaning the material shows ductile behavior); otherwise, it exhibits brittle deformation behavior. Figure 5a shows the variation in the ratio of the bulk modulus to shear modulus with the increase of pressure. As can be seen from the diagram, the value is always greater than 1.75 B/G and tends to grow with the increase of pressure. This illustrates the toughness of anhydrite crystals under conditions of low pressure. In addition, Frantsevich uses Poisson’s ratios to reflect the brittle behavior of materials [23]. If υ < 0.26, this indicates that the material is a brittle material; otherwise, it is a ductile material. Figure 5b is the Poisson’s ratio of the anhydrite crystal change with pressure. As can be seen in the picture, the Poisson’s ratio of anhydrite tends to grow with the increase of pressure, and the Poisson’s ratios are always greater than 0.26 under a pressure in the range of 0~120 MPa. This shows that anhydrite crystals exhibit ductile behavior in this region.
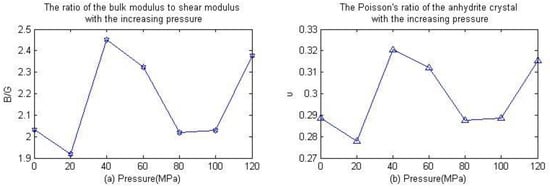
Figure 5.
Ratio of bulk modulus to shear modulus and Poisson’s ratio as a function of pressure.
The Cauchy pressure of a crystal is expressed as the difference between two given elastic constants , , [24]. Figure 6 shows the variation of the three Cauchy pressures. The higher the Cauchy pressure, the greater the toughness of the material; otherwise, the material is brittle. If the Cauchy pressure is positive, the material is characterized by ductile behavior; otherwise, the material exhibits brittle behavior. As can be seen from the graph, the Cauchy pressure is negative in direction c, and in the other two directions, the Cauchy pressure is positive. Therefore, the toughness of anhydrite in direction b is inferior compared to in the other two directions.
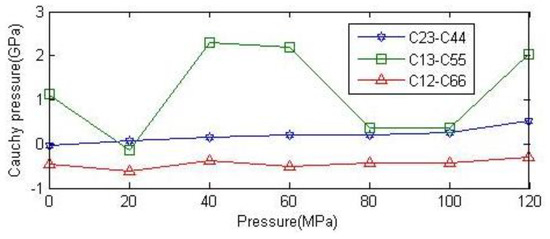
Figure 6.
Relationship between Cauchy pressure of anhydrite crystals and ambient pressure.
Hardness is a material’s resistance to elasto-plastic deformation under external load, which is related to the elastic constant, plasticity, strain, brittleness, strength and other characteristics of the material. Theoretically, the hardness (H) of the material can be obtained by the following equation [25]:
In order to visually show the relationship between hardness and pressure of anhydrite crystal, the hardness as a function of pressure was plotted, as shown in Figure 7.
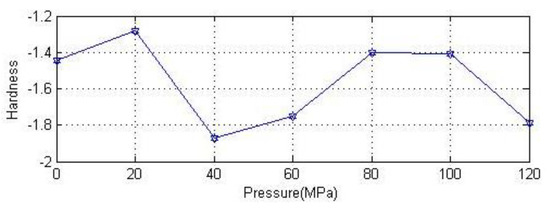
Figure 7.
Relation of the hardness of anhydrite crystal with pressure.
It is well known that all crystals are anisotropic. Therefore, the study of the anisotropic properties of crystals is of great significance to crystal physics and engineering science. The compression anisotropy factors, shear anisotropy factors and general anisotropy factors can be obtained by the following formula [26,27]:
Figure 8 is the variation of anisotropic characteristic parameters for anhydrite crystals under different pressures. The anisotropy factor is zero for isotropic crystals. Regarding the difference between the anisotropy factor and zero reflection degree of the anisotropic elasticity of crystals, Figure 8a shows that the compression anisotropy factor of anhydrite tends to increase slightly with increasing pressure. Figure 8b,c shows that the shear anisotropy factor and general anisotropy factor increase slightly with the increase of pressure. Therefore, the compression and shear anisotropic characteristics of anhydrite crystal have the same tendency with increasing pressure. In addition, the directivity of the Young’s modulus reflects the elastic anisotropic characteristics of the crystal.
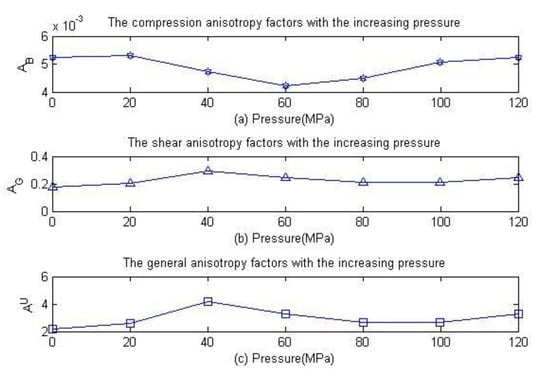
Figure 8.
Relationship of the anisotropic percentage of anhydrite crystals with pressure.
In materials science, elastic anisotropy is the directional dependence of physical properties of materials. Most materials exhibit elastic anisotropy. The bulk modulus, Young’s modulus, shear modulus and Poisson’s ratio are directional.
The bulk modulus of uniaxial compression along directions a and c is obtained by the following:
As can be seen from Figure 9, Ba and Bc have exhibit similar trends as a function of pressure, showing a gradual increasing trend with the increase of pressure. The fluctuation of data may be caused by the convergence accuracy of the calculation program.
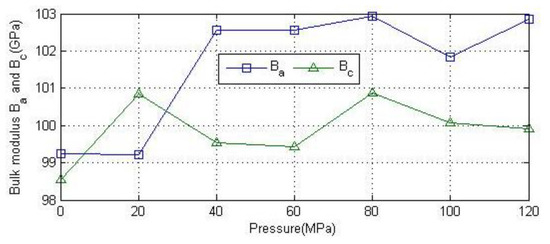
Figure 9.
Relationship between bulk modulus and pressure along the a and c axes under uniaxial compression.
Equation (15) is the calculation formula for the Young’s modulus, shear modulus and bulk modulus in the direction [28]. is the cosine direction for the radius vector r. In order to make the anisotropic properties of materials more intuitive, the Young’s modulus, shear modulus and bulk modulus of the material in all directions are shown with a cloud chart. Figure 10 is the cloud chart for the bulk modulus, Young’s modulus and shear modulus of anhydrite crystals at 0 MPa, 60 MPa and 120 MPa, respectively. It can be seen from the figure that the bulk moduli of anisotropic characteristics of anhydrite crystals under pressures of 0 MPa and 60 MPa are different from several other anisotropic characteristics. The shear modulus and Young’s modulus of anisotropic characteristics are the same under various pressures.
where B is the bulk modulus, G is the shear modulus, E is Young’s modulus, and S is the flexible tensor.
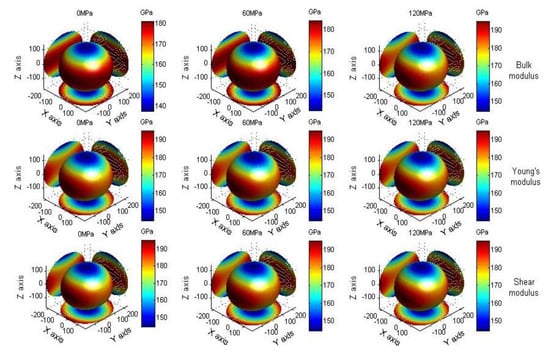
Figure 10.
The modulus of anhydrite crystals at pressures of 0 MPa, 60 MPa and 120 MPa.
3.4. Pressure-Dependent Wave Velocity and Thermal Conductivity
The wave velocities are related to the symmetry of the crystal structure and have directionality. For orthogonal crystal systems, elastic waves have pure longitudinal and transverse waves in the three directions [100], [010] and [001], while other directions have quasi-longitudinal or quasi-transverse waves [25]:
Then, the average elastic wave velocity is
Figure 11 shows the relationship between the longitudinal wave velocity, transverse wave velocity and average wave velocity of polycrystalline anhydrite and pressure. It can be seen from the figure that the polycrystalline wave velocity fluctuates slightly under different pressures and tends to stabilize between 0 MPa and 120 MPa.
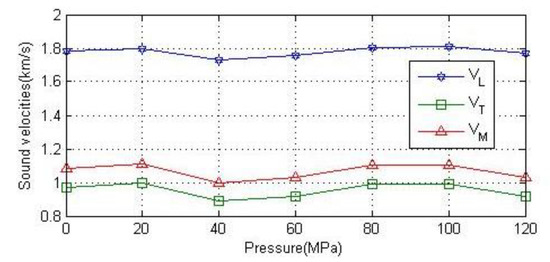
Figure 11.
Variation of longitudinal, transverse and average sound velocity of polycrystalline anhydrite with pressure.
To study the directivity of the crystal wave velocity, the slowness surface equation is taken as follows:
where is the direction cosine vector of the wave vector, and is the velocity of the wave.
Then, the matrix element of the Christoffel tensor of an orthogonal crystal system is [29]
Taking the wave vector k directions as [100], [001] and [110], and substituting Equation (19) into Equation (18) to obtain the longitudinal wave velocity and transverse wave velocity in each direction yields the following:
where , , respectively, represent the first and second transverse wave velocities, and is the mass density of the crystal. Then, the minimum thermal conductivity can be obtained by the following formula [30]:
where is the density of atoms per volume. Because the total thermal conductivity is already treated as the summation of one longitudinal and two transverse acoustic branches, the equation might be suitable to study the anisotropic thermal conductivities of the crystal.
Figure 12 shows the variation of the longitudinal and transverse sound velocities of anhydrite crystals along the [100], [001], [110] directions with pressure. It can be seen from the graph that the sound velocities from all the three directions remain relatively unchanged with the increase of pressure. The longitudinal sound velocities in the three directions are almost equal. The transverse sound velocity appears to have a large difference in different directions, and the transverse sound velocity of direction [001] is minimal. This also reflects the anisotropic characteristics of anhydrite crystals.
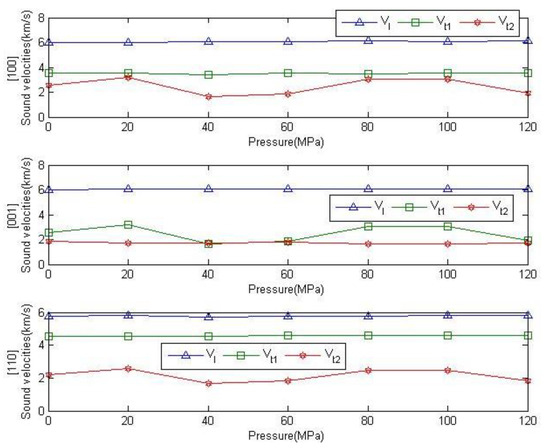
Figure 12.
Relationship between wave velocity and pressure in the [100], [001] and [110] directions of anhydrite crystals.
Figure 13 shows the minimum thermal conductivity for anhydrite crystals along the [100], [001], [110] directions. It is concluded from the figure that the minimum thermal conductivity remains relatively unchanged with the increase of pressure. The fluctuation of data may be caused by the convergence accuracy of the calculation program because of the small pressure difference. The thermal conductivity was similar in the directions [100] and [110]. The thermal conductivity is largest value in the [110] direction; this shows that anhydrite crystals in the axial direction of the thermal conductivity are worse than in the other direction.
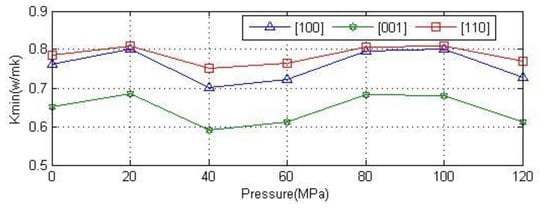
Figure 13.
Relationship between the minimum thermal conductivity and pressure in the [100], [001] and [110] directions of anhydrite crystals.
4. Conclusions
The structure and anisotropic elastic properties of anhydrite crystals were studied by the first-principles method at a pressure in the range of 0~120 MPa. The optimized structure constants of anhydrite crystal remain strikingly similar to the previous experimental values and theoretical calculation values reported by other scholars, and the elastic tensor of anhydrite crystals was obtained under different pressures. The mechanical stability was ascertained by using elastic constants at each stage. The results show that the elastic constants meet the stability conditions effectively under all pressures. By studying the Young’s modulus, anisotropy factor, sound velocity and other properties of anhydrite, it was found that the value of the bulk modulus and the anisotropy factor increase slowly with increasing pressure from Figure 4 and Figure 8, respectively. The anisotropy characteristics of the Young’s modulus and shear modulus of anhydrite were consistent under different pressures, and the anisotropic characteristics of the bulk modulus were different from Figure 10. The sound velocity of anhydrite crystal is essentially unchanged under a pressure of 0~120 MPa. The minimum thermal conductivity also remains relatively unchanged with the increase of pressure. The hardness of anhydrite crystal declines with increasing pressure, as shown in Figure 7. In this paper, the results of this study carry important implications regarding the understanding of dynamic characteristics of deep rock mass.
Author Contributions
X.Z. and S.Y. conceived and designed the calculations; X.Z. and L.L. performed the calculations; G.H. and W.Z. analyzed the data; Z.L. contributed analysis tools; X.Z., S.Y. and Y.X. wrote the paper. All authors have read and agree to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 51375416) and the Project of Science Research of Department of Education of Hunan Province (No. 15K131).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Peng, F.L.; Qiao, Y.K.; Zhao, J.W.; Liu, K.; Li, J.C. Planning and implementation of underground space in Chinese central business district (CBD): A case of Shanghai Hongqiao CBD. Tunn. Undergr. Space Technol. 2020, 95, 103176. [Google Scholar] [CrossRef]
- Ning, Y.B.; Tang, H.M.; Zhang, B.C.; Shen, P.W.; Zhang, G.C.; Xia, D. Research on rock similar material proportioning test based on orthogonal design and its application in base friction physical model test. Rock Soil Mech. 2020, 6, 1–11. [Google Scholar]
- Chikhaoui, M.; Belayachi, N.; Nechnech, A.; Hoxha, D. Experimental characterization of the hydromechanical properties of the gypsum soil of Sebkha of Oran. Period. Polytech Civ. Eng. 2017, 61, 706–717. [Google Scholar] [CrossRef][Green Version]
- Marius, M.; Amalia, D.F.; Philippe, D.; Michael, A.; Dubois, P. Polylactide compositions. Part 1: Effect of filler content and size on mechanical properties of PLA/calcium sulfate composites. Polymer 2008, 48, 2613–2618. [Google Scholar]
- Austad, T.; Shariatpanahi, S.F.; Strand, S.; Aksulu, H.; Puntervold, T. Low Salinity EOR Effects in Limestone Reservoir Cores Containing Anhydrite: A Discussion of the Chemical Mechanism. Energy Fuels 2015, 29, 6903–6911. [Google Scholar] [CrossRef]
- Antao, S.M. Crystal-structure analysis of four mineral samples of anhydrite, CaSO4, using synchrotron high-resolution powder X-ray diffraction data. Powder Diffr. 2011, 26, 326–330. [Google Scholar] [CrossRef]
- Azimi, G.; Papangelakis, V.G. Mechanism and kinetics of gypsum–anhydrite transformation in aqueous electrolyte solutions. Hydrometallurgy 2011, 108, 122–129. [Google Scholar] [CrossRef]
- Liu, C.J.; Zheng, H.F. A new approach to kinetics study of the anhydrite crystallization at 373 K using a diamond anvil cell with Raman spectroscopy. Rev. Sci. Instrum. 2013, 84, 044501. [Google Scholar] [CrossRef]
- Tang, Y.; Gao, J.; Liu, C.; Chen, X.; Zhao, Y. Dehydration Pathways of Gypsum and the Rehydration Mechanism of Soluble Anhydrite γ-CaSO4. ACS Omega 2019, 4, 7636–7642. [Google Scholar] [CrossRef]
- Aquilano, D.; Rubbo, M.; Catti, M.; Pavese, A.; Ugliengo, P. Theoretical equilibrium and growth morphology of anhydrite (CaSO4) crystal. J. Cryst. Growth 1992, 125, 519–532. [Google Scholar] [CrossRef]
- Rao, E.N.; Vaitheeswaran, G.; Reshak, A.H.; Auluck, S. Effect of lead and caesium on the mechanical, vibrational and thermodynamic properties of hexagonal fluorocarbonates: A comparative first principles study. RSC Adv. 2016, 6, 99885–99897. [Google Scholar] [CrossRef]
- Etienne, B.; Marc, B.; Carlos, P.; Michele, L. First-principles modeling of sulfate incorporation and 34S/32S isotopic fractionation in different calcium carbonates. Chem. Geol. 2014, 374, 84–91. [Google Scholar]
- Philippe, F.W.; Eunja, K.; Carlos, F.J.C.; David, C.S. First-principles study of anhydrite, polyhalite and carnallite. Chem. Phys. Lett. 2014, 594, 1–5. [Google Scholar]
- Benmakhlouf, A.; Errandonea, D.; Bouchenafa, M.; Maabed, S.; Bouhemadou, A.; Bentabet, A. New pressure-induced polymorphic transitions of anhydrous magnesium sulfate. Dalton Trans. 2017, 46, 5058–5068. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.M.; Becker, U. Uranyl (VI) and neptunyl (V) incorporation in carbonate and sulfate minerals: Insight from first-principles. Geochim. Cosmochim. Acta 2015, 161, 19–35. [Google Scholar] [CrossRef]
- Zhao, J.H.; Zhou, B.; Liu, B.G.; Guo, W.L. Elasticity of Single-Crystal Calcite by First-Principles Calculations. J. Comput. Theor. Nanosci. 2009, 6, 1181–1188. [Google Scholar] [CrossRef]
- Korabel’nikov, D.V.; Zhuravlev, Y.N. Structural elastic electronic and vibrational properties of a series of sulfates from first principles calculations. J. Phys. Chem. Solids 2018, 119, 114–121. [Google Scholar] [CrossRef]
- Myhill, R. The elastic solid solution model for minerals at high pressures and temperatures. Contrib. Mineral. Petrol. 2018, 173, 12. [Google Scholar] [CrossRef]
- Reshak, A.H.; Jamal, M. DFT calculation for elastic constants of orthorhombic structure within WIEN2K code: A new package (ortho-elastic). J. Alloys Compd. 2012, 543, 147–151. [Google Scholar] [CrossRef]
- Xu, Y.Q.; Wu, S.Y.; Ding, C.C.; Wu, L.N.; Zhang, G.J. First-principles investigation on the mechanism of photocatalytic properties for cubic and orthorhombic KNbO3. Chem. Phys. 2018, 504, 66–71. [Google Scholar] [CrossRef]
- Chen, H.C.; Tian, W.Y. First-principles investigation of the physical properties of cubic and orthorhombic phase Na3UO4. Phys. B 2017, 524, 144–148. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Elastic Constants and Elastic Moduli of Metals and Insulators Handbook; Frantsevich, I.N., Ed.; Naukova Dumka: Kiev, Ukraine, 1983; pp. 60–180. [Google Scholar]
- Jund, P.; Viennois, R.; Tao, X.M.; Niedziolka, K.; Tedenac, J.C. Physical properties of thermoelectric zinc antimonide using first-principles calculations. Phys. Rev. B 2012, 85, 224105. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Intrinsic correlation between hardness and elasticity in polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The elastic anisotropy of crystals. J. Appl. Phys. 1967, 38, 2010–2012. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Bai, X. Study on Pure Mode Axes of Orthorhombic System Crystals. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2016. [Google Scholar]
- Cahill, D.G.; Watson, S.K.; Pohl, R.O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 1992, 46, 6131–6140. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).