Mixed Oscillation Flow of Binary Fluid with Minus One Capillary Ratio in the Czochralski Crystal Growth Model
Abstract
1. Introduction
2. Model Formulation and Numerical Methodology
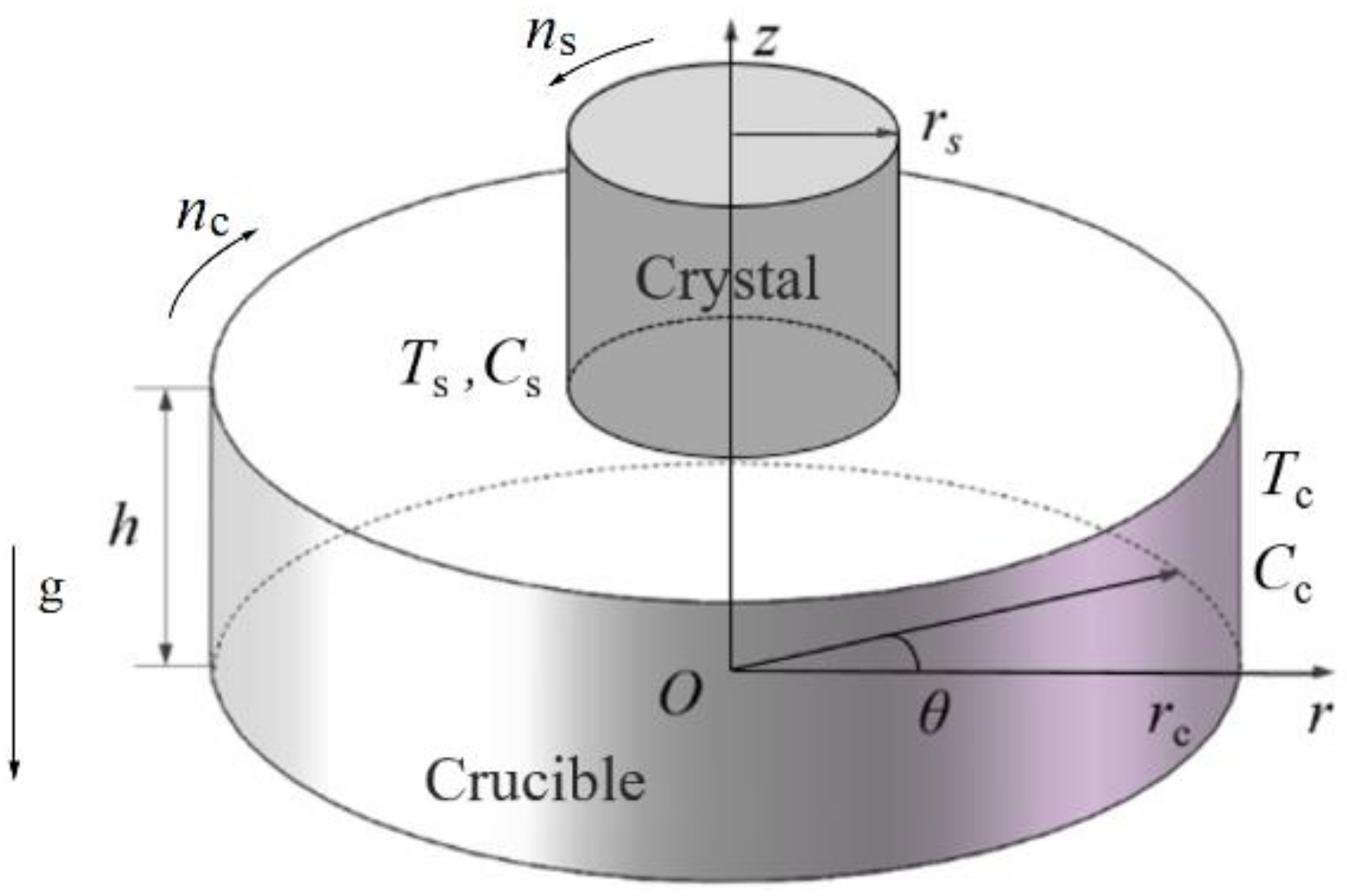
2.1. Physical Model and Basic Assumption
2.2. Mathematical Formulation
2.3. Numerical Procedure and Method Validation
3. Results and Discussions
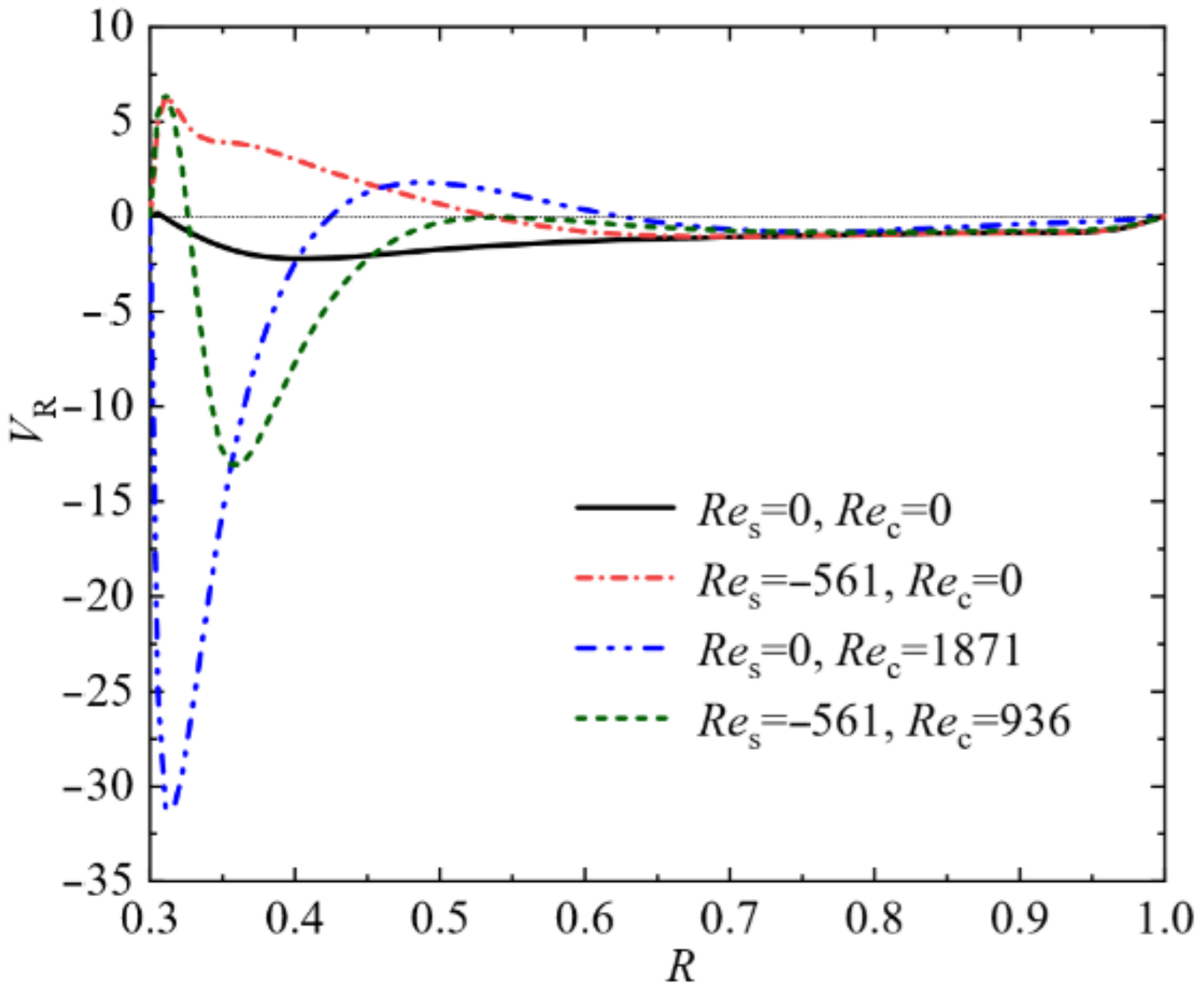
3.1. Basic Two-Dimensional Flow and Stability
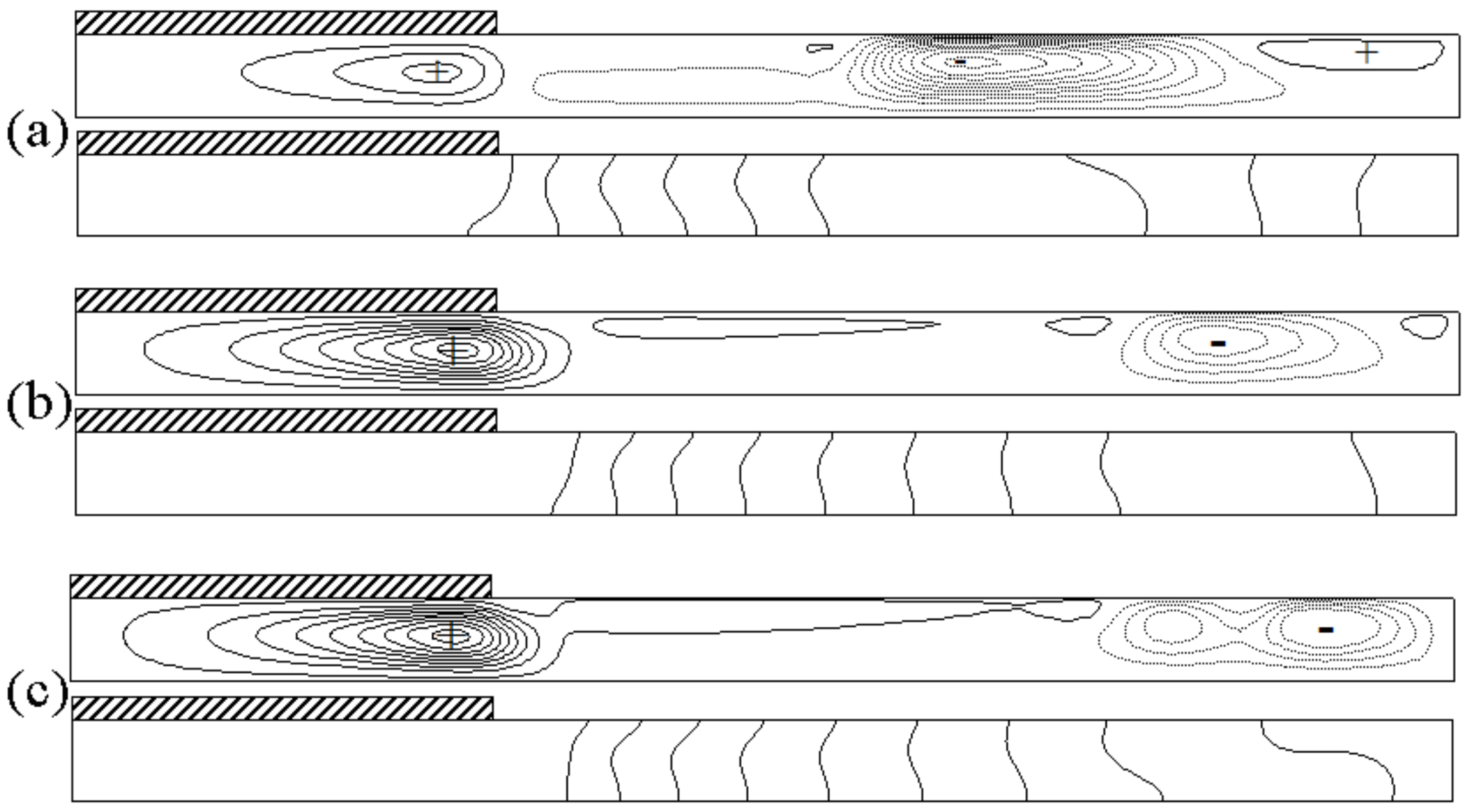
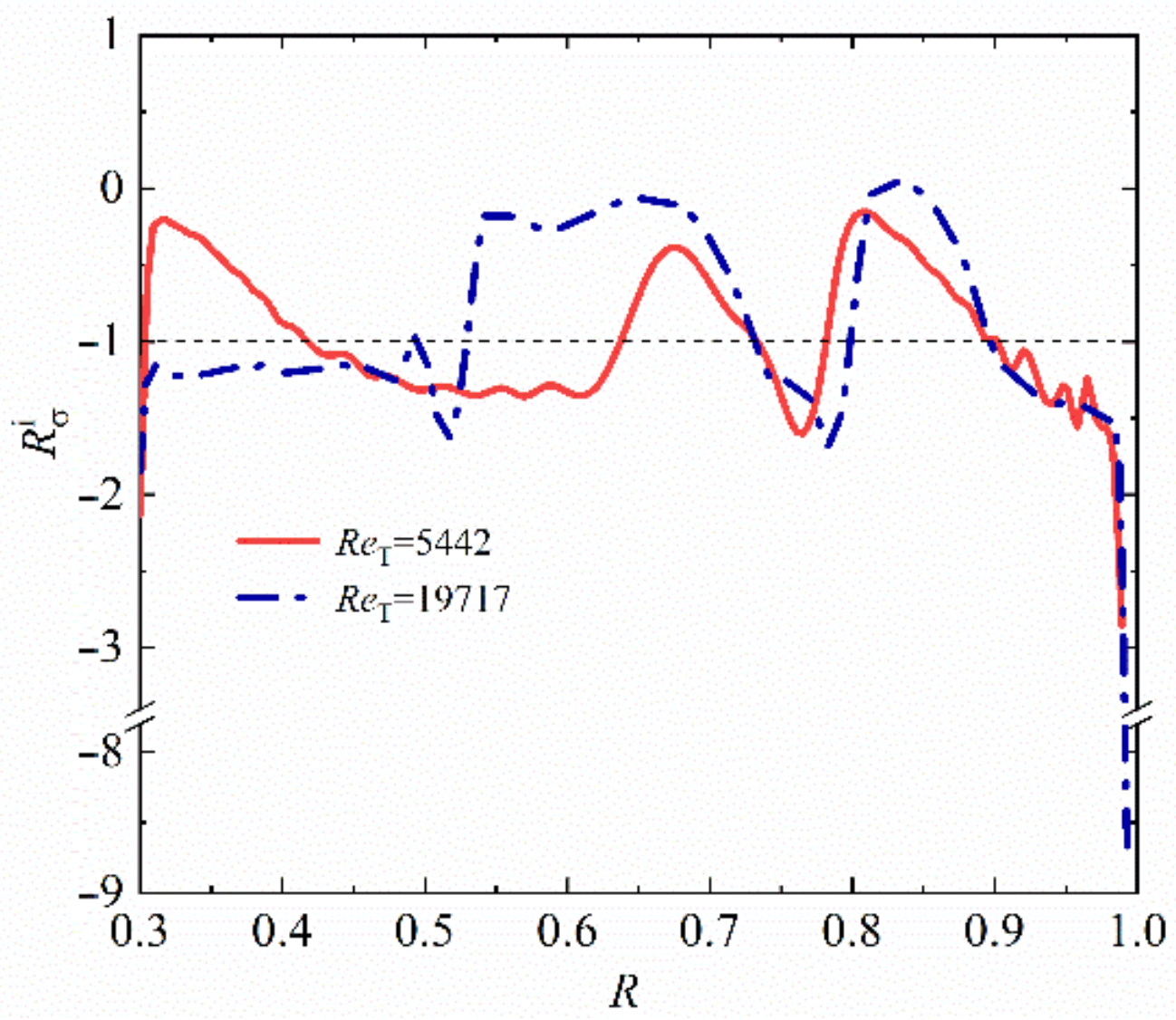
3.2. Three-Dimensional Steady Flow
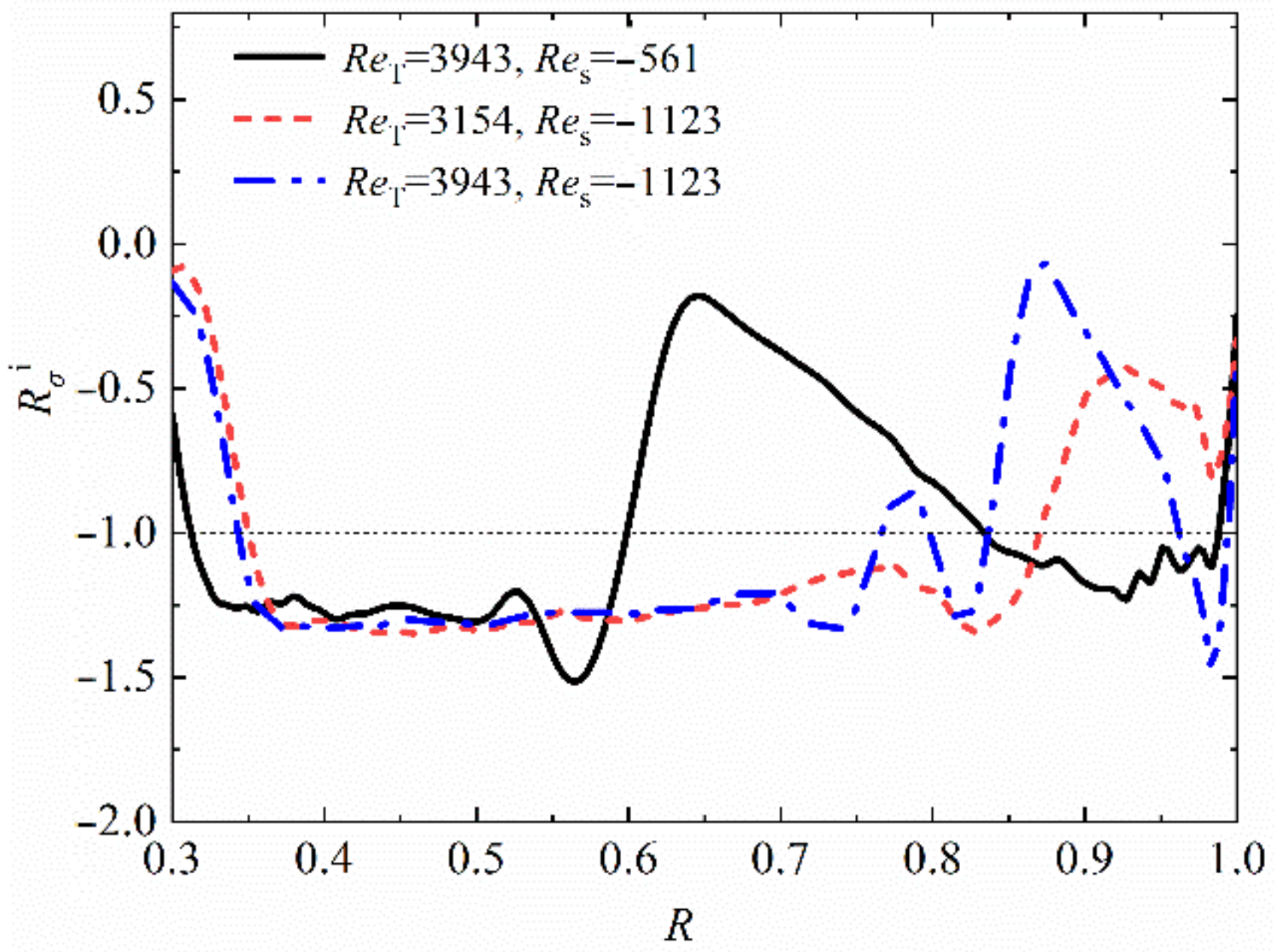
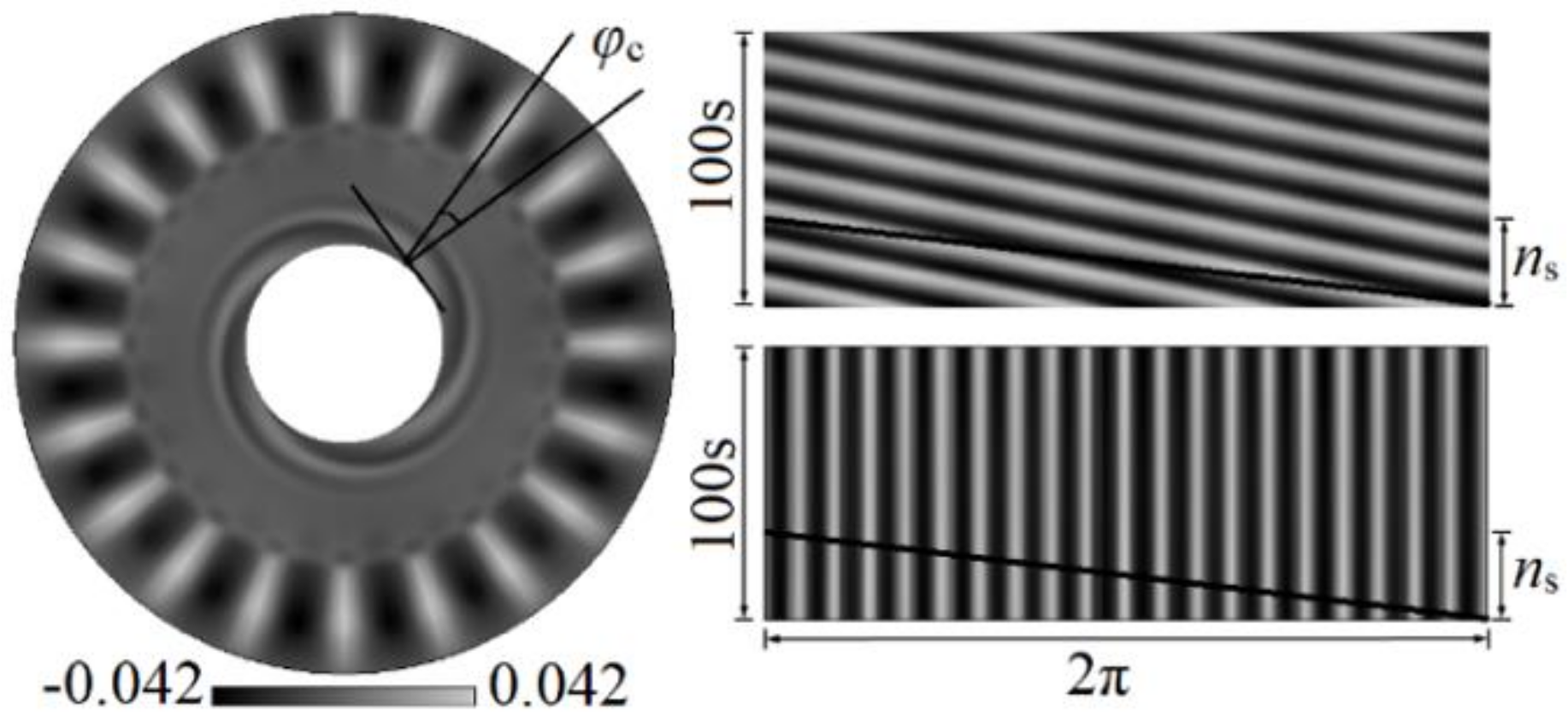
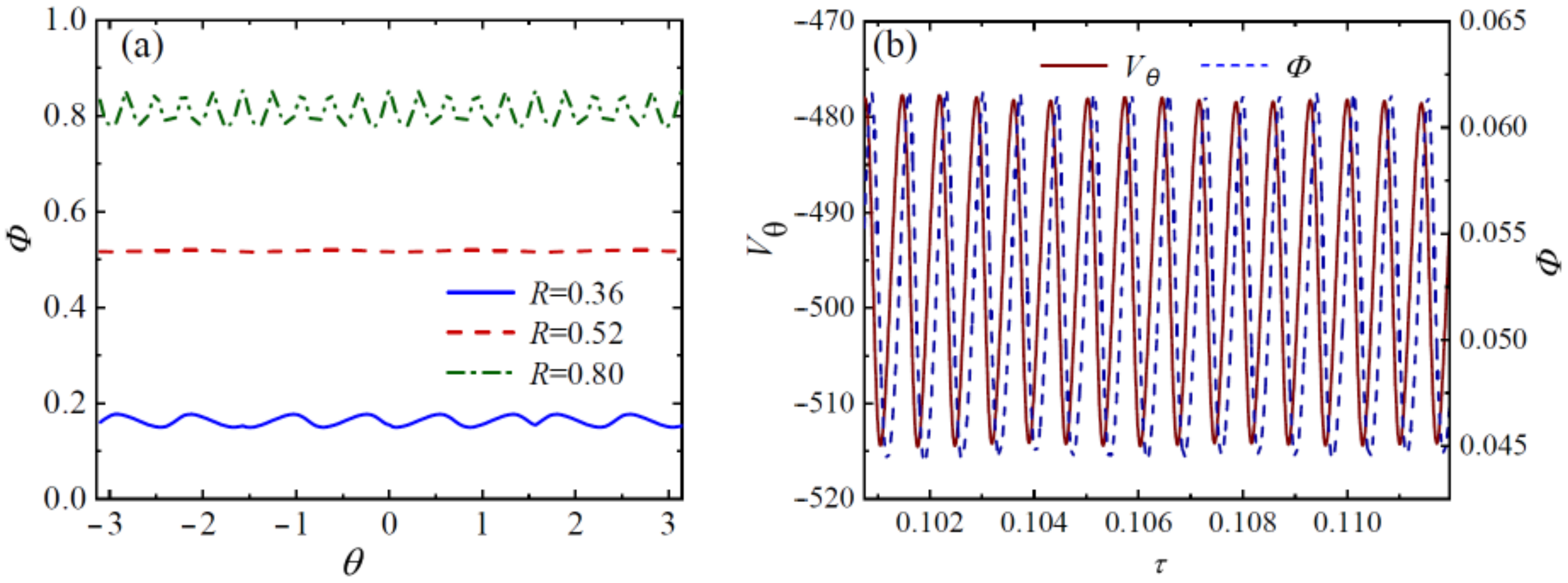
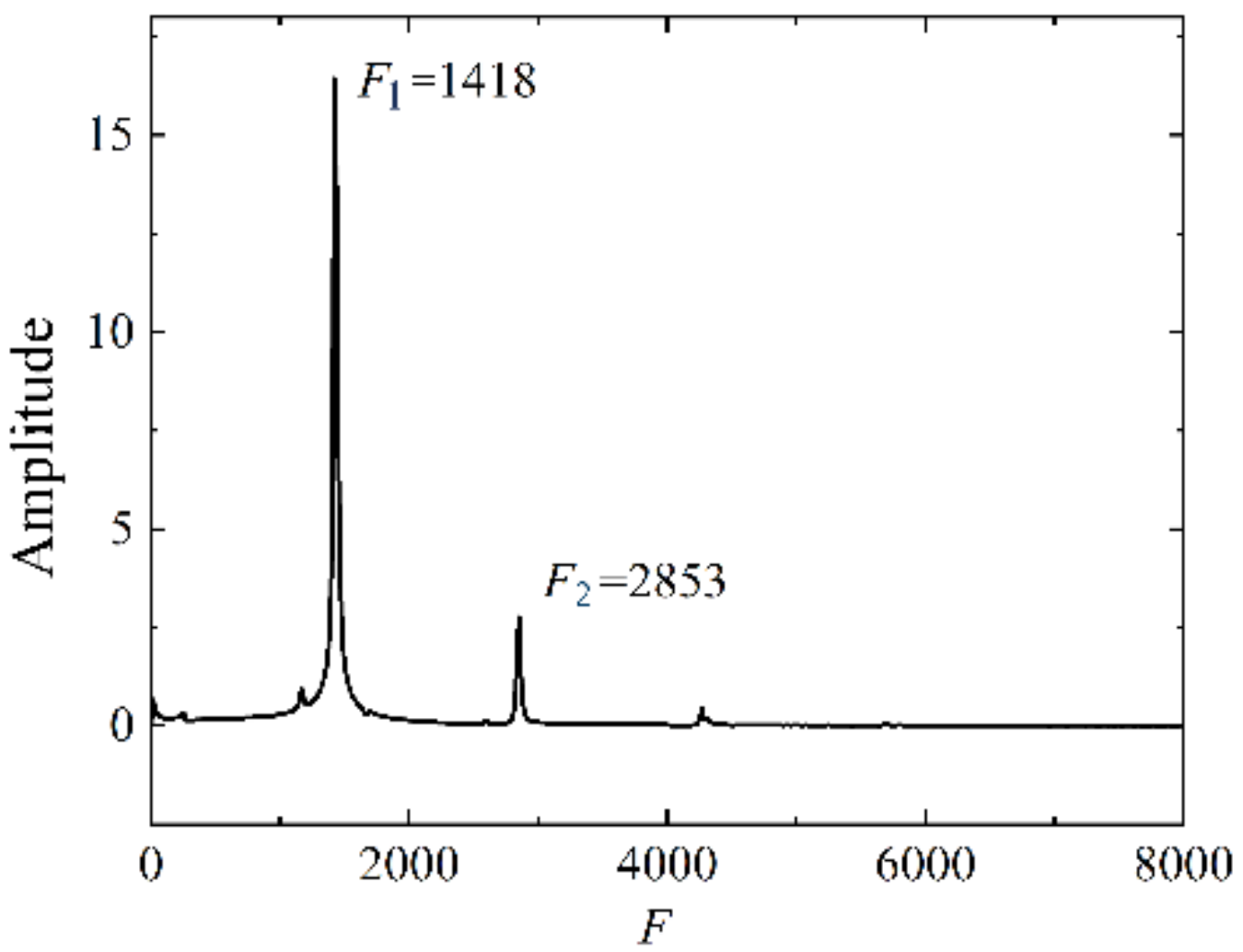
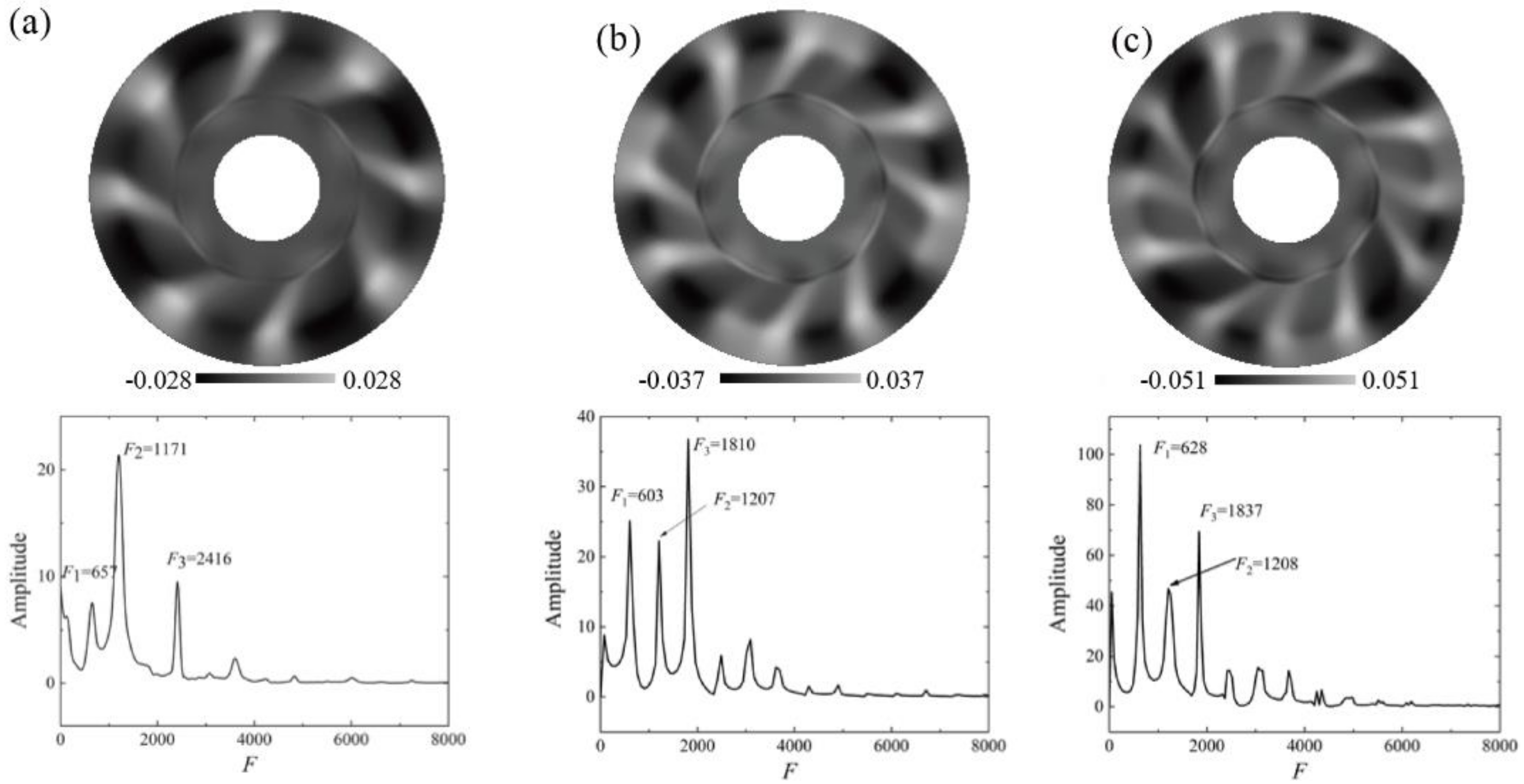
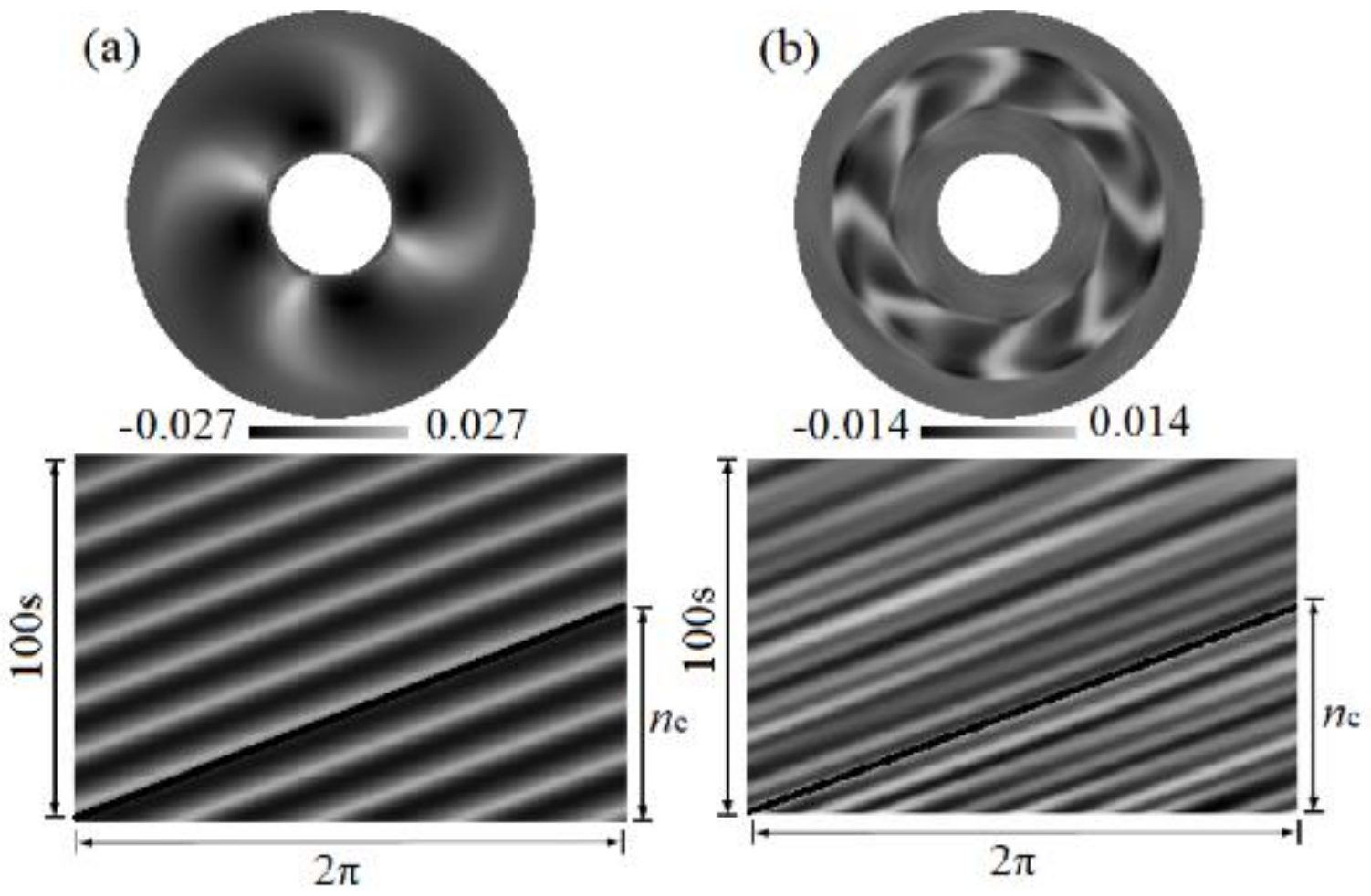
3.3. Three-Dimensional Oscillatory Flow
4. Conclusions
- (a)
- For the mixture with capillary ratio of minus one, the total thermal and solutocapillary forces are counterbalanced. The introduction of buoyancy force leads to the disturbance of the balance, generating the mixed capillary-buoyancy convection. For a small concentration gradient, the flow is in two-dimensional steady state. Owing to the good fluidity and thermal uniformity, this state is important for the growth of high quality of crystals. The coupled capillary and buoyancy flow in the crucible is presented as a large counterclockwise circulation. When the rotations of the crystal and crucible are considered, the mixed natural and forced flow structures are more complex, and the directions of the rolling cells are associated with the competitions among the driving forces.
- (b)
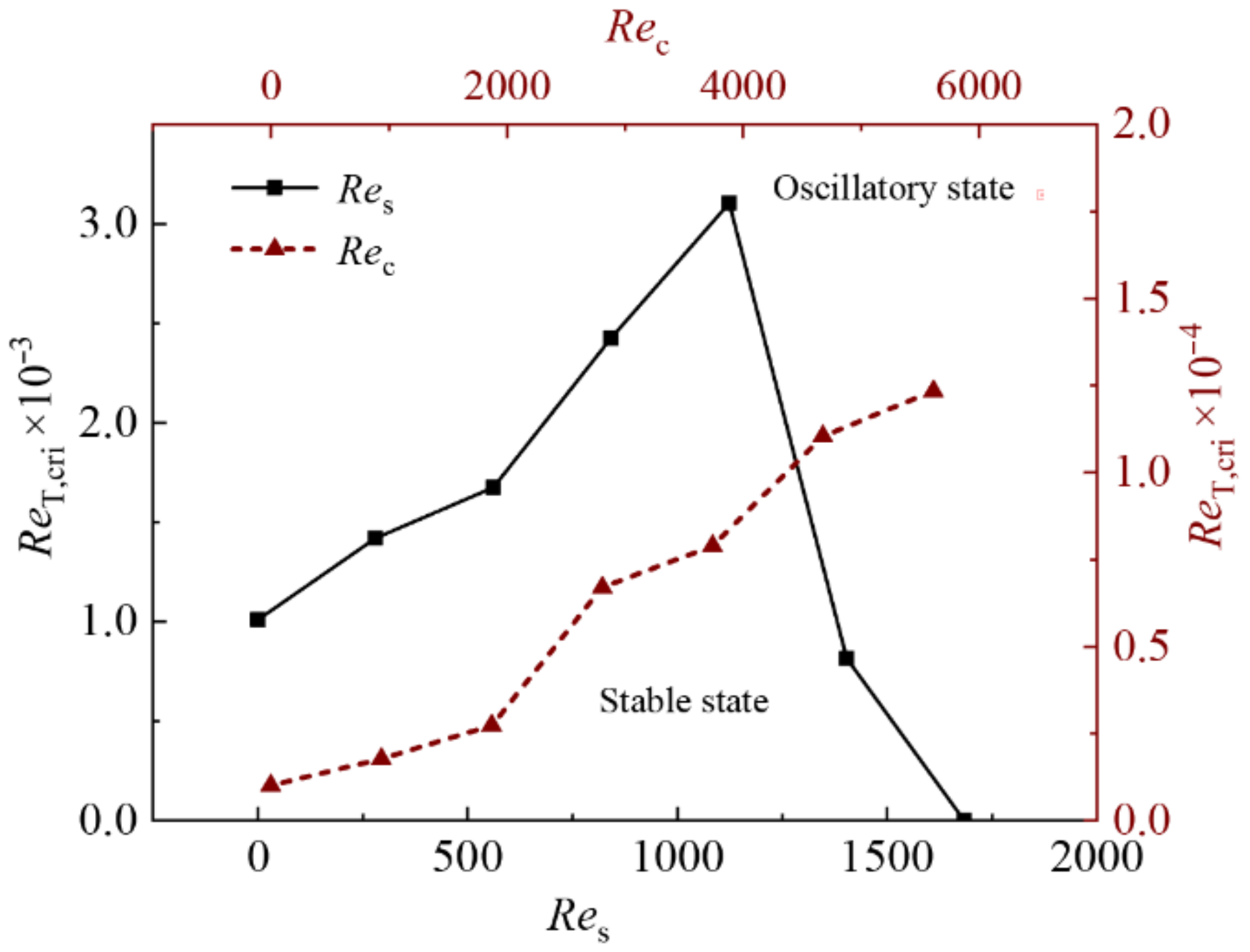
- When the capillary force is greater than a certain value, the basic flow transits to three-dimensional state. The critical conditions for the mixed flow transitions at different rotation rates are obtained. Crucible rotation can obviously strengthen the flow stability. Influenced by the crystal rotation, the critical thermocapillary Reynolds number increases until it reaches a turning point. With the enhancement of crystal rotation driven flow, a dramatic decrease of the critical value is observed.
- (c)
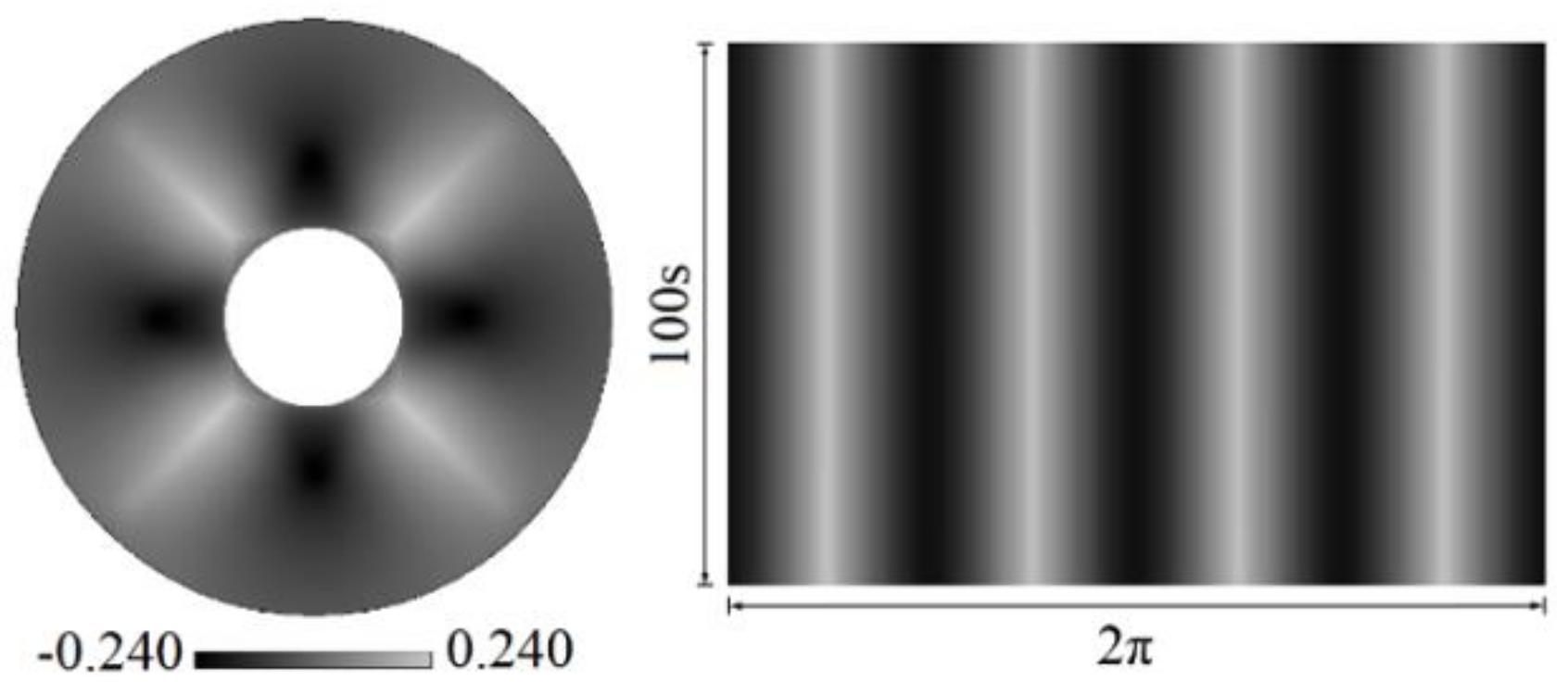
- Once the instability is incubated, the basic mixed flow firstly bifurcates to the three-dimensional steady state, which oscillates spatially along the circumferential direction. Driven by the competition among the capillary-buoyancy forces, centrifugal, and Coriolis forces, the surface fluctuations are presented as spokes, rosebud, and pulsating ring. With the enhanced flow instabilities, three-dimensional unsteady oscillation occurs. Prosperous oscillation patterns are discussed, including the spiral hydrosoultal waves, superimposition of spirals and spokes, as well as rotating waves.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, X.F.; Liu, X.; Nakano, S.; Harada, H.; Miyamura, Y.; Kakimoto, K. 3D Numerical analysis of the asymmetric three-phase line of floating zone for silicon crystal growth. Crystals 2020, 10, 121. [Google Scholar] [CrossRef]
- Nguyen, T.H.T.; Chen, J.C.; Hu, C.; Chen, C.H.; Huang, Y.H.; Lin, H.W.; Yu, A.; Hsu, B.; Yang, M.; Yang, R. Numerical study of the thermal and flow fields during the growth process of 800 kg and 1600 kg silicon feedstock. Crystals 2017, 7, 74. [Google Scholar] [CrossRef]
- Miller, W.; Abrosimov, N.; Fischer, J.; Gybin, A.; Juda, U.; Kayser, S.; Janicskó-Csáthy, J. Quasi-transient calculation of Czochralski growth of Ge crystals using the software elmer. Crystals 2020, 10, 18. [Google Scholar] [CrossRef]
- Guo, F.Y.; Li, Q.Y.; Zhang, H.M.; Yang, S.H.; Tao, Z.; Chen, X.; Chen, J.Z. Czochralski growth, magnetic properties and faraday characteristics of CeAlO3 crystals. Crystals 2019, 9, 245. [Google Scholar] [CrossRef]
- Nguyen, T.H.T.; Chen, J.C.; Hu, C.; Chen, C.H. Numerical simulation of heat and mass transfer during Czochralski silicon crystal growth under the application of crystal-crucible counter- and iso-rotations. J. Cryst. Growth 2019, 507, 50–57. [Google Scholar] [CrossRef]
- Nguyen, T.H.T.; Chen, J.C.; Hu, C.; Chen, C.H. Effects of crystal-crucible iso-rotation and a balanced/unbalanced cusp magnetic field on the heat, flow, and oxygen transport in a Czochralski silicon melt. J. Cryst. Growth 2020, 531, 125373. [Google Scholar] [CrossRef]
- Mittal, N.; Satheesh, A.; Kumar, D.S. Numerical simulation of mixed-convection flow in a lid-driven porous cavity using different nanofluids. Heat Transf. Asian Res. 2014, 43, 1–16. [Google Scholar] [CrossRef]
- Mittal, N.; Manoj, V.; Kumar, D.S.; Satheesh, A. Numerical simulation of mixed convection in a porous medium filled with water/Al2O3 nanofluid. Heat Transf. Asian Res. 2013, 42, 46–59. [Google Scholar] [CrossRef]
- Miller, W.; Böttcher, K.; Galazka, Z.; Schreuer, J. Numerical modelling of the Czochralski growth of β-Ga2O3. Crystals 2017, 7, 26. [Google Scholar] [CrossRef]
- Lyubimova, T.P.; Skuridin, R.V. Control of thermo- and solutocapillary flows in FZ crystal growth by high-frequency vibrations. J. Appl. Mech. Tech. Phy. 2017, 58, 1159–1170. [Google Scholar] [CrossRef]
- Lappa, M. Thermal convection and related instabilities in models of crystal growth from the melt on earth and in microgravity: Past history and current status. Cryst. Res. Technol. 2005, 40, 531–549. [Google Scholar] [CrossRef]
- McTaggart, C.L. Convection driven by concentration and temperature-dependent surface tension. J. Fluid Mech. 1983, 134, 301–310. [Google Scholar] [CrossRef]
- Ho, K.L.; Chang, H.C. On nonlinear doubly-diffusive Marangoni instability. AIChE J. 1988, 34, 705–722. [Google Scholar] [CrossRef]
- Castillo, J.L.; Velarde, M.G. Microgravity and the thermo-convective stability of a binary-liquid layer open to the ambient air. J. Non-Equilib. Thermodyn. 1980, 5, 111–124. [Google Scholar] [CrossRef]
- Castillo, J.L.; Velarde, M.G. Thermal-diffusion and Marangoni-Bénard instability of a 2-component fluid layer heated from below. Phys. Lett. A 1978, 66, 489–491. [Google Scholar] [CrossRef]
- Bergeon, A.; Henry, D.; Benhadid, H.; Tuckerman, L.S. Marangoni convection in binary mixtures with Soret effect. J. Fluid Mech. 1998, 375, 143–177. [Google Scholar] [CrossRef]
- Bergeon, A.; Knobloch, E. Oscillatory Marangoni convection in binary mixtures in square and nearly square containers. Phys. Fluids 2004, 16, 360–372. [Google Scholar] [CrossRef]
- Podolny, A.; Oron, A.; Nepomnyashchy, A.A. Long-wave Marangoni instability in a binary-liquid layer with deformable interface in the presence of Soret effect: Linear Theory. Phys. Fluids 2005, 17, 104104. [Google Scholar] [CrossRef]
- Shklyaev, S.; Nepomnyashchy, A.A.; Oron, A. Marangoni convection in a binary liquid layer with Soret effect at small Lewis number: Linear stability analysis. Phys. Fluids 2009, 21, 054101. [Google Scholar] [CrossRef]
- Morozov, M.; Oron, A.; Nepomnyashchy, A.A. Long-wave Marangoni convection in a layer of surfactant solution: Bifurcation analysis. Phys. Fluids 2015, 27, 082107. [Google Scholar] [CrossRef]
- Köhler, W.; Morozov, K.I. The Soret effect in liquid mixtures–a review. J. Non-Equilib. Thermodyn. 2016, 41, 151–197. [Google Scholar] [CrossRef]
- Braibanti, M.; Artola, P.A.; Baaske, P.; Bataller, H.; Bazile, J.P.; Bou-Ali, M.M.; Cannell, D.S.; Carpineti, M.; Cerbino, R.; Croccolo, F.; et al. European Space Agency experiments on thermodiffusion of fluid mixtures in space. Eur. Phys. J. E 2019, 42, 86. [Google Scholar] [CrossRef] [PubMed]
- Croccolo, F.; García-Fernández, L.; Bataller, H.; Vailati, A.; Ortiz De Zárate, J.M. Propagating modes in a binary liquid mixture under thermal stress. Phys. Rev. E 2019, 99, 012602. [Google Scholar] [CrossRef] [PubMed]
- Bergman, T.L. Numerical simulation of double-diffusive Marangoni convection. Phys. Fluids 1986, 29, 2103–2108. [Google Scholar] [CrossRef]
- Chen, Z.W.; Li, Y.S.; Zhan, J.M. Double-diffusive Marangoni convection in a rectangular cavity: Onset of convection. Phys. Fluids 2010, 22, 034106. [Google Scholar] [CrossRef]
- Li, Y.S.; Chen, Z.W.; Zhan, J.M. Double-diffusive Marangoni convection in a rectangular cavity: Transition to chaos. Int. J. Heat Mass Transf. 2010, 53, 5223–5231. [Google Scholar] [CrossRef]
- Zhou, X.; Huai, X. Influence of thermal and solutal Marangoni effects on free surface deformation in an open rectangular cavity. J. Therm. Sci. 2017, 26, 255–262. [Google Scholar] [CrossRef]
- Zhou, X.; Huai, X. Thermosolutocapillary convection in an open rectangular cavity with dynamic free surface. J. Heat Transf. 2015, 137, 082901. [Google Scholar] [CrossRef]
- Zou, Q.; Ding, L.; Wang, H.; Wang, J.; Zhang, L. Two-degree-of-freedom flow-induced vibration of a rotating circular cylinder. Ocean Eng. 2019, 191, 106505. [Google Scholar] [CrossRef]
- Lopez, J.M.; Marques, F. Rapidly rotating precessing cylinder flows: Forced triadic resonances. J. Fluid Mech. 2018, 839, 239–270. [Google Scholar] [CrossRef]
- Ding, L.; Yang, L.; Yang, Z.M.; Zhang, L.; Wu, C.M.; Yan, B.W. Performance improvement of aeroelastic energy harvesters with two symmetrical fin-shaped rods. J. Wind Eng. Ind. Aerodyn. 2020, 196, 104051. [Google Scholar] [CrossRef]
- Zebib, A. Thermocapillary instabilities with system rotation. Phys. Fluids 1996, 8, 3209–3211. [Google Scholar] [CrossRef]
- Tian, Z.A.; Zeng, Z.; Liu, H.; Yin, L.; Zhang, L.; Qiao, L. Linear stability analysis of thermocapillary flow in rotating shallow pools heated from inner wall. J. Therm. Sci. 2020, 29, 251–259. [Google Scholar] [CrossRef]
- Shen, T.; Wu, C.M.; Zhang, L.; Li, Y.R. Experimental investigation on effects of crystal and crucible rotation on thermal convection in a model Czochralski configuration. J. Cryst. Growth 2016, 438, 55–62. [Google Scholar] [CrossRef]
- Shen, T.; Wu, C.M.; Li, Y.R. Numerical simulation on effect of rotation on thermal convection in a shallow model Czochralski configuration with a heated bottom. Cryst. Res. Technol. 2018, 53, 1700268. [Google Scholar] [CrossRef]
- Wu, C.M.; Ruan, D.F.; Li, Y.R.; Liao, R.J. Flow pattern transition driven by the combined marangoni effect and rotation of crucible and crystal in a Czochralski configuration. Int. J. Therm. Sci. 2014, 86, 394–407. [Google Scholar] [CrossRef]
- Wu, C.M.; Li, Y.R.; Liao, R.J. Instability of three-dimensional flow due to rotation and surface-tension driven effects in a shallow pool with partly free surface. Int. J. Heat Mass Transf. 2014, 79, 968–980. [Google Scholar] [CrossRef]
- Cröll, A.; Mitric, A.; Aniol, O.; Schütt, S.; Simon, P. Solutocapillary convection in germanium-silicon melts. Cryst. Res. Technol. 2009, 44, 1101–1108. [Google Scholar] [CrossRef]
- Campbell, T.A.; Schweizer, M.; Dold, P.; Cröll, A.; Benz, K.W. Float zone growth and characterization of Ge1-xSix (x ≤ 10 at %) single crystals. J. Cryst. Growth 2001, 226, 231–239. [Google Scholar] [CrossRef]
- Sorgenfrei, T. 30 years of crystal growth under microgravity conditions in freiburg: An overview of past activities. Cryst. Res. Technol. 2018, 53, 1700265. [Google Scholar] [CrossRef]
- Wu, C.M.; Yuan, B.; Li, Y.R. Flow instabilities of coupled rotation and thermal-solutal capillary convection of binary mixture in Czochralski configuration. Crystals 2019, 9, 72. [Google Scholar] [CrossRef]
- Abbasoglu, S.; Sezai, I. Three-dimensional modelling of melt flow and segregation during Czochralski growth of gexsi1-x single crystals. Int. J. Therm. Sci. 2007, 46, 561–572. [Google Scholar] [CrossRef]
- Montalenti, F.; Rovaris, F.; Bergamaschini, R.; Miglio, L.; Salvalaglio, M.; Isella, G.; Isa, F.; Känel, H.V. Dislocation-free SiGe/Si heterostructures. Crystals 2018, 8, 257. [Google Scholar] [CrossRef]
- Kanda, I. A Laboratory study of two-dimensional and three-dimensional instabilities in a quasi-two-dimensional flow driven by differential rotation of a cylindrical tank and a disc on the free surface. Phys. Fluids 2004, 16, 3325–3340. [Google Scholar] [CrossRef]
- Zhan, J.M.; Chen, Z.W.; Li, Y.S.; Nie, Y.H. Three-dimensional double-diffusive Marangoni convection in a cubic cavity with horizontal temperature and concentration gradients. Phys. Rev. E 2010, 82, 066305. [Google Scholar] [CrossRef]
- Smith, M.K.; Davis, S.H. Instabilities of dynamic thermocapillary liquid layers. Part 1. Convective instabilities. J. Fluid Mech. 1983, 132, 119–144. [Google Scholar] [CrossRef]




| Property | Symbol | Unit | Value |
|---|---|---|---|
| Kinematic viscosity | ν | m2/s | 1.4 × 10−7 |
| Thermal diffusivity | α | m2/s | 2.2 × 10−5 |
| Mass diffusivity | D | m2/s | 1.0 × 10−8 |
| Temperature coefficient of surface tension | γT | N/(m·k) | 8.1 × 10−5 |
| Concentration coefficient of surface tension | γC | N/m | −0.54 |
| Prandtl number | Pr | - | 6.4 × 10−3 |
| Lewis number | Le | - | 2197.8 |
| Mesh | m | F1 | F2 |
|---|---|---|---|
| 60R × 20Z × 80θ | 8 | 650 | 1165 |
| 80R × 35Z × 120θ | 8 | 665 | 1177 |
| 100R × 35Z × 160θ | 8 | 657 | 1171 |
| 120R × 55Z × 200θ | 8 | 659 | 1167 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Chen, J.; Li, Y. Mixed Oscillation Flow of Binary Fluid with Minus One Capillary Ratio in the Czochralski Crystal Growth Model. Crystals 2020, 10, 213. https://doi.org/10.3390/cryst10030213
Wu C, Chen J, Li Y. Mixed Oscillation Flow of Binary Fluid with Minus One Capillary Ratio in the Czochralski Crystal Growth Model. Crystals. 2020; 10(3):213. https://doi.org/10.3390/cryst10030213
Chicago/Turabian StyleWu, Chunmei, Jinhui Chen, and Yourong Li. 2020. "Mixed Oscillation Flow of Binary Fluid with Minus One Capillary Ratio in the Czochralski Crystal Growth Model" Crystals 10, no. 3: 213. https://doi.org/10.3390/cryst10030213
APA StyleWu, C., Chen, J., & Li, Y. (2020). Mixed Oscillation Flow of Binary Fluid with Minus One Capillary Ratio in the Czochralski Crystal Growth Model. Crystals, 10(3), 213. https://doi.org/10.3390/cryst10030213




