Abstract
We investigated the elastic properties of the HfV2O7 high-temperature phase, exhibiting negative thermal expansion, in a synergetic strategy of first-principle calculations and nanoindentation experiments performed on sputtered films. Self-consistent results were obtained for the measured elastic modulus (73 ± 14 GPa) and dispersion-corrected density functional theory calculations. The elastic properties of HfV2O7 are affected by long-range dispersion interaction, which may be induced by severe modification in the second-nearest neighbor O-O bond distance as obtained upon compression. HfV2O7 is composed of HfO6, VO4, and V2O7 building blocks, whereby the latter is characterized by an increasing V-O(-V) bond length upon compression.
1. Introduction
Near-zero expansion composites are contrived for applications in environments with rapidly changing temperatures to guarantee unaltered material performance [1,2,3,4]. Negative thermal expansion (NTE) phases are implemented in these composites as thermal expansion compensators [3,4,5,6]. The cubic high-temperature (HT) phase of HfV2O7 (space group: Pa, 40 atoms per cell) [6,7,8], which is stable at temperatures above ~370 K [6,9], constitutes a promising candidate due to its isotropic NTE [6,7,9] with a thermal expansion coefficient of −7.2 × 10−6 1/K [10]. Upon cooling, the HT phase transforms into an incommensurate structure between 369 K and 340 K [9]. Below 340 K, HfV2O7 exhibits a cubic 3 × 3 × 3 superstructure [6,7,9,11] (space group: Pa, 1080 atoms per cell). However, NTE is only reported for the HT phase [6,7,9], which is reasoned by phonon modes involving translational and librational movements of the quasi-rigid octahedral HfO6 and tetrahedral VO4 units [7,9]. These translations and librations substantially soften upon compression of the lattice which leads to its thermal compression [7,9]. For the application of HfV2O7 in a composite, understanding its elastic behavior is important for multiple reasons: the elastic properties of an NTE phase used in a composite not only determine the overall elastic properties of the composite [12], but also its mechanical response in rapid heating or cooling processes which induce thermal stress due to the different coefficients of thermal expansion [13]. Additionally, the ability of the NTE phase to counteract positive thermal expansion depends on its elastic properties [14]. However, the elastic behavior of HT HfV2O7, with its quasi-rigid HfO6 and tetrahedral VO4 building blocks, has not been investigated yet.
In this work, a synergetic strategy of theory and experiments was devised to examine the elastic behavior of the HfV2O7 HT phase. Since conventional density functional theory (DFT) [15] calculations do not accurately describe dispersion interaction [16,17,18,19,20,21] which might influence the elastic properties of HT HfV2O7, various DFT approaches, including dispersion-corrected DFT, were employed to calculate the elastic constants. Based on the analysis of the atomic rearrangement upon compression of first (metal-oxide) and second (oxygen-oxygen) nearest neighbors, the various theoretical results were critically appraised. Finally, HfV2O7 thin films were synthesized and nanoindentation experiments were carried out to validate the theoretical predictions.
2. Computational and Experimental Details
Ground state electronic structure calculations were performed employing the Vienna Ab initio Simulation Package (VASP) [22] with projector augmented-wave potentials within the framework of DFT [15]. The generalized gradient approximation (GGA), as introduced by Perdew, Burke, and Ernzerhof (PBE) [23], was applied. Integration in the Brillouin zone was performed on a 12 × 12 × 12 k-point grid for the cubic HfV2O7 unit cell (40 atoms), according to Monkhorst and Pack [24]. The convergence criterion for the total energy was set to 0.01 meV within a 500 eV cut-off. The equilibrium volume and energy were determined by the Birch–Murnaghan equation of state [25,26], applying two procedures for relaxation: (i) structural relaxation only at equilibrium volume, denoted as static calculation (SC), and (ii) full relaxation (FR) of the cell at each volume and deformation (minimization of interatomic forces) for determination of lattice parameter and elastic constants. These two approaches are referred to as DFT-SC and DFT-FR, respectively, throughout this paper. It has been shown that DFT-SC, as a computationally less expensive approach compared to FR, yields accurate bulk modulus data for isotropic cubic materials [27]. To explicitly include dispersion interaction (weak correlations), additional calculations were performed employing (ii-1) the VASP DFT-D3 method with zero damping, as introduced by Grimme et al. [16], and (ii-2) the self-consistent screening (non-local correlations) method by Tkatchenko and Scheffler [28] (DFT-TS). The cubic shear elastic constants C’ = (C11–C12)/2 and C44 were determined by employing the strain-energy method for all four approaches, using volume-conserving distortions of ±1% and ±2% [29,30], which are well within the commonly employed range for elastic constant calculations [29,31,32]. Elastic (Young’s) modulus (E) and shear modulus (G), as well as Poisson’s ratio (v) were calculated from the elastic constants using the Hill method [33].
HfV2O7 thin films were deposited on 50 mm diameter sapphire (0001) substrates by direct current magnetron sputtering of elemental Hf and V targets (50 mm diameter, 99.95% purity) at base pressures below 1 × 10−4 Pa. The target-to-substrate distance was set to 100 mm. The V and Hf target power was set to 200 W and 63 W, respectively, in order to achieve a stoichiometry of 2:1 on the metal sublattice. A mixture of argon (99.9999% purity) and oxygen (99.999% purity) was used as sputtering gas. Depositions were carried out at an oxygen partial pressure of 4.7 × 10−2 Pa and an overall deposition pressure of 8.6 × 10−1 Pa. The deposition temperatures were selected to be 200 °C, 350 °C and 450 °C. The deposited thin films were characterized using X-ray diffraction (XRD), carried out in a Bruker AXS D8 Discover XRD (Bruker Corporation, Billerica, MA, USA), which was equipped with a general area detector diffraction system, using a Cu Kα X-ray source at an acceleration voltage of 40 kV and a current of 40 mA with an incidence angle of 15°. The chemical composition of the as-deposited thin films was analyzed in terms of the Hf to V ratio by energy dispersive X-ray spectroscopy (EDX) in a JEOL JFM-6480 scanning electron microscope (JEOL Ltd., Tokyo, Japan) equipped with an EDAX Genesis 2000 (EDAX Inc., Mahwah, NJ, USA) and operated at an acceleration voltage of 20 kV. To measure non-conducting HfV2O7 thin films by EDX, the films were capped with approximately 10 nm Nb, which had been sputtered at 200 W subsequent to the cooling process without intentional heating. Nanoindentation was carried out in a Hysitron TriboIndenterTM (Hysitron Inc., Eden Prairie, MN, USA) with a 100 nm radius Berkovich diamond tip at the loads of 0.15 mN, 0.2 mN and 0.3 mN, all corresponding to a penetration depth below 10% of the thickness of the uncapped sample. For each load, a grid of 6 × 6 points was measured for sufficient statistics. The reduced modulus ER was determined using the Oliver–Pharr method [34]. ER can be converted into the elastic modulus of the specimen according to
where i and s refer to the indenter and sample, respectively. Ei and vi were taken to be 1140 GPa and 0.07, respectively.
3. Results and Discussion
Energy-volume curves for the HT phase of cubic HfV2O7 in the case of static calculation (SC) and full structural relaxation (FR) are shown in Figure 1.
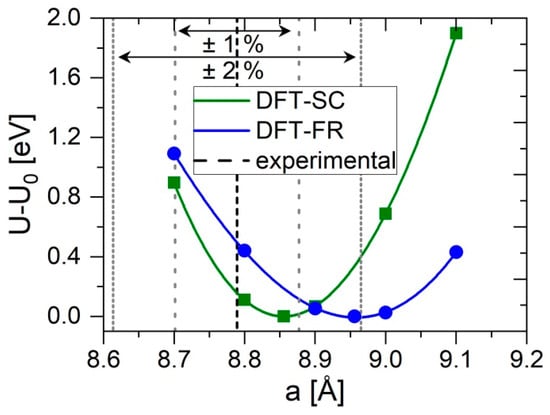
Figure 1.
Calculated change in energy U-U0 as a function of the lattice parameter a of cubic HfV2O7. Density functional theory calculations were performed with structural relaxation only at equilibrium volume (DFT-SC) and full structural relaxation at each volume (DFT-FR). The dashed line represents the experimentally obtained lattice parameter (480 K) [6]. The grey dashed and dotted lines represent a deviation of 1% and 2% from the experimentally determined lattice parameter, respectively.
It can be seen that the curves are affected significantly depending on the calculation approach employed. Enabling full structural relaxation at every volume has a two-fold effect compared to the static calculation. First, the minimum (equilibrium lattice parameter at 0 K) is shifted to larger values. Comparison with the experimental lattice parameter of 8.7862 Å, determined at 480 K, [6] yield deviations below 2% for both employed calculations and they are, thus, considered to be in reasonable agreement with the experiment. DFT calculations of equilibrium lattice parameters using PBE functionals tend to overestimate experimentally determined values within 2% [35]. Moreover, given a thermal expansion coefficient of −7.2 × 10−6 1/K [10], the calculated lattice parameter at 0 K should be decreased by 0.35% at 480 K. Second, the energetic response to deviations from equilibrium volume is significantly stronger for the static calculation than for the full relaxation case. This shape of the curves is directly related to the bulk modulus (B), representing the energetic response to uniform compression (hydrostatic pressure with uniform uniaxial strains), and is, therefore, indicating a considerably smaller B in the case of full structural relaxation at every volume. Furthermore, the curve becomes more asymmetric which has implications for the pressure derivative of the bulk modulus (B’), as elaborated below. The obtained differences between these two approaches suggest dynamic changes in the internal free parameters upon deformation having a pronounced impact on the elastic behavior. Thus, the structure of HT HfV2O7, as depicted in Figure 2a, is examined in more detail.
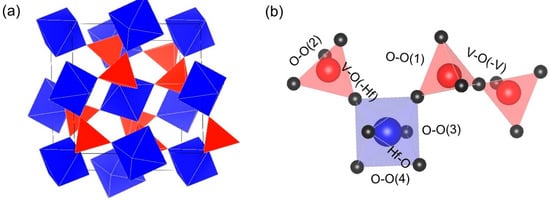
Figure 2.
(a) Structure of the HfV2O7 high-temperature phase, containing the HfO6 octahedra (blue) and VO4 tetrahedra (red). (b) Section of interconnected polyhedra with examples of individual bonds formed within the structure.
HfV2O7 is composed of HfO6 octahedra and VO4 tetrahedra, which are connected by corner-sharing oxygen atoms, forming an openly-packed network structure [8]. While all oxygen atoms in a HfO6 octahedron are shared with neighboring VO4 tetrahedra, only three of four oxygen atoms in VO4 are shared with HfO6 octahedra, whereas one is forming another VO4 tetrahedron, therefore creating a V2O7 unit. Within this V2O7 unit, the V-O-V bonds maintain an angle of 180°, as set by the space group. In contrast to the NTE material ZrW2O8, in which one W-O bond is non-bridging, all oxygen atoms in HfV2O7 exhibit a two-fold coordination lowering the flexibility of the structure [36].
To study the structural changes in HfV2O7 upon compression in the case of full structural relaxation at every volume (FR), the change in the bond length of the first (metal-oxygen) and second (oxygen-oxygen) nearest neighbors is examined and summarized in Table 1. Examples of the individual bonds formed within the structure are illustrated in Figure 2b.

Table 1.
Comparison of individual bond lengths in equilibrium and upon uniform compression (5 GPa), that is, hydrostatic pressure with uniform uniaxial strains, for the full relaxation at every volume (FR) approach.
Uniform compression without structural relaxation at every volume (SC) pushes all atoms closer together so that all bond lengths decrease. In contrast, allowing for full structural relaxation at every volume (FR) reveals a complex structural response of cubic HfV2O7 to the imposed compression, as shown in Table 1. While the Hf-O and V-O(-Hf) (shared oxygen between HfO6 octahedra and VO4 tetrahedra) bond distances are decreasing by ≥ 1% for a compression of 5 GPa, an increase in bond length of 0.3% for the rigid V-O(-V) bonds, present in the formed V2O7 unit (see Figure 2b), is obtained. Thus, static calculations fail to capture the pronounced atomic rearrangement and are consequently considered to be inappropriate to describe the elastic behavior of HfV2O7.
It has been shown that full structural relaxation is also required for systems with dominant dispersion (van der Waals) interaction [27,37,38,39], suggesting that dispersion interaction may be important in HfV2O7. An investigation of the second-nearest neighbor interaction (see Table 1) revealed severe modifications in the O-O distance. The change in bond distance is ranging from a reduction of 3.9%, obtained within the HfO6 octahedra, to an increase of 1.5%, as observed within the VO4 tetrahedra. It seems that long-range O-O interactions are subtle and may affect the elastic properties. However, conventional DFT calculations with GGA do not accurately describe dispersion interaction [16,17,18,19,20,21]. Hence, two additional dispersion-corrected DFT calculations were performed (DFT-D3 and DFT-TS). In general, these calculations are reported to describe a variety of compounds with dispersion interaction more accurately, for example, graphene [17,40], graphite [17,18,19,41], hexagonal boron nitride [17], MoS2 [19,20,40,42,43], and V2O5 [19,44,45]. The calculated elastic properties and lattice parameters using the various approaches are summarized in Table 2.

Table 2.
Comparison of the calculated lattice parameter a and the elastic properties (B: Bulk modulus, B’: pressure derivative of B, Cij: Elastic constants, ν: Poisson’s ratio, E: Elastic modulus, G: Shear modulus) of HfV2O7 using DFT. Calculations were performed with structural relaxation only at equilibrium volume (SC), at every volume without dispersion correction (FR), as well as with dispersion correction, by applying methods according to Grimme et al. [16] (D3) and Tkatchenko and Scheffler [28] (TS).
The introduced dispersion interaction (DFT-D3 and DFT-TS) has only a minor effect on the resulting lattice parameter, whereas the elastic properties are altered significantly. For dispersion-corrected DFT according to Tkatchenko and Scheffler [28], B is reduced to 40% and 73% of the initial value obtained for static calculation and full structural relaxation, respectively. Furthermore, for all calculations with enabled full structural relaxation at every volume and deformation (DFT-FR, DFT-D3, and DFT-TS), the first derivative of the bulk modulus with respect to pressure, B’, is predicted to be negative, which is common for NTE compounds and is known as pressure-induced softening [1,46]. For comparison, B’ calculated by DFT-SC is positive, confirming that the elastic behavior of NTE HfV2O7 is not properly captured within this static approach, which is consequently neglected in the following discussion.
Despite the reasonable agreement in B between DFT-FR and dispersion-corrected DFT, pronounced deviations for the single-crystal elastic constants Cij and the resulting elastic constants E, G, and v of a polycrystalline aggregate, approximated according to Hill [33], are obtained. The elastic moduli E (shear moduli G) are about 2.0 (2.4) and 2.6 (3.0) times lower for DFT-D3 and DFT-TS, respectively, compared to the full relaxation case. Between both dispersion-corrected DFT calculations, however, a maximum deviation (predicted for C11) of 27% was obtained. At this stage, it is not confirmed that dispersion-corrected DFT, which also considers long-range interaction [16,17,18,19,20,21], yields a more realistic description of the elastic behavior of NTE HfV2O7.
To evaluate the reliability of the predicted elasticity data, results are to be compared to experimental values. However, experimental data about the elastic properties of the HT phase, exhibiting NTE, are missing. Experimental room temperature studies on the 3 × 3 × 3 superstructure of HfV2O7 revealed a surprisingly low B of 12.8 ± 0.4 GPa [8]. The experimentally determined bulk modulus of the HfV2O7 3 × 3 × 3 superstructure deviates, as expected, from the calculated bulk moduli of HT HfV2O7, ranging between 56 GPa and 77 GPa, as shown in Table 2. The structural difference between the low-temperature 3 × 3 × 3 superstructure and the HT phase may account for the obtained difference in bulk moduli since similar densities for both structures are expected, according to Baran [11]. At the example of isostructural ZrV2O7, it has been found that some of the V-O(-V) bonds are bent away from 180° in the 3 × 3 × 3 superstructure [47]. For the HT phase of HfV2O7, these rigid V-O(-V) bonds resist the imposed compression and even elongate upon compression, as discussed above (see Table 1). Hence, it may be speculated that the higher resistance to compression of the HT phase originates from the 180° V-O(-V) bonds. Furthermore, it needs to be considered that elastic properties are generally calculated in the ground state (0 K), whereas experiments are often conducted at ambient temperatures. While the bulk moduli of common compounds show only small temperature dependency [48], the bulk moduli of NTE phases, as HfV2O7, are reported to be highly temperature dependent [1,46,48,49]. For example, for NTE ZrW2O8, an exceptional increase in bulk modulus of 40% upon cooling from 300 K to 0 K is reported [48].
In order to critically appraise the reliability of the DFT predictions, more experimental elasticity data of HfV2O7 are required. Therefore, HfV2O7 samples were synthesized using magnetron sputtering and were subsequently characterized by nanoindentation to study the elastic modulus. For this purpose, HfV2O7 phase formation studies were conducted. The influence of temperature was investigated by depositing stoichiometric thin films at 200 °C, 350 °C and 450 °C. The resulting diffractograms are shown in Figure 3.
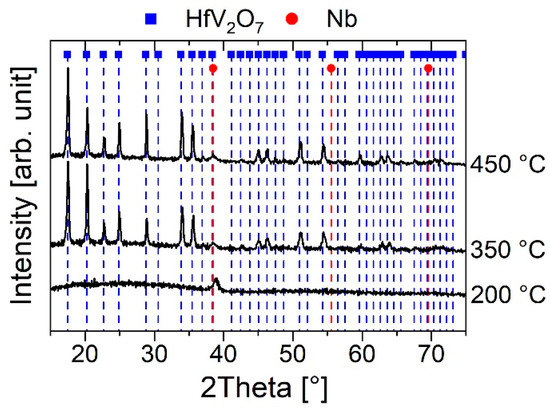
Figure 3.
Diffractograms of HfV2O7 thin films deposited at different temperatures. The films were capped with a ~10 nm thick Nb layer.
The thin film deposited at 200 °C is X-ray amorphous, showing only a peak at 39° which can be attributed to bcc Nb [50], originating from the Nb capping layer. With an increase in temperature to 350 °C, additional peaks can be observed which can all be assigned to the HfV2O7 HT structure [6]. Characteristic peaks for the low-temperature 3 × 3 × 3 superstructure [6,7,11] were not detected. Hence, based on these XRD results it was assumed that the HT phase is present. With a further increase in temperature to 450 °C, no structural changes based on XRD and no change in chemical composition based on EDX were observed. The lattice parameter was determined to be 8.76 ± 0.01 Å, deviating by less than 2% from the dispersion-corrected DFT results. This value is in very good agreement with the experimental lattice parameter of 8.7862 Å reported in the literature [6]. The reduced modulus of HfV2O7 was subsequently measured by nanoindentation to be 74 ± 14 GPa. Employing the calculated Poisson’s ratio based on DFT-FR of 0.11 in Equation (1) yields an elastic modulus of HfV2O7 of 78 ± 16 GPa which is inconsistent with the predicted value of 178 GPa (see Table 2). On the other hand, using the Poisson’s ratios of dispersion-corrected DFT (DFT-D3 and DFT-TS) reveal experimentally determined elastic moduli of HfV2O7 of 72 ± 14 GPa and 73 ± 14 GPa, respectively. The DFT-TS calculated modulus of 69 GPa, based on the Hill average, deviates by 5% from this experimentally determined value. The upper and lower bound of this value, applying the Voigt [51] and Reuss [52] method, were calculated to lie in the narrow range between 70 GPa and 68 GPa, respectively. Hence, dispersion-corrected DFT, using the self-consistent screening (non-local correlations) method by Tkatchenko and Scheffler [28], is suggested to yield the most accurate estimate of the elastic properties of HfV2O7 which is self-consistent with the experimental results obtained. Nevertheless, it still needs to be considered that the proposed reliability of the predicted ground state properties is based on the comparison to experimental values determined at room temperature. As already discussed, the bulk modulus of NTE ZrW2O8 exhibits an exceptional increase of 40% upon cooling from 300 K to 0 K [48], while the elastic modulus and Poisson’s ratio only increase by 12% and 13%, respectively, [48] implying that the elastic modulus for the comparison of theory and experiment is less prone to temperature influence. Consequently, the results suggest that the elastic properties of HfV2O7 are affected by the long-range dispersion interaction, which may be ascribed to the severe modification in the second-nearest neighbor O-O bond distance obtained upon compression.
4. Conclusions
The work aimed to study the elastic properties of the HT phase of HfV2O7, exhibiting NTE, in a synergetic strategy using both, ground state DFT calculations and nanoindentation experiments on sputtered HfV2O7 thin films. Employing dispersion-corrected DFT calculations according to Tkatchenko and Scheffler [28], the elastic properties of HT HfV2O7 were determined, proving to be self-consistent with the elastic modulus data obtained by experiment (deviations within 5%). The structural analysis revealed that the V-O(-V) bonds elongate upon compression possibly explaining the higher resistance of the HT phase to compression compared to the 3 × 3 × 3 superstructure. Furthermore, dispersion interaction plays a major role in HfV2O7, which may be attributed to the pronounced modifications found for the O-O bond distances upon compression. The good agreement between the theoretical and experimental data, presented in this work, may encourage additional experimental studies on the elastic properties of HfV2O7 and other NTE materials.
Author Contributions
Conceptualization, A.L.R., P.K., D.M. and J.M.S.; methodology, A.L.R., P.K. and D.M.; formal analysis, A.L.R., P.K. and D.J.M.; investigation, A.L.R. and P.K.; resources, J.M.S.; calculation, A.L.R., P.K. and D.M.; writing—original draft preparation, A.L.R. and P.K.; writing—review and editing, A.L.R., P.K., D.M., D.J.M. and J.M.S.; supervision, D.M. and J.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Calculations were performed with the computing resources granted by JARA HPC from RWTH Aachen University under Project No. JARA0131.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dove, M.T.; Fang, H. Negative thermal expansion and associated anomalous physical properties: Review of the lattice dynamics theoretical foundation. Rep. Prog. Phys. 2016, 79. [Google Scholar] [CrossRef] [PubMed]
- Grima, J.N.; Zammit, V.; Gatt, R. Negative Thermal Expansion. Xjenza 2006, 11, 17–29. [Google Scholar]
- Takenaka, K. Negative thermal expansion materials: Technological key for control of thermal expansion. Sci. Technol. Adv. Mater. 2012, 13. [Google Scholar] [CrossRef]
- Lind, C. Two Decades of Negative Thermal Expansion Research: Where Do We Stand? Materials 2012, 5, 1125–1154. [Google Scholar] [CrossRef]
- Jakubinek, M.; Whitman, C.; White, M. Negative thermal expansion materials - Thermal properties and implications for composite materials. J. Therm. Anal. Calorim. 2009, 99. [Google Scholar] [CrossRef]
- Turquat, C.; Muller, C.; Nigrelli, E.; Leroux, C.; Soubeyroux, J.L.; Nihoul, G. Structural investigation of temperature-induced phase transitions in HfV2O7. Eur. J. Phys. Appl. Phys. 2000, 10, 15–27. [Google Scholar] [CrossRef]
- Mittal, R.; Chaplot, S.L. Lattice dynamical calculation of negative thermal expansion in ZrV2O7 and HfV2O7. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Hemamala, U.L.C.; El-Ghussein, F.; Goedken, A.M.; Chen, B.; Leroux, C.; Kruger, M.B. High-pressure x-ray diffraction and Raman spectroscopy of HfV2O7. Phys. Rev. B 2004, 70. [Google Scholar] [CrossRef]
- Yamamura, Y.; Horikoshi, A.; Yasuzuka, S.; Saitoh, H.; Saito, K. Negative thermal expansion emerging upon structural phase transition in ZrV2O7 and HfV2O7. Dalton Trans. 2011, 40, 2242–2248. [Google Scholar] [CrossRef]
- Hisashige, T.; Yamaghuchi, T.; Tsuji, T.; Yamamura, Y. Phase Transition of Zr1-xHfxV2O7 Solid Solutions Having Negative Thermal Expansion. J. Ceram. Soc. Jpn. 2006, 114, 607–611. [Google Scholar] [CrossRef]
- Baran, E.J. The unit cell of hafnium divanadate. J. Less Common M. 1976, 46, 343–345. [Google Scholar] [CrossRef]
- Grima, J.N.; Ellul, B.; Attard, D.; Gatt, R.; Attard, M. Composites with needle-like inclusions exhibiting negative thermal expansion: A preliminary investigation. Compos. Sci. Technol. 2010, 70, 2248–2252. [Google Scholar] [CrossRef]
- Romao, C.P.; Miller, K.J.; Whitman, C.A.; White, M.A. Comprehensive Inorganic Chemistry II - Negative Thermal Expansion (Thermomiotic) Materials; Elsevier: Oxford, UK, 2013; Volume 4, pp. 128–151. [Google Scholar]
- Romao, C.P.; Marinkovic, B.A.; Werner-Zwanziger, U.; White, M.A. Thermal Expansion Reduction in Alumina-Toughened Zirconia by Incorporation of Zirconium Tungstate and Aluminum Tungstate. J. Am. Ceram. Soc. 2015, 98, 2858–2865. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, S. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132. [Google Scholar] [CrossRef]
- Lebedeva, I.V.; Lebedeva, A.V.; Popov, A.M.; Knizhnik, A.A. Comparison of performance of van der Waals-corrected exchange-correlation functionals for interlayer interaction in graphene and hexagonal boron nitride. Comput. Mater. Sci. 2017, 128, 45–58. [Google Scholar] [CrossRef]
- Lebègue, S.; Harl, J.; Gould, T.; Ángyán, J.G.; Kresse, G.; Dobson, J.F. Cohesive Properties and Asymptotics of the Dispersion Interaction in Graphite by Random Phase Approximation. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef]
- Reckien, W.; Janetzko, F.; Peintinger, M.F.; Bredow, T. Implementation of Empirical Dispersion Corrections to Density Functional Theory for Periodic Systems. J. Comput. Chem. 2012, 33, 2023–2031. [Google Scholar] [CrossRef]
- Rosen, A.S.; Notestein, J.M.; Snurr, R.Q. Comprehensive Phase Diagrams of MoS2 Edge Sites Using Dispersion-Corrected DFT Free Energy Calculations. J. Phys. Chem. A 2018, 122, 15318–15329. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, Y.; Si, K.; Ren, Z.; Bai, J.; Xu, X. Elastic, electronic, and dielectric properties of bulk and monolayer ZrS2, ZrSe2, HfS2, HfSe2 from van der Waals density-functional theory. Phys. Status Solidi B 2017, 254. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 1169–1186. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The Compressibility of Media under Extreme Pressures. Proc. Natl. Acad. Sci. USA 1944, 15, 244–247. [Google Scholar] [CrossRef]
- Kim, E.; Chen, C. Calculation of bulk modulus for highly anisotropic materials. Phys. Lett. A 2004, 326, 442–448. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102. [Google Scholar] [CrossRef]
- Music, D.; Takahashi, T.; Vitos, L.; Asker, C.; Abrikosov, I.A.; Schneider, J.M. Elastic properties of Fe–Mn random alloys studied by ab initio calculations. Appl. Phys. Lett. 2007, 91. [Google Scholar] [CrossRef]
- Friák, M.; Hichel, T.; Körmann, F.; Udyansky, A.; Dick, A.; Pezold, J.V.; Ma, D.; Kim, O.; Counts, W.A.; Sob, M.; et al. Determining the Elasticity of Materials Employing Quantum-mechanical Approaches: From the Electronic Ground State to the Limits of Materials Stability. Steel Res. 2011, 82, 86–100. [Google Scholar] [CrossRef]
- Fast, L.; Wills, J.M.; Johansson, B.; Eriksson, O. Elastic constants of hexagonal transition metals: Theory. Phys. Rev. B 1995, 51, 17431–17438. [Google Scholar] [CrossRef]
- Mehl, M.J.; Osburn, J.E.; Papaconstantopoulos, D.A.; Klein, B.M. Structural properties of ordered high-melting-temperature intermetallic alloys from first-principles total-energy calculations. Phys. Rev. B 1990, 41, 10311–10323. [Google Scholar] [CrossRef] [PubMed]
- Hill, R. A general method of analysis for metal-working processes. J. Mech. Phys. Solids 1963, 11, 305–326. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Paier, J.; Marsman, M.; Hummer, K.; Kessel, G.; Gerber, C.; Ángyán, J.G. Screened hybrid density functionals applied to solids. J. Chem. Phys. 2006, 124. [Google Scholar] [CrossRef]
- Pryde, A.K.A.; Hammonds, K.D.; Dove, M.R.; Henne, V.; Gale, J.D.; Warren, M.C. Origin of the negative thermal expansion in ZrW2O8 and ZrV2O7. J. Phys.: Condens. Matter 1996, 8, 10973–10982. [Google Scholar] [CrossRef]
- Albe, K. Theoretical study of boron nitride modifications at hydrostatic pressures. Phys. Rev. B 1997, 55, 6203–6210. [Google Scholar] [CrossRef]
- Ooi, N.; Rairkar, A.; Adams, J.B. Density functional study of graphite bulk and surface properties. Carbon 2006, 44, 231–242. [Google Scholar] [CrossRef]
- Reeswinkel, T.; Music, D.; Schneider, J.M. Ab initio calculations of the structure and mechanical properties of vanadium oxides. J. Phys. Condens. Matter 2009, 21. [Google Scholar] [CrossRef]
- Mehmood, F.; Pachter, R. Density functional theory study of chemical sensing on surfaces of single-layer MoS2 and graphene. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Thinius, S.; Islam, M.M.; Heitjans, P.; Bredow, T. Theoretical Study of Li Migration in Lithium-Graphite Intercalation Compounds with Dispersion-Corrected DFT Methods. J. Phys. Chem. A 2014, 118, 2273–2280. [Google Scholar] [CrossRef]
- Nguyen, C.V.; Hieu, N.N.; Nguyen, D.T. Dispersion-Corrected Density Functional Theory Investigations of Structural and Electronic Properties of Bulk MoS2: Effect of Uniaxial Strain. Nanoscale Res. Lett. 2015. [Google Scholar] [CrossRef] [PubMed]
- Oviedo, J.P.; KC, S.; Lu, N.; Wang, J.; Cho, K.; Wallace, R.M.; Kim, M.J. In Situ TEM Characterization of Shear-Stress-Induced Interlayer Sliding in the Cross Section View of Molybdenum Disulfide. ACS Nano 2015, 9, 1543–1551. [Google Scholar] [CrossRef] [PubMed]
- Londero, E.; Schröder, E. Role of van der Waals bonding in the layered oxide V2O5: First-principles density-functional calculations. Phys. Rev. B 2010, 82. [Google Scholar] [CrossRef]
- Londero, E.; Schröder, E. Vanadium pentoxide (V2O5): A van der Waals density functional study. Comput. Phys. Commun. 2011, 182, 1805–1809. [Google Scholar] [CrossRef]
- Fang, H.; Dove, M.T.; Phillips, A.E. Common origin of negative thermal expansion and other exotic properties in ceramic and hybrid materials. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Korthuis, V.; Khosrovani, N.; Sleight, A.W.; Roberts, N.; Dupree, R.; Warren, W.W. Negative Thermal Expansion and Phase Transitions in the ZrV2-xPxO7 Series. Chem. Mater. 1995, 7, 412–417. [Google Scholar] [CrossRef]
- Drymiotis, F.R.; Ledbetter, H.; Betts, J.B.; Kumura, R.; Lashley, J.C.; Migliori, A.; Ramirez, A.P.; Kowach, G.R.; Duijn, J.v. Monocrystal Elastic Constants of the Negative-Thermal-Expansion Compound Zirconium Tungstate (ZrW2O8). Phys. Rev. Lett. 2004, 93. [Google Scholar] [CrossRef]
- Gallington, L.C.; Chapman, K.W.; Morelock, C.R.; Chupas, P.H.; Wilkinson, A.P. Dramatic softening of the negative thermal expansion material HfW2O8 upon heating through its WO4 orientational order-disorder phase transition. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Nadler, M.R.; Kempter, C.P. Niobium. Anal. Chem. 1959, 31, 1922. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; Springer Fachmedien Wiesbaden GmbH: Leipzig, Germany, 1910. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. J. Appl. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).