Surface Roughness Changes Induced by Stoichiometric Deviation in Ambient Phase for Two-Component Semiconductor Crystals
Abstract
1. Introduction
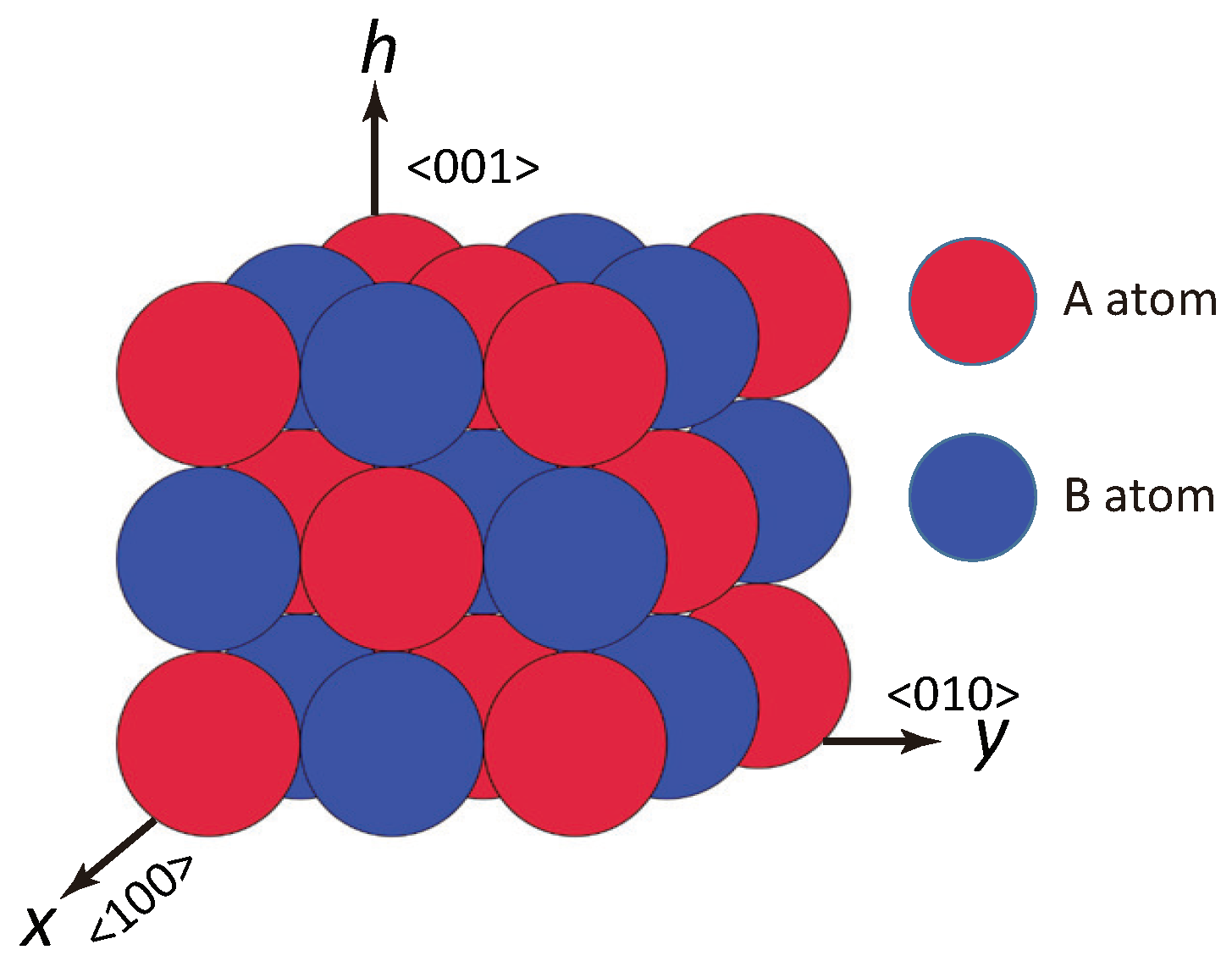
2. Surface Model
2.1. Surface Hamiltonian
2.2. Monte Carlo Method
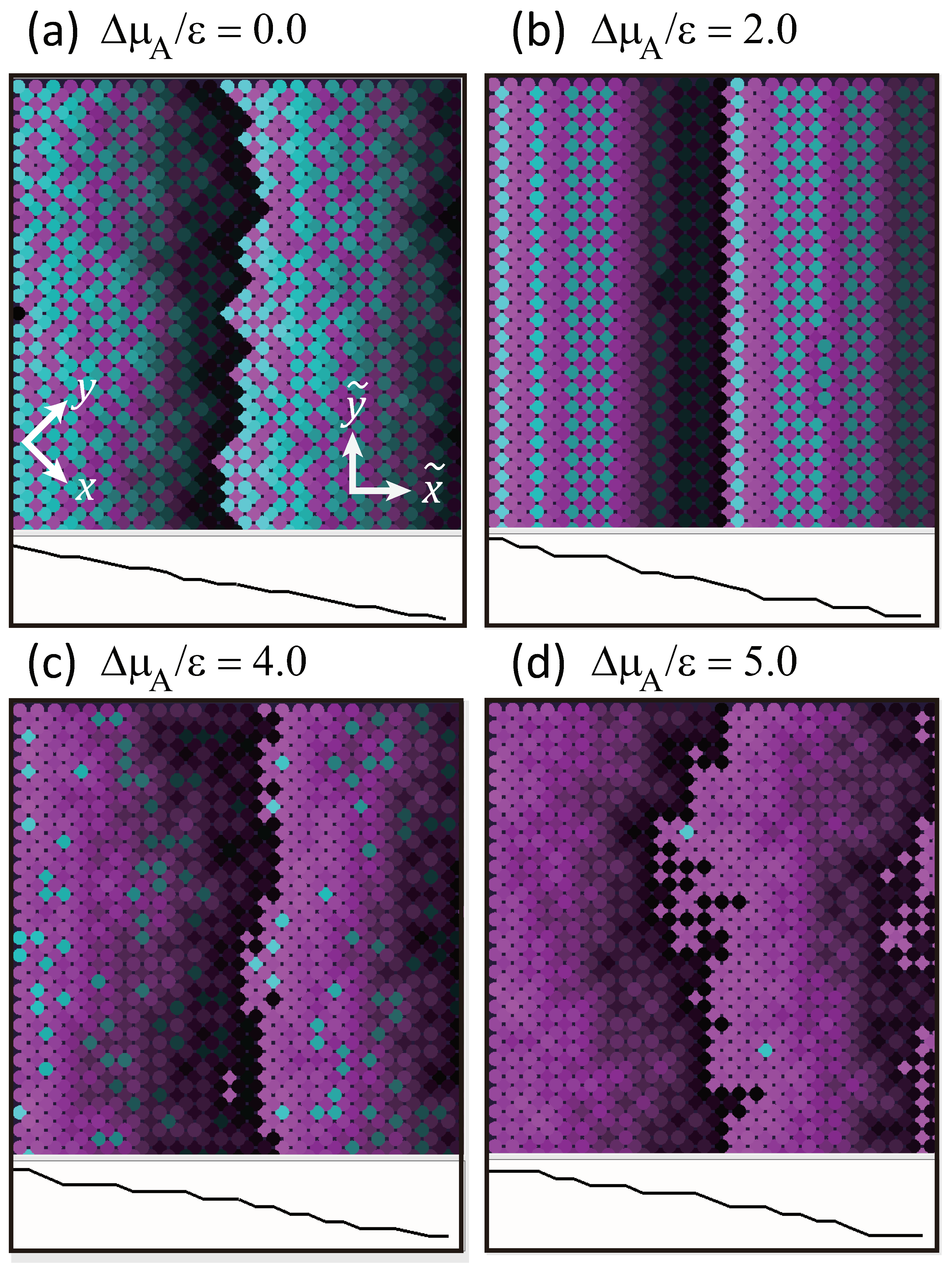
3. Decrease in Roughness Due to Locally Merged Steps
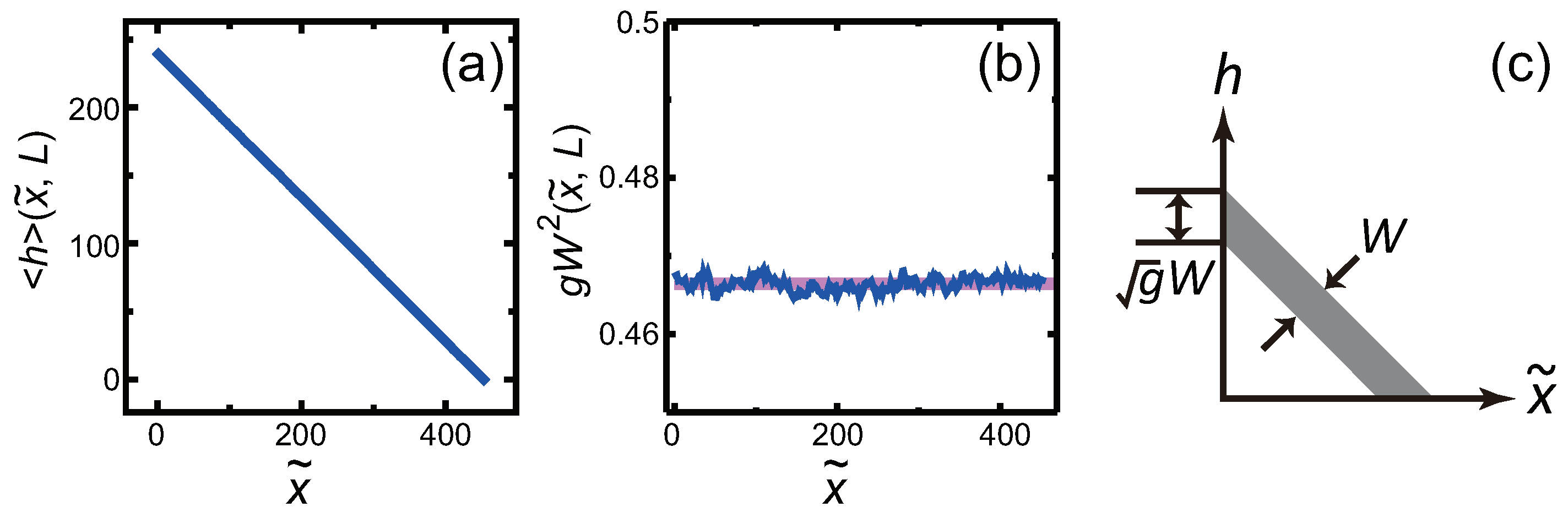
3.1. Mean Height of Local Merged Steps
3.2. No Step Faceting
3.3. Dependence of Surface Roughness
4. Surface Roughness
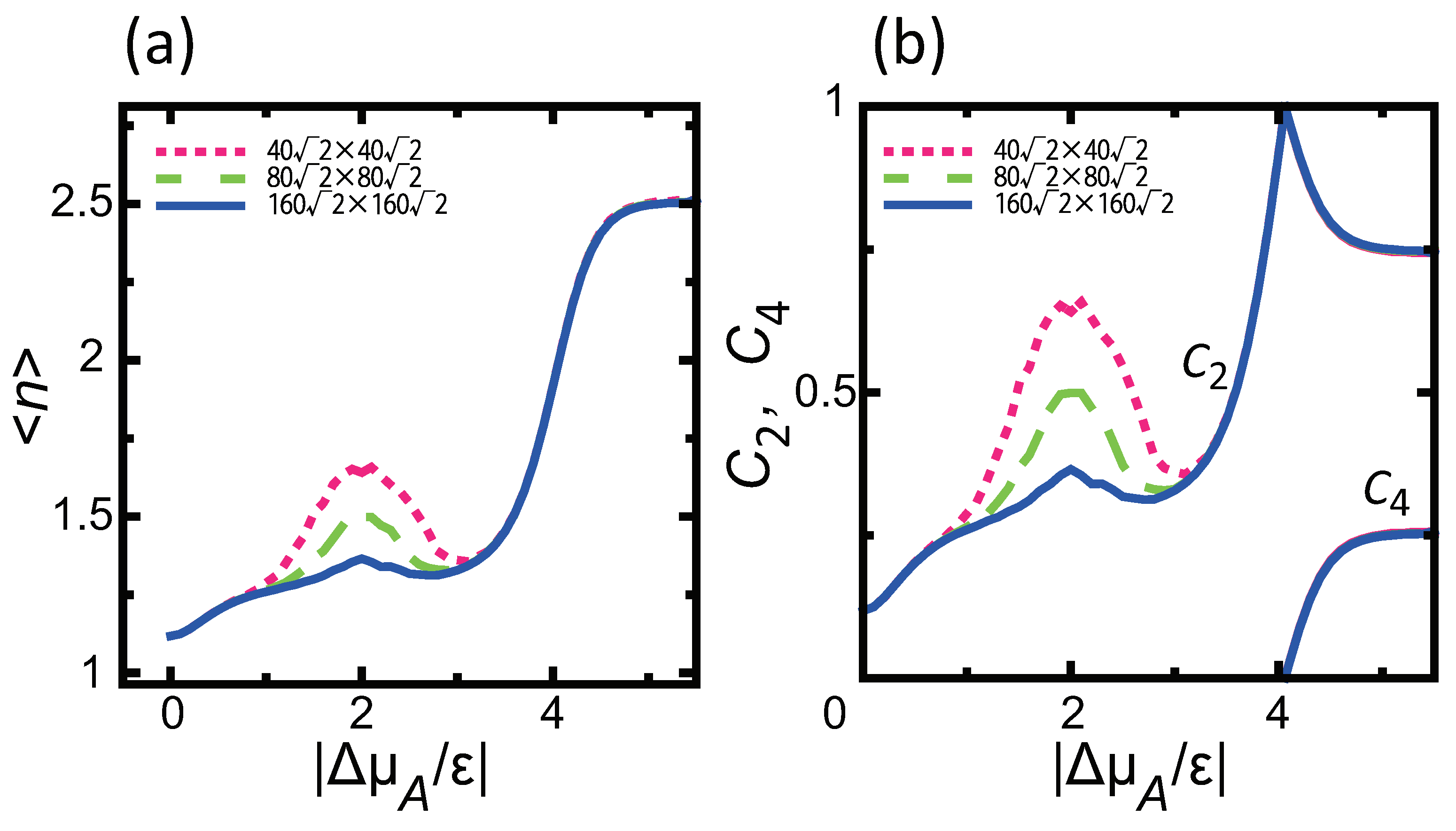
4.1. Effect of Component Deviation on Roughness Exponent
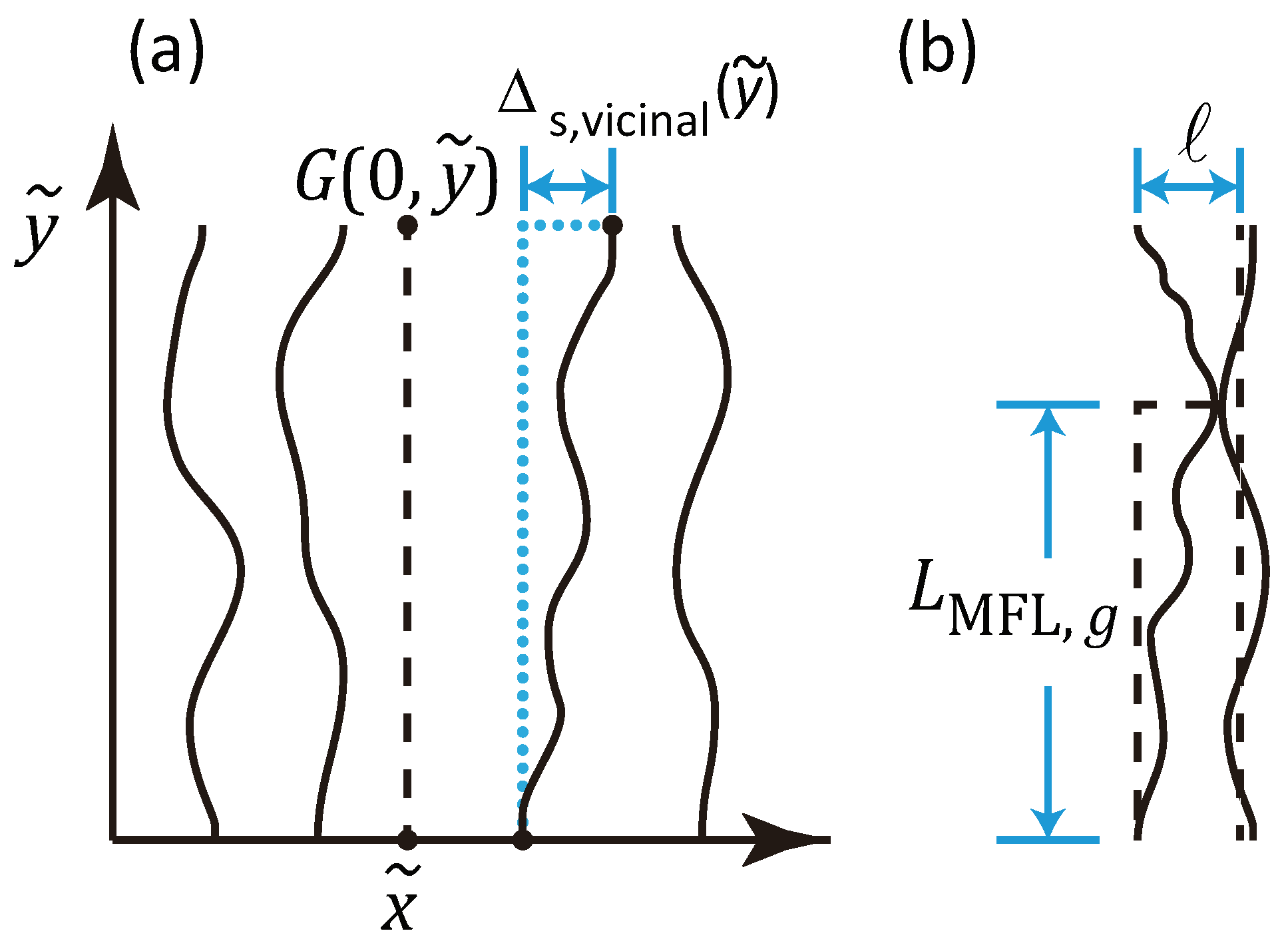
4.2. Mean Free Length
4.3. Analysis Based on Two-Dimensional Lattice Gas Model
4.4. Relationship between Surface Width and Step Width
4.5. Small Systems
5. Conclusions
- A component deviation in the ambient phase does not cause macrostep self-organization.
- does not affect the roughness exponent; i.e., the roughness exponent . For , the squared surface width logarithmically diverges with respect to .
- () stabilizes polar surfaces by lowering the surface energy. This changes the morphology of the crystal through the anisotropy of the surface tension and step tension. This also causes non-monotonic changes of , , , , and step stiffness with respect to .
- Double steps and quadruple steps form locally for and , respectively.
- For , is proportional to L; for , is constant, making the surface similar to a smooth surface.
- is about 160a, where a is the lattice constant, around . At lower temperatures, becomes substantially longer.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ECS | Equilibrium crystal shape |
| RSOS | Restricted solid-on-solid |
| st-RSOS | Staggered restricted solid-on-solid |
| nn | Nearest neighbor |
| DMRG | Density matrix renormalization group |
| DFT | Density functional theory |
| GMPT | Gruber–Mullins–Pokrovsky–Talapov |
| MCS | Monte Carlo steps |
| IPW | Imaginary-path-weight random walk |
| MBE | Molecular beam epitaxy |
| MFL | Mean free length |
Appendix A. Chemical Potentials
Appendix B. Two-Dimensional Lattice Gas Model
References
- Mitani, T.; Komatsu, N.; Takahashi, T.; Kato, T.; Harada, S.; Ujihara, T.; Matsumoto, Y.; Kurashige, K.; Okumura, H. Effect of aluminum addition on the surface step morphology of 4H–SiC grown from Si–Cr–C solution. J. Cryst. Growth 2015, 423, 45–49. [Google Scholar] [CrossRef]
- Akutsu, N. Thermal step bunching on the restricted solid-on-solid model with point contact inter-step attractions. Appl. Surf. Sci. 2009, 256, 1205–1209. [Google Scholar] [CrossRef]
- Akutsu, N. Non-universal equilibrium crystal shape results from sticky steps. J. Phys. Condens. Matter 2011, 23, 485004. [Google Scholar] [CrossRef] [PubMed]
- Akutsu, N. Pinning of steps near equilibrium without impurities, adsorbates, or dislocations. J. Cryst. Growth 2014, 401, 72–77. [Google Scholar] [CrossRef]
- Akutsu, N.; Yamamoto, T. Rough-Smooth Transition of Step and Surface. In Handbook of Crystal Growth; Nishinaga, T., Ed.; Elsevier: London, UK, 2015; Volume I, p. 265. [Google Scholar]
- Einstein, T.L. Equilibrium Shape of Crystals. In Handbook of Crystal Growth; Nishinaga, T., Ed.; Elsevier: London, UK, 2015; Volume I, p. 216. [Google Scholar]
- Akutsu, N. Faceting diagram for sticky steps. AIP Adv. 2016, 6, 035301. [Google Scholar] [CrossRef]
- Akutsu, N. Effect of the roughening transition on the vicinal surface in the step droplet zone. J. Cryst. Growth 2017, 468, 57–62. [Google Scholar] [CrossRef]
- Akutsu, N. Profile of a Faceted Macrostep Caused by Anomalous Surface Tension. Adv. Condens. Matter Phys. 2017, 2017, 2021510. [Google Scholar] [CrossRef]
- Akutsu, N. Sticky steps inhibit step motions near equilibrium. Phys. Rev. E 2012, 86, 061604. [Google Scholar] [CrossRef]
- Akutsu, N. Disassembly of Faceted Macrosteps in the Step Droplet Zone in Non-Equilibrium Steady State. Crystals 2017, 7, 42. [Google Scholar] [CrossRef]
- Akutsu, N. Height of a faceted macrostep for sticky steps in a step-faceting zone. Phys. Rev. Mater. 2018, 2, 023603. [Google Scholar] [CrossRef]
- Akutsu, N. Relationship Between Macrostep Height and Surface Velocity for a Reaction-Limited Crystal Growth Process. Cryst. Growth Des. 2019, 19, 2970–2978. [Google Scholar] [CrossRef]
- Williams, E.D.; Phaneuf, R.J.; Wei, J.; Bartelt, N.C.; Einstein, T.L. Thermodynamics and statistical mechanics of the faceting of stepped Si (111). Surf. Sci. 1993, 294, 219–242, Erratum to “Thermodynamics and statistical mechanics of the faceting of stepped Si (111)” [Surf. Sci. 1993, 294, 219], Surf. Sci. 1994, 310, 451. [Google Scholar] [CrossRef]
- Burton, W.K.; Cabrera, N.; Frank, F.C. The growth of crystals and the equilibrium structure of their surfaces. Philos. Trans. R. Soc. Lond. A 1951, 243, 299–358. [Google Scholar]
- Weeks, J.D.; Gilmer, G.H.; Leamy, H.J. Structural Transition in the Ising-Model Interface. Phys. Rev. Lett. 1973, 20, 549–551. [Google Scholar] [CrossRef]
- Chui, S.T.; Weeks, J.D. Phase transition in the two-dimensional Coulomb gas, and the interfacial roughening transition. Phys. Rev. B 1976, 14, 4978–4982. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Knops, H.J.F. Exact Relation between the Solid-on-Solid Model and the XY Model. Phys. Rev. Lett. 1977, 39, 766–769. [Google Scholar] [CrossRef]
- Van Beijeren, H. Exactly Solvable Model for the Roughening Transition of a Crystal Surface. Phys. Rev. Lett. 1977, 38, 993–996. [Google Scholar] [CrossRef]
- Weeks, J.D. Ordering in Strongly Fluctuation Condensed Matter Systems; Riste, T., Ed.; Plenum: New York, NY, USA; London, UK, 1980; p. 293. [Google Scholar]
- Jayaprakash, C.; Saam, W.F.; Teitel, S. Roughening and facet formation in crystals. Phys. Rev. Lett. 1983, 50, 2017–2020. [Google Scholar] [CrossRef]
- Rottman, C.; Wortis, M. Equilibrium crystal shapes for lattice models with nearest- and next-nearest-neighbor interactions. Phys. Rev. B 1984, 29, 328–339. [Google Scholar] [CrossRef]
- Rottman, C.; Wortis, M. Statistical mechanics of equilibrium crystal shapes: Interfacial phase diagrams and phase transitions. Phys. Rep. 1984, 103, 59–79. [Google Scholar] [CrossRef]
- Wortis, M. Chemistry and Physics of Solid Surface VII; Vanselow, R., Howe, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 367–405. [Google Scholar]
- Beijeren, V.H.; Nolden, I. Structure and Dynamics of Surfaces; Schommers, W., Blancken-Hagen, V., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; Volume 2, p. 259. [Google Scholar]
- Gruber, E.E.; Mullins, W.W. On the theory of anisotropy of crystalline surface tension. J. Phys. Chem. Solids 1967, 28, 875–887. [Google Scholar] [CrossRef]
- Pokrovsky, V.L.; Talapov, A.L. Ground state, spectrum, and phase diagram of two-dimensional incommensurate crystals. Phys. Rev. Lett. 1979, 42, 65–67. [Google Scholar] [CrossRef]
- Jayaprakash, C.; Rottman, C.; Saam, W.F. Simple model for crystal shapes: Step-step interactions and facet edges. Phys. Rev. B 1984, 30, 6549–6554. [Google Scholar] [CrossRef]
- Akutsu, Y.; Akutsu, N.; Yamamoto, T. Universal jump of Gaussian curvature at the facet edge of a crystal. Phys. Rev. Lett. 1988, 61, 424–427. [Google Scholar] [CrossRef]
- Yamamoto, T.; Akutsu, Y.; Akutsu, N. Universal Behavior of the Equilibrium Crystal Shape near the Facet Edge. I. A Generalized Terrace-Step-Kink Model. J. Phys. Soc. Jpn. 1988, 57, 453–460. [Google Scholar] [CrossRef]
- Mikheev, L.V.; Pokrovsky, V.L. Free-fermion solution for overall equilibrium crystal shape. J. Phys. I 1991, 1, 373–382. [Google Scholar] [CrossRef]
- Huse, D.A.; van Saarloos, W.; Weeks, J.D. Interface Hamiltonians and bulk critical behavior. Phys. Rev. B 1985, 32, 233–246. [Google Scholar] [CrossRef] [PubMed]
- Barabasi, A.L.; Stanley, H.E. Fractal Concepts in Surface Growth; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Akutsu, N.; Akutsu, Y. Roughening, faceting and equilibrium shape of two-dimensional anisotropic interface. I. Thermodynamics of interface fluctuations and geometry of equilibrium crystal shape. J. Phys. Soc. Jpn. 1987, 56, 1443–1453. [Google Scholar] [CrossRef]
- Yamamoto, T.; Akutsu, Y.; Akutsu, N. Fluctuation of a single step on the vicinal surface-universal and non-universal behaviors. J. Phys. Soc. Jpn. 1994, 63, 915–925. [Google Scholar] [CrossRef]
- Akutsu, Y.; Akutsu, N.; Yamamoto, T. Logarithmic step fluctuations in vicinal surface: A Monte Carlo study. J. Phys. Soc. Jpn. 1994, 63, 2032–2036. [Google Scholar] [CrossRef]
- Takata, M.; Ookawa, A. On the growth mechanism of an A-B crystal. J. Cryst. Growth 1974, 24/25, 515–518. [Google Scholar] [CrossRef]
- Ookawa, A.; Akutsu, N.; Asakura, Y. The growth characteristics of the III-V compound-like crystals affected by the relative activity. In Morphology and Growth Unit of Crystals; Sunagawa, I., Ed.; Terra Scientific Publishing Company: Tokyo, Japan, 1989; pp. 49–50. [Google Scholar]
- Akutsu, N. Equilibrium Crystal Shape of Planar Ising Antiferromagnets in External Fields. J. Phys. Soc. Jpn. 1992, 61, 477–498. [Google Scholar] [CrossRef]
- Nishizawa, S.; Pons, M. Growth and Doping Modeling of SiC–CVD in a Horizontal Hot-Wall Reactor. Chem. Vap. Depos. 2006, 12, 516–522. [Google Scholar] [CrossRef]
- Robertson, N.F.; Jacobsen, J.L.; Saleur, H. Conformally invariant boundary conditions in the antiferromagnetic Potts model and the SL(2,R)/U(1) sigma model. High Energy Phys. 2019, 254, 1–51. [Google Scholar]
- Hsue, C.S.; Lin, K.Y.; Wu, F.Y. Staggered eight-vertex model. Phys. Rev. B 1975, 12, 429–437. [Google Scholar] [CrossRef]
- Kaku, M. Strings, Conformal Fields, and Topology: An Introduction; Springer: New York, NY, USA, 1991. [Google Scholar]
- De Walle, C.G.V.; Neugebauer, J. First-Principles Surface Phase Diagram for Hydrogen on GaN Surfaces. Phys. Rev. Lett. 2002, 88, 066103. [Google Scholar] [CrossRef]
- De Walle, C.G.V.; Neugebauer, J. Structure and energetics of nitride surfaces under MOCVD growth conditions. J. Cryst. Growth 2003, 248, 8–13. [Google Scholar] [CrossRef]
- Akiyama, T.; Yamashita, T.; Nakamura, K.; Ito, T. Stability of hydroben on nonpolar and semipolar nitride surfaces: Role of surface orientation. J. Cryst. Growth 2011, 318, 79–83. [Google Scholar] [CrossRef]
- Kangawa, Y.; Akiyama, T.; Ito, T.; Shiraishi, K.; Nakayama, T. Surface Stability and Growth Kinetics of Compount Semiconductors: An Ab Initio- Based Approach. Materials 2013, 6, 3309–3360. [Google Scholar] [CrossRef]
- Kempisty, P.; Strak, P.; Sakowski, K.; Kangawa, Y.; Krukowski, S. Thermodyamic foundations of application of ab initio methods for determination of the adsorbate equilibria: Hydrogen at the GaN(0001) surface. Phys. Chem. Chem. Phys. 2017, 19, 29676–29684. [Google Scholar] [CrossRef] [PubMed]
- Kempisty, P.; Kangawa, Y. Evolution of the free energy of the GaN(0001) surface based on first-principles phonon calculations. Phys. Rev. B 2019, 100, 085304. [Google Scholar] [CrossRef]
- Krzyzewski, F.; Zaluska-Kotur, M.A. Coexistence of bunching and meandering instability in simulated growth of 4H-SiC(0001) surface. J. Appl. Phys. 2014, 115, 213517. [Google Scholar] [CrossRef]
- Ehrlich, G.; Hudda, F.G. Atomic View of Surface Self-Diffusion: Tungsten on Tungsten. J. Chem. Phys. 1966, 44, 1039. [Google Scholar] [CrossRef]
- Schwoebel, R.L.; Shipsey, E.J. Step Motion on Crystal Surfaces. J. Appl. Phys. 1966, 37, 3682. [Google Scholar] [CrossRef]
- Alerhand, O.L.; Vanderbilt, D.; Meade, R.D.; Joannopoulos, J.D. Spontaneous formation of stress domains on crystal surfaces. Phys. Rev. Lett. 1988, 61, 1973–1976. [Google Scholar] [CrossRef]
- Keshishev, K.O.; Parshin, A.Y.; Babkin, A.V. Crystallization Waves in 4He. Sov. Phys. JETP 1981, 53, 362–369. [Google Scholar]
- Noziéres, P. Liquid and Solid Helium: A Probe of Condensed Matter Phenomena. Phys. Scr. 1987, 1987, 589–593. [Google Scholar] [CrossRef]
- Balibar, S.; Guthmann, C.; Rolley, E. From vicinal to rough crystal surfaces. J. Phys. I 1993, 3, 1475–1491. [Google Scholar] [CrossRef]
- Balibar, S.; Alles, H.; Parshin, A.Y. The surface of helium crystals. Rev. Mod. Phys. 2005, 77, 318–370. [Google Scholar] [CrossRef]
- Abe, H.; Saitoh, Y.; Ueda, T.; Ogasavara, F.; Nomura, R.; Okuda, Y.; Parshin, A.Y. Facet Growth of 4He Crystal Induced by Acoustic Wave. J. Phys. Soc. Jpn. 2006, 75, 023601. [Google Scholar] [CrossRef]
- Nishinaga, T.; Sasaoka, C.; Chernov, A.A. A numerical analysis for the supersaturation distribution around LPE macrostep. Morphology and Growth Unit of Crystals; Sunagawa, I., Ed.; Terra Scientific Publishing Company: Tokyo, Japan, 1989. [Google Scholar]
- Broughton, J.Q.; Gilmer, G.H. Molecular dynamics investigation of the crystal-fluid interface. II. Structures of the fcc (111), (100), and (110) crystal-vapor systems. J. Chem. Phys. 1983, 79, 5105. [Google Scholar] [CrossRef]
- Broughton, J.Q.; Gilmer, G.H. Molecular dynamics investigation of the crystal-fluid interface. III. Dynamical properties of fcc crystal-vapor systems. J. Chem. Phys. 1983, 79, 5119. [Google Scholar] [CrossRef]
- Kangawa, Y.; Ito, T.; Taguchi, A.; Shiraishi, K.; Ohachi, T. A new theoretical approach to adsorption–desorption behavior of Ga on GaAs surfaces. Surf. Sci. 2001, 493, 178–181. [Google Scholar] [CrossRef]
- Widom, B. Statistical Mechanics: A Concise Introduction for Chemists; Cambridge University Press: London, UK, 2002. [Google Scholar]
- Cabrera, N. The equilibrium of crystal surfaces. Surf. Sci. 1964, 2, 320–345. [Google Scholar] [CrossRef]
- Laue, V.M. Der Wulffsche Satz für die Gleichgewichtsform von Kristallen. Z. Kristallogr. 1944, 105, 124–133. [Google Scholar] [CrossRef]
- Herring, C. Some theorems on the free energies of crystal surfaces. Phys. Rev. 1951, 82, 87–93. [Google Scholar] [CrossRef]
- MacKenzie, J.K.; Moore, A.J.W.; Nicholas, J.F. Bonds broken at atomically flat crystal surfaces—I: Face-centred and body-centred cubic crystals. J. Chem. Phys. Solids 1962, 23, 185–196. [Google Scholar] [CrossRef]
- Den Nijs, M. Corrections to scaling and self-duality in the restricted solid-on-solid model. J. Phys. A Math. Gen. 1985, 18, L549–L556. [Google Scholar] [CrossRef]
- Akutsu, N.; Akutsu, Y. Thermal evolution of step stiffness on the Si (001) surface: Temperature-rescaled Ising-model approach. Phys. Rev. B 1998, 57, R4233–R4236. [Google Scholar] [CrossRef]
- Akutsu, N.; Akutsu, Y. The Equilibrium Facet Shape of the Staggered Body-Centered-Cubic Solid-on-Solid Model—A Density Matrix Renormalization Group Study—. Prog. Theor. Phys. 2006, 116, 983–1003. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one-or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133–1136, Erratum in 1966, 17, 1307. [Google Scholar] [CrossRef]
- Müller-Krumbhaar, H. Kinetics of crystal growth. In Current Topics in Materials Science; Kaldis, E., Ed.; North-Holland Publishing: Amsterdam, The Nethlands, 1978; Volume 1, Chapter 1; pp. 1–46. [Google Scholar]
- Akutsu, N.; Akutsu, Y. Equilibrium Crystal Shape: Two Dimensions and Three Dimensions. J. Phys. Soc. Jpn. 1987, 56, 2248–2251. [Google Scholar] [CrossRef]
- Akutsu, Y.; Akutsu, N. Interface tension, equilibrium crystal shape, and imaginary zeros of partition function: Planar Ising systems. Phys. Rev. Lett. 1990, 64, 1189–1192. [Google Scholar] [CrossRef] [PubMed]
- Akutsu, N.; Akutsu, Y. An Imaginary Path-Weight Random-Walk Method for Calculation of One-Dimensional Interface Tension. J. Phys. Soc. Jpn. 1990, 59, 3041–3044. [Google Scholar] [CrossRef]
- Akutsu, N.; Akutsu, Y. Step stiffness and equilibrium island shape of Si(100) surface: Statistical-mechanical calculation by the imaginary path weight random-walk method. Surf. Sci. 1997, 376, 92–98. [Google Scholar] [CrossRef]
- Akutsu, N.; Akutsu, Y. Statistical mechanical calculation of anisotropic step stiffness of a two-dimensional hexagonal lattice-gas model with next-nearest-neighbor interactkions: Application to Si(111) surface. J. Phys. Condens. Matter 1999, 11, 6635–6652. [Google Scholar] [CrossRef]
- Akutsu, N. Measurement of microscopic coupling constants between atoms on a surface: Combination of LEEM observation with lattice model analysis. Surf. Sci. 2014, 630, 109–115. [Google Scholar] [CrossRef]
- Bricmont, J.; Lebowitz, J.L.; Pfister, C.E. On the Local Structure of the Phase Separation Line in the Two-Dimensional Ising System. J. Stat. Phys. 1981, 26, 313–332. [Google Scholar] [CrossRef]
- Akutsu, Y.; Akutsu, N. Intrinsic structure of the phase-separation line in the two-dimensional Ising model. J. Phys. A 1987, 20, 5981–5990. [Google Scholar] [CrossRef]
- Akutsu, Y.; Akutsu, N. Relationship between the anisotropic interface tension, the scaled interface width and the equilibrium shape in two dimensions. J. Phys. 1986, A19, 2813–2820. [Google Scholar] [CrossRef]
- Swartzentruber, B.S.; Mo, Y.-W.; Kariotis, R.; Lagally, M.G.; Webb, M.B. Direct determination of step and kink energies on vicinal Si(001). Phys. Rev. Lett. 1990, 65, 1913–1916. [Google Scholar] [CrossRef] [PubMed]
- Swartzentruber, B.S.; Schacht, M. Kinetics of atomic-scale fluctuations of steps on Si (001) measured with variable-temperature STM. Surf. Sci. 1995, 322, 83–89. [Google Scholar] [CrossRef]
- Nozawa, J.; Uda, S.; Guo, S.; Toyotama, A.; Yamanaka, J.; Ihara, N.; Okada, J. Kink Distance and Binding Energy of Colloidal Crystals. Cryst. Growth Des. 2018, 18, 6078–6083. [Google Scholar] [CrossRef]
- Markov, I.V. Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy, 2nd ed.; World Scientific: Singapore, 2003. [Google Scholar]
- Kashchiev, D. Nucleation: Basic Theory with Applications; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]

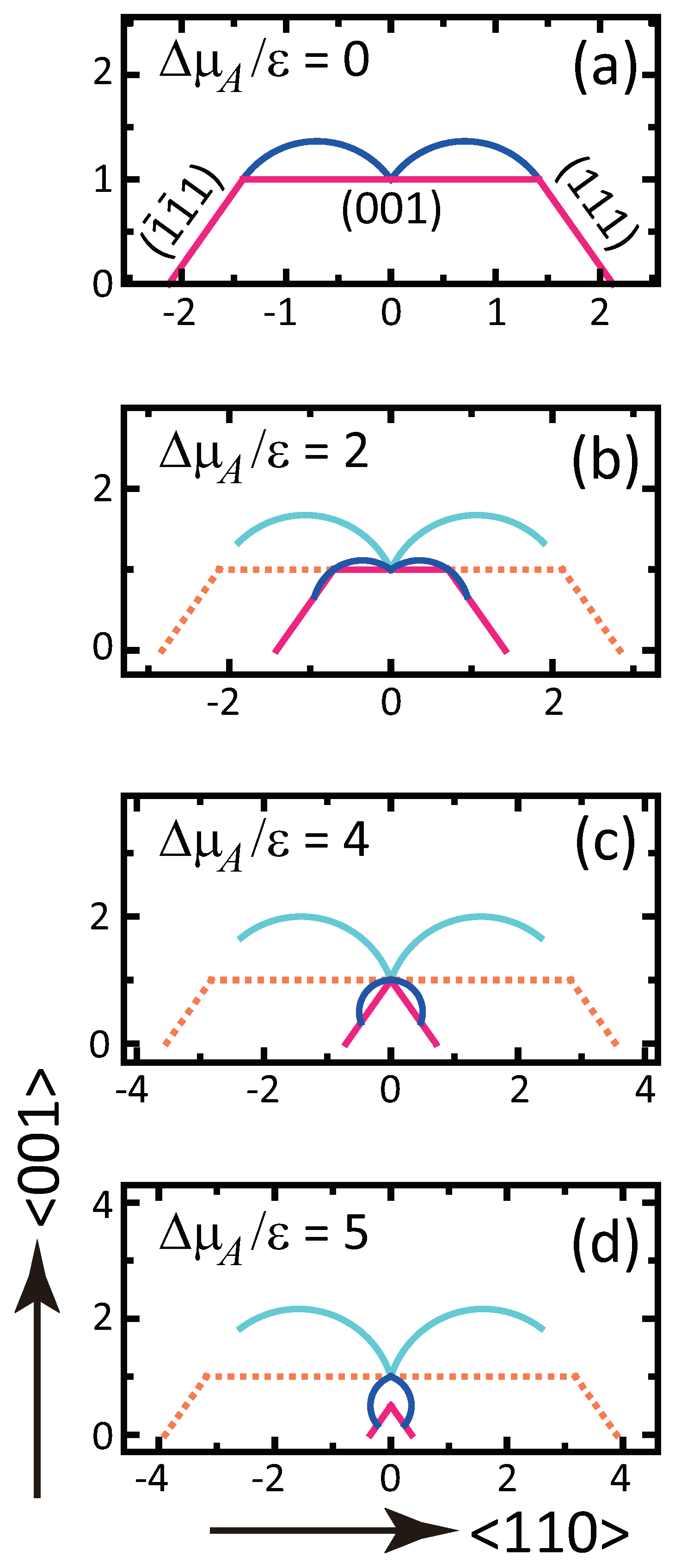

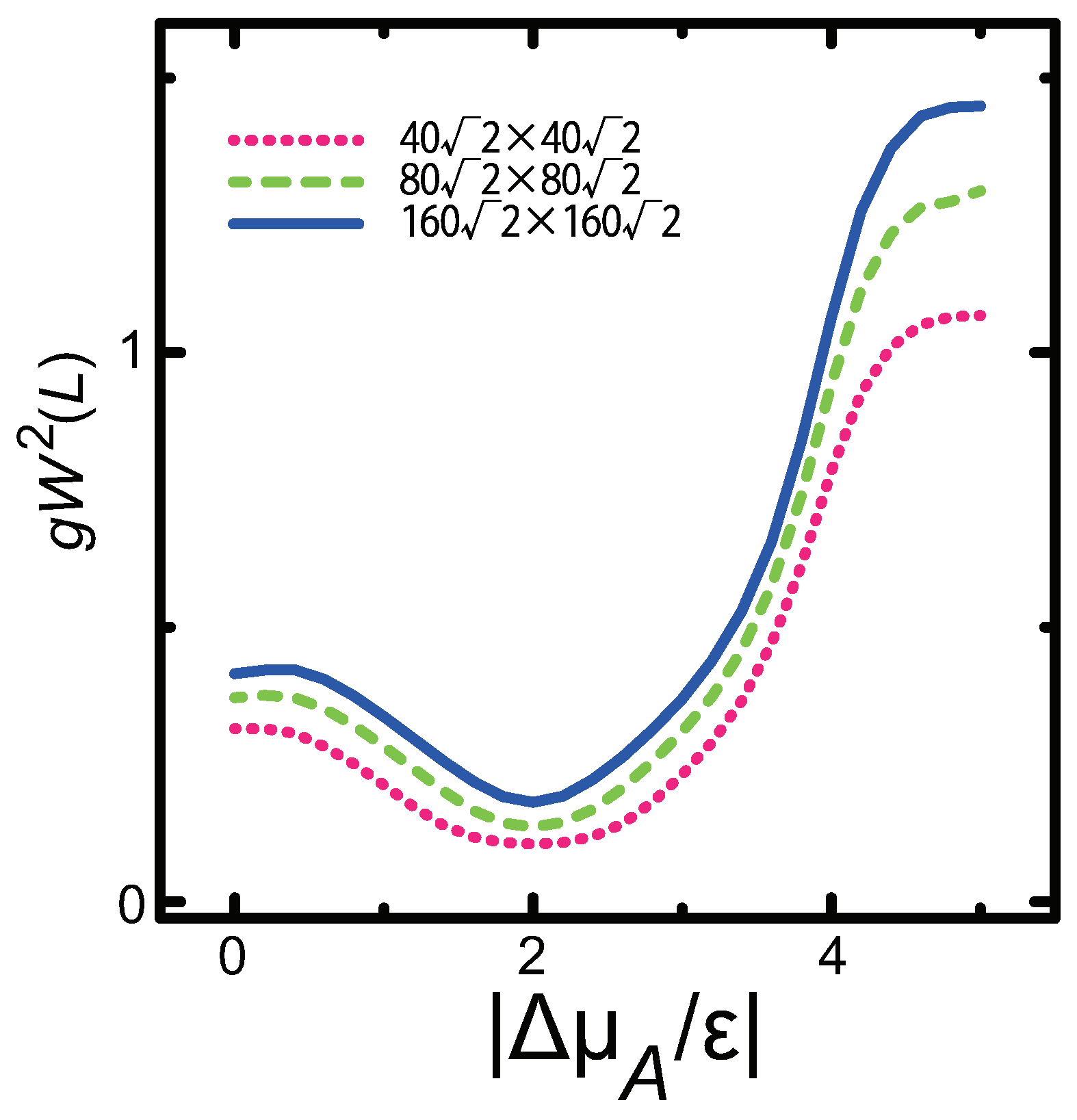
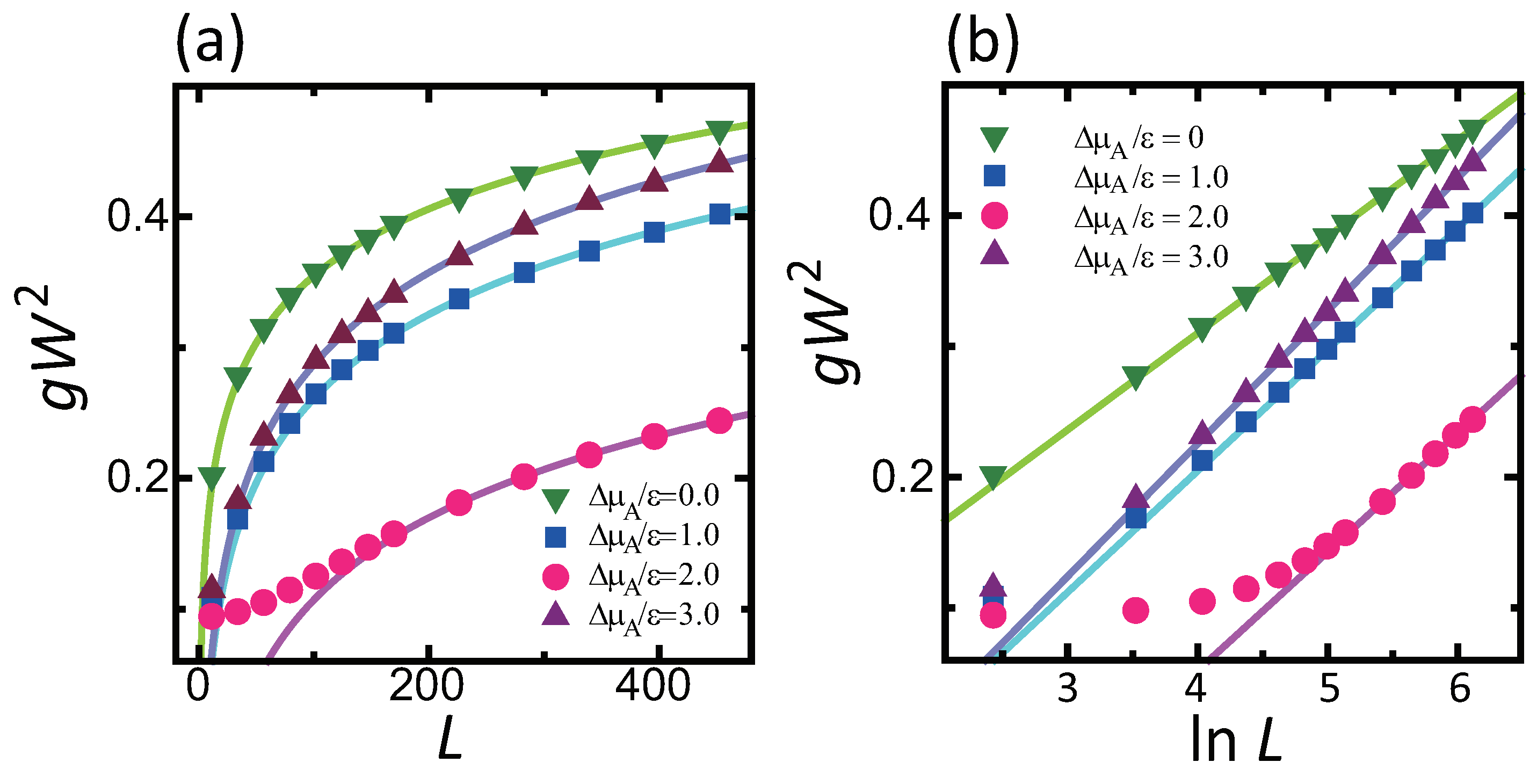
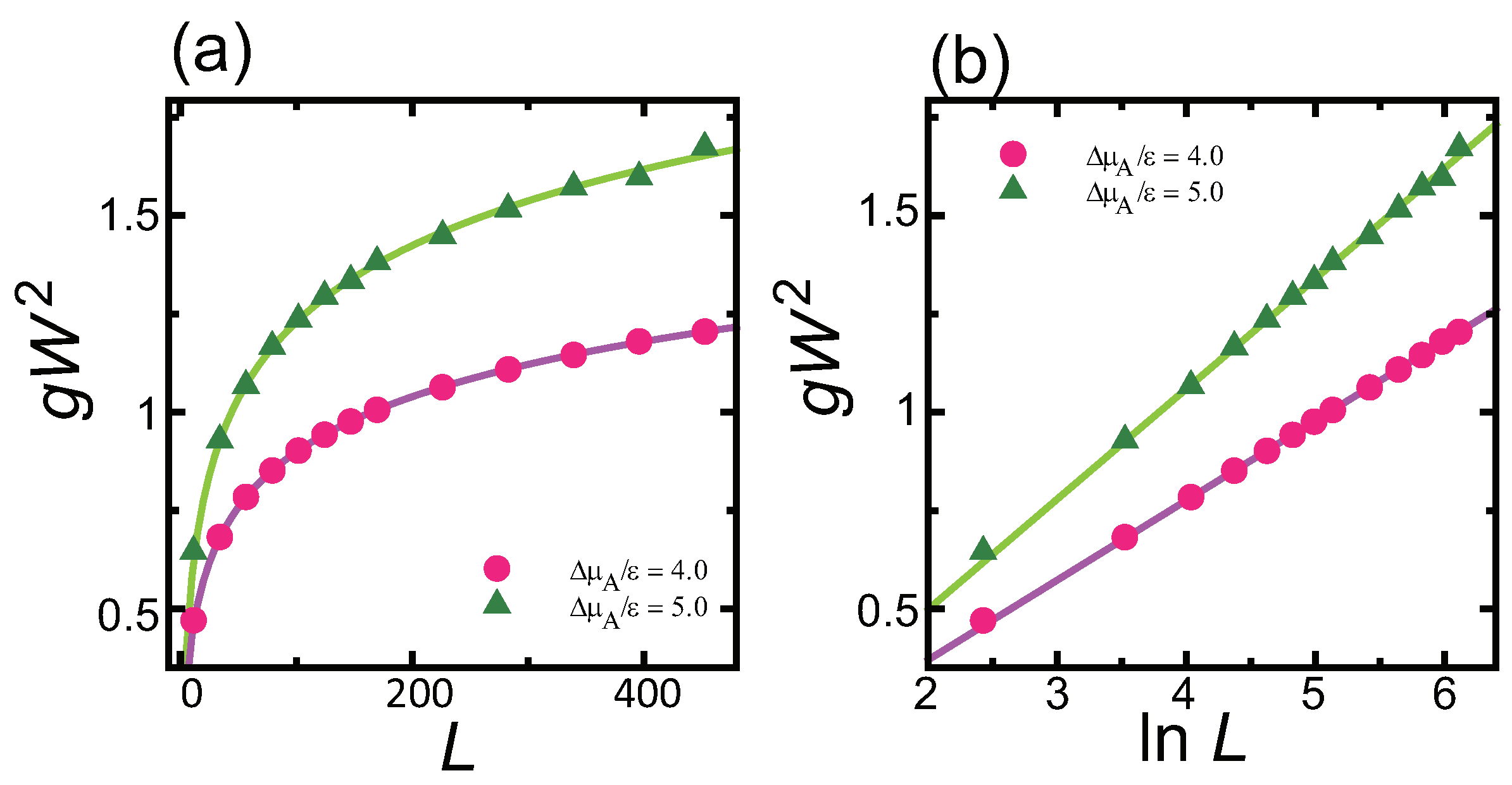

| Amplitude | Step Tension | Step Stiffness | |||||
|---|---|---|---|---|---|---|---|
| ΔμA/ϵ | A | LMFL | |||||
| Equation (22) | Equation (22) | Ref. [40] | Ref. [40] | ϕ = 45° | ϕ = 45° | ||
| 0.0 | 0.0739 | 6.1 | 1 | 2.44 | 0.565 | 1 | 1 |
| 1.0 | 0.0928 | 31 | 5.0 | 2.08 | 2.00 | 1.07 | 4.42 |
| 2.0 | 0.0907 | 156 | 26 | 1.41 | 10.5 | 0.722 | 23.2 |
| 3.0 | 0.1015 | 24 | 3.9 | 0.662 | 1.45 | 0.340 | 3.21 |
| 4.0 | 0.203 | 2.7 | 0.45 | 0 | 0 | 0 | 0 |
| 5.0 | 0.280 | 2.1 | 0.35 | 0 | 0 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akutsu, N.; Sugioka, Y.; Murata, N. Surface Roughness Changes Induced by Stoichiometric Deviation in Ambient Phase for Two-Component Semiconductor Crystals. Crystals 2020, 10, 151. https://doi.org/10.3390/cryst10030151
Akutsu N, Sugioka Y, Murata N. Surface Roughness Changes Induced by Stoichiometric Deviation in Ambient Phase for Two-Component Semiconductor Crystals. Crystals. 2020; 10(3):151. https://doi.org/10.3390/cryst10030151
Chicago/Turabian StyleAkutsu, Noriko, Yoshiki Sugioka, and Naoya Murata. 2020. "Surface Roughness Changes Induced by Stoichiometric Deviation in Ambient Phase for Two-Component Semiconductor Crystals" Crystals 10, no. 3: 151. https://doi.org/10.3390/cryst10030151
APA StyleAkutsu, N., Sugioka, Y., & Murata, N. (2020). Surface Roughness Changes Induced by Stoichiometric Deviation in Ambient Phase for Two-Component Semiconductor Crystals. Crystals, 10(3), 151. https://doi.org/10.3390/cryst10030151





