Abstract
High-pressure chemistry of organic compounds is a hot topic of modern chemistry. In this work, basic computational concepts for high-pressure phase transition studies in molecular crystals are described, showing their advantages and disadvantages. The interconnection of experimental and computational methods is highlighted, showing the importance of energy calculations in this field. Based on our deep understanding of methods’ limitations, we suggested the most convenient scheme for the computational study of high-pressure crystal structure changes. Finally, challenges and possible ways for progress in high-pressure phase transitions research of organic compounds are briefly discussed.
1. Introduction
High-pressure chemistry and particularly crystallography is developing fast in recent decades [1,2,3]. High-pressure effects are known to be studied originally and mainly by physicists and geologists [4,5]. Such significant interest in various minerals at high pressure and extreme temperatures is caused by questions that usually arise from geology—how substances act in Earth’s crust and mantle and how do they transform further when temperature and pressure decreases. To describe mineral behavior, many theoretical and experimental works have been done, resulting in a deep understanding of the formation of our and other planets [6]. Among more practical results, one should point out equations of state (EoS) many of which were originally developed for minerals and combined in special software [7,8,9,10] but now used frequently in different fields [11,12,13].
Construction and functional materials are also known for both precise and vast investigations [14,15,16]. One can easily understand that many of the materials we use every day are exposed to relatively high pressures and sometimes high temperatures and, for sure, should be studied for possible undesirable phase transitions. Another application of high pressures is discovering new forms of different elements and substances, which may exhibit new valuable properties [17,18,19,20,21,22]. Stabilizing new forms obtained at high pressures at ambient conditions is an ambitious aim for applied science and industry—graphite transforming to diamonds is the most popular example of this possible process. The importance of finding and stabilizing new inorganic and metal-organic phases that may arise at high pressure is evident. These materials are almost in every part of different devices and constructions surrounding us.
Nevertheless, new forms of organic substances are also in demand by industry [23,24,25]. Production of different forms of active pharmaceutical ingredients is a hot topic of crystallography of organic substances and can be used in practice [25,26,27,28]. Among others, one can find the application of high-pressure being a non-trivial way for obtaining new polymorphs of desired substances [29,30,31,32]. Several groups are doing extensive work looking over many organic substances for new phases at high pressure. Nowadays, there are more than 1000 structures at high pressure according to the CCDC database, and its number is growing steadily [33].
Thus, one can understand that a high-pressure phase transition study in molecular crystals is an important field of modern chemistry and as any advanced direction should be studied both experimentally and computationally.
2. The Main Research Directions
High-pressure phase transitions can be studied mainly using two different concepts:
- Experimental techniques usually provided in diamond anvil cells (DAC) by X-Ray diffraction and Raman spectroscopy [1] but not limited to these methods [34,35]. Significant progress in engineering made these experiments possible and even routine in some sense, but still, very time consuming and complicated. These experiments give atomic coordinates and unit cell parameters of molecular crystal and rarely some information on atom/functional groups motion, which can be interpreted in terms of energetic characteristics.
- Computational methods, which can be divided into DFT and Force Field (FF) groups, provide direct energetic characteristics of studied materials.
- FF methods are implemented in PIXEL [36,37] and CrystalExplorer17 [38,39,40] software for convenient work with molecular crystals. Very accurate parametrization [39] makes these methods being reliable and very fast in the estimation of lattice energies of organic crystals.
- DFT methods have many implementations for periodic systems, most popular are VASP [41,42,43], QuantumEspresso [44,45], CPMD [46], CASTEP [47] and CRYSTAL [48] codes, but researcher’s choice is not limited to abovementioned software. Reasonable choice of level of theory (LOT), which combines many parameters, gives very accurate energies of investigated systems but requires much more resources and time in comparison to FF methods.
Here can be also mentioned many specific methods that can shed some light on different aspects of structures’ nature or phase transitions, including electron/charge density analysis [49,50]. Nevertheless, these methods are relatively rarely used for molecular crystals at high-pressure conditions and have a specific discussion in literature [51,52], thus would not be described further in this work. We also do not describe molecular dynamics (MD) methods which are very useful [53,54,55], having not much experience in these methods. Modern machine learning and big data approaches are also not specified here, showing significant progress in the crystal structure and properties prediction, but not being applied to high-pressure phase transitions in molecular crystals [56,57,58,59,60].
Important to understand that both computational DFT and FF methods can barely be used without experiments being done at all because atom coordinates are needed for calculations [13,61]. Nevertheless, computational methods should be used when possible to understand and explain the nature of phase transitions of molecular crystals at high pressure because crystallographic and spectroscopic data rarely gives unambiguous reasons for phase transitions and can be interpreted differently by different scientific groups [61,62,63,64,65,66,67].
2.1. Force Field Methods
Force Field methods represent the functional form and parameter sets used to calculate the potential energy of a system of atoms or coarse-grained particles in molecular mechanics and molecular dynamics simulations. They are known widely due to their implementation in molecular dynamics for different systems, including biological ones [68,69]. Much less known but still frequently used “static” FF methods can evaluate lattice energies and some properties of molecular crystals [70,71,72,73,74]. The first successful attempt (accepted by the scientific community) was made by A. Gavezzotti, showing AA-CLP method for very fast evaluation of lattice energy and enthalpy of molecular crystals, based on atomic charges [36]. In this work [36], it has been postulated that “Structural papers with discussions of crystal packing involving user-selected atom–atom distances or geometries only should no longer be allowed in the literature” and gave the right direction of further research on molecular crystals and their forms. Later this method was substituted by more precise and sophisticated PIXEL [37], which used electron density for energy evaluation and Gaussian software [75] as a backend for this type of calculations. The energy of pair-wise interactions was described as a sum of different terms (Etot = Eele + Epol + Edis + Erep), which are given in analytical form [37]. Summation of these pair-wise interactions over a cluster of molecules in the crystal structure of radius equal to 20–50 A3 (depending on the system) gives total lattice energy (Etot). This leads to a very fast estimation of energies and, what is more important, to the “chemical” partition of different energy terms. Definitely, this very clear energy concept together with DFT was applied to high-pressure research to find the reasons for phase transition at extreme conditions [67,76,77]. One of the pioneer works in this direction was done by Wood et al. [67] who combined experimental study with extensive computational work, where both DFT and FF methods were used. Relatively good convergence with DFT methods has been shown, taking into account some limitations applied to DFT optimization procedure. Moreover, energies of structures of L-serine polymorphs were reasonable and close for both DFT and PIXEL calculations. The most valuable feature is that the energy of intermolecular interactions can be monitored for experimental structures at different pressures, and it is possible to divide into chemically sensible terms and visualize using new CE17 implementation [40]. Another important feature is the possibility to monitor the energy of any pair-wise interaction in the crystal structure and thus follow phase transitions at high pressure at a molecular level. If one needs to understand deeply what the reason for a phase transition is and why some interactions or H-bonds are broken and new appeared, energy calculations are mandatory and should be done if atom coordinates are known for different crystal phases at high pressures.
Nevertheless, one should understand that despite FF methods are very fast and relatively easy to use, they should be checked carefully for specific tasks, one of which is high-pressure research. Energy is written as a summation of different terms with coefficients Etot = keleEele + kpolEpol + kdispEdisp + krepErep, where ki is parametrized on DFT energies or experimental enthalpies (depending on implementation) for molecular crystals at ambient conditions. H-bond length is also parametrized for ambient condition calculations, and cannot be switched off due to the very low precision of X-ray experimental measurements in defining hydrogen bond lengths. Summing up, an extensive benchmark on high-pressure data is needed to use FF methods unambiguously for high-pressure research in molecular crystals or should be critically checked by DFT calculations.
2.2. DFT Methods
In contrast to FF methods, DFT calculations for systems with periodic boundary conditions prove to give very accurate energies if multiple parameters are used correctly [78,79,80,81,82]. Discussing any phase transition, we assume that Gibbs energy change should be negative for spontaneous phase transition, which can be estimated from enthalpy and entropy terms. Entropy term is frequently neglected (especially if space group preserves after phase transition), supposing to have a small impact on Gibbs energy, while enthalpy can be calculated relatively easy [61,67,80,81,83]. Nevertheless, a lack of entropy calculations can lead to significant mistakes in the prediction of phase stability, which was shown for many inorganic materials [84,85]. The introduction of thermal effects in phase stability (DFT-QHA) increases computational costs drastically, but phonon effects are crucial to define accurate thermodynamic properties and Gibbs energies [86]. Calculation of all terms of Gibbs energy is strongly recommended to correctly predict stability and (subtle) phase transitions at high-pressure and temperature conditions [85,87,88]. Thus, the enthalpy diagram should be used as the first step of an investigation. Enthalpy is a sum of internal energy and PV term, where internal energy can be described as lattice energy—a sum of intermolecular and intramolecular (conformational) interactions. The thing that can be calculated using FF methods is intermolecular interactions only, while conformational (relaxation) energies should be calculated using DFT methods [80,81]. Constant-pressure (or, more precisely, fixed-stress) geometry optimization has to be carried out in DFT energy calculations to accurately define static pressure. Then, P-V-T EoS of the substance must be known via phonon dispersion calculations to define total pressure as a sum of static, zero-point and thermal contributions. Correct assessment of PV term at high-pressure and temperature conditions could be rather complex and expensive from a computational point of view and could strongly affect P-T location of phase transition boundaries [88]. Despite the abovementioned statements were supported mostly by examples from inorganic materials, we do not see any significant difference when these calculations applied to molecular crystals. Following Gibbs energy contributions can lead to a new understanding of reasons for phase transitions for any crystalline material. In some cases, it is possible to claim volume change (PV), energy (Einter or Eintra), enthalpy (H) or entropy (S) as a driving force for phase transition [61,67,81,89]
DFT methods can be applied to experimental structures, obtained at some pressure, and all the above-mentioned parameters can be calculated. If one needs thermodynamic parameters for crystal structure at a pressure where no experimental data available, there are two main possibilities. The first is to calculate the equation of state for the phase and estimate the volume of the system, which will be fixed during ionic relaxation (structure optimization) to obtain energies. It is important to note that all calculations, in this case, should be performed for fixed unit cell volume. This technique is dependent on the accuracy of the equation of state, which needs at least 5–7 pressure-energy points within a pressure interval of a couple of GPa [90]. In this case, the quality of experimental data is very important because it influences the whole procedure of calculations. More convenient and independent from the number and quality of experimental data is the procedure with programmed pressure, e.g., as a starting structure can be taken one at ambient conditions and optimized to programmed pressure of, e.g., 3 GPa (e.g. PSTRESS option at VASP package). It was shown before that this kind of optimization to programmed pressure works accurately [61,91]. In this case, the volume is not fixed. In the case of DFT calculations enthalpy, the sum of inter- and intramolecular interactions (Ucrystal), entropy and PV term are obtained, which may give unambiguous answers with reasons for a pressure-induced phase transition. It is recommended to verify computational parameters (functional, dispersion correction scheme, k-points, and Ecutoff, etc.) on the structure, which is used as a guess structure for further calculations, usually ambient-pressure experimental data. One of the most important parameters is dispersion correction, which is crucial for accurate simulation of molecular crystals at ambient and non-ambient conditions. Nowadays, highly sophisticated density functionals are available to account for dispersive interactions in DFT (e.g., DFT-D3, B3LYP-D*, HF-3c, DFT-TS, M06, etc.) [92,93,94,95,96,97,98,99].
In relation to FF methods no “chemical” (electrostatic, polarization, dispersion, repulsion) terms are obtained in case of DFT calculations, but in common case gives more reliable energies. The advantages and disadvantages of DFT and FF methods applied to high-pressure researches are summarized in Table 1.

Table 1.
Advantages and disadvantages of DFT and FF methods applied for high-pressure research of organic substances.
2.3. Combined Techniques
Recently we suggested the scheme where different phases are simulated not only in the intervals of their stability according to experimental data but also out of these intervals [61], and used it later for another system [91]. To the best of our knowledge, these are the first examples of such calculations for organic systems, studying intrinsic vs. extrinsic phase stability of polymorphs for molecular crystals. Nevertheless, it is widely used for inorganic systems, e.g., [85,100]. This helps to understand what would happen to the polymorph structure if no phase transition occurs. Such simulation provides structural and energy data to direct comparison of all phases at the same conditions, even if some phases are not found at these pressures experimentally (Figure 1).
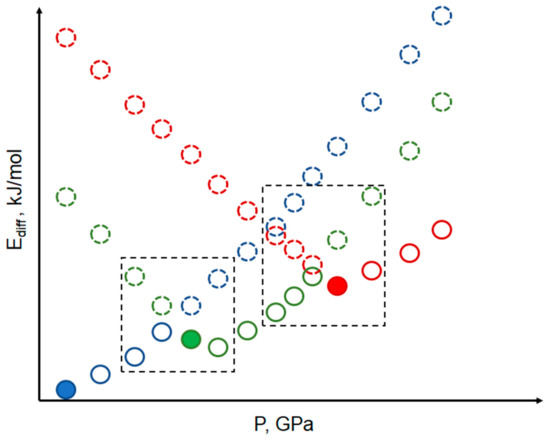
Figure 1.
Schematic representation of calculated energy parameters (∆Ucrystal, ∆H, etc.) for different phases in the whole pressure range, even at pressures where a specific phase is not found experimentally. Solid dots filled with color, starting experimental structure for DFT optimization; solid empty dots, DFT optimized structure at fixed pressure as observed experimentally; dashed dots, DFT optimized structure at fixed pressure out of experimental pressure range. Blue, phase I; green, phase II; red, phase III. Dashed squares show pressure-energy conditions close to high-pressure phase transitions.
In previous work, we also simulated pair-wise interactions using DFT gas-phase calculations with fixed geometries after solid state optimization. This simulation shows energy changes when distance decreases at pressure, building energy well for each H-bond [61]. This kind of energy well simulation is definitely not perfect due to the absence of molecular conformation change because of the molecular surrounding. This possibly could be also simulated using FF methods as described before and was done in other works [67,80,81,101].
Summing up, we suggest that the following scheme should be applied for high-pressure phase transition research of molecular crystals (Scheme 1).
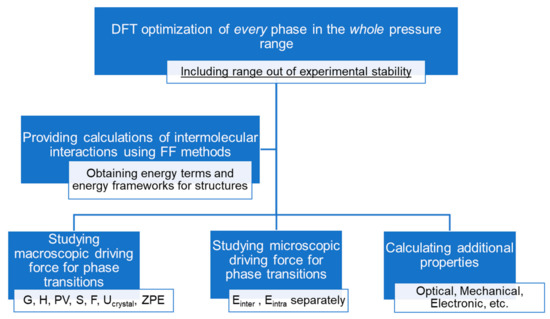
Scheme 1.
A suggested scheme for the computational study of high-pressure phase transitions of molecular crystals. All steps are calculated for structures both in and out of structural stability regions.
Finally, we would like to point out that scrupulous checks for the validity of all parameters and methods should be done for every particular system. If this is done correctly, one can assume this computational scheme is a numerical experiment aimed at understanding the reasons and mechanisms of phase transitions of molecular crystals at high pressure.
In this review, we put aside many questions related to high-pressure polymorphism of organic compounds: kinetic barriers for phase transitions which play an important role [102,103,104,105], temperature corrections for DFT methods [106,107,108], prediction of new phases (which in future can significantly decrease amount of experimental work) [109,110,111], etc. Nevertheless, as it is shown above, current computational methods can bring out many more answers than pure experimental results.
3. Prospects
To the best of our knowledge, there is no specific method or software for computationally studying high-pressure phase transitions in molecular crystals. Still, wise usage of already developed methods and their implementations with appropriate validation of different parameters can unveil reasons and even some mechanisms for phase transitions. We hope that in the future all experimental works be complemented with computational techniques. This may bring out true reasons and a deep understanding of already observed phase transitions and the prediction of new polymorphs. Finally, taking into account progress in crystal structure prediction [109,112], one can expect the prediction of new structures of molecular crystals at extreme conditions. Nevertheless, we are sure that the concept shown in this work gives the most convenient and all-round scheme for high-pressure research of organic compounds using computational methods and can be improved by obtaining different more specific properties: mechanical, electronic, optical, etc. Finally, we do not see any issues that can prevent usage of the proposed scheme for metal-organic and inorganic materials if proper parameters of the simulation are chosen.
Funding
Funding for this research was provided by Russian Science Foundation grant No. 18-73-00154.
Acknowledgments
The Siberian Branch of the Russian Academy of Sciences (SB RAS) Siberian Supercomputer Center is gratefully acknowledged for providing supercomputer facilities (http://www.sscc. icmmg.nsc.ru). The author also acknowledges the Supercomputing Center of the Novosibirsk State University (http:// nusc.nsu.ru) for provided computational resources. ISSCM SB RAS is acknowledged for free access to the literature used for this review.
Conflicts of Interest
The author declares no conflict of interest.
References
- Katrusiak, A. High-pressure crystallography. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 135–148. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.-K.; Chen, B.; Chen, J.; Li, K.; Lin, J.-F.; Yang, W.; Zheng, H. Recent advances in high-pressure science and technology. Matter Radiat. Extrem. 2016, 1, 59–75. [Google Scholar] [CrossRef]
- Tse, J.S. A Chemical Perspective on High Pressure Crystal Structures and Properties. Natl. Sci. Rev. 2019, 1, 53. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Duffy, T.S.; Shen, G.; Dobrzhinetskaya, L.F. (Eds.) Advances in High-Pressure Technology Geophysical Application; Elsevier: Amsterdam, The Netherlands, 2005; ISBN 9780444519795. [Google Scholar]
- Gonzalez-Platas, J.; Rodriguez-Hernandez, P.; Muñoz, A.; Rodríguez-Mendoza, U.R.; Nénert, G.; Errandonea, D. A High-Pressure Investigation of the Synthetic Analogue of Chalcomenite, CuSeO3∙2H2O. Crystals 2019, 9, 643. [Google Scholar] [CrossRef]
- Oganov, A.R.; Price, G.D.; Scandolo, S. Ab initio theory of planetary materials. Zeitschrift für Krist. Cryst. Mater. 2005, 220, 531–548. [Google Scholar] [CrossRef]
- Angel, R.J. Equations of State. Rev. Mineral. Geochem. 2000, 41, 35–59. [Google Scholar] [CrossRef]
- Angel, R.J. High-Pressure Structural Phase Transitions. Rev. Mineral. Geochem. 2000, 39, 85–104. [Google Scholar] [CrossRef]
- Angel, R.J.; Alvaro, M.; Gonzalez-Platas, J. EosFit7c and a Fortran module (library) for equation of state calculations. Zeitschrift für Krist.Cryst. Mater. 2014, 229, 405–419. [Google Scholar] [CrossRef]
- Gonzalez-Platas, J.; Alvaro, M.; Nestola, F.; Angel, R. EosFit7-GUI: A new graphical user interface for equation of state calculations, analyses and teaching. J. Appl. Crystallogr. 2016, 49, 1377–1382. [Google Scholar] [CrossRef]
- Bull, C.L.; Playford, H.Y.; Knight, K.S.; Marshall, W.G.; Stenning, G.B.G.; Smith, R.I.; Hart, Z. New insights into the phase diagram of a magnetic perovskite, LaCo 1/3 Mn 2/3 O 3. J. Phys. Condens. Matter 2015, 27, 165401. [Google Scholar] [CrossRef]
- Errandonea, D.; Muñoz, A.; Gonzalez-Platas, J. Comment on “High-pressure x-ray diffraction study of YBO 3 /Eu 3+, GdBO 3, and EuBO 3: Pressure-induced amorphization in GdBO 3”. J. Appl. Phys. 2014, 115, 216101. [Google Scholar] [CrossRef]
- Hunter, S.; Sutinen, T.; Parker, S.F.; Morrison, C.A.; Williamson, D.M.; Thompson, S.; Gould, P.J.; Pulham, C.R. Experimental and DFT-D Studies of the Molecular Organic Energetic Material RDX. J. Phys. Chem. C 2013, 117, 8062–8071. [Google Scholar] [CrossRef]
- Sharma, S.M.; Garg, N. Material Studies at High Pressure. In Materials Under Extreme Conditions; Elsevier: Amsterdam, The Netherlands, 2017; pp. 1–47. ISBN 9780128014424. [Google Scholar]
- Millar, D.I.A. Energetic Materials at Extreme Conditions; Springer Berlin Heidelberg: Berlin, Heidelberg, 2012; ISBN 978-3-642-23131-5. [Google Scholar]
- Dubrovinsky, L.; Dubrovinskaia, N.; Bykova, E.; Bykov, M.; Prakapenka, V.; Prescher, C.; Glazyrin, K.; Liermann, H.-P.; Hanfland, M.; Ekholm, M.; et al. The most incompressible metal osmium at static pressures above 750 gigapascals. Nature 2015, 525, 226–229. [Google Scholar] [CrossRef] [PubMed]
- Gao, G.; Oganov, A.R.; Ma, Y.; Wang, H.; Li, P.; Li, Y.; Iitaka, T.; Zou, G. Dissociation of methane under high pressure. J. Chem. Phys. 2010, 133, 144508. [Google Scholar] [CrossRef]
- Zhang, W.; Oganov, A.R.; Goncharov, A.F.; Zhu, Q.; Boulfelfel, S.E.; Lyakhov, A.O.; Stavrou, E.; Somayazulu, M.; Prakapenka, V.B.; Konopkova, Z. Unexpected Stable Stoichiometries of Sodium Chlorides. Science 2013, 342, 1502–1505. [Google Scholar] [CrossRef] [PubMed]
- Zentkova, M.; Mihalik, M. The Effect of Pressure on Magnetic Properties of Prussian Blue Analogues. Crystals 2019, 9, 112. [Google Scholar] [CrossRef]
- Manjón, F.J.; Sans, J.A.; Ibáñez, J.; Pereira, A.L.J. Pressure-Induced Phase Transitions in Sesquioxides. Crystals 2019, 9, 630. [Google Scholar] [CrossRef]
- Yang, X.; Wang, X.; Wang, Y.; Li, K.; Zheng, H. From Molecules to Carbon Materials—High Pressure Induced Polymerization and Bonding Mechanisms of Unsaturated Compounds. Crystals 2019, 9, 490. [Google Scholar] [CrossRef]
- Cazorla, C.; MacLeod, S.G.; Errandonea, D.; Munro, K.A.; McMahon, M.I.; Popescu, C. Thallium under extreme compression. J. Phys. Condens. Matter 2016, 28, 445401. [Google Scholar] [CrossRef]
- Barrio, M.; Maccaroni, E.; Rietveld, I.B.; Malpezzi, L.; Masciocchi, N.; Céolin, R.; Tamarit, J.-L. Pressure-temperature state diagram for the phase relationships between benfluorex hydrochloride forms I and II: A case of enantiotropic behavior. J. Pharm. Sci. 2012, 101, 1073–1078. [Google Scholar] [CrossRef]
- Neumann, M.A.; van de Streek, J.; Fabbiani, F.P.A.; Hidber, P.; Grassmann, O. Combined crystal structure prediction and high-pressure crystallization in rational pharmaceutical polymorph screening. Nat. Commun. 2015, 6, 7793. [Google Scholar] [CrossRef]
- Fabbiani, F.P.A.; Pulham, C.R. High-pressure studies of pharmaceutical compounds and energetic materials. Chem. Soc. Rev. 2006, 35, 932. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, J. Polymorphism—A Perspective. Cryst. Growth Des. 2011, 11, 632–650. [Google Scholar] [CrossRef]
- Bučar, D.-K.; Lancaster, R.W.; Bernstein, J. Disappearing Polymorphs Revisited. Angew. Chemie Int. Ed. 2015, 54, 6972–6993. [Google Scholar] [CrossRef]
- Konieczny, K.; Ciesielski, A.; Bąkowicz, J.; Galica, T.; Turowska-Tyrk, I. Structural Transformations in Crystals Induced by Radiation and Pressure. Part 7. Molecular and Crystal Geometries as Factors Deciding about Photochemical Reactivity under Ambient and High Pressures. Crystals 2018, 8, 299. [Google Scholar] [CrossRef]
- Bernstein, J. Polymorphism in Molecular Crystals; Oxford University Press: New York, NY, USA, 2002; Volume 14, ISBN 978-0-19-923656-5. [Google Scholar]
- Boldyreva, E.V.; Shakhtshneider, T.P.; Ahsbahs, H.; Sowa, H.; Uchtmann, H. Effect of high pressure on the polymorphs of paracetamol. J. Therm. Anal. Calori. 2002, 68, 437–452. [Google Scholar]
- Seryotkin, Y.V.; Drebushchak, T.N.; Boldyreva, E.V. A high-pressure polymorph of chlorpropamide formed on hydrostatic compression of the α-form in saturated ethanol solution. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2013, 69, 77–85. [Google Scholar] [CrossRef]
- Görbitz, C.H. Crystal structures of amino acids: from bond lengths in glycine to metal complexes and high-pressure polymorphs. Crystallogr. Rev. 2015, 21, 160–212. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Anzellini, S.; Errandonea, D.; Cazorla, C.; MacLeod, S.; Monteseguro, V.; Boccato, S.; Bandiello, E.; Anichtchenko, D.D.; Popescu, C.; Beavers, C.M. Thermal equation of state of ruthenium characterized by resistively heated diamond anvil cell. Sci. Rep. 2019, 9, 14459. [Google Scholar] [CrossRef]
- Knudson, M.D.; Desjarlais, M.P.; Dolan, D.H. Shock-Wave Exploration of the High-Pressure Phases of Carbon. Science 2008, 322, 1822–1825. [Google Scholar] [CrossRef] [PubMed]
- Gavezzotti, A. Efficient computer modeling of organic materials. The atom–atom, Coulomb–London–Pauli (AA-CLP) model for intermolecular electrostatic-polarization, dispersion and repulsion energies. New J. Chem. 2011, 35, 1360. [Google Scholar] [CrossRef]
- Gavezzotti, A. Calculation of lattice energies of organic crystals: the PIXEL integration method in comparison with more traditional methods. Zeitschrift für Krist. Cryst. Mater. 2005, 220, 499–510. [Google Scholar] [CrossRef]
- Edwards, A.J.; Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Intermolecular interactions in molecular crystals: What’s in a name? Faraday Discuss. 2017, 203, 93–112. [Google Scholar] [CrossRef]
- Thomas, S.P.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Accurate Lattice Energies for Molecular Crystals from Experimental Crystal Structures. J. Chem. Theory Comput. 2018, 14, 1614–1623. [Google Scholar] [CrossRef]
- Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer model energies and energy frameworks: extension to metal coordination compounds, organic salts, solvates and open-shell systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- CPMD.org. Available online: http://www.cpmd.org/ (accessed on 7 October 2015).
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Zeitschrift für Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Macchi, P.; Casati, N.; Kleppe, A.; Jephcoat, A. Electron density of molecular crystals at high pressure from synchrotron data. Acta Crystallogr. Sect. A Found. Adv. 2014, 70, C1340. [Google Scholar] [CrossRef]
- Casati, N.; Kleppe, A.; Jephcoat, A.P.; Macchi, P. Putting pressure on aromaticity along with in situ experimental electron density of a molecular crystal. Nat. Commun. 2016, 7, 10901. [Google Scholar] [CrossRef] [PubMed]
- Spackman, M.A. How Reliable Are Intermolecular Interaction Energies Estimated from Topological Analysis of Experimental Electron Densities? Cryst. Growth Des. 2015, 15, 5624–5628. [Google Scholar] [CrossRef]
- Kumar, P.; Cabaj, M.K.; Dominiak, P.M. Intermolecular Interactions in Ionic Crystals of Nucleobase Chlorides—Combining Topological Analysis of Electron Densities with Energies of Electrostatic Interactions. Crystals 2019, 9, 668. [Google Scholar] [CrossRef]
- Mahesta, R.; Mochizuki, K. Stepwise Homogeneous Melting of Benzene Phase I at High Pressure. Crystals 2019, 9, 279. [Google Scholar] [CrossRef]
- Nemkevich, A.; Bürgi, H.-B.; Spackman, M.A.; Corry, B. Molecular dynamics simulations of structure and dynamics of organic molecular crystals. Phys. Chem. Chem. Phys. 2010, 12, 14916. [Google Scholar] [CrossRef]
- Iyer, S.; Slagg, N. Energetic Materials; Boddu, V., Redner, P., Eds.; CRC Press: Boca Raton, FL, USA, 2010; Volume 2, ISBN 978-1-4398-3513-5. [Google Scholar]
- Musil, F.; De, S.; Yang, J.; Campbell, J.E.; Day, G.M.; Ceriotti, M. Machine learning for the structure-energy-property landscapes of molecular crystals. Chem. Sci. 2018, 9, 1289–1300. [Google Scholar] [CrossRef]
- Wicker, J.G.P.; Cooper, R.I. Will it crystallise? Predicting crystallinity of molecular materials. CrystEngComm 2015, 17, 1927–1934. [Google Scholar] [CrossRef]
- Wicker, J.G.P.; Crowley, L.M.; Robshaw, O.; Little, E.J.; Stokes, S.P.; Cooper, R.I.; Lawrence, S.E. Will they co-crystallize? CrystEngComm 2017, 19, 5336–5340. [Google Scholar] [CrossRef]
- Podryabinkin, E.V.; Tikhonov, E.V.; Shapeev, A.V.; Oganov, A.R. Accelerating crystal structure prediction by machine-learning interatomic potentials with active learning. Phys. Rev. B 2019, 99, 064114. [Google Scholar] [CrossRef]
- Evans, J.D.; Coudert, F.-X. Predicting the Mechanical Properties of Zeolite Frameworks by Machine Learning. Chem. Mater. 2017, 29, 7833–7839. [Google Scholar] [CrossRef]
- Rychkov, D.A.; Stare, J.; Boldyreva, E.V. Pressure-driven phase transition mechanisms revealed by quantum chemistry: l -serine polymorphs. Phys. Chem. Chem. Phys. 2017, 19, 6671–6676. [Google Scholar] [CrossRef]
- Kolesnik, E.N.; Goryainov, S.V.; Boldyreva, E.V. Different behavior of L- and DL-serine crystals at high pressures: Phase transitions in L-serine and stability of the DL-serine structure. Dokl. Phys. Chem. 2005, 404, 169–172. [Google Scholar] [CrossRef]
- Moggach, S.A.; Allan, D.R.; Morrison, C.A.; Parsons, S.; Sawyer, L. Effect of pressure on the crystal structure of L-serine-I and the crystal structure of L-serine-II at 5.4 GPa. Acta Crystallogr. Sect. B Struct. Sci. 2005, 61, 58–68. [Google Scholar] [CrossRef]
- Drebushchak, T.N.; Sowa, H.; Seryotkin, Y.V.; Boldyreva, E.V.; Ahsbahs, H. L-Serine III at 8.0 GPa. Acta Crystallogr. Sect. E Struct. Rep. Online 2006, 62, 4052–4054. [Google Scholar] [CrossRef]
- Boldyreva, E.V.; Sowa, H.; Seryotkin, Y.V.; Drebushchak, T.N.; Ahsbahs, H.; Chernyshev, V.; Dmitriev, V. Pressure-induced phase transitions in crystalline l-serine studied by single-crystal and high-resolution powder X-ray diffraction. Chem. Phys. Lett. 2006, 429, 474–478. [Google Scholar] [CrossRef]
- Moggach, S.A.; Marshall, W.G.; Parsons, S. High-pressure neutron diffraction study of L-serine-I and L-serine-II, and the structure of L-serine-III at 8.1 GPa. Acta Crystallogr. Sect. B Struct. Sci. 2006, 62, 815–825. [Google Scholar] [CrossRef]
- Wood, P.A.; Francis, D.; Marshall, W.G.; Moggach, S.A.; Parsons, S.; Pidcock, E.; Rohl, A.L. A study of the high-pressure polymorphs of L-serine using ab initio structures and PIXEL calculations. CrystEngComm 2008, 10, 1154. [Google Scholar] [CrossRef]
- Antila, H.S.; Salonen, E. Biomolecular Simulations; Monticelli, L., Salonen, E., Eds.; Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2013; Volume 924, ISBN 978-1-62703-016-8. [Google Scholar]
- Kukol, A. (Ed.) Molecular Modeling of Proteins; Methods in Molecular Biology; Springer New York: New York, NY, USA, 2015; Volume 1215, ISBN 978-1-4939-1464-7. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007; Volume 2, ISBN 9780470058046. [Google Scholar]
- Turner, M.J.; Thomas, S.P.; Shi, M.W.; Jayatilaka, D.; Spackman, M.A. Energy frameworks: Insights into interaction anisotropy and the mechanical properties of molecular crystals. Chem. Commun. 2015, 51, 3735–3738. [Google Scholar] [CrossRef]
- Rychkov, D.; Arkhipov, S.; Boldyreva, E. Structure-forming units of amino acid maleates. Case study of L-valinium hydrogen maleate. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 160–163. [Google Scholar] [CrossRef]
- Binns, J.; Parsons, S.; McIntyre, G.J. Accurate hydrogen parameters for the amino acid l -leucine. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 885–892. [Google Scholar] [CrossRef]
- Moggach, S.A.; Marshall, W.G.; Rogers, D.M.; Parsons, S. How focussing on hydrogen bonding interactions in amino acids can miss the bigger picture: A high-pressure neutron powder diffraction study of ε-glycine. CrystEngComm 2015, 17, 5315–5328. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B. Gaussian 09. Expanding the limits of computational chemistry. 2009. Available online: https://gaussian.com/g09citation/ (accessed on 30 January 2020).
- Johnstone, R.D.L.; Lennie, A.R.; Parker, S.F.; Parsons, S.; Pidcock, E.; Richardson, P.R.; Warren, J.E.; Wood, P.A. High-pressure polymorphism in salicylamide. CrystEngComm 2010, 12, 1065. [Google Scholar] [CrossRef]
- Munday, L.B.; Chung, P.W.; Rice, B.M.; Solares, S.D. Simulations of High-Pressure Phases in RDX. J. Phys. Chem. B 2011, 115, 4378–4386. [Google Scholar] [CrossRef]
- Dolgonos, G.A.; Hoja, J.; Boese, A.D. Revised values for the X23 benchmark set of molecular crystals. Phys. Chem. Chem. Phys. 2019, 21, 24333–24344. [Google Scholar] [CrossRef]
- Colmenero, F. Mechanical properties of anhydrous oxalic acid and oxalic acid dihydrate. Phys. Chem. Chem. Phys. 2019, 21, 2673–2690. [Google Scholar] [CrossRef]
- Giordano, N.; Beavers, C.M.; Kamenev, K.V.; Marshall, W.G.; Moggach, S.A.; Patterson, S.D.; Teat, S.J.; Warren, J.E.; Wood, P.A.; Parsons, S. High-pressure polymorphism in l-threonine between ambient pressure and 22 GPa. CrystEngComm 2019, 21, 4444–4456. [Google Scholar] [CrossRef]
- Giordano, N.; Afanasjevs, S.; Beavers, C.M.; Hobday, C.L.; Kamenev, K.V.; O’Bannon, E.F.; Ruiz-Fuertes, J.; Teat, S.J.; Valiente, R.; Parsons, S. The Effect of Pressure on Halogen Bonding in 4-Iodobenzonitrile. Molecules 2019, 24, 2018. [Google Scholar] [CrossRef]
- Abraham, B.M.; Vaitheeswaran, G. First principles study of pressure induced polymorphic phase transition in trimethylamine. In Proceedings of the AIP Conference Proceedings. AIP Conf. Proc. 2018, 1942, 030006. [Google Scholar]
- Wen, X.D.; Hoffmann, R.; Ashcroft, N.W. Benzene under high pressure: A story of molecular crystals transforming to saturated networks, with a possible intermediate metallic phase. J. Am. Chem. Soc. 2011, 133, 9023–9035. [Google Scholar] [CrossRef]
- Zucchini, A.; Prencipe, M.; Belmonte, D.; Comodi, P. Ab initio study of the dolomite to dolomite-II high-pressure phase transition. Eur. J. Mineral. 2017, 29, 227–238. [Google Scholar] [CrossRef]
- Belmonte, D.; Ottonello, G.; Zuccolini, M.V. Ab initio-assisted assessment of the CaO-SiO2 system under pressure. Calphad 2017, 59, 12–30. [Google Scholar] [CrossRef]
- Belmonte, D.; Gatti, C.; Ottonello, G.; Richet, P.; Zuccolini, M.V. Ab initio thermodynamic and thermophysical properties of sodium metasilicate, Na2SiO3, and their electron-density and electron-pair-density counterparts. J. Phys. Chem. A 2016, 120, 8881–8895. [Google Scholar] [CrossRef] [PubMed]
- Wdowik, U.D. Structural stability and thermal properties of BeO from the quasiharmonic approximation. J. Phys. Condens. Matter 2010, 22, 045404. [Google Scholar] [CrossRef] [PubMed]
- Belmonte, D. First Principles Thermodynamics of Minerals at HP–HT Conditions: MgO as a Prototypical Material. Minerals 2017, 7, 183. [Google Scholar] [CrossRef]
- Moses Abraham, B.; Adivaiah, B.; Vaitheeswaran, G. Microscopic origin of pressure-induced phase-transitions in urea: A detailed investigation through first principles calculations. Phys. Chem. Chem. Phys. 2019, 21, 884–900. [Google Scholar] [CrossRef]
- Katrusiak, A.; McMillan, P.F. High-Pressure Crystallography; Katrusiak, A., McMillan, P., Eds.; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Fedorov, A.Y.; Rychkov, D.A.; Losev, E.A.; Zakharov, B.A.; Stare, J.; Boldyreva, E.V. Effect of pressure on two polymorphs of tolazamide: Why no interconversion? CrystEngComm 2017, 19, 2243–2252. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef] [PubMed]
- Brandenburg, J.G.; Grimme, S. Dispersion Corrected Hartree–Fock and Density Functional Theory for Organic Crystal Structure Prediction. In Peptide-Based Materials; Springer: Dordrecht, The Netherlands, 2013; Volume 310, pp. 1–23. [Google Scholar]
- Klimeš, J.; Michaelides, A. Perspective: Advances and challenges in treating van der Waals dispersion forces in density functional theory. J. Chem. Phys. 2012, 137, 120901. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Kronik, L.; Tkatchenko, A. Understanding Molecular Crystals with Dispersion-Inclusive Density Functional Theory: Pairwise Corrections and Beyond. Acc. Chem. Res. 2014, 47, 3208–3216. [Google Scholar] [CrossRef] [PubMed]
- Brandenburg, J.G.; Grimme, S. Accurate Modeling of Organic Molecular Crystals by Dispersion-Corrected Density Functional Tight Binding (DFTB). J. Phys. Chem. Lett. 2014, 5, 1785–1789. [Google Scholar] [CrossRef]
- Marom, N.; DiStasio, R.A.; Atalla, V.; Levchenko, S.; Reilly, A.M.; Chelikowsky, J.R.; Leiserowitz, L.; Tkatchenko, A. Many-Body Dispersion Interactions in Molecular Crystal Polymorphism. Angew. Chemie Int. Ed. 2013, 52, 6629–6632. [Google Scholar] [CrossRef]
- Jahn, S. High-pressure phase transitions in MgSiO3 orthoenstatite studied by atomistic computer simulation. Am. Mineral. 2008, 93, 528–532. [Google Scholar] [CrossRef][Green Version]
- Giordano, N.; Beavers, C.M.; Campbell, B.J.; Eigner, V.; Gregoryanz, E.; Marshall, W.G.; Peña-Álvarez, M.; Teat, S.J.; Vennari, C.E.; Parsons, S. High-pressure polymorphism in pyridine. IUCrJ 2020, 7, 58–70. [Google Scholar] [CrossRef]
- Boldyreva, E. High-Pressure Polymorphs of Molecular Solids: When Are They Formed, and When Are They Not? Some Examples of the Role of Kinetic Control. Cryst. Growth Des. 2007, 7, 1662–1668. [Google Scholar]
- Fisch, M.; Lanza, A.; Boldyreva, E.; Macchi, P.; Casati, N. Kinetic Control of High-Pressure Solid-State Phase Transitions: A Case Study on l-Serine. J. Phys. Chem. C 2015, 119, 18611–18617. [Google Scholar] [CrossRef]
- Bhardwaj, P.; Singh, S. Pressure induced structural phase transitions—A review. Open Chem. 2012, 10, 1391–1422. [Google Scholar] [CrossRef]
- Han, Y.; Liu, J.; Huang, L.; He, X.; Li, J. Predicting the phase diagram of solid carbon dioxide at high pressure from first principles. npj Quantum Mater. 2019, 4, 10. [Google Scholar] [CrossRef]
- Smith, J.C.; Sagredo, F.; Burke, K. Warming Up Density Functional Theory. In Frontiers of Quantum Chemistry; Springer: Singapore, 2018. [Google Scholar]
- Majewski, A.R.; Billman, C.R.; Cheng, H.-P.; Sullivan, N.S. DFT Calculations of Temperature-Dependent NQR Parameters in alpha-paradichlorobenzene and beta-HMX. arXiv 2019, arXiv:1903.10097. [Google Scholar]
- Hickel, T.; Grabowski, B.; Körmann, F.; Neugebauer, J. Advancing density functional theory to finite temperatures: Methods and applications in steel design. J. Phys. Condens. Matter 2012, 24, 053202. [Google Scholar] [CrossRef]
- Reilly, A.M.; Cooper, R.I.; Adjiman, C.S.; Bhattacharya, S.; Boese, A.D.; Brandenburg, J.G.; Bygrave, P.J.; Bylsma, R.; Campbell, J.E.; Car, R.; et al. Report on the sixth blind test of organic crystal structure prediction methods. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 439–459. [Google Scholar]
- Iuzzolino, L.; McCabe, P.; Price, S.L.; Brandenburg, J.G. Crystal structure prediction of flexible pharmaceutical-like molecules: Density functional tight-binding as an intermediate optimisation method and for free energy estimation. Faraday Discuss. 2018, 211, 275–296. [Google Scholar] [CrossRef]
- Price, S.L.; Reutzel-Edens, S.M. The potential of computed crystal energy landscapes to aid solid-form development. Drug Discov. Today 2016, 21, 912–923. [Google Scholar]
- Zurek, E.; Grochala, W. Predicting crystal structures and properties of matter under extreme conditions via quantum mechanics: The pressure is on. Phys. Chem. Chem. Phys. 2015, 17, 2917–2934. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).