Effects of Pulsed Magnetic Fields of Different Intensities on Dislocation Density, Residual Stress, and Hardness of Cr4Mo4V Steel
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Materials Characterization
2.3. EBSD Tests
2.4. Residual Stress Measurement
2.5. Vickers Hardness Measurement
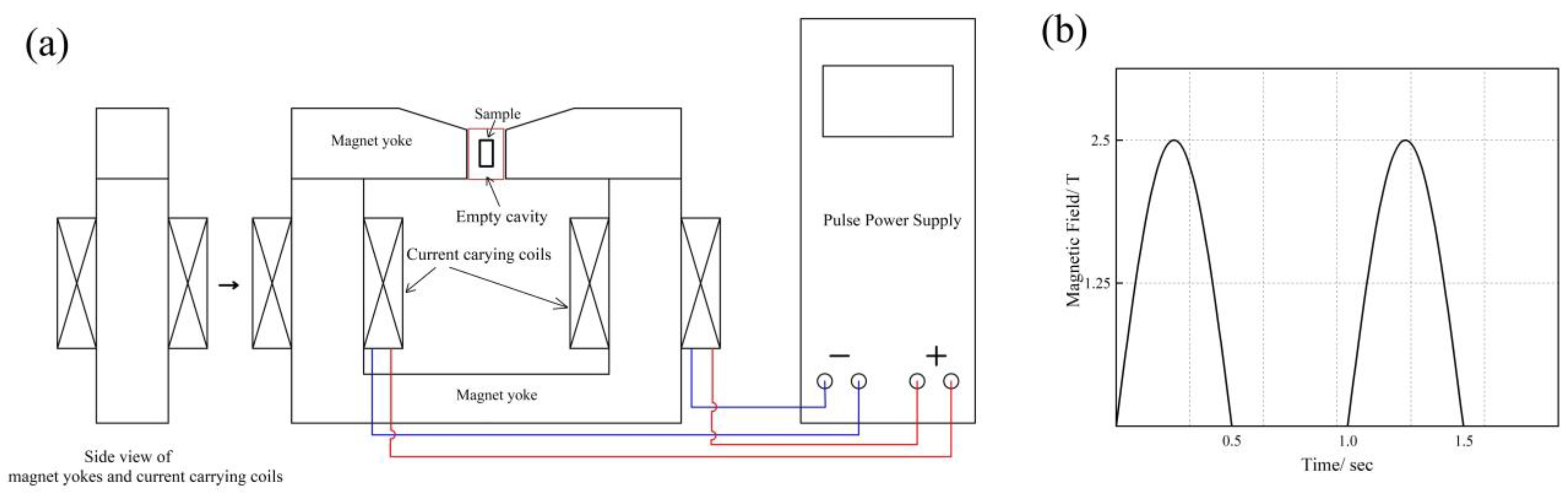
2.6. Pulsed Magnetic Field Treatment
3. Experiment Results
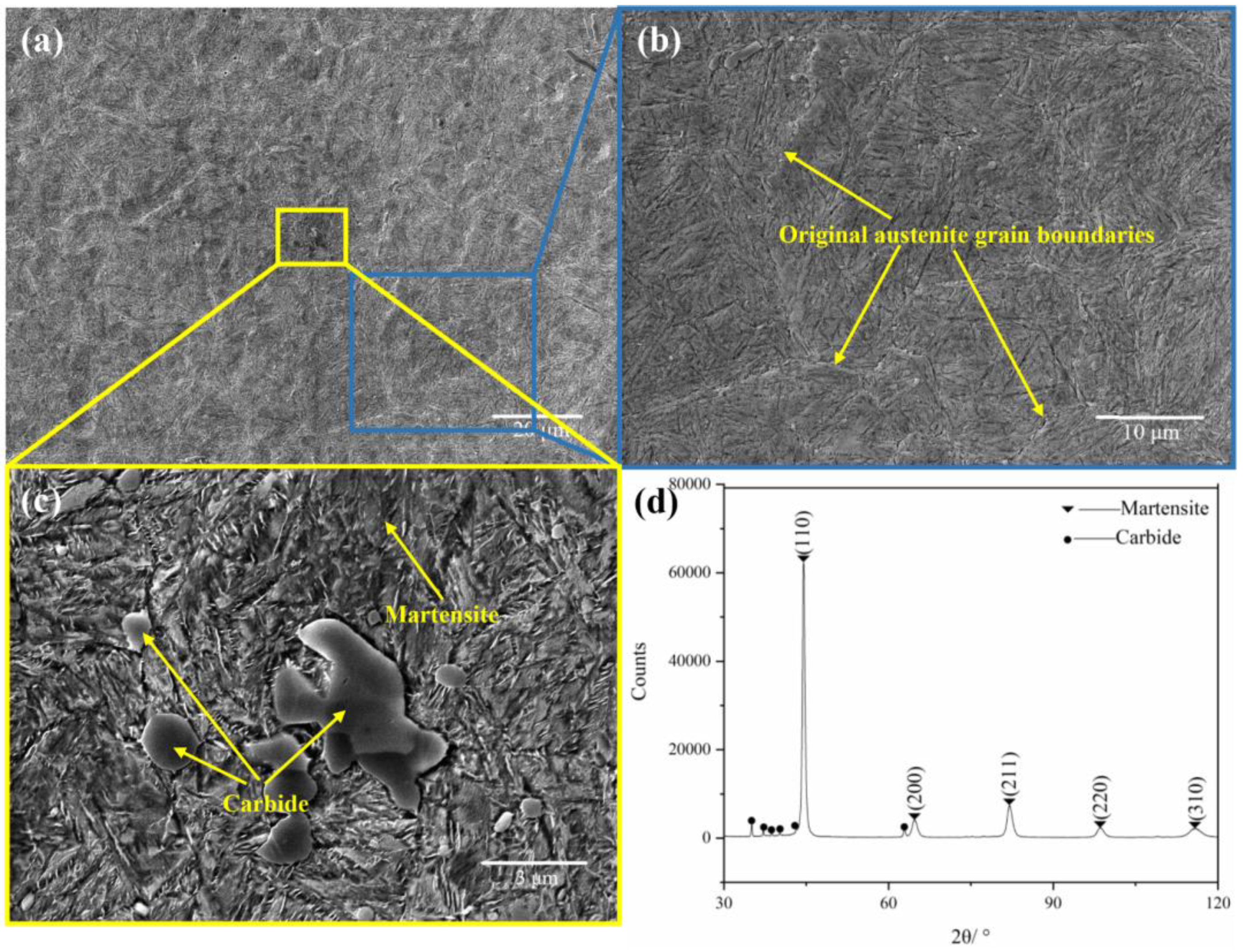
3.1. Materials Characterization
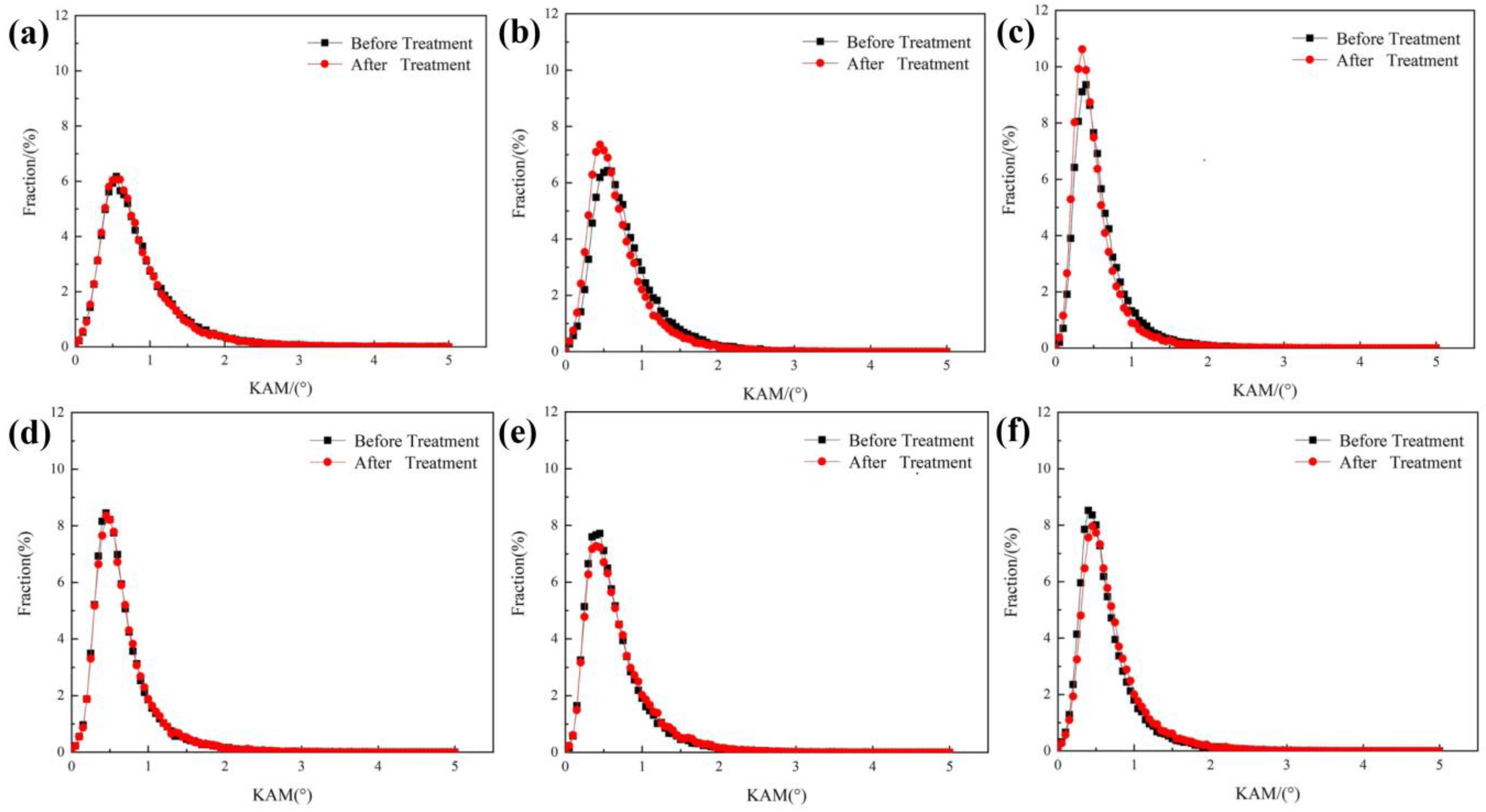
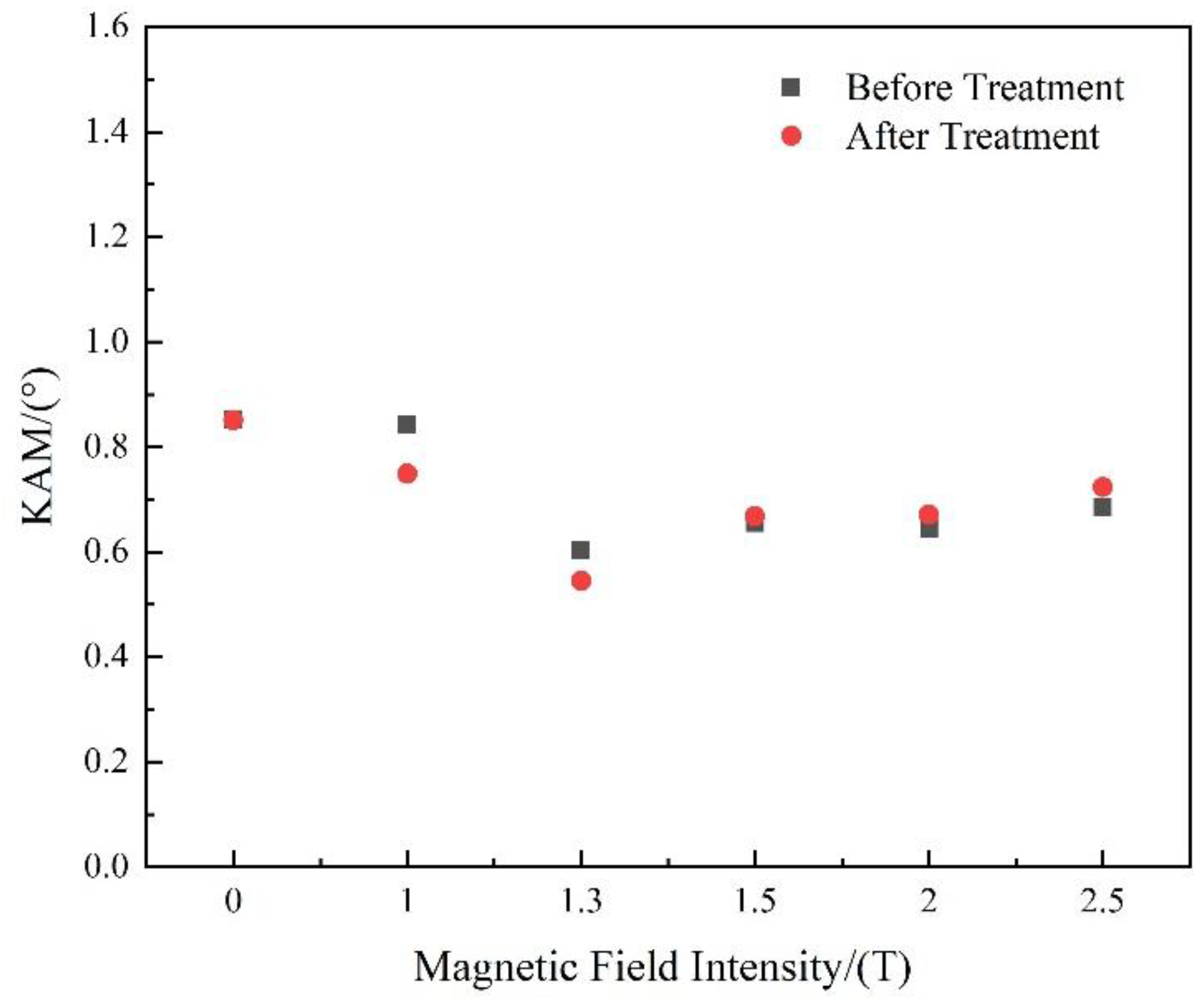
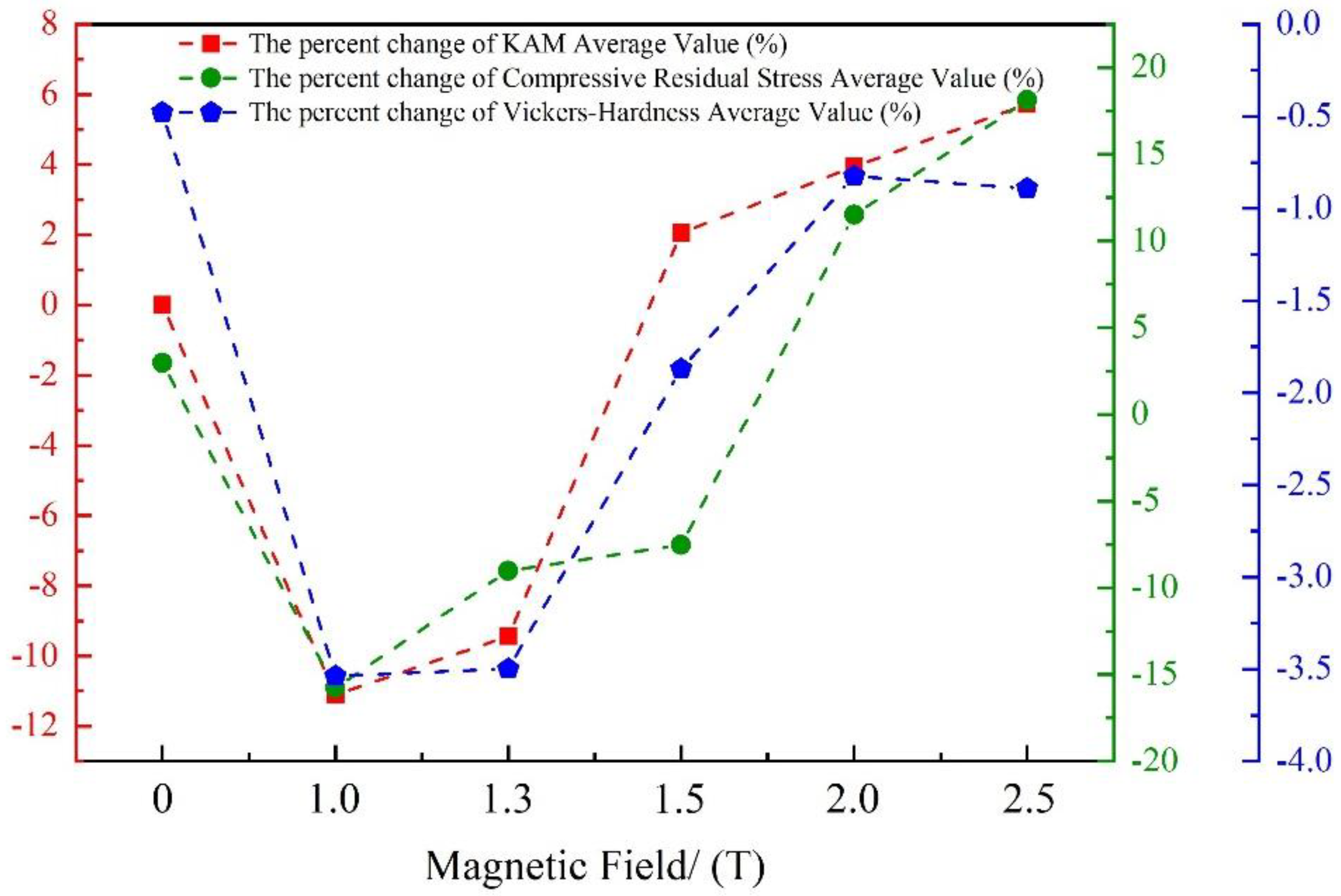
3.2. Dislocations
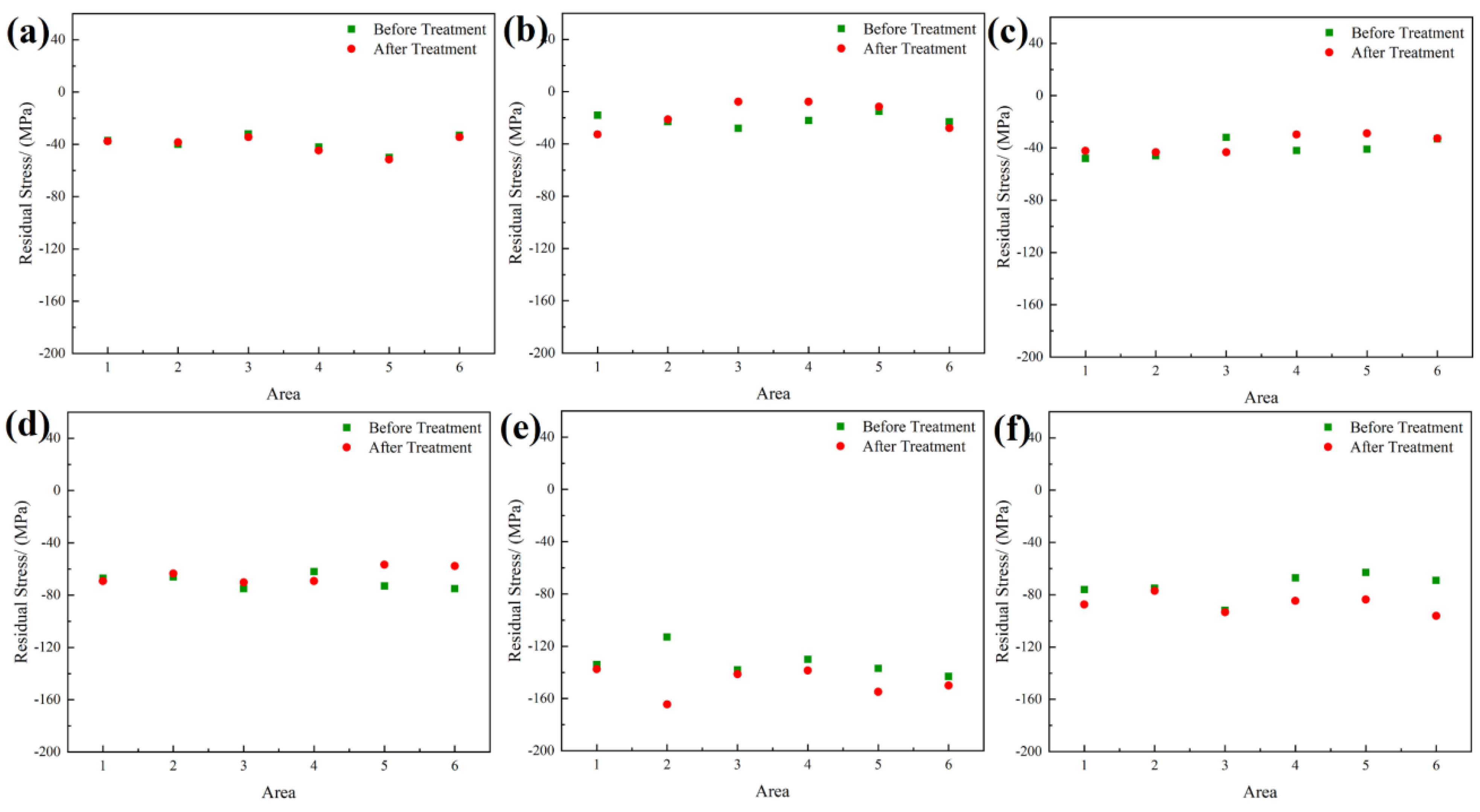
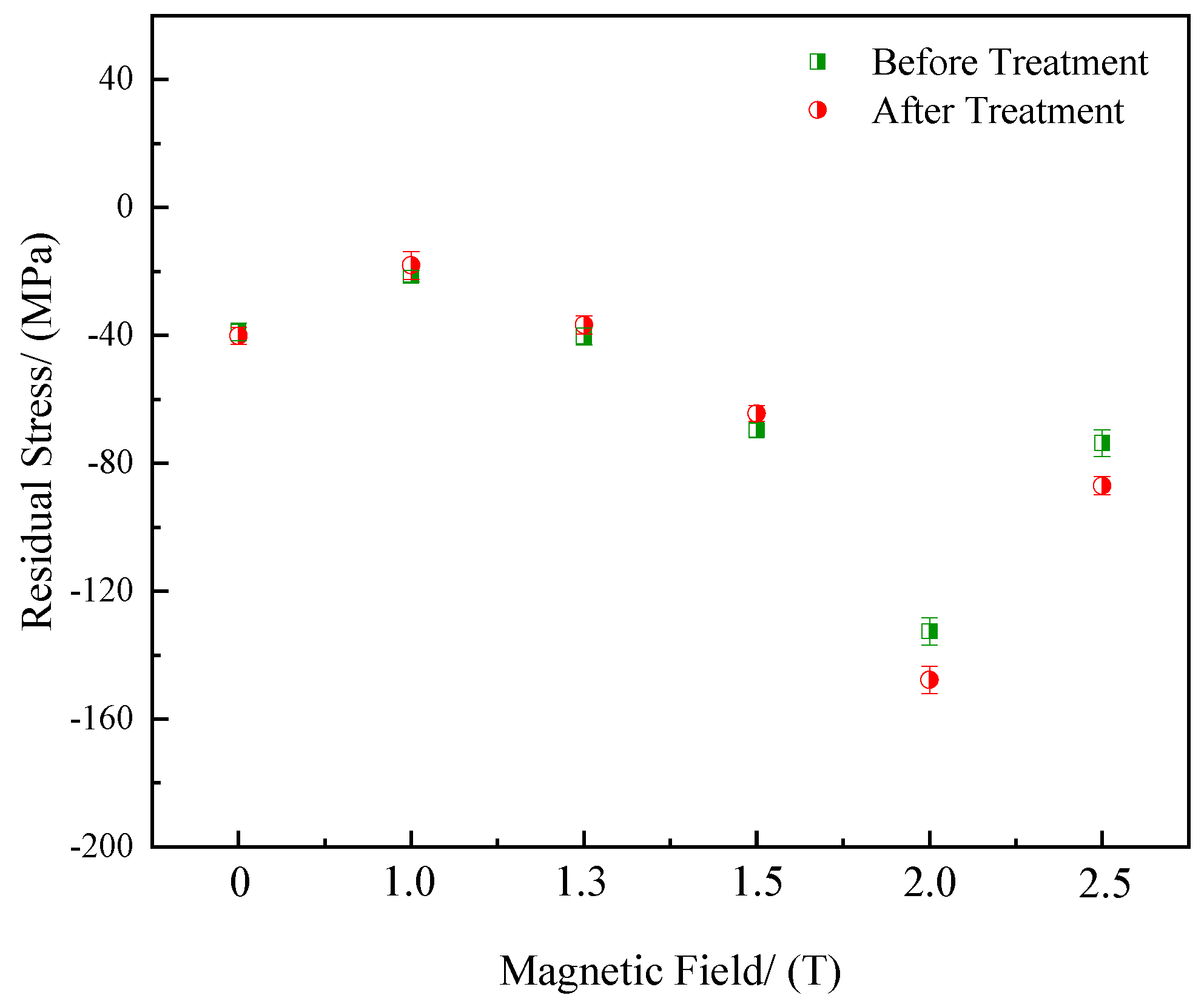
3.3. Residual Stress
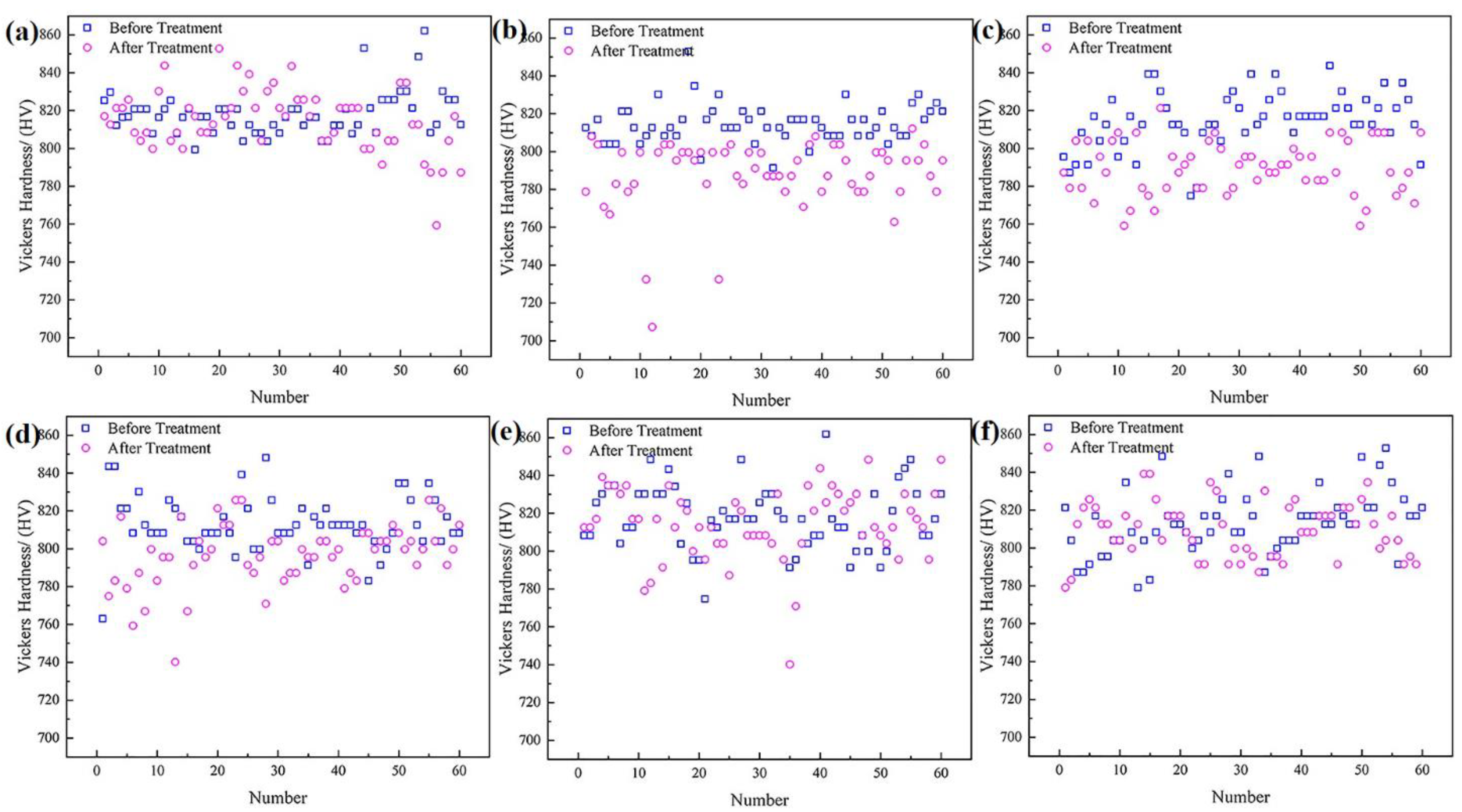
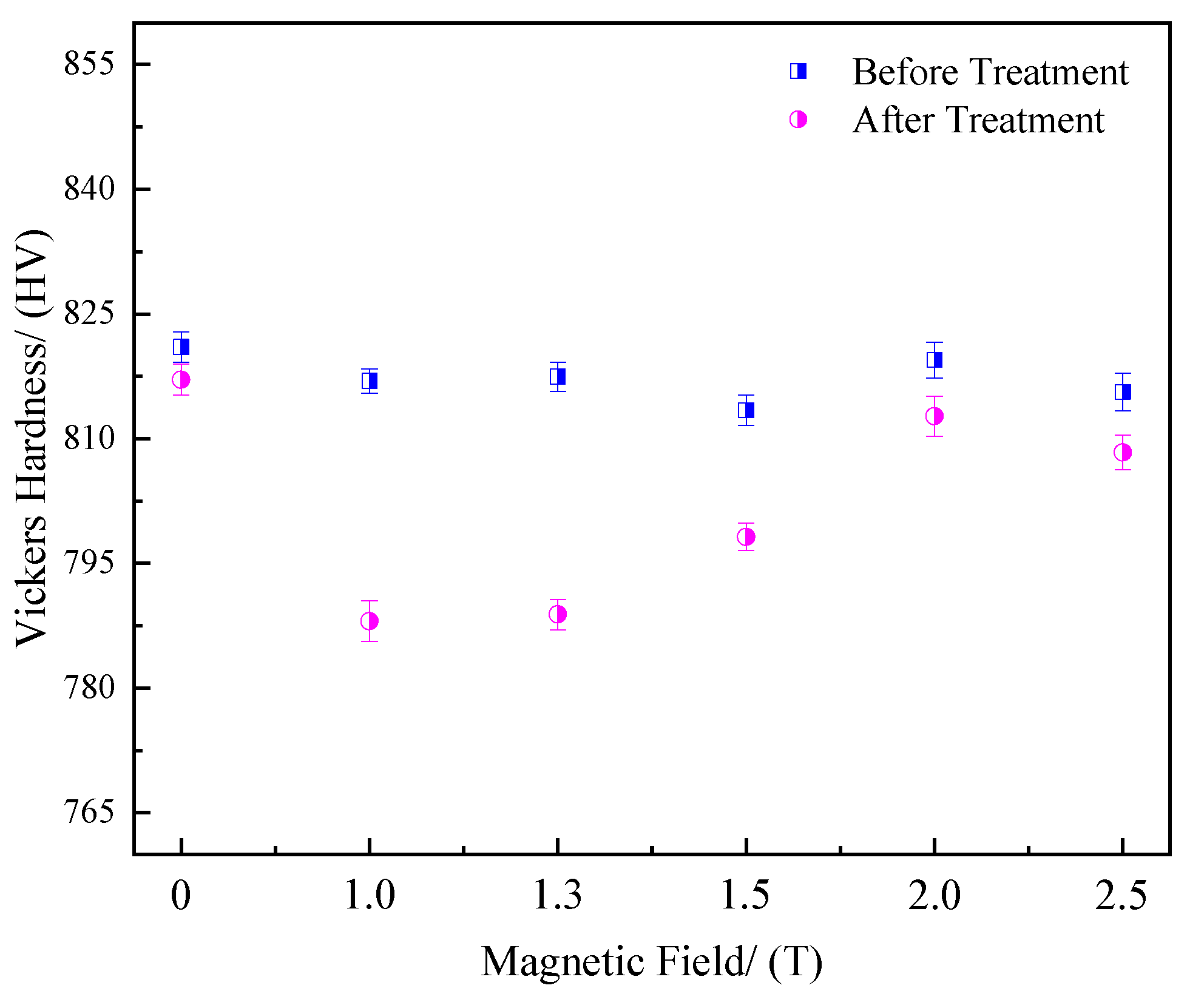
3.4. Vickers Hardness
4. Discussion
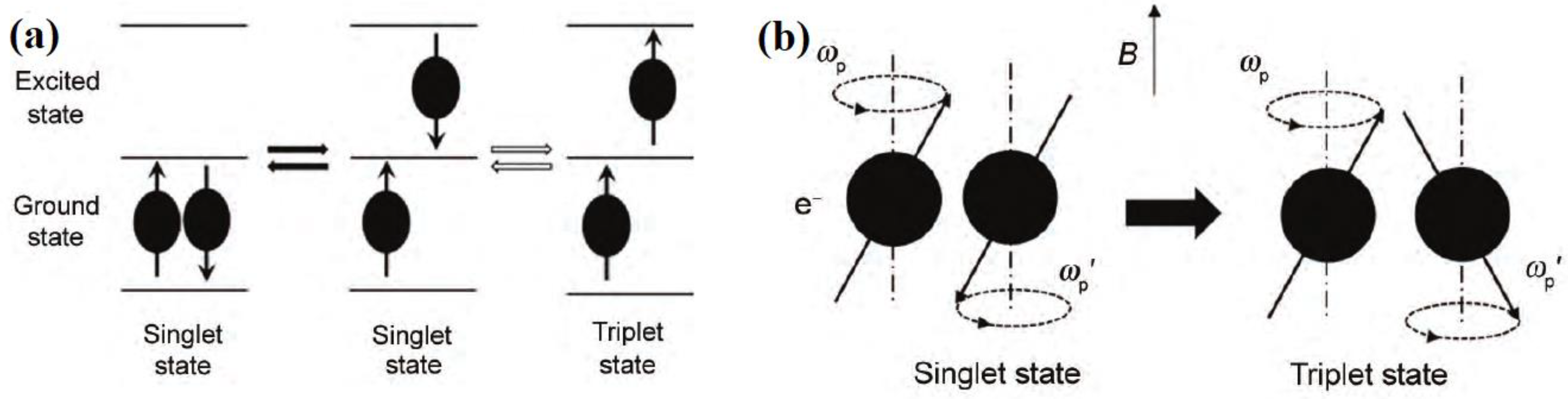
4.1. Mechanism of Dislocation Movement with Magnetic Treatment
4.2. Mechanism of Residual Stress Change
4.3. Mechanism of Hardness Change
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mukhopadhyay, P.; Kannaki, P.S.; Srinivas, M.; Roy, M. Microstructural developments during abrasion of M50 bearing steel. Wear 2014, 315, 31–37. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Steels for bearings. Prog. Mater. Sci. 2012, 57, 268–435. [Google Scholar] [CrossRef]
- Wang, F.; Qian, D.S.; Hua, L.; Lu, X.H. The effect of prior cold rolling on the carbide dissolution, precipitation and dry wear behaviors of M50 bearing steel. Tribol. Int. 2019, 132, 253–264. [Google Scholar] [CrossRef]
- Guan, J.; Wang, L.Q.; Mao, Y.Z.; Shi, X.J.; Ma, X.X.; Hu, B. A continuum damage mechanics based approach to damage evolution of M50 bearing steel considering residual stress induced by shot peening. Tribol. Int. 2018, 126, 218–228. [Google Scholar] [CrossRef]
- Allison, B.; Subhash, G.; Arakere, N.; Haluck, D.A.; Chin, H. Influence of initial residual stress on material properties of bearing steel during rolling contact fatigue. Tribol. Trans. 2014, 57, 533–545. [Google Scholar] [CrossRef]
- Dommarco, R.C.; Kozaczek, K.J.; Bastias, P.C.; Hahn, G.T.; Rubin, C.A. Residual stresses and retained austenite evolution in SAE 52100 steel under non-ideal rolling contact loading. Wear 2004, 257, 1081–1088. [Google Scholar] [CrossRef]
- Choi, Y. A study on the effects of machining-induced residual stress on rolling contact fatigue. Int. J. Fatigue 2009, 31, 1517–1523. [Google Scholar] [CrossRef]
- Guo, Y.B.; Barkey, M.E. Modeling of rolling contact fatigue for hard machined components with process-induced residual stress. Int. J. Fatigue 2004, 26, 605–613. [Google Scholar] [CrossRef]
- Shen, Y.; Moghadam, S.M.; Sadeghi, F.; Paulson, K.; Trice, R.W. Effect of retained austenite compressive residual stresses on rolling contact fatigue life of carburized AISI 8620 steel. Int. J. Fatigue 2015, 75, 135–144. [Google Scholar] [CrossRef]
- Shao, Q.; Kang, J.J.; Xing, Z.G.; Wang, H.D.; Huang, Y.F.; Ma, G.Z.; Liu, H.P. Effect of pulsed magnetic field treatment on the residual stress of 20Cr2Ni4A steel. J. Magn. Magn. Mater. 2019, 476, 218–224. [Google Scholar] [CrossRef]
- Cai, Z.P.; Lin, J.A.; Zhou, L.A.; Zhao, H.Y. Evaluation of effect of magnetostriction on residual stress relief by pulsed magnetic treatment. Mater. Sci. Technol. 2004, 20, 1563–1566. [Google Scholar] [CrossRef]
- Cai, Z.P.; Huang, X.Q. Residual stress reduction by combined treatment of pulsed magnetic field and pulsed current. Mater. Sci. Eng. A. 2011, 528, 6287–6292. [Google Scholar] [CrossRef]
- Fu, L.C.; Zhou, L.P. Effect of applied magnetic field on wear behavior of martensitic steel. J. Mater. Res. Technol. 2019, 28, 2880–2886. [Google Scholar] [CrossRef]
- Choi, K.J.; Yoo, S.C.; Ham, J.; Kim, J.H.; Jeong, S.Y.; Choi, Y.S. Fatigue behavior of AISI 8620 steel exposed to magnetic field. J. Alloy. Compd. 2018, 764, 73–79. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Gorley, M.; Kabra, S.; Surrey, E. Influence of a 1.5 T magnetic field on the tensile properties of Eurofer-97 steel. Fusion Eng. Des. 2019, 141, 68–72. [Google Scholar] [CrossRef]
- Paulmiera, D.; Zaidia, H.; Bedria, R.; Kadiri, E.K.; Pan, L.; Jiang, Q. Steel surface modifications in magnetised sliding contact. Surf. Coat. Technol. 1995, 76–77, 583–588. [Google Scholar] [CrossRef]
- Lu, B.T.; Qiao, S.R.; Sun, X.Y. Exploration on repairing fatigue damage of steel specimens with magnetic treatment. Scr. Mater. 1999, 40, 767–771. [Google Scholar]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Jiang, J.; Britton, T.B.; Wilkinson, A.J. Measurement of geometrically necessary dislocation density with high resolution electron backscatter diffraction: Effects of detector binning and step size. Ultramicroscopy 2013, 125, 1–9. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Harrington, T.; Gray, G.T., III; Vecchio, K.S. Dislocation-type evolution in quasi-statically compressed polycrystalline nickel. Acta Mater. 2018, 155, 104–116. [Google Scholar] [CrossRef]
- Rui, S.S.; Niu, L.S.; Shi, H.J.; Wei, S.L.; Tasan, C.C. Diffraction-based misorientation mapping: A continuum mechanics description. J. Mech. Phys. Solids 2019, 133, 103709. [Google Scholar] [CrossRef]
- Calcagnotto, M.; Ponge, D.; Demir, E.; Raabe, D. Orientation gradients and geometrically necessary dislocations in ultrafine grained dual-phase steels studied by 2D and 3D EBSD. Mater. Sci. Eng. A 2010, 527, 2738–2746. [Google Scholar] [CrossRef]
- Nye, J.F. Some geometrical relations in dislocated crystals Quelques relations géométriques dams des cristaux disloqués Einige geometrische beziehungen in verformten kristallen. Acta Metall. 1953, 1, 153–162. [Google Scholar] [CrossRef]
- Arsenlis, A.; Parks, D.M. Crystallographic aspects of geometrically-necessary and statistically-stored dislocation density. Acta Mater. 1999, 47, 1597–1611. [Google Scholar] [CrossRef]
- Gussev, M.N.; Leonard, K.J. In situ SEM-EBSD analysis of plastic deformation mechanisms in neutron-irradiated austenitic steel. J. Nucl. Mater. 2019, 517, 45–56. [Google Scholar] [CrossRef]
- Zaretsky, E.V. Rolling bearing steels-a technical and historical perspective. Mater. Sci. Technol. 2012, 28, 58–69. [Google Scholar] [CrossRef]
- Cui, W.; Martin, D.S.; Pedro, E.J. Towards efficient microstructural design and hardness prediction of bearing steels—An integrated experimental and numerical study. Mater. Des. 2017, 133, 464–475. [Google Scholar] [CrossRef]
- Bhaumik, S.; Molodova, X.; Molodov, D.A.; Gottstein, G. Magnetically enhanced recrystallization in an aluminum alloy. Scr. Mater. 2006, 55, 995–998. [Google Scholar] [CrossRef]
- Alshits, V.I.; Darinskaya, E.V.; Koldaeva, M.V.; Petrzhik, E.A. Magnetoplastic effect: Basic properties and physical mechanisms. Crystallogr. Rep. 2003, 48, 768–795. [Google Scholar] [CrossRef]
- Xu, Q.D.; Li, K.J.; Cai, Z.P.; Wu, Y. Effect of Pulsed Magnetic Field on the Microstructure of TC4 Titanium Alloy and Its Mechanism. Acta Metall. Sin. 2019, 55, 489–495. [Google Scholar]
- Molotskii, M.I.; Kris, R.E.; Fleurov, V. Internal friction of dislocations in a magnetic field. Phys. Rev. B 1995, 51, 12531–12536. [Google Scholar] [CrossRef] [PubMed]
- Golovin, Y.I. Study on the relationship between magneto-vibration and residual stress in steel materials. J. Mater. Sci. 2004, 39, 5129–5134. [Google Scholar] [CrossRef]
- Wang, F.E. Bonding Theory for Metals and Alloys; Elsevier: Amsterdam, The Netherlands, 2005; pp. 6–7. [Google Scholar]
- Zhang, X.; Zhao, Q.; Cai, Z.P.; Pan, J.L. Effects of Magnetic Field on the Residual Stress and Structural Defects of Ti-6Al-4V. Metals 2020, 10, 141. [Google Scholar] [CrossRef]
- Tang, G.Y.; Xu, Z.H.; Tang, M.; Chen, X.H.; Zhou, H.H.; Lu, A.L. Effect of a pulsed magnetic treatment on the dislocation substructure of a commercial high strength steel. Mater. Sci. Eng. A 2003, 48, 768–795. [Google Scholar] [CrossRef]
- Lin, J.; Zhao, H.Y.; Cai, Z.P.; Lei, Y.P. Study on the relationship between magneto-vibration and residual stress in steel materials. Acta Metall. Sin. 2008, 44, 451–456. [Google Scholar]
- Lu, A.L.; Tang, F.; Luo, X.J.; Mei, J.F.; Fang, H.Z. Research on residual-stress reduction by strong pulsed magnetic treatment. J. Mater. Process. Technol. 1998, 74, 259–262. [Google Scholar] [CrossRef]
- Vohringer, O. Relaxation of residual stresses by annealing or mechanical treatment. Adv. Surf. Treat. 1987, 4, 367–396. [Google Scholar]
- Prussin, S. Generation and Distribution of Dislocations by Solute Diffusion. J. Appl. Phys. 1961, 32, 1876–1881. [Google Scholar] [CrossRef]
- Dowling, N.E. Mechanical Behavior of Materials; Pearson Education: Boston, MA, USA, 2013; p. 118. [Google Scholar]
- Meyers, M.A.; Chawla, K.K. Mechanical Behavior of Materials; Cambridge University Press: Cambridge, UK, 2009; pp. 2–3. [Google Scholar]
- Blum, W.; Gotz, G. Evolution of dislocation structure in martensitic steels: The subgrain size as a sensor for creep strain and residual creep life. Mater. Technol. 1999, 70, 274–278. [Google Scholar] [CrossRef]


| Steel | Cr | Mo | V | C | Mn | Si | Ni | Cu | S | P |
|---|---|---|---|---|---|---|---|---|---|---|
| Cr4Mo4V steel | 4 | 4 | 1 | 0.72 | 0.30 | 0.20 | 0.10 | 0.05 | 0.01 | 0.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, M.; Li, K.; Li, X.; Zhang, X.; Rui, S.; Wu, Y.; Cai, Z. Effects of Pulsed Magnetic Fields of Different Intensities on Dislocation Density, Residual Stress, and Hardness of Cr4Mo4V Steel. Crystals 2020, 10, 115. https://doi.org/10.3390/cryst10020115
Hou M, Li K, Li X, Zhang X, Rui S, Wu Y, Cai Z. Effects of Pulsed Magnetic Fields of Different Intensities on Dislocation Density, Residual Stress, and Hardness of Cr4Mo4V Steel. Crystals. 2020; 10(2):115. https://doi.org/10.3390/cryst10020115
Chicago/Turabian StyleHou, Mingdong, Kejian Li, Xiaogang Li, Xu Zhang, Shaoshi Rui, Yao Wu, and Zhipeng Cai. 2020. "Effects of Pulsed Magnetic Fields of Different Intensities on Dislocation Density, Residual Stress, and Hardness of Cr4Mo4V Steel" Crystals 10, no. 2: 115. https://doi.org/10.3390/cryst10020115
APA StyleHou, M., Li, K., Li, X., Zhang, X., Rui, S., Wu, Y., & Cai, Z. (2020). Effects of Pulsed Magnetic Fields of Different Intensities on Dislocation Density, Residual Stress, and Hardness of Cr4Mo4V Steel. Crystals, 10(2), 115. https://doi.org/10.3390/cryst10020115






