Reaction Initiation in Enzyme Crystals by Diffusion of Substrate
Abstract
1. Introduction
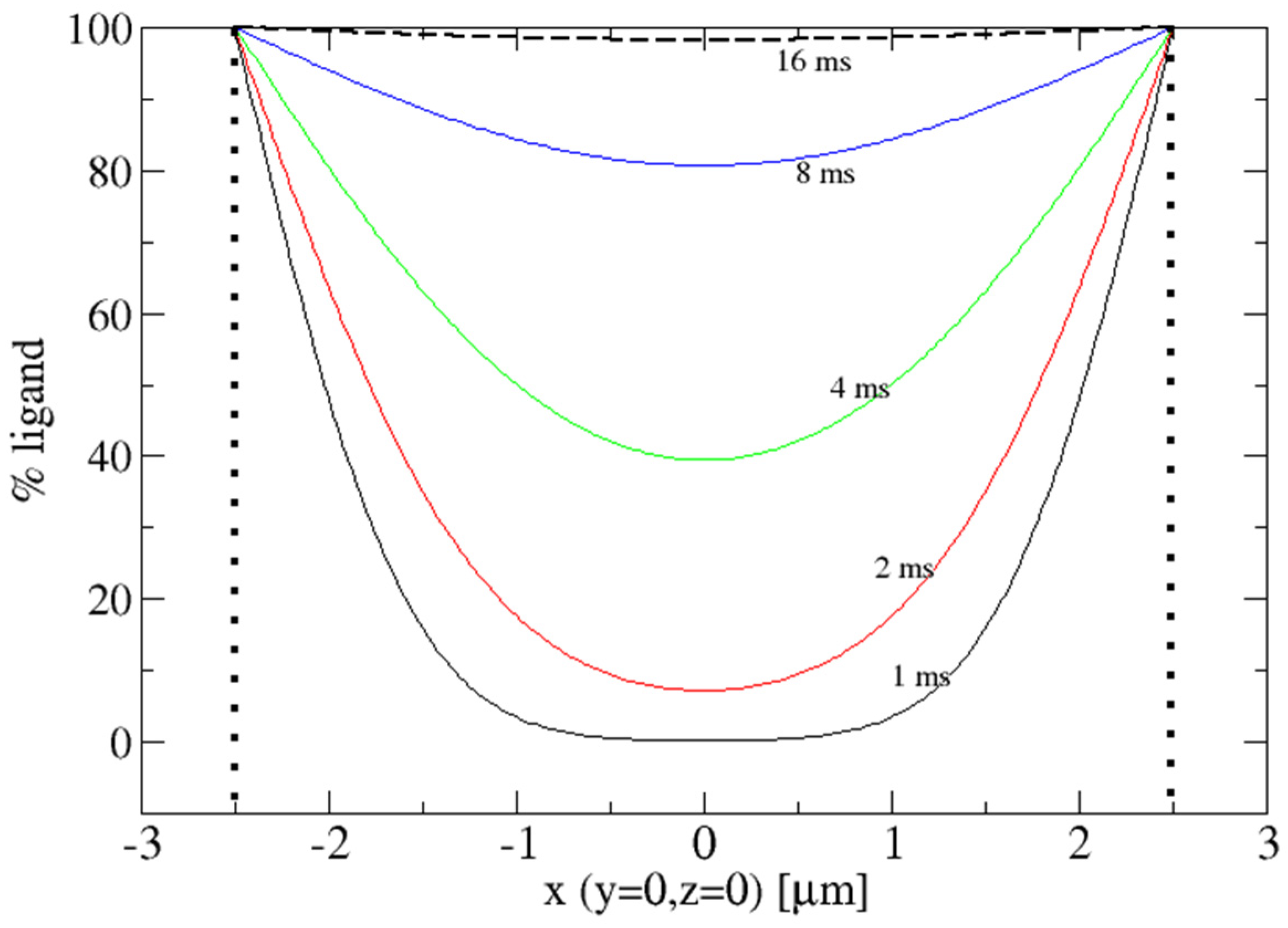
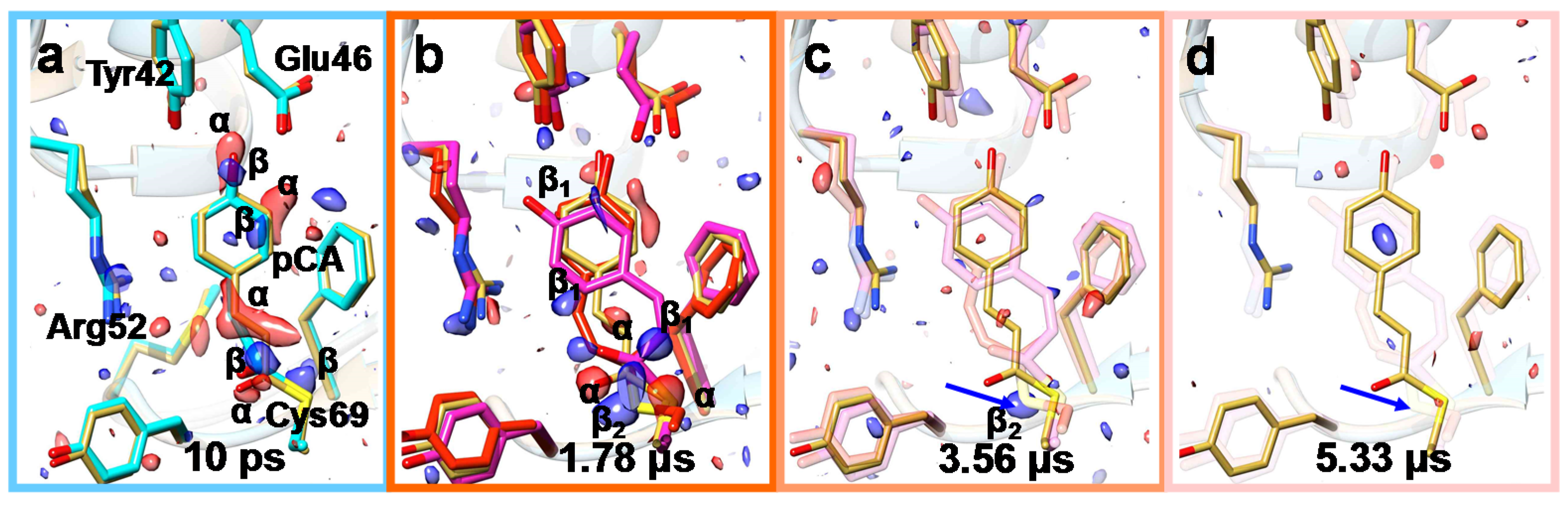
2. Diffusion into Protein Crystals
3. X-ray Light Sources and Techniques that Support Mixing Experiments
4. Mixing Techniques for Structure-Based Enzymology
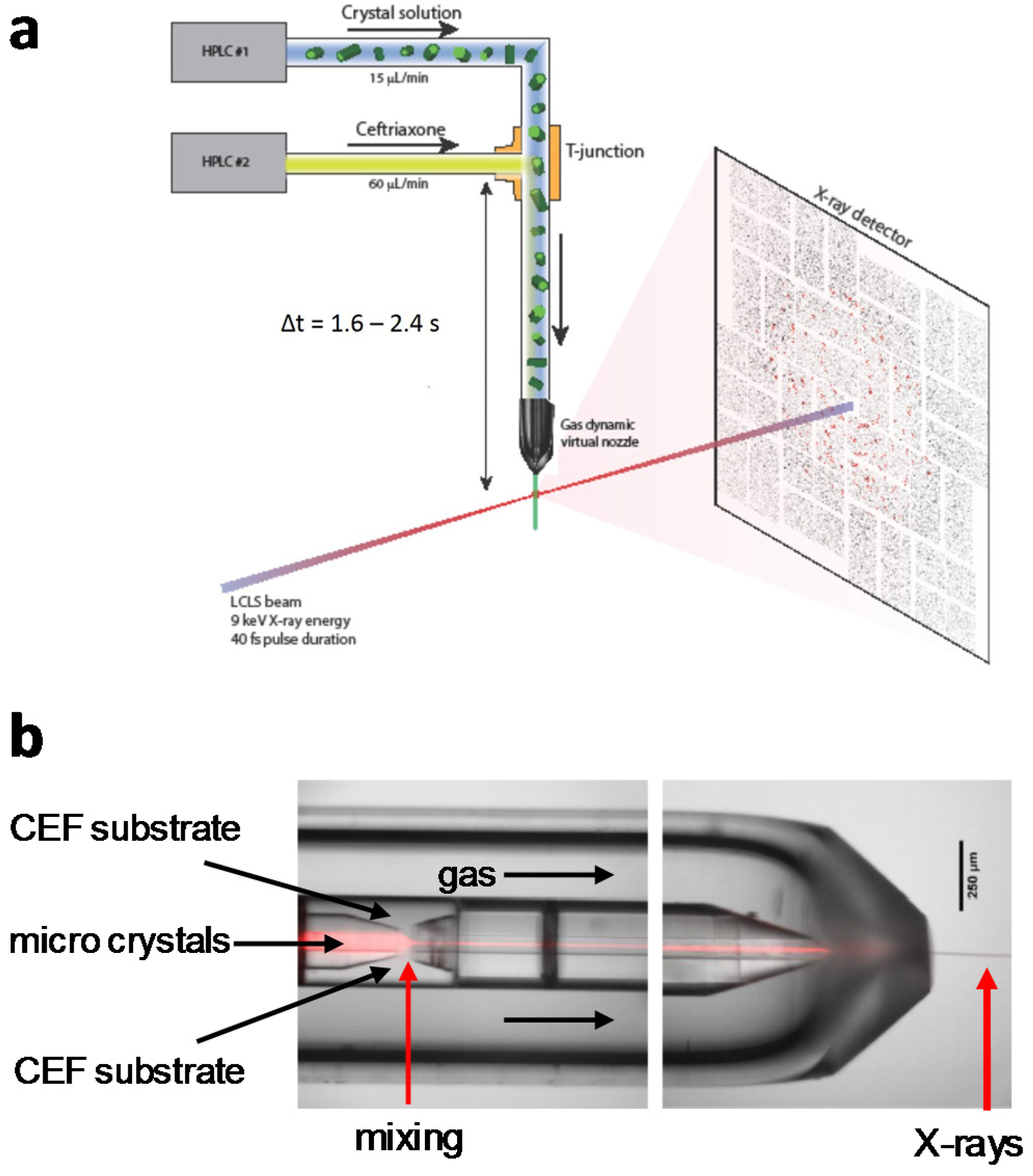
4.1. Jet Based Technique
4.2. Mixing on Fixed Targets
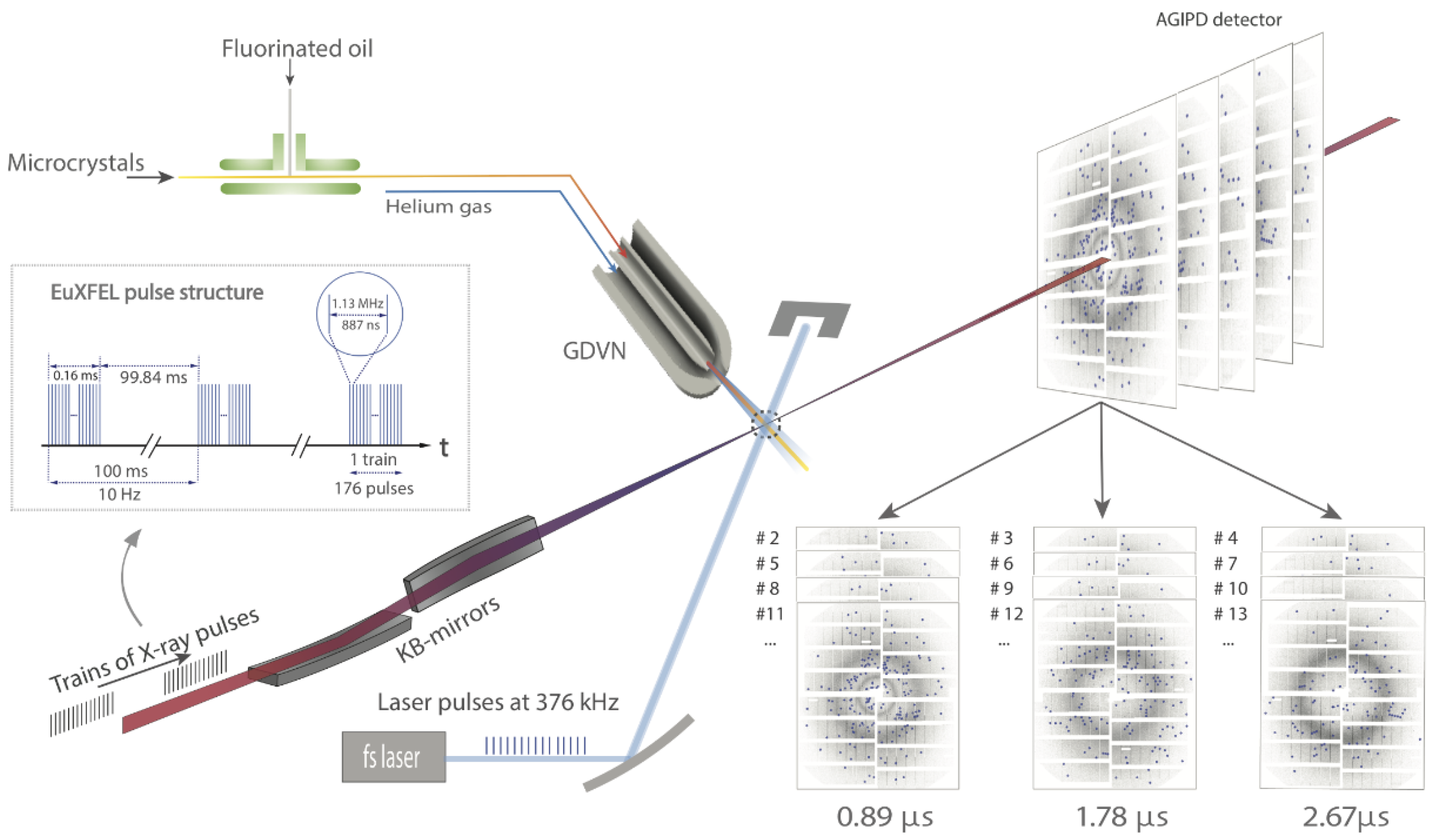
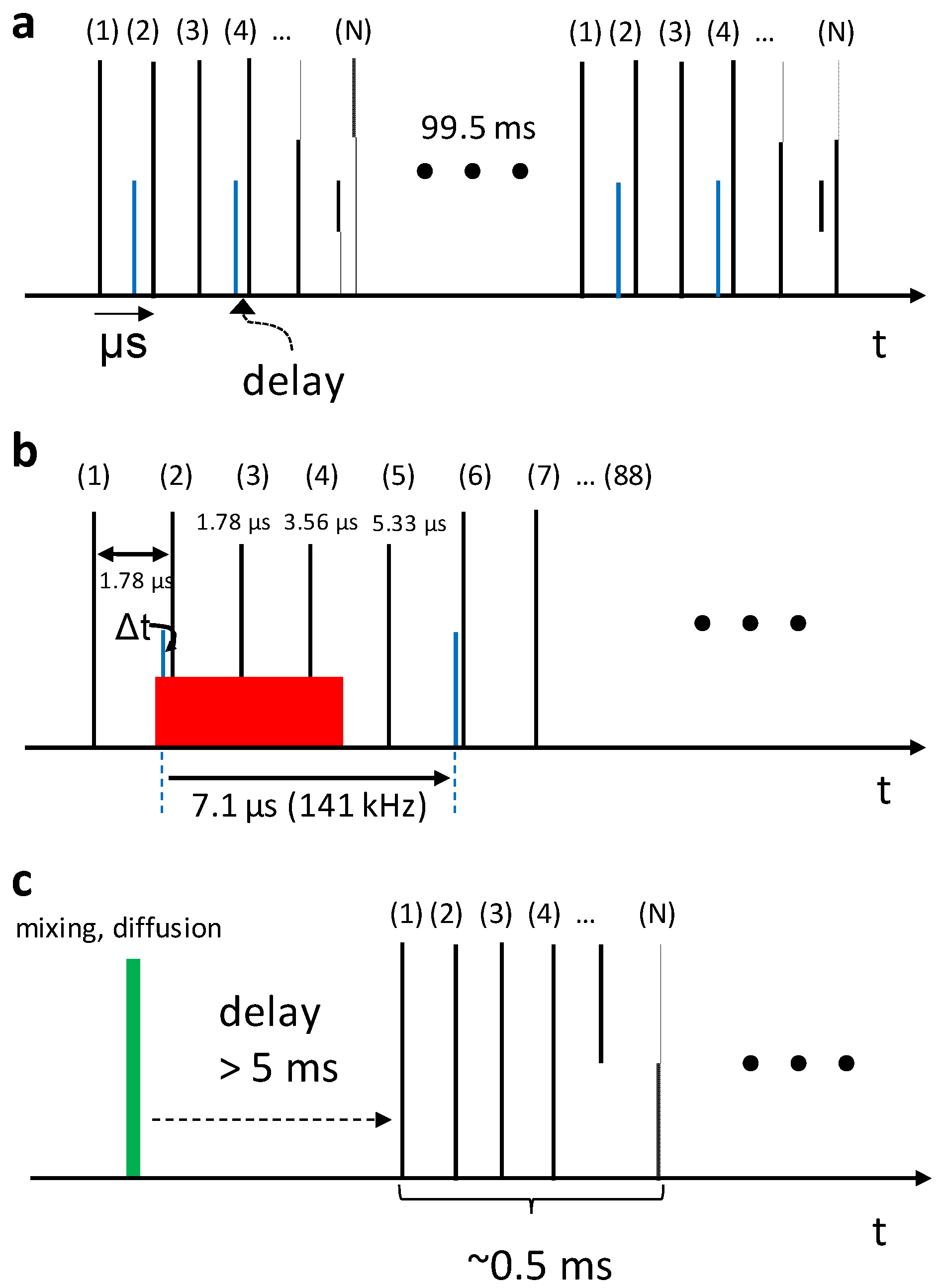
5. High Repetition Rate XFELs
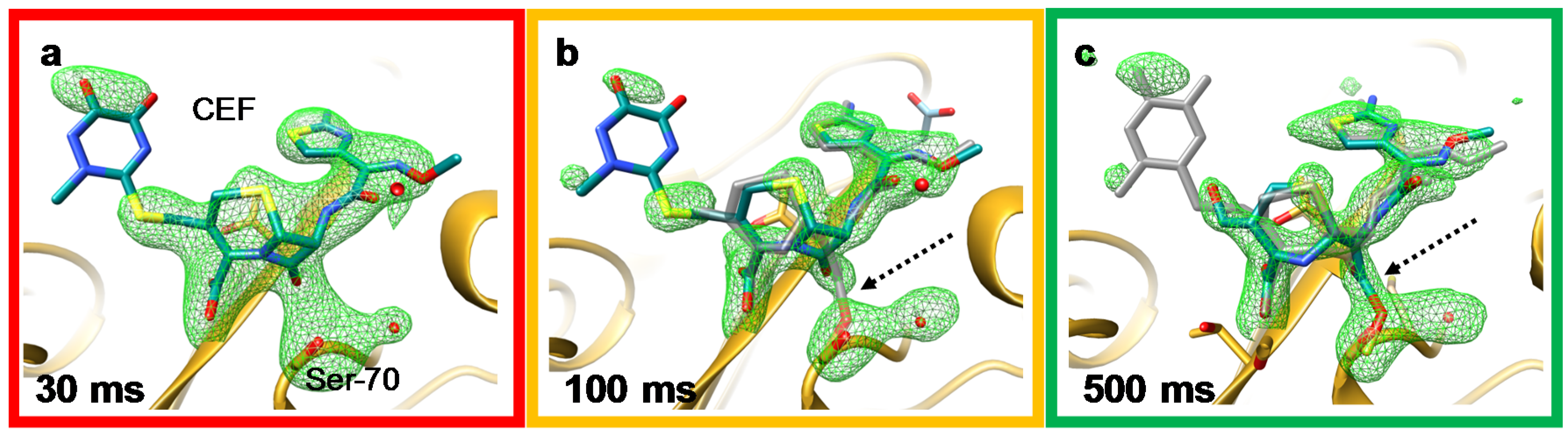
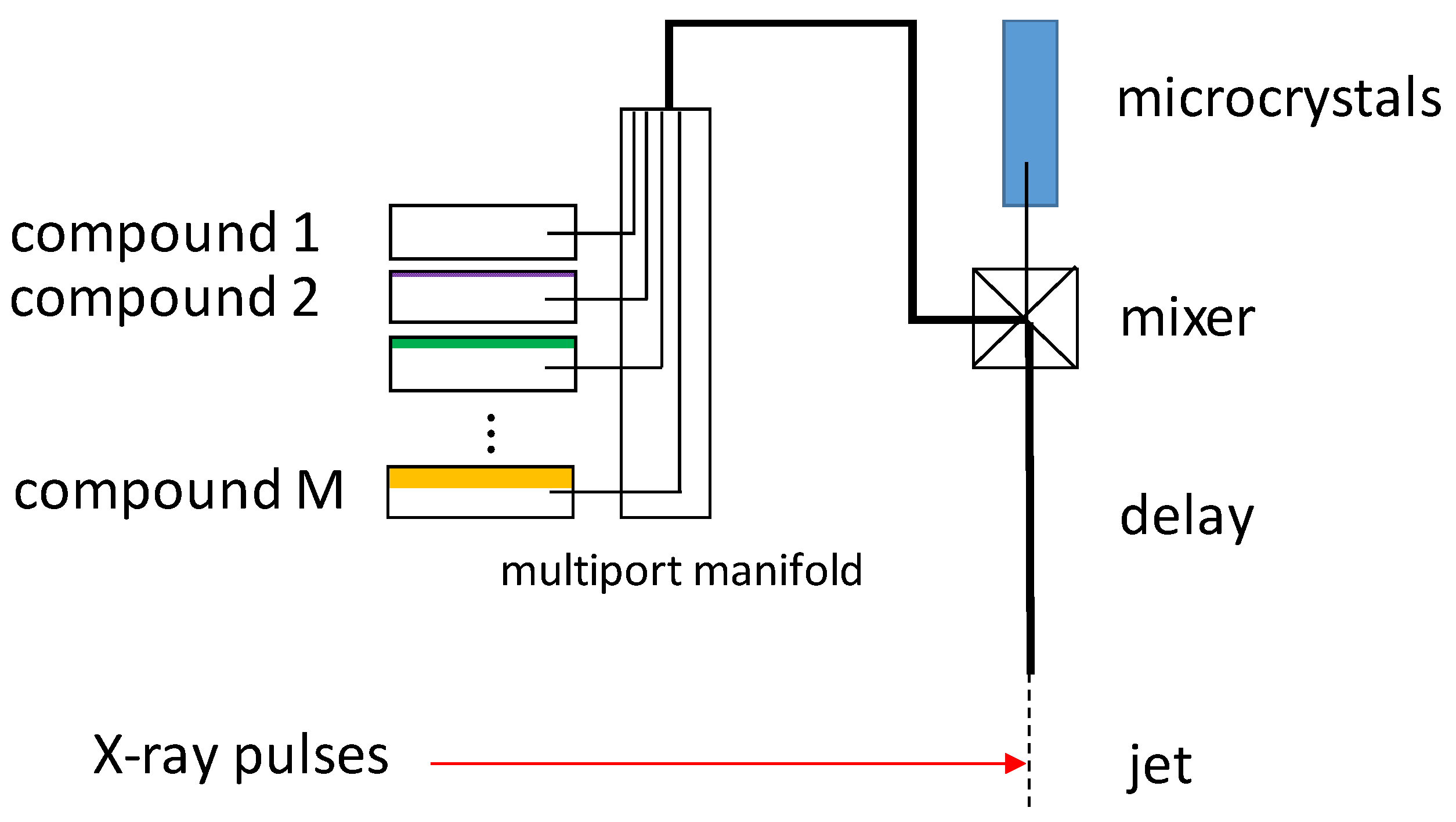
6. Mix-and-Inject Experiments at High Repetition Rate XFELs
Funding
Conflicts of Interest
References
- Rupp, B. Biomolecular Crystallography: Principles, Practice, and Application to Structural Biology; Garland Science: New York, NY, USA, 2009. [Google Scholar]
- McPherson, A. Crystallization of Biological Macromolecules; Cold Spring Harbor Laboratory Press: New York, NY, USA, 1999. [Google Scholar]
- Carugo, O.; Blatova, O.A.; Medrish, E.O.; Blatov, V.A.; Proserpio, D.M. Packing topology in crystals of proteins and small molecules: A comparison. Sci. Rep. 2017, 7, 13209. [Google Scholar] [CrossRef]
- Kendrew, J.C.; Bodo, G.; Dintzis, H.M.; Parrish, R.G.; Wyckoff, H.; Phillips, D.C. A three-dimensional model of the myoglobin molecule obtained by x-ray analysis. Nature 1958, 181, 662–666. [Google Scholar] [CrossRef]
- Blake, C.C.; Koenig, D.F.; Mair, G.A.; North, A.C.; Phillips, D.C.; Sarma, V.R. Structure of hen egg-white lysozyme. A three-dimensional Fourier synthesis at 2 Angstrom resolution. Nature 1965, 206, 757–761. [Google Scholar] [CrossRef]
- Sluyterman, L.A.; de Graaf, M.J. The activity of papain in the crystalline state. Biochim. Biophys. Acta 1969, 171, 277–287. [Google Scholar] [CrossRef]
- Hajdu, J.; Neutze, R.; Sjogren, T.; Edman, K.; Szoke, A.; Wilmouth, R.C.; Wilmot, C.M. Analyzing protein functions in four dimensions. Nat. Struct. Biol. 2000, 7, 1006–1012. [Google Scholar] [CrossRef]
- Schmidt, M. Mix and Inject, Reaction Initiation by Diffusion for Time-Resolved Macromolecular Crystallography. Adv. Condens. Matter Phys. 2013, 1–10. [Google Scholar] [CrossRef]
- Moffat, K.; Chen, Y.; Ng, K.M.; Mcree, D.; Getzoff, E.D. Time-Resolved Crystallography—Principles, Problems and Practice. Philos. Trans. R. Soc. A 1992, 340, 175–189. [Google Scholar]
- Schmidt, M. Structure Based Enzyme Kinetics by Time-Resolved X-Ray Crystallography, Ultrashort Laser Pulses in Medicine and Biology; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Olmos, J.L., Jr.; Pandey, S.; Martin-Garcia, J.M.; Calvey, G.; Katz, A.; Knoska, J.; Kupitz, C.; Hunter, M.S.; Liang, M.; Oberthuer, D.; et al. Enzyme intermediates captured “on the fly” by mix-and-inject serial crystallography. BMC Biol. 2018, 16, 59. [Google Scholar] [CrossRef]
- Parak, F.; Hartmann, H.; Schmidt, M.; Corongiu, G.; Clementi, E. The hydration shell of myoglobin. Eur. Biophys. J. EBJ 1992, 21, 313–320. [Google Scholar] [CrossRef]
- Schmidt, M.; Srajer, V.; Henning, R.; Ihee, H.; Purwar, N.; Tenboer, J.; Tripathi, S. Protein energy landscapes determined by five-dimensional crystallography. Acta Crystallogr. D Biol. Crystallogr. 2013, 69, 2534–2542. [Google Scholar] [CrossRef]
- Beale, J.H.; Bolton, R.; Marshall, S.A.; Beale, E.; Carr, S.B.; Ebrahim, A.; Moreno-Chicano, T.; Hough, M.A.; Worrall, J.A.R.; Tews, I.; et al. Successful sample preparation for serialcrystallography experiments. J. Appl. Cryst. 2019. [Google Scholar] [CrossRef]
- Geremia, S.; Campagnolo, M.; Demitri, N.; Johnson, L.N. Simulation of diffusion time of small molecules in protein crystals. Structure 2006, 14, 393–400. [Google Scholar] [CrossRef]
- Helliwell, J.R.; Nieh, Y.P.; Raftery, J.; Cassetta, A.; Habash, J.; Carr, P.D.; Ursby, T.; Wulff, M.; Thompson, A.W.; Niemann, A.C.; et al. Time-resolved structures of hydroxymethylbilane synthase (Lys59Gln mutant) as it is loaded with substrate in the crystal determined by Laue diffraction. J. Chem. Soc. Faraday Trans. 1998, 94, 2615–2622. [Google Scholar] [CrossRef]
- Stoddard, B.L.; Cohen, B.E.; Brubaker, M.; Mesecar, A.D.; Koshland, D.E., Jr. Millisecond Laue structures of an enzyme-product complex using photocaged substrate analogs. Nat. Struct. Biol. 1998, 5, 891–897. [Google Scholar] [CrossRef]
- Stoddard, B.L. New results using Laue diffraction and time-resolved crystallography. Curr. Opin. Struct. Biol. 1998, 8, 612–618. [Google Scholar] [CrossRef]
- Moffat, K.; Szebenyi, D.; Bilderback, D. X-ray Laue Diffraction from Protein Crystals. Science 1984, 223, 1423–1425. [Google Scholar] [CrossRef]
- Ren, Z.; Bourgeois, D.; Helliwell, J.R.; Moffat, K.; Srajer, V.; Stoddard, B.L. Laue crystallography: Coming of age. J. Synchrotron Radiat. 1999, 6, 891–917. [Google Scholar] [CrossRef]
- Martin-Garcia, J.M.; Conrad, C.E.; Nelson, G.; Stander, N.; Zatsepin, N.A.; Zook, J.; Zhu, L.; Geiger, J.; Chun, E.; Kissick, D.; et al. Serial millisecond crystallography of membrane and soluble protein microcrystals using synchrotron radiation. IUCrJ 2017, 4, 439–454. [Google Scholar] [CrossRef]
- Meents, A.; Wiedorn, M.O.; Srajer, V.; Henning, R.; Sarrou, I.; Bergtholdt, J.; Barthelmess, M.; Reinke, P.Y.A.; Dierksmeyer, D.; Tolstikova, A.; et al. Pink-beam serial crystallography. Nat. Commun. 2017, 8, 1281. [Google Scholar] [CrossRef]
- Kirian, R.A.; Wang, X.; Weierstall, U.; Schmidt, K.E.; Spence, J.C.; Hunter, M.; Fromme, P.; White, T.; Chapman, H.N.; Holton, J. Femtosecond protein nanocrystallography-data analysis methods. Opt. Express 2010, 18, 5713–5723. [Google Scholar] [CrossRef]
- Tenboer, J.; Basu, S.; Zatsepin, N.; Pande, K.; Milathianaki, D.; Frank, M.; Hunter, M.; Boutet, S.; Williams, G.J.; Koglin, J.E.; et al. Time-resolved serial crystallography captures high-resolution intermediates of photoactive yellow protein. Science 2014, 346, 1242–1246. [Google Scholar] [CrossRef] [PubMed]
- Boutet, S.; Lomb, L.; Williams, G.J.; Barends, T.R.; Aquila, A.; Doak, R.B.; Weierstall, U.; DePonte, D.P.; Steinbrener, J.; Shoeman, R.L.; et al. High-resolution protein structure determination by serial femtosecond crystallography. Science 2012, 337, 362–364. [Google Scholar] [CrossRef] [PubMed]
- Chapman, H.N.; Fromme, P.; Barty, A.; White, T.A.; Kirian, R.A.; Aquila, A.; Hunter, M.S.; Schulz, J.; DePonte, D.P.; Weierstall, U.; et al. Femtosecond X-ray protein nanocrystallography. Nature 2011, 470, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Lomb, L.; Barends, T.R.; Kassemeyer, S.; Aquila, A.; Epp, S.W.; Erk, B.; Foucar, L.; Hartmann, R.; Rudek, B.; Rolles, D.; et al. Radiation damage in protein serial femtosecond crystallography using an x-ray free-electron laser. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 214111. [Google Scholar] [CrossRef]
- Spence, J.C.; Hawkes, P.W. Diffract-and-destroy: Can X-ray lasers “solve“ the radiation damage problem? Ultramicroscopy 2008, 108, 1502–1503. [Google Scholar] [CrossRef]
- Neutze, R.; Wouts, R.; van der Spoel, D.; Weckert, E.; Hajdu, J. Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 2000, 406, 752–757. [Google Scholar] [CrossRef]
- Chapman, H.N.; Barty, A.; Bogan, M.J.; Boutet, S.; Frank, M.; Hau-Riege, S.P.; Marchesini, S.; Woods, B.W.; Bajt, S.; Benner, H.; et al. Femtosecond diffractive imaging with a soft-X-ray free-electron laser. Nat. Phys. 2006, 2, 839–843. [Google Scholar] [CrossRef]
- Chapman, H.N.; Caleman, C.; Timneanu, N. Diffraction before destruction. Philos. Trans. R. Soc. B 2014. [Google Scholar] [CrossRef]
- Aquila, A.; Hunter, M.S.; Doak, R.B.; Kirian, R.A.; Fromme, P.; White, T.A.; Andreasson, J.; Arnlund, D.; Bajt, S.; Barends, T.R.; et al. Time-resolved protein nanocrystallography using an X-ray free-electron laser. Opt. Express 2012, 20, 2706–2716. [Google Scholar] [CrossRef]
- DePonte, D.P.; Weierstall, U.; Schmidt, K.; Warner, J.; Starodub, D.; Spence, J.C.H.; Doak, R.B. Gas dynamic virtual nozzle for generation of microscopic droplet streams. J. Phys. D Appl. Phys. 2008, 41, 19. [Google Scholar] [CrossRef]
- Stellato, F.; Oberthuer, D.; Mengning, L.; Bean, R.; Gati, C.; Yefanov, O.; Barty, A.; Burkhardt, K. Room-temperature macromolecular serial crystallography using synchrotron radiation. IUCrJ 2014, 1, 204–212. [Google Scholar] [CrossRef] [PubMed]
- Nogly, P.; James, D.; Wang, D.; White, T.A.; Zatsepin, N.; Shilova, A.; Nelson, G.; Liu, H.; Johansson, L.; Heymann, M.; et al. Lipidic cubic phase serial millisecond crystallography using synchrotron radiation. IUCrJ 2015, 2, 168–176. [Google Scholar] [CrossRef] [PubMed]
- Tolstikova, A.; Levantino, M.; Yefanov, O.; Hennicke, V.; Fischer, P.; Meyer, J.; Mozzanica, A.; Redford, S.; Crosas, E.; Opara, N.L.; et al. 1 kHz fixed-target serial crystallography using a multilayer monochromator and an integrating pixel detector. IUCrJ 2019, 6, 927–937. [Google Scholar] [CrossRef]
- Coquelle, N.; Brewster, A.S.; Kapp, U.; Shilova, A.; Weinhausen, B.; Burghammer, M.; Colletier, J.P. Raster-scanning serial protein crystallography using micro- and nano-focused synchrotron beams. Acta Crystallogr. D Biol. Crystallogr. 2015, 71, 1184–1196. [Google Scholar] [CrossRef] [PubMed]
- Kupitz, C.; Olmos, J.L., Jr.; Holl, M.; Tremblay, L.; Pande, K.; Pandey, S.; Oberthur, D.; Hunter, M.; Liang, M.; Aquila, A.; et al. Structural enzymology using X-ray free electron lasers. Struct. Dyn. 2017, 4, 044003. [Google Scholar] [CrossRef] [PubMed]
- Stagno, J.R.; Liu, Y.; Bhandari, Y.R.; Conrad, C.E.; Panja, S.; Swain, M.; Fan, L.; Nelson, G.; Li, C.; Wendel, D.R.; et al. Structures of riboswitch RNA reaction states by mix-and-inject XFEL serial crystallography. Nature 2017, 541, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, M.; Budday, D.; de Oliveira, S.H.P.; Madzelan, P.; Marchany-Rivera, D.; Seravalli, J.; Hayes, B.; Sierra, R.G.; Boutet, S.; Hunter, M.S.; et al. Mix-and-inject XFEL crystallography reveals gated conformational dynamics during enzyme catalysis. Proc. Natl. Acad. Sci. USA 2019. [Google Scholar] [CrossRef]
- Mehrabi, P.; Schulz, E.C.; Agthe, M.; Horrell, S.; Bourenkov, G.; von Stetten, D.; Leimkohl, J.P.; Schikora, H.; Schneider, T.R.; Pearson, A.R.; et al. Liquid application method for time-resolved analyses by serial synchrotron crystallography. Nat. Methods 2019, 16, 979–982. [Google Scholar] [CrossRef]
- Roessler, C.G.; Agarwal, R.; Allaire, M.; Alonso-Mori, R.; Andi, B.; Bachega, J.F.; Bommer, M.; Brewster, A.S.; Browne, M.C.; Chatterjee, R.; et al. Acoustic Injectors for Drop-On-Demand Serial Femtosecond Crystallography. Structure 2016, 24, 631–640. [Google Scholar] [CrossRef]
- Beyerlein, K.R.; Dierksmeyer, D.; Mariani, V.; Kuhn, M.; Sarrou, I.; Ottaviano, A.; Awel, S.; Knoska, J.; Fuglerud, S.; Jonsson, O.; et al. Mix-and-diffuse serial synchrotron crystallography. IUCrJ 2017, 4, 769–777. [Google Scholar] [CrossRef]
- Calvey, G.D.; Katz, A.M.; Pollack, L. Microfluidic Mixing Injector Holder Enables Routine Structural Enzymology Measurements with Mix-and-Inject Serial Crystallography Using X-ray Free Electron Lasers. Anal. Chem. 2019, 91, 7139–7144. [Google Scholar] [CrossRef] [PubMed]
- Calvey, G.D.; Katz, A.M.; Schaffer, C.B.; Pollack, L. Mixing injector enables time-resolved crystallography with high hit rate at X-ray free electron lasers. Struct. Dyn. 2016, 3, 054301. [Google Scholar] [CrossRef] [PubMed]
- Ishigami, I.; Lewis-Ballester, A.; Echelmeier, A.; Brehm, G.; Zatsepin, N.A.; Grant, T.D.; Coe, J.D.; Lisova, S.; Nelson, G.; Zhang, S.; et al. Snapshot of an oxygen intermediate in the catalytic reaction of cytochrome c oxidase. Proc. Natl. Acad. Sci. USA 2019, 116, 3572–3577. [Google Scholar] [CrossRef] [PubMed]
- Sierra, R.G.; Gati, C.; Laksmono, H.; Dao, E.H.; Gul, S.; Fuller, F.; Kern, J.; Chatterjee, R.; Ibrahim, M.; Brewster, A.S.; et al. Concentric-flow electrokinetic injector enables serial crystallography of ribosome and photosystem II. Nat. Methods 2016, 13, 59–62. [Google Scholar] [CrossRef]
- Sherwood, A.V.; Henkin, T.M. Riboswitch-Mediated Gene Regulation: Novel RNA Architectures Dictate Gene Expression Responses. Annu. Rev. Microbiol. 2016, 70, 361–374. [Google Scholar] [CrossRef]
- Shelby, M.; Gilbile, D.; Grant, T.; Seuring, C.; Segelke, B.; He, W.; Evans, A.; Pakendorf, T.; Fischer, P.; Hunter, M.; et al. Fixed Target Delivery for Serial Femtosecond Crystallography of Weakly-Diffracting Objects. Protein Sci. 2019, 28, 109–110. [Google Scholar]
- Hunter, M.S.; Segelke, B.; Messerschmidt, M.; Williams, G.J.; Zatsepin, N.A.; Barty, A.; Benner, W.H.; Carlson, D.B.; Coleman, M.; Graf, A.; et al. Fixed-target protein serial microcrystallography with an x-ray free electron laser. Sci. Rep. 2014, 4, 6026. [Google Scholar] [CrossRef]
- Zarrine-Afsar, A.; Barends, T.R.M.; Muller, C.; Fuchs, M.R.; Lomb, L.; Schlichting, I.; Miller, R.J.D. Crystallography on a chip. Acta Crystallogr. D 2012, 68, 321–323. [Google Scholar] [CrossRef]
- Sui, S.; Wang, Y.X.; Kolewe, K.W.; Srajer, V.; Henning, R.; Schiffman, J.D.; Dimitrakopoulos, C.; Perry, S.L. Graphene-based microfluidics for serial crystallography. Lab A Chip 2016, 16, 3082–3096. [Google Scholar] [CrossRef]
- Kern, J.; Chatterjee, R.; Young, I.D.; Fuller, F.D.; Lassalle, L.; Ibrahim, M.; Gul, S.; Fransson, T.; Brewster, A.S.; Alonso-Mori, R.; et al. Structures of the intermediates of Kok’s photosynthetic water oxidation clock. Nature 2018, 563, 421–425. [Google Scholar] [CrossRef]
- Casadei, C.M.; Nass, K.; Barty, A.; Hunter, M.S.; Padeste, C.; Tsai, C.J.; Boutet, S.; Messerschmidt, M.; Sala, L.; Williams, G.J.; et al. Structure-factor amplitude reconstruction from serial femtosecond crystallography of two-dimensional membrane-protein crystals. IUCrJ 2019, 6, 34–45. [Google Scholar] [CrossRef] [PubMed]
- Li, C.F.; Li, X.X.; Kirian, R.; Spence, J.C.H.; Liu, H.G.; Zatsepin, N.A. SPIND: A reference-based auto-indexing algorithm for sparse serial crystallography data. IUCrJ 2019, 6, 72–84. [Google Scholar] [CrossRef] [PubMed]
- Schulz, E.C.; Mehrabi, P.; Muller-Werkmeister, H.M.; Tellkamp, F.; Jha, A.; Stuart, W.; Persch, E.; De Gasparo, R.; Diederich, F.; Pai, E.F.; et al. The hit-and-return system enables efficient time-resolved serial synchrotron crystallography. Nat. Methods 2018, 15, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Altarelli, M.; Mancuso, A.P. Structural biology at the European X-ray free-electron laser facility. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2014, 369, 20130311. [Google Scholar] [CrossRef]
- Mancuso, A. The Single Particles, Clusters and Biomolecules (SPB) Instrument at the European XFEL. Acta Crystallogr. A Found. Adv. 2013, 69, S143. [Google Scholar] [CrossRef]
- Galler, A.; Gawelda, W.; Biednov, M.; Bomer, C.; Britz, A.; Brockhauser, S.; Choi, T.K.; Diez, M.; Frankenberger, P.; French, M.; et al. Scientific instrument Femtosecond X-ray Experiments (FXE): Instrumentation and baseline experimental capabilities. J. Synchrotron Radiat. 2019, 26, 1432–1447. [Google Scholar] [CrossRef]
- Allahgholi, A.; Becker, J.; Delfs, A.; Dinapoli, R.; Goettlicher, P.; Greiffenberg, D.; Henrich, B.; Hirsemann, H.; Kuhn, M.; Klanner, R.; et al. The Adaptive Gain Integrating Pixel Detector at the European XFEL. J. Synchrotron Radiat. 2019, 26, 74–82. [Google Scholar] [CrossRef]
- Greiffenberg, D.; Collaboration, A. The AGIPD detector for the European XFEL. J. Instrum. 2012, 7. [Google Scholar] [CrossRef]
- Wiedorn, M.O.; Oberthur, D.; Bean, R.; Schubert, R.; Werner, N.; Abbey, B.; Aepfelbacher, M.; Adriano, L.; Allahgholi, A.; Al-Qudami, N.; et al. Megahertz serial crystallography. Nat. Commun. 2018, 9, 4025. [Google Scholar] [CrossRef]
- Yefanov, O.; Oberthur, D.; Bean, R.; Wiedorn, M.O.; Knoska, J.; Pena, G.; Awel, S.; Gumprecht, L.; Domaracky, M.; Sarrou, I.; et al. Evaluation of serial crystallographic structure determination within megahertz pulse trains. Struct. Dyn. 2019, 6, 064702. [Google Scholar] [CrossRef]
- Gisriel, C.; Coe, J.; Letrun, R.; Yefanov, O.M.; Luna-Chavez, C.; Stander, N.E.; Lisova, S.; Mariani, V.; Kuhn, M.; Aplin, S.; et al. Membrane protein megahertz crystallography at the European XFEL. Nat. Commun. 2019, 10, 5021. [Google Scholar] [CrossRef]
- Stan, C.A.; Milathianaki, D.; Laksmono, H.; Sierra, R.G.; McQueen, T.A.; Messerschmidt, M.; Williams, G.J.; Koglin, J.E.; Lane, T.J.; Hayes, M.J.; et al. Liquid explosions induced by X-ray laser pulses. Nat. Phys. 2016, 12, 966–971. [Google Scholar] [CrossRef]
- Grunbein, M.L.; Bielecki, J.; Gorel, A.; Stricker, M.; Bean, R.; Cammarata, M.; Dorner, K.; Frohlich, L.; Hartmann, E.; Hauf, S.; et al. Megahertz data collection from protein microcrystals at an X-ray free-electron laser. Nat. Commun. 2018, 9, 3487. [Google Scholar] [CrossRef]
- Pandey, S.; Bean, R.; Sato, T.; Poudyal, I.; Bielecki, J.; Cruz Villarreal, J.; Yefanov, O.; Mariani, V.; White, T.A.; Kupitz, C.; et al. Time-resolved serial femtosecond crystallography at the European XFEL. Nat. Methods 2019. [Google Scholar] [CrossRef]
- Palmer, G.; Kellert, M.; Wang, J.X.; Emons, M.; Wegner, U.; Kane, D.; Pallas, F.; Jezynski, T.; Venkatesan, S.; Rompotis, D.; et al. Pump-probe laser system at the FXE and SPB/SFX instruments of the European X-ray Free-Electron Laser Facility. J. Synchrotron Radiat. 2019, 26, 328–332. [Google Scholar] [CrossRef]
- Mancuso, A.P.; Aquila, A.; Batchelor, L.; Bean, R.J.; Bielecki, J.; Borchers, G.; Doerner, K.; Giewekemeyer, K.; Graceffa, R.; Kelsey, O.D.; et al. The Single Particles, Clusters and Biomolecules andSerial Femtosecond Crystallography instrument ofthe European XFEL: Initial installation. J. Synchrotron Radiat. 2019, 26, 660–676. [Google Scholar] [CrossRef]
- Pande, K.; Hutchison, C.D.M.; Groenhof, G.; Aquila, A.; Robinson, J.S.; Tenboer, J.; Basu, S.; Boutet, S.; Deponte, D.; Liang, M.; et al. Femtosecond Structural Dynamics Drives the Trans/Cis Isomerization in Photoactive Yellow Protein. Science 2016, 352, 725–729. [Google Scholar] [CrossRef]
- Jung, Y.O.; Lee, J.H.; Kim, J.; Schmidt, M.; Moffat, K.; Srajer, V.; Ihee, H. Volume-conserving trans-cis isomerization pathways in photoactive yellow protein visualized by picosecond X-ray crystallography. Nat. Chem. 2013, 5, 212–220. [Google Scholar] [CrossRef]
- Schotte, F.; Cho, H.S.; Kaila, V.R.; Kamikubo, H.; Dashdorj, N.; Henry, E.R.; Graber, T.J.; Henning, R.; Wulff, M.; Hummer, G.; et al. Watching a signaling protein function in real time via 100-ps time-resolved Laue crystallography. Proc. Natl. Acad. Sci. USA 2012, 109, 19256–19261. [Google Scholar] [CrossRef]
- Schmidt, M. Time-Resolved Macromolecular Crystallography at Pulsed X-ray Sources. Int. J. Mol. Sci. 2019, 20, 1401. [Google Scholar] [CrossRef]
- Thomas, S.E.; Collins, P.; James, R.H.; Mendes, V.; Charoensutthivarakul, S.; Radoux, C.; Abell, C.; Coyne, A.G.; Floto, R.A.; von Delft, F.; et al. Structure-guided fragment-based drug discovery at the synchrotron: Screening binding sites and correlations with hotspot mapping. Philos Trans. A Math. Phys. Eng. Sci. 2019, 377, 20180422. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, M. Reaction Initiation in Enzyme Crystals by Diffusion of Substrate. Crystals 2020, 10, 116. https://doi.org/10.3390/cryst10020116
Schmidt M. Reaction Initiation in Enzyme Crystals by Diffusion of Substrate. Crystals. 2020; 10(2):116. https://doi.org/10.3390/cryst10020116
Chicago/Turabian StyleSchmidt, Marius. 2020. "Reaction Initiation in Enzyme Crystals by Diffusion of Substrate" Crystals 10, no. 2: 116. https://doi.org/10.3390/cryst10020116
APA StyleSchmidt, M. (2020). Reaction Initiation in Enzyme Crystals by Diffusion of Substrate. Crystals, 10(2), 116. https://doi.org/10.3390/cryst10020116




