Detector Tilt Considerations in Bragg Coherent Diffraction Imaging: A Simulation Study
Abstract
1. Introduction
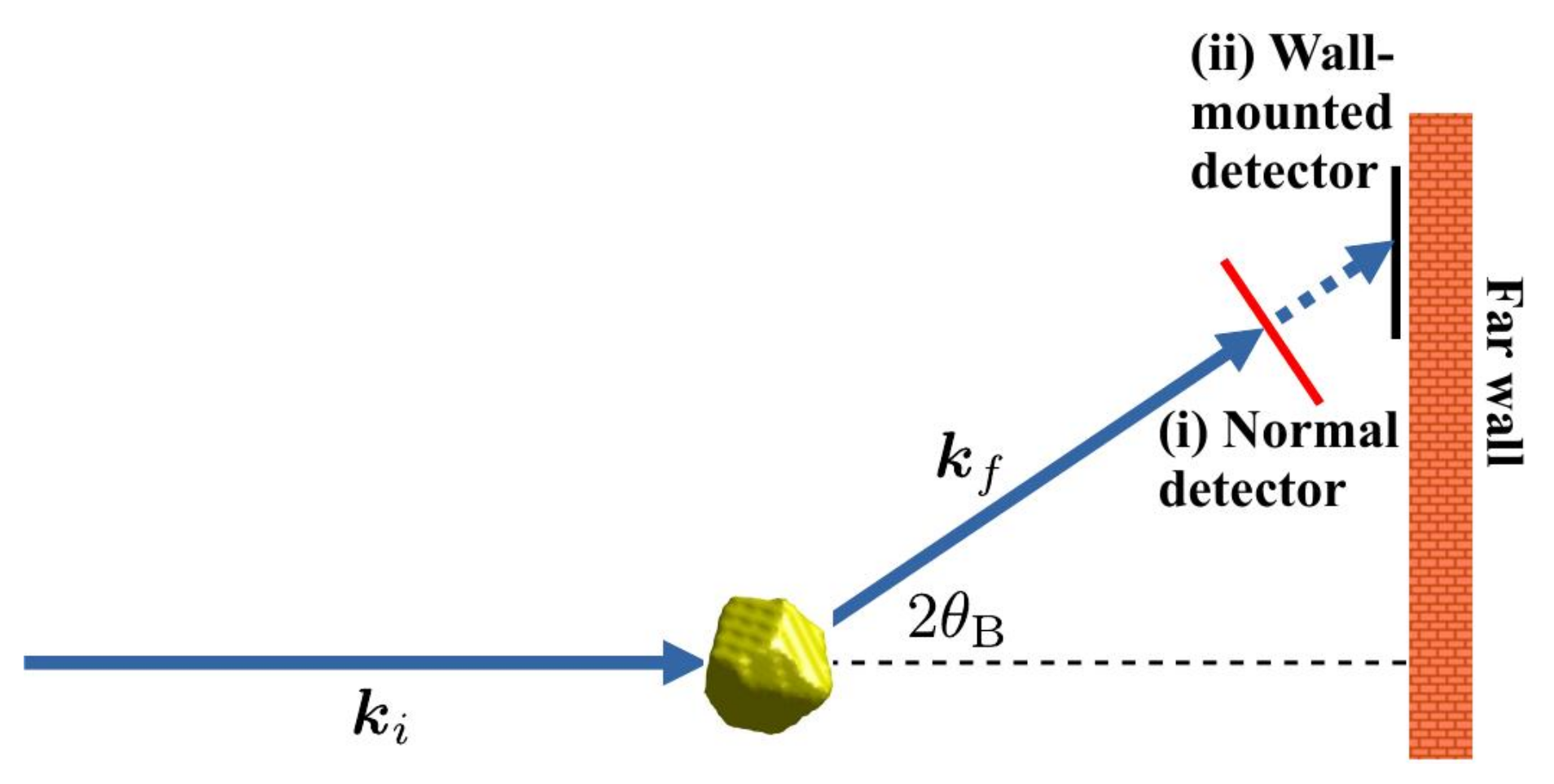
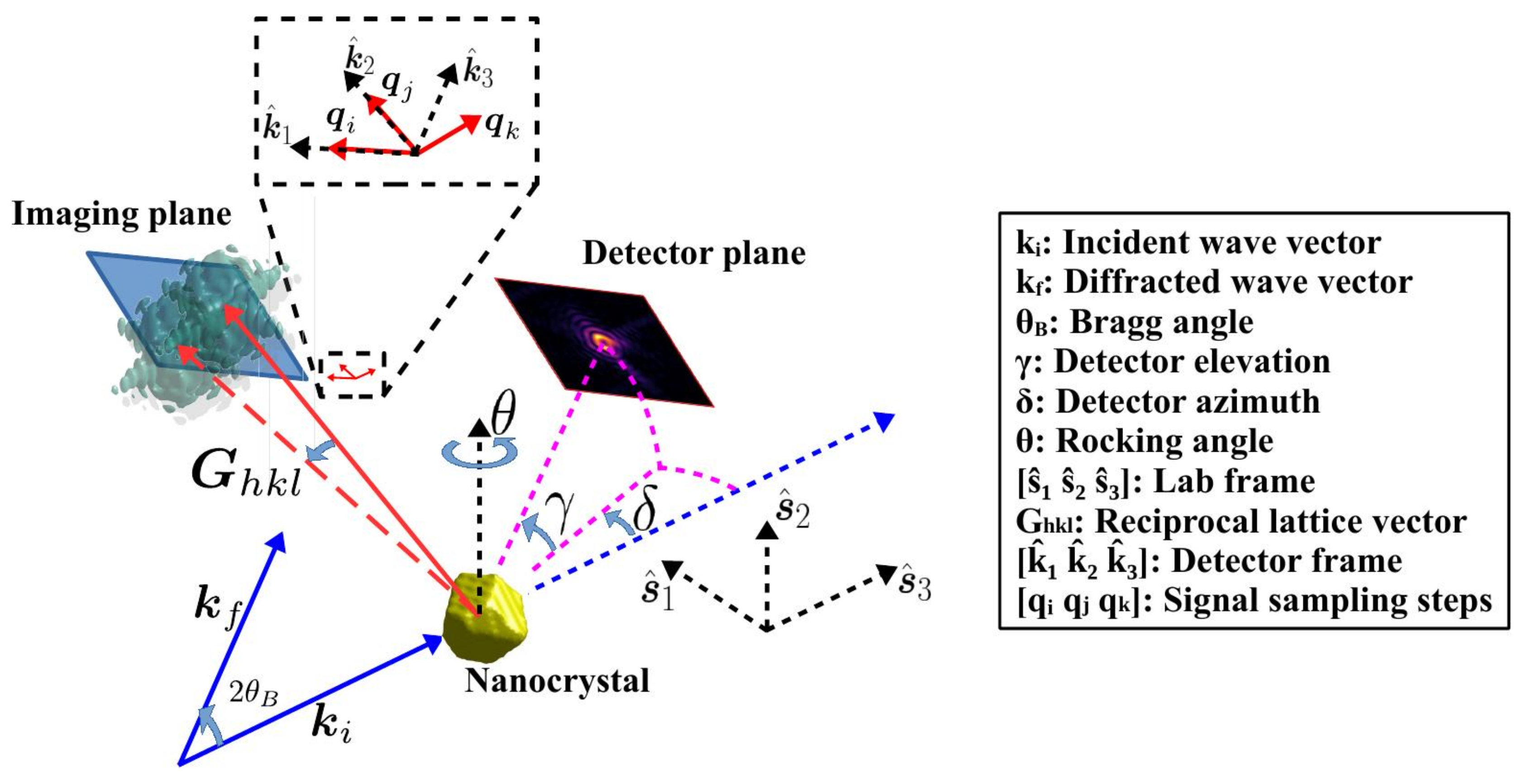
- The scattering geometry with the incident and diffracted wave vectors and , respectively, along with the scattering angle . is the reciprocal lattice vector corresponding to the active Bragg reflection. Here, in the crystallographers’ convention, where is the wavelength of the nominally monochromatic X-rays. Their respective directions are given by those of the incident and diffracted beams.
- The orthonormal laboratory frame .
- The orthonormal frame , where and span the plane normal to the exit beam (the “imaging plane”). The direction is perpendicular to the imaging plane along the nominal exit beam direction. This is identical to the frame from [23].
- The rocking angle , in this case about , but in general about any direction permissible by the experimental arrangement.
- Most importantly, the discrete sampling steps in Fourier space corresponding to the detector pixels, represented as the columns of a matrix: . Here, and are the reciprocal-space steps defined by the pixel dimensions along and . The incremental migration of the 3D diffraction signal through the imaging plane by virtue of the rotation is denoted in this convention by and is independent of the detector pixel dimensions.
2. A Tilted Detector
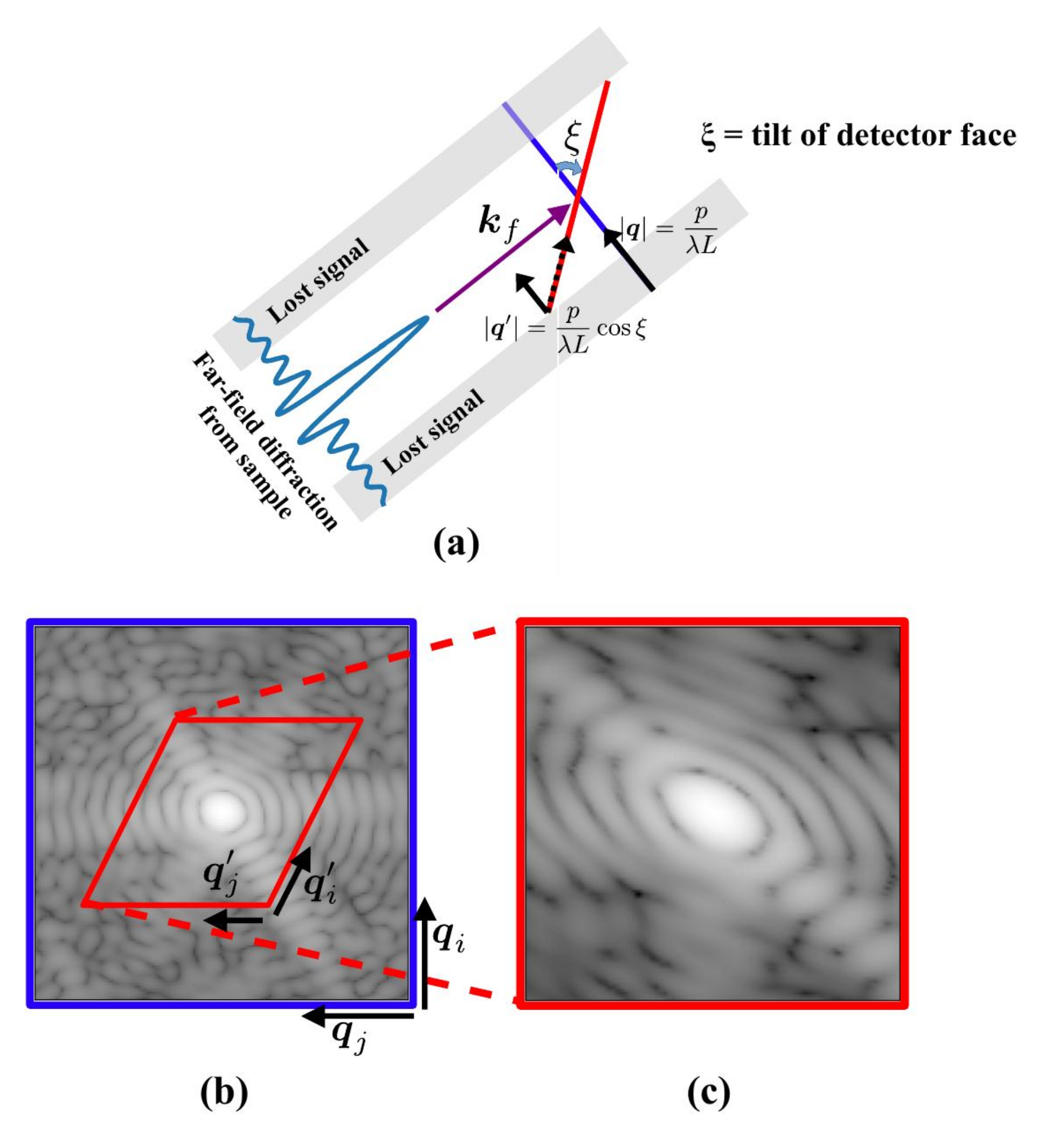
- The third sampling vector is not modified by the tilt of the detector, since it depends only on the Bragg reflection of interest and the direction of scatterer rocking.
- The information of the detector tilt is introduced into and not through the projection operator , but the now out-of-plane vectors and .
- As seen in Figure 3c, a tilted detector results in the measurements of a distorted diffraction pattern , which in turn corresponds to the distorted wave field . Here, denotes the wave field resulting from the in-plane distortion, while the complex exponential phase ramp parameterized by a constant vector denotes the distribution of the phase lag in the interrogated wave field relative to the phase profile at the imaging plane. This additional linearly varying phase clearly does not influence the measured signal and is therefore not considered from here on, assuming the measurements are in fact made in the far-field regime.
3. Simulation Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BCDI | Bragg coherent diffraction imaging |
| ESRF-EBS | European Synchrotron Radiation Facility—Extremely Brilliant Source |
| APS-U | Advanced Photon Source—Upgraded |
| FFT | Fast Fourier transform |
| IFFT | Inverse Fourier transform |
| SNR | Signal-to-noise ratio |
Appendix A. Simulating Diffraction with a Tilted Detector through Fourier Space Resampling
- A rotation by an angle about an axis in the imaging plane followed by…
- A rotation by an angle about the exit beam direction.
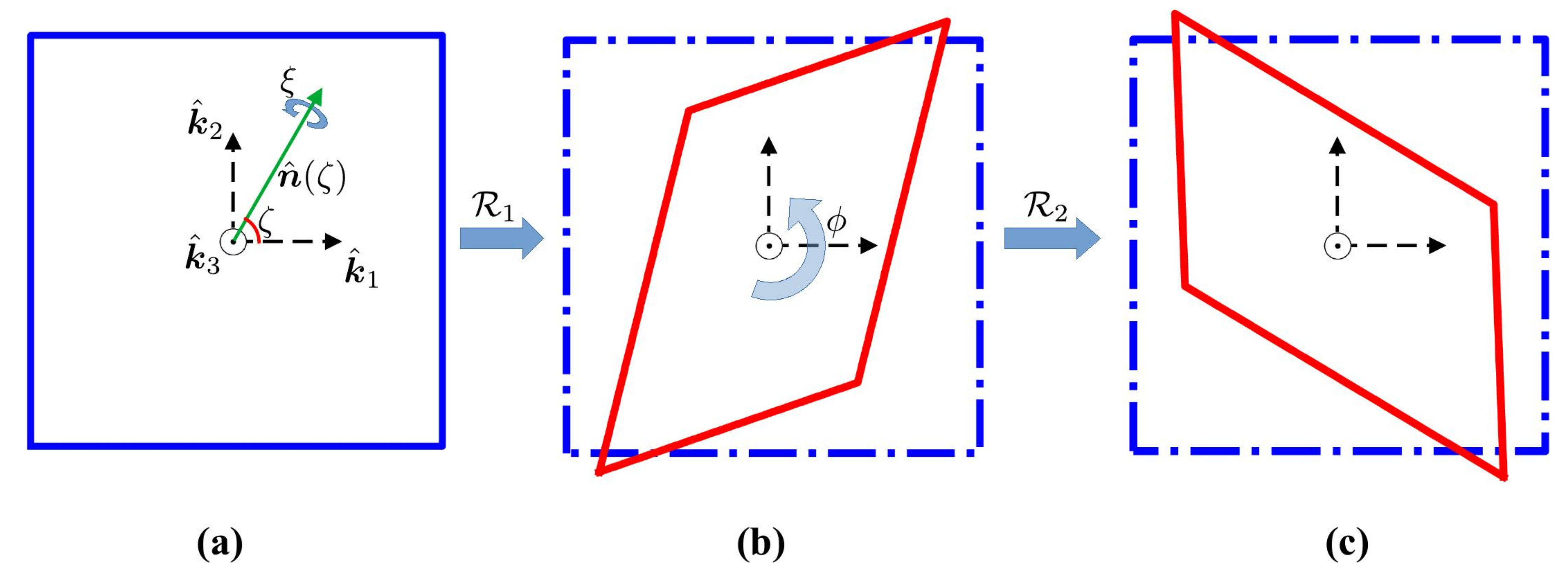
- The signal sampling shear in the imaging plane is computed using Equation (A8).
- The Fourier-space incremental step due to sample rocking is sheared in its first two dimensions by: .
- The scatterer is re-sampled in its first two dimensions by: .
| Parameter | Value | Description |
|---|---|---|
| E | 9 keV | Beam energy |
| Å | Wavelength | |
| Angular increment | ||
| L | m | Object detector distance |
| Detector alignment (elevation) | ||
| Detector alignment (azimuth) | ||
| p | m | Pixel size |
| Pixel array dimensions |
References
- Robinson, I.K.; Vartanyants, I.A.; Williams, G.J.; Pfeifer, M.A.; Pitney, J.A. Reconstruction of the Shapes of Gold Nanocrystals Using Coherent X-ray Diffraction. Phys. Rev. Lett. 2001, 87, 195505. [Google Scholar] [CrossRef]
- Williams, G.; Pfeifer, M.; Vartanyants, I.; Robinson, I. Three-dimensional imaging of microstructure in Au nanocrystals. Phys. Rev. Lett. 2003, 90, 175501. [Google Scholar] [CrossRef] [PubMed]
- Pfeifer, M.A.; Williams, G.J.; Vartanyants, I.A.; Harder, R.; Robinson, I.K. Three-dimensional mapping of a deformation field inside a nanocrystal. Nature 2006, 442, 63–66. [Google Scholar] [CrossRef] [PubMed]
- Williams, G.; Pfeifer, M.; Vartanyants, I.; Robinson, I. Internal structure in small Au crystals resolved by three-dimensional inversion of coherent X-ray diffraction. Phys. Rev. B 2006, 73, 094112. [Google Scholar] [CrossRef]
- Newton, M.C.; Leake, S.J.; Harder, R.; Robinson, I.K. Three-dimensional imaging of strain in a single ZnO nanorod. Nat. Mater. 2010, 9, 120–124. [Google Scholar] [CrossRef]
- Harder, R.; Liang, M.; Sun, Y.; Xia, Y.; Robinson, I. Imaging of complex density in silver nanocubes by coherent X-ray diffraction. New J. Phys. 2010, 12, 035019. [Google Scholar] [CrossRef]
- Newton, M.C.; Harder, R.; Huang, X.; Xiong, G.; Robinson, I.K. Phase retrieval of diffraction from highly strained crystals. Phys. Rev. B 2010, 82, 165436. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef]
- Fienup, J.R.; Wackerman, C.C. Phase-retrieval stagnation problems and solutions. J. Opt. Soc. Am. A 1986, 3, 1897–1907. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, B.; Morrison, G.R.; Vila-Comamala, J.; Guizar-Sicairos, M.; Robinson, I.K. Phase retrieval by coherent modulation imaging. Nat. Commun. 2016, 7, 1–8. [Google Scholar] [CrossRef]
- Guizar-Sicairos, M.; Fienup, J.R. Phase retrieval with transverse translation diversity: A nonlinear optimization approach. Opt. Express 2008, 16, 7264–7278. [Google Scholar] [CrossRef]
- Godard, P.; Carbone, G.; Allain, M.; Mastropietro, F.; Chen, G.; Capello, L.; Diaz, A.; Metzger, T.H.; Stangl, J.; Chamard, V. Three-dimensional high-resolution quantitative microscopy of extended crystals. Nat. Commun. 2011, 2, 1–6. [Google Scholar] [CrossRef]
- Hruszkewycz, S.; Holt, M.; Murray, C.; Bruley, J.; Holt, J.; Tripathi, A.; Shpyrko, O.; McNulty, I.; Highland, M.; Fuoss, P. Quantitative nanoscale imaging of lattice distortions in epitaxial semiconductor heterostructures using nanofocused X-ray Bragg projection ptychography. Nano Lett. 2012, 12, 5148–5154. [Google Scholar] [CrossRef]
- Pateras, A. Three Dimensional X-ray Bragg Ptychography of an Extended Semiconductor Heterostructure. Ph.D. Thesis, Aix Marseille University, Marseille, France, 2015. [Google Scholar]
- Hruszkewycz, S.O.; Allain, M.; Holt, M.V.; Murray, C.E.; Holt, J.R.; Fuoss, P.H.; Chamard, V. High-resolution three-dimensional structural microscopy by single-angle Bragg ptychography. Nat. Mater. 2017, 16, 244–251. [Google Scholar] [CrossRef]
- Hill, M.O.; Calvo-Almazan, I.; Allain, M.; Holt, M.V.; Ulvestad, A.; Treu, J.; Koblmuller, G.; Huang, C.; Huang, X.; Yan, H.; et al. Measuring Three-Dimensional Strain and Structural Defects in a Single InGaAs Nanowire Using Coherent X-ray Multiangle Bragg Projection Ptychography. Nano Lett. 2018, 18, 811–819. [Google Scholar] [CrossRef]
- Karpov, D.; Liu, Z.; Rolo, T.d.S.; Harder, R.; Balachandran, P.V.; Xue, D.; Lookman, T.; Fohtung, E. Three-dimensional imaging of vortex structure in a ferroelectric nanoparticle driven by an electric field. Nat. Commun. 2017, 8, 280. [Google Scholar] [CrossRef]
- Labat, S.; Richard, M.I.; Dupraz, M.; Gailhanou, M.; Beutier, G.; Verdier, M.; Mastropietro, F.; Cornelius, T.W.; Schülli, T.U.; Eymery, J.; et al. Inversion Domain Boundaries in GaN Wires Revealed by Coherent Bragg Imaging. ACS Nano 2015, 9, 9210–9216. [Google Scholar] [CrossRef]
- Ulvestad, A.; Singer, A.; Clark, J.; Cho, J.; Kim, J.W.; Harder, R.; Maser, J.; Meng, S.; Shpyrko, O. Topological Defect Dynamics in Operando Battery Nanoparticles. Science 2015, 348, 1344–1347. [Google Scholar] [CrossRef]
- Ulvestad, A.; Welland, M.J.; Cha, W.; Liu, Y.; Kim, J.W.; Harder, R.; Maxey, E.; Clark, J.N.; Highland, M.J.; You, H.; et al. Three-dimensional imaging of dislocation dynamics during the hydriding phase transformation. Nat. Mater. 2017, 16, 565–571. [Google Scholar] [CrossRef]
- Singer, A.; Zhang, M.; Hy, S.; Cela, D.; Fang, C.; Wynn, T.A.; Qiu, B.; Xia, Y.; Liu, Z.; Ulvestad, A.; et al. Nucleation of dislocations and their dynamics in layered oxide cathode materials during battery charging. Nat. Energy 2018, 3, 641–647. [Google Scholar] [CrossRef]
- Maddali, S.; Park, J.S.; Sharma, H.; Shastri, S.; Kenesei, P.; Almer, J.; Harder, R.; Highland, M.J.; Nashed, Y.; Hruszkewycz, S.O. High-Energy Coherent X-Ray Diffraction Microscopy of Polycrystal Grains: Steps toward a Multiscale Approach. Phys. Rev. Appl. 2020, 14, 024085. [Google Scholar] [CrossRef]
- Maddali, S.; Li, P.; Pateras, A.; Timbie, D.; Delegan, N.; Crook, A.L.; Lee, H.; Calvo-Almazan, I.; Sheyfer, D.; Cha, W.; et al. General approaches for shear-correcting coordinate transformations in Bragg coherent diffraction imaging. Part I. J. Appl. Crystallogr. 2020, 53. [Google Scholar] [CrossRef]
- Li, P.; Maddali, S.; Pateras, A.; Calvo-Almazan, I.; Hruszkewycz, S.; Cha, W.; Chamard, V.; Allain, M. General approaches for shear-correcting coordinate transformations in Bragg coherent diffraction imaging. Part II. J. Appl. Crystallogr. 2020, 53. [Google Scholar] [CrossRef]
- Kriegner, D.; Wintersberger, E.; Stangl, J. xrayutilities: A versatile tool for reciprocal space conversion of scattering data recorded with linear and area detectors. J. Appl. Crystallogr. 2013, 46, 1162–1170. [Google Scholar] [CrossRef]
- Rüter, T.; Hauf, S.; Kuster, M.; Strüder, L. Effects of Oblique Incidence in Pixel Detectors on Diffraction Experiments. In Proceedings of the 2017 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), Atlanta, GA, USA, 21–28 October 2017; pp. 1–3. [Google Scholar]
- Bracewell, R.N. Strip Integration in Radio Astronomy. Aust. J. Phys. 1956, 9, 198–217. [Google Scholar] [CrossRef]
- Bracewell, R.N. Numerical Transforms. Science 1990, 248, 697–704. [Google Scholar] [CrossRef]
- Unser, M.; Thevenaz, P.; Yaroslavsky, L. Convolution-based interpolation for fast, high-quality rotation of images. IEEE Trans. Image Process. 1995, 4, 1371–1381. [Google Scholar] [CrossRef]
- Larkin, K.G.; Oldfield, M.A.; Klemm, H. Fast Fourier method for the accurate rotation of sampled images. Opt. Commun. 1997, 139, 99–106. [Google Scholar] [CrossRef]
- Chen, B.; Kaufman, A. 3D volume rotation using shear transformations. Graph. Model. 2000, 62, 308–322. [Google Scholar] [CrossRef]
- Thévenaz, P.; Blu, T.; Unser, M. Interpolation revisited [medical images application]. IEEE Trans. Med. Imaging 2000, 19, 739–758. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maddali, S.; Allain, M.; Li, P.; Chamard, V.; Hruszkewycz, S.O. Detector Tilt Considerations in Bragg Coherent Diffraction Imaging: A Simulation Study. Crystals 2020, 10, 1150. https://doi.org/10.3390/cryst10121150
Maddali S, Allain M, Li P, Chamard V, Hruszkewycz SO. Detector Tilt Considerations in Bragg Coherent Diffraction Imaging: A Simulation Study. Crystals. 2020; 10(12):1150. https://doi.org/10.3390/cryst10121150
Chicago/Turabian StyleMaddali, Siddharth, Marc Allain, Peng Li, Virginie Chamard, and Stephan O. Hruszkewycz. 2020. "Detector Tilt Considerations in Bragg Coherent Diffraction Imaging: A Simulation Study" Crystals 10, no. 12: 1150. https://doi.org/10.3390/cryst10121150
APA StyleMaddali, S., Allain, M., Li, P., Chamard, V., & Hruszkewycz, S. O. (2020). Detector Tilt Considerations in Bragg Coherent Diffraction Imaging: A Simulation Study. Crystals, 10(12), 1150. https://doi.org/10.3390/cryst10121150






